
Deviations in Birth Rates with Respect to the Day of the Week and the
Month for a 100 Year Period Regarding Social and Medical Aspects in
Explaining Models
Fabian Schuster
1
, Thomas Ostermann
2
, Reinhard Schuster
3
and Timo Emcke
4
1
Faculty of Law, European University Viadrina Frankfurt (Oder), 15230 Frankfurt (Oder), Germany
2
Chair of Research Methodology and Statistics in Psychology, Witten/Herdecke University, 58313 Herdecke, Germany
3
Chair of Department of Health Economics, Epidemiology and Medical Informatics, Medical Advisory board of Statutory
Health Insurance in Northern Germany (MDK), 23554 L
¨
ubeck, Germany
4
Chair of Department of Prescription Analysis, Association of Statutory Health Insurance Physicians,
23795 Bad Segeberg, Germany
Keywords:
Sunday Births, Long Time Considerations, Social Aspects, Instable Problems, Shannon Entropy, Gini
Coeffient.
Abstract:
During the last hundred years the birth rates on Sundays changed dramatically with a neutral point around
1955. Modern birth regulation is considered as the main reason for that. Medical backgrounds for this situation
were discussed in the 1970s. Prior to that no analysis has relevant case numbers. The time from conception
to birth measured in days is divisable by 7. The time of conception is relevant in relation to social aspects.
Conception rates can be determined under the assumption that we can split up the population in a low and a
high risk share. This consideration principally leads to an instable problem on a discrete cyclic space. But
using some limiting considerations we get a numerically stable solution with feasible characteristics. For
observing long time changes we need a relevant smoothing operator. In numerical calculations we look for a
quadratic minimum solution or alternatively a linear program. For the discussion of inequality the concept of
Shannon entropy as well as and Lorenz curve and Gini coefficient are relevant.
1 INTRODUCTION
We will consider, how the birth rate per weekday
has changed in the last hundred years using data of
the statutory health and care insurances. Reduced
birthrates at weekends are usually discussed in the
context of elective interventions. Larger birth rates at
Sundays at the beginning of the 20th century should
be discussed in the social context. One has to take
into account that it is not possible to measure real
birth rates from 1900-1950 but only the component
related to insurance benefits decades later. Even sur-
vival rates may depend on weekday of birth. On the
other hand the benefits of health insurance may de-
pend on the underlying risk structure. Even the health
status (”medical age”) may also depend on the week-
day of birth.
Next we consider different daily birth rates and health
costs with respect to the month of birth during differ-
ent decades of the last century. Social and medical in-
Long time deviations of births on Tuesday, Wednesday and Sunday 1910-2005
-20,0%
-15,0%
-10,0%
-5,0%
0,0%
5,0%
10,0%
1910 1915 1920 1925 1930 1935 1940 1945 1950 1955 1960 1965 1970 1975 1980 1985 1990 1995 2000 2005
year
deviation
Tue
Wed
Sun
Figure 1: Long term development of birth rates on Tuesday,
Wednesday and Sunday 1910-2005.
fluences cause short and long term changes. In order
to avoid large variations we use a 5 year smoothing of
data. Interesting points are the day of birth and day
of fertilization 100-85 years ago with varying social
background. Large amounts of data are required to
determine significant statistical effects. For this time
Schuster F., Ostermann T., Schuster R. and Emcke T.
Deviations in Birth Rates with Respect to the Day of the Week and the Month for a 100 Year Period Regarding Social and Medical Aspects in Explaining Models.
DOI: 10.5220/0006114900410047
In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 41-47
ISBN: 978-989-758-213-4
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
41

period no register data are digitally available in the ex-
tend needed. One has to take into account the exten-
sive migration movements during the last 100 years.
A possible solution might be given by aggregated dig-
ital administrative data of health and care insurances.
But precise resolution (day) is rarely available after
aggregation has been done for other reasons. The
first discussion of the influence of the weekday of
birth on a large data base was given in (Macfarlane,
1978) and (Mathers, 1983) using birth data of the
seventies, our data focuses on some decades before.
Furthermore the number of births with respect to the
weekday differs much from the current pattern. Re-
lated backgrounds are discussed in the stated refer-
ences (cf.(Kibele et al., 2013), (Klein et al., 2001),
(Klein and Unger, 2002), (Lampert and Kroll, 2014),
(Ma et al., 2012), (Mackenbach, 2006), (Schnell and
Trappmann, 2006), (Schuster and Emcke, 2016), (Os-
termann and Schuster, 2015)).
2 MATERIAL AND METHODS
We use health and care insurance data from a German
federal state. With respect to sufficient statistical sig-
nificance in the care insurance field we can go as far
back as people born in 1905 by using data from 1998
till 2006, in the health insurance data from 2006 one
can track back until 1920. Although we only need
aggregated data, such data with a weekday resolution
are rarely available.
We use the script language perl in order to aggregate
data and for the association of day of the week and
date. If we refer to birth rates with respect to months
we have to take into account their different lengths.
Gender was only available for the care insurance data.
The detailed insurance can be identified by a 9-digit
identification code (IK-number). We used a reference
table containing the insurance type in order to get a
known social indication.
If we use drug data, there is information about addi-
tional private payment of patients. Patients with low
social status have an additional payment exemption.
There is also a mixed status in which patients get an
additional payment exemption after having payed a
certain amount themselves. We are interested in the
social circumstances during birth, but we measure the
social status many years later. A Markov model for
transition of states would be useful. But there is no
real information about transition rates. If we assume
that the states are stable, we underestimate social ef-
fects.
Another type of analysis could combine low and high
risk at birth with a survival in the following cate-
gories: first three days after birth and mothers with
an age under or over 50 years. A derived, more de-
tailed refinement could lead to mortality tables in de-
pendence of the day and month of birth. Due to the
low availability of historical information this remains
a modeling challenge.
The time from the last menstrual period (LMP) to
childbirth is usually taken as 40 weeks or 280 days.
Pregnancy from conception to childbirth is 38 weeks
or 266 days long. But there are no large scale mea-
surements for mean values and standard deviations
and in particular about deviations from normal dis-
tribution. We can divide the population into two sub-
sets with respect to high and low pregnancy risk: X =
X
1
+X
2
as random variables. Let s(X) be the standard
deviation of X. We use s(X
1
) < s(X
2
). It is known
from literature that we have 9 < s(X) < 13. We use
s(X
1
) = 1,2, 3. X
1
leads to increasing peaks, X
2
gives
a nearly uniform variation to all days. If fertilization
data would be given, the distribution of the random
variable length of pregnancy would be a smoothing
parameter on cyclic space (with discretization to days
of week). But if we have given the birth data and
want to derive the weekday distribution of the fertil-
ization we get an inversion operator which tends to be
instable. Constraints lead to numerical stabilization.
We start with a quadratic-deviations model. Let f(i)
be the observed deviation from 1/7 for likelihood of
birth at day i (i = 0, 1,...,6) and w(i) the fertilization
deviation pattern at day i (i = 0, 1,..., 6). Than d
s
( j)
shall be the translation of j days by normal distribu-
tion with standard deviation s using integer intervals.
We look for the quadratic minimum:
6
∑
i=0
f (i) −
30
∑
j=−30
d(i − j)w( j)
!
2
−→ Min!
with the constraints −1 < −a < w(i) < b < 1. Prac-
tically we use a = b = 1/(7 ∗ 5) in order to limit the
deviation for each day with respect to the mean of the
week to 20 %. Alternatively we could use linear pro-
gramming:
f (i) −
30
∑
j=−30
d(i − j)w( j)
< s,s −→ Min!
For calculations we use Microsoft Excel and Mathe-
matica from Wolfram Research.
In order consider the different deviations during the
considered time period we use the concept of Shan-
non entropie
∑
6
i=0
− p
i
ln(p
i
) for the birth rates p
i
at day i. The same considerations we can adopt to
months instead of the weekdays. Alternative mea-
sures of the inequality are given by the Lorenz Curve
and the related Gini coefficient. In order to quan-
HEALTHINF 2017 - 10th International Conference on Health Informatics
42

tify the deviation from the equal distribution we de-
fine x
i
= p
i
− 1/7 and from
∑
6
i=0
p
i
= 1 it follows
∑
6
i=0
x
i
= 0. The function (1/7 + x)ln(1/7 + x) has
the Taylor series: −ln(7)/7 + x(1 − ln(7)) + 7x
2
/2 −
49x
3
/6 + O(x
4
) . As result we get a constant if we
sum up the index i from 0 to 6 (with respect to the
weekdays, with respect to the months we have to sum
up from 0 to 11). Therefore the entropy reflects a
quadratic (non-linear) property with respect to the p
i
.
The Gini coefficient is in contrast to that linear in the
p
i
with weighting coefficients depending of the order
up to a constant
∑
6
i=0
(1 − p)p
i
with monotonically
increasing p
i
. First we consider an empiric connec-
tion between Shannon entropy and Gini coefficient
looking at 5 year periods. Second we compare the
Taylor series to the quadratic term of the function
(1/7 + x) ln(1/7 + x):
- 0.06 - 0.04 - 0.02 0.02 0.04 0.06
- 0.002
- 0.001
0.001
0.002
0.003
0.004
Figure 2: Difference of term in the Shannon sum and its
quadratic Taylor series representation.
3 RESULTS
If we use data of the care insurance from 1998-2006,
we can consider deviations of the birth rates back to
1905 in Figure 3.
On Saturdays and Sundays we have increased birth
rates, lower ones on Tuesdays and Wednesdays. The
Deviations in the weekday of birth (care insurace)
-6,0%
-4,0%
-2,0%
0,0%
2,0%
4,0%
6,0%
Monday Tuesday Wednesday Thursday Friday Saturday Sunday
J 1905-1909
J 1910-1914
J 1915-1919
J 1920-1924
J 1925-1929
Figure 3: Deviations of birth rates in dependence of the
weekday (care insurance data).
other weekdays are somewhere between with instabil-
ities with respect to time periods. One has to take into
consideration that only about 20% of the people ever
get benefits of care insurance. In contrast to this the
great majority of older people gets at least one drug
each year. If we use drug prescription data of 2006
we get the distribution of birth rates in Figure 4. There
Deviations in the weekday of birth (weighted)
-6,0%
-4,0%
-2,0%
0,0%
2,0%
4,0%
6,0%
Monday Tuesday Wednesday Thursday Friday Saturday Sunday
J 1905-1909
J 1910-1914
J 1915-1919
J 1920-1924
J 1925-1929
Figure 4: Deviations of birth rates in dependence of the
weekday (health insurance data).
are only small differences if we use drug prescription
data of 2007 or 2008. At Saturdays the birth rates are
less increased compared to care insurance, the rates
at Sundays are even larger. The reduced birth rates
on Tuesdays and Wednesdays correspond with the re-
sults from the care insurance analysis.
If we compare the drug costs of the patients born
between 1920 and 1924 with those born between
1925 and 1929 we find an average annual increase
of 1.51%. For such considerations it is important to
use an age group with monotonously increasing drug
costs. Having regard to that we create subgroups with
respect to the weekday of birth, cf. Figure 5.
drug cost deviations in 2006
n=144.533 patients
-2,5%
-2,0%
-1,5%
-1,0%
-0,5%
0,0%
0,5%
1,0%
1,5%
2,0%
2,5%
Mon Tue Wed Thu Fri Sat Sun
day of week
dev.
dev. 1920-24
dev. 1925-29
Figure 5: Drug costs in dependence of the weekday of birth
for age groups born 1920-24 and 1925-29.
The weekdays with increased and reduced costs do
not match those of increased and reduced birth rates.
The 1.51% increased drug costs of patients born on
Saturdays can be interpreted as having a one year
higher biological age than calendar age. On the
other hand the people born on Thursdays are one year
Deviations in Birth Rates with Respect to the Day of the Week and the Month for a 100 Year Period Regarding Social and Medical Aspects
in Explaining Models
43

younger biologically.
Using the data of care insurance, we find a relevant
gender dependent difference in the birth rates on Sun-
days, cf. Figure 6.
Deviation of birth rates on Sundays in dependence of gender
-6%
-4%
-2%
0%
2%
4%
6%
8%
10%
1900 1905 1910 1915 1920 1925 1930 1935 1940 1945 1950
w
m
Figure 6: Deviations of the birth rates on Sundays with re-
spect to gender.
Next we consider subgroups with respect to the social
status. We use additional payment as a proxy.
Deviation of the birth rates from social status 1920-24
-10%
-8%
-6%
-4%
-2%
0%
2%
4%
6%
8%
Mon Tue Wed Thu Fri Sat Sun
day of week
deviation
no copaiment
copaiment
mixed
Figure 7: Birth rates in dependence of the social status and
the weekday of birth for the period 1920-24.
The group of patients of births for the 1925-29 period
and a socially week status show a lower increase in
rates on Sundays and higher reduction on Tuesdays,
cf. Figure 7 . In the next five year period the situation
is quite different, cf. Figure 8.
Deviation of the birth rates from social status 1920-24
-6%
-4%
-2%
0%
2%
4%
6%
8%
10%
Mon Tue Wed Thu Fri Sat Sun
no copaiment
copaiment
mixed
Figure 8: Birth rates in dependence of the social status and
the weekday of birth for the period 1925-29.
Social week patients show an even higher increase in
birth rates on Sundays but no significant differences
in reduced birth rates on Tuesdays. We can compare
the rate changes on Thursdays and Sundays directly,
cf. Figure 9 and 9.
Deviation of the birth rates from social status
-10,0%
-9,0%
-8,0%
-7,0%
-6,0%
-5,0%
-4,0%
-3,0%
-2,0%
-1,0%
0,0%
no copaiment copaiment mixed
category
deviation
J 1920-24
J 1925-29
Figure 9: Birth rates on Tuesdays in dependence of the so-
cial status in 1920-24 vs. 1925-29.
Deviation of the birth rates from social status
0%
1%
2%
3%
4%
5%
6%
7%
8%
9%
10%
no copaiment copaiment mixed
category
deviation
J 1920-24
J 1925-29
Figure 10: Birth rates on Sundays in dependence of the so-
cial status in 1920-24 vs. 1925-29.
Additionally we can use social information using the
type of insurance, cf. Figure 11.
Deviations for birth rates on Sundays in dependence of socials status due to insurance type
-2%
-1%
0%
1%
2%
3%
4%
5%
6%
7%
8%
1900 1905 1910 1915 1920 1925 1930 1935 1940 1945 1950
year
deviation
social week
none week
Figure 11: Birth rates on Sundays in dependence of the so-
cial status using health insurance type.
We will consider the low risk population and cal-
culate the different fertility rates by the considered
quadratic-deviations model with standard deviations
1, 2 and 3 and a limitation of the rate deviations by
20%, cf. Figure 12.
HEALTHINF 2017 - 10th International Conference on Health Informatics
44

Deviations in the day of the week
-25%
-20%
-15%
-10%
-5%
0%
5%
10%
15%
20%
25%
Sun Mon Tue Wed Thu Fry Sat
weekday
deviation
ori
v 1
v 2
v 3
Figure 12: Calculated deviation of the fertility rates with
standard deviations 1, 2 and 3.
We see that in general the effects at Saturday and
Sundays are increased, the effects at Tuesdays and
Wednesdays are reduced. We have used the 20%
value in order to limit instabilities. If we would use
values from 10% to 25%, we would get the same re-
sult for the distribution to the weekdays. Unfortu-
nately we get no further information about a true limit
value.
Shannon entropy and Gini coefficients have the same
behavior with respect to local maxima and minima.
Additionally we can use social information using the
type of insurance, cf. Figure 13.
Entropy with respect to the day of birth (x 1000)
0
5
10
15
20
25
1905 1910 1915 1920 1925 1930 1935 1940 1945 1950 1955 1960 1965 1970 1975 1980 1985 1990 1995 2000 2005
Figure 13: Shannon entropy with respect to the weekdays
of birth in dependence of 5 year periods.
Gini coefficient (x 1000)
0%
2%
4%
6%
8%
10%
12%
14%
16%
18%
20%
1905 1910 1915 1920 1925 1930 1935 1940 1945 1950 1955 1960 1965 1970 1975 1980 1985 1990 1995 2000 2005
Figure 14: Gini coefficient with respect to the weekdays of
birth in dependence of 5 year periods.
Both results show the global minimum for the year
1955. We remember that this year separates the age
of increased and that of reduced Sunday birth rates.
There is a different resolution between the entropy
and the Gini result. The Shannon entropy result uses a
nonlinear effect but does not order the used rates, the
Gini result is linear but uses ordered rates. Thereby it
is interesting that both results coincide so much.
Till now we have considered the weekday period. It
is also interesting to consider months.
-25%
-20%
-15%
-10%
-5%
0%
5%
10%
15%
20%
1905
1910
1915
1920
1925
1930
1935
1940
1945
1950
1955
1960
1965
1970
1975
1980
1985
1990
1995
2000
2005
deviation
5-year period
birth rates in dependence of the quater of birth
quater 1
quater 2
quater 3
quater 4
Figure 15: Birth rates in dependence of the quarter of birth.
In 1920-1980 for the first six months there are in-
creased birth rates. Reduced birth dates we have since
1920. Before 1920 the situation is quite different. The
mean costs in dependence of the month of birth are
quite heterogeneous with respect to different histori-
cal periods, cf. Figure 16.
cost deviations in dependence of the birth months
-2,0%
-1,5%
-1,0%
-0,5%
0,0%
0,5%
1,0%
1,5%
2,0%
Jan Feb Mar Apr May June July Aug Sept Oct Nov Dec
1910-1930
1935-1980
1910-1980
1960-1980
Figure 16: Deviations in drug costs in dependence of the
month of birth during different historical periods.
If we consider the period from 1920 till 1980, we have
increased costs during the first half of the year and re-
duced costs during the second half of the year. One
explanation could be, that the month of birth has dif-
ferent influences due to the historical period of birth.
On the other hand the effect can depend on the age
of the persons. We compare the mean effect for birth
rates and drug costs from 1920 till 1980 with respect
to the quarters of the year, we see that generally in-
creased birth rates and health status measured by drug
costs behave reverse, cf. Figure 17.
Deviations in Birth Rates with Respect to the Day of the Week and the Month for a 100 Year Period Regarding Social and Medical Aspects
in Explaining Models
45
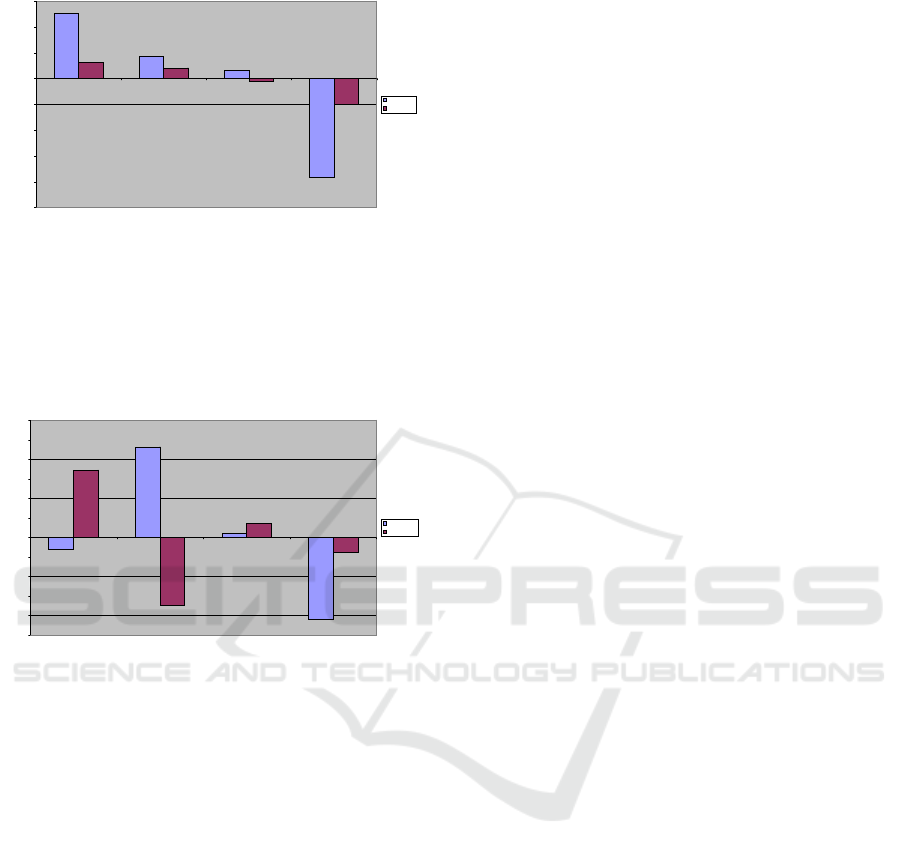
birth rates and cost deviations
-5,0%
-4,0%
-3,0%
-2,0%
-1,0%
0,0%
1,0%
2,0%
3,0%
Q1 Q2 Q3 Q4
quater
deviation
birth rates
cost dev.
Figure 17: Deviations in birth rates and drug costs with in
dependence of the quarters of the year.
Last we compare drug costs in dependence of the
quarter of the year for the two groups born from 1910
till 1930 versus the group born between 1960 an 1980,
cf. Figure 18.
deviations in drug costs 1910-1930 vs. 1960-1980
-1,0%
-0,8%
-0,6%
-0,4%
-0,2%
0,0%
0,2%
0,4%
0,6%
0,8%
1,0%
1,2%
Q 1 Q 2 Q 3 Q4
1910-1930
1960-1980
Figure 18: Deviations in drug costs in dependence of the
month of birth during different historical periods.
The highest difference we have at quarter two. It can
be a consequence of different historical health condi-
tions near to birth. An other explanation would be an
age dependent effect.
4 CONCLUSIONS
In order to consider the time between birth and mea-
surements using data of health and care insurance the
following statements and guesses can be made regard-
ing the results.
In scenario 1 more births measured in insurance data
can be caused by more real births in the considered
time 1915-1930. That can be due to different concep-
tion and/or fertilization possibilities depending on the
day of the week. A bias may be caused by migration.
In scenario 2 the day of birth may causes different sur-
vival expectancies in the critical first three days after
birth and the related health conditions during these
days. That is why we analyze drug costs in depen-
dence of the day of birth. As we already stated, drug
costs increase in the mean by 1.5 % per year between
the considered two age groups. As a modeling con-
sideration one can use drug costs as a proxy for bio-
logical age, comparing it with calendar age. Due to
the considered age dependent drug cost increase we
can suspect a strong connection to the residual life ex-
pectancy. Thursday births around 90 years ago have
a one year higher residual life expectancy. Saturday
births have a one year lower residual life expectancy,
Sunday births have 4 months higher residual life ex-
pectancy. In contrast to the situation stated in Macfar-
lane (1978) lower perinatal mortality rates at week-
ends can be caused by the fact that quality of care was
higher due to family background. In those times spe-
cialist obstetric services have been less common com-
pared to later decades. It is quite important, that the
psycho-social near birth circumstances 90 years ago
may induce significant differences today.
REFERENCES
Kibele, E. U., Jasilionis, D., and Shkolnikov, V. M.
(2013). Widening socioeconomic differences in mor-
tality among men aged 65 years and older in Germany.
J Epidemiol Community Health, 67(1):453–457.
Klein, T., Schneider, S., and L
¨
owel, H. (2001). Bildung
und Mortalit
¨
at. die Bedeutung gesundheitsrelevanter
Aspekte des Lebensstils. Zeitschrift f
¨
ur Soziologie,
30(5):384–400.
Klein, T. and Unger, R. (2002). Aktive Lebenserwartung in
Deutschland und in den USA. Zeitschrift f
¨
ur Geron-
tologie und Geriatrie, 35:528–539.
Lampert, T. and Kroll, L. (2014). Soziale Unterschiede
in der Mortalitt und Lebenserwartung. Hrsg. Robert
Koch-Institut, Berlin, 5(2).
Ma, J., Xu, J., Anderson, R., and Jemal, A. (2012). Widen-
ing educational disparities in premature death rates
in twenty six states in the United States, 1993-2007.
PloS one, 7(7).
Macfarlane, A. (1978). Variations in number of births and
perinatal mortality by day of week in England and
Wales. British Medical Journal, 2:1670–1673.
Mackenbach, J. (2006). Health inequalities: Europe in pro-
file. An independent expert report commissioned by
the UK Presidency of the EU. Department of Health,
London.
Mathers, C. (1983). Births and perinatal deaths in Australia:
variations by day of week. Journal of Epidemiology
and Community Health, 37:57–62.
Ostermann, T. and Schuster, R. (2015). An Information-
theoretical Approach to Classify Hospitals with Re-
spect to Their Diagnostic Diversity using Shannon’s
Entropy. HEALTHINF.
Schnell, R. and Trappmann, M. (2006). Konsequen-
zen der Panelmortalitt im SOEP fr Sch
¨
atzungen der
HEALTHINF 2017 - 10th International Conference on Health Informatics
46

Lebenserwartung. Arbeitspapier. Zentrum f
¨
ur Quan-
titative Methoden und Surveyforschung, Mannheim,
Konstanz., 2.
Schuster, R. and Emcke, T. (2016). Unterj
¨
ahrige
Schwankungen bei den Arzneimittelverschreibungen
und bei der Anzahl der Patienten pro Arzt: eine Base-
line f
¨
ur den vertrags
¨
arztlichen Bereich. HEC 2016.
M
¨
unchen.
Deviations in Birth Rates with Respect to the Day of the Week and the Month for a 100 Year Period Regarding Social and Medical Aspects
in Explaining Models
47
