
A Simplified Low Rank and Sparse Model for Visual Tracking
Mi Wang, Huaxin Xiao, Yu Liu, Wei Xu and Maojun Zhang
Institute of Information Systems and Management, National University of Defense,
No. 109 Deya Road Kaifu District Changsha City Hunan Prov., 410073, Changsha, China
{coolsa007, huaxin_xiao}@163.com, jasonyuliu@nudt.edu.cn, {545406612, 1023133126}@qq.com
Keywords: Visual Tracking, Sparse and Low-Rank Representation.
Abstract: Object tracking is the process of determining the states of a target in consecutive video frames based on
properties of motion and appearance consistency. Numerous tracking methods using low-rank and sparse
constraints perform well in visual tracking. However, these methods cannot reasonably balance the two
characteristics. Sparsity always pursues a sparse enough solution that ignores the low-rank structure and vice
versa. Therefore, this paper replaces the low-rank and sparse constraints with
2,1
l
norm. A simplified low-
rank and sparse model for visual tracking (LRSVT), which is built upon the particle filter framework, is
proposed in this paper. The proposed method first prunes particles which are different with the object and
selects candidate particles for efficiency. A dictionary is then constructed to represent the candidate particles.
The proposed LRSVT algorithm is evaluated against three related tracking methods on a set of seven
challenging image sequences. Experimental results show that the LRSVT algorithm favorably performs
against state-of-the-art tracking methods with regard to accuracy and execution time.
1 INTRODUCTION
Visual tracking finds a region in the current image
that matches the given object. It is a well-known
problem in computer vision with numerous
applications including surveillance, driver assistance,
robotics, human-computer interaction, and motion
analysis (Zhang T et al. 2014). Despite demonstrated
success, it remains challenging to design a robust
visual tracking algorithm due to factors such as
occlusion, background clutter, varying viewpoints,
and illumination and scale changes (Wang L et al.
2015).
Recently, sparse and low-rank representation has
cause for concern in many aspects (R. Xia et al. 2014,
Zhang C et al. 2015). These tracking methods express
a target by a sparse linear combination of the
templates in a dictionary (Zhang T et al. 2014). These
algorithms based on
1
l
minimization have been
demonstrated time-consuming. Then they set up low-
rank representation and sparse representation to solve
the problem. However, they can not balance the two
characteristics in good reason. Sparse always pursue
a sparse enough solution, which ignoring the low-
rank structure. At the same time,
2,1
l
norm has been
proved effective at represent both low-rank and
sparse in some paper (Zhao M et al. 2014). Besides,
the
2,1
l
norm avoid the time-consuming process of
nuclear norm.
This paper, we use norm which can combine the low-
rank and sparse characteristic to learn robust linear
representations for efficient and effective object
tracking. The proposed visual tracking algorithm is
developed based on the particle filter. We can see the
process in Fig. 1.
Fig. 1 shows the flowchart of the enforcement of the
proposed algorithm by pruning particles. First, the
target is selected from the first frame. Second, all
particles are sampled based on the previous object.
Third, the particles are pruned using the
reconstruction error to prune particles. Finally, the
object is selected using our LRSVT algorithm in the
next frame, which enforces sparsely low-rank
properties.
Wang, M., Xiao, H., Liu, Y., Xu, W. and Zhang, M.
A Simplified Low Rank and Sparse Model for Visual Tracking.
DOI: 10.5220/0006117003010308
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 301-308
ISBN: 978-989-758-222-6
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
301

Figure 1: Enforcing the sparsity, low-rank properties in the proposed LRSVT algorithm. (1) The frame at time t(t=1). (2) All
particles sampled based on previous object. Here the number of particle is = 400. (3) Particles are pruned using the
reconstruction error
0
e
. 25 candidate particles are obtained after pruning. (4) The frame at time t(t=2), object is selected
using our LRSVT algorithm in the next frame.
Object tracking is formulated as a sparse and low-
rank representation problem from a new perspective,
which is carried out by exploiting the relationship
between the observations of the particle samples and
jointly representing them using a dictionary of
templates with an online update. The resulting
sparsely low-rank representation of candidate
particles facilitates robust performance for visual
tracking. The relationship of these algorithms and the
importance of each property for visual tracking are
shown.
2 RELATED WORKS
The recent years have witnessed significant progress
in tracking with sparse and low-rank representation.
Most recently, an algorithm that jointly learns the
sparse and low-rank representations of all particles
(Zhang, K. et al. 2012; Zhang, T. et al. 2012–2014) is
proposed for object tracking. Solutions to low-rank
matrix minimization and completion problems have
also achieved considerable progress. Zhou X et al
(Zhou X et al. 2012) demonstrated that the image
sequence of a cardiac cycle can be well approximated
with a low-rank matrix. Zhang C (Zhang C et al.
2014) learned the observation model by extracting
low-rank features. Yehui Yang et al (W Hu et al.
2016) developed a comprehensive study of the
2,1
l
norm to tolerate the sudden changes between two
adjacent frames that exploits the low-rank structure
among consecutive target observations.
3 LOW RANK SPARSE VISUAL
TRACKING
In this section, we present the proposed tracking
algorithm based on low-rank sparse representations
of particle samples.
3.1 Consistent Low-rank Sparse
Representation
In this work, particles are sampled from previous
object locations to predict the state
t
s
of the target at
time t, from which the region of interest
t
y
is
cropped in the current image and normalized to the
template size. The state transition function
1
(| )
tt
ps s
is modeled by an affine motion model
with a diagonal Gaussian distribution. The
observation model
(|)
tt
py s
reflects a similarity
between an observed image region
t
y
corresponding
to a particle
t
s
and the templates of the current
dictionary. In this paper,
(|)
tt
py s
is computed as a
function of the difference between the consistent low-
rank sparse representation of the target based on
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
302

object templates and its representation based on
background templates. The particle that maximizes
this function is selected as the tracked target at each
time instance. At time t,
0
n
sampled particles and
corresponding vectorized gray-scale image
observations form a matrix
0
012
[ , ,..., ]
n
X
xx x
,
wherein the observation with regard to the i-th
particle is denoted as
d
i
x
R
. Each observation is
represented as a linear combination of templates from
a dictionary
12
, ,...,
tm
D
dd d
, such that
0 tt
XDZ
. The columns of
0
12
[ , ,..., ]
tn
Z
zz z
denote the
representations of particle observations with regard to
t
D
. The dictionary columns contain templates used
to represent each particle, including image
observations of the tracked object and the
background. Misalignment between dictionary
templates and particle observations may lead to
tracking drifts because representation is constructed
on the pixel level. The dictionary
t
D
can be
constructed from an over-complete set using
transformed templates of the target and background
classes to alleviate this problem. This dictionary is
also updated progressively. Temporal consistency is
exploited to prune particles for efficient and effective
tracking. A particle is considered temporally
inconsistent if its observation is not linearly well
represented by the dictionary
t
D
and the
representation of the tracked target in the previous
frame, which is denoted as
0
z . More specifically, the
particle is pruned in the current frame if the
2
l
reconstruction error
0
2
it
x
Dz
is sufficiently
large, thereby leaving a number of
i
x
; therefore, the
number is set as n. In this work, temporal consistency
is exploited as the appearances of the tracked
object.Consequently, this process effectively reduces
the number of particles to be represented from
0
n
to
n
, where
0
nn
in most cases. Next, the ones left
after pruning are denoted as candidate particles, in
which their corresponding observations are
dn
X
R
and their representations are
mn
Z
R
.
The representation of each candidate particle is
based on the following observations. (1) After
pruning, the candidate particle observations can be
modeled by a low-rank subspace (i.e., X is low-rank);
therefore, Z (i.e., their representations with regard to
t
D
) is expected to be low-ranked. (2) The
observation
i
x
of a good candidate particle can be
modeled by a small number of nonzero coefficients in
its corresponding representation
i
z . (3) The aim of
object tracking is to search for patches (with regard to
particles) that have a representation similar to
previous tracking results. Therefore, a “good”
representation should be consistent over time. In the
work of CLRST [4], the tracking problem is
formulated by min Z, E
12 304
* 1,1 2,1 1,1
,
min
..
ZE
Z
ZZZ E
sj X DZ E
(1)
where
1
,
q
p
q
p
ij
pq
ji
ZZ
(2)
12
*1,1
Z
Z
as
1
2,1
Z
is replaced in this
paper.
The
2,1
l
norm encourages the columns of Z to be
zero, which assumes that the corruptions are “sample-
specific” (i.e., several data vectors are corrupted and
the others are clean) (Zhang X et al. 2012) to ensure
that Z has a low-rank and sparse property.
1304
2,1 2,1 1,1
,
min
..
ZE
Z
ZZ E
sj X DZ E
(3)
E is the error which is attributed to noise as well
as occlusion.
We then lead in two equality constraints, and the
equation and constraint becomes
11 3 2 4
2,1 2,1 1,1
,
3
31
320
min
..
ZE
Z
ZE
XDZ E
sj Z Z
ZZZ
(4)
In this formulation,
i
, i = 1, 3, 4 are weights that
quantify the trade-off between the different terms
discussed below. In addition,
ij
Z
denotes the entry
at the i-th row and j-th column of Z. The
representation of the previous tracking result is
denoted with regard to
t
D
as
0
z . The matrix
00
1
Z
z
is a rank one matrix, where each column is
0
z
.
3.1.1 Low-Rank and Sparse:
2,1
Z
In CLRST formulation,
*
Z
is used to minimize the
matrix rank of representations of all candidate
particles together. Their sparse representation scheme
A Simplified Low Rank and Sparse Model for Visual Tracking
303

is
1,1
Z
, which has been shown to be robust to
occlusion or noise in visual tracking.
2,1
Z
is
considered to replace
12
*1,1
Z
Z
which is the
sparse congruency constraint on matrix Z. This
constraint only allows a few rows of Z to become
nonzero, thereby deleting the ambiguous bases and
maintaining principal bases. Therefore, the samples
belonging to the same class are more likely to choose
the same atom in their representation and share the
same sparse pattern in their SR coefficient vectors.
Thus, Z is sparse and low-rank. By contrast, the
sparse congruency constraint considers the global
structure of Z and eliminates rows of elements that
have a slight contribution to the representation of the
dataset and do not affect the low-rank structure of Z.
Thus, the contribution time is greatly reduced (Zhao
M et al. 2014).
3.1.2 Temporal
0
2,1
ZZ
and Reconstruction
Error
1,1
E
Temporal representation allows only a small number
of particles to have representations different from the
previous tracking results. The values and support of
the columns in E are informative because these values
indicate the presence of occlusion (substantial values
but sparse support) and determines whether a
candidate particle is sampled from the background
(substantial values with non-sparse support) (Zhao M
et al. 2014).
3.2 Solving
3.2.1 Solving Equation
1,2,3 1,2,3 1,2,3
11 3 2 4
1,2 2,1 1,1
2
1
13 3
2
2
231 31
2
3
33 2 0 3 2 0
,, ,
2
2
2
T
F
T
F
T
F
LZ EY u
ZZ E
u
tr Y X DZ E X DZ E
u
tr Y Z Z Z Z
u
tr Y Z Z Z Z Z Z
(5)
3.2.2 Solving
12 3
,,,
Z
ZEZ in Turn
1
2
2
*
1
11132
1,2
22
32
2
11
arg min
2
1
= +
F
u
Z
ZZZY
uu
ZY
u
L
(6)
3
3
2
*
3
222303
2,1
33
30 3
3
11
arg min +
2
1
= +
F
u
Z
ZZZZY
uu
ZZ Y
u
L
(7)
1,
4
1
2
*
4
31
1
11
31
1
11
arg min
2
1
=
F
u
EEEXDZY
uu
XDZ Y
u
S
(8)
And
*
313
2
1
3
2
2
231 31
2
3
33 2 0 3 2 0
123
arg min
2
2
2
T
F
T
F
T
F
T
ZtrYXDZE
u
XDZ E
u
tr Y Z Z Z Z
u
tr Y Z Z Z Z Z Z
GD X E G G
(9)
Where
1
23
1
11
T
uu
GDD I I
uu
(10)
23
21 20
11
uu
GZ ZZ
uu
(11)
and
3123
1
1
T
GDYYY
u
(12)
3.2.3 Update
1,2,3 1,2,3
,Yu
111 3
22231
3333 2 0
112 23 3
;;;
YYuXDZ E
YYuZZ
YYuZZZ
uuu uuu
(13)
3.3 Adaptive Dictionary
The dictionary
t
D is initialized by sampling image
patches around the initial target position. The
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
304

dictionary is updated in successive frames to model
the change in appearance of the target object and to
ensure accuracy in the tracking.
t
D
is augmented
with representative templates of the background to
alleviate the problem of tracking drift, such that
[]
tOB
D
DD
, where
O
D
and
B
D represent the
target object and background templates, respectively.
Thus, the representation
k
z
of a particle comprised
an object representation
O
k
z
and a background
representation
B
k
z
. The tracking result
t
y
at instance
t is the particle
i
x
, such that
kk
11
k=1,...,
i=arg max z - z
OB
n
(14)
which encourages good modeling of the tracking
result using object templates and not using
background templates. Discriminative information
was also employed to design a systematic procedure
for updating
t
D
.
4 EXPERIMENT
In this section, the experimental results on the
evaluation of the proposed tracking algorithm against
several state-of-the-art methods were evaluated.
4.1 Datasets
Twenty-five challenging videos with ground truth
object locations, including basketball, football,
singer1, singer2, singer1(low frame rate), skating1,
and skating2 were used for analysis. These videos
contain complex scenes with challenging factors
(e.g., cluttered background, moving camera, fast
movement, large variation in pose and scale,
occlusion, shape deformation, and distortion).
4.2 Evaluated Algorithms
The proposed tracking methods (SLRVT) are
compared with three state-of-the-art visual trackers,
including FCT (Zhang K et al. 2014),
1
l (Zhao M et
al. 2014), and CLRST (Mei X et al. 2011). Publicly
available sources or binary codes provided by the
authors are used for fair comparisons. The same
initialization and parameter settings in all
experiments are also used.
4.3 Evaluation Criteria
Two metrics are used to evaluate tracking
performance. The first metric is the center location
error, which is the Euclidean distance between the
central location of a tracked target and the manually
labeled ground truth. The second metric is an overlap
ratio based on the PASCAL challenge object
detection score (Everingham B M. et al. 2010). Given
tracked bounding box
T
R
OI
and the ground truth
bounding box
GT
R
OI
, the overlap score can be
computed as
()
()
TGT
TGT
area ROI ROI
score
area ROI ROI
(15)
The average overlap score across all frames of each
image sequence is computed to rank the tracking
performance.
4.4 Implementation Details
All experiments are carried out in MATLAB on a 3.2
GHz Intel Corei5–4460 Duo machine with 4 GB
RAM. Template size d, which is manually initialized
in the first frame, is set to half the size of the target
object. The affine transformation, where the state
transitional probability
-1
(| )
tt
p
ys is modeled by a
zero-mean Gaussian distribution and a diagonal
covariance matrix
0
with values (0.03, 0.0005,
0.0005,0.03, 1, 1):
-1 0
(| )~(0,)
tt
py s N
, is used.
The definition of
(|)
tt
p
ys is
i
(|) z( 1,2,...,)
tt
p
ys i n
. The representation
threshold is set to 0.5. Parameter
is set to 1.0 in
the CLRST method to prune particles. The number of
particles
0
n is set to 400 and total number of
templates m is set to 25.
5 TEST RESULTS
5.1 Parameter Analysis
Several parameters play important roles in the
proposed tracking algorithm. In this section,
determining the values and effects of these
parameters on tracking performance is shown.
Effect of
:
The objective function has three parameters, namely,
A Simplified Low Rank and Sparse Model for Visual Tracking
305

Table 1: a. The distance value with the change of
1
. b. The distance value with the change of
3
.
a. The distance on the value of
1
1
:
0.0001 0.5 0.9 1 1.1 2 5 10
Distance 50.1 54 50.6 33.7 54.3 53.2 55.8 58.4
b. The distance on the value of
3
3
: 0.0001 0.5 0.9 1 1.1 2 5 10
Distance 55.5 54 51.5 41.7 54.6 44.8 52 51.1
Figure 2: Tracking result on 7 image sequences. LRSVT、FCT (Zhang K et al. 2014)、CLRST (Zhao M et al. 2014)、
1
l
(Mei X et al. 2011)are respectively displayed in red
、
green
、
blue and yellow.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
306
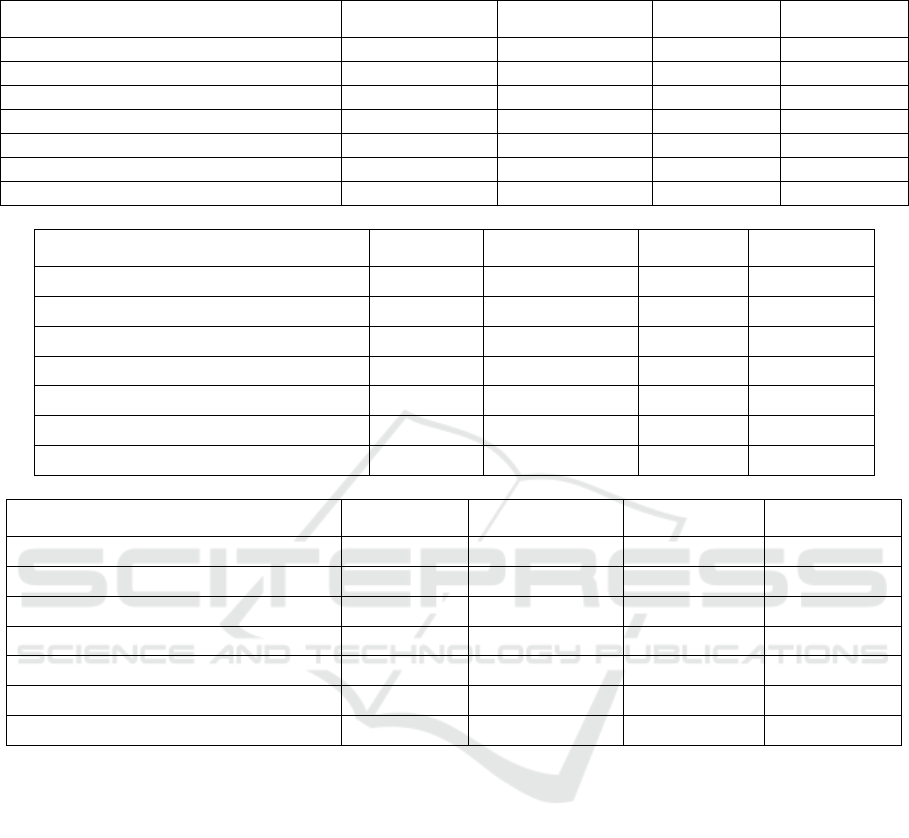
Table 2: Overlap、distance and time result on 7 image sequences with LRSVT、CLRST、FCT and
1
l methods.
a. Overlap
LRSVT CLRST
FCT
football(280fps) 0.262 0.312 0.582 0.283
basketball(141fps) 0.381 0.506 0.661 0.501
singer2(366fps) 0.436 0.588 0.408 0.328
singer1(351fps) 0.436 0.588 0.818 0.047
skating2(707fps) 0.284 0.17 0.101 0.255
singer1(low frame rate) (181fps) 0.592 0.095 0.344 0.255
skating1(285fps) 0.511 0.642 0.411 0.669
b. Distance
LRSVT CLRST FCT
football(280fps) 5.2 4.2 11.4 6
basketball(141fps) 9 23.3 23 16.5
singer2(366fps) 130 133.7 35.1 49.7
singer1(351fps) 130 133.7 3.5 22.4
skating2(707fps) 98.4 64.2 184.8 127.6
singer1(low frame rate)(181fps) 4.7 162.7 37 127.6
skating1(285fps) 24.4 8.3 35.9 18.3
c. Time
LRSVT CLRST FCT
football(280fps) 0.431 1.597 0.00027 0.0178
basketball(141fps) 0.563 2.354 0.000269 0.0195
singer2(366fps) 0.59 2.555 0.000089 0.0174
singer1(351fps) 0.59 2.555 0.000136 0.0186
skating2(707fps) 0.821 1.608 0.000085 0.019
singer1(low frame rate) (181fps) 0.581 2.65 0.000194 0.019
skating1(285fps) 0.586 2.674 0.000216 0.018
1
,
3
, and
4
(1). Because
1
and
3
are related to
the coefficients Z and
4
is related to E,
4
= 1 was
fixed and other parameter values were changed. All
1,3
i
i=
are parameterized by a discrete set Λ for
sensitivity analysis, in which Λ = {0.0001, 0.5, 0.9,1,
1.1, 2, 5, 10.0}. The different combinations of these
values were analyzed on video with 100 frames. The
average distance score from all frames was computed
for each combination. The corresponding results were
obtained for different
1
, as shown in Table 1.a.
Table 1 shows the sensitivity analysis of
=1,3i
i
.
From on these results, we can set
1
= 1,
3
= 1, and
4
= 1 for the objective function (1).
5.2 Qualitative Comparison
Fig. 2 and Table 2 show the tracking results of four
trackers on seven sequences. Three norms are
included: overlap, distance, and time.
Singer1(low frame rate) has better tracking
performance based on the visual effect of the views
of football, basketball, and singer1. The proposed
method performed well in terms of position and size
of the target. The singer2 sequence contains
significant illumination, scale, and viewpoint
changes. skating2 contains Abrupt Motion,
Illumination Change, and Occlusion. Therefore, most
trackers drift away from the target object in these two
sequences. In the Singer2 sequence, only the result of
the LRSVT method falls on the screen. In Skating1
sequence, length and width did not fully track the
target in terms of the basic location of the tracking
target.
1
l
1
l
1
l
A Simplified Low Rank and Sparse Model for Visual Tracking
307

LRSVT performed well at overlap in singer1(low
frame rate) and at the distance in basketball than any
of the other methods. Among all sequences, the time
consumed from fastest to slowest is in the order of
1
l
, FCT, LRSVT, and CLRST.
6 CONCLUSION
This paper conducted based on the CLRST method.
2,1
l
norm was used to represent low-rank and sparse,
which differs from CLRST. The performance of the
tracking algorithms against three competing state-of-
the-art methods on seven challenging image
sequences was analyzed extensively. The proposed
method significantly reduced computation time than
CLRST. The result maintained more than twice the
speed of operation with the same overlap and
distance. The results are in line with expectations.
ACKNOWLEDGEMENT
This research was partially sponsored by National
Natural Science Foundation (NSFC) of China under
project No.61403403 and No.61402491.
REFERENCES
Zhang, T., Liu, S., Ahuja, N., Yang, M. H., & Ghanem, B.
(2014). Robust visual tracking via consistent low-rank
sparse learning. International Journal of Computer
Vision, 111(2), 171-190.
Shen, Z., Toh, K. C., & Yun, S. (2011). An accelerated
proximal gradient algorithm for frame-based image
restoration via the balanced approach. Siam Journal on
Imaging Sciences, 4(2), 573-596.
Zhang, K., Zhang, L., & Yang, M. H. (2012). Real-Time
Compressive Tracking. European Conference on
Computer Vision (Vol.7574, pp.864-877). Springer-
Verlag.
Zhang, T., Ghanem, B., & Ahuja, N. (2012). Robust multi-
object tracking via cross-domain contextual
information for sports video analysis. , 22(10), 985-988.
Zhang, T., Ghanem, B., Xu, C., & Ahuja, N. (2013). Object
tracking by occlusion detection via structured sparse
learning. , 71(4), 1033-1040.
Zhang, T., Ghanem, B., Liu, S., & Ahuja, N. (2012). Robust
visual tracking via multi-task sparse learning. , 157(10),
2042-2049.
Zhang, T., Ghanem, B., Liu, S., & Ahuja, N. (2013). Robust
visual tracking via structured multi-task sparse
learning. International Journal of Computer Vision,
101(2), 367-383.
Zhang, T., Ghanem, B., Liu, S., Xu, C., & Ahuja, N. (2013).
Low-Rank Sparse Coding for Image Classification.
IEEE International Conference on Computer Vision
(pp.281-288).
Zhang, T., Ghanem, B., Xu, C., & Ahuja, N. (2013). Object
tracking by occlusion detection via structured sparse
learning. , 71(4), 1033-1040.
Zhang, X., Ma, Y., Lin, Z., Gao, H., Zhuang, L., & Yu, N.
(2012). Non-negative low rank and sparse graph for
semi-supervised learning. IEEE Conference on
Computer Vision & Pattern Recognition (Vol.157,
pp.2328 - 2335).
Zhang, T., Ghanem, B., Liu, S., & Ahuja, N. (2012). Low-
Rank Sparse Learning for Robust Visual Tracking.
Computer Vision – ECCV 2012. Springer Berlin
Heidelberg.
Zhao, M., Jiao, L., Feng, J., & Liu, T. (2014). A simplified
low rank and sparse graph for semi-supervised learning
☆. Neurocomputing, 140(Supplement 1), 84-96.
Zhang, K., Zhang, L., & Yang, M. H. (2014). Fast
compressive tracking. IEEE Transactions on Pattern
Analysis & Machine Intelligence, 36(10), 2002-15.
Everingham, M., Zisserman, A., Williams, C. K. I., Van
Gool, L., Allan, M., & Bishop, C. M., et al. (2006). The
2005 pascal visual object classes challenge. Lecture
Notes in Computer Science, 111(1), 117-176.
Wang, L., Ouyang, W., Wang, X., & Lu, H. (2015). Visual
Tracking with Fully Convolutional Networks. IEEE
International Conference on Computer Vision
(pp.3119-3127). IEEE.
Zhang, C., Fu, H., Liu, S., Liu, G., & Cao, X. (2015). Low-
Rank Tensor Constrained Multiview Subspace
Clustering. IEEE International Conference on
Computer Vision. IEEE.
Xia, R., Pan, Y., Du, L., & Yin, J. (2014). Robust multi-
view spectral clustering via low-rank and sparse
decomposition. Twenty-Eighth AAAI Conference on
Artificial Intelligence. AAAI Press
Mei, X., Ling, H., Wu, Y., Blasch, E., & Bai, L. (2011).
Minimum error bounded efficient l1 tracker with
occlusion detection (preprint). Proceedings / CVPR,
IEEE Computer Society Conference on Computer
Vision and Pattern Recognition. IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition, 1257-1264.
Zhou, X., Yang, C., & Yu, W. (2012). Moving object
detection by detecting contiguous outliers in the low-
rank representation. IEEE Transactions on Software
Engineering, 35(3), 597-610.
Hu, W., Yang, Y., Zhang, W., & Xie, Y. (2016). Moving
object detection using tensor based low-rank and
saliently fused-sparse decomposition. , PP(99), 1-1.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
308
