Shape-based Trajectory Clustering

Telmo J. P. Pires and M

ario A. T. Figueiredo

Instituto de Telecomunicac¸

oes and Instituto Superior T

ecnico, Universidade de Lisboa, Lisboa, Portugal

{telmopires, mario.ﬁgueiredo}@tecnico.ulisboa.pt

Keywords:

Unsupervised Learning, Directional Statistics, k-means, EM Algorithm, Nonnegative Matrix Factorization,

Trajectory Clustering.

Abstract:

Automatic trajectory classiﬁcation has countless applications, ranging from the natural sciences, such as zo-

ology and meteorology, to urban planning, sports analysis, and surveillance, and has generated great research

interest. This paper proposes and evaluates three new methods for trajectory clustering, strictly based on the

trajectory shapes, thus invariant under changes in spatial position and scale (and, optionally, orientation). To

extract shape information, the trajectories are ﬁrst uniformly resampled using splines, and then described by

the sequence of tangent angles at the resampled points. Dealing with angular data is challenging, namely due

to its periodic nature, which needs to be taken into account when designing any clustering technique. In this

context, we propose three methods: a variant of the k-means algorithm, based on a dissimilarity measure that

is adequate for angular data; a ﬁnite mixture of multivariate Von Mises distributions, which is ﬁtted using

an EM algorithm; sparse nonnegative matrix factorization, using complex representation of the angular data.

Methods for the automatic selection of the number of clusters are also introduced. Finally, these techniques

are tested and compared on both real and synthetic data, demonstrating their viability.

1 INTRODUCTION

In recent years, an exponential growth in the amount

of available data for analysis has been experienced in

most ﬁelds of knowledge. These huge data quanti-

ties, far beyond the scope of manual analysis, have

stimulated a growing interest in automated methods.

Trajectory data is no exception, thanks to the grow-

ing number of tracking devices, including GPS re-

ceivers, RFID tags, tracking cameras, and even cell-

phone call traces (Becker et al., 2011). This has led to

a growing interest in automatic trajectory clustering,

as a means to perform activity recognition and clas-

siﬁcation. The study of trafﬁc patterns, human mo-

bility, and even air pollution exposure of populations

(Demirbas et al., 2009); the detection of common be-

haviors in meteorological phenomena (Elsner, 2003);

animal movement analysis (Brillinger et al., 2004);

automated sports analysis; and automatic surveillance

are just a few of the applications of these techniques.

Besides being inﬂuenced by many factors not di-

rectly related to the phenomenon in study, such as sea-

sonality, in the case of hurricane tracks, trajectories

introduce many challenges by being represented by a

sequence of space-time data points:

1. Differences in the speed of tracked objects cause

misalignments in the trajectories, as illustrated in

Figure 1(a). Varying sampling rates have a similar

effect.

2. Similar trajectories may have a different number

of points, as illustrated in Figure 1(b).

3. In some applications, trajectories differing only in

a translation (and possibly orientation) should be

treated as being similar.

4. Besides being affected by noise, trajectories can

also have big, but sparse errors, called outliers.

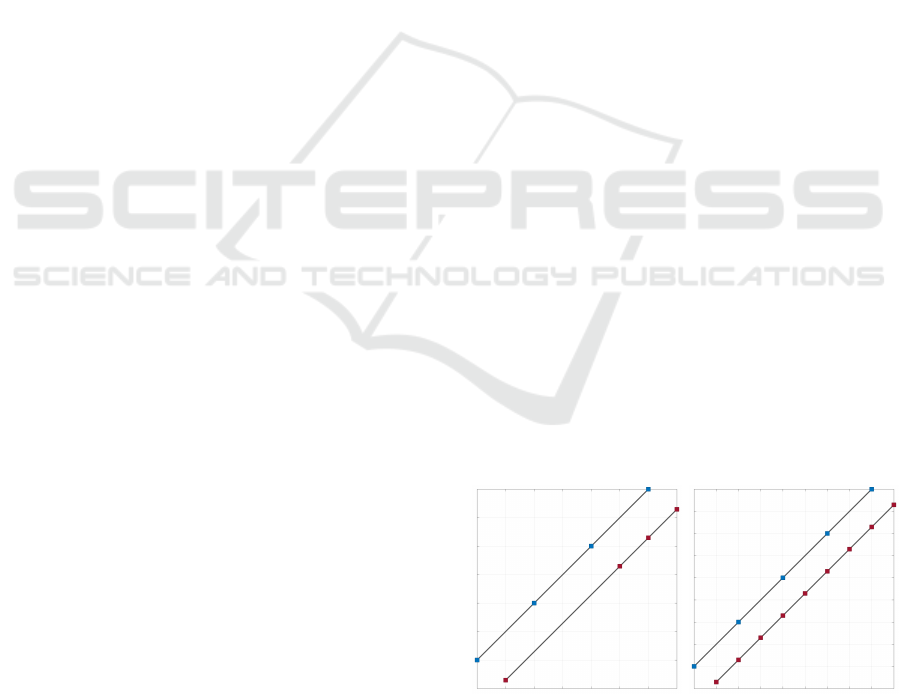
(a) Objects moving at differ-

ent speeds, leading to mis-

aligned, but similar tracks.

(b) Similar tracks with a dif-

ferent number of points.

Figure 1: Some of the challenges faced with trajectory data.

In this paper, a novel approach is introduced for

Pires, T. and Figueiredo, M.

Shape-based Trajectory Clustering.

DOI: 10.5220/0006117400710081

In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 71-81

ISBN: 978-989-758-222-6

clustering 2D trajectories, based exclusively on their

shapes. This means trajectories are clustered inde-

pendently of their location and of a global change of

scale. Optionally, it is also possible to have orienta-

tion invariance.

2 PREVIOUS WORKS

Other authors have studied the problem of trajectory

clustering. Their approaches can be divided into two

main groups: the distance metric approach and the

model based (generative) approach.

2.1 Distance Metric Approaches

These approaches aim to ﬁnd (dis)similarity measures

between trajectories, and then cluster them based on

those measures. For example, the Euclidean distance

is used in (Fu et al., 2005) and (Hu et al., 2007),

which requires trajectories with the same number of

points and uniformly sampled, so a preprocessing step

is needed.

To avoid the need for uniformly sampled trajecto-

ries, methods that try to ﬁnd an optimal alignment be-

tween time-varying sequences, such as dynamic time

warping (Pierobon et al., 2005) and longest common

subsequence (Vlachos et al., 2002) have been suc-

cessfully applied to trajectory clustering.

Another important method is TRACLUS (Lee

et al., 2007). This method allows sub-trajectory

clustering, instead of clustering the trajectories as a

whole, which may be useful in some applications.

This method works by partitioning trajectories in sub-

trajectories, and then performing density-based clus-

tering, using a specially deﬁned metric.

2.2 Model-based Approaches

Model-based methods, on the other hand, attempt to

ﬁnd a model capable of describing the whole dataset,

instead of directly comparing trajectories.

In (Gaffney and Smyth, 1999), trajectories are

represented as polynomial functions of time, and the

parameters of these functions are modeled as a ﬁnite

mixture. A similar approach is used in (Wei et al.,

2011), but trajectories are modeled using B-splines.

Another common approach to trajectory cluster-

ing models trajectories as vector ﬁelds. Some of these

works are (Ferreira et al., 2012), in which a variant of

k-means for vector ﬁelds was proposed, and (Nasci-

mento et al., 2013), where a mixture of vector ﬁelds

model allowing transitions between ﬁelds was pro-

posed.

3 DATA PRE-PROCESSING

Trajectories are usually given as sequences of points,

so a pre-processing step is needed in order to capture

their shapes. In our case, shape is characterized as

a sequence of angles: the angles of the tangents to

the trajectory, sampled at uniformly spaced points, as

illustrated in Figure 2. As seen below, the sequence

of angles is invariant under changes in location and

scale of the trajectory.

Figure 2: Uniformly resampled trajectory and respective

tangents. Shape is characterized by the angles of the tan-

gent vectors w.r.t. the horizontal.

This pre-processing step solves the problem of tra-

jectories having different lengths and the problem of

misalignment, by assuring all trajectories are simi-

larly sampled. In this work, the resampling is per-

formed using cubic splines, ﬁtted separately for both

the x and y coordinates. In order to ﬁt splines, an

independent variable is needed, and it must be the

same for each coordinate. A natural choice is time,

but many datasets only have spatial information. In

these cases, the independent variable must be esti-

mated from data, using

p+1

= τ

(i)

p+1

− x

(i)

)

+ (y

(i)

p+1

− y

(i)

)

, (1)

with τ

= 0, where we assume that the speed is uni-

form.

To reduce the inﬂuence of noise, we use smooth-

ing splines, which are ﬁtted by minimizing the cost

(De Boor, 2001)

∑

i=1

(x(τ

)− f (τ

))

+(1− p)

f (τ))

dτ, (2)

where p is a parameter that controls the trade-off be-

tween smoothness and accuracy, w

are weights we

set to 1, and D

f (τ) is the second derivative of func-

tion f . Many implementations of these algorithms are

readily available, such as the Curve Fitting toolbox in

MATLAB, which was used in this work.

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

For a uniform resampling to d points, splines

should be evaluated at:

= τ

− τ

d − 1

(i − 1) , i = 1,.. . ,d,

where τ

and τ

are the τ’s calculated according to

Eq. (1).

The angles of the tangents are obtained by

(i)

= atan2(D f

(i)

(τ

),D f

(i)

(τ

)) , ω

(i)

∈ [−π, π] ,

where atan2(·) is the 4-quadrant inverse tangent func-

tion and D f

(i)

(τ

) and D f

(i)

(τ

) refer to the ﬁrst

derivatives of the ﬁtted splines, evaluated at τ

. This

way, we get a d-dimensional vector ω

(i)

describing

the trajectory.

Besides being invariant to spatial translation and

scaling, another interesting property of this formula-

tion is that it allows trajectories to be invariant to ro-

tation with a small modiﬁcation: by working with the

differences between consecutive angles, instead of the

angles themselves.

3.1 Choosing Parameters p and d

The pre-processing step requires two input parame-

ters: p and d. For choosing p, no systematic proce-

dure is available, and so we try several values until a

good one is found. The choice of d, on the other hand,

can be automated. This is done by ﬁnding the small-

est number of points that can accurately describe a

trajectory, called the characteristic points, which pro-

vides a lower bound for d, as the characteristic points

may not be equally spaced. In order to fully charac-

terize the trajectories, we use d approximately 5 times

the maximum number of characteristic points found

in the given dataset.

In (Lee et al., 2007), a method for ﬁnding the char-

acteristic points of a trajectory was proposed, which

uses the minimum description length (MDL) prin-

ciple. The idea is to loop though all the points in

a trajectory and to compute, MDL

par

start

, p

curr

the MDL cost assuming p

start

and p

curr

are the only

characteristic points in the interval p

start

,. . ., p

curr

and MDL

nopar

start index

, p

curr index

), the MDL cost

preserving the original trajectory. If MDL

par

≤

MDL

nopar

, then choosing p

curr

as a characteristic

point makes the MDL cost lower. This procedure is

shown in algorithm 1.

The MDL cost, or MDL length, of a given

partitioning consists of two components, L(H) and

L(D|H), given by

L(H) =

par

−1

∑

j=1

log

(length(p

j+1

)),

Algorithm 1: Approximate Trajectory Partitioning.

Input: A trajectory, as a sequence of points,

,. . ., p

Output: N

, the number of characteristic points

1 N

= 1 // Add the starting point

2 start index = 1 length = 1 while

start index + length ≤ m do

3 curr index = start index + length

cost

par

= MDL

par

start index

, p

curr index

)

cost

nopar

MDL

nopar

start index

, p

curr index

) if

cost

par

> cost

nopar

then

// Partition at the previous

point

4 N

= N

+ 1

start index = curr index − 1

length = 1

5 else

6 length = length + 1

7 end

8 end

9 N

= N

+ 1 // Add the ending point

L(D|H) =

par

−1

∑

j=1

j+1

−1

∑

k=c

log

⊥

j+1

, p

k+1

))

+ log

j+1

, p

k+1

))

where par

is the number of characteristic points in

trajectory i, length(·) is the Euclidean length of a seg-

ment, p

is the segment deﬁned by points p

and

and d

⊥

and d

are the perpendicular and angular

distances, deﬁned as:

⊥

) =

⊥1

+ l

⊥2

⊥1

+ l

⊥2

) =

(

length(s

) × sin θ 0 ≤ θ < π/2

length(s

), π/2 ≤ θ ≤ π

where l

⊥1

and l

⊥2

are the distances illustrated in Fig-

ure 3.

Figure 3: Deﬁnition of distance functions from TRACLUS.

Image from (Lee et al., 2007).

To reduce the inﬂuence of noise in the procedure

above, we only apply it to estimate d after having

Shape-based Trajectory Clustering

smoothed the trajectories with the p given by the user

and using d twice the length of a trajectory, to assure

its shape is well captured.

From this point on, whenever we mention trajecto-

ries we mean the trajectories after pre-processing, i.e.,

the set {ω

(1)

,. . .,ω

(m)

}, where each trajectory ω

(i)

a sequence of angles (ω

(i)

,. . .,ω

(i)

4 K-MEANS

4.1 Introduction

The k-means algorithm is one of the most famous

clustering techniques (Jain, 2010), despite offering no

global optimality guarantees. Arguably, its popularity

is due to the fact that it is a very simple and fast ap-

proach to clustering.

Given a set of points and the number of de-

sired clusters, k-means stores a set of k centroids,

,. . .,µ

, and alternates between two steps: assign-

ment and centroid update.

1. Assignment step: set c

(i)

:= arg min

(i)

− µ

for all i, where c

(i)

= j if the ith input sample be-

longs to cluster j. In other words, assign each

sample to the closest centroid. Possible ties are

broken by some arbitrary rule.

2. Centroid update step: set µ

∑

i=1

1{c

(i)

= j}x

(i)

∑

i=1

1{c

(i)

= j}

for

all j, where 1{c

(i)

= j} is an indicator function,

taking the value 1 if c

(i)

= j and 0 otherwise, that

is, move each centroid to the mean of the points

assigned to it.

Originally, k-means was developed to work with

Euclidean distances, although many other versions

have been proposed in the literature. In our case, we

need to adapt it to handle the sequences of angles that

describe each trajectory.

4.2 Measuring Distances

A classical measure of the distance between two an-

gles is the length of the chord between them, as illus-

trated in Figure 4. It can be shown that, if the dif-

ference between two angles is ∆ω, the length of the

corresponding chord (red line in Fig. 4) is given by

2sin

∆ω

. Since sin is an odd function, it returns a

negative length if the angular difference is negative.

This is unintended, so we take the squares,

Figure 4: Relationship between angular difference and

chord (in red) in a unit circle.



2sin

∆ω



= 2 (1 − cos ∆ω) ∝ 1 − cos ∆ω,

where the constant “2” is irrelevant and dropped,

since this function will only be used to compare dis-

tances. Thus, the ﬁnal metric is 1 − cos ∆ω. The

extension of this expression to d-dimensional data is

trivial:

(ω

(1)

,ω

(2)

) =

∑

p=1



1 − cos(ω

(1)

− ω

(2)

)



, (3)

where the ω

(i)

’s are angular vectors and ω

(i)

is the

pth component of vector i. The notation D

is used to

indicate this metric is a squared value (of the chord).

4.3 Updating the Centroids

The arithmetic mean cannot be used for updating the

coordinates of a centroid, as it does not work well

with circular data. In this work, we deﬁne the mean

of a sequence of angles {ω

(1)

,. . .,ω

(m)

} as:

ω = atan2

∑

i=1

sinω

(i)

∑

i=1

cosω

(i)

(4)

The extension of this result to vectorial data is

straightforward: the mean of an angular vector is the

angular mean of each of its coordinates.

4.4 Algorithm Description

For the algorithm to be completely described, initial-

ization and stopping criteria must be speciﬁed. Re-

garding initialization, k-means++ (Arthur and Vassil-

vitskii, 2007) is used, but using Eq. (3) instead of

the Euclidean distance. The termination condition is

when the assignments no longer change between con-

secutive iterations.

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

Algorithm 2: circular k − means algorithm.

Input: Data set, {ω

(1)

,. . .,ω

(m)

}, and number

of clusters, k

Output: Cluster centroids, µ

,. . .,µ

, and

cluster assignments, c

(1)

,. . .,c

(m)

1 Initialize k cluster centroids: µ

,. . .,µ

2 repeat

3 foreach i do

4 Set c

(i)

:= arg min

D(ω

(i)

,µ

)

// Assign centroids to samples

5 end

6 foreach j do

7 Set µ

= atan2



∑

i=1

1{c

(i)

= j}sin ω

(i)

∑

i=1

1{c

(i)

= j}cos ω

(i)



for p = 1,... ,d // Update each

coordinate of the centroids

8 end

9 until convergence

4.5 Model Selection

In real-world situations, the number of clusters, k, is

not given, and it is necessary to estimate it. One com-

mon choice used in conjunction with k-means is the

so-called elbow method. This method involves com-

puting a distortion function for several values of k and

ﬁnding an elbow, that is, a point after which the rate of

decrease is signiﬁcantly smaller. The distortion func-

tion is just the sum of the distances of each data sam-

ple to the respective centroid. For circular k-means,

this is given by

J(ω

(1)

,. . .,ω

(m)

(1)

,. . .,c

(m)

,µ

,. . .,µ

)

∑

i=1

∑

p=1



1 − cos(ω

(i)

− µ

(i)

)



5 FINITE MIXTURE MODELS

Given a set of d-dimensional trajectories,

{ω

(1)

,. . .,ω

(m)

}, which is to be partitioned into

k clusters, we can model this set as i.i.d. samples of a

ﬁnite mixture,

p(ω

(i)

|θ

θ) =

∑

j=1

p(ω

(i)

= j,θ

θ),

where the z

(i)

’s are latent variables, with z

(i)

= j

meaning the ith trajectory belongs to cluster j. Each

parameter α

= p(z

(i)

= j) is the mixing probability,

and θ

θ a set of parameters characterizing the distribu-

tions. The likelihood function of the given set of tra-

jectories can be written as

p(ω

(1)

,. . .,ω

(m)

|α

α,θ

θ) =

∏

i=1

p(ω

(i)

|α

α,θ

θ)

∏

i=1

∑

j=1

p(ω

(i)

= j,θ

θ). (5)

A popular distribution for modeling circular data

is the Von Mises distribution, making it a natu-

ral choice for our mixture model. This way, the

p(ω

(i)

= j,θ

θ) are Von Mises pdf’s. The pdf of

a multivariate Von Mises is (Mardia et al., 2008)

p(ω

ω;µ

µ,κ

κ,Λ

Λ) = T (κ

κ,Λ

Λ)

−1

exp



c(ω

ω,µ

µ)

s(ω

ω,µ

µ)

Λ s(ω

ω,µ

µ)



, (6)

where

c(ω

ω,µ

µ)

= [cos(ω

− µ

), ... , cos(ω

− µ

)],

s(ω

ω,µ

µ)

= [sin(ω

− µ

), ... , sin(ω

− µ

)],

and T (κ

κ,Λ

Λ)

−1

is a normalizing constant, which is un-

known in explicit form for d > 2. Parameters µ

µ and

κ are the d-dimensional mean and concentration of

the distribution; Λ

Λ is a d × d symmetric matrix (with

zeros in the diagonal), where entry Λ

i j

measures the

dependence between ω

and ω

. Matrix Λ

Λ can be seen

as the analogous to the covariance matrix in a Gaus-

sian distribution.

The usual choice for obtaining maximum like-

lihood (ML) or maximum a posteriori (MAP) esti-

mates of the mixture parameters is the EM algorithm

(Dempster et al., 1977), which is an iterative proce-

dure with two steps:

• E-step: Set w

(i)

= p(z

(i)

= j|ω

(i)

;α

α,M

M,K

K, L

L),

where M

M, K

K, and L

L are used in place of

{µ

,. . .,µ

}, {κ

,. . .,κ

}, and {Λ

,. . .,Λ

}, re-

spectively.

Using Bayes’ Theorem, the E-step reduces to

computing, for every i and j,

(i)

p(ω

(i)

= j; µ

,κ

,Λ

)

∑

l=1

p(ω

(i)

= l; µ

,κ

,Λ

)

, (7)

where p(ω

(i)

= j;µ

,κ

,Λ

) is a multivariate

Von Mises pdf.

• M-step: this step requires maximizing the follow-

ing function, with respect to the parameters of the

model:

∑

i=1

∑

j=1

(i)

p(ω

(i)

= j;µ

,κ

,Λ

)p(z

(i)

= j;α

α)

(i)

Shape-based Trajectory Clustering

The multivariate Von Mises pdf depends on

T (κ

,Λ

), an unknown constant, which presents

a challenge for ML or MAP estimation. To avoid

having to use special numeric procedures, we as-

sume that the components of the ω

(i)

vector are

independent of the others, which makes the mul-

tivariate Von Mises distribution equivalent to the

product of d (the number of features) univariate

Von Mises distributions:

p(ω

(i)

= j; µ

,κ

,Λ

) =

∏

p=1

cos(ω

(i)

−µ

)

2πI

(κ

)

(8)

where µ

, κ

, and ω

(i)

refer to the pth component

of vectors µ

, κ

and ω

(i)

, respectively, and I

the modiﬁed Bessel function of ﬁrst kind and or-

der 0.

Using ML estimation, the update equations for µ

(the qth component of µ

), α

and κ

are as fol-

lows:

= atan2

∑

i=1

(i)

sinω

(i)

∑

i=1

(i)

cosω

(i)

, (9)

∑

i=1

(i)

, (10)

= A

−1

∑

i=1

(i)

cos(ω

(i)

− µ

)

∑

i=1

(i)

, (11)

where A

(·) =

(·)

, with I

and I

denoting the

modiﬁed Bessel functions of the ﬁrst kind and or-

ders 1 and 0, respectively.

In some cases, it is of interest to restrict κ

, in

order to avoid overﬁtting small datasets. We refer

to this variant as a constrained Von Mises mixture

(VMM), as opposed to the unconstrained (previous)

case. To constrain the concentration parameter, the

components of the κ

are forced to be the same, i.e.,

= κ

= . . . = κ

= κ

, so (11) is replaced by

= A

−1

∑

p=1

∑

i=1

(i)

cos(ω

(i)

− µ

)

∑

i=1

(i)

. (12)

5.1 Prior on the Concentration

Parameter

Due to the asymptotic behavior of the A

−1

function,

the estimation of the concentration parameter is prone

to numerical problems. One way to deal with this is

to introduce a prior, limiting its range of possible val-

ues. In this work, the conjugate prior of the Von Mises

distribution is used (Fink, 1997),

p(κ;c, R

) =

(

κR

(κ)

, κ > 0

0 , otherwise,

(13)

where K =

∞

κR

(κ)

is a normalizing constant, and

c > 0 and R

≤ c are parameters that control the shape

of the prior. Using this prior, the update rule for κ

is:

= A

−1



1+c



∑

i=1

(i)

cos(ω

(i)

−µ

)

∑

i=1

(i)

+ R



(14)

When constraining κ

, a similar expression is ob-

tained, but whose argument is averaged over the d di-

mensions.

5.2 Algorithm Description

Algorithm 3: Mixture of Von Mises for trajectory

clustering algorithm.

Input: {ω

(1)

,. . .,ω

(m)

} and the number of

clusters, k

Output: {µ

,. . .,µ

}, {κ

,. . .,κ

} and α

1 Initialize α

α, {µ

,. . .,µ

}, {κ

,. . .,κ

}

2 repeat

// E-step

3 foreach i, j do

4 Set w

(i)

p(ω

(i)

= j;µ

,κ

)

∑

j=1

p(ω

(i)

=l;µ

,κ

)

5 end

// M-step

6 Update α

with Eq. (10) for j = 1..., k

7 Update µ

with Eq. (9) for j = 1..., k and

p = 1,.. . ,d

8 Update κ

with Eq. (11), (12), or (14) for

j = 1 ..., k and p = 1,. ..,d

9 until convergence condition is satisﬁed

// Compute cluster assignments

10 foreach i = 1,. ..,m do

11 c

(i)

= arg max

j=1,...,k

(i)

12 end

To completely described the algorithm, an ini-

tialization procedure and a termination condition are

needed. Regarding initialization, we set α

,∀ j,

that is, we assume all clusters are equally likely; κ

initialized with the global κ over all dimensions and

all samples; the centroids are initialized with the re-

sults of running k-means with k-means++ initializa-

tion. Regarding termination, the algorithms are exe-

cuted until the change in log-likelihood is less than a

fraction ε = 10

−4

of its current value.

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

5.3 Model Selection

One advantage of using probabilistic methods is the

ability to use formal approaches for model selection,

such as the MDL principle (Lee, 2001), (Rissanen,

1978).

The MDL cost has two components: the length of

the model, L(H), and the length of data encoded with

the model, L(D|H). In our case, the MDL cost can be

shown to be

MDL

cost

−

∑

i=1

∑

j=1

p(ω

(i)

= j,µ

,κ

) +

lnm,

where c is the number of parameters of the model.

For unconstrained VMM’s, c = k × (2d + 1); for con-

strained, c = k × (d + 2).

For selecting the number of clusters, several val-

ues are tried, and the one minimizing the MDL cost

is chosen. To avoid local optima, EM is run several

times for each k, and only the highest likelihood solu-

tion is considered (Lee, 2001).

6 MATRIX FACTORIZATION

Nonnegative matrix factorization (NMF) is a special

type of matrix factorization where a nonnegative data

matrix, V , is decomposed as the product of two low-

rank matrices, W and H, also nonnegative (Lee and

Seung, 1999). One of the many reasons for the re-

cent interest NMF has received is its close relation-

ship with k-means. In fact, it has been shown that it

is equivalent to k-means, with appropriate constraints.

Since we are sometimes interested in factorizing ma-

trices with negative entries, variants such as semi-

NMF have been proposed (Caner T

urkmen, 2015).

Unfortunately, the constraints that make NMF

equivalent to k-means lead to an intractable problem,

thus they must be relaxed. One way to do this is

by using sparse semi-NMF (SSNMF) (Li and Ngom,

2013), which solves the following optimization prob-

lem:

min

W,H≥0

kV −W Hk

+ ηkW k

+ β

∑

i=1

, (15)

where |h

| is the `

-norm of the ith column of H, while

η and β are tuning parameters: η > 0 controls the size

of the elements of W, while β > 0 controls the trade-

off between sparseness and accuracy of the approxi-

mation.

6.1 Application to Circular Data

Unfortunately, the standard factorization techniques

do not directly work with circular data. One way

to deal with this is to convert the angles to unit vec-

tors, which do not have the problems of circular data.

This can be done by stacking the set of trajectories,

{ω

(1)

,. . .,ω

(m)

}, as columns of the Ω

Ω

Ω matrix, and use

the duality between 2D vectors and complex numbers.

This way, we can deﬁne matrix V as:

V = e

jΩ

Ω





| | |

jω

(1)

jω

(2)

·· · e

jω

(m)

| | |





where j is the imaginary unit and e

jω

(i)

is the complex

vector:

jω

(i)



jω

(i)

,. . .,e

jω

(i)



where ω

(i)

is the pth entry of trajectory ω

(i)

. In this

work we use the exponential of a matrix as the expo-

nential of its entries. It can be shown that factorizing

this matrix is approximately equivalent to minimizing

the squares of the chords corresponding to the differ-

ences between angles.

Using this matrix, we may use SSNMF for clus-

tering. One last step can be applied to avoid work-

ing with complex valued matrices: since the real and

imaginary parts of matrix V are treated independently,

one can get the same results by factorizing V

instead,

where



ℜ{e

jΩ

Ω

}

ℑ{e

jΩ

Ω

}



. (16)

The W matrix will change by a similar transformation.

Since we are only interested in the angles, and not the

vectors themselves, the matrix of the shape centroids

W = arg



+ jW



, (17)

where W

and W

are, respectively, the top and bottom

halves of the W

matrix obtained by factorizing V

Function arg(·) returns the argument of each entry of

the input matrix. In this work, “The NMF MATLAB

Toolbox” was used (Li and Ngom, 2013).

6.2 Algorithm Description

The complete clustering algorithm using SSNMF is

described in Algorithm 4.

The η parameter is set to 0 in our tests, as there is

no interest in constraining the W matrix. For β, the

default value is 0.1.

Shape-based Trajectory Clustering

Algorithm 4: Sparse NMF applied to clustering of tra-

jectories.

Input: Set of trajectories, {ω

(1)

,. . .,ω

(m)

number of desired clusters, k and η and

β parameters

Output: Clustering assignments, c

(i)

’s, and, if

needed, centroid matrix, W

1 Compute V

matrix from Eq. (16).

2 Using “The NMF MATLAB Toolbox”, ﬁnd W

and H minimizing Eq. (15).

3 Compute W from Eq. (17). // Compute

cluster assignments

4 foreach i = 1,. ..,m do

5 c

(i)

= arg max

j=1,...,k

6 end

6.3 Model Selection

The MDL principle can not be directly applied to SS-

NMF, but other methods can be used. The elbow

method works as for k-means, but uses a different cost

function: J(V

,H) = kV

−W

. The so-called

consistency method works as follows (Kim and Park,

2008):

1. For each k, compute the consistency matrix:

(i, j) = 1 ⇐⇒ i and j are in the same cluster

2. Repeat the previous step multiple times, and com-

pute the mean consistency matrix.

3. Finally, compute the consistency of each cluster-

ing using:

∑

i=1

∑

j=1



(i, j) −



, 0 ≤ ρ

≤ 1,

and choose k where ρ

drops.

The reasoning behind this choice for k is that, for

the right k, SSNMF should be consistent, but not for

higher k’s. For smaller ones, it may or may not be so.

7 RESULTS

In this section, k-means, unconstrained and con-

strained VMM’s, and SSNMF are tested and com-

pared, on both synthetic and real datasets.

7.1 Synthetic Datasets

The performance of the proposed algorithms is ana-

lyzed using the following two datasets:

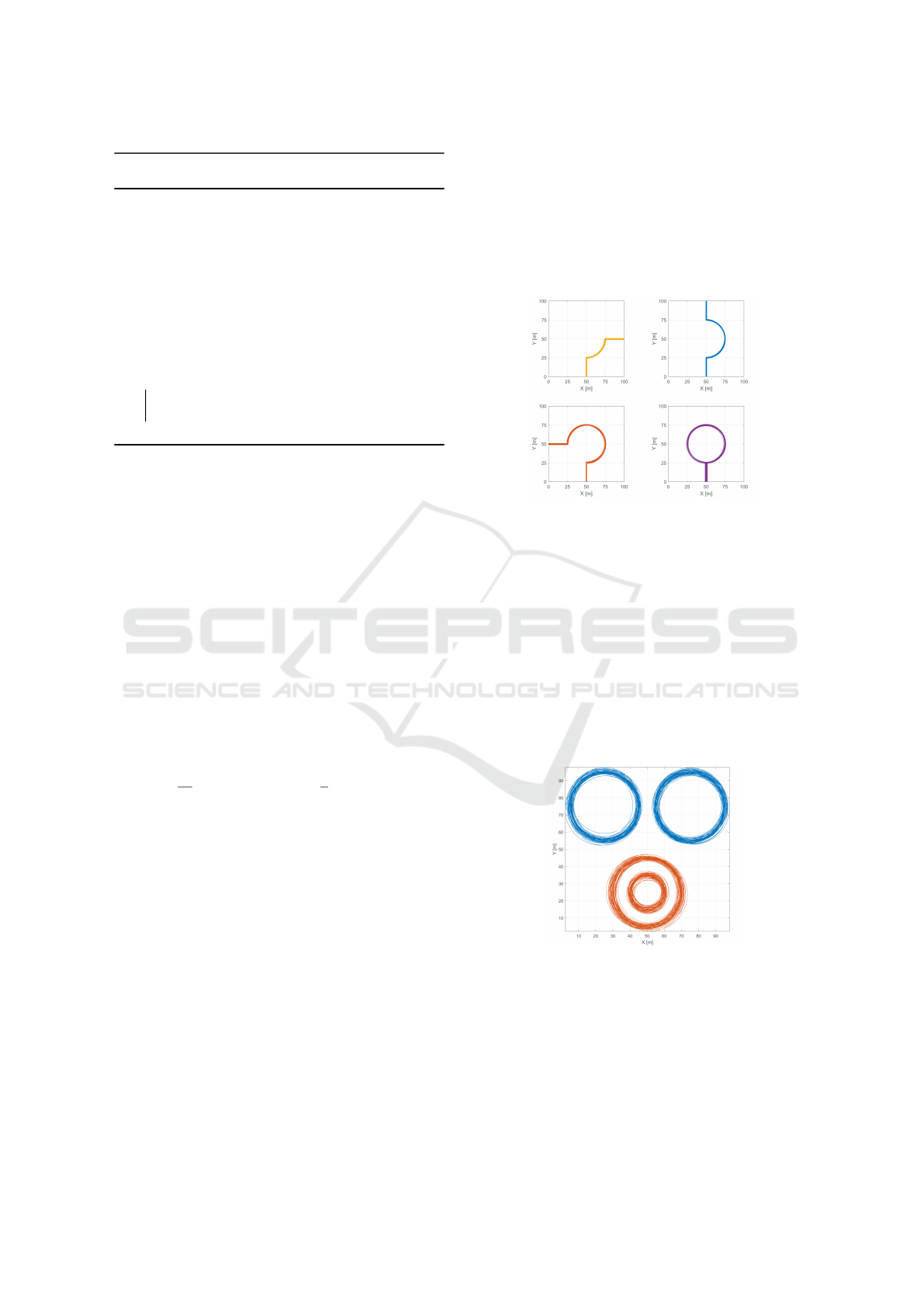
• The roundabout dataset (Figure 5) models a

roundabout where vehicles enter at the bottom and

circulate counterclockwise. There are 4 possible

exits, and each of these 4 clusters is composed of

20 noiseless trajectories. The radius and the cen-

ter of the roundabout were randomly generated for

each trajectory, making their shapes a little differ-

ent.

Figure 5: Roundabout synthetic dataset and its 4 clusters.

• The circles dataset (Figure 6) shows 100 circular

trajectories, in 4 equal size clusters. The top two

clusters correspond to objects circulating counter-

clockwise, while the bottom two, to objects circu-

lating clockwise. The radius and center of each

trajectory change between samples, and each tra-

jectory starts at a random orientation in the inter-

val [0,2π[. To ignore the changes in orientation,

we cluster the differences between angles of the

tangents, instead of the angles themselves. This

way, there are two distinguishable clusters in the

dataset, composed by the top and bottom circles.

Figure 6: Circles dataset and its 2 clusters. The two top

circles rotate counterclockwise, while the bottom two rotate

clockwise.

• The Noisy dataset (Figure 7(a)) was designed for

testing the effect of noise on the performance

of the algorithms. This dataset has 4 clusters,

with 50 trajectories each, and is corrupted by zero

mean Gaussian noise, with a standard deviation of

1.5 m.

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

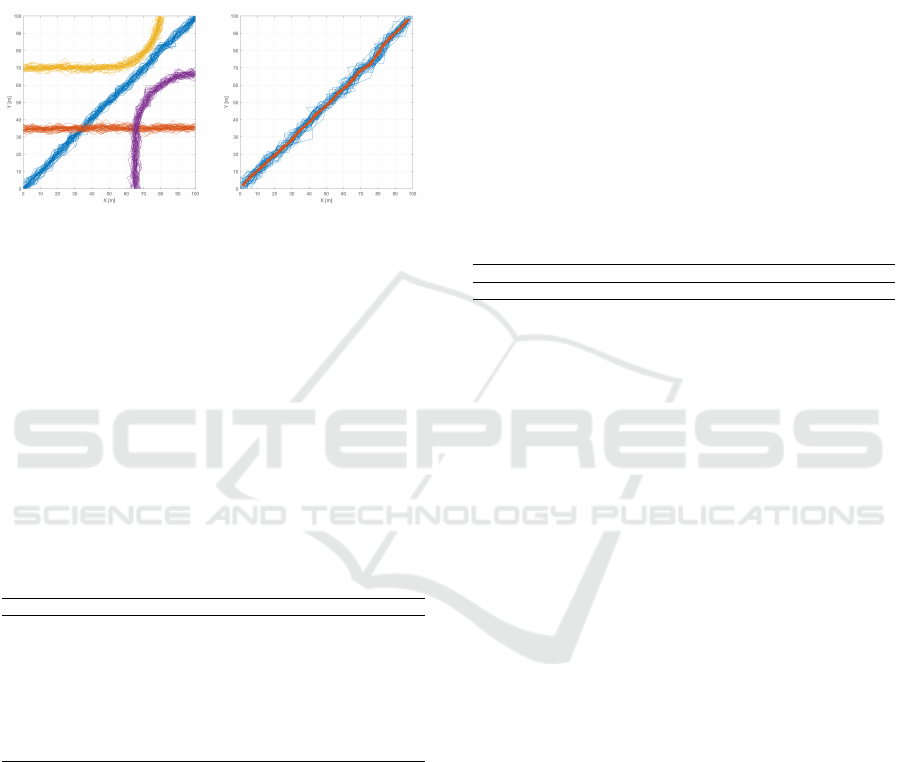
• The Concentration dataset (Figure 7(b)) was cre-

ated to illustrate the advantages of probabilis-

tic modeling (VMM’s) over the other techniques.

This dataset contains 100 trajectories, equally dis-

tributed between the two clusters, and was gener-

ated by the same mean trajectory, but with differ-

ent variances (standard deviations of 0.5 m and 2

m).

(a) Noisy Tracks synthetic

dataset, with 4 clusters.

(b) Concentration dataset

and its 2 clusters.

Figure 7: Noisy datasets.

For the noiseless and Concentration datasets, no

smoothing was used. For the Noisy dataset, several

possible values for p were tested. In the noiseless

datasets, 50 features were used, and 30 in the other

two. Each of the 4 clustering algorithms was run on

these datasets and given the right number of clusters.

This was repeated 1000 times, and the percentage of

trials the correct clustering was found is shown in Ta-

ble 1.

Table 1: Percentage of times the optimal assignment was

achieved out of 1000 trials in the synthetic datasets. The ‘*’

indicate numerical issues.

Dataset k-means unconstrained VMM constrained VMM SSNMF

Roundabout 96.7% 96.7% 96.7% 100.0%

Circles 100.0% 100.0%* 100.0%* 100.0%

Noisy (p = 1) 58.1% 58.4% 58.4% 42.6%

Noisy (p = 0.5) 58.8% 59.0% 59.0% 64.3%

Noisy (p = 0.1) 65.4% 65.4% 65.4% 83.6%

Noisy (p = 0.01) 82.4% 82.4% 82.4% 92.4%

Noisy (p = 1e − 5) 99.1% 99.1% 99.1% 35.7%

Noisy (p = 0) 99.7% 99.7% 99.7% 34.6%

Concentration 0.0% 68.9% 79.4% 0.0%

In both noiseless datasets, the true clusterings

were found most of the time. There were some nu-

merical issues with the circles dataset, as the trajec-

tories are too similar. To avoid this, a prior with

c = −R

= 5e − 5 was introduced and used in this

and all the following tests. In the Noisy dataset, it

was observed that below a certain level of smooth-

ing, all algorithms performed better with the decrease

in p. Stronger smoothing led to poorer results for

SSNMF, but better for the other methods. It is impor-

tant to note, however, that shape information is lost

with too much smoothing, so it is not advised. Over-

all, the best results were obtained for p = 0.01. In the

Concentration dataset, only the VMM’s were able to

ﬁnd the right clusters, as expected. It is interesting

to note that the constrained version outperformed the

unconstrained one, probably due to the latter having

too many degrees of freedom for the available dataset.

7.2 Inﬂuence of β on SSNMF Results

In the previous tests, the β parameter of SSNMF was

set to 0.1. To determine its effect on the results,

a parametric study was conducted, using the Noisy

dataset. With p = 0.01, β was varied, and the tests

were repeated 100 times. Table 2 summarizes the re-

sults. For β ∈ [0.1,0.5], performance is approximately

constant, thus justifying the choice of β used. Low

and high β’s give poorer results.

Table 2: Percentage of times the optimal assignment was

achieved out of 100 trials for various values for β.

β 0 10

−3

0.01 0.1 0.2 0.5 1 2 5 10

Results 1% 32% 92% 94% 92% 91% 82% 63% 61% 63%

7.3 Model Selection on the Synthetic

Datasets

In the previous tests, the algorithms were given the

correct number of clusters. Since this is not the case

in real problems, we now evaluate the model selection

criteria. For this, k was varied in the range 1, . .., 10

and the tests were repeated 20 times for each k, to

avoid local optima, for each dataset and algorithm.

A parametric study of the inﬂuence of p on model

selection was also performed. Results are shown in

tables 3 and 4.

In the noiseless datasets, the elbow method (us-

ing k-means and SSNMF) found the right number of

clusters. MDL minimization using an unconstrained

VMM also found the right k in these cases and in

the Concentration dataset. In the noisy dataset, only

MDL minimization using an unconstrained VMM

found the true k, except for very small p’s. This

is because too much smoothing makes local patterns

emerge, and also causes higher likelihoods. The other

two criteria, MDL minimization using constrained

VMM’s and consistency performed poorly. The for-

mer performed poorly because the VMM uses very

few parameters, and so too complex models are not

penalized enough. The latter, on the other hand, per-

formed badly because SSNMF was consistent even

for values of k higher than the true one.

Shape-based Trajectory Clustering

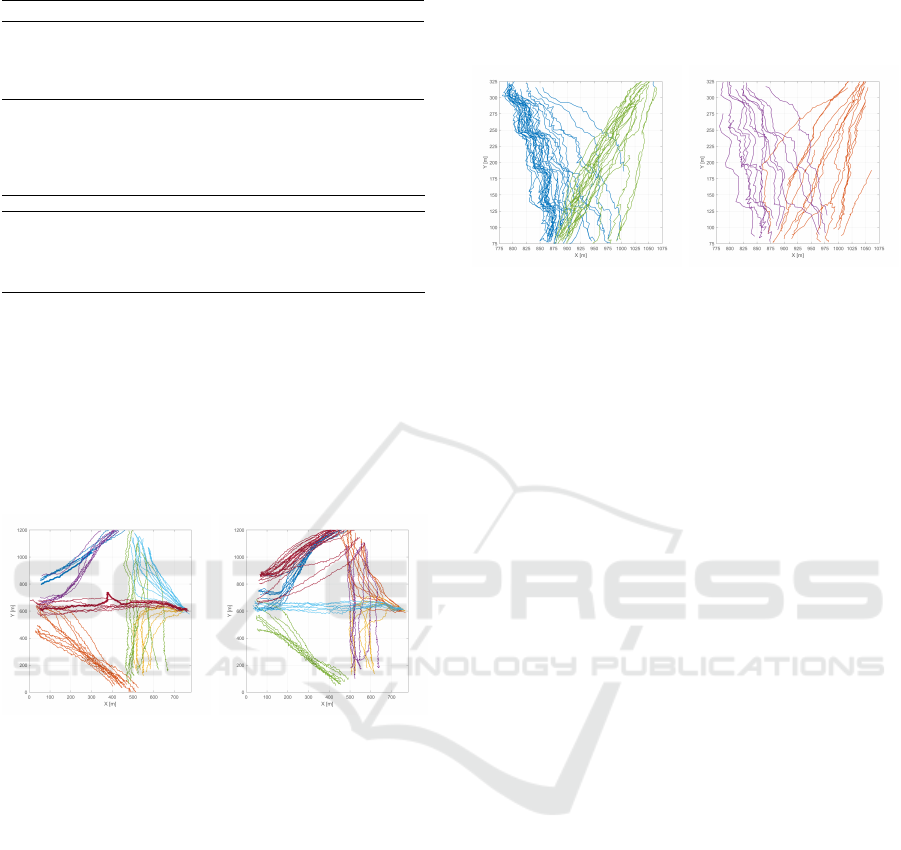
Table 3: Results of automatic model selection criteria.

Method Roundabout Circles Concentration

Unconstrained VMM 4 2 4

Constrained VMM 10 2 5

k-means 4 2 –

SSNMF (elbow/consistency) 4/5 2/3 –/–

Table 4: Inﬂuence of p on model selection in the noisy

tracks dataset. The true number of clusters is 4 and the ‘*’

indicates no clear k could be chosen.

Algorithm p = 1 p = 0.5 p = 0.1 p = 0.01 p = 10

−5

p = 0

Unconstrained VMM 4 4 4 4 9 7

Constrained VMM 7 5 5 7 10 10

k-means 4 4/5* 4/5* 4/5* 4 4

SSNMF (elbow method) 3 3 3 3/4* 4 2

SSNMF (consistency) 3 3 3 3 2 2

7.4 Real Datasets

The campus dataset is shown in Fig. 8, and is com-

posed of 134 trajectories. Since the number of clus-

ters is unknown, the methods for model selection

were executed 20 times for each k between 1 and 20.

By trial-and-error, we set p = 0.001 and 100 features

were used.

(a) 7 of the 14 clusters found

in the IST Campus dataset.

(b) The other 7 clusters.

Figure 8: The 14 clusters found in IST Campus dataset.

They are separated over 2 plots for facility of visualization.

Only the MDL minimization using the uncon-

strained VMM, which found the 14 clusters shown

in Fig. 8, gave meaningful results. For having few

parameters, MDL minimization with the constrained

VMM chooses the biggest k tested. Using the el-

bow method, on the other hand, no elbow was found

for k-means, and only a “weak” elbow was found at

k = 3 using SSNMF, but it gives meaningless clusters.

SSNMF was highly consistent for all k’s, and the only

sharp decrease happened at k = 4, which gives poor

clusters.

The staircase dataset is shown in Fig. 9. It shows a

series of people going up and down the stairs, tracked

from two different views, totaling 90 different trajec-

tories. By trial an error, p = 0.01 was found, and 50

features were used. The number of clusters was var-

ied from 1 to 12 and the tests were repeated 20 times,

to avoid bad local optima. In this case, all methods ex-

cept MDL minimization using the constrained VMM

found 4 clusters, shown in Fig. 9. This criteria failed

for not penalizing enough more complex models.

(a) 2 clusters of people going

down the stairs.

(b) The other 2 clusters, with

people going up the stairs.

Figure 9: Clusters found in the Staircase dataset.

8 CONCLUSIONS

In this work, we have presented a novel approach

to trajectory clustering, based on shape, and 3 al-

gorithms were developed for this purposed. These

methods were then tested on both synthetic and real

datasets. In both cases, all algorithms could ﬁnd good

cluster assignments when given the desired number

of clusters. With model selection, the results differed

much between techniques. Overall, the best method

was MDL minimization using unconstrained VMM’s,

which found good clusters most of the time.

Possible future work includes an extension of

this methodology to 3-dimensional trajectories and an

adaptation of this methodology to clustering parts of

trajectories.

ACKNOWLEDGEMENT

This work was partially supported by FCT (Fundac¸

para a Ci

encia e Tecnologia), grants PTDC/EEI-

PRO/0426/2014 and UID/EEA/5008/2013.

An extended version of this work can be found in

(Pires, 2016).

REFERENCES

Arthur, D. and Vassilvitskii, S. (2007). K-means++: The

Advantages of Careful Seeding. In Proceedings of

the Eighteenth Annual ACM-SIAM Symposium on

Discrete Algorithms, SODA ’07, pages 1027–1035,

Philadelphia, PA, USA. Society for Industrial and Ap-

plied Mathematics.

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

Becker, R. A., Caceres, R., Hanson, K., Loh, J. M., Ur-

banek, S., Varshavsky, A., and Volinsky, C. (2011).

Route Classiﬁcation Using Cellular Handoff Patterns.

In Proceedings of the 13th International Conference

on Ubiquitous Computing, UbiComp ’11, pages 123–

132, New York, NY, USA. ACM.

Brillinger, D., Preisler, H. K., Ager, A. A., and Kie, J. G.

(2004). An exploratory data analysis (EDA) of paths

of moving animals. In Journal of Statistical Planning

and Inference, pages 43–63.

Caner T

urkmen, A. (2015). A Review of Nonnegative Ma-

trix Factorization Methods for Clustering. ArXiv e-

prints.

De Boor, C. (2001). A Practical Guide to Splines. Applied

Mathematical Sciences. Springer, Berlin.

Demirbas, M., Rudra, C., Rudra, A., and Bayir, M. A.

(2009). iMAP: Indirect measurement of air pollution

with cellphones. In Pervasive Computing and Com-

munications, 2009. PerCom 2009. IEEE International

Conference on, pages 1–6.

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).

Maximum likelihood from incomplete data via the

EM algorithm. Journal of the Royal Statistical So-

ciety: Series B, 39(1):1–38.

Elsner, J. B. (2003). Tracking Hurricanes. Bulletin of the

American Meteorological Society, 84(3):353–356.

Ferreira, N., Klosowski, J. T., Scheidegger, C. E., and Silva,

C. T. (2012). Vector Field k-Means: Clustering Tra-

jectories by Fitting Multiple Vector Fields. CoRR,

abs/1208.5801.

Fink, D. (1997). A compendium of conjugate priors.

Fu, Z., Hu, W., and Tan, T. (2005). Similarity based vehicle

trajectory clustering and anomaly detection. In IEEE

International Conference on Image Processing 2005,

volume 2, pages II–602–5.

Gaffney, S. and Smyth, P. (1999). Trajectory Clustering

with Mixtures of Regression Models. In Proceedings

of the Fifth ACM SIGKDD International Conference

on Knowledge Discovery and Data Mining, KDD ’99,

pages 63–72, New York, NY, USA. ACM.

Hu, W., Xie, D., Fu, Z., Zeng, W., and Maybank, S. (2007).

Semantic-Based Surveillance Video Retrieval. IEEE

Transactions on Image Processing, 16(4):1168–1181.

Jain, A. K. (2010). Data Clustering: 50 Years Beyond K-

means. Pattern Recognition Letters, 31(8):651–666.

Kim, J. and Park, H. (2008). Sparse Nonnegative Matrix

Factorization for Clustering.

Lee, D. D. and Seung, H. S. (1999). Learning the parts of

objects by non-negative matrix factorization. Nature,

401:788–791.

Lee, J., Han, J., and Whang, K. (2007). Trajectory Clus-

tering: A Partition-and-Group Framework. In In SIG-

MOD, pages 593–604.

Lee, T. C. M. (2001). An Introduction to Coding Theory and

the Two-Part Minimum Description Length Principle.

International Statistical Review, 69(2):169–183.

Li, Y. and Ngom, A. (2013). The non-negative matrix fac-

torization toolbox for biological data mining. Source

Code for Biology and Medicine, 8(1):1–15.

Mardia, K. V., Hughes, G., Taylor, C. C., and Singh, H.

(2008). A Multivariate Von Mises Distribution with

Applications to Bioinformatics. The Canadian Jour-

nal of Statistics / La Revue Canadienne de Statistique,

36(1):99–109.

Nascimento, J. C., Figueiredo, M. A. T., and Marques, J. S.

(2013). Activity Recognition Using a Mixture of Vec-

tor Fields. IEEE Transactions on Image Processing,

22(5):1712–1725.

Pierobon, M., Marcon, M., Sarti, A., and Tubaro, S.

(2005). Clustering of human actions using invari-

ant body shape descriptor and dynamic time warping.

In IEEE Conference on Advanced Video and Signal

Based Surveillance, 2005., pages 22–27.

Pires, T. (2016). Shape-based Trajectory Clustering. Mas-

ter’s thesis, Instituto Superior Tcnico, Universidade de

Lisboa.

Rissanen, J. (1978). Modeling by shortest data description.

Automatica, 14(5):465 – 471.

Vlachos, M., Kollios, G., and Gunopulos, D. (2002). Dis-

covering similar multidimensional trajectories. In

Data Engineering, 2002. Proceedings. 18th Interna-

tional Conference on, pages 673–684.

Wei, J., Yu, H., Chen, J. H., and Ma, K. L. (2011). Parallel

clustering for visualizing large scientiﬁc line data. In

Large Data Analysis and Visualization (LDAV), 2011

IEEE Symposium on, pages 47–55.

Shape-based Trajectory Clustering