Spontaneous Facial Expression Recognition using Sparse Representation

Dawood Al Chanti and Alice Caplier

Univ. Grenoble Alpes, GIPSA-Lab, F-38000 Grenoble, France

CNRS, GIPSA-Lab, F-38000 Grenoble, France

Keywords:

Dictionary Learning, Random Projection, Spontaneous Facial Expression, Sparse Representation.

Abstract:

Facial expression is the most natural means for human beings to communicate their emotions. Most facial

expression analysis studies consider the case of acted expressions. Spontaneous facial expression recognition

is signiﬁcantly more challenging since each person has a different way to react to a given emotion. We

consider the problem of recognizing spontaneous facial expression by learning discriminative dictionaries for

sparse representation. Facial images are represented as a sparse linear combination of prototype atoms via

Orthogonal Matching Pursuit algorithm. Sparse codes are then used to train an SVM classiﬁer dedicated to

the recognition task. The dictionary that sparsiﬁes the facial images (feature points with the same class labels

should have similar sparse codes) is crucial for robust classiﬁcation. Learning sparsifying dictionaries heavily

relies on the initialization process of the dictionary. To improve the performance of dictionaries, a random face

feature descriptor based on the Random Projection concept is developed. The effectiveness of the proposed

method is evaluated through several experiments on the spontaneous facial expressions DynEmo database. It

is also estimated on the well-known acted facial expressions JAFFE database for a purpose of comparison with

state-of-the-art methods.

1 INTRODUCTION

An increasing number of techniques have been pro-

posed in the literature for emotional facial expressions

analysis since emotion is an essential component of

interpersonal relationships and communication. Hu-

man behavior is central to research concerning inter-

action processes. A facial image contains much in-

formation about a person identity but also about emo-

tion and state of mind. Emotion cues show how we

feel about ourselves and others. The cues are repre-

sented through facial components (eyes, nose, mouth,

cheeks, eyebrow,forehead, etc) which are the region

of interest (ROI) for emotional recognition system.

Facial expression recognition system utilized in locat-

ing and extracting different facial motions and facial

feature changes from the ROI region and classifying

into one of the emotional or mental states. The poten-

tial utility of a system capable of analyzing sponta-

neous facial expressions automatically is considerable

in terms of its potential applications: human machine

interaction, detection of mental disorders, remote de-

tection of people in trouble, detection of malicious

behavior and multimedia facial queries (Tong et al.,

2007). The current researches about facial expres-

sion recognition can be divided into two categories

(Peng et al., 2009): recognition of facial affect and

recognition of facial muscle actions. In this paper, fa-

cial affect recognition is considered for observable ex-

pressions of emotion displayed through facial expres-

sions. Our choice comes from the fact that it provides

simplicity in identiﬁcation of the various emotions via

extracting information about facial expressions from

images. However, facial action units (AUs) which are

related to the contraction of speciﬁc facial muscles,

consist of 44 action units. Although the number of

atomic action units is small, more than 7,000 combi-

nations of action units have been observed (Scherer

and Ekman, 1982).

As far as automatic facial affect recognition is

concerned, most of the existing efforts focused on the

six basic Ekman’s-emotions (Ekman, 1999) because

those emotions have universal properties. Moreover,

relevant training and test materials are available (e.g.,

(Kanade et al., 2000) and (Lyons et al., 1998)). These

studies are limited to exaggerated expressions and

controlled environments. There are a few tentatives

efforts to detect non-basic affective states including

mental states (“irritated”, “worried”...) (El Kaliouby

and Robinson, 2005). But those expressions are

closer to natural behavior. Additionally, the fact

is that spontaneous facial expressions have differ-

Al Chanti D. and Caplier A.

Spontaneous Facial Expression Recognition using Sparse Representation.

DOI: 10.5220/0006118000640074

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 64-74

ISBN: 978-989-758-226-4

ent temporal and morphological characteristics than

posed ones.

The purpose of our work is to demonstrate that

sparse representation is an efﬁcient model in order to

classify and to increase the accuracy rate of predict-

ing the spontaneous facial expressions using sponta-

neous facial images. Sparse representation provides

higher or lower dimensional representations which in-

duce the likelihood that image classes will be possi-

bly linearly separable. The sparse discriminative fea-

ture set provides the main interface through which a

machine learning algorithm can infer about the data.

More precisely, the main issue with sparse represen-

tation being dictionary learning and due to the fact

that the original facial image has a very high dimen-

sion, the straightforward application of sparse repre-

sentation for sparse feature extraction from raw im-

ages does not lead to a meaningful sparse representa-

tion. Thus we present an efﬁcient initialization strat-

egy and dimensionality reduction technique via de-

veloping an optimized random face feature descriptor

(RFFD) based on the random projection (RP) concept

(Vempala, 2005). RFFD aims at projecting the fa-

cial images into a lower dimensional space and at se-

lecting the most discriminative feature sets that min-

imizes the correlation between different facial image

classes while maximizing the correlation within fa-

cial image classes, in an attempt to ensure the unique-

ness of the atoms selection from the dictionary during

sparse coding process. Our pre-training step allows us

to avoid high computational resources (memory usage

and training time) required during dictionary training

which is an important requirement for developing a

real-time automatic facial expression recognition sys-

tem. Experimental results on the JAFFE acted facial

expression database and on the DynEmo spontaneous

expression database demonstrate that our algorithm

outperforms many recently proposed sparse represen-

tation and dictionary learning based approaches. Our

algorithm has the capacity to be trained on a small or a

big dataset and to provide a high accuracy rate, which

can be considered as an advantage compared to deep

learning approaches which are doing great nowadays

only if a big dataset is provided.

2 RELATED WORK

Numerous methods for extracting discriminative in-

formation about facial expressions from images have

been developed. For example, Eigenfaces, Fisher-

faces, and Laplacianfaces have been used on full face

images (Buciu and Pitas, 2004). Gabor ﬁlter banks

also have been successfully used as an efﬁcient facial

feature ((Candes and Romberg, 2005) and (Cand

et al., 2006)) because these features are locally con-

centrated and have been shown to be robust to block

occlusion (Donoho, 2006). Once the feature vector

is extracted from an image, this vector feeds a classi-

ﬁer which gives the recognized expression. A survey

of automatic facial expression recognition methods is

presented in (Hoyer, 2003).

A noteworthy contribution of sparse representa-

tions of signals has been reported in recent years. It

has been successfully applied to a variety of prob-

lems in computer vision and image analysis, includ-

ing image denoising (Elad and Aharon, 2006), image

restoration (Mairal et al., 2008) and image classiﬁ-

cation (Yang et al., 2009), (Wright et al., 2009) and

(Bradley and Bagnell, 2008). Sparse representation

modeling of data assumes an ability to describe sig-

nals as linear combinations of few atoms from a pre-

speciﬁed dictionary. The success of the model relies

on the quality of the dictionary that sparsiﬁes the sig-

nals. The choice of a proper dictionary can be done

using one of two following ways (Rubinstein et al.,

2010): building a sparsifying dictionary based on a

mathematical model of the data (wavelets, wavelet

packets, contourlets, and curvelets), or learning a dic-

tionary to perform best on a training set. Reference

(Wright et al., 2009) employs the entire set of train-

ing samples as the dictionary for discriminative sparse

coding, and achieves impressive performance for face

recognition. Many algorithms ((Mairal et al., 2010)

and (Wang et al., 2010)) have been proposed to ef-

ﬁciently learn an over-complete dictionary (the num-

ber of prototype signals, referred as atoms, is much

greater than the features size) that enforces some dis-

criminative criteria. Recently, another sparse rep-

resentation for object representation and recognition

was proposed in the seminal work (Wright et al.,

2009). In (Jiang et al., 2013), the class labels of

training data are used to learn a discriminative dic-

tionary for sparse coding. In addition, label informa-

tion is associated with each dictionary item to enforce

discriminability in sparse codes during the dictionary

learning process. More speciﬁcally, a new label con-

sistency constraint called “discriminative sparse-code

error” is introduced and combined with the recon-

struction error and the classiﬁcation error to form a

uniﬁed objective function.

Our work is inspired by the good reputation of

sparse representation in both theoretical research and

practical applications ((Yang et al., 2009), (Wright

et al., 2009), (Bradley and Bagnell, 2008) and (Mairal

et al., 2008)). Moreover, our choice comes from the

fact that sparse representation has the ability to pro-

vide sparse vectors that can share the same sparsity

Spontaneous Facial Expression Recognition using Sparse Representation

pattern at class level if it is correctly built.

3 MODEL ARCHITECTURE

Figure 1 presents the global architecture of the pro-

posed algorithm for facial expression recognition.

Figure 1: Global architecture of spontaneous facial expres-

sion recognition algorithm (SFER).

3.1 Dimensionality Reduction and

Dictionary Pre-training Stage

We aim to leverage the random projection (RP) tech-

nique (Sulic et al., 2010) to develop a random face

feature descriptor (RFFD) for dictionary pre-training

that elegantly solves the problem of shared subspace

distribution. It also projects the raw data into a lower-

dimensional space, while preserving their reconstruc-

tive and discriminative properties. Beside, it seeks

for the best transformation matrix that maximizes the

separation between the multiple classes which is the

main key to induce sparsity.

As a pre-processing stage, a face detector (Zhu

and Ramanan, 2012) is applied in order to detect and

locate a bounding box around the face. Facial im-

ages are cropped to focus on the expressive parts only:

eyes, eye-brows, mouth and nose, in order to reduce

the effect of background variation. Then, RFFD is ap-

plied in order to project the data into a lower dimen-

sional subspace and to extract the most informative

and discriminative independent features. The pro-

jected data serve as dictionary initialization. Thus, the

dictionary is pre-trained with feature vectors sharing

same patterns within class label while feature vectors

from different classes have different patterns.

Random Projection Theory and Concept:

Random projection is a powerful data dimension

reduction technique because it is capable to preserve

the reconstructive properties of the data (Sulic et al.,

2010). It uses random projection matrices whose

columns have unit length to project data from high-

dimensional subspace to a low-dimensional subspace.

It is a computationally simple and efﬁcient method

that preserves the structure of the data without signif-

icant distortion (Sanghai et al., 2005).

The concept of RP is as follows: Given a data

matrix X, the dimensionality of data can be reduced

by projecting it onto a lower-dimensional subspace

formed by a set of random vectors:

m×N

= R

m×d

· X

d×N

(1)

where N is the total number of points, d is the

original dimension, and m is the desired lower di-

mension, R is the random transoformation matrix and

A is the projected data. The central idea of RP is

based on the Johnson-Lindenstrauss lemma. For com-

plete proofs of the lemma refer to (Tsagkatakis and

Savakis, 2009).

The choice of the random matrix R is one of the

crucial points of interest. Reference (Tsagkatakis and

Savakis, 2009) employs a random matrix R whose el-

ements are drawn independently and are identically

distributed (i.i.d.) from a zero mean, bounded vari-

ance distribution. There are many choices for the ran-

dom matrix. A random matrix with elements gener-

ated by a normal distribution r

i, j

∼ N(0, 1) being one

of the simplest in terms of analysis (Tsagkatakis and

Savakis, 2009) has been chosen in this work.

Random Face Feature Descriptor Algorithm:

A Random Face Feature Descriptor based on RP

concept is designed. RFFD ﬁrstly tackles the curse of

dimensionality in which each image is projected onto

m-dimensional vector with a randomly generated pro-

jection matrix R from a zero-mean normal distribu-

tion. Each row of the transformation random matrix

is l

normalized. RFFD aims at minimizing the corre-

lation between different classes while maximizing the

correlation within-classes. It preserves discriminative

properties of the input data.

Figure 2 presents the RFFD algorithm. It looks

for the best projection matrix R and the best dimen-

sion of projection m that preserve the structure and

the reconstructive properties of the original data. The

intuition behind this algorithm is as follows: since R

is generated randomly, it is not guaranteed to have

good quality features. A good quality feature vector

, i = [1, ..., m], is a vector where its most entire el-

ements are not full of zeros. The quality of the pro-

jected matrix A

m×N

(ﬁgure 2 step iii) is checked by

thresholding the norm of every column vector A

. If

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

Input:

• X ∈ R

d×N

: is the input matrix, where each column

represents one sample. d is the original dimension

of the image and N is the total number of samples.

• M = [m

, m

, ..., m

]: a list of possible desired

lower dimensions.

• rn: is the desired number for generating good ran-

dom matrices.

Algorithm:

1. For each m in M

(a) While j in rn

i. Generate random matrix R

[m×d]

from zero

mean, normal distribution N(0, 1) and l

nor-

malized columns.

ii. Compute A

[m×N]

= R

[m×d]

· X

[d×N]

iii. Check the quality of the obtained features in

[m×N]

iv. If A

[m×N]

has good quality features, add A

[m×N]

to a list L

(b) For each A in L

i. Apply Linear SVM over the obtained (A) with

cross validation.

ii. Store the recognition rate.

that reaches

the highest classiﬁcation accuracy rate.

(d) Add best A and its classiﬁcation accuracy rate to

a list L

2. Pick up in the L

list the A that reaches the highest

accuracy rate and the corresponding best transfor-

mation matrix R

Output:

• Projected data A

[m×N]

from the optimal R and m.

• Optimal projection matrix R that generates the best

discriminative features.

• Optimal lower dimension m.

Figure 2: Random Face Feature Descriptor Algorithm.

the norm of A

is smaller than a given threshold, it is

considered as a bad feature vector.

Once a good data projection A

(m,N)

is obtained, R

is considered as good random transformation matrix.

Moreover, the quality of the features vectors A

from

two different good transformation matrices R and R

can vary. We aim at picking out R that induce the most

discriminability between classes. Selecting the best R

among a set of R’s is then important (ﬁgure 2 steps

b and c). In addition, selecting the best dimension

m that preserves the discriminative properties of the

original data with minimal distortion has a great effect

on the ﬁnal recognition rate (ﬁgure 2 steps d and 2).

The projected data obtained as the output of the

RFFD process is used to initialize the dictionary that

is required for the sparse representation process. This

step is important to induce sparsity during learning

process by initializing the dictionary with atoms that

are highly informative and that have maximum sepa-

ration between multiple classes.

3.2 Dictionary Reﬁning and Sparse

Coding Stage

The second step of the algorithm (see ﬁgure 1) ﬁrstly

aims at reﬁning the pre-trained dictionary to sparsify

the images via K-Singular Value Decomposition (K-

SVD) algorithm (Rubinstein et al., 2008). Secondly it

aims at deriving the sparse code associated to each

signal by solving l

-norm regularization to enforce

sparsity by using an approximate sparse reconstruc-

tion algorithm, Orthogonal Matching Pursuit (OMP)

(Tropp, 2004).

Given a dataset Y ∈ R

n×N

and a target sparsity level

L (maximum number of atoms allowed in each rep-

resentation) the problem is to build the dictionary

D ∈ R

n×K

and the sparse matrix X ∈ R

K×N

such that

Y ≈ DX. The problem can be formulated as:

< D, X >= argmin

D,X

||Y − DX||

such that (2)

∀

, i ∈ [1, N], ||x

≤ L

∀

, j ∈ [1, K], ||d

= 1

where:

• ||x

is ||l||

pseudo norm, deﬁned by the number

of non-zero coefﬁcients in column x

• ||E||

is the Frobenius norm.

• columns d

is l

normalized atom of the dictionary

Equation 2 can be solved by an alternating two

step optimization process :

1. Sparse Coding: Keep the pre-trained dictionary

D ﬁxed and estimate X such as:

X = argmin

||Y − DX||

such that ∀

, ||x

≤ L

(3)

The sparse representation X is optimized by using

the OMP algorithm. Compared with other alterna-

tive methods for sparse coding, a major advantage

of the OMP is its simplicity and fast implementa-

tion.

2. Dictionary Reﬁning: Keep the obtained sparse

matrix X ﬁxed and update the pre-trained dictio-

nary D via K-SVD algorithm to better ﬁt the data.

Spontaneous Facial Expression Recognition using Sparse Representation

To recap, the search for the sparse representation

of facial expression images over a pre-trained dictio-

nary is achieved by optimizing an objective function

(equation 2) that includes two terms: one that mea-

sures the signal reconstruction error and the other that

measures the best sparsity level to ensure the correct

representation of the signals.

3.3 Classiﬁcation Stage

In the last step (see ﬁgure 1), the sparse matrix X is

directly used as feature vectors for classiﬁcation. Our

model trains a “Multinomial Linear Support Vector

Machine” classiﬁer (Vapnik, 2013) for the purpose

of facial expression recognition. We consider linear

SVM classiﬁer among the others well-known classi-

ﬁers (i.e., K-Means, Ada Boost and Decision Tree)

since it shows the best results. In the training step, the

sparse matrix X

training data

is used to learn a predic-

tive model to recognize facial expressions. The test

sparse matrix X

test data

is used for generalization pur-

pose: the capability of the model to predict unseen

facial expression is tested. Grid search is applied to

ﬁnd the best parameter C (regularization parameter)

to tune the linear SVM classiﬁer.

4 EXPERIMENTAL SETUP AND

ANALYSIS

A critical experimental evaluation of the proposed ap-

proach is presented. Two public data sets that exhibit

various emotions in different conditions, starting from

acted facial expressions: the JAFFE database (Lyons

et al., 1998), to everyday natural and spontaneous fa-

cial expressions: the DynEmo database (Tcherkas-

sof et al., 2013), are used. The effectiveness of the

proposed random face feature descriptor as a dimen-

sion reduction technique and dictionary pre-training

method is analyzed by considering ﬁrst the acted and

controlled JAFFE database. This database is also used

for fair comparison with the state of the art methods.

Then experiments on the DynEmo database are re-

ported since spontaneous facial expressions recogni-

tion is our main goal.

4.1 Model Validation Over the JAFFE

Database

The JAFFE Database: The Japanese Female Fa-

cial Expression (JAFFE) database is a well-known

database made of acted facial expressions related to

Figure 3: Examples of facial expressions from JAFFE

database.

Eckman’s emotions. It contains 213 images of fe-

male facial expressions including: “happy”, “anger”,

“sadness”, “surprise”, “disgust”, “fear” and “neutral”.

Resolution of original facial images is 256 × 256 pix-

els. After cropping, each image has a resolution of

138 × 128 pixels. The head is almost in frontal pose.

The number of images corresponding to each of the

seven categories of expressions is roughly the same

(around 30 images per class). A few of them are

shown in ﬁgure 3. It is obvious that expressions are

over exaggerated. Nonetheless this database has often

been used in literature to evaluate the performance of

some facial expressions recognition algorithms.

JAFFE Database Protocol: Identities that appear in

the training data sets do not appear in the test set.

1. train set: 20 images per class are picked out as

training set. In total we have 143 facial expres-

sion images, randomly shufﬂed, for training our

algorithm.

2. development set: Leave-one-out cross validation

is considered over the training set to tune the al-

gorithm parameters.

3. test set: 10 images per class are picked out as test

set. In total we have 70 facial expression images,

randomly shufﬂed, to test the performance of our

algorithm.

Experimental Setup and Analysis:

The efﬁciency of our approach and its capability to

recognize acted facial expressions beforehand testing

it on spontaneous facial expressions is evaluated and

demonstrated as a control experiment.

Firstly, the dataset is divided into two portions

based on the number of images per class as deﬁned

in the previous JAFFE dataset protocol. Figure 4

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

Table 1: RFFD versus PCA Performance on the JAFFE

Database.

JAFFE database

Projection Method Average recognition rate %

RFFD (ours) 70

PCA 30

represents the evaluation of the random face feature

descriptor. The x-axis represents the generation of

different random matrix R for the same desired di-

mension m. The y-axis represents the ﬁnal aver-

age classiﬁcation rate over the projected data. To

evaluate the performance of RFFD over the JAFFE

database, we deﬁne a list of desired lower dimen-

sions, m: 600, 650, 700, 750, 800, 900, and1000. For

each dimension, different random matrices R

are gen-

erated. For a given dimension, R that reaches the max-

imum average classiﬁcation accuracy rate is picked

out. Finally, both the best dimension and the best R

are derived. Figure 4 shows that the optimal random

projection matrix is R

700

. Which means, the optimal

dimension is found to be 700 at random matrix R

this set. The projected data from R

700

reaches an av-

erage classiﬁcation rate of 70%.

We compare the proposed dimension reduction

method with PCA which is probably the most popular

method for dimensionality reduction. Our method out

performs PCA method as shown in table 1.

For illustration, the ﬁrst three feature vectors for

20 images per class before and after RFFD over the

test data are displayed. Figure 5 shows that the data

have a shared subspace before projection. This prob-

lem is solved by the proposed RFFD method since the

data are then partially linearly separable. This reaches

our main concern to obtain highly informative and in-

dependent feature vectors between different classes.

Secondly, the optimal data projection is used to

initialize the dictionary D

(0)

, of size (700 features,

143 atoms (K)) (under-complete dictionary: number

of the atoms is smaller than the feature size). Each

column of the dictionary is normalized to have unit

norm, which ensures that the angle is proportional to

the inner product. K-SVD algorithm is applied to re-

ﬁne the initialized dictionary and the sparse matrix

is computed via OMP algorithm. The optimal dic-

tionary is obtained. It yields to a signal representa-

tion with the smallest possible support while the es-

timated signal is still close to the observation. The

choice of L is estimated to 15% of the dictionary size

by controlling the absolute reconstruction error (ﬁg-

ure 6) and the discriminability of the obtained sparse

code (ﬁgure 7). Figure 6 shows the ability of the

trained dictionary to reconstruct the test samples with

minimal reconstruction error and with low sparsity

level (21 non-zero coefﬁcient at maximum). Figure

Table 2: Recognition Rate per Class % on the JAFFE

Database.

Class Recognition Rate %

AN 99

DI 90

FE 95

HA 89

SA 100

SU 100

NE 91

Table 3: Classiﬁcation Accuracies (%) on the JAFFE

Database.

Approach Average Recognition Rate %

SFER (ours) 94.85

LC-KSVD-1 76

LC-KSVD-2 78

CAE-based 95.8

FIS 87.6

Sobel-based 93.1

7 represents the sparse code coefﬁcients of a given

image of the following expressions: ”Anger”, ”Dis-

gust”, ”Fear”, ”Happy”, ”Sad”, ”Surprise” and ”Neu-

tral” respectively from top to bottom. The x-axis rep-

resents the dictionary atoms (basis vectors) in which

the coming facial image is encoded from while the y-

axis represents the coefﬁcients value. Figure 7 shows

that each expression is encoded by a different set of

atoms with different weights coefﬁcients. The dis-

criminability of the sparse code is a very important

property for robust classiﬁcation. The other point to

be noticed is that under-complete dictionary allows

faster computation, since OMP algorithm will pick

out at most L out of K atoms (greedy algorithm).

Finally, after deriving the test and the train spar-

sity matrices via OMP algorithm based on the reﬁned

dictionary via K-SVD algorithm, a linear SVM clas-

siﬁer is trained over the training sparse matrix (143:

samples, 143: sparse feature vector size). The test

sparsity matrix (70, 143) is used to assess the ability

of the classiﬁer to generalize. A grid search is applied

to ﬁnd the best regularization parameter C, and C is

found to be 1.

Table 2 presents the recognition rate per class. It

shows that expressions “anger” (AN), “sadness” (SA)

and “surprise” (SU), are perfectly classiﬁed. For the

expressions “disgust” (DI), “happy” (HA) and “neu-

tral” (NE) the system is able to recognize them with

91% classiﬁcation accuracy rate. “Fear” (FE) got

95% recognition rate. The ﬁnal average recognition

rate is 94.85%.

We compare our approach with other sparse ap-

proaches LC-KSVD1 and LC-KSVD2 (Jiang et al.,

Spontaneous Facial Expression Recognition using Sparse Representation

Figure 4: Random Face Feature Descriptor Evaluation over the JAFFE Database.

2013) but also with other techniques: Convolutional

Autoencoder, Sobel-Based, Fuzzy Inference System

(Hamester et al., 2015). Table 3, shows the average

recognition rate for those different approaches. It is

obvious that our approach outperforms other sparse

approaches and exhibits performance similar to those

of the most recent state of the art methods.

4.2 Model Evaluation Over the

DynEmo Database

The DynEmo Database: DynEmo is a database con-

taining dynamic and natural emotional facial expres-

sions (EFEs). It is made of six spontaneous ex-

pressions which are: “irritation”, “curiosity”, “hap-

piness”, “worried”, “astonishment”, and “fear” (see

ﬁgure 8). Those expressions have been elicited by

showing some emotive short clips to volunteer sub-

jects. The database contains a set of 125 record-

ings of EFE of ordinary Caucasian people (ages 25 to

65, 182 females and 176 males) ﬁlmed in natural but

standardized conditions. In this set, EFE recordings

are both associated with the affective state of the ex-

presser itself and with continuous annotations of ob-

servers’ ratings of the emotions displayed throughout

the recording (see ﬁgure 9). The x-axis of ﬁgure 9

represents the time line, while the y-axis represents

the probability of judgment for each frame. In the rest

of this paper, we will refer to the expresser as encoder

and to the observer as decoder. Figure 9 shows that

10% of the decoders recognized the feeling of the en-

coder as irritation at the beginning of the video (time

line: frame 1 to frame 20). While for the time line be-

tween frame 21 and frame 76, the judgement of differ-

ent decoders led to different results. To overcome this

problem, when different decoders judge with differ-

ent classes, we associate to each frame the class that

gets the highest probability. For example, for the time

line corresponding to frames between 36 and 41, the

apex (maximum expressiveness of the emotion) is as-

sociated to the astonishment class with a probability

of 70%. In some cases, when the probability of two

or more different classes is the same, we refer to the

previous frame judgment as additional information to

judge the current frame.

We built a labelled spontaneous database in which

the frames are extracted based on the previous de-

ﬁned ground truth. 480 images of female and male

facial expressions of 65 different identities form the

database. Each image has a resolution of 239 × 200

pixels after face detection and cropping. The head is

not totally in frontal pose. The number of images cor-

responding to each of the six categories of expressions

is roughly the same (80 images per class). The dataset

is challenging since it is closer to natural human be-

haviour and ﬁgure 10 shows that even for the same

emotion, people can perform it in different ways.

DynEmo Database Protocol: Identities that appear

in the training data sets do not appear in the test set.

1. train set: 60 images per class are picked out as

training set. In total we have 360 facial expres-

sion images, randomly shufﬂed, for training our

algorithm.

2. development set: Leave-one-out cross validation

is considered over the training set to tune the al-

gorithm parameters.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

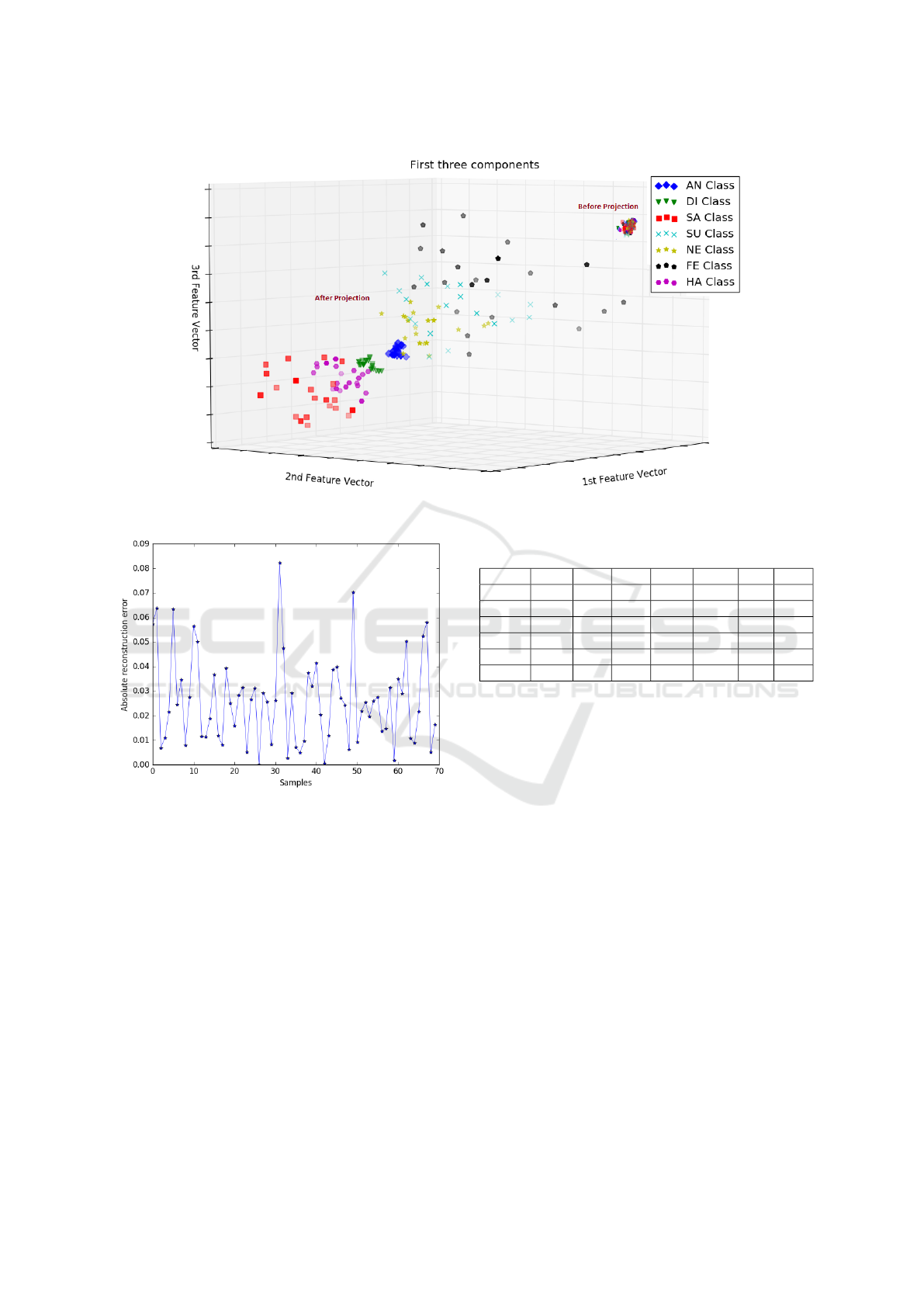
Figure 5: Data distribution before and after projection.

Figure 6: Absolute reconstruction error for test samples.

3. test set: 20 images per class are picked out as test

set. In total we have 120 facial expression images,

randomly shufﬂed, to test the performance of our

algorithm.

Experimental Setup and Analysis:

Same experimental setup as in the control exper-

iment has been followed. Firstly, the dataset is di-

vided into two portions based on the number of im-

ages per class as deﬁned in the previous DynEmo

dataset protocol. Then, RFFD is applied in which the

optimal random matrix that generates good discrim-

inative features and the optimal dimensionality size

(n-features = 250 feature points) are derived. There-

fore, passing through the ﬁrst stage of SFER algo-

rithm, we get a training set with 360 images and 250

Table 4: Confusion Matrix and average recognition rate per

class (RR) in % .

Class IRR CU HA WO AST FE RR

IRR 85 5 5 0 5 0 81

CU 5 95 0 0 0 0 95

DI 0 0 95 5 0 0 93

WO 15 0 5 80 0 0 86

AST 0 0 0 0 100 0 98

FE 5 0 0 0 0 95 97

feature points (n) in addition to a testing set of 120

images and 250 feature points. The average recogni-

tion rate over the projected data prior to the second

stage of SFER algorithm is 68.4%. The performance

of RFFD is compared with PCA which achieves an

average recognition rate of 24% only. It is obvious

that PCA is not powerful at all to extract good dis-

criminative features compared to RFFD when consid-

ering spontaneous facial expressions.

Secondly, a dictionary of size (250 features, 360

atoms (K)) is initialized (projected training set). The

sparsity level (L) is estimated to 10% of the dictionary

size by controlling the absolute reconstruction error.

The dictionary is reﬁned via K-SVD and the sparse

matrix is derived via OMP algorithm.

Finally, a linear SVM classiﬁer is trained over the

training matrix (360, 360). The test sparsity matrix

(120, 360) is used to assess the ability of the classiﬁer

for generalization. A grid search is applied to ﬁnd the

best regularization parameter C, where C is found to

be 10.

Table 4 shows the confusion matrix and the aver-

age recognition rate per class. It appears that the high-

Spontaneous Facial Expression Recognition using Sparse Representation

Figure 7: Sparse code coefﬁcients of signals representing AN, DI, FE, HA, SA, SU and NE expressions respectively from top

to bottom.

Figure 8: Examples of spontaneous facial expressions from

the DynEmo database.

Figure 9: Time line of continuous annotations.

Figure 10: Same spontaneous emotion (disgust) expressed

by different encoders.

Table 5: Classiﬁcation Accuracies (%) on the DynEmo

Database.

Approach Average Recognition Rate %

SFER (ours) 91.68

LC-KSVD-1 20.1

LC-KSVD-2 85.4

est number of misclassiﬁcations is obtained for “irri-

tation” (IRR) and “worried” (WO). Figure 8 shows

that WO and IRR expressions are visually close to

each other. For the rest of the classes like “curious”

(CU), “astonishment” (AST) and “fear” (FE), the ob-

tained recognition rate is above 95%. The class “dis-

gust” (DI) got a 93% recognition rate. The average

recognition rate is 91.67%. Table 5 shows the recog-

nition rate on the DynEmo dataset compared to the

other sparse approaches. It can be seen that our ap-

proach performs much better than LC-K-SVD1 and

LC-K-SVD2.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

Table 6: Average recognition rate using SFER approach.

Number of

images per class

AN IRR SU CU SA AST HA WO DI FE

Training set 20 60 20 60 20 60 20 60 80 80

Test set 10 20 10 20 10 20 10 20 30 30

Average recognition

Rate per class in %

93 78 94 90 88 92 89 83 89 88

Final average

recognition rate

88.4 %

4.3 Generalization Performance

The system’s generalization performance is evaluated

on the combination of the two datasets: JAFFE +

DynEmo. Table 6 show the distribution of the new

database, the average recognition per class and the

ﬁnal average recognition rate obtained over the new

database. Same experimental setup as the two pre-

vious experiments has been followed. The model is

tuned by performing 10-folds cross validation over

the training set and tested over the test set. Table 6

shows that our model is capable of recognizing dif-

ferent classes related to different emotions and mental

states. 88.4 % as an average recognition rate over the

10 classes is achieved.

5 CONCLUSION

In this paper, a robust spontaneous facial expression

recognition algorithm (SFER) based on facial im-

ages that recognizes non-basic affective state includ-

ing mental state is presented. We developed a method

to pre-train the dictionary that enforces sparsity and

enhances dictionary performance. We shown that it

was possible to learn under-complete dictionary once

good discriminative features are extracted prior to dic-

tionary reﬁning stage which ensures the uniqueness

of the selected atoms from the dictionary during the

optimization process. We proposed the use of ran-

dom projection as a mean of dimensionality reduction

and as a mean of solving the problem of shared sub-

space. We exhibited very good recognition rates over

the recent spontaneous facial database DynEmo. A

possible work for the future is exploiting the tempo-

ral dynamics of facial expressions in order to improve

the recognition rates. Temporal information might be

useful since expressions not only vary in their facial

deformations but also in their onset, apex, and offset

timings.

REFERENCES

Bradley, D. M. and Bagnell, J. A. (2008). Differential sparse

coding.

Buciu, I. and Pitas, I. (2004). Application of non-negative

and local non negative matrix factorization to facial

expression recognition. In Pattern Recognition, 2004.

ICPR 2004. Proceedings of the 17th International

Conference on, volume 1, pages 288–291. IEEE.

Candes, E. and Romberg, J. (2005). l1-magic: Recov-

ery of sparse signals via convex programming. URL:

www. acm. caltech. edu/l1magic/downloads/l1magic.

pdf, 4:46.

Cand

es, E. J., Romberg, J., and Tao, T. (2006). Robust un-

certainty principles: Exact signal reconstruction from

highly incomplete frequency information. Informa-

tion Theory, IEEE Transactions on, 52(2):489–509.

Donoho, D. L. (2006). Compressed sensing. Information

Theory, IEEE Transactions on, 52(4):1289–1306.

Ekman, P. (1999). Basic emotions. Handbook of cognition

and emotion, 98:45–60.

El Kaliouby, R. and Robinson, P. (2005). Real-time infer-

ence of complex mental states from facial expressions

and head gestures. In Real-time vision for human-

computer interaction, pages 181–200. Springer.

Elad, M. and Aharon, M. (2006). Image denoising via

sparse and redundant representations over learned dic-

tionaries. Image Processing, IEEE Transactions on,

15(12):3736–3745.

Hamester, D., Barros, P., and Wermter, S. (2015). Face ex-

pression recognition with a 2-channel convolutional

neural network. In 2015 International Joint Confer-

ence on Neural Networks (IJCNN), pages 1–8. IEEE.

Hoyer, P. O. (2003). Modeling receptive ﬁelds with non-

negative sparse coding. Neurocomputing, 52:547–

552.

Jiang, Z., Lin, Z., and Davis, L. S. (2013). Label consistent

k-svd: Learning a discriminative dictionary for recog-

nition. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 35(11):2651–2664.

Kanade, T., Cohn, J. F., and Tian, Y. (2000). Comprehen-

sive database for facial expression analysis. In Auto-

matic Face and Gesture Recognition, 2000. Proceed-

ings. Fourth IEEE International Conference on, pages

46–53. IEEE.

Lyons, M., Akamatsu, S., Kamachi, M., and Gyoba,

J. (1998). Coding facial expressions with gabor

Spontaneous Facial Expression Recognition using Sparse Representation

wavelets. In Automatic Face and Gesture Recognition,

1998. Proceedings. Third IEEE International Confer-

ence on, pages 200–205. IEEE.

Mairal, J., Bach, F., Ponce, J., and Sapiro, G. (2010). Online

learning for matrix factorization and sparse coding.

The Journal of Machine Learning Research, 11:19–

60.

Mairal, J., Elad, M., and Sapiro, G. (2008). Sparse represen-

tation for color image restoration. Image Processing,

IEEE Transactions on, 17(1):53–69.

Peng, X., Zou, B., Tang, L., and Luo, P. (2009). Research

on dynamic facial expressions recognition. Modern

Applied Science, 3(5):31.

Rubinstein, R., Bruckstein, A. M., and Elad, M. (2010).

Dictionaries for sparse representation modeling. Pro-

ceedings of the IEEE, 98(6):1045–1057.

Rubinstein, R., Zibulevsky, M., and Elad, M. (2008). Ef-

ﬁcient implementation of the k-svd algorithm using

batch orthogonal matching pursuit. CS Technion,

40(8):1–15.

Sanghai, K., Su, T., Dy, J., and Kaeli, D. (2005). A multino-

mial clustering model for fast simulation of computer

architecture designs. In Proceedings of the eleventh

ACM SIGKDD international conference on Knowl-

edge discovery in data mining, pages 808–813. ACM.

Scherer, K. R. and Ekman, P. (1982). Handbook of methods

in nonverbal behavior research, volume 2. Cambridge

University Press Cambridge.

Sulic, V., Per

s, J., Kristan, M., and Kovacic, S. (2010). Ef-

ﬁcient dimensionality reduction using random projec-

tion. In 15th Computer Vision Winter Workshop, pages

29–36.

Tcherkassof, A., Dupr

e, D., Meillon, B., Mandran, N.,

Dubois, M., and Adam, J.-M. (2013). Dynemo: A

video database of natural facial expressions of emo-

tions. The International Journal of Multimedia & Its

Applications, 5(5):61–80.

Tong, Y., Liao, W., and Ji, Q. (2007). Facial action unit

recognition by exploiting their dynamic and semantic

relationships. IEEE Transactions on Pattern Analysis

& Machine Intelligence, (10):1683–1699.

Tropp, J. A. (2004). Greed is good: Algorithmic results for

sparse approximation. IEEE Transactions on Infor-

mation theory, 50(10):2231–2242.

Tsagkatakis, G. and Savakis, A. (2009). A random pro-

jections model for object tracking under variable pose

and multi-camera views. In Distributed Smart Cam-

eras, 2009. ICDSC 2009. Third ACM/IEEE Interna-

tional Conference on, pages 1–7. IEEE.

Vapnik, V. (2013). The nature of statistical learning theory.

Springer Science & Business Media.

Vempala, S. S. (2005). The random projection method, vol-

ume 65. American Mathematical Soc.

Wang, J., Yang, J., Yu, K., Lv, F., Huang, T., and Gong,

Y. (2010). Locality-constrained linear coding for

image classiﬁcation. In Computer Vision and Pat-

tern Recognition (CVPR), 2010 IEEE Conference on,

pages 3360–3367. IEEE.

Wright, J., Yang, A. Y., Ganesh, A., Sastry, S. S., and Ma,

Y. (2009). Robust face recognition via sparse repre-

sentation. Pattern Analysis and Machine Intelligence,

IEEE Transactions on, 31(2):210–227.

Yang, J., Yu, K., Gong, Y., and Huang, T. (2009). Lin-

ear spatial pyramid matching using sparse coding for

image classiﬁcation. In Computer Vision and Pattern

Recognition, 2009. CVPR 2009. IEEE Conference on,

pages 1794–1801. IEEE.

Zhu, X. and Ramanan, D. (2012). Face detection, pose es-

timation, and landmark localization in the wild. In

Computer Vision and Pattern Recognition (CVPR),

2012 IEEE Conference on, pages 2879–2886. IEEE.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications