
Adjusting Word Embeddings by Deep Neural Networks
Xiaoyang Gao
1
and Ryutaro Ichise
2,3
1
School of Electronics Engineering and Computer Science, Peking University, Beijing, China
2
National Institute of Informatics, Tokyo, Japan
3
National Institute of Advanced Industrial Science and Technology, Tokyo, Japan
Keywords:
NLP, Word Embeddings, Deep Learning, Neural Network.
Abstract:
Continuous representations language models have gained popularity in many NLP tasks. To measure the
similarity of two words, we have to calculate their cosine distances. However the qualities of word embeddings
depend on the corpus selected. As for word2vec, we observe that the vectors are far apart to each other.
Furthermore, synonym words with low occurrences or w ith multi ple meanings are even further in distance.
In these cases, cosine similarities are no longer appropriate to evaluate how similar the words are. And
considering about the structures of most of the language models, they are not as deep as we supposed. “Deep”
here refers to setting more layers in the neural network. Based on these observations, we implement a mixed
system with two kinds of architectures. We show that adjustment can be done on word embeddings in both
unsupervised and supervised ways. Remarkably, this approach can successfully handle the cases mentioned
above by largely increasing most of synonyms similarities. It is also easy to train and adapt to certain tasks by
changing the training target and dataset.
1 INTRODUCTION
To understand the meanings of words is the core
task of natura l language processing models. While
still hard to compete with a human-like brain,
many models successfully reveal cer ta in aspects of
similarity relatedness using distributed representa-
tion. These word embeddings are trained over
large and unlabeled text corpus leveraging different
kinds of neural networks (Bengio et al.(2003)Bengio,
Ducharme, Vincent, and Jauvin; Collobert and
Weston(2008); Mnih and Hinton(2009); Mikolov
et al.(2011)Mikolov, Kombrink, Burget,
ˇ
Cernock`y,
and Khudanpur) and have obtained much attention
in many fields, such as part-of- speech tagging (Col-
lobert et al.(2011)Collobert, Weston, Bottou, Kar-
len, K avukcuoglu, and Kuksa), dependency parsing
(Chen and Manning(2014)), syntactic parsing (Socher
et al.(2013) Socher, Bauer, Manning, and Ng), etc.
One of the popular neural-network models is
word2vec (Mikolov et al.(2013a)Mikolov, Chen, Cor-
rado, and Dean; Mikolov an d Dean(2013b)), in which
words are embedded into a low-dimensional vector
space, which corresponds to words in a way based
on the distributional hypothesis: word s that occur in
similar context should have similar meanings. The
hypothesis captures the semantic and syntactic relati-
ons between words, and learned vectors encode these
properties. Both o f the semantic and synta c tic regula-
rities can be revealed from linear calculation between
word pairs: boys - boy ≈ cars - car, and k ing - man
≈ queen - woman. The mean s of measuring the si-
milarity between the source word and the target word
is to calculate the cosin e distance. Bigger cosine si-
milarity indicates that the target word is more similar
to the source word than the others. After applying the
model, the embedded vectors are spread in a large Eu-
clidean space in which words are separated far from
others, lead ing to sparse vecto rs. Traditional methods
to measure the semantic similarity are o ften operated
on the taxonomic dictionary WordNet (Miller(1995))
and exploit the hierarchy stru c ture. (Men´e ndez-Mora
and Ic hise(2011)) prop osed a new mode l which modi-
fies the trad itional WordNet-based semantic similarity
metrics. But these m ethods do not consider the con-
text of words, and it is hard to figure out the syntactic
properties and linguistic regularities. A good idea is
to combine WordNet with neural network models for
deep learning.
Words that are synonyms denote that they mean
nearly the same sense in the same langu age and they
are interchangeable in certain c ontexts. For exam-
398
Gao X. and Ichise R.
Adjusting Word Embeddings by Deep Neural Networks.
DOI: 10.5220/0006120003980406
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 398-406
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: The framework of our system. We feed word
representations to a deep neural network for pre-training,
and then use learned parameters for a deep neural network
which implements for fine-tuning. x is the input, h
1
and h
2
are the learned hidden representations from unsupervised
model. Synonym dataset is used for supervised learning in
fine-tuning model.
ple, blush and flush c a n be both interpreted as be-
coming red in the face when feeling embarrassed
or shamed, but the cosine similarity between words
is only around 0.2 when we obtain the vector by
word2vec. It is also observed that word2vec doesn’t
recover another kind of relational similarity, for ex-
ample, regularize and regularise are totally the same,
but such word pair only gains around 0.7 cosine si-
milarity which illustrate the sparse and scattered pro-
perties of word 2vec representations. In this p aper, we
propose two different deep neural networks to com-
press the vectors and reduce the dimensionality in
both supervised a nd u nsupervised ways. Unsupervi-
sed deep neural networks are usually applied for pre-
training and extracting meaningful features, and can
achieve better performance comparing to the results
without unsupervised learning proc e ss. Considering
there is only one hid den layer in word2vec, we show
that leveraging deep ne ural networks on learned vec-
tors can lead to competitive and state-of-the-ar t re-
sults. By adjusting the elements in the vector, we
found that u sing autoenc oders can improve the simi-
larity between synonyms, exhibitin g the nature of this
relation, ma king the cosine similarity more plausible
to h uman perception. Without using other datasets
like WordNet and regardless of the corpus used, stac-
ked autoencoders can automatically enable the syno-
nyms to get closer in th e space.
A key insight of the work is that vecto rs from
word2vec can be learned deeply by the neural net-
work. Deep neural networks(DNNs) have achieve re-
markable performances in many critical tasks compa-
ring to traditional machine learning methods. (Kriz-
hevsky et al.(2012)Krizhevsky, Sutskever, and Hin-
ton) proposed a deep convolutional neural network
which achieved record-breaking results on Image N et
classfication. (Dahl et al.(2012)Dah l, Yu, Deng , a nd
Acero) also presented a novel DNN model with deep
belief network for pre-training in spee ch recognition.
The model reduced relative e rror and outperformed
conventional models. Previous works inspire us to
use DNNs on raw word representations. After adjust-
ment, th e model produces markedly different word re-
presentations and we find that the cosine similarities
between most of the synonyms are improved. Toget-
her with a fine-tu ning m odel and a novel loss function,
all com pressed word embeddings fro m hidden lay-
ers achieve state-of-the-art performances at recove-
ring th e synonym relation and deceasing distances be-
tween non-synonym word pairs. This result r eflects
the potential energy of autoenco ders and the space for
deep learning of the vectors from word2vec.
In this paper, we will introduce related work in
Section 2, and pr esent our deep learning m odel in
Section 3 . The experiment setup and results will b e
presented in Section 4, a s well as the discussion. We
will conclude our system and findings in Section 5 .
2 RELATED WORK
Traditional langua ge models r e construct certain word
co-occurrence ma trix and represent words as high
dimensional but sparse vectors, then r e duce the di-
mension by matrix-factorization methods, such as
SVD (Bullinaria and Levy(2007)), or LDA (Blei
et al.(2003)Blei, Ng, and Jordan). Recently, dense
vectors fro m neural network langu a ge models refer-
red to as “word embedding” perform well in a variety
of NLP tasks.
Neural network lang uage models (NNLMs) “em-
bed” words from large, unlabeled corpus into a low-
dimensional vector space and outperfo rm traditio-
nal models. Moreover, neural-network based mo-
dels have been successfully a pplied in many speci-
fied fields, such as ana logy answer tasks, named en-
tity recognition, etc. In NNLMs, each word is presen-
ted as a k-dimensio n vector with real numbers, and
two vectors that have a high cosine similarity result
indicate that the cor responding words are semanti-
cally or syntactically related. Among all these mo-
dels, word2vec which largely reduced the compu ta ti-
onal complexity gains the most popularity. The word
Adjusting Word Embeddings by Deep Neural Networks
399

embedd ings of the model capture the attributional si-
milarities f or words that occ ur in the similar context.
As for word2vec, the model increases th e dot product
of words that co-occur in the corpus, and this leads
to the result tha t words that are semantic or syntactic
related are closed to each o ther in the representation
space. There are two structures for the m odel, each
has its own characteristics and ap plicability in d if-
ferent cases. The continuous bag-of-words (CBOW)
predict the target word by the window of words to the
left as well as to the right of it. The Skip-gram model
predicts the words in the window from cu rrent word.
However, we can find some problems in the mo-
del. Words in English always have multiple mea-
nings. To deal with this issue, WordNet, a lexical
ontology, distinguishes different meanings of one spe-
cific word by attributing it to different synsets. (Bol-
legala et al.(2015)Bollegala, Mohamm e d, Mae hara,
and Kawarabayashi) used a semantic lexicon an d a
corpus to learn word representations. Their method
utilizes co-occurrence matrix and the lexical on to-
logy instead of the neural network and outperforms
both CBOW and Skip-gram by calculating the corre-
lation coefficient between cosine similarities and ben-
chmark datasets. Also there will be an intersection for
senses of two words if they refer to the same mea ning
in the certain context. But bec a use of different usages
and writing habits, some words with the sam e m ea-
ning may occur in distinc t contexts or ap pear infre-
quently in the text. For example, the cosine similarity
for “let” and “allow” is smaller than human intuition
judgement, and except “letting”, “lets”, the most simi-
lar word to “let” is “want”. This indicates the sparse
property of word embe ddings learned by the model.
Considering about two words, each word has a vari-
ety of meanin gs, but they shar e a few of them, in this
case, they are widely spread in representation space
by this model and far apart to each other. Moreover,
one word can have different forms, for example, “re-
gularize” can also be written in the form of “regula-
rise”, wh ile in fact they are the same. However, when
we use word representations to calculate the cosine
similarities in the se cases we get unreasonable scores
which fail to accurately measure the similarity bet-
ween words. To deal with these kinds of sparsity, and
considerin g abo ut the “depth” of NNLMs, we propose
a deep neural network and this will be discussed later
in the following section. Currently not so many works
focus on addressing these problems.
3 PROPOSED APPROACH
We propose a novel de ep neural network with pre -
train process by using stacked autoencoders. Figure 1
illustrates the data flow of our architecture. First we
process the input for pre-training to get latent para-
meters. After pre-training the raw input, we reduce
the dimensionality to get better representations. The
parameters of fine-tuning model are initialized by le-
arned weights and biases. Both parts of the system
leverage back propagation method for training. In the
fine-tunin g part we exhibit an innovative loss function
which enables the model to increase the quality of si-
milarities between synonym words as well as unrela-
ted words.
3.1 Pre-train Model
An autoencoder (Rumelhart et al.(1985)Rumelhart,
Hinton, and Williams; Hinton and Salakhutdi-
nov(2006)) is a neural network for the purpose of re-
ducing dimension, encod ing origina l representations
of the data in an unsu pervised way. It is widely used
for pre-training the data before classification tasks due
to their strong d ependen cy on the representation. By
learning better r epresentation s,a n auto-encoder redu-
ces noise and extracts meaningful features, which im-
prove performance of classifiers. (Kamyshanska and
Memisevic(2015)) presents the potential energy of
autoencoder using different activation functio ns and
how different autoencoders achieve competitive per-
formances in classification tasks. This inspires us to
implement the network on word embeddings.
For an autoencoder, the network uses a mapping
function f
θ
to enco de the inpu t x
x
x into hidden rep resen-
tations y
y
y, wher e θ = {W
W
W , b
b
b}, W
W
W is the weight matrix
and b
b
b is the bias term. Then the autoencoder decodes
the hidden representations to re construct the input ˆx
ˆx
ˆx
via W
W
W
T
and another bias te rm for the output layer. h
is the activation functions, Sigmoid and ReLU are fre-
quently used.
y
y
y = h(W
W
Wx
x
x +b
b
b) (1)
ˆx
ˆx
ˆx = h
W
W
W
T
h (W
W
Wx
x
x +b
b
b)+
ˆ
b
ˆ
b
ˆ
b
(2)
The goa l of the autoencoder is to compa re the recon-
structed output to the or iginal in put and minimize the
error so that output can be as close as po ssible to the
input.
We leverage autoencoders to word emb eddings le-
arned by word2vec for the following three reaso ns:
1. We use the autoencoder to denoise and lea rn better
representations.
2. Polysemous words spread widely in the represen -
tation space , far fro m their similar words, while
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
400
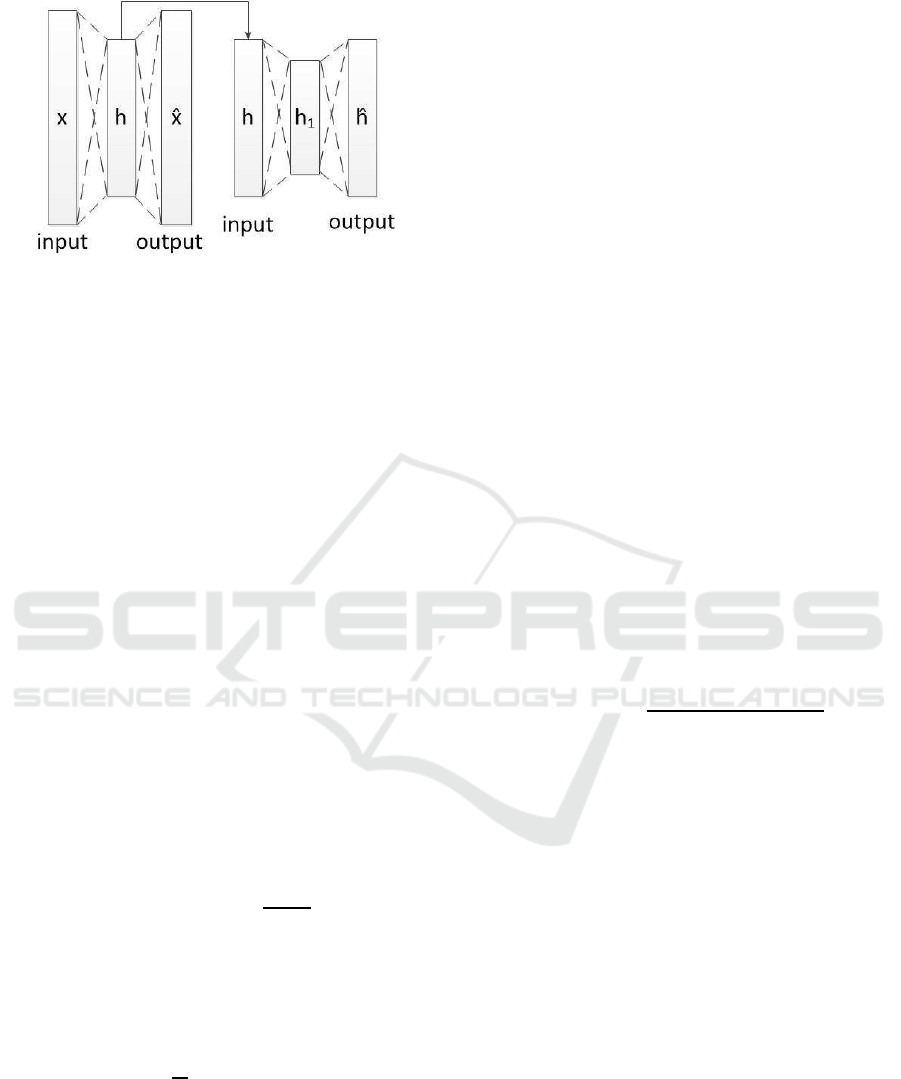
Figure 2: Stacked autoencoders with 2 hidden layers. Train
the fi r st autoencoder on the input to learn new features h.
Then feed new features to the second autoencoder to obtain
secondary features h
1
.
autoencoder can compress the vectors and make
them closer.
3. Representations of deeper hidde n layers are rela-
tively r obust and steady to the input so we will
reduce the dimensionality at least twice.
An advanced form of applying the red uction is
stacked autoencod ers. This neural network consists
of multip le layers of sparse autoencoders in which
the output of each layer is the input of the succes-
sive layer. The best way to train the stacked autoen-
coders is to use greedy layer-wise training. To do
this, we first train one autoencoder for dimensiona-
lity reduc tion to obtain the weigh t matrix and bias.
Then use the latent representation as the input for the
next autoencoder. Follow this meth od in the subse-
quent layers, and finally a fine-tuning model is used to
confirm and optimize the convergence of whole neu-
ral networks by the backpropag a tion method. In our
system, we first use stacked autoencoders to obtain
more robust representations tha n the corrupted input
from word2vec as the pre-train step. Figure 2 shows
the ar c hitecture of this step. Additionally, the activa-
tion function f (x) = tanh(x) =
1−e
−2x
1+e
−2x
is used in the
intermediate layers, and the ou tput lay er is also tanh
because word representations shou ld inc lude positive
as we ll as negative values.
In order to have the output as close as p ossible to
the input, w e use mean squar e d loss function
L
L
L =
1
N
N
∑
i=1
||x
i
x
i
x
i
− ˆx
i
ˆx
i
ˆx
i
||
2
(3)
where x
i
denotes the representation of a word in the
corpus, and N is the total number of words. Using
this function, the output will be as close as p ossible to
the input.
3.2 Fine-tuning Model
The second part of our system is a n ovel fine-tuning
model, constituted by a dee p neural network. Unlike
the fine-tunin g model f or autoencoder s talked about in
the p revious section, we remove the symmetric struc-
ture of the network bec ause we raise a new kind of
loss function fo r lear ning dee per level representati-
ons. But the parameters are still initialized by learned
weights and biases from stacked autoencoders for the
purpose of fine-tuning. Figure 3 shows the architec-
ture of th e model.
We use the synonym dataset from WordNet to
train the model. Th e dataset consists of words and
their corresponding synsets IDs. I f two words have
the same synset ID, they denote the same concept. We
iterate the whole dataset, each time we choose a word
and find all the synonym words to it. At the same
time, we ran domly select 5 negative samples. Word
negative me ans they are non-synonym instances to the
present word. We utilize a innovative loss function
for processing with word representations following
the inspiration from (Huang et al.(2015)Huang, Heck,
and Ji; Shen et al.(2014 )Shen, He , Gao , Deng, and
Mesnil)
L
L
L = −log
∏
(w
+
,w)
P
w
+
|w
(4)
P(w
j
|w
i
) =
exp (sim(w
j
, w
i
))
∑
w
′
∈E
i
exp (sim(w
′
, w
i
))
(5)
where w
+
denotes one related sy nonym word accor-
ding to the cu rrent input instance in the dataset, and
E
i
is the set of instances which are not related or re-
lated to the input in any sense. We use one back-
propagation method to minimize the loss to get op-
timal results, and in order to avoid overfitting, 10-fold
cross-validation is imp le mented for determining mo-
del param eters after randomly sorting the vocabulary
list. We set the first hidden layer to 150 neura l units,
and 100 for the next. On the top of the network, we
output representations of positive and negative instan-
ces, and calculate the cosine similarity for word pairs
so that we ca n measure the loss and update the p ara-
meters. By calculating the posterior pr obability and
the loss, the model will in c rease the cosine similari-
ties between synonym word pairs, and decrease those
for non-synonym word pairs simultaneously. Also
in this supervised way, we can save artificial efforts
and obtain competitive or even state-of-the-art results
comparing to word embeddings without learning by
deep neural network.
Adjusting Word Embeddings by Deep Neural Networks
401
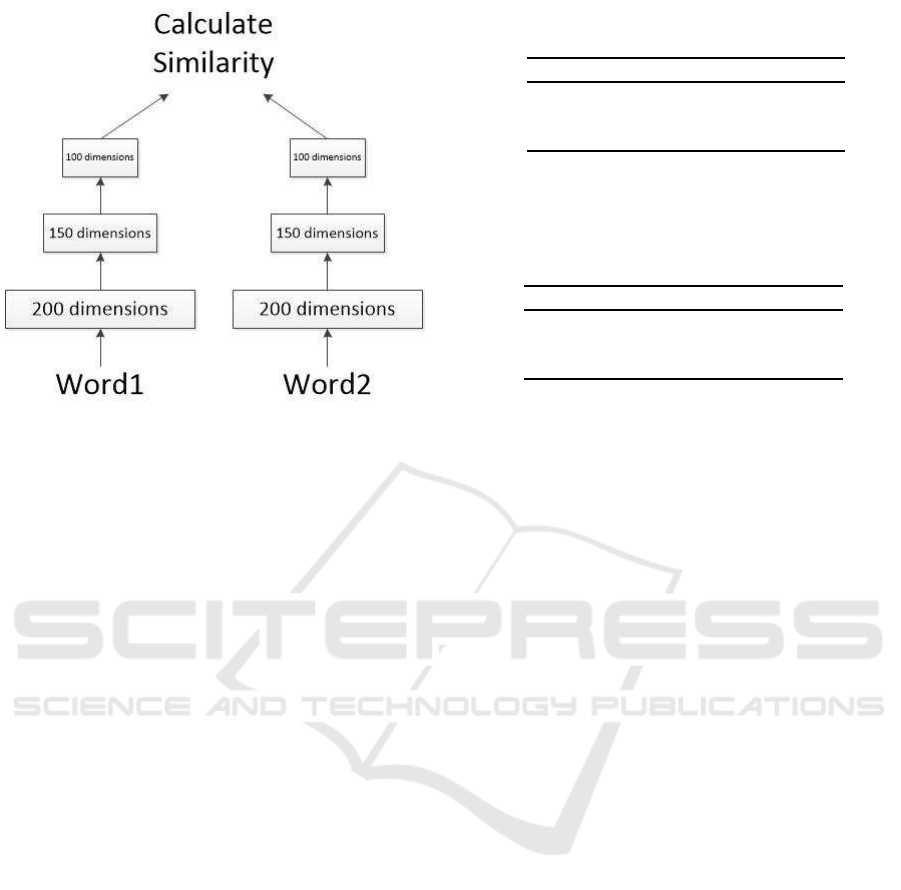
Figure 3: The structure of the fine-tuning model. Each time
the input is the current word we come across in the dataset
and we find a synonym of the word, we calculate the cosine
similarity between them. We also choose a certain number
of negative words which are not related to the current word.
4 EXPERIMENTS
We evaluate the learned representations of stacked au-
toencod ers and the fine-tuning model, comparing to a
variety of dimensions from word2vec without hand -
ling to show the performan ce of our system. For the
experiment we use English Wikipedia dump collected
in June of 2016. As processing, the corpus was lower-
cased and a ll punctuatio ns are eliminated, phrases are
separated so that words in them are treated indepen-
dently. We set word2vec to apply CBOW instead o f
Skip-gram because there’s little difference, negative
sampling instead of hierarchy softmax. For parame-
ters in the model, the size of dimension is 200 and
the minimum count is 5 0. As a result we get 473926
words in total. Initially we reduced 200-dimension
vectors learne d by word2vec to 150 dimension. We
use Adam algorithm which proposed by (Kin gma and
Ba(2014)) to minimize the loss function because of
its computational efficiency. For the first a utoenco-
der, the input is the original word representations from
word2vec. After training to reach convergence, the
first autoencoder produces dime nsionality reduced re-
presentations and is used for the next autoencoder. By
stacking the ne ural networks, we obtain embeddings
of different dim ensions. In this way we fed the en-
semble of real value vecto rs which are of 150 dimen-
sion all the way to the secondary autoencoder to get
100 dimension results. We preserved weights and bias
terms o f each level for the initialization of the fine tu-
Table 1: The empirical results for stacked autoencoders and
the input is vectors of 200 dimension.
Dimensionality 150-ae 100-ae
200 73.54% 83.77%
150 49.00% 75.07%
100 27.50% 58.17%
Table 2: Results of the stacked autoencoders with 300 di-
mension vectors as input. In this experiment we compressed
the vectors more times comparing to the previous one. The
comparison between Table 1 shows that the deeper neural
networks perform better.
Dimensionality 150-ae 100-ae
200 85.31% 88.11%
150 75.06% 83.87%
100 55.76% 73.46%
ning model. We did not implement Mini-Batch Gra-
dient De scent considering about the unique property
of each word. The whole train ing pro cess usually
takes more than 10000 iterations and 12 hours on a
single CPU. Meanwhile we dealt with 300-dimension
embedd ings for c omparison sin c e we found that the
obtained results hold interesting tre nds and we want
to see if the same case will happen for the same size
of dimensio nality, and to find out whether the depth
influences the performance. Acco rdingly, vector s di-
mensionality of 200, 150 and 100 from word2vec are
for comparison to our system’s output latent repre -
sentations. As for fine-tunin g pa rt, after filtering the
instances in the dataset that do not o ccur in the corpus
or are phrases, the total words for trainin g the fine-
tuning model is 55823 with 77538 different senses.
Because we don’t have test datasets for the work and
in case of overfitting, we use 10-fold cross-validation
to evaluate th e average results about proportions be -
tween the numbe r of synonym word pairs of which
cosine similarities have been improved and the total
number of pairs in the set.
4.1 Experiment 1
We first evaluate the results of the pr e-train model.
The idea to use autoencoders is that we can get bet-
ter vector rep resentations which own less noise, more
robust fea tures and it can make related words closer.
The input is vectors of 200 dimen sio n from word2vec,
and reduced the dimensionality to 150 by the first le-
vel autoencoder. Then we use learne d re presentations
as input for the second level to get dimension ality of
100. The evaluation is to calculate the average per-
formances for test sets. We want to see how many
synonym word pairs in the set whose cosine similari-
ties have been improved. In this way we will calculate
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
402

the proportion of improved word pairs and present the
percentage in the following tables. To ensure the con-
vergence, the iteratin g stops when we obtain the loss
value as small as possible and it remains invariant for
a period of time.
Table 1 shows some interesting findings. The row
in Table 1 represents word embeddings of 200, 150
and 100 from word2vec respectively. The column
stands for 150 and 100 dimension hidden represen-
tations after we used stacked au toencoders. We set
the baseline as original cosine similarities, and calcu-
late after we reduced the dimension, h ow many syno-
nym word pairs’ similarities have been improved. For
150 dimension vectors obtained from the autoe nco-
der, 73.54% of synonym word pairs have b e en impro-
ved considering their cosine similarities, comparing
to the raw input of 20 0 dimension. This de monstra-
tes that after encoding, synonyms becom e closer in an
unsuper vised way. But for 150 dimension original re-
presentations, only 49% of word pairs have been im-
proved which can be regarded as competitive results,
and 27.50% for 100 d imension. The decreasing trend
by virtue of the mechanism in word2vec, the smal-
ler the dimensionality is, the higher cosine similarity
results we get, however the represen ta tions still hold
the d eficiencies of the model. Then the secondary en-
coded vectors of 100 dimension give better results,
83.97% of word pairs have been improved, outp erfor-
ming the previous on e. Even we r educe the d imension
twice, the encoded representations still hold the de-
creasing trend. As for 200 and 150 dimensions, h id-
den representations significantly promote the quality
of similarity between synonym words without sp eci-
fic corpus in which the characteristics of sy nonyms
in specific c ontexts are well preserved. Comparing to
the same size, we still g et competitive results, nonet-
heless, the 100 dimension latent re presentations p er-
form better than 150 in the same case. To consolidate
our idea and to exploit more of the strength of stac-
ked autoencoders, w e reduced 300 dimension to 150
dimension a s well as 100 dimension by a 50 dimen-
sion drop for each reduction. This time w e encoded
the vectors 3 times and 4 times to ge t latent repre-
sentations. In Table 2, the 150 and 100 dimension
in column come from one different stacked a utoenco-
ders model and possess more reduc tion times compa-
ring to hidden representation s in the Table 1 column.
After raising the reduction times, we can see the re-
sults become even better, and the reduction amo unt
between adjacent layers is decreasing. The cosine si-
milarities of the 150 and 100 dimension representati-
ons are greatly improved, an d as for the same size of
word2vec vectors, the results are beyond competitive.
We can conclude that “the deeper, the better”, deeper
Table 3: Overall performances of fine-tuning model. The
representations from two hidden layers are evaluated for
computing the proportion between improved i nstances and
the total number.
Dimensionality 150-bp 100-bp
200 94.37% 80.76%
150 92.36% 79.65%
100 88.91% 78.60%
layer representations are m ore compact. In this way,
we denoise so that related words get closer a nd the
similarities of sy nonym words become higher, whic h
seems more reasona ble to human perception.
This pre-training method is an au tomatic learning
process for the input, and the model develops bet-
ter representations for synonym word pairs. We can
argue th at the stacked autoencoders is powerful to
address the problem of ambiguity between synonym
words and scattering vectors by reducing the dimen-
sion. This novel approach on dealing with word2vec
vectors demonstrates that these vectors can still be le-
arned by deep neu ral networks. It ca n be utilized to
extract meaningful features in embeddings so that we
can explore the properties held in them.
4.2 Experiment 2
In order to fine-tune the pa rameters, we propose a
deep synonym relatedness m odel to learn late nt re-
presentations after pre-training. Following the ar-
chitecture shown in Figure 3, we use 10-fold cross-
validation and evaluate the average pe rformances for
learned representations from two hidden layer. The
whole training process takes rougly 7 hours on a sin-
gle machine. In Table 3, 150-bp an d 100-bp repre-
sent learned hidden re presentations after using back-
propagation m e thod from fine-tuning model. The row
in the table means the same as previous tables. In
Table 3 we can see that, in 94.37% of the instances,
the similarities of words have been improved, in com-
parison to dimensionalities of 200 and 150, and the
results are also significantly better than deep stacked
autoencoders. As for 100 dimension in fine-tuning
model, it is only competitive to the same dimension
from p re-train model. From the table we can see
that after fine-tuning, the representations still hold the
decreasing trend when comparing with the original
vectors, the same behaviour with pre-training results.
But the model improves the pe rformance of latent re-
presentations on the same dimension and the smal-
ler dimension. Considering about th e 27.50% and
49.00% improvement in Table 1, we acq uire 88.91%
and 92.36% which are notable results. We can argue
that even if we don’t use autoencoders to encode and
Adjusting Word Embeddings by Deep Neural Networks
403
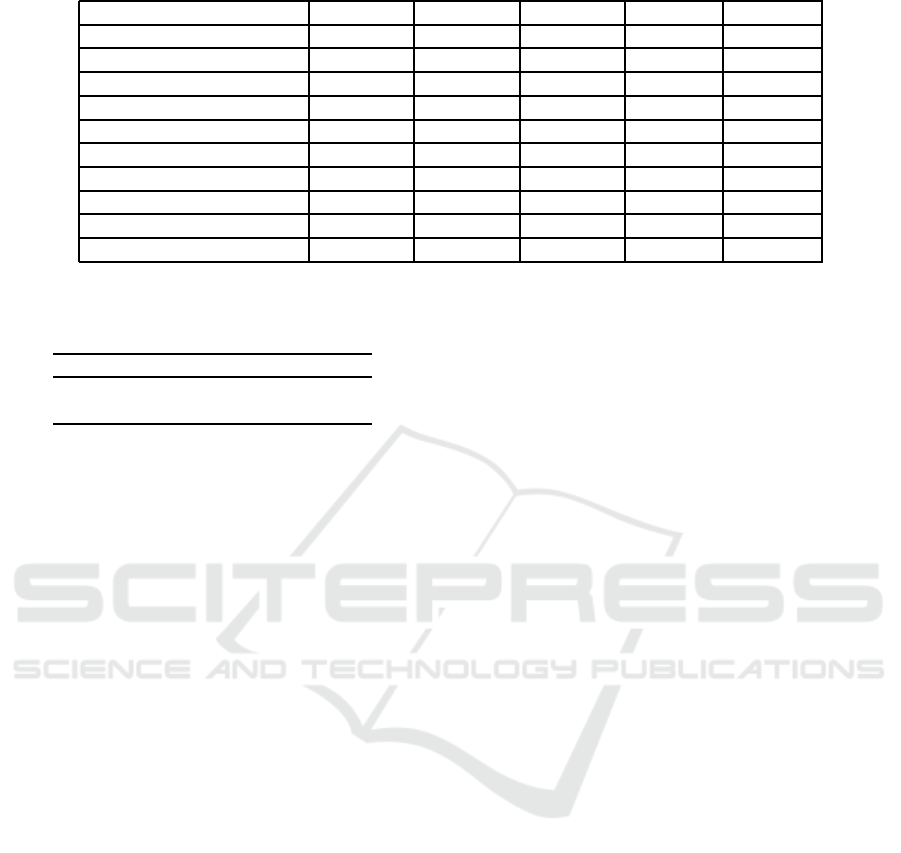
Table 4: Examples of synonym words and the comparison between different dimensions of vectors.
Synonyms 200 150 100 150-bp 100-bp
regularize & regularise 0.661886 0.710118 0.702691 0.801452 0.999723
changeless & unalterable 0.500718 0.578448 0.640918 0.694430 0.918739
respectful & reverential 0.654054 0.683833 0.719712 0.742635 0.884301
repair & fix 0.452142 0.467059 0.474660 0.628190 0.997788
fortun a te ly & fortuitously 0.3 95465 0.432642 0.428508 0.442118 0.963096
promoter & booster 0.043374 0.028916 -0.038873 0.240978 0.216803
curb & kerb 0.317527 0.346058 0.325593 0.618310 0.684300
dusk & nigh tfall 0.694591 0.723055 0.746611 0.804976 0.936354
awake & arouse 0.127879 0.134865 0.146026 0.397994 0.772240
run & consort -0.189202 -0.221867 -0.267452 0.183840 0.269530
Table 5: Comparison between representations of two layer
stacked autoencoders and fine-tuning model.
Dimensionality 150-bp 100-bp
150-ae 91.94% 79.45%
100-ae 86.95% 77.55%
compress th e vectors, by using the fin e-tuning mo-
del an d the novel loss function, we can still promote
the similarities between synonym words an d d ecrease
the similarities between non-synonym pairs. We u se
the similarities from word2vec as baselines and ma-
nually inspect similarities after fine-tuning(Tab le 4).
Run and consort can mean the same when referring
to hanging out with someone. Th e cosine similarity
of two words are negative which makes no sense. Af-
ter fine-tu ning, the similarity is improved to more than
0.183840. Arouse and awake are interch angeable but
they get poor 0.1278 79 cosine similarity r e sults, ho-
wever for 100 dimension represen ta tions it can get
0.772240 instead . Regularize and regularise are the
same, the similarity is around 0.710118 because of th e
scattering and sparsity problem in word2vec, the fine-
tuning result for 100 d imension is notably 0.999732,
nearly 1 . Repair and fix have only poor 0.474660 si-
milarity, and the model impr ove it to 0.997788. These
examples demonstrate tha t 100 dimensio n vectors af-
ter fine-tuning gain the largest improvement, better
than 150 dimension. I t seems reasonable because of
the grad ie nt vanishing. But we still found that for just
a few instances, 100 dimension results are even lower
than original vector s. This may because we should
add some regularize rs or smooth parameters.
The supervised learning me thod verifies the idea
that deep neural networks can be applied on word2vec
vectors for spec ific tasks by artificially adjusting. Be-
cause the model is for fine-tuning, so we will com-
pare the results between autoen coders’ vectors and
fine-tuned vectors. We can see from Table 5 that by
using the architec ture without reducing dimensiona-
lity, the similarities between sy nonym words get furt-
her improvement. 150-bp and 100-bp stand for the
hidden representations from the fine-tuning model,
while 150-ae and 100-ae still represent the reduced
vectors fro m hidden layers of stacked autoencoders.
As for 15 0 dimension latent representations in stac-
ked autoencoders, around 91.94% of synonym word
pairs’ similarities have been increased, indicating that
the d e ep ne ural network is more effective because of
supervised learning. But it is still uncertain why the
performance of 100 dimension after back-propagation
method is worse than 150 dimension. Maybe we can
assume that the space of 100 dimension representati-
ons to be impr oved is not as much as 150 dimension,
this also demonstrates that deeper u nsupervised mo-
dels have already denoise more and decrease the spar-
sity. Even witho ut the initialization from pre-trainin g
process, if we inco rporate more training data, the mo-
del can reform word embedding s with better quality.
It is possible to utilize the n eural network with ap-
propriate data an d more types of knowledge to learn
representations that are suitable for certain tasks.
5 CONCLUSIONS AND FUTURE
WORK
We have introduced a combined sy stem with two
kinds of neura l networks to handle the word embed-
dings of word2vec. From the results we can say, stac-
ked autoencoders are strong en ough to encode and
compact the vectors in the space. Due to different
conditions for the used corpora and its restriction,
word2vec will not produce word embeddings with
good quality. Some sy nonyms are rarely seen in the
text, so the similarities could be even negative values
in word2vec. And some synonyms have not only a
few same mea nings but also other different senses.
In this case, words are spread far apart in the space
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
404

with extremely low cosine similarities. By using au -
toencod ers in an unsupervised approach, we get more
compact representations with less noise which auto-
matically disambiguate the similarities between syn-
onyms. T he fine-tuning model also indicates th e po-
tential of representation s to be learned by deep neu-
ral networks with carefully designed loss functions
and knowledge graphs or lexical datasets. In this pa-
per, we set the loss function in a softmax form with
a dataset of WordNet synsets to calculate the poste-
rior probability, this method improves cosine simila-
rities between syno nym words and decreases similari-
ties of non-syn onym ones. Un like the idea in stacked
autoencoders, by encoding word embeddings in a su-
pervised way, the model only extracts useful sem antic
features for synonyms, and makes them closer.
Both of the models achieved significantly better
performance than word2 vec on measuring synonym
relatedness, shed light on exploiting word embed-
dings in a supervised or unsupervised way. But these
two models come up from different ideas and there is
still something confuses u s, th e deeper stack autoen-
coders we use, the loss wh e n converging will be big-
ger for each autoen c oder in the network, we will keep
studying o n this phenomenon in the future to probe
the features of autoencoders and word representati-
ons. For unsupervised learnin g, we plan to compre-
hensively evaluate the energy of autoencoders. We
will explore the changes in linguistic regularities of
latent repre sentations, and discover the patterns of se-
mantic and syntactic properties in embedding s. Au-
toencod er may be a good toolkit to clarify the mea-
ning of opaque vectors. Our future work will also fo-
cus on disambig uating entities types by setting a clas-
sifier on the top layer of the network.
ACKNOWLEDGMENT
This work was partially supp orted by NEDO (New
Energy and Industrial Te chnology Development Or-
ganization ).
REFERENCES
Yoshua Bengio, R´ejean Ducharme, Pascal Vincent, and
Christian Jauvin. A neural probabilistic language mo-
del. Journal of machine learning research, 3(Feb):
1137–1155, 2003.
David M Blei, Andrew Y Ng, and Michael I Jordan. La-
tent dirichlet allocation. Journal of machine Learning
research, 3(Jan):993–1022, 2003.
Danushka Bollegala, Alsuhaibani Mohammed, Takanori
Maehara, and Ken-ichi Kawarabayashi. Joint word
representation learning using a corpus and a semantic
lexicon. arXiv preprint arXiv:1511.06438, 2015.
John A Bullinaria and Joseph P Levy. E xtracti ng semantic
representations from word co-occurrence statistics: A
computational study. Behavior research methods, 39
(3):510–526, 2007.
Danqi Chen and Christopher D Manning. A fast and accu-
rate dependency parser using neural networks. In P ro-
ceedings of the 2014 Conference on Empirical Met-
hods i n Natural Language Processing (EMNLP), pa-
ges 740–750, 2014.
Ronan Collobert and Jason Weston. A unified architec-
ture for natural language processing: Deep neural net-
works with multit ask learning. In Proceedings of the
25th International Conference on Machine learning,
pages 160–167. ACM, 2008.
Ronan Collobert, Jason Weston, L´eon Bottou, Michael Kar-
len, Koray Kavukcuoglu, and Pavel Kuksa. Natural
language processing (almost) from scratch. Journal
of Machine Learning Research, 12(Aug):2493–2537,
2011.
George E Dahl, Dong Yu, Li Deng, and Alex Acero.
Context-dependent pre-trained deep neural networks
for large-vocabulary speech recognition. IEEE Tran-
sactions on Audio, Speech, and Language Processing,
20(1):30–42, 2012.
Geoffrey E Hinton and Ruslan R Salakhutdinov. Redu-
cing the dimensionality of data wit h neural networks.
Science, 313(5786):504–507, 2006.
Hongzhao Huang, Larry Heck, and Heng Ji. Leveraging
deep neural networks and knowledge graphs for entity
disambiguation. arXiv preprint arXiv:1504.07678,
2015.
Hanna Kamyshanska and Roland Memisevic. The potential
energy of an autoencoder. IEEE transactions on pat-
tern analysis and machine intelligence, 37(6):1261–
1273, 2015.
Diederik Kingma and Jimmy Ba. Adam: A method for sto-
chastic optimization. arXiv preprint arXiv:1412.6980,
2014.
Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton.
Imagenet classification with deep convolutional neu-
ral networks. In Advances in neural information pro-
cessing systems, pages 1097–1105, 2012.
Ra´ul Ernesto Men´endez-Mora and Ryutaro Ichise. Toward
simulating the human way of comparing concepts.
IEICE TRANSACTIONS on Information and Systems,
94(7):1419–1429, 2011.
Tomas Mikolov and J Dean. Distributed representations of
words and phrases and their compositionality. 2013b.
Tomas Mikolov, Stefan Kombrink, Luk´aˇs Burget, Jan
ˇ
Cernock`y, and Sanjeev Khudanpur. Extensions of re-
current neural network language model. In 2011 IEEE
International Conference on Acoustics, Speech and
Signal Processing (ICASSP), pages 5528–5531. IEEE ,
2011.
Tomas Mikolov, Kai Chen, Greg Corrado, and Jeffrey Dean.
Efficient estimation of word representations in vector
space. arXiv preprint arXiv:1301.3781, 2013a.
George A Miller. Wordnet: a lexical database for english.
Communications of the ACM, 38(11):39–41, 1995.
Adjusting Word Embeddings by Deep Neural Networks
405

Andriy Mnih and Geoffrey E Hinton. A scalable hierarchi-
cal distr ibuted language model. In Advances in neu-
ral information processing systems, pages 1081–1088,
2009.
David E R umelhart, Geoffrey E Hinton, and Ronald J Wil-
liams. Learning internal representations by error pro-
pagation. Technical report, DTIC Document, 1985.
Yelong Shen, Xiaodong He, Jianfeng Gao, Li Deng, and
Gr´egoire Mesnil. Learning semantic representations
using convolutional neural networks for web search.
In Proceedings of the 23rd International Conference
on World Wide Web, pages 373–374. ACM, 2014.
Richard Socher, John Bauer, Christopher D Manning, and
Andrew Y Ng. Parsing with compositional vector
grammars. In Proceedings of the Annual Meeting of
the Association for C omputational Linguistics, pages
455–465, 2013.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
406
