
Recognition of Handwritten Music Symbols using Meta-features
Obtained from Weak Classifiers based on Nearest Neighbor
Jorge Calvo-Zaragoza, Jose J. Valero-Mas and Juan R. Rico-Juan
Department of Software and Computing Systems, University of Alicante,
Carretera San Vicente del Raspeig s/n, Alicante, Spain
{jcalvo, jjvalero, juanra}@dlsi.ua.es
Keywords:
Optical Music Recognition, Music Symbols, Handwriting Recognition, Symbol Classification, Meta-features
Space.
Abstract:
The classification of musical symbols is an important step for Optical Music Recognition systems. However,
little progress has been made so far in the recognition of handwritten notation. This paper considers a scheme
that combines ideas from ensemble classifiers and dissimilarity space to improve the classification of hand-
written musical symbols. Several sets of features are extracted from the input. Instead of combining them,
each set of features is used to train a weak classifier that gives a confidence for each possible category of the
task based on distance-based probability estimation. These confidences are not combined directly but used
to build a new set of features called Confidence Matrix, which eventually feeds a final classifier. Our work
demonstrates that using this set of features as input to the classifiers significantly improves the classification
results of handwritten music symbols with respect to other features directly retrieved from the image.
1 INTRODUCTION
Composing music with pen and paper is still a com-
mon procedure for most musicians. Nevertheless,
digital versions of music scores offer a great deal of
advantages with respect to the physical ones. For
instance, issues related to the storage, distribution,
preservation, and reproduction of the information are
straightforwardly solved in the digital domain. Also,
having such music information encoded in a struc-
tured format opens the possibility of applying com-
putational music tools for tasks such as content-based
music searches, musicological analysis or organiza-
tion in digital libraries, among others.
In order to take advantage of the aforementioned
processes, handwritten scores need to be transcribed
onto a digital version. Most commonly, this is done
by hand using some kind of software for music score
edition. Unfortunately, the process can be very te-
dious since the complexity of music notation in-
evitably leads to burdensome and uncomfortable in-
terfaces based on drag and drop actions with the
mouse.
An effortless alternative for the user to obtain the
digital version of a handwritten music composition is
to resort to an Optical Music Recognition (OMR) sys-
tem (Bainbridge and Bell, 2001). These systems im-
port a scanned version of the music sheet and try to
automatically export the information to some type of
machine-readable format such as MusicXML, MIDI
or MEI (see Fig. 1).
(a) Example of input score for an OMR system
(b) Symbolic representation of the input score
Figure 1: The task of Optical Music Recognition (OMR) is
to analyze an image containing a music score to export its
musical content into some machine-readable format.
Given the particularities of music notation, an
OMR system usually follows a segmentation-based
approach: isolated symbols are initially detected and,
then, classified. The process starts with a preprocess-
ing stage, which focuses on providing robustness to
the system by means of binarization and deskewing.
Then, a process for the detection and removal of staff
lines takes place. Although these lines are necessary
96
Calvo-Zaragoza, J., Valero-Mas, J. and Rico-Juan, J.
Recognition of Handwritten Music Symbols using Meta-features Obtained from Weak Classifiers based on Nearest Neighbor.
DOI: 10.5220/0006120200960104
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 96-104
ISBN: 978-989-758-222-6
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

for human readability, they complicate the segmenta-
tion of musical symbols. Given that, the more accu-
rate this process, the better the detection of musical
symbols, much research effort has been devoted to
this process, which can be considered nowadays as a
research topic by itself (Dalitz et al., 2008). After this
stage, symbol detection is performed by searching the
remaining meaningful objects of the score. Finally,
once single pieces of the score have been isolated, a
hypothesis about the type of each one is emitted in
the classification stage. A comprehensive experimen-
tation was carried out by Rebelo et al. (Rebelo et al.,
2010), which presented a comparative study on diffe-
rent algorithms for the classification of musical sym-
bols.
Unfortunately, the classification of music symbols
is still far from achieving accurate results, especially
for handwritten scores (Rebelo et al., 2012). The
great variability in the manner of writing the musical
symbols is the main difficulty to overcome, similarly
to the field of handwritten text recognition (Romero
et al., 2012). Thus, there is still a need for developing
algorithms that can provide a more accurate classifi-
cation of handwritten music symbols.
This work presents the classification of iso-
lated handwritten music symbols by means of meta-
features extracted from the decisions of weak classi-
fiers, each of which focuses on different features of
the input. This strategy has been proven to be very ac-
curate in the context of shape recognition (Rico-Juan
and Calvo-Zaragoza, 2015), yet its performance in the
context of handwritten music notation remains unex-
plored.
The remaining of the paper is organized as
follows: the classification approach is described in
depth in Section 2. The set of experiments carried
out over a comprehensive dataset of isolated music
symbols is presented in Section 3. Finally, Section 4
concludes the work and proposes future work to be
explored.
2 CLASSIFICATION WITH
META-FEATURES BASED ON
WEAK CLASSIFIERS
Classification systems have been widely studied in
pattern recognition tasks. Typically, these schemes
work on a sequential fashion: first of all, a set of
features is extracted from the sample at issue; then,
these features are fed into a classification scheme,
which has been trained previously with a set of exam-
ples, to obtain a hypothesis about its class (Duda and
Hart, 1973). Under this premise, a great variety of
techniques have been proposed in order to improve
classification accuracy, being Artificial Neural Net-
works (Jain et al., 1996) and Support Vector Machines
(Burges, 1998) some representative examples of re-
markably successful methods.
The evolution in this field has led to the develop-
ment of new schemes. Among the large amount of
techniques proposed, ensemble methods constitute a
particular methodology with considerable relevance
in this work. The idea behind these schemes is that it
is more robust to combine a set of simple hypotheses
obtained with a set of basic classifiers than to use just
one complex hypothesis computed by a more com-
plex scheme (Kittler et al., 1998).
This paper bases on the idea of ensemble classi-
fiers and expands it by considering a more sophisti-
cated approach for the particular case of the classi-
fication of isolated music symbols: first, a set of
weak classifiers is considered, each of which provides
the probability of belonging to each of the possible
classes for a given sample to classify; then, all these
probabilities are combined to form a meta-feature set
that is used as input to a final classifier. An overview
of the process is illustrated in Fig. 2.
In formal terms, let Ω be the set of possible class
labels and D the set of weak classifiers considered. A
matrix M of dimensions |D|×|Ω| is computed, which
contains the confidence (represented as probabilities)
that each of the |D| weak classifiers gives to the sam-
ple at issue of belonging to each of the |Ω| classes.
That is, M
i j
represents the probability of sample be-
longing to the class Ω
i
based on the weak classifier
D
j
. The matrix can thus be viewed as a new feature
representation (meta-features) that can be used to feed
the final classifier rather than using the original fea-
tures. This idea is based on the Decision Templates
proposed by (Kuncheva, 2001). The difference in our
case is that the probabilities are computed from just
one classifier, instead of using many of them.
The construction of this matrix therefore requires
different groups of features to be extracted from the
original image. Each weak classifier is trained for a
particular set of features, thus producing confidence
values that work on the different points of view of
the input data. Note that all weak classifiers retrieve
a vector of size |Ω| (probability of the sample of be-
longing to each of the possible classes) independently
of the dimensionality of the input for each of them,
thus allowing to group the results in a single matrix.
However, as the different weak classifiers are totally
independent, each one may use different methods or
measures to estimate the probability.
The use of such Confidence Matrix (CM) repre-
Recognition of Handwritten Music Symbols using Meta-features Obtained from Weak Classifiers based on Nearest Neighbor
97
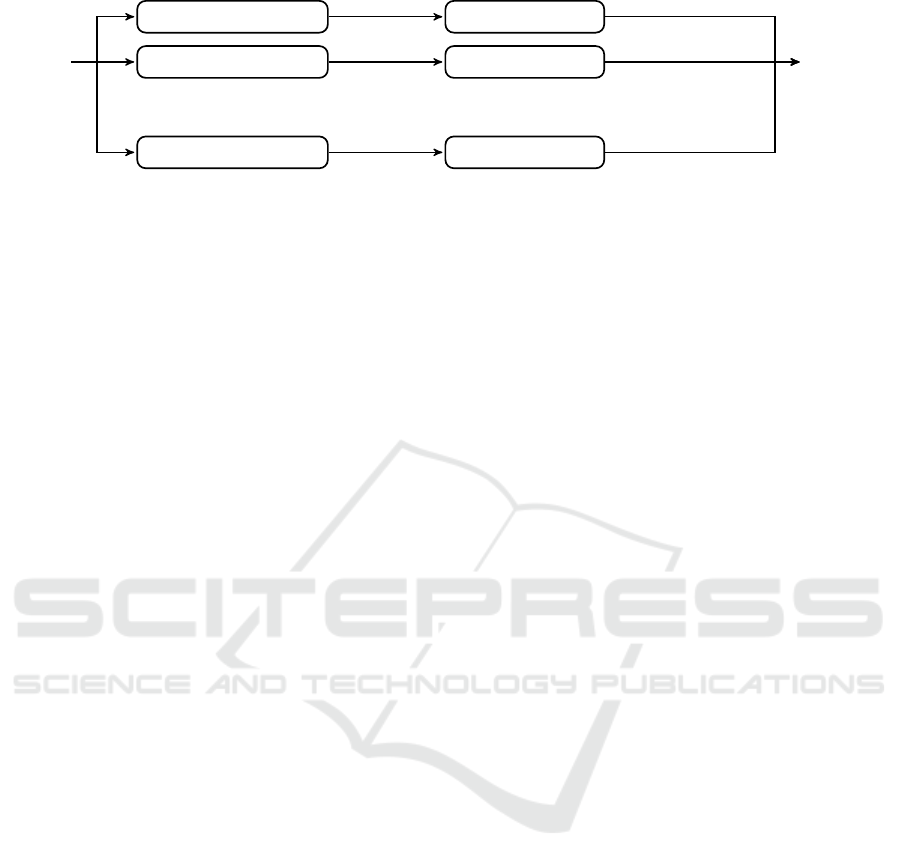
Sample
Feature Extraction 1
Feature Extraction 2
...
Feature Extraction |D|
Weak classifier 1
Weak classifier 2
...
Weak classifier |D|
Confidence
Matrix
(|D| × |Ω|)
Features 1
Features 2
Features |D|
Confidence values 1
Confidence values 2
Confidence values |D|
Figure 2: Graphical scheme of the construction of a Confidence Matrix representation.
sentation entails a set of intrinsic advantages. A first
one is that, unlike classical approaches in which the
final classifier has the responsibility of discovering
the different points of view of the signal, the final
classifier in this matrix representation is already pro-
vided with this segmentation by weak classifiers. Fur-
thermore, in contrast to ensemble classifiers, this new
scheme avoids the need for defining distinct dissimi-
larity measures or types of weak classifiers as features
may be grouped according to their nature, which is of-
ten relatively simple for a user with domain expertise.
From an algorithmic point of view, some addi-
tional advantages are its straightforward implemen-
tation and that the pipeline of the algorithm can be
easily parallelized so that each weak classifier runs at
the same time. Additionally, there may be some sce-
narios in which the CM is not only helpful but also
necessary. For example, when several input features
from the same sample come from different, incompat-
ible structures (eg. trees, strings or feature vectors).
In these cases, scores from weak classifiers trained
separately with each kind of structure can be easily
combined within the matrix representation.
Note, however, that this new scheme does not pro-
duce a final decision. It merely maps the input fea-
tures into another space (meta-features). This signi-
fies that it is necessary to use an algorithm that em-
ploys the matrix to make a decision using it as a set of
features.
We shall now introduce the different elements
comprising the proposed scheme: the initial features
directly retrieved from the image, the features ob-
tained considering the set of weak classifiers, and the
schemes considered for the final classification stage.
2.1 Groups of Features from Isolated
Music Symbols
Given an input image depicting an isolated music
symbol that has undergone a binarization process, a
preprocessing stage is performed first. A morpholog-
ical closing filter (Serra, 1982) is applied in order to
correct any gaps and spurious points that may have
appeared in the binarization process. In the next step,
.......................................................
.......................................................
................................*.*******..............
...............................************............
.............................***************...........
..........................*******************..........
....................*************************..........
...................****************.....******.........
...................*************.........*****.........
..................*********..*...........*****.........
................**********...............*****.........
..............***********................*****.........
.............**********..................*****.........
.............**********..................*****.........
.............*********..................******.........
.............*********..................*****..........
..............********.................*****...........
..............*******.................******...........
................*****.................******...........
................*****................******............
................*****...............******.............
................****...............******..............
...............*****.............*******...............
...............*****...........*******.................
..............******.........********..................
..............******........********...................
..............******......*********....................
..............******.....********......................
..............******..**********.......................
..............*****************........................
.............*****************.........................
............*****************..........................
...........*****************...........................
...........*************...............................
...........***********.................................
............*******....................................
............*****......................................
...........******......................................
...........******......................................
...........******......................................
...........******......................................
...........******......................................
...........******......................................
...........******......................................
..........******.......................................
..........******.......................................
..........******.......................................
..........******.......................................
..........*****........................................
.........******........................................
.........*****.........................................
.........*****.........................................
..........****.........................................
...........***.........................................
.......................................................
Figure 3: Example of binary input representing an isolated
handwritten Half Note (
˘
“
).
the character is located in the image and the region of
interest (ROI) is selected.
Once the image has been preprocessed, the fea-
ture extraction takes place. The image is divided into
a sub-structure of smaller regions in order to extract
local features. The number of sub-regions must be
fixed empirically.
For the sake of clarity in the explanation, let us
consider the input image shown in Fig. 3 as example,
which depicts an isolated Half Note. Three groups of
features are considered for this work:
• Foreground area: a vector with the foreground
area in terms of pixels for each sub-region of the
image is produced (see Fig. 4). Note that, if one
pixel belongs to more than one region it is counted
proportionally within each one.
• Background area: this feature extraction, which is
based on that of (Vellasques et al., 2006), com-
putes four projections (up, down, left, and right)
for each pixel in the image; a counter is set to
zero for each pixel in the image and, when any of
these projections touches the foreground object,
the counter associated to that pixel increases in
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
98

.........1111111111111111111111111111111111111.........
.........1111111111111111111111111111111111111.........
11111111122222222222222222222222*3*******22222111111111
1111111112222222222222222222222************222111111111
11111111122222222222222222222***************22111111111
11111111122222222222222222*******************2111111111
11111111122222222222*************************2111111111
1111111112222222222****************55555******111111111
1111111112222222222*************555555555*****111111111
111111111222222222*********55*55555555555*****111111111
1111111112222222**********555555555555555*****111111111
11111111122222***********5555555555555555*****111111111
1111111112222***********55555555555555555*****111111111
1111111112222**********555555555555555555*****111111111
1111111112222*********555555555555555555******111111111
1111111112222*********555555555555555555*****2111111111
11111111122223********55555555555555555*****22111111111
11111111122223*******55555555555555555******22111111111
111111111222233******55555555555555555******22111111111
1111111112222333*****5555555555555555******222111111111
1111111112222333*****555555555555555******2222111111111
1111111112222333****555555555555555******22222111111111
111111111222233*****5555555555555*******222222111111111
111111111222233*****55555555555*******22222222111111111
11111111122223******555555555********222222222111111111
11111111122223******55555555********2222222222111111111
11111111122223******555555*********22222222222111111111
11111111122223******55555********2222222222222111111111
11111111122223*******5**********22222222222222111111111
11111111122223*****************222222222222222111111111
1111111112222*****************2222222222222222111111111
111111111222*****************22222222222222222111111111
11111111122*****************222222222222222222111111111
11111111122*************2222222222222222222222111111111
11111111122***********222222222222222222222222111111111
111111111223*******222222222222222222222222222111111111
111111111223******2222222222222222222222222222111111111
11111111122******22222222222222222222222222222111111111
11111111122******22222222222222222222222222222111111111
11111111122******22222222222222222222222222222111111111
11111111122******22222222222222222222222222222111111111
11111111122******22222222222222222222222222222111111111
11111111122******22222222222222222222222222222111111111
11111111122******22222222222222222222222222222111111111
1111111112******222222222222222222222222222222111111111
1111111112******222222222222222222222222222222111111111
1111111112******222222222222222222222222222222111111111
1111111112******222222222222222222222222222222111111111
1111111112*****2222222222222222222222222222222111111111
111111111******2222222222222222222222222222222111111111
111111111*****22222222222222222222222222222222111111111
111111111*****22222222222222222222222222222222111111111
1111111112****22222222222222222222222222222222111111111
11111111122***22222222222222222222222222222222111111111
.........1111111111111111111111111111111111111.........
1:
266.5 257.0
266.5 257.0
2:
186.5 274.5
91.0 475.0
3:
20.5 4.5
5.0 0.0
4:
0.0 0.0
0.0 0.0
5:
101.0 174.5
3.5 0.0
Figure 4: Background features extracted from input consid-
ering 4 sub-regions.
.......................................................
.......................................................
................................1.1111111..............
...............................111111111111............
.............................111111111111111...........
..........................1111111111111111111..........
....................1111111111111111111111111..........
...................1111111111111111.....111111.........
...................1111111111111.........11111.........
..................111111111..1...........11111.........
................1111111111...............11111.........
..............11111111111................11111.........
.............11111111111.................11111.........
.............1111111111..................11111.........
.............111111111..................111111.........
.............111111111..................11111..........
..............11111111.................11111...........
..............1111111.................111111...........
...............111111.................111111...........
................11111................111111............
................11111...............111111.............
................1111...............111111..............
...............11111.............1111111...............
...............11111...........1111111.................
..............111111.........11111111..................
..............111111........11111111...................
..............111111......111111111....................
..............111111.....11111111......................
..............1111111.1111111111.......................
..............11111111111111111........................
.............11111111111111111.........................
............11111111111111111..........................
...........11111111111111111...........................
...........1111111111111...............................
...........11111111111.................................
............1111111....................................
............111111.....................................
...........111111......................................
...........111111......................................
...........111111......................................
...........111111......................................
...........111111......................................
...........111111......................................
...........111111......................................
..........111111.......................................
..........111111.......................................
..........111111.......................................
..........111111.......................................
..........11111........................................
.........111111........................................
.........11111.........................................
.........11111.........................................
..........1111.........................................
...........111.........................................
.......................................................
163.75 207.75
205.50 15.00
Figure 5: Foreground features extracted from input consid-
ering 4 sub-regions.
one unit. This process allows to distinguish four
different categories of background pixels, accor-
ding to their projection values (1, 2, 3, 4). Zero-
valued counters are discarded. An additional cate-
gory with value 5 is added to provide disambigua-
tion information: this value substitutes the value
of 4 if the pixel lies in an isolated background
area. Eventually, the feature vector derived for
each sub-region contains five descriptors which
depict the proportion of pixel area covered by
each of the projection categories considered. An
example can be seen in Fig. 5.
• Contour area: the contour of the object is encoded
by the links between each pair of 8-neighbor
pixels using 4-chain codes in the manner proposed
by (Oda et al., 2006). These codes are used to ex-
tract four vectors (one for each direction), and the
proportion of pixel area covered by the number of
each code is counted for the different sub-regions
considered. Figure 6 shows an example of this
feature extraction process.
1:
22.5 18.0
35.5 0.0
2:
18.5 25.5
14.0 6.0
3:
12.5 23.0
10.0 0.5
4:
1.0 6.0
1.0 0.0
.......................................................
...............................3333333334..............
..............................2..........34............
............................32.............4...........
.........................332................4..........
...................333332....................1.........
..................2..........................1.........
..................1................3334.......1........
.................2..............332....4......1........
...............32.............32........1.....1........
.............32...........3332..........1.....1........
............2............2..............1.....1........
............1...........2...............1.....1........
............1..........2...............2......1........
............1.........2................1......1........
............1.........1...............2......2.........
............1.........1..............2......2..........
.............1.......2...............1......1..........
.............1.......1..............2.......1..........
..............4......1.............2.......2...........
...............2.....1............2.......2............
..............2.....2...........32.......2.............
..............1.....1.........32........2..............
.............2......1.......32........32...............
.............1......1......2.........2.................
.............1......1....32.........2..................
.............1......1...2..........2...................
.............1.......332.........32....................
.............1..................2......................
............2..................2.......................
...........2..................2........................
..........2..................2.........................
..........1.................2..........................
..........1.............3332...........................
..........1...........32...............................
..........1........332.................................
..........1.......2....................................
..........1......2.....................................
..........1......1.....................................
..........1......1.....................................
..........1......1.....................................
..........1......1.....................................
..........1......1.....................................
.........2.......1.....................................
.........1......2......................................
.........1......1......................................
.........1......1......................................
.........1......1......................................
........2......2.......................................
........1......1.......................................
........1.....2........................................
........1.....1........................................
........1.....1........................................
.........4....1........................................
..........3332.........................................
Figure 6: Contour features extracted from input considering
4 sub-regions.
2.2 Meta-features based on Weak
Classifiers
As discussed previously, a set of weak classifiers with
which to map each group of features onto confidence
values is needed. In this regard, each weak classifier
has been obtained considering a formula based on the
Nearest Neighbor (NN) rule (Cover and Hart, 1967)
given its conceptual simplicity.
Each weak classifier is trained using a leaving-
one-out scheme: each single sample is isolated from
the training set T and the rest are used in combination
with the NN to produce the confidence values. The
formula detailed below is inspired by (P
´
erez-Cort
´
es
et al., 2000). If x is a training sample, then the confi-
dence value for each possible class w ∈ Ω to represent
instance x is based on the following equation:
p(w|x) =
1
min
x
0
∈T
w
,x6=x
0
d(x, x
0
) + ε
(1)
where T
w
is the training set for w label and ε is a
non-zero value provided to avoid infinity values. In
our experiments, the dissimilarity measure d(·, ·) is
the Euclidean distance. After calculating the proba-
bility for each class, the values are normalized such
that
∑
w∈Ω
p(w|x) = 1.
Once each training sample has been mapped onto
the probability matrix M, the samples can be used in
the test phase.
2.3 Final Classifiers
Once the meta-features have been calculated they are
fed into a conventional classifier to compute a class
hypothesis. Given that each of the |D| weak classifiers
is retrieving a vector of |Ω| features, two classification
paradigms may be considered for this last stage: on
the one hand, we may construct the M matrix by
Recognition of Handwritten Music Symbols using Meta-features Obtained from Weak Classifiers based on Nearest Neighbor
99

grouping all the features from the weak classifiers and
then use a single classification algorithm; on the other
hand, a meta-classifier which takes as separate inputs
the |D| feature vectors from the weak classifiers may
be also considered.
The underlying idea of meta-classification is to
solve a labeling problem by combining the decisions
of individual classifiers in order to combine them into
a unique final decision (late fusion). Thus, the main
reason for considering the aforementioned strategies
for the final classification stage is to discard the possi-
bility of observing an improvement in the results with
the proposed idea produced by the use of too simple
classifiers. In addition, note that our intention in this
work is to check whether the proposed representation
can improve the performance achieved with classical
feature vectors for the precise task of classifying iso-
lated music symbols and not necessarily trying to out-
perform the existing late fusion techniques.
In terms of actual algorithms, we considered
three different classifiers for each of the two men-
tioned categories: as of conventional classifiers we
considered Nearest Neighbor, Support Vector Ma-
chine, and Multi-Layer Perceptron; in terms of meta-
classifiers, we chose Maximum Average Class Prob-
ability, Stacking-C, and Rotation Forest. For all of
them, we have considered the Waikato Environment
for Knowledge Analysis (WEKA) library (Hall et al.,
2009), each one with their default parameterization.
We shall now briefly introduce these schemes.
2.3.1 Nearest Neighbor
The previously introduced Nearest Neighbor (NN)
rule can also be directly used for classification. Let
X = (x
1
, . . . ,x
n
) be a set of labeled samples and let
x
0
∈ X be the sample that minimizes a dissimilarity
measure d(x, x
0
) to a test point x. The NN rule (Aha
et al., 1991) assigns to x the label associated with x
0
.
2.3.2 Support Vector Machines
Support Vector Machine (SVM) is a supervised
learning algorithm developed by Vapnik (Vapnik,
1998). It seeks for a hyperplane which maximizes the
separation (margin) between the hyperplane and the
nearest samples of each class (support vectors). SVM
assumes a binary classification problem and thus
needs an extension to tackle multi-class problems. In
this work we shall use the one-vs-one scheme, which
creates an SVM classifier for each pair of classes.
Additionally, as SVM relies on the use of a Kernel
function to deal with non-linearly separable problems,
we shall consider a first-order polynomial kernel for
that purpose.
Finally, the training of the SVM considered in this
work is conducted by the Sequential Minimal Opti-
mization (SMO) algorithm (Platt, 1999).
2.3.3 Muti-Layer Percepton
Artificial Neural Networks is a family of structures
developed in an attempt to mimic the operation of
the nervous system to solve machine learning prob-
lems. The topology of a neural network can be quite
varied. For this work, the common neural network
called Multi-Layer Perceptron (MLP) is used.
2.3.4 Stacking-C
Given that our classification scheme is based on the
main idea of Stacking algorithms (i.e., training a
system to classify with the results of other inde-
pendent classifiers), we have included this algorithm
to prove the improvement that can be obtained by
means of the use of meta-features. We have selected
one of the most successful algorithms from this fa-
mily: Stacking-C (Seewald, 2002), an extension to
Stacking to accurately address multi-class problems.
2.3.5 Rotation Forest
Rotation Forest (RoF) (Rodriguez et al., 2006) is an
ensemble method that focuses on building accurate
and diverse classifiers. It trains a set of decision trees
(forest), each of which uses an independent feature
extraction. RoF makes use of a base classifier to
generate its decision trees. In our work, two alter-
natives will be considered: C4.5 (Quinlan, 1993) (J48
implementation (Hall et al., 2009)) and Random Fo-
rest (RaF) (Breiman, 2001). The first alternative is
proposed by the original article, whilst the latter is
considered due to its remarkably good performance
shown in our preliminary experiments.
2.3.6 Maximum Average Class Profile
In contrast to the previous meta-classifiers consi-
dered, a decision can be taken by combining the in-
dividual decisions of each weak classifier. In this re-
gard we have considered the Maximum Average Class
Probability (MACP) (Kuncheva, 2004), which labels
the input query with the class that maximizes the ave-
rage of the probabilities given by each of the weak
classifiers.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
100

3 EXPERIMENTS
3.1 Corpus
The HOMUS dataset (Calvo-Zaragoza and Oncina,
2014) of musical symbols will be used in this ex-
perimentation
1
. This set contains 15200 handwritten
musical symbols from 100 different musicians spread
over 32 of the most common music symbols. It is
important to stress that the corpus was collected en-
couraging the users to write the symbols as natural as
possible, thereby leading to a high variability in the
music notation found within the dataset, as depicted
in Table 1.
3.2 Evaluation
The evaluation of our method consists in comparing
the proposed strategy against conventional classifica-
tion methods. It is also interesting to know whether
results achieved by our proposal are caused by the
group of features selected or by the CM represen-
tation based on weak classifiers. Therefore, experi-
ments report the results with and without using the
meta-feature representation considered. In the for-
mer case, both the raw input image (pixel values after
rescaling the binarised image to 20 × 20, to compare
with previous works (Rebelo et al., 2010)) and the set
of features selected is considered.
Table 2 shows the average results in terms of error
rates obtained in the experimentation considering a 4-
fold cross-validation scheme. A first remark to point
out is that classification results when considering the
raw image exhibit high error rates since almost all
classifiers depict error figures around 25 % and 35 %.
The highest error value can be seen in the MLP classi-
fier as it only properly performs in 25 % of the situa-
tions whereas the best performing algorithm is the
Random Forest ensemble (RoF RaF).
When considering the group of features for enco-
ding the image instead of its raw version, a remar-
kable improvement in the results is observed. Almost
all classifiers exhibit a decrease ranging around 10 %
and 15 % in their error rates, being SVM the one
achieving the best classification performance. The
only exception to this general improvement is found
in the MLP classifier in which these features do not re-
port an improvement compared to the raw image case,
thus still exhibiting the lowest performance among
the different methods considered.
1
The dataset is freely available at http://grfia.dlsi.
ua.es/homus/
Focusing now on the use of the CM representa-
tion, it can be checked that this representation en-
tails some additional improvements in the results with
respect to the group of features initially considered
for the image. Particularly, the CM representation
reduces the observed error rate in around 5 % to
7 % with respect to the previous representation, be-
ing again SVM the classifier outperforming the rest
with roughly a 10 % of error rate, which represents
a particularly good result given that there are more
than 30 different classes. The NN classifier consti-
tutes the only case for which the use of this represen-
tation does not suppose an improvement in the results.
Lastly, and in spite of exhibiting the highest error rate
for all classifier using the CM set of features, MLP re-
sults undergo a remarkable improvement with respect
to the two previous data representations of close to a
50 % in terms of error rate.
This general improvement in the results when con-
sidering the CM representation for all algorithms (ex-
cept for NN, in which results hardly change) suggests
that the accuracy boost is due to this alternative
feature representation and not to the use of meta-
classification schemes rather than simpler metho-
dologies. That is, independently of the classification
scheme considered, an improvement is generally ob-
served when the feature representation is based on
CM.
Finally, results obtained with the MACP strategy
also point out that a basic combination of the deci-
sions of each weak classifier instead of using them as
features for a final classification stage may be enough
for achieving a competitive error rate (around 17 %
for the data considered). More precisely, as it can be
observed, MACP outperforms on average rather com-
plex schemes such as MLP or Stacking-C.
In order to provide consistent conclusions of our
work, these results must be validated objectively
through statistical tests (Demsar, 2006). In this case
we have considered the Wilcoxon rank-sum tests that
allow a pairwise comparison between different clas-
sification configurations. Our main intention is to
check whether our approach improves significantly
the conventional classification scheme consisting of a
set of extracted features plus direct classification. To
this end, Table 3 shows the results of this test com-
paring classification with the proposed set of meta-
features (CM) against the results obtained consider-
ing the raw input image and the group of features ini-
tially extracted from the image. The significance of p
has been established to 0.05. Note that a comparison
between each classifier with CM and the MACP en-
semble is also checked. While we are aware that re-
sults from a 4-fold cross-validation scheme may not
Recognition of Handwritten Music Symbols using Meta-features Obtained from Weak Classifiers based on Nearest Neighbor
101
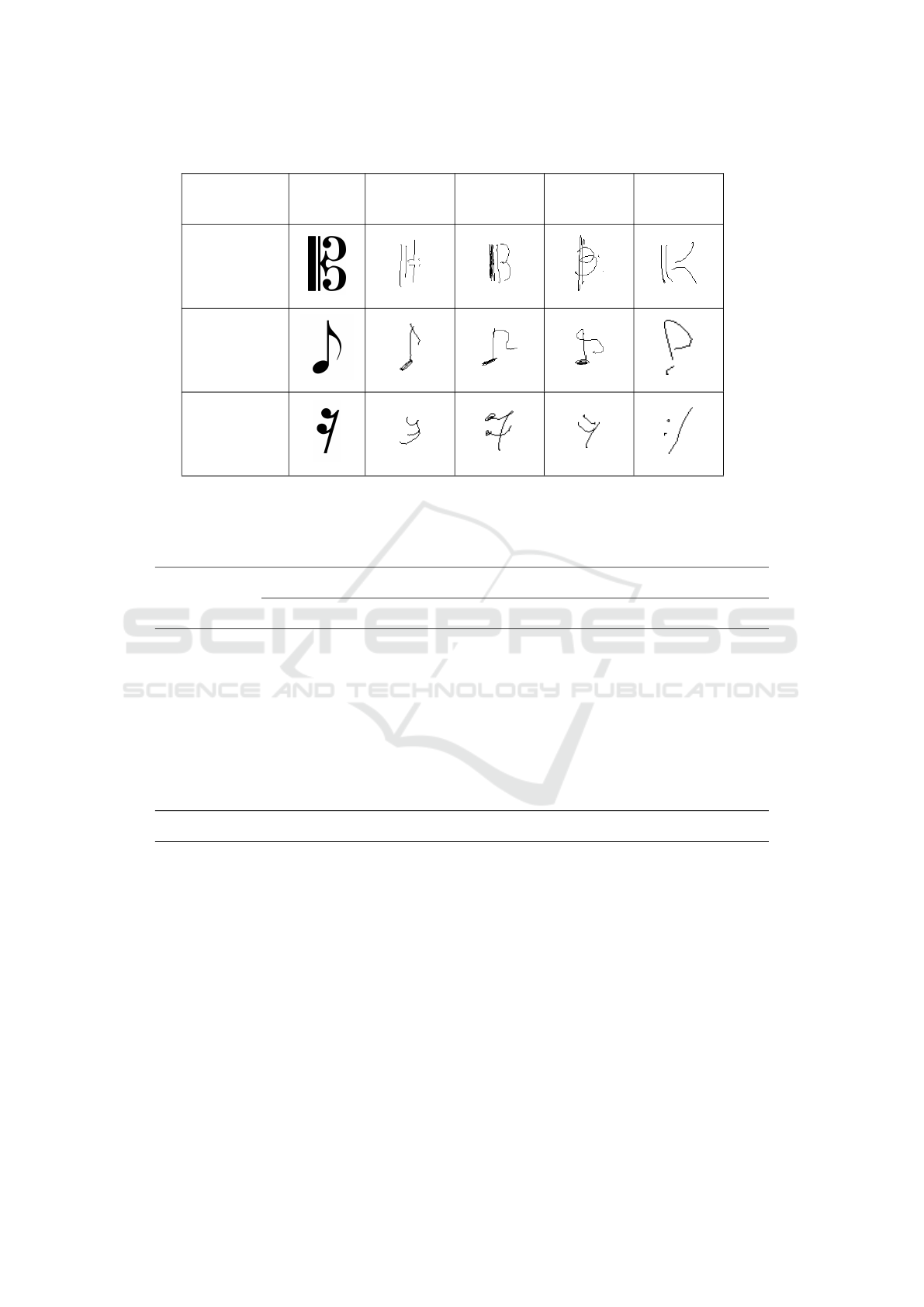
Table 1: Examples of variability in handwritten musical symbols from HOMUS dataset among different musicians.
Label Symbol Musician 1 Musician 2 Musician 3 Musician 4
C-Clef
Eighth Note
Sixteenth
Rest
Table 2: Comparison of the error rate (%) shown by the different classifiers considered when the input representation is based
on the raw image, the set of image features or the matrix representation based on weak classifiers. The subregion parameter
for the feature extraction has been optimized for each particular classifier. Additionally, the results when considering the
MACP scheme for combining the decisions of each weak classifier is included.
Classifier
Input representation
Raw image Groups of features Confidence Matrix
NN 32.5 19.7 21.0
SVM 32.4 18.6 11.8
MLP 75.2 75.4 24.2
StackingC 33.4 23.2 18.9
RoF J48 35.6 20.8 16.1
RoF RaF 25.1 18.9 15.4
MACP
17.4
be enough for a robust statistical analysis, it allows
depicting the general behavior of the algorithms.
As observed, the use of the CM features entails
a significant accuracy improvement over the raw im-
age for all classifiers considered. Additionally, when
compared to the initial group of features extracted
from the image, CM also significantly outperforms
the results except for the case of the NN classifier,
in which this analysis does not evidence any statis-
tical difference between the use of these two set of
features.
Finally, the statistical comparison between the
MACP combination of single decisions and the use of
a last classification stage for the CM features shows
some interesting results. Rotation Forest ensembles
(both RoF J48 and RoF RaF) as well as SVM are able
to significantly outperform the MACP strategy. On
the contrary, NN and MLP show a significantly worse
performance than the aforementioned decision com-
bination strategy. Lastly, Stacking-C does not show
a statistically relevant difference in performance with
respect to MACP.
4 CONCLUSIONS
The classification of handwritten music symbols is a
remarkably useful process in the field of Optical Mu-
sic Recognition which turns to be a quite challenging
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
102

Table 3: Results obtained for the statistical significance tests comparing the accuracy of the classifier depicted in the row using
CM-based classification against the accuracy of the same final classifier when considering the raw image and the features from
the figure (columns). An additional comparison with the MACP ensemble technique is made to assess the performance of
CM against a basic combinations of decisions. Symbols 3, 7 and = state that results achieved by elements in the rows
significantly improve, decrease or do not differ respectively to the results by the elements in the columns. Significance has
been set to p < 0.05.
CM Ensemble
Raw features Groups of features MACP
NN
3 = 7
SVM
3 3 3
MLP
3 3 7
StackingC
3 3 =
RoF J48
3 3 3
RoF RaF
3 3 3
problem given the variability expected in the musical
symbols.
In this paper we considered an ensemble-based
strategy which consists in extracting heterogeneous
features that are eventually mapped onto a Confidence
Matrix (CM) as a set of posterior probability values
obtained by a group of weak classifiers. This ap-
proach enables the features to be transformed into a
new space (meta-features), thus allowing the dimen-
sionality of the data (in our case) to be reduced and a
more meaningful value to be provided in each dimen-
sion. This is expected to help to reduce the error rate
of the final classifier.
Our results show that the use of this alternative
space provides significant improvements in the results
with respect to the use of image-based features for
most classifiers studied. Among the figures obtained,
Support Vector Machine with the Confidence Matrix
representation yields the best results, which is even-
tually estimated in around 10 % of error rate for the
considered handwritten music symbol data.
Future work considers the inclusion of this pro-
posal in a functional Optical Musical Recognition
system to study its impact in a real-world context.
Additionally, with the intention of still lowering the
error rate obtained, we aim at exploration Convolu-
tional Neural Networks given their reported success
in image processing tasks.
ACKNOWLEDGEMENTS
This work has been supported by the Spanish Ministe-
rio de Educaci
´
on, Cultura y Deporte through FPU fel-
lowship (AP2012-0939), Vicerrectorado de Investi-
gaci
´
on, Desarrollo e Innovaci
´
on de la Universidad de
Alicante through the FPU programme (UAFPU2014–
5883) and the Spanish Ministerio de Econom
´
ıa y
Competitividad Project TIMuL (No. TIN2013–
48152–C2–1–R supported by UE FEDER funds).
REFERENCES
Aha, D. W., Kibler, D., and Albert, M. K. (1991). Instance-
based learning algorithms. Mach. Learn., 6(1):37–66.
Bainbridge, D. and Bell, T. (2001). The challenge of optical
music recognition. Computers and the Humanities,
35(2):95–121.
Breiman, L. (2001). Random forests. Machine learning,
45(1):5–32.
Burges, C. J. C. (1998). A tutorial on support vector
machines for pattern recognition. Data Mining and
Knowledge Discovery, 2:121–167.
Calvo-Zaragoza, J. and Oncina, J. (2014). Recognition of
pen-based music notation: The HOMUS dataset. In
22nd International Conference on Pattern Recogni-
tion, ICPR 2014, Stockholm, Sweden, August 24-28,
2014, pages 3038–3043.
Cover, T. and Hart, P. (1967). Nearest neighbor pattern clas-
sification. IEEE Transactions on Information Theory,
13(1):21–27.
Dalitz, C., Droettboom, M., Pranzas, B., and Fujinaga, I.
(2008). A comparative study of staff removal al-
gorithms. IEEE Trans. Pattern Anal. Mach. Intell.,
30(5):753–766.
Demsar, J. (2006). Statistical comparisons of classifiers
over multiple data sets. Journal of Machine Learning
Research, 7:1–30.
Duda, R. O. and Hart, P. E. (1973). Pattern Recognition and
Scene Analysis. John Wiley and Sons, New York.
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,
P., and Witten, I. H. (2009). The weka data min-
Recognition of Handwritten Music Symbols using Meta-features Obtained from Weak Classifiers based on Nearest Neighbor
103

ing software: An update. SIGKDD Explor. Newsl.,
11(1):10–18.
Jain, A. K., Mao, J., and Mohiuddin, K. M. (1996). Artifi-
cial neural networks: A tutorial. Computer, 29(3):31–
44.
Kittler, J., Hatef, M., Duin, R. P. W., and Matas, J. (1998).
On combining classifiers. IEEE Trans. on Patt. Anal.
Machine Intelligencet, 20:226–239.
Kuncheva, L. I. (2001). Using measures of similarity and in-
clusion for multiple classifier fusion by decision tem-
plates. Fuzzy sets and systems, 122(3):401–407.
Kuncheva, L. I. (2004). Combining pattern classifiers :
methods and algorithms. John Wiley & Sons.
Oda, H., Zhu, B., Tokuno, J., Onuma, M., Kitadai, A., and
Nakagawa, M. (2006). A Compact On-line and Off-
line Combined Recognizer. In Tenth International
Workshop on Frontiers in Handwriting Recogntion,
volume 1, pages 133–138.
P
´
erez-Cort
´
es, J. C., Llobet, R., and Arlandis, J. (2000). Fast
and Accurate Handwritten Character Recognition Us-
ing Approximate Nearest Neighbours Search on Large
Databases. In Ferri, F. J., I
˜
nesta, J. M., Amin, A., and
Pudil, P., editors, Advances in Pattern Recognition,
volume 1876 of Lecture Notes in Computer Science,
pages 767–776, Berlin. Springer-Verlag.
Platt, J. C. (1999). Advances in kernel methods. chapter
Fast training of support vector machines using sequen-
tial minimal optimization, pages 185–208. MIT Press,
Cambridge, MA, USA.
Quinlan, J. R. (1993). C4.5: Programs for machine learn-
ing. Machine Learning.
Rebelo, A., Capela, G., and Cardoso, J. S. (2010). Optical
recognition of music symbols: A comparative study.
Int. J. Doc. Anal. Recognit., 13(1):19–31.
Rebelo, A., Fujinaga, I., Paszkiewicz, F., Marcal, A.,
Guedes, C., and Cardoso, J. (2012). Optical music
recognition: state-of-the-art and open issues. Inter-
national Journal of Multimedia Information Retrieval,
1(3):173–190.
Rico-Juan, J. R. and Calvo-Zaragoza, J. (2015). Improv-
ing classification using a confidence matrix based on
weak classifiers applied to OCR. Neurocomputing,
151:1354–1361.
Rodriguez, J., Kuncheva, L., and Alonso, C. (2006). Rota-
tion forest: A new classifier ensemble method. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 28(10):1619–1630.
Romero, V., Toselli, A. H., and Vidal, E. (2012). Multi-
modal Interactive Handwritten Text Transcription. Se-
ries in Machine Perception and Artificial Intelligence
(MPAI). World Scientific Publishing.
Seewald, A. K. (2002). How to make stacking better and
faster while also taking care of an unknown weak-
ness. In Proceedings of the Nineteenth International
Conference on Machine Learning, ICML ’02, pages
554–561, San Francisco, CA, USA. Morgan Kauf-
mann Publishers Inc.
Serra, J. (1982). Image Analysis and mathematical mor-
phology. Academic Press.
Vapnik, V. N. (1998). Statistical learning theory. Wiley, 1
edition.
Vellasques, E., Oliveira, L., Jr., A. B., Koerich, A., and
Sabourin, R. (2006). Modeling Segmentation Cuts
Using Support Vector Machines. In Tenth Interna-
tional Workshop on Frontiers in Handwriting Recogn-
tion, volume 1, pages 41–46.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
104
