Multi-agent based Synchronous Communication for Dynamic
Rescheduling in Railway Network
Krishnendu Kundu and Animesh Dutta
Department of Information Technology, National Institute of Technology, Durgapur, India
Keywords:
Message Passing, DCOP, Multi-agent based Modeling, Selective Flooding.
Abstract:
This paper presents a multi-agent based solution to change a predefined Railway schedule dynamically. This
paper models a railway network consisting of passenger and freight trains, along with their fixed schedules
following the rules of Indian Railways. The trains in the system are modelled as Train Agents and rail segments
as Segment Agents. Delay of a single train due to unavoidable hazards like track related problems, rain, fog
may cause severe delays for next trains in sequence. This paper proposes a method to suggest overtaking
maneuvers for trains by passing different types of messages between Train Agents and Segment Agents. This
paper proposes Selective Flooding of messages to avoid congestion overhead. All types of messages passed
are elaborately described in the problem formulation section. This paper also contains a theoretical proof
showing that Selective Flooding technique is always able to reach every node required. The proposed method
has been simulated using JADE platform and the results are presented.
1 INTRODUCTION
Creation of optimal timetable for Railway Network
and introducing new train according to requirement
are time consuming processes for the countries where
Railway Network is maintained manually. Most of
the research works done on railway scheduling have
focused on creating optimal timetable that maintains
the constraints provided by the railway operators.
Apart from optimizing the schedule there are other
issues that should be taken care of. Some dynamic
strategies should be there to handle unavoidable haz-
ards that may occur in railway network. Schedule of
a train can be affected by unpredictable delay due to
meteorological conditions such as rain, fog or track
related issue. This paper aims to implement the ro-
bustness feature along with the optimal timetable so
that delay of one passenger or freight train can not af-
fect others severely. In Indian Railways freight trains
generally do not have any fixed schedule. So, on de-
mand scheduling should be there to handle freight
trains along with passenger trains. During last few
years distributed approaches of solving any real time
problem have been admired rather than centralized
approach. To take the rescheduling decision dynam-
ically multiple autonomous entities or Agents can be
introduced to solve the issues stated above.
The main focus of this work is to model N-track
railway network in which passenger and freight trains
are scheduled and rescheduled dynamically with the
notion of Distributed Constraint Optimization Prob-
lem (DCOP). Each train and segment acts as an au-
tonomous agent (termed as Train Agent and Station
Agent). Based on different types of delay objective
functions are formed depending on certain constraints
related to Indian Railways. The agents communicate
among themselves to find a way out when disturbance
occurs. The total procedure of sharing, updating, tak-
ing decisions are properly stated in proposed algo-
rithm.
2 RELATED WORK
Authors of (Takeuchi et al., 2007) have used Monte
Carlo technique to calculate robustness index that rep-
resents passengers disutility when delay occurs. Au-
thors of (Liebchen et al., 2010) have shown five possi-
ble types of activities and tried to minimize the objec-
tive function which considers different kinds of delay
associated to each activity along with number of pas-
sengers on the train. Space graph strategies were pro-
posed in (Cacchiani and Toth, 2012) where four dif-
ferent arcs starting, segment, station, ending are used
and each arc has initial profit. If global profit of any
train becomes NULL or negative train cancellation is
Kundu K. and Dutta A.
Multi-agent based Synchronous Communication for Dynamic Rescheduling in Railway Network.
DOI: 10.5220/0006120901370144
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 137-144
ISBN: 978-989-758-219-6
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
137

allowed. Authors of (Fischetti and Monaci, 2009)
have proposed a light robustness technique which is
flexible to allow the violation of constraints while im-
posing a maximum efficiency loss. Authors of (Ci-
cerone et al., 2009) have measured price of robustness
by the ratio between recoverable robust timetable and
the optimal non-robust solution. They have shown
that problem of finding optimal recoverable robust
timetables is NP-hard. Authors of (Sahana et al.,
2014) have proposed ant colony based optimization
for solving scheduling problem for train having same
speed and for different speed also. But they have not
focused on unpredictable delay. Genetic Algorithms
proposed by (Tormos et al., 2008) and (Chung et al.,
2009) are appropriate methods to explore the search
space of this complex problem but they have not con-
sidered the robustness related issue. In (Kiekintveld
et al., 2010) authors have proposed k-distance opti-
mality using Subset Locking and Partial Synchroniza-
tion. Bipartite factor graph is used in (Farinelli et al.,
2008) for sending messages. (Kuo et al., 2010) con-
tains a process to schedule freight train dynamically.
Agent based approach for modeling domain depen-
dent constraint satisfaction problem has been shown
in (Salido et al., 2007).
3 SCOPE OF THE WORK
In case of railway scheduling most of the research pa-
pers focused on creating optimal timetable that main-
tains the constraints provided by the railway opera-
tors. Using different objective functions they have
tried to solve Railway scheduling problem where
delay management problem has not been addressed
properly. This paper considers a railway network
of passenger and freight trains along with a given
timetable. If a train becomes affected by severe delay
the predefined schedule becomes inefficient. The aim
of this paper is to take dynamic overtaking decision to
improve roubustness of overall Railway Network. Im-
plementation of robustness feature which maintains
the overall system utility is a good scope to work on.
In some cases overtaking should be allowed without
violating the hard constraints. But there are also such
scenarios where change of ordering bring more devas-
tating result. This paper identifies the utility for both
of the cases and takes a decision.
4 SYSTEM MODEL
All possible types of junction points (where trains
can change their track) are not considered in this pa-
per. Alternatively junction points are assumed to be
present at the both end of each station. So, signal
points are available only before entering and exiting
each station. The portion of railway track between
two consecutive signal points is called segment. Ga-
lop train does not stop at those stations where it has
no commercial stop.
SEG
j
is ordered set of segments that train j ∈
N ∪ M has to cover. S
j
is ordered set of stations
from originating station to final destination of train
j ∈ N ∪ M.
N = Set of all passenger trains.
M = Set of all fright trains.
SEG = Set of all segments.
ET
j
is ordered set of all events that a train j ∈
N ∪ M has to go through. ln
j
is the last event of set
ET
j
.
N S
j
is the set of stations where train j ∈ N has
commercial stop.
ES
k
is ordered set of all events that are scheduled
to occur at segment k ∈ SEG. Each event in ES
k
on segment k has originating point OP
k
and finish-
ing point FP
k
where OP
k
,FP
k
∈ SEG
k
. ln
k
is the last
event of ES
k
.
If v and v
0
are two same directional events of
segment k, then OP
v
= OP
0
v
and headway distance
∆
same
= |x
end
v
− x
beg
v
0
|
UT
k
and DT
k
are set of up tracks and down tracks
of segment k.
U
old
is the overall system utility if overtaking is
not granted, U
new
is the new utility if overtaking re-
quest is granted.
4.1 Binary Functions
ADJ(i,k) =
(
1, if segment i, k is adjacent.
0, otherwise.
UP(k,i) =
(
1, if k is towards up from i.
0, otherwise.
DOW N(k,i) =
(
1, if k is towards down from i.
0, otherwise.
LOOP(k) =
(
1, if segment k has a loop line.
0, otherwise.
FREE(l
k
) =
(
1, if track l of k ∈ SEG is free.
0, otherwise.
REC(msg) =
(
1, if msg has been received.
0, otherwise.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
138

PREC(v,v
0
) =
(
1, if event v ≺ v
0
in schedule.
0, otherwise.
4.2 Train Agent and Segment Agent
Each segment consists of one Segment Agent (SA)
that maintains all records of that particular segment
and communicate with other SAs and Train Agents.
Each of the passenger and freight trains consist of
one Train Agent (TA) which can communicate only
with 3 segments- current, previous and next. We are
avoiding the communications among different TAs to
reduce communication hazard.
∀ event ∈ ET
j
, Train Agent j stores the FT
j
. Num-
ber of event in ET
j
is equal to the number of seg-
ments to cross. ∀ event∈ ES
k
, Segment Agent k stores
f inish time and start time as per predefined sched-
ule. actual start and finishing time are ST
j
,FT
j
.
4.3 Directions and Fields of Messages
Direction of messages
Message type SA to
TA
SA to
SA
TA to
SA
ARR no no yes
LINK PROB no yes no
DEPT no yes no
REQ no yes no
WAIT yes yes no
GRANT yes yes no
OT RQ no yes no
OT GRANT yes yes no
T H U T IL no no yes
Two functions send() and receive() are used to
send and receive messages. Fields of different
messages are as follows.
ARR(train,track, prevSA,nextSA, currentSA,time)
LINK PROB(segment,track,tolerance, f lag)
DEPT (train,track,time)
REQ(train,track,sender segment)
WAIT (train, segment, loopline)
GRANT (train,segment, f ree track)
OT RQ(train behind,train heading,requesting SA,
time,count,U
old
,U
new
)
OT GRANT (train, green signal)
T H U T IL(train,U
T h
j
)
5 METRIC DEFINITION
Here is a list of metrics to calculate the delay fac-
tor that helps the agents to take decisions. All of the
utility factors have negative impact and have a range
[0,1].
• Utility of delay of freight train j (U
δ
f
j
): Accord-
ing to Indian Railways departure of a freight train
from originating point is officially decided at least
before 3 hours of departure. So we can assume
freight trains do not have fixed schedule. They
have deadlines to reach at the final destination and
almost fixed route to follow.
• Utility of arrival at commercial stop (U
δ
a
j
): For
passenger trains arrival delay is calculated at each
commercial stop except the originating station. If
a passenger train has reached all the commercial
stop on time except one stop, then also it can not
have the best utility 0.
• Utility of delay of departure from commercial
stop (U
δ
d
j
): Our proposed method calculates this
utility at each commercial stop except the final
destination of passenger train.
• Threshold delay (U
T h
j
): This threshold utility cal-
culation is done for each passenger train at the fi-
nal station.
6 PROBLEM FORMULATION
This paper does not concentrate on adding a new
train in the schedule or creating a optimal timetable
from the scratch. The main concern of this paper
is to reschedule some predefined events (ES) so that
overall system performance does not downgrade too
much. There is already a fixed predefined schedule
given for each and every train j ∈ M ∪N. Each SA (let
k) contains information about which train is sched-
uled to cross it in form of ES
k
along with start time
ST
i
and FT
i
where i ∈ ES
k
.
6.1 Delay Measurement
6.1.1 Delay Measurement for Freight Train
For freight train there is prior knowledge about the
deadline. Initial utilityl is 0 and maximum value of
utility can be reached when (∆t
j
×
1
t
d
j
−t
e
j
) × p
j
be-
comes 1 for freight train j where,
∆t
j
= total delay of freight train j.
t
d
j
= deadline for freight train j, where t
d
j
> t
e
j
.
t
e
j
= expected finish time for freight train j.
p
j
= priority of train j. For higher priority train
(containing special goods) must reach at final stop
within time. So, for them p
j
= 1. They suffer
maximum negative weightage when ∆t
j
<= t
d
j
−t
e
j
.
Multi-agent based Synchronous Communication for Dynamic Rescheduling in Railway Network
139

But lower priority train may some relaxation on their
deadline by assigning p
j
value less than 1.
U
δ
f
j
= min((∆t
j
×
1
t
d
j
−t
e
j
) × p
j
,1) (1)
6.1.2 Delay Measurement for Arrival
No credit is given to a passenger train for early ar-
rival (arrive δ
ji
= 0) at it’s commercial stop . If a
train arrives early that means it has to wait more at
station and thus free platform resources decrease. Ar-
rival time delay generally affects the utility of the train
itself. Suppose, a train j delays arrive δ
ji
to arrive
at station i and jrny time
j
is scheduled journey time
of train j from originating station to final destination,
then utility for a single train j,
U
δ
a
j
= min(
|N S
j
|
∑
i=1
(arrive δ
ji
/ jrny time
j
),1) (2)
6.1.3 Delay Measurement for Departure
Departure of a passenger train can’t be allowed be-
fore predefined scheduled. On the other hand depar-
ture time delay affects the following train in sequence.
Arrival time and Departure time delay are measured
at each scheduled commercial stop.Suppose, a train
j delays dept δ
ji
before leaving station i, then utility
for a single train j,
U
δ
d
j
= min(
|N S
j
|
∑
i=1
(dept δ
ji
/ jrny time
j
),1) (3)
6.1.4 Threshold on Delay
Depending on the priority, each of the passenger
trains has certain level of delay threshold. T h
j
indi-
cates the maximum tolerable delay of train j in arrival
time at the final destination.
U
T h
j
= max(b(r time
j
− jrny time
j
)/T h
j
c,0) (4)
where, r time
j
is the actual journey time of train j. As
the worst value of threshold utility is 1 at the final sta-
tion when train exceeds threshold delay. So, if a train
is being delayed beyond its threshold permit it can
not be reflected in the objective functions. A restric-
tion must be there to save a lower priority train to be a
victim of huge delay. A train j can suffer from a huge
delay if following trains in sequence are allowed to
overtake train j to minimize their delay. Always aim-
ing for the betterment of overall system is impractical,
if a particular train is suffering from too much delay.
To avoid this starvation problem we must introduced a
constant OT
j
for each of the train j that indicates how
many train can overtake j during its whole journey.
The cost associated to deviation from actual ar-
rival and departure time of passenger train and vio-
lation of deadline by freight can be measured by fol-
lowing objective function:
min(
|M|
∑
j=1
U
δ
f
j
+
|N|
∑
j=1
U
δ
a
j
+
|N|
∑
j=1
U
δ
d
j
+
|N|
∑
j=1
U
T h
j
) (5)
6.2 SA - SA Communications
Segment k sends LINK PROB message to the adja-
cent segments if there is a problematic track in seg-
ment k. If a train is delayed by problem in certain
track there is no logic to go for overtaking. If a haz-
ard is there in a particular segment, it affects all of the
train in same direction. Initially ∆ allowed
kl
is reset
to 0. It gets some positive value in presence of any
track error in the Railway Network. Algorithm 1 de-
scribes the steps followed by sender of LINK PROB
message. If a problem occurs in the UP link then
sender SA sends message only to adjacent UP SA.
Receiver SA repeats this process using Algorithm 2
and updates ∆ allowed
kl
accordingly. If the problem
occurs in DOWN link rather than UP link same pro-
cesses are followed up towards DOWN direction.
6.3 TA - SA Communications
As TA is mobile entity, critical decisions should not
depend on communication involving TA. Most of all
types of signaling decisions are taken depending on
the SA to SA communication. TA asks each segment
before entering into that whether it is meeting the en-
try criteria.
When a freight train i ∈ M is about to enter a seg-
ment having loop line the SA must check whether fol-
lowing passenger train j ∈ N needs to overtake i as de-
scribed in Algorithm 4. Overtaking can be scheduled
in following three cases:
• The freight train was already scheduled to wait at
the loop line.
• There is a j behind freight train i where j is sup-
posed to be in front of i. For some reason j is
suffering from delay.
• i is suffering from delay and there is a follow-
ing passenger train j running on time. So, there
should a procedure to pass that passenger train j
by make i waiting in the loop line.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
140

6.4 Overtaking Decision
If a train is late for more than ∆ allowed
kl
at segment
k and still not getting free slot or green signal for en-
tering next segment, the segment k sends OT REQ
message to the next segment in sequence. If prior-
ity of train i is less than the preceding train j, i is
not allowed to overtake train j unless it is a presched-
uled overtaking. Otherwise overtaking decision can
be taken after following conditions are satisfied.
6.4.1 Recalculate Objective Function Value
If a train i overtakes train j, i needs and extra time
of ∆ cross
i j
and j needs an extra time of ∆ cross
i j
+
δ
i j
(line 5 of Algorithm 7). ∆ cross
i j
depends on how
much time train i takes to change the track and gets
back to the previous track after overtaking j. In real
scenario ∆ cross
i j
is not constant. But we are as-
suming it as a constant for a particular railway net-
work as ‘how to optimally change track at junction
point’ is not main concern of this paper. δ
i j
depends
on how much time train j takes to regain its original
speed after getting back to its own track in addition
with the time taken by train i to cross the headway
distance ∆
same
. We are not considering δ accelerate
i
(time required to accelarate and get back the normal
velocity V
i
), as it is already included in ∆ cross
i j
.
δ
i j
= δ accelerate
j
+ ∆
same
/V
i
.
Objective function value can be recalculated prop-
erly considering the whole route of two trains. The
technique is optimal for betterment of threshold util-
ity. But to decrease arrival and departure delay at each
segment we must take Zonal decision. Indian Railway
uses Zonal management and decision strategy man-
ually. Our proposed technique reflects the existing
policy. In Zonal decision strategy objective function
value is recalculated up to a constant number of seg-
ments .
6.4.2 Check for Feasibility
If overtaking is not feasible due to unavailability of
free slots for overtaking, rescheduling decision should
not be finalized. To check the rescheduling feasibility
we are following almost same strategy as described
by author of (Dalapati et al., 2014). But unlike (Dala-
pati et al., 2014) SA does not contain all information
in our proposed method. So, SA needs to commu-
nicate with other SAs and TAs to calculate objective
function. In this paper all segments towards destina-
tion segment are considered and each SA k updates
event list ES
k
after finalizing the rescheduled over-
taking. The event list of all TA remain unchanged
as each train is following the order in which they are
supposed to cross the segments.
6.5 Message Passing
When a TA enters a segment it sends ARR using Al-
gorithm 3. On receiving ARR using Algorithm 6, the
SA sends the followings
• REQ to the next SA in sequence.
• DEPT to the previous segment.
• Overtaking request OT REQ if required.
After receiving DEPT using Algorithm 5, SA calcu-
lates U
δ
d
j
and set the track free. On receiving REQ
the SA sends followings according to Algorithm 4
• GRANT to SA and TA when track is free.
• WAIT to both of SA and TA.
Line 9 and 10 of Algorithm 4 create a loop if there
is no free track. The loop breaks immediately when
a track becomes available. On receiving GRANT and
WAIT the SA provides proper signal to TA using Al-
gorithm 5. An extra security is provided by Algorithm
8 as TA also receives WAIT and GRANT along with
traditional signal. Algorithm 7 describes the method
to check the requirement and feasibility of overtak-
ing and send OT GRANT which is received by Algo-
rithm 5. In Algorithm 7 Zonal decision is taken within
next 10 segments (line 6,7). The segment comes af-
ter 10th segment takes the final decision depending on
received U
old
and U
new
.
6.6 Selective Flooding of LINK PROB
After detecting the link related problem LINK PROB
message is required to be sent to other Segemnt
Agents. The naive approach is to inform all Segment
Agents in the railway Network. But to reduce mes-
sage passing complexity and avoid broadcast storm
problem, Selecting Flooding can be introduced. In
Selective Flooding technique the messages are sent
to selective Segment Agents. Algorithm 1 and Algo-
rithm 2 describe the procedure how Segement Agents
are selected from the total set of segments SEG.
Algorithm 1: SA detects track related problem.
1: k ← ID of SA where problem occurs at Track l
2: tol ← predicted delay of crossing track k
3: ∆ allowed
kl
← (∆ allowed
kl
+tol)
4: for i ∈ SEG do
5: if (l ∈ U T
k
) then
6: if (ADJ(i,k) = 1 ∧ DOW N(k,i) = 1) then
7: send (LINK
PROB(k,l,tol,1), i)
8: else if (ADJ(i,k) = 1 ∧UP(k, i) = 1) then
9: send (LINK PROB(k,l,tol,0), i)
Multi-agent based Synchronous Communication for Dynamic Rescheduling in Railway Network
141

Algorithm 2: On receiving LINK PROB(segment,track,
tol, f lag) message by SA from other SA.
1: receive (LINK PROB(k,l,tol, f lag))
2: i ← ID of receiving SA
3: ∆ allowed
il
← (∆ allowed
il
+tol)
4: if ( f lag = 1) then
5: for i ∈ SEG do
6: if (ADJ(i,k) = 1 ∧ DOW N(k,i) = 1) then
7: send(LINK PROB(k,l,tol, 1),i)
8: else if (ADJ(i,k) = 1 ∧UP(k, i) = 1) then
9: send (LINK PROB(k,l,tol,1), i)
Algorithm 3: On arriving of TA j at track l of segment sc at
time t.
1: send (ARR( j, l,sp,sn,t),sc)
2: FT
sc
← t
3: if (sc = ln
j
) then
4: calculate U
T h
j
using Equation 4
5: send (TH UT IL( j,U
T h
j
),sc)
Algorithm 4 : On receiving REQ(train,track, sender
segment) message by SA k from other SA.
1: receive(REQ( j, l,s))
2: if ( j ∈ M)
3: calculate U
δ
f
j
using Equation 1
4: if(REC(OT RQ, j
0
) = 1 ∧ PREC( j, j
0
) = 1 ∧
j
0
∈ N ∧LOOP(k) = 1 ∧ FREE(lt
k
) = 1)
5: send(WAIT ( j, k,lt
k
),s)
6: send(WAIT ( j, k,lt
k
), j)
7: FREE(lt
k
) ← 0
8: EXIT
9: if ∀l
0
∈ UT
k
∪ DT
k
,connected to l and FREE(l
0
) = 0
10: go to line 9
11: FREE(l
0
) ← 0
12: send(GRANT ( j,k, l
0
),s)
13: send(GRANT ( j,k, l
0
), j)
claim: The Selective Flooding technique de-
scribed by Algorithm 1 and Algorithm 2 covers suffi-
ciently large portion of network and the unaware SAs
do not require this LINK PROB message from seg-
ment k.
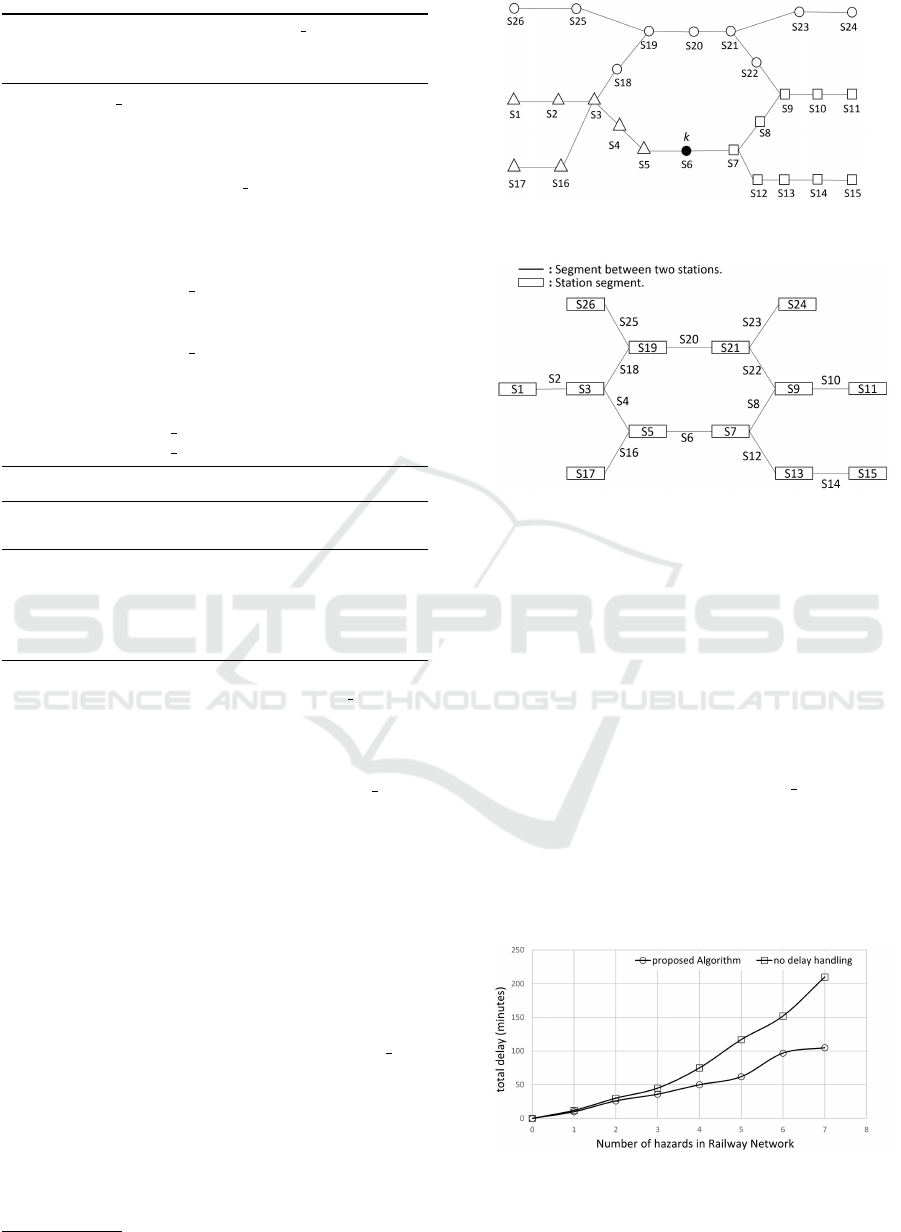
Proof: In figure 1 k is an arbitrary segment among
a set of segments represented by nodes. A join-
ing arc connecting two segments represents suitable
entry and exit criteria of the connecting segments.
The triangle(T) shaped segments indicate the UP seg-
ments with respect to segment k and square(S) shaped
segments represent DOWN segments with respect to
k. The round white(RW ) segments are not sharing any
route with segment k. According to Indian railway a
train can be either UP or DOWN directed. If a train
has a route that consist of UP directed route followed
by a Down directed route, Indian railway uses two
Algorithm 5: On receiving DEPT ( j,l,t), GRANT ( j,k,l
0
),
WAIT( j, k,lt
k
), OT GRANT ( j,g) message by SA from
SA.
1: msg ←receive()
2: if (type(msg) = DEPT ) then
3: FT
j
← t
4: dept δ
ji
← (FT
j
− f inish time
j
)
5: if(i ∈ N S
j
) then
6: calculate U
δ
d
j
using Equation 3
7: FREE(l) ← 1
8: else if (type(msg) = GRANT ) then
9: send green signal to j to enter track l
0
of segment k
10: else if (type(msg) = WAIT ) then
11: send signal to j to enter loop track lt
k
of segment k
12: else if (type(msg) = OT GRANT ) then
13: if(g=1) then
14: check feasibility by sending REQ to sn
15: else
16: Stop train j and wait for REQ
Algorithm 6 : On receiving ARR(train,track, previousSA,
nextSA,currentSA,time) message by SA i from TA j.
1: receive (ARR( j,l,sp,sn,t),sc)
2: send(DEPT ( j,l,t),sp)
3: s ← i
4: send(REQ( j, l,s), sn)
5: ST
j
← t
6: arrive δ
ji
← ST
j
− start time
j
7: if(i ∈ N S
j
) then
8: calculate U
δ
a
j
using Equation 2
9: if j ∈ N then
10: if ((∆ allowed
i j
< arrive δ
ji
)∧GRANT message
not received from sn) then
11: send(OT RQ( j, 0,i,t,0,0,0),sn)
different numbers of the train for two different direc-
tions. So, logically each train can have only one direc-
tion. We categorize all segments into 3 sets (S,T,RW )
from the perspective of segment k. According to pro-
posed formulation for i ∈ S, U P(k,i) function returns
1, for i ∈ T, DOW N(k,i) returns 1 and for i ∈ RW
both functions returns 0 .
Suppose segment k finds a problem in UP track
and it informs the adjacent segments towards UP di-
rection. Let us assume that there be a segment k0 ∈ T
so that DOW N(k, k0) = 1 and k0 does not receive
LINK PROB initiated by segment k. If k0 does not
receive LINK PROB that means there is no segment
i ∈ T \k,k0 such that line 6 of Algorithm 2 is satis-
fied. As railway network is connected graph there
must be a path from k to k0. As i ∈ T , the existing
path from k to k0 must be completely UP directed.
So, second condition in line 6 of Algorithm 2 is true
∀i ∈ T. If there is n nodes in between k to k0 (let
i
1
,i
2
...i
n
), then DOW N(k,i
1
) = 1,DOW N(i
1
,i
2
) =
1...DOW N(i
n−1
,i
n
) = 1 and DOW N(i
n
,k0) = 1. So,
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
142

Algorithm 7: On receiving OT RQ(trainbehind,
trainheading,requesting SA,time, count,U
old
,U
new
) mes-
sage by SA from other SA.
1: receive(OT RQ( j, j
0
,s,t,c,x,y))
2: if( j /∈ ES
k
) // the SA who do not have j as event
3: EXIT
4: U
old
← (U
old
jk
+U
old
j
0
k
+ x)
5: calculate U
new
considering ∆ cross
i j
+ δ
i j
using t
6: if(c <= 10) then //restricting zonal decision
7: c ← c + 1
8: if(UP(k,s) = 1) then
9: for ∀k
0
∈ SEG ∧ ADJ(k,k
0
) ∧UP(k, k
0
)
10: send(OT RQ( j, j
0
,s,t,c,U
old
,U
new
),k
0
)
11: else
12: for ∀k
0
∈ SEG ∧ ADJ(k,k
0
) ∧ DOW N(k,k
0
)
13: send(OT RQ( j, j
0
,s,t,c,U
old
,U
new
),k
0
)
14: else
15: calculate Objective function using Equation 5
16: if (new value of objective function is minimum)
17: send(OT GRANT ( j,1),s)
18: send(OT GRANT ( j
0
,0), sn)
Algorithm 8: On receiving GRANT ( j, k,l
0
) or
WAIT( j, k,lt
k
) message by TA from SA.
1: msg ←receive()
2: if (type(msg) = GRANT ) then
3: enter segment k using track l
0
4: else if (type(msg) = WAIT ) then
5: wait at loop line lt
k
of segment k
Algorithm 2 guarantees delivery of LINK PROB to
each node i ∈ T except the following situation.
If all nodes in T are adjacent of k, then 2nd con-
dition of line 6 of Algorithm 2 becomes false. In that
case Algorithm 1 guarantees delivery of LINK
PROB
message to all of the adjacent nodes of k. So our as-
sumption was wrong and we conclude that all nodes
in set T receive the message.
7 EXPERIMENT AND RESULTS
As depicted in Figure 2 a small Railway Network
is considered which consists of 26 segments (among
them 13 segments are stations) along with 10 passen-
ger trains and 3 freight trains. The longest jrny time
is of 180 minutes. Segment and Train Agents are cre-
ated using JADE
1
(Java Agent Development Frame-
work) where different types of messages are created
by different formatives of ACL message. In our sim-
ulation 7 different types of abnormal delay (hazards)
are created randomly at different segments.
1
http://jade.tilab.com/
Figure 1: Segments towards UP and DOWN from SA k.
Figure 2: Railway Network having 13 stations.
7.1 Delay Handling
Figure 3 shows simulation result where our proposed
method restricts the delay from being severe. It is ob-
vious that the overtaking of trains takes some addi-
tional time, but that helps to minimize the delay as
shown Figure 3. Delay canot be minimised too much
as maximum journey time is too small in our simu-
lation environment(only 180 minutes). In case of a
real time scenario (having long journey time) the de-
lay can be reduced a lot by speeding up the affected
train after overtaking. In case of hazard number 6 our
algorithm does not provide better result as it is track
related issue as described in algorithm 1. If a track is
in problematic state then overtaking is illogical.
Figure 3: Overall delay comparison.
Multi-agent based Synchronous Communication for Dynamic Rescheduling in Railway Network
143

Figure 4: Summary of message passing.
7.2 Communication Overhead
Each TA sends two types of messages - ARR and
T H U T IL. During any type of hazard TA need not to
send any extra message. So according to figure 4 the
number of messages sent by all Train Agents remains
same irrespective of number of hazards occured. Each
Segment Agent sends 7 types of messages. Number
of messages REQ, DEPT , WAIT and GRANT re-
mains unchanged irespective of number of hazards.
But number of OT GRANT , OT REQ, LINK PROB
messages changes depending on the number and type
of hazards. As shown in Figure 4 number of messages
sent by all Segment Agents is not increased a lot with
the increase of number of hazards.
8 CONCLUSION
With the increase in number of trains and tracks in
Indian Railways, the on demand scheduling task be-
comes time consuming. As per the case study it is evi-
dent that Multi-agent based approach described in this
paper has promising aspects for taking dynamic deci-
sion more accurately. As Railway Network graph is
not too much complex as complete graph, no prepro-
cessing is required like other DCOP algorithms like
(Petcu and Faltings, 2005) and (Modi et al., 2005). It
is a major advantage to have additional time for multi-
agent communication. In this paper robustness is im-
plemented in Railway Network. To support this re-
search the microscopic view of ‘how to change track
and optimize the delay at junction points’ should be
taken under consideration in the near future.
ACKNOWLEDGEMENT
This research work is funded by Visvesvaraya PhD
scheme of DeitY (Department of Electronics & Infor-
mation Technology), Govt. of India.
REFERENCES
Cacchiani, V. and Toth, P. (2012). Nominal and robust train
timetabling problems. European Journal of Opera-
tional Research, 219(3):727–737.
Chung, J.-W., Oh, S.-M., and Choi, I.-C. (2009). A hybrid
genetic algorithm for train sequencing in the korean
railway. Omega, 37(3):555–565.
Cicerone, S., DAngelo, G., Di Stefano, G., Frigioni, D., and
Navarra, A. (2009). Recoverable robust timetabling
for single delay: Complexity and polynomial algo-
rithms for special cases. Journal of Combinatorial
Optimization, 18(3):229–257.
Dalapati, P., Singh, A., Dutta, A., and Bhattacharya, S.
(2014). Multi agent based railway scheduling and op-
timization. pages 1–6.
Farinelli, A., Rogers, A., Petcu, A., and Jennings, N. R.
(2008). Decentralised coordination of low-power em-
bedded devices using the max-sum algorithm. pages
639–646.
Fischetti, M. and Monaci, M. (2009). Lecture notes in
computer science. Robust and Online Large-Scale
Optimization,R.K. Ahuja, R. Moehring, C. Zaroliagis
(Eds.), 5868:61–84.
Kiekintveld, C., Yin, Z., Kumar, A., and Tambe, M. (2010).
Asynchronous algorithms for approximate distributed
constraint optimization with quality bounds. pages
133–140.
Kuo, A., Miller-Hooks, E., and Mahmassani, H. S. (2010).
Freight train scheduling with elastic demand. Trans-
portation Research Part E: Logistics and Transporta-
tion Review, 46(6):1057–1070.
Liebchen, C., Schachtebeck, M., Sch
¨
obel, A., Stiller, S.,
and Prigge, A. (2010). Computing delay resistant rail-
way timetables. Computers & Operations Research,
37(5):857–868.
Modi, P. J., Shen, W.-M., Tambe, M., and Yokoo, M.
(2005). Adopt: Asynchronous distributed constraint
optimization with quality guarantees. Artificial Intel-
ligence, 161(1):149–180.
Petcu, A. and Faltings, B. (2005). A scalable method for
multiagent constraint optimization. IJCAI, pages 266–
271.
Sahana, S. K., Jain, A., and Mahanti, P. K. (2014). Ant
colony optimization for train scheduling: an analysis.
International Journal of Intelligent Systems and Ap-
plications, 6(2):29.
Salido, M. A., Abril, M., Barber, F., Ingolotti, L., Tor-
mos, P., and Lova, A. (2007). Domain-dependent dis-
tributed models for railway scheduling. Knowledge-
Based Systems, 20(2):186–194.
Takeuchi, Y., Tomii, N., and Hirai, C. (2007). Evaluation
method of robustness for train schedules. Quarterly
Report of RTRI, 48(4):197–201.
Tormos, P., Lova, A., Barber, F., Ingolotti, L., Abril, M.,
and Salido, M. (2008). A genetic algorithm for rail-
way scheduling problems. Studies in Computa- tional
Intelligence (SCI), page 255276.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
144