
Matching of Line Segment for Stereo Computation
O. Martorell, A. Buades and B. Coll
Dpt. Mathematics and Computer Science, Universitat de les Illes Balears,
carret. Valldemossa, km 7,5, 07122 Palma, Spain
Keywords:
Stereo, Matching, Segments, Diffusion, T-junction, Convexity Points.
Abstract:
A stereo algorithm based on the matching of line segments between two images is proposed. We extract
several characteristics of the segments which permit its matching across the two images. A depth ordering
computed from the line segments of the reference image allows us to attribute the match disparity to the
correct pixels. This depth sketch is computed by joining close line segments and identifying T-junctions and
convexity points. The disparity computed for segments is then extrapolated to the rest of the image by means
of a diffusion process. The performance of the proposed algorithm is illustrated by applying the procedure to
synthetic stereo pairs.
1 INTRODUCTION
The human visual system has the ability to infer the
depth of a scene from the two images captured by the
eyes. Our brain is responsible for merging the infor-
mation from the 2D images in order to determine the
depth ordering of objects in scene. This process is
called stereopsis.
The computation of the depth of objects in a scene
is one of the main problems in computer vision. The
computation of such depth has been an intensive re-
search area. If the images are stereo rectified, mean-
ing that the epipolar lines are both horizontal, the
computation of the distance between the observer and
each 3D point, reduces to the computation of the dis-
parity or difference of horizontal coordinates of the
same point in both images.
Numerous algorithms have been proposed in or-
der to compute correspondences between points in
both images. The main classification separates lo-
cal from global algorithms (Scharstein and Szeliski,
2002). Local algorithms match a small window
around each pixel with the most similar window in
the same epipolar line in the second image. Only dis-
tinctive patches can be matched correctly. Small win-
dows without texture or geometry are matched am-
biguously, and therefore matches are discarded. The
most common metrics for this window matching are
based on correlation, intensity differences, and rank
metrics (Tombari et al., 2008). Recent methods adapts
the shape and size of the window to the image content
itself. Windows are preferred to contain only pixels
with the same disparity (Buades and Facciolo, 2015;
Hirschm
¨
uller et al., 2002) or at least belonging to the
same physical object (Patricio et al., 2004; Yoon and
Kweon, 2006; Wang et al., 2006; Rhemann et al.,
2011).
We find local algorithms matching features as
edge segments or contours. These methods are fea-
ture based instead of intensity based, see for in-
stance (Brown et al., 2003) for a review. Even if
feature based matching is less popular than intensity
based, there’s a prominent literature in the field. In
(Nasrabadi, 1992), a stereo matching algorithm based
on the generalized Hough transform of small edge
segments had proposed. In the same line, Ma, Si
and Chen (Ma et al., 1992) utilized a curve based ap-
proach to perform matching by assuming that quadric
based curves exist on the surfaces of the objects in
the scene. Robert and Faugeras (Robert and Faugeras,
1992) approximated edge contours as B- splines and
use these as their matching primitives. In (McCane
and de Vel, 1994), the authors presented a stereo
algorithm based on the matching of free-form con-
tours. This matching process was proposed as a near-
est neighbor problem by using a set of features ex-
tracted from each of the contours.
In contrast to local methods, global methods aim
to determine disparities for all reference image pix-
els at once (Szeliski et al., 2008). This is achieved by
minimizing an energy function composed of a corre-
spondence data term and a regularization term. The
410
Martorell O., Buades A. and Coll B.
Matching of Line Segment for Stereo Computation.
DOI: 10.5220/0006121004100417
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 410-417
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

most commonly used optimization methods for mini-
mization of energy functions are based on graph cuts
(Kolmogorov and Zabih, 2001) and belief propaga-
tion (Sun et al., 2003). Global methods depend on ad-
ditional parameters difficult to fix in general, its value
being different for each stereo pair.
Finally, monocular algorithms are also proposed
in the literature. These algorithms use a single im-
age to infer the depth ordering of objects in the
scene. Making use of a single image, these algorithms
can not estimate the actual depth of the objects but
only which are further or closer. These methods are
based on the computation of T-junctions, convexity
clues and occlusion detection (Dimiccoli et al., 2008;
Calderero and Caselles, 2013; Palou and Salembier,
2013). The algorithm in (Dimiccoli et al., 2008) de-
tects local depth cues based on the response of a line
segment detector LSD, (Grompone von Gioi et al.,
2010). The LSD method is aimed at detecting lo-
cally straight contours on images by using a contrario
validation approach according to Helmholtz princi-
ple. This algorithm joins the Burn’s segment detector
(Burns et al., 1986) with a contrario validation tech-
niques (Desolneux et al., 2000).
In this work, we propose a feature matching al-
gorithm for depth estimation from a stereo pair. We
match line segments across the two images to obtain
a disparity estimate for points belonging to these seg-
ments. Being segment points at the boundary between
two different objects, it is not clear from the segment
description which pixels in the image should have
the estimated disparity. We use the monocular depth
sketch obtained with (Dimiccoli et al., 2008) to re-
move this ambiguity and give the computed estimate
to the closer object. This local depth information de-
fined only on the segments is extrapolated to all the
pixels of the image by applying a non-linear diffusion
process.
The rest of the paper is organized as follows. Sec-
tion 2 introduces the LSD algorithm (Grompone von
Gioi et al., 2010). In Section 3 we describe the
monocular algorithm proposed in (Dimiccoli et al.,
2008). Section 4 presents the proposed algorithm for
stereo matching. In Section 5 we show a set of experi-
ments to validate the proposed algorithm followed by
the conclusion n Section 6.
2 LINE SEGMENT DETECTION
ALGORITHM
In this section we describe the LSD algorithm for de-
tecting line segments introduced by (Grompone von
Gioi et al., 2010), (Grompone von Gioi et al., 2012).
In practice, the LSD algorithm takes a gray-level im-
age as input and returns a list of detected line seg-
ments.
First of all, the algorithm computes a unit vector
field for each pixel of the image, called the level-line
angle, such that all vectors are tangent to the level line
going through their base point. That produces a vec-
tor field in all the image. Then, the vector field is
segmented into connected regions of pixels that share
the same level-line angle up to a threshold parame-
ter. These connected regions of vector fields are called
line support regions. At this point, each line support
region is a candidate for a line segment. The main
rectangle direction is taken as the principal inertial
axis of the line support region. In order to validate or
not the rectangle as a detected line segment, the total
number of pixels in the rectangle, n, and its number
of aligned points, k, are used.
The validation process is based on the a contrario
approach and the Helmholtz principle. This princi-
ple states that no perception (or detection) should be
produced on an image of noise. Then, an event is
validated if the expected number of events as good
as the observed one is small on the a contrario model.
Then, a number of false alarms (NFA) associated with
a rectangle r, gives us the lower bound for the valida-
tion of r.
More concretely, the steps of the algorithm are the
followings:
• The image gradient is computed at each pixel us-
ing a 2 × 2 mask by applying a difference scheme
and using a threshold ρ which depends of the an-
gle tolerance to be used in the region growing al-
gorithm.
• Pixels are classified into the bins according to
their gradient magnitude which correspond to the
more contrasted contours. A threshold is used for
accepting or rejecting the gradient magnitude.
• Starting from a seed pixel in the ordered list of un-
used pixels, a region growing algorithm is applied
to form a line-support region.
• A rectangle associated to a line-support region
must be found. The center of mass of the region is
selected as the center of the rectangle and the main
direction of the rectangle is set to the first inertia
axis of the region. For the width and length of
the rectangles, the parameters are set to the small-
est values that make the rectangle to cover the full
line-support region.
• The pixels in the rectangle whose level-line angle
is equal to the main direction, up to a tolerance pπ,
are called p-aligned points. If the total number
of pixels in the rectangle is denoted by n and the
Matching of Line Segment for Stereo Computation
411

number of p-aligned points is denoted by k, then,
then the number of false alarms (NFA) associated
with the rectangle r is computed in the form
NFA(r) = (NM)
5/2
γB(n,k, p),
where N and M are the number of columns and
rows of the image and B(n, k, p) is the binomial
tail
B(n,k, p) =
n
∑
j=k
n
j
p
j
(1 − p)
n− j
.
Finally, only the rectangles with a NFA less than
a threshold are validated as a detections.
Figure 1: On the left, original image. On the right, the de-
tected segments by applying the LSD algorithm.
3 RELATIVE DEPTH ORDER IN
A SIMPLE IMAGE
In the field of computer vision, the monocular depth
estimation problem tries to extract the depth order of
the objects present in a scene using only information
from a single view or image. Since this information
is partial, in general, the extracted depth relations are
relative in the sense that we can not deduce the abso-
lute depth position of an object in the scene.
In this section, we describe the method (Dimic-
coli et al., 2008) that we will use with minor modifi-
cations. The algorithm estimates the occlusions (be-
tween overlapping objects) and convex contours of
objects. From this low-level features, the depth or-
dering is computed.
For the estimation of the occlusions and convex
contours, we use the list of detected segments of the
image computed from the LSD algorithm. From that,
we found all possible local configurations of the seg-
ments which allow us to detect the T -junctions and
the convexity points. Remember that a T -junction
configuration is formed by the confluence of the
boundary of two different objects and the intersection
point is called a T -junction point. Based on the set of
segments of the image, we define a T -junction point a
point where meet the ends of three different segments
or two segments, and the latter case, only one of them
by the end. By the contrary, a convexity point is a
point where meet the ends of two different segments
and with different slope.
3.1 Algorithm for the T -junction and
Convexity Points Estimation
From the set S = {s
1
,. .. ,s
n
} of detected segment by
applying the LSD algorithm, the output parameters
are the ends segment points, (x
1
i
,y
1
i
) and (x
2
i
,y
2
i
) and
the angle of the slope, θ
i
, i = 1, .. ., n. Note that we
can define a lexicographic order on the ends segment
points by the following rule: (x
1
i
,y
1
i
) ≤ (x
2
i
,y
2
i
) if and
only if x
1
i
< x
2
i
and y
1
i
< y
2
i
if x
1
i
= x
2
i
.
Given two different segments, we define the fol-
lowing rules to decide their relative position.
a) Intersection point: we call X the point of inter-
section of the straight lines which contain the two
segments.
b) Proximity of the segments to the intersection
point: we say that a segment s is near the point of
intersection X if one of the following conditions
holds:
b.1) the end nearest of s to X , ( ¯x, ¯y), satisfy that
the distance d(( ¯x, ¯y),X) is lesser than a certain
threshold.
b.2) the point X belongs to s.
c) Relative position of the segments s
1
and s
2
to be
part of a convexity or T -junction: the difference of
the angles |θ
1
− θ
2
| must be greater than a certain
threshold.
d) Parallel segments: two segments s
1
and s
2
, with
ends segment points, (x
1
l
,y
1
l
) and (x
2
l
,y
2
l
), l = 1,2,
are parallel if the difference |θ
1
− θ
2
| is smaller
than a given threshold. Furthermore, the point of
intersection X must be the midpoint between the
end points (x
1
1
,y
1
1
) and (x
2
2
,y
2
2
) or between (x
2
1
,y
2
1
)
and (x
1
2
,y
1
2
). In both cases, these ends points are
the ends closer.
From these rules, we can define the algorithm to
search T -junction and convexity points.
• A point X is a T -junction point if satisfies one of
the following conditions:
I) In the case of three different segments, it must
be fulfilled the following two conditions:
i1) There exist two segments s
1
and s
2
, with
intersection point X, satisfying conditions a),
b1) and c); or conditions a), b1) and d).
i2) There exist another segment s
3
satisfying
b1), with respect to X , and c), with respect to
s
1
and s
2
.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
412

II) In the case of two different segments, it must
be fulfilled the following two conditions:
i3) There exist two segments s
1
and s
2
, with
intersection point X, satisfying conditions a),
b2) and c).
i4) If X belongs to s
1
, then the distance of the
end nearest of s
1
to X must be greater than a
certain threshold and the distance of the end
nearest of s
2
to X must be lesser than a given
threshold.
• A point X is a convexity point if there exist two
segments s
1
and s
2
, with intersection point X, sat-
isfying conditions a), b1) and c).
3.2 Computation of the Depth
Once calculated the T -junction and convexity points,
the configuration of its neighborhood allows us to
classify the type of singularity. In most situations the
T -junction configuration is formed when two sets A
and B are occluded by a third one C. That means the
neighborhood of the singularity is segmented by three
different regions where region A and B are behind and
C is in front. By the contrary, in the convexity config-
uration, only two regions A and B are determined in
a neighborhood of the singularity.
Let us take a point representative of each of these
regions and assign labels depending on whether the
region is in front (FSP: Foreground Source Point) or
behind (BSP: Background Source Point). In addition,
each label is assigned a numerical value which then
will allow us to extrapolate information from these
points to the other parts of the image using a diffusion
filtering.
For the T-junction configuration, we take the
points m
3
, m
4
and m
1
that represent each region and
are calculated as follows: first we determine the seg-
ment s that separates the regions A and B and compute
the points m
1
and m
2
, which are at the same distance
from the center of the T-junction P and on the straight
line containing s. In this way, thus m
1
is inside C and
m
2
is on s. Now we calculate m
3
and m
4
: they are in
the perpendicular direction to s passing per m
2
and at
the same distance from m
2
, see Figure 2. Since A and
B are behind and C is in front, m
1
is labeled as FSP
while m
3
and m
4
are labeled as BSP.
In the case of convexity configuration, we choose
the points m
1
and m
2
that represent each region and
are calculated as follows: take the points X
1
and X
2
,
which are located on each of the segments and at the
same distance d of the point of intersection of the
two segments P. Then, we choose m
1
and m
2
on the
straight line perpendicular to the line joining X
1
and
X
2
and at the same distance from P, see Figure 3. In
this case, due to the convexity configuration, we as-
sign m
1
and m
2
the labels BSP and FSP, respectively.
The recovery of the relative depth order on the im-
age is achieved by global integration of these local
depth information from the same object by applying a
non-linear diffusion filtering, the Depth Diffusion Fil-
ter (DDF), see (Dimiccoli et al., 2008). To do that, we
consider z(x) the depth value of pixel x. We initialize
as z(x) = 1 the points labeled as FSP while the other
points (labeled as BSP and not labeled) are initialized
as z(x) = 0. Then we apply the DDF:
DDF
r,δ
z(x) = max
y∈B
r
(x)
z(y) · w(x, y), (1)
where
w(x,y) =
1 si |I(x) −I(y)| ≤ δ,
0 si |I(x) −I(y)| > δ.
In the application of this diffusion filter, we need
an additional constraint for the separation of the ob-
jects. In fact, the points labeled as BSP and FSP,
which are in neighboring regions, are related because
we want to preserve the different depth in the inter-
polation process. To do that, we impose that the dif-
ference absolute value between each pair of BSP and
FSP is greater than 1. In Figure 4 we give an example
of the application of the algorithm.
Figure 2: On the left, the T -junction configuration. On the
right, the starting points for the depth computation.
Figure 3: On the left, the convexity point configuration. On
the right, the starting points for the depth computation.
4 STEREO MATCHING
ALGORITHM
We propose an algorithm for computing line segment
correspondences between two images of a stereo pair.
Matching of Line Segment for Stereo Computation
413

Figure 4: On the left, the original image where the three
polygons overlap with each other. On the right, the result
after applying the algorithm. The black color corresponds
to the value of depth three, thus making the rectangle on the
right is ahead of the rest. Furthermore, how strong is gray,
the greater the depth value.
We assume that the images are rectified in epipolar
geometry. We associate to each segment a descriptor
containing several characteristics of it. A cost func-
tion is defined to compare two segments based on
their characteristics. For each segment in the refer-
ence image, the segment in the second image match-
ing with minimum cost is selected.
4.1 Matching Segments
We extract the following features from each segment:
c(1) length of the segment,
c(2) angle of the slope of the segment,
c(3) y-coordinate of the centroid of the segment,
c(4) x-coordinate of the centroid of the segment,
c(5) contrast sign of the segment, which is given by
the sign of the majority of pixels that belong to the
segment. By definition, sign(x,y) = sign(I(x , y)−
I(x +1,y)), where I is the grey level image.
In order to reduce ambiguity in the segment
matching between images I
1
and I
2
, we start discard-
ing those matches which do not agree with the epipo-
lar restriction or would have a too large disparity com-
pared to the camera motion. We apply the following
criteria:
• From the epipolar assumption, if the difference
of the y-centroids between the segment s
1
of I
1
and the segment s
2
of I
2
is greater than a certain
threshold (in practice 5), then we discard the cor-
respondence between s
1
and s
2
.
• Assuming we have some knowledge about the dis-
placement of the camera and from the epipolar
assumption, we also discard the correspondences
between s
1
and s
2
if the difference of their x-
centroids is greater than a certain threshold.
• If the difference between the angles of the seg-
ments s
1
and s
2
is greater than a certain threshold
(in practice π/10), then we discard the correspon-
dence between s
1
and s
2
.
• We also discard the correspondence of a pair of
segments having a different sign contrast.
For the remaining possible correspondences, we com-
pute a cost for each match depending on the charac-
teristics c(k), k = 1, 2,3.
We denote by c
li
(k), k = 1,··· , 3 the features of
the indexed segment s
i
from the left image and by
c
r j
(k), k = 1,··· ,3 the features of the indexed seg-
ment s
j
from the right image. Then the cost function
to match segment s
i
with segment s
j
is defined as
C(i, j) =
3
∑
k=1
W
k
·
c
li
(k) −c
r j
(k)
,
where the weights W
k
, k = 1,2,3, gives more impor-
tance to certain features. Note that for a given seg-
ment s
i
of the left image, min
j
C(i, j) is reached for
some s
¯
j
, where s
¯
j
is a segment of the right image.
Then, we put in correspondence segment s
i
with seg-
ment s
¯
j
.
4.2 Computation of the Disparity Map
Once segment correspondences are estimated we as-
sociate a disparity value to each pixel of the segment.
For a given segment s
i
, suppose that s
¯
j
is the corre-
spondence segment. Let d
1
= x
1
i
−x
1
¯
j
and d
2
= x
2
i
−x
2
¯
j
be the difference between the x -coordinate of both
ends of the paired segments. The disparity value of
all pixels (x,y) of s
i
is given by
d
0
(x,y) = (d
2
− d
1
) · L(x, y) + d
1
, (2)
being
L(x,y) =
q
(x − x
1
i
)
2
+ (y − y
1
i
)
2
q
(x
2
i
− x
1
i
)
2
+ (y
2
i
− y
1
i
)
2
.
That is, the estimated disparity varies linearly be-
tween the disparity of the two end points.
Being a segment the boundary between two ob-
jects, the disparity given to the segment actually is
due to the motion of the occluding object. That is, we
must give this disparity only to pixels belonging to the
occluding object. We use at this point the depth order-
ing computed from the reference image as described
in Section 3.
• Compute the monocular depth for the reference
image.
• For each pixel of the segment, we give the esti-
mated disparity computed in (2) to the neighbor-
ing pixels which are closer to the observer. We
use a mask M to identify pixels (x, y) for which
an estimate was given, M (x,y) = 1. Otherwise,
M(x,y) = 0.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
414
Finally, an iterative diffusion process assigns for a
given pixel, the average of the disparity values of its
neighboring pixels, called Average Depth Diffusion
Filter (ADDF). This average updates only the value
of pixels for which the disparity was not estimated by
the matching process. That is, the values computed
by the segment matching process are maintained con-
stant during the whole process permitting its diffusion
to the rest of pixels. Specifically, we apply the filter
ADDF
r,δ
d(x, y) =
1
W
∑
(i, j)∈B
r
(x,y)
d(i, j) · w(x,y,i, j),
(3)
for pixels with M(x, y) = 0, while originally estimated
pixels are not modified, d(x,y) = d
0
(x,y) if M(x,y) =
1. The weight distribution averages pixels expected to
belong to the same object,
w(x,y,i, j ) =
1 si |I
1
(x,y) −I
1
(i, j)| ≤ δ,
0 si |I
1
(x,y) −I
1
(i, j)| > δ,
and W =
∑
(i, j)∈B
r
(x,y)
w(x,y,i, j ). In practice, the val-
ues of δ and r are fixed to 5 and 3, respectively.
5 EXPERIMENTS
In this section a series of test figures are examined in
order to provide more intuition and understanding of
the proposed method.
First of all, we want to note that for displaying the
disparity on the corresponding image, there is a differ-
ence on the background color of the output disparity
image.
• When the background color is white, all objects
have moved to the left with respect to their posi-
tion in the reference image. And the closer the
level of gray to black, the displacement has been
greater.
• When the background color is black, all objects
have moved to the right with respect to their po-
sition in the reference image. And the closer the
level of gray to white, the displacement has been
greater.
• When the background color is gray level, there ex-
ist objects that have been moved in one direction
or the other. More concretely, objects with color
close to white are shifted to the right and objects
with color close to black, to the left.
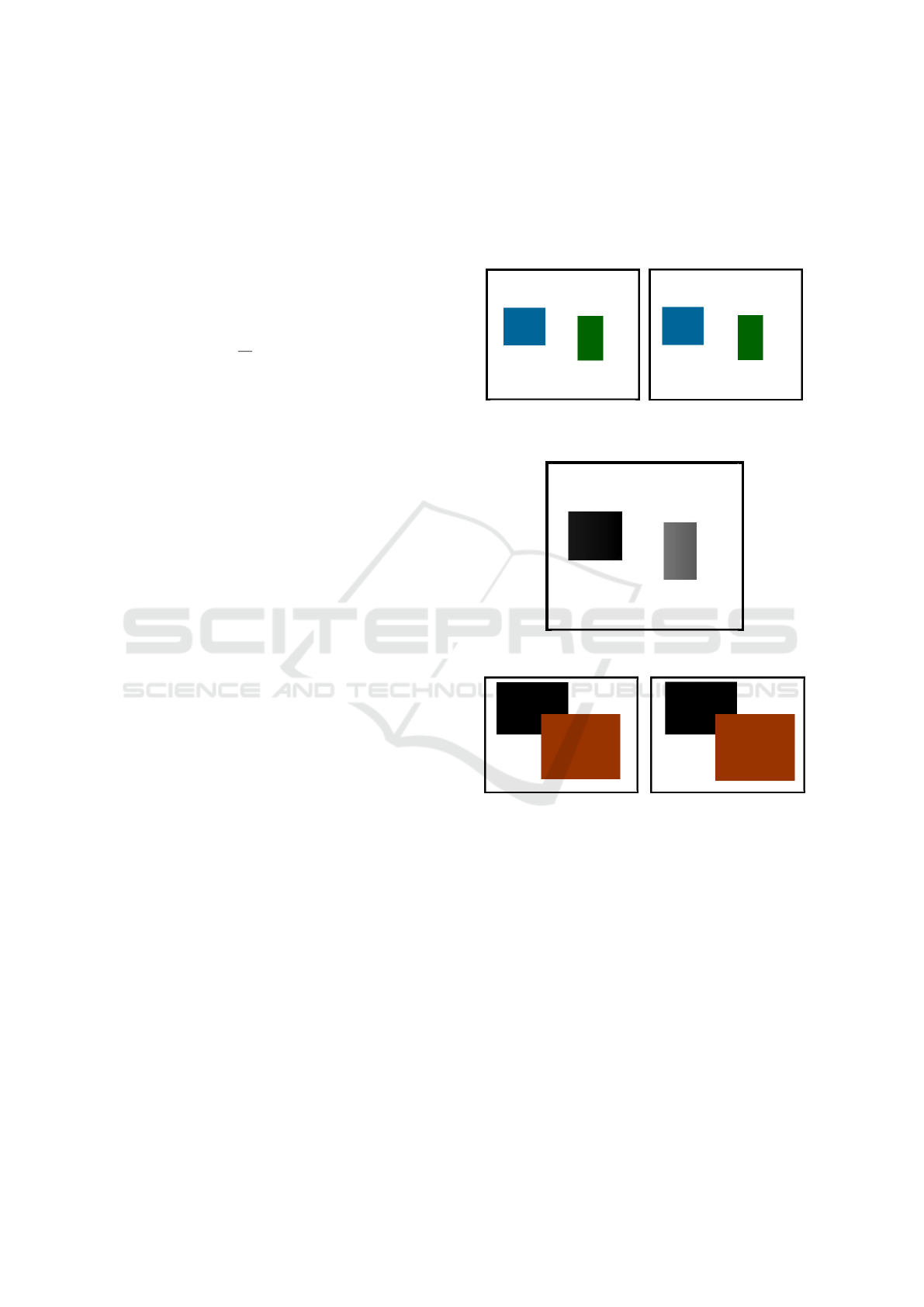
Figure 5 is an example of a pair of stereo images
consisting of two rectangles. The displacement of
each rectangle is different from the other, but the two
movements are uniform. The result is given in Figure
6. The fact that the color is different comes from each
rectangle has moved a different distance and therefore
have a different disparity value. As a consequence,
we can deduce that the blue rectangle is the closest to
the eye or the camera, because it is what is associated
with a greater displacement.
Figure 5: An example of a pair of stereo images with two
rectangles non-overlapping.
Figure 6: The result of the disparity map.
Figure 7: An example of a pair of stereo images consisting
of two overlapping rectangles.
Figure 7 is an example of a pair of stereo images
consisting of two overlapping rectangles that have
moved in the same direction. As in previous example,
the displacement of each rectangle is different from
the other, but the two movements are uniform. Figure
8 shows the final result. Because the background is
black, the two objects have been moved to the right
with respect to its position in the reference image and
the rectangle in front has moved more than the other.
In the following experience, the displacement of
the objects is not uniform, see Figure 9. From the al-
gorithm we get that each segment that makes up the
border of the object tends to have a different dispar-
ity. Applying the filter DDF (1), the result is a jump
disparity between neighboring pixels. However, if we
Matching of Line Segment for Stereo Computation
415

Figure 8: The disparity map after applying our proposed
algorithm to the pair of images of Figure 7.
Figure 9: The pair of stereo images where we suppose that
the displacement of the object is not uniform.
use the averaging filter ADDF (3), then the disparity
is gradually increased, thus causing the grow of the
disparity value is more smooth and continuous from
one border to another one of the polygon. Figure 10
shows the result by the application of the algorithm
to Figure 9. We can see that the gray level increases
from left to right, as the object is displaced in a uni-
form manner. Specifically, the left side has had a dis-
placement greater than the right side. This example
justifies the use of an interpolation method for calcu-
lation of disparity in all the points of a segment: if we
didn’t use this method, the algorithm would give us
the same disparity for all points of the segment, when
really every point of the segment has a different dis-
placement.
Finally, we present an experiment given by the
movement of two rectangles but the polygons are not
parallel to the horizontal axis, which gives lead to ge-
ometrical shape of a rhombus. In addition, each poly-
gon is moving in a different direction, see Figure 11.
Applying the algorithm, we can show the disparity
map on Figure 12. We can observe that each rect-
angle has moved in a different direction and the black
rectangle is closer as it has a greater disparity.
6 CONCLUSIONS
The aim of this work has been to propose a feature
matching algorithm for the stereo vision problem by
using the segments of the image. The experimental
Figure 10: The result of the disparity map. We can see that
the left side has had a displacement greater than the right
side.
Figure 11: The pair of stereo images where the main seg-
ments of the T -junctions are not parallel to the the horizon-
tal axis.
Figure 12: The result of the disparity map. We observe that
each rectangle has moved in a different direction and the
black rectangle is closer as it has a greater disparity.
tests indicate that results are promising for both uni-
form and non-uniform movements and geometric im-
ages.
The future work includes the application of this
algorithm to real stereo pairs and the use of curves
additionally to line segments.
ACKNOWLEDGEMENTS
This work has been partially supported by the Minis-
terio de Ciencia e Innovaci
´
on of the Spanish Govern-
ment under grant TIN2014-53772-R.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
416

REFERENCES
Brown, M. Z., Burschka, D., and Hager, G. D. (2003). Ad-
vances in computational stereo. IEEE Trans. Pattern
Anal. Mach. Intell., 25(8):993–1008.
Buades, A. and Facciolo, G. (2015). Reliable multiscale
and multiwindow stereo matching. SIAM Journal on
Imaging Sciences, 8(2):888–915.
Burns, J., Hanson, H. R., and Riseman, E. M. (1986). Ex-
tracting straight lines. EEE Transactions on PAMI,
8(4):425–455.
Calderero, F. and Caselles, V. (2013). Recovering rela-
tive depth from low-level features without explicit t-
junction detection and interpretation. Int. J. Comput.
Vision, 104(1):38–68.
Desolneux, A., Moisan, L., and Morel, J. (2000). Mean-
ingful alignments. International Journal of Computer
Vision, 40(1):7–23.
Dimiccoli, M., Morel, J.-M., and Salembier, P. (2008).
Monocular depth by nonlinear diffusion. In Proceed-
ings of the 2008 Sixth Indian Conference on Computer
Vision, Graphics & Image Processing, ICVGIP ’08,
pages 95–102, Washington, DC, USA. IEEE Com-
puter Society.
Grompone von Gioi, R., Jakubowicz, J., Morel, J., and G.,
R. (2010). Lsd: A fast line segment detector with a
false detection control. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 32(4):722–732.
Grompone von Gioi, R., Jakubowicz, J., Morel, J.-M., and
Randall, G. (2012). LSD: a Line Segment Detector.
Image Processing On Line, 2:35–55.
Hirschm
¨
uller, H., Innocent, P. R., and Garibaldi, J. (2002).
Real-time correlation-based stereo vision with re-
duced border errors. International Journal of Com-
puter Vision, 47(1-3):229–246.
Kolmogorov, V. and Zabih, R. (2001). Computing vi-
sual correspondence with occlusions using graph cuts.
In Computer Vision, 2001. ICCV 2001. Proceedings.
Eighth IEEE International Conference on, volume 2,
pages 508–515. IEEE.
Ma, S. D., Si, S. H., and Chen, Z. Y. (1992). Quadric curve
based stereo. In ICPR 92, pages 1–4. IEEE.
McCane, B. J. and de Vel, O. (1994). A stereo matching
algorithm using curve segments and cluster analysis.
Technical report, Citeseer.
Nasrabadi, N. M. (1992). A stereo vision technique using
curve-segments and relaxation matching. IEEE Trans.
Pattern Anal. Mach. Intell., 14(5):566–572.
Palou, G. and Salembier, P. (2013). Monocular depth or-
dering using t-junctions and convexity occlusion cues.
IEEE transactions on image processing, 22(5):1926–
1939.
Patricio, M. P., Cabestaing, F., Colot, O., and Bonnet, P.
(2004). A similarity-based adaptive neighborhood
method for correlation-based stereo matching. In Im-
age Processing, 2004. ICIP’04. 2004 International
Conference on, volume 2, pages 1341–1344. IEEE.
Rhemann, C., Hosni, A., Bleyer, M., Rother, C., and
Gelautz, M. (2011). Fast cost-volume filtering for vi-
sual correspondence and beyond. In Computer Vision
and Pattern Recognition (CVPR), 2011 IEEE Confer-
ence on, pages 3017–3024. IEEE.
Robert, L. and Faugeras, O. D. (1992). Curve based stereo:
figural continuity and curvature. In CVPR 91, pages
57–62. IEEE.
Scharstein, D. and Szeliski, R. (2002). A taxonomy and
evaluation of dense two-frame stereo correspondence
algorithms. International journal of computer vision,
47(1-3):7–42.
Sun, J., Zheng, N.-N., and Shum, H.-Y. (2003). Stereo
matching using belief propagation. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
25(7):787–800.
Szeliski, R., Zabih, R., Scharstein, D., Veksler, O., Rother,
C., Kolmogorov, V., Agarwala, A., Tappen, M., and
Rother, C. (2008). A comparative study of energy
minimization methods for markov random fields with
smoothness-based priors. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 30(6):1068–
80.
Tombari, F., Mattocia, S., Stefano, L., and Addimanda, E.
(2008). Classification and evaluation of cost aggrega-
tion methods for stereo correspondence. In Computer
Vision and Pattern Recognition, 2008. CVPR 2008.
IEEE Conference on, pages 1–8. IEEE.
Wang, L., Liao, M., Gong, M., Yang, R., and Nister, D.
(2006). High-quality real-time stereo using adap-
tive cost aggregation and dynamic programming. In
3D Data Processing, Visualization, and Transmission,
Third International Symposium on, pages 798–805.
IEEE.
Yoon, K.-J. and Kweon, I. S. (2006). Adaptive support-
weight approach for correspondence search. IEEE
Transactions on Pattern Analysis & Machine Intelli-
gence, (4):650–656.
Matching of Line Segment for Stereo Computation
417
