Optimizing Distributed Resource Allocation using Epistemic Game

Theory: A Model-driven Engineering Approach

Fazle Rabbi

1,2

, Lars Michael Kristensen

and Yngve Lamo

Bergen University College, Bergen, Norway

University of Oslo, Oslo, Norway

Keywords:

Metamodelling, Epistemic Game Theory, Model Transformation, Optimization, Distributed Systems.

Abstract:

Distributed systems modelling often involves a set of heterogeneous models where each model speciﬁes a

set of local constraints capturing a speciﬁc view of the system. In real life, distributed systems are often

loosely connected and interdependencies are not deﬁned into their software models. This limits the scope of

optimization of distributed resources. In this paper, we merge heterogeneous models of distributed systems

and articulate distributed resource constraints via inter-metamodel constraints. We apply model-driven en-

gineering and use model transformation rules to construct an epistemic game theory model for the purpose

of optimizing distributed resource allocation. Since the application of transformation rules normally do not

guarantee the satisfaction of constraints when applied on a model, it requires a conformance checking which

is an expensive operation. To overcome this problem, we introduce the concept of compliant rule for eﬃcient

model transformation.

1 INTRODUCTION

Distributed systems are organized in a modular,

loosely coupled fashion such as in healthcare organi-

zations, where separate departments deliver diﬀerent

types of healthcare. Each unit in a healthcare orga-

nization deals with a diﬀerent set of operational con-

straints (Pinelle and Gutwin, 2006). Patients often re-

quire a diverse set of services which are provided by

diﬀerent health facilities. However, the medical care

provided by various health facilities are not neces-

sarily optimized to reduce patients’ waiting time and

other important aspects of getting healthcare services.

While optimizing the resource allocation of a

healthcare system, game theory is more suitable

choice as there are many participants and it is required

to reason about optimality respecting patients prefer-

ences and priorities. Healthcare systems need to be

equipped with uncertainty management as many pa-

tients attending do not have an obvious diagnosis at

presentation; also there are varieties of uncertainty in

healthcare (Han et al., 2011). We propose to use epis-

temic game theory for optimizing the use of health-

care resources with the aim of improving the quality

and eﬃciency of healthcare services. Game theory is

the discipline of science that models strategic situa-

tions where individuals reason about others choices

for decision making. Epistemic game theory (Perea,

2012; Perea, 2014) can be viewed as rational deci-

sion making under uncertainty. It can play an im-

portant role in coordinating distributed systems or in

the design of interconnected systems. A model driven

approach for meta-modelling epistemic game theory

was introduced in (Rabbi et al., 2016a). We inves-

tigated how distributed systems may be coordinated

to optimize their resources respecting a distributed

set of local constraints (Rabbi et al., 2016a). How-

ever, there are situations where loosely coupled dis-

tributed systems have to deal with a set of global con-

straints. For instance, patients scheduled appointment

time for getting a healthcare service should not con-

ﬂict with other scheduled appointments for getting

other healthcare services. In this paper, we enhance

the approach with inter-metamodel (i.e., global) con-

straints.

We present our approach with a running example

from the healthcare domain. Let us consider that you

and Barbara are two orthopedic patients at the same

hospital. Both you and Barbara are asked to visit the

department of orthopedic surgery on the same day at

9am. When you report to the front desk of the or-

thopedic department you are asked to take an X-ray

from the radiology department which is located on the

same ﬂoor as the orthopedic department. The ortho-

Rabbi F., Kristensen L. and Lamo Y.

Optimizing Distributed Resource Allocation using Epistemic Game Theory: A Model-driven Engineering Approach.

DOI: 10.5220/0006121400410052

In Proceedings of the 5th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2017), pages 41-52

ISBN: 978-989-758-210-3

pedic department sends an imaging order electroni-

cally to the radiology department which includes pa-

tients information and an instruction about the X-ray.

It took some time for you to reach to the radiology de-

partment as you have a long leg cast. Barbara reported

to the front desk right after you, but she reached the

radiology department before you. The radiology de-

partment is equipped with a queue automation and

therefore you will be served after Barbara. While you

are waiting for your turn at the radiology department

you do not know that Dr. Logan (your doctor) will be

out soon for his round at the inpatient medical wards.

Barbara also does not know that she will not be served

at the orthopedic department before 10.30am because

there are more patients waiting to see her doctor Dr.

Bryan. When you are done with the X-ray and return

to the orthopedic department, you ﬁnd that Dr. Lo-

gan is out for the rounds and you will have to wait

until 12pm. It could have been an optimal decision

to have your X-ray done before Barbara as Barbara

will have to wait until 10.30am anyway. Even though

the orthopedic department and the radiology depart-

ment are located on the same ﬂoor they do not share

their appointment schedules and as a result, the over-

all wait time for patients to get health services are in-

creased. We propose to use epistemic game theory for

optimizing the use of distributed resources and add re-

source constraints to game theory. This paper presents

a formal treatment of distributed resource constraints

via inter-metamodel constraints. For the eﬃcient con-

struction of game theory models we introduce the idea

of compliant rules.

The paper is organized as follows: In section 2, we

present a formal model for distributed resource con-

straints. Section 3 presents a model transformation

technique for resource allocation. Section 4 presents

a game theory model for optimizing resource alloca-

tion. Section 5 introduces compliant rules and co-

ordination of transformation rules, section 6 presents

some related works and section 7 concludes the paper.

2 MODELLING RESOURCE

CONSTRAINTS

Our approach is based on category theory (Barr and

Wells, 1995), model transformations (Ehrig et al.,

2006) and epistemic game theory (Perea, 2012). We

use Diagrammatic Logic (Diskin and Wolter, 2008)

and the Diagram Predicate Framework (DPF) (Rutle,

2010) for the formal development of metamodel spec-

iﬁcations. DPF is suitable for developing domain

speciﬁc modelling languages and has support for an

unbounded number of metalevels. In DPF, a model

is represented by a diagrammatic speciﬁcation S =

(S,C

: Σ) consisting of an underlying graph S to-

gether with a set of atomic constraints C

speciﬁed

by a predicate signature Σ. A predicate signature con-

sists of a collection of predicates, each having a name,

an arity (or shape graph), a visualization, and a se-

mantic interpretation (see Table 1). A predicate is

used to specify a constraint in a model by means of

graph homomorphisms. An atomic constraint (p, δ)

is added to a graph S by a predicate symbol p and

a graph homomorphism δ : α

(p) → S where α

(p)

represents the shape graph of predicate p. DPF pro-

vides a formalization of multi level meta-modelling

by deﬁning the conformance relation between mod-

els at adjacent levels of a meta-modelling hierarchy.

There are two kinds of conformance: typed by and

satisfaction of constraints. Figure 1(i) and (ii) shows

the DPF metamodel speciﬁcations of an orthopedic

department (S

) and a radiology department (S

), re-

spectively. These speciﬁcations are constrained by

predicates from Table 1.

Constraints are added into the speciﬁcations by

graph homomorphisms from the shape graph of the

predicates to the model elements. Below is a list of

constraints speciﬁed in S

and S

• C1. A patient must have exactly one birthdate in

an instance of S

(speciﬁed by <mult(1,1)> )

• C2. A person must have exactly one birthdate in

an instance of S

(speciﬁed by <mult(1,1)> )

• C3. An appointment time-slot (i.e., TS@Dept)

allocated to a patient in an instance of S

must

belong to that patients assigned doctor (speciﬁed

by <composite>)

• C4. A person can only check-in for an exami-

nation in an instance of S

if the person has an

imaging order (speciﬁed by <pre-condition>)

• C5. Only registered persons are allocated with

examination time-slots (i.e., TS@Lab) in an in-

stance of S

(speciﬁed by <pre-condition>)

• C6. An appointment time-slot in an instance of

must not be allocated to more than one patient

(speciﬁed by <injective>)

• C7. An exam time-slot in an instance of S

must

not be allocated to more than one person (speci-

ﬁed by <injective>)

2.1 Distributed Resource Constraints

Usually orthopedic doctors need to inspect the X-ray

reports of the patient during consultation. Therefore

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development

TS@Dept

assigned

Doctor

[1..1]

belongsTo

birthdate

Imaging

Exam

hasOrder

admittedTo

Doctor

Patient

Department

Date

Prescription

[comp]

TS@Lab

checkin

[1..1]

birthdate

Imaging

Exam

hasOrder

Registration

Person

Dept

Date

Report

[Pcond]

birthdate

Imaging

Exam

hasOrder

Patient

Dept

Date

( i )

( iii )

( ii )

TS@Dept

assigned

Doctor

[1..1]

belongsTo

checkin

admittedTo

orderingDept

Doctor

Patient

Dept

Registration

Imaging

Exam

[comp]

Prescription

Date

birthdate

Report

[Pcond]

TS@Lab

( iv )

[1..1]

Figure 1: (i) Metamodel speciﬁcation of an orthopedic department, (ii) Metamodel speciﬁcation of a radiology department,

(iii) overlap speciﬁcation, (iv) merged metamodel speciﬁcation with an inter-metamodel constraint.

Table 1: Predicates of a signature, Σ.

p Arity Visualization Semantic interpretation

f must have at least n and

at most m instances for

each instance of X

For each instance of f there

exists an instance of g with the

same source node

For each composition of

instances f;g, there exists an

instance of h

If there are instances of f and g

with the same source node,

then there exists an ordering of

values between instances of Y

and Z

Instances of f never maps

distinct elements of its domain

to the same element of its

codomain

<mult

(n,m

<pre

condition>

1 2

X Y

[Pcond]

[n..m]

[comp]

X Y

[prcd]

1 2

[inj]

α (p)

∑

orthopedic patients’ time-slot at the radiology depart-

ment must be preceded by the time-slot at the orthope-

dic department. We will refer to this constraint as C8.

We use the concept ‘time-slot’ for an appointment or

an examination to represent the time assigned for a

scheduled job. A time-slot t2 which include informa-

tion about the start-time and end-time of a scheduled

job is preceded by a time-slot t1 if the end-time of t2

are less than the end-time of t1. To model this dis-

tributed resource constraint, we need to merge speci-

ﬁcations S

and S

While merging speciﬁcations, atomic constraints

speciﬁed in the component metamodel speciﬁcations

need to be preserved. We merge speciﬁcations in such

a way that for any component metamodel speciﬁca-

tion S

there exists a speciﬁcation morphism from S

to the merged metamodel speciﬁcation. The deﬁni-

tion of speciﬁcation morphism is given below (Rutle,

2010):

Deﬁnition 1 (Speciﬁcation Morphism). Given two

speciﬁcations S = (S,C

: Σ) and S

= (S

: Σ),

a speciﬁcation morphism φ : S → S

is a graph

homomorphism φ : S → S

such that for any atomic

constraint (p, δ) ∈ C

implies (p,δ; φ) ∈ C

illustrated in the following diagram.

α (p)

∑

’

δ;Ф

Diskin et al. presented an approach of merging

metamodels by making metamodels explicit and by

introducing a correspondence span between compo-

nent metamodels (Diskin et al., 2010) (Diskin, 2011).

We adapt the approach with speciﬁcation morphisms

in order to preserve constraints into the merged meta-

model speciﬁcations. Details of merging heteroge-

neous metamodels and specifying inter-metamodel

constraints can be found in (Diskin et al., 2010). Un-

like (Diskin et al., 2010), in our approach the head

of the span is an overlap speciﬁcation given in DPF

which speciﬁes the common concepts of both meta-

models and the legs of the span are speciﬁcation

Optimizing Distributed Resource Allocation using Epistemic Game Theory: A Model-driven Engineering Approach

morphisms. Figure 1(iii) shows the overlap speciﬁ-

cation S

= (S

: Σ) (highlighted in grey) and

Figure 1(iv) shows the merged metamodel speciﬁca-

tion S

= (S

: Σ). S

is constructed by merg-

ing component metamodel speciﬁcations S

and S

modulo their overlap S

(i.e., common elements ap-

pear only once in the merge). Overlaps are speciﬁed

by two speciﬁcation morphisms S

←−− S

−−→ S

where S

contains all common concepts, S

and S

are the underlying graphs of speciﬁcations S

and

. Any pair of elements x

∈ S

and x

∈ S

are

considered to be the same if there is an element

x ∈ S

such that ψ

(x) = x

and ψ

(x) = x

. Fol-

lowing (Diskin et al., 2010), we call this conﬁgu-

ration of metamodel speciﬁcations and mappings a

multi-metamodel speciﬁcation M, and write M =

, S

, ψ

). The multi-metamodel speciﬁ-

cation M declares the uniﬁcation of concepts Date,

birthdate, hasOrder, ImagingE xam, orderingDept

and uniﬁes also the following concepts:

• Patient and Person since ψ

(Patient) = Patient

and ψ

(Patient) = Person

• Department and Dept since ψ

(Dept) =

Department and ψ

(Dept) = Dept

The mappings φ

: S

→ S

and φ

: S

→ S

in Figure 1 maps elements from S

and S

to the cor-

responding elements in S

Deﬁnition 2 (Merged Metamodel Speciﬁcation).

Given two (component) metamodel speciﬁcations

= (S

: Σ) and S

= (S

: Σ), a merged

metamodel speciﬁcation S

= (S

: Σ) of S

and S

is given by two speciﬁcation morphisms

: S

→ S

, φ

: S

→ S

and a multi-metamodel

speciﬁcation M = (S

, S

, ψ

) such that the

graph S

is obtained by the pushout of ψ

and ψ

This is illustrated in the following diagram:

∑

α (p ) ....

δ ;

∑

... α (q )

δ'

δ‘ ;

∑

α (d )

...

δ ; = δ ;

The binary case can be generalized to the N-ary

case by constructing S

as a so-called colimit and

preserving all the atomic constraints speciﬁed in the

component metamodels. Constraints of component

metamodel speciﬁcations are preserved in a merged

metamodel speciﬁcation. Additional constraints may

be added into a merged metamodel speciﬁcation.

The distributed resource constraints are added into

the merged metamodel speciﬁcation by means of

inter-metamodel constraints. The distributed resource

constraint C8 is added into S

by using the predicate

<precede>. In general, merged metamodel speciﬁca-

tions have the following properties:

Theorem 1. Let S

be a merged metamodel spec-

iﬁcation obtained from component metamodel spec-

iﬁcations S

, . . . S

. For any component metamodel

speciﬁcation S

(1 ≤ i ≤ n), there exists a speciﬁcation

morphism from S

to S

Proof. This follows directly from the deﬁnition of

merged metamodel speciﬁcation. 

A model (I,ι) of a metamodel speciﬁcation S =

(S,C

: Σ) is a graph I together with a typing graph

homomorphism ι : I → S . In order to be a valid model

of a metamodel speciﬁcation S the typing morphism

must satisfy the atomic constraints speciﬁed in C

Here we deﬁne the merged model of two component

models.

Deﬁnition 3. Given two (component) models

, ι

), (I

, ι

) of metamodel speciﬁcations S

, S

and an overlap model I

←−− I

−−→ I

typed by the

overlap speciﬁcation of S

and S

. The merged

model is a graph I

together with a typing graph

homomorphism ι

: I

→ S

where S

is the under-

lying graph of the merged metamodel speciﬁcations

of S

, S

such that the graph I

is obtained by the

pushout of g

and g

and the top face constitute a

van Kampen square in the category of Graph as

illustrated in the following diagram:

(top)

The reader interested in the property of van Kam-

pen square may wish to consult (Mantz, 2014). It is

possible that the atomic constraints when preserved in

a merged metamodel speciﬁcation may conﬂict with

other constraints or may become redundant. There

exists some research for detecting these problems au-

tomatically such as the alloy analyzer which may be

used to detect these problems by speciﬁcation anal-

ysis (Wang et al., 2015). An atomic constraint speci-

ﬁed in a component metamodel and satisﬁed in a com-

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development

ponent model may become unsatisﬁable in a merged

model or vice versa. Figure 2 shows an example of

a model merge where a component model (I

, ι

) is

typed by the underlying graph S

of the metamodel

speciﬁcation S

. The predicate p is used to con-

straint S

by a graph homomorphism δ : α

(p) → S

The edge 1

−−→ 2 is mapped to A

−→ B and the edge

−−→ 1 is mapped to B

−→ A. The overlap speciﬁ-

cation is given by (S

, S

, ψ

) which uniﬁes

of the following concepts: A and AA, B and BB. To

check if (I

, ι

) satisﬁes the constraint (p, δ) we extract

the fragment (O

∗

) of the component model that is af-

fected by the constraint. Again, to check if the merged

model (I

, ι

) satisﬁes the constraint (p, δ;φ

) we ex-

tract the fragment (O

∗

) of the merged model that is af-

fected by the constraint. The object O

∗

is obtained by

the pullback of α

(p)

−→ S

←− I

and the object O

∗

is obtained by the pullback of α

(p)

δ;φ

−−−−→ S

←−− I

Since we obtain two diﬀerent objects by the pullback

operation, it is possible that the satisfaction of the lo-

cal constraint will vary.

Typing, l

1 2

(p)

∑

PB(1)

δ*

AA BB AA BB

a b

AA BB

δ*

PB(2)

Ф*

δ;

Figure 2: Construction of pullback for a component model

and merged model I

3 RESOURCE ALLOCATION

Our example introduced earlier consists of two com-

ponent metamodels representing two distributed sys-

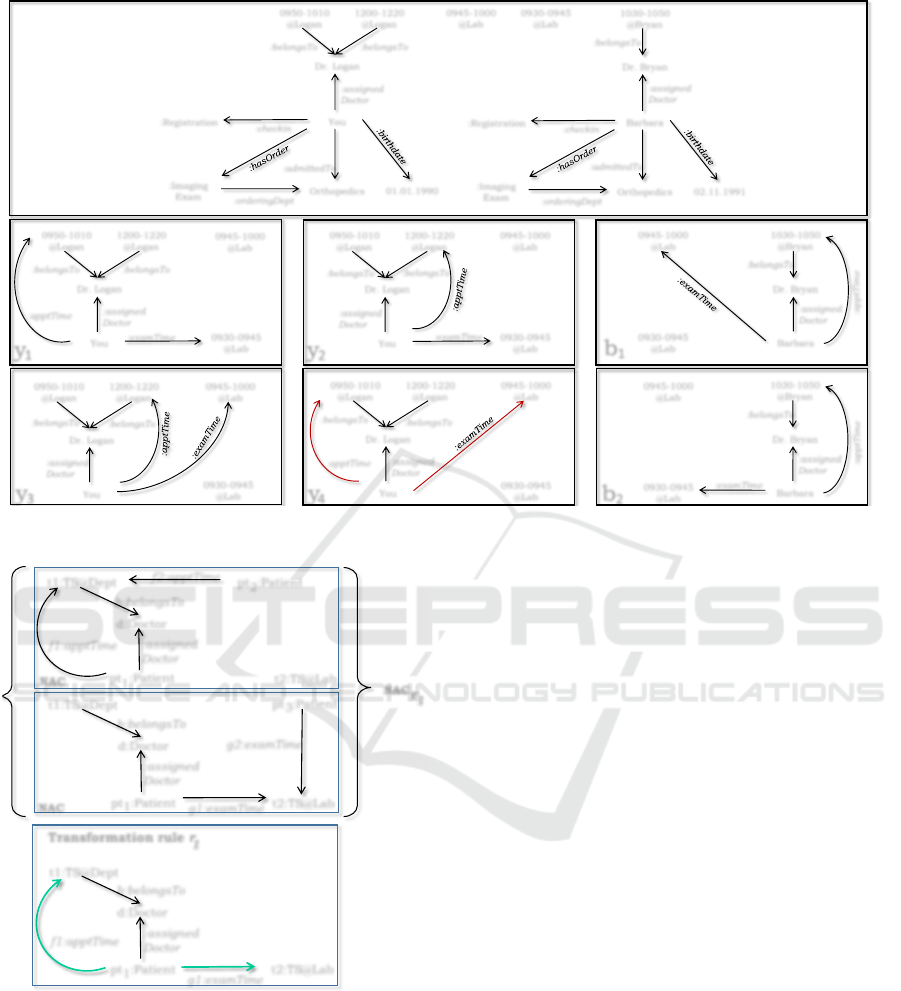
tems and an inter-metamodel constraint C8. Figure 3

shows a model (I, ι

) of the merged metamodel S

of Figure 1. The typing ι

of the modelling elements

are not explicitly represented in the ﬁgure. In the ﬁg-

ure, You and Barbara are instances of Patient, your

assigned doctor is Dr.Logan and Barbara’s assigned

doctor is Dr.Bryan. Dr. Logan has two available time-

slots: 0950 − 1010@Logan and 1200 − 1220@Logan

and Dr. Bryan has one available time-slot: 1030 −

1050@Bryan. There are two available time-slots

at the radiology department: 0945 − 1000@Lab and

0930− 0945@Lab. In time-slot 0950− 1010@Logan,

09:50 is the start time and 10:10 is the end time.

Model (I,ι

) need to be completed with resource al-

location for you and Barbara at the radiology and or-

thopedic department. One can ﬁnd that there are four

possible choices of resource allocation for you and

two possible choices of resource allocation for Bar-

bara with the available resources.

We use a transformation approach where transfor-

mation rules have a set of negative application condi-

tions proposed by Lambers et al., in (Lambers et al.,

2008) for allocating resources to the patients. Figure 4

illustrates a rule r

typed by the merged metamodel

. The typing information of a modelling element

in r

appears after a colon (:). The rule speciﬁes that

a patient pt

is allocated with an appointment time-

slot t1 and an exam time-slot t2 if t1 belongs to pt

’s

assigned doctor d and t1, t2 are not allocated to any

other patient. The green color is used to indicate el-

ements that the rule is going to produce. Negative

application conditions (NACs) are typically used in

graph transformation to prohibit an inﬁnite number of

rule applications.

The rule can be applied over the model (I,ι

) in

six diﬀerent ways since there are six matches. Fig-

ure 3 shows brieﬂy the choices of resource allocation

for you in y

− y

and for Barbara in b

, b

. y

shows a

resource allocation where you are assigned with exam

time-slot 0930 − 0945@Lab at the radiology depart-

ment and appointment time-slot 0950− 1010@Logan

at the orthopedics department with Dr. Logan. This

resource distribution is valid since it is not violating

any constraint. Similarly, other valid resource distri-

butions are y

, y

, b

and b

. However y

is not valid

as it is violating the distributed resource constraint

C8: your exam time-slot 0945 − 1000@Lab must

be preceded by your appointment time-slot 0950 −

1010@Logan.

We apply epistemic game theory for the optimiza-

tion of resources over the valid choices of resource

allocation. Epistemic game theory is a broad area of

research that formalizes the assumptions about ratio-

nality and mutual beliefs in a formal language to an-

alyze games. It introduces a Bayesian perspective on

decision-making in strategic situations. In a strate-

gic game, the outcome does not only depend on the

choice of a single player but also on the choices of

other players. The combination of all the players’

choices is called a strategy proﬁle. From an epistemic

point of view, the strategy proﬁle should include the

beliefs players have about each other’s possible ac-

tions (and beliefs). This model of interdependent de-

cision making can essentially represent a wide array

of social interactions. A metamodel for modelling

epistemic aspects of a system as presented in (Rabbi

et al., 2016a) is shown in Figure 5. Players in an epis-

Optimizing Distributed Resource Allocation using Epistemic Game Theory: A Model-driven Engineering Approach

:assigned

Doctor

:belongsTo

:checkin

:admittedTo

:orderingDept

Dr. Logan

You

Orthopedics

:Registration

:Imaging

Exam

01.01.1990

0945-1000

@Lab

:assigned

Doctor

:belongsTo

:checkin

:admittedTo

:orderingDept

Dr. Bryan

Barbara

Orthopedics

:Registration

:Imaging

Exam

02.11.1991

0930-0945

@Lab

0950-1010

@Logan

1200-1220

@Logan

:belongsTo

1030-1050

@Bryan

:assigned

Doctor

:belongsTo

Dr. Logan

You

0945-1000

@Lab

0930-0945

@Lab

0950-1010

@Logan

1200-1220

@Logan

:belongsTo

:examTime

:apptTime

:assigned

Doctor

:belongsTo

Dr. Logan

You

0945-1000

@Lab

0930-0945

@Lab

0950-1010

@Logan

1200-1220

@Logan

:belongsTo

:assigned

Doctor

:belongsTo

Dr. Logan

You

0945-1000

@Lab

:assigned

Doctor

:belongsTo

Dr. Bryan

Barbara

0950-1010

@Logan

1200-1220

@Logan

:belongsTo

1030-1050

@Bryan

:apptTime

:assigned

Doctor

:belongsTo

Dr. Logan

You

0945-1000

@Lab

:assigned

Doctor

:belongsTo

Dr. Bryan

Barbara

0950-1010

@Logan

1200-1220

@Logan

:belongsTo

1030-1050

@Bryan

:apptTime

:examTime

:apptTime

0930-0945

@Lab

0930-0945

@Lab

:examTime

0945-1000

@Lab

0930-0945

@Lab

0945-1000

@Lab

0930-0945

@Lab

Figure 3: A model (I,ι

) of S

(top) and individual resource allocation.

pt :Patient

t1:TS@Dept

pt :Patient

f2:apptTime

pt :Patient

t2:TS@Lab

f1:apptTime

b:belongsTo

t1:TS@Dept

g1:examTime

d:Doctor

:assigned

Doctor

f1:apptTime

g1:examTime

pt :Patient

t2:TS@Lab

pt :Patient

g2:examTime

Transformation rule r

NAC

b:belongsTo

d:Doctor

:assigned

Doctor

b:belongsTo

d:Doctor

:assigned

Doctor

t1:TS@Dept

t2:TS@Lab

Figure 4: Transformation rule r

for individual resource al-

location of patients.

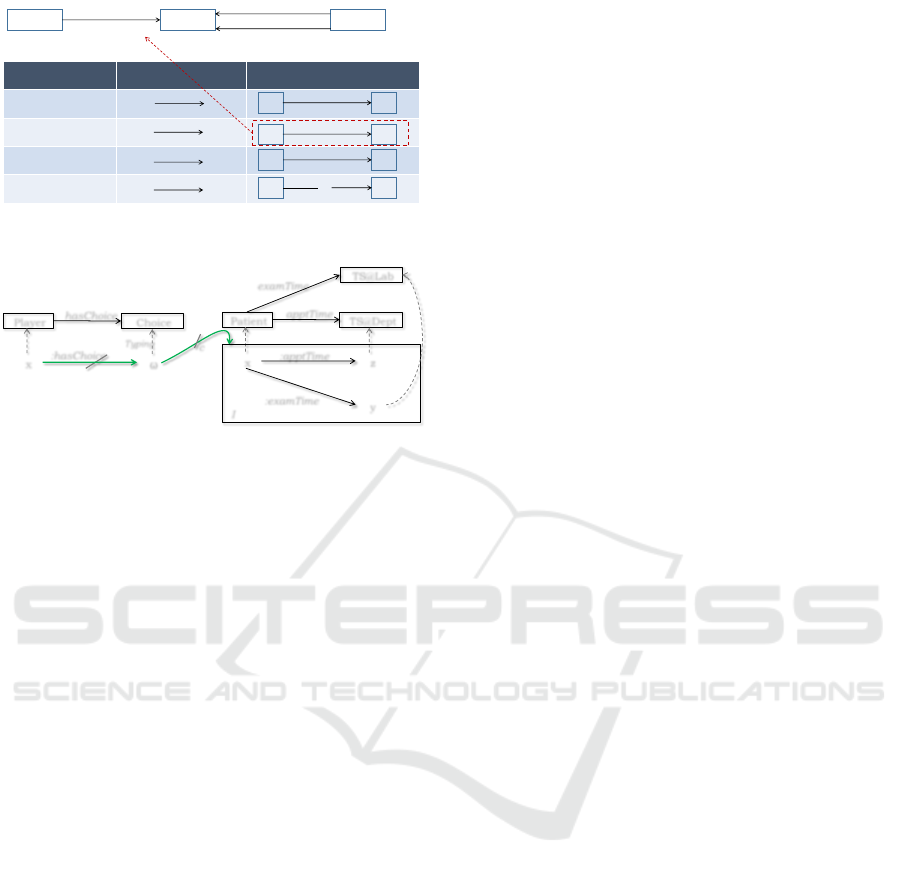
temic game may have choices. The surjective con-

straint imposed on the hasChoice relation ensures that

instances of Choice must be associated with players.

An instance of Belie f connects the choices of a player

with other players’ choices denoting the choice com-

bination of players. In game theory, utility represents

the motivation or satisfaction of players. The higher

the utility the more the outcome is preferred. We use

the <utility(n)> predicate to assign utility to an in-

stance of a belief. A utility assigned to an instance of

a belief denotes the utility that a player derives from

the outcome induced by the choice combination. We

use the <prob(r)> predicate to annotate an instance

of a belief with probability. Of course in a healthcare

setting, patients do not have to know about each oth-

ers choices; they are not expected to make decisions

for mutual beneﬁts. We propose to construct a strat-

egy proﬁle for them indirectly with an aim to optimize

resource allocation respecting patients’ preferences.

Given an initial epistemic model ξ of the meta-

model in Figure 5 with two instances of Player: You

and Barbara, we use coupled model transformation

rules to automatically produce choices for you and

Barbara. For each valid choice of resource alloca-

tion of individual patients from Figure 3, we create

choices in ξ. The special kind of coupled transfor-

mation rule with coordinating edges creates choices ξ

and establishes links from choices to instances of the

merged metamodel S

. Coordinating edges are used

to co-ordinate between heterogeneous models and or

modelling elements (Rabbi et al., 2014) (Rabbi et al.,

2015). Figure 6 shows a transformation rule that iden-

tiﬁes a player and produces choices for the player.

The rule speciﬁes that if we have an instance x of type

Player in the epistemic model and x is an instance of

Patient in a model (I, ι

) of S

, such that x is allocated

with an appointment time-slot z and an exam time-slot

y, then we create an epistemic choice ω for player x

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development

Player Choice Belief

source

[1..*]

hasChoice

[surj]

Predicate, p Arity Visualization

mult(n,m)>

surjective>

prob(r)>

utility(n)>

X Y

[n..m]

X Y

[surj]

1 2

target

[1..*]

1 2

X Y

(r)

constraint

1 2

X Y

Figure 5: Metamodel for modelling epistemic aspects.

Typing

Patient

TS@Dept

x z

:apptTime

apptTime

Player

Choice

:hasChoice

hasChoice

:examTime

TS@Lab

examTime

Typing, ι

Model (I, ι )

Figure 6: Transformation rule r

for producing epistemic

choices.

in the epistemic model and create a coordinating edge

c linking the choice ω to the model (I,ι

Figure 7 illustrates the result of the application

of this transformation rule over the possible choices

of resource allocation from Figure 3. Figure 7(left)

shows an epistemic model ξ where You and Barbara

are instances of Player. Choices for you and Bar-

bara are produced in ξ where the choices are linked

to the models of the merged metamodel S

in Fig-

ure 7(right) by coordinating edges shown in blue.

Note that we only produce epistemic choices for valid

models of the entity metamodel. Since y

is not a

valid model, we did not produce any epistemic choice

for y

Figure 8 brieﬂy presents the coordinating meta-

model used for coordinating heterogeneous metamod-

elling hierarchies. The coordinating metamodel spec-

iﬁes that we may have coordinating-edges between

nodes. The coordinating-edge may be instantiated

in an arbitrary level of a metamodelling hierarchy.

Rossini et al. presented a formal way of specify-

ing this requirement in DPF using deep metamod-

elling (Rossini et al., 2012). A reference with multi-

potency at a metalevel i can be instantiated in all

metalevels below i. Since the coordinating-edge has

multi-potency, it can be instantiated in an arbitrary

metalevel. In Figure 8, S

, y

are placeholder

nodes representing the identity of the (meta)models.

The instance of the coordinating-edge c

establishes

a link between an epistemic choice instance to the in-

stance y

by referring to the node y

4 OPTIMIZATION OF

RESOURCE ALLOCATION

In this section we discuss how resource allocation

of distributed systems may be optimized using epis-

temic game theory. In our example, the patients were

asked to come to the hospital at 9am and the clinic

at the orthopedic department remains open until 5pm.

Therefore, the maximum time spent by the patients

to get healthcare services could be 8 hours (480 min-

utes). We calculate the utility based on the time spent

at the hospital by the patients to get healthcare ser-

vices. If a patient spends m minutes in total to get

services, then her utitity is (480 − m). Therefore, the

longer the patients are waiting, the lower utility they

get. Our target is to optimize the resource alloca-

tion for the patients so that their wait time will be

reduced. Consider the choice y

for you, which rep-

resents the resource allocation of 0930 − 0945@Lab

and 0950 − 1010@Logan. This gives a utility of

480 − 70 = 410 as you are spending only 70 minutes

at the hospital to get your services. Similarly, we can

calculate Barbara and your utilities and complete the

epistemic model ξ with belief instances by perform-

ing a Cartesian product of Barbara and your choices

as shown in Figure 9. Curved arrows in Figure 9 are

representing belief instances which will be referred to

as belief arrows. The belief arrow from y

to b

with

an attribute 410 is representing an instance of Belie f

with utility 410.

An essential element of epistemic game theory

analysis is the notion of belief hierarchies which are

used to characterize solution concepts. We obtain be-

lief hierarchies from an epistemic model by following

belief arrows starting from any choice of a player. In

our epistemic model we are only considering simple

belief hierarchies. The idea of a simple belief hier-

archy states that the whole belief hierarchy may be

summarized by a combination of beliefs about play-

ers’ choices. A belief hierarchy is simple if it con-

tains at most one belief of each player. The epistemic

model in Figure 9 represents six simple belief hier-

archies of which three are: (i) y

410

−−−→ b

370

−−−→ y

; (ii)

410

−−−→ b

370

−−−→ y

; (iii) y

280

−−−→ b

370

−−−→ y

. Typically a

belief hierarchy speciﬁes a player’s belief over other

players’ beliefs but in the healthcare context we use a

belief hierarchy to specify a systems belief about pa-

tient’s choices. The belief hierarchy y

410

−−−→ b

370

−−−→ y

can be read as: the system believes that you will con-

sider making appointments represented in y

if Bar-

bara considers making appointments represented in

; and Barbara considers making appointments rep-

resented in b

if you consider making appointments

Optimizing Distributed Resource Allocation using Epistemic Game Theory: A Model-driven Engineering Approach

:assigned

Doctor

:belongsTo

Dr. Bryan

Barbara

1030-1050

@Dept

:examTime

:apptTime

0945-1000

@Lab

0930-0945

@Lab

:assigned

Doctor

:belongsTo

Dr. Bryan

Barbara

1030-1050

@Dept

:apptTime

0945-1000

@Lab

0930-0945

@Lab

:assigned

Doctor

:belongsTo

Dr. Logan

You

0945-1000

@Lab

0930-0945

@Lab

0950-1010

@Dept

1200-1220

@Dept

:belongsTo

:assigned

Doctor

:belongsTo

Dr. Logan

You

0945-1000

@Lab

0950-1010

@Dept

1200-1220

@Dept

:belongsTo

0930-0945

@Lab

:examTime

Entity models (Instances of the merged

metamodel shown in Figure 1)

Epistemic model

Barbara

:hasChoice

:assigned

Doctor

:belongsTo

Dr. Logan

You

0945-1000

@Lab

0930-0945

@Lab

0950-1010

@Logan

1200-1220

@Logan

:belongsTo

:examTime

:apptTime

You

:hasChoice

y ( )

0930-0945@Lab

0950-1010@Logan

y ( )

0930-0945@Lab

1200-1220@Logan

y ( )

0945-1000@Lab

1200-1220@Logan

b ( )

0945-1000@Lab

1030-1050@Bryan

b ( )

0930-0945@Lab

1030-1050@Bryan

Figure 7: Epistemic choices produced by the application of model transformation rules.

0950-1010

@Logan

:belongsTo

:assign

Doctor

Dr. Logan

You

0950-1010

@Logan

120

:belongsTo

:apptTime

0950-1010

@Logan

:belongsTo

:assign

Doctor

:be

Dr. Logan

You

0950-1010

@Logan

120

:belongsTo

:apptTime

You

:hasChoice

y ( )

0930-0945@Lab

0950-1010@Logan

y ( )

0930-0945@Lab

1200-1220@Logan

Node

coordinating-edge

arrow

TS@Dept

belongsTo

checkin

Registration

[comp]

[Pcond]

TS@Lab

Player Choice

[1..*]

hasChoice

[surj]

[1..*]

Figure 8: Heterogeneous metamodelling with Coordinating

metamodel.

Barbara

You

:hasChoice

y ( )

0930-0945@Lab

0950-1010@Logan

y ( )

0930-0945@Lab

1200-1220@Logan

y ( )

0945-1000@Lab

1200-1220@Logan

b ( )

0945-1000@Lab

1030-1050@Bryan

b ( )

0930-0945@Lab

1030-1050@Bryan

410

370

410

370

280

370

280

370

280

370

280

370

Figure 9: Epistemic model with combination of beliefs.

represented in y

. In our approach, uncertainty can

be modelled by assigning probability to the belief ar-

rows.

An important concern regarding the belief hierar-

chies is their consistency. A consistent belief hier-

archy represents a solution concept that satisﬁes all

the constraints speciﬁed in the metamodel speciﬁca-

tions. Following (Rabbi et al., 2016a) we determine

how inconsistent combination of beliefs can be au-

tomatically removed from an epistemic model. If a

combination of beliefs includes choices from a ho-

mogeneous metamodel, then the models are merged

into a single model. For instance if we wish to check

if the combination of beliefs represented by the be-

lief hierarchy y

410

−−−→ b

370

−−−→ y

is consistent, we need

to merge the models linked to y

and b

since they

are typed by the merged metamodel S

. The merged

model is then checked for consistency and if it vi-

olates any constraint speciﬁed in its metamodel, we

conclude that the combination of beliefs is incon-

sistent and should be discarded from the epistemic

model.

The combination of beliefs represented by the be-

lief hierarchy y

410

−−−→ b

370

−−−→ y

is inconsistent as the

merged instance is violating constraint C7 (see sec-

tion 2). The reason is that according to the injec-

tive constraint imposed on the reference examT ime,

patients cannot have the same time-slot. Therefore,

assigning time-slot 0930 − 0945@Lab to both of you

and Barbara is making the merged instance inconsis-

tent. To check that a constraint is satisﬁed in a given

model of a metamodel, we inspect the part of a model

which is aﬀected by the constraint. This is checked

by projecting out the part of the model which is af-

fected by the constraint. This is formally deﬁned as a

pullback operation in category theory.

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development

Similarly we can show that the combination of

beliefs represented by the belief hierarchies y

280

−−−→

370

−−−→ y

, y

280

−−−→ b

370

−−−→ y

are inconsistent. Fig-

ure 10 shows an epistemic model with only consistent

combination of beliefs.

Barbara

You

:hasChoice

y ( )

0930-0945@Lab

0950-1010@Logan

y ( )

0930-0945@Lab

1200-1220@Logan

y ( )

0945-1000@Lab

1200-1220@Logan

b ( )

0945-1000@Lab

1030-1050@Bryan

b ( )

0930-0945@Lab

1030-1050@Bryan

410

370

280

370

280

370

Figure 10: Epistemic model with consistent combination of

beliefs.

Barbara

You

:hasChoice

y ( )

0930-0945@Lab

0950-1010@Logan

y ( )

0930-0945@Lab

1200-1220@Logan

y ( )

0945-1000@Lab

1200-1220@Logan

b ( )

0945-1000@Lab

1030-1050@Bryan

b ( )

0930-0945@Lab

1030-1050@Bryan

410

370

280

370

Figure 11: Epistemic model with rational combination of

beliefs.

The epistemic choice y

which represents the re-

source allocation of 0930 − 0945@Lab and 1200 −

1220@Logan is not a rational choice since this is not

optimal for any of the epistemic choices for Barbara.

If you are allocated with time-slot 0930 − 0945@Lab

at the radiology department, it will be optimal for

you to see the doctor in appointment time-slot 0950 −

1010@Logan. Therefore, the epistemic choice y

dominated by y

. The epistemic choice y

is a ratio-

nal choice since this is optimal if Barbara is allocated

with time-slot 0930 − 0945@Lab at the radiology de-

partment.

Figure 11 shows belief combinations with rational

choices. The combination of beliefs is rational as the

choices consist of the belief combinations are all ra-

tional choices with respect to the choice combination

represented by the combination of beliefs.

Following (Perea, 2012) (Rabbi et al., 2016a), a

simple belief hierarchy generated by a combination

of beliefs leads to a Nash equilibrium if the combi-

nation of beliefs is rational. Therefore, we obtain two

Nash equilibria from the epistemic model represented

in Figure 11:

• Allocating time-slot 0930 − 0945@Lab and

0950 − 1010@Logan for you is rational if time-

slot 0945 − 1000@Lab and 1030 − 1050@Bryan

are allocated to Barbara gives a total utility of

(410 + 370) = 780;

• Allocating time-slot 0945 − 1000@Lab and

1200 − 1220@Logan for you is rational if time-

slot 0930 − 0945@Lab and 1030 − 1050@Bryan

are allocated to Barbara gives a total utility of

(280 + 370) = 650.

However, the ﬁrst equilibrium has a higher total

utility for the system.

5 COORDINATION OF

TRANSFORMATION RULES

Scalability is an important issue regarding the appli-

cation of optimization techniques in real-life scenario.

In our approach, we proposed to use model transfor-

mation rules for allocating resources. In general, the

result of the application of a model transformation

rule may become inconsistent i.e., may violate the

constraints speciﬁed in a metamodel. Therefore, the

application of a model transformation rule requires a

consistency checking which is a time consuming op-

eration. To tackle this problem, we need techniques

to reduce the complexity of consistency checking. In

this section, we introduce the idea of a compliant rule

that preserves the validity of a model.

The transformation rule r

presented in Figure 4

is not compliant with the set of atomic constraints

speciﬁed in the merged metamodel speciﬁcation S

of Figure 1. If the rule is applied over a valid model,

it does not guarantee that the result will be a valid

model conforming to S

. The rule can be enhanced

so that while matching with a model it makes sure that

the result will be a valid model.

Deﬁnition 4 (Compliant Rule). Given a metamodel

speciﬁcation S = (S,C

: Σ). A transformation rule

r is compliant with a set of atomic constraints from

if the application of r over any valid model of S

results in a valid model of S.

Figure 12 shows a transformation rule r

which

is compliant with the set of atomic constraints C

speciﬁed in S

(Figure 1). The addition of new in-

stances of examT ime and apptT ime in a valid model

of S

can possibly violate atomic constraints C3, C5,

C6, C7 and C8. The transformation rule r

makes

sure that when applied on a valid model of S

, the

addition of new elements does not violate any of the

above mentioned constraints. The additional match-

ing condition endT ime(t2) < endT ime(t1) speciﬁed in

makes sure that C8 is not violated. Therefore the

application of r

will not require any further consis-

tency checking.

Optimizing Distributed Resource Allocation using Epistemic Game Theory: A Model-driven Engineering Approach

pt :Patient

t1:TS@Dept

pt :Patient

f2:apptTime

pt :Patient

t2:TS@Lab

f1:apptTime

b:belongsTo

t1:TS@Dept

g1:examTime

d:Doctor

:assigned

Doctor

f1:apptTime

g1:examTime

pt :Patient

t2:TS@Lab

pt :Patient

g2:examTime

Transformation rule r

NAC

e:Imaging

Exam

h:hasOrder

Additional Matching Condition, MC =

{ ‘endTime(t2) < endTime(t1)’ }

t2:TS@Lab

b:belongsTo

t1:TS@Dept

d:Doctor

:assigned

Doctor

e:Imaging

Exam

h:hasOrder

b:belongsTo

d:Doctor

:assigned

Doctor

e:Imaging

Exam

h:hasOrder

Figure 12: Transformation rule r

for individual resource

allocation of patients.

Further enhancement of the rule is performed by

amalgamation of rule r

(Figure 12) and r

(Fig-

ure 6). Rule amalgamation is a model transformation

technique commonly used for coordinating rules with

overlapping parts (Lamo et al., 2013). To apply a rule

over a source model requires to perform an injective

matching. In order to reduce the number of match-

ing we coordinate rule r

and r

. Figure 13 shows a

transformation rule r

that we formulate by combin-

ing r

and r

. While allocating resources for individ-

ual patients the rule r

produces epistemic choices at

the same time. The rule is also compliant with the

set of constraints speciﬁed in the merged metamodel

speciﬁcation and therefore if the rule is applied over a

valid model, it guarantees consistency.

6 RELATED WORK

The necessity of merging diﬀerent formalisms of soft-

ware speciﬁcations is intrinsic to the discipline of

software engineering. Category theory has been con-

sidered to be a viable solution to accommodate the di-

versity of formalisms (Fiadeiro and Maibaum, 1995;

Diskin et al., 2010; Rutle, 2010). Diskin et al.,

(Diskin et al., 2010) introduced the concept of inter-

metamodel constraints to specify constraints over in-

terdependent models and later on K

onig et al., (K

onig

and Diskin, 2016) proposed an advanced consistency

checking algorithm for inter-metamodel constraints.

A slight diﬀerent but related idea was presented by

Rabbi et al., in (Rabbi et al., 2014) which formalizes

the co-ordination among metamodels, using a linguis-

tic extension of the metamodelling hierarchy. The

proposed linguistic extension is based on an added

metalevel which models the integration of two or

more diﬀerent aspects of a system.

Bak et al. presented a language called Clafer that

uniﬁes features and class modelling (Bak et al., 2016).

The language is supported by a tool that supports

model based analyses such as consistency checking,

instance completion, single and multi-objective opti-

mization. The tool utilizes existing model based an-

alyzers such as Alloy (relational logic solver) (Jack-

son, 2002), Z3 (SMT solver) (De Moura and Bjørner,

2008), Choco 3 (constraint satisfaction problems and

constraint programming solver) (Jussien et al., 2008)

by translating Clafer models into the backend solvers.

While Clafer provides a concise notation for feature

modeling it does not support modelling distributed

systems with inter-metamodel constraints. Also the

optimization technique is diﬀerent in contrast to the

optimization technique of epistemic game theory.

Alanen and Porres investigated an approach for

automatic discovery of the diﬀerence and union of

models in the context of a version control system

(Alanen and Porres, 2003). They presented algo-

rithms to calculate the diﬀerence between models for

MOF-based models. This work can be adapted in or-

der to identify overlaps between component models

for merging DPF (meta)model speciﬁcations.

7 CONCLUSION

This paper is based on the metamodelling epistemic

game theory approach introduced in (Rabbi et al.,

2016a). Epistemic games are relevant for modeling

distributed systems in order to optimize the use of

shared resources. We proposed several enhancement

in this paper by incorporating model merge with inter-

metamodel constraints and compliant rules.

In this paper, we adopted merged metamodel

speciﬁcations and speciﬁed distributed resource con-

straints via inter-metamodel constraints. We applied

model transformations to produce epistemic game

theory models for the purpose of optimizing the use

of distributed resources. Currently we are investigat-

ing the Clafer (Bak et al., 2016) and WebDPF tool

(Rabbi et al., 2016b) for reasoning over DPF meta-

models. In order to apply the proposed method eﬃ-

ciently, we presented the concept of compliant rules.

An automatic resolution of compliant rules is out of

scope of this paper and it is currently under investiga-

tion.

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development

pt :Patient

t1:TS@Dept

pt :Patient

f2:apptTime

pt :Patient

t2:TS@Lab

f1:apptTime

b:belongsTo

t1:TS@Dept

g1:examTime

d:Doctor

:assigned

Doctor

f1:apptTime

g1:examTime

pt :Patient

t2:TS@Lab

pt :Patient

g2:examTime

NAC

e:Imaging

Exam

h:hasOrder

Additional Matching Condition, MC =

{ ‘endTime(t2) < endTime(t1)’ }

t2:TS@Lab

b:belongsTo

t1:TS@Dept

d:Doctor

:assigned

Doctor

e:Imaging

Exam

h:hasOrder

b:belongsTo

d:Doctor

:assigned

Doctor

e:Imaging

Exam

h:hasOrder

Typing

Player

Choice

:hasChoice

hasChoice

Instance, (I, ι )

Figure 13: Transformation rule r

for resource allocation and producing epistemic choices.

REFERENCES

Alanen, M. and Porres, I. (2003). Diﬀerence and Union

of Models, pages 2–17. Springer Berlin Heidelberg,

Berlin, Heidelberg.

Bak, K., Diskin, Z., Antkiewicz, M., Czarnecki, K., and

Wasowski, A. (2016). Clafer: unifying class and

feature modeling. Software and System Modeling,

15(3):811–845.

Barr, M. and Wells, C., editors (1995). Category Theory

for Computing Science, 2nd Ed. Prentice Hall Inter-

national (UK) Ltd., Hertfordshire, UK.

De Moura, L. and Bjørner, N. (2008). Z3: An eﬃcient smt

solver. In Proceedings of the Theory and Practice of

Software, 14th International Conference on Tools and

Algorithms for the Construction and Analysis of Sys-

tems, TACAS’08/ETAPS’08, pages 337–340, Berlin,

Heidelberg. Springer-Verlag.

Diskin, Z. (2011). Model Synchronization: Mappings, Tiles,

and Categories, pages 92–165. Springer Berlin Hei-

delberg, Berlin, Heidelberg.

Diskin, Z. and Wolter, U. (2008). A diagrammatic logic for

object-oriented visual modeling. Electronic Notes in

Theoretical Computer Science, 203(6):19 – 41. Pro-

ceedings of the Second Workshop on ACCAT, 2007.

Diskin, Z., Xiong, Y., and Czarnecki, K. (2010). Specify-

ing overlaps of heterogeneous models for global con-

sistency checking. In Proceedings of the First Inter-

national Workshop on Model-Driven Interoperability,

MDI ’10, pages 42–51, NY, USA. ACM.

Ehrig, H., Ehrig, K., Prange, U., and Taentzer, G.

(2006). Fundamentals of Algebraic Graph Transfor-

mation. Monographs in Theoretical Computer Sci-

ence. Springer.

Fiadeiro, J. L. and Maibaum, T. (1995). Interconnecting

formalisms: Supporting modularity, reuse and incre-

mentality. SIGSOFT Softw. Eng. Notes, 20(4):72–80.

Han, P. K., Klein, W. M., and Arora, N. K. (2011). Vari-

eties of uncertainty in health care: A conceptual tax-

onomy. Medical decision making: an international

journal of the Society for Medical Decision Making,

31(6):828–838.

Jackson, D. (2002). Alloy: A lightweight object mod-

elling notation. ACM Trans. Softw. Eng. Methodol.,

11(2):256–290.

Jussien, N., Rochart, G., and Lorca, X. (2008). Choco: an

Open Source Java Constraint Programming Library.

In CPAIOR’08 Workshop on Open-Source Software

for Integer and Contraint Programming (OSSICP’08),

pages 1–10, Paris, France, France.

onig, H. and Diskin, Z. (2016). Advanced local checking

of global consistency in heterogeneous multimodel-

ing. In Wasowski, A. and L

onn, H., editors, Modelling

Foundations and Applications - 12th European Con-

ference, ECMFA’16/STAF’16, volume 9764 of LNCS,

pages 19–35. Springer.

Lambers, L., Ehrig, H., Prange, U., and Orejas, F. (2008).

Embedding and Conﬂuence of Graph Transformations

with Negative Application Conditions, pages 162–

177. Springer Berlin Heidelberg.

Lamo, Y., Mantz, F., Rutle, A., and de Lara, J. (2013).

A declarative and bidirectional model transformation

approach based on graph co-spans. In Proceedings

of the 15th Symposium on Principles and Practice

of Declarative Programming, PPDP ’13, pages 1–12,

NY, USA. ACM.

Mantz, F. (2014). Coupled Transformations of Graph Struc-

tures applied to Model Migration. PhD thesis, De-

partment of Mathematics and Informatics, Philipps-

Universit

at Marburg, Germany.

Perea, A. (2012). Epistemic Game Theory: Reasoning and

Choice. Cambridge University Press, 1 edition.

Optimizing Distributed Resource Allocation using Epistemic Game Theory: A Model-driven Engineering Approach

Perea, A. (2014). Fron classical to epistemic game theory.

International Game Theory Review, 16(01):1440001.

Pinelle, D. and Gutwin, C. (2006). Loose coupling and

healthcare organizations: Deployment strategies for

groupware. Comput. Supported Coop. Work, 15(5-

6):537–572.

Rabbi, F., Lamo, Y., and MacCaull, W. (2014). Co-

ordination of multiple metamodels, with application

to healthcare systems. In 1st International Workshop

on (Meta)modelling for Healthcare Systems (MMHS),

2014, volume 37 of Procedia Computer Science,

pages 473–480. Elsevier.

Rabbi, F., Lamo, Y., and Yu, I. C. (2016a). Towards a cate-

gorical approach for meta-modelling epistemic game

theory. In Proceedings of the ACM/IEEE 19th Interna-

tional Conference on Model Driven Engineering Lan-

guages and Systems, pages 57–64. ACM.

Rabbi, F., Lamo, Y., Yu, I. C., and Kristensen, L. M. (2015).

Towards a Multi Metamodelling Approach for Devel-

oping Distributed Healthcare Applications. . NIK:

Norsk Informatikkonferanse, ISSN: 1892-0721.

Rabbi, F., Lamo, Y., Yu, I. C., and Kristensen, L. M.

(2016b). WebDPF: A web-based metamodelling

and model transformation environment. In MOD-

ELSWARD 2016 - Proceedings of the 4rd Interna-

tional Conference on Model-Driven Engineering and

Software Development, Rome, Italy, 19-21 February,

2016., pages 87–98. SciTePress.

Rossini, A., de Lara, J., Guerra, E., Rutle, A., and Lamo, Y.

(2012). A graph transformation-based semantics for

deep metamodelling. In Proceedings of the 4th Inter-

national Conference on Applications of Graph Trans-

formations with Industrial Relevance, AGTIVE’11,

pages 19–34. Springer-Verlag.

Rutle, A. (2010). Diagram Predicate Framework: A For-

mal Approach to MDE. PhD thesis, Department of

Informatics, University of Bergen, Norway.

Wang, X., Rutle, A., and Lamo, Y. (2015). To-

wards user-friendly and eﬃcient analysis with al-

loy. In Proceedings of the 12th Workshop on

Model-Driven Engineering, Veriﬁcation and Valida-

tion, MoDeVVa@MoDELS 2015, volume 1514 of

CEUR Workshop Proceedings, pages 28–37. CEUR-

WS.org.

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development