Partially Coherent Linearly Polarized Sources with Inhomogeneous

Azimuth

Juan Carlos Gonz

alez de Sande

, Rosario Mart

ınez-Herrero

, Gemma Piquero

and David Maluenda

ETSIS de Telecomunicaci

on, Universidad Polit

ecnica de Madrid, Campus Sur 28031, Madrid, Spain

Departamento de

Optica, Universidad Complutense de Madrid, Ciudad Universitaria 28040, Madrid, Spain

Keywords:

Coherence, Polarization.

Abstract:

A new model of physically realizable electromagnetic source is proposed. The source is partially coherent

and non-uniformly totally polarized. The coherence and polarization characteristics of this new source are

analyzed. The spatial coherence area of the source can be easily modiﬁed at will. The state of polarization is

linear across the transverse plane of the source with an azimuth that varies from point to point in a different

way depending on the selected values of the parameters that deﬁne the source.

1 INTRODUCTION

Recently there is a great interest in proposing new

sources of light with special characteristics of coher-

ence and polarization including non uniformly polar-

ized ﬁelds with controllable distributions across the

transversal section (Ambrosini et al., 1994; Gori et al.,

1998; Seshadri, 1999; Gori et al., 2000; Gori, 2001;

Gori et al., 2001; Piquero et al., 2002; P

akk

onen

et al., 2002; Shirai et al., 2005; Mart

ınez-Herrero

et al., 2008; Mart

ınez-Herrero and Mej

ıas, 2008;

Zhan, 2009; Brown and Zhan, 2010; Liang et al.,

2014; Rodrigo and Alieva, 2015; Borghi et al., 2015;

Mei and Korotkova, 2016; Wang and Korotkova,

2016). Works can be found in the literature that deal

with partially coherent and partially or totally polar-

ized sources, from both theoretical and experimental

points of view (Friberg and Sudol, 1982; Friberg and

Turunen, 1988; Serna et al., 1992; Santarsiero et al.,

1999; Piquero et al., 2002; Santarsiero et al., 2009;

Ram

ırez-S

anchez et al., 2010; de Sande et al., 2012;

Maluenda et al., 2013). The goal for proposing dif-

ferent kind of light sources generally is to get a bet-

ter performance of different optical devices and tech-

niques where speciﬁc characteristics of the used light

are required depending on the application.

A big issue when a new source model is pro-

posed, is to prove its physical realizability. The non-

negativeness condition must be satisﬁed by the cross

spectral density function in the scalar case or by the

cross spectral density matrix in the vectorial case

(Mandel and Wolf, 1995). Recently, some results

have been derived that solve this task (Gori and San-

tarsiero, 2007; Gori et al., 2008; Mart

ınez-Herrero

et al., 2009a; Mart

ınez-Herrero and Mej

ıas, 2009;

Gori et al., 2009).

In this paper we introduce a new class of vectorial

source whose cross spectral density matrix (CSDM)

ensures its physical realizability. The source is par-

tially coherent non-uniformly totally polarized and

present the particularity that its state of polarization

is linear with inhomogeneous azimuth.

The paper is structured as follows: in Section

2, some concepts and parameters to be used in the

present work are deﬁned; in Section 3, the new

CSDM is presented together with a proposal to ex-

perimentally synthesize it; in Section 4 we character-

ize the source by means of different parameters as the

degree of polarization, Stokes parameters, radial po-

larization content, and degree of coherence; ﬁnally in

Section 5, the main conclusions of this work are de-

rived.

2 BASIC CONCEPTS

Stochastic, statistically stationary electromagnetic

light sources can be appropriately described by

their corresponding cross-spectral density matrix

W (r

) (Mandel and Wolf, 1995; Mart

ınez-Herrero

et al., 2009b). The vectors r

= (r

,θ

) with j =

1,2 are position vectors across the source plane with

,θ

) denoting the radial and angular coordinates,

202

de Sande J., MartÃ nez-Herrero R., Piquero G. and Maluenda D.

Partially Coherent Linearly Polarized Sources with Inhomogeneous Azimuth.

DOI: 10.5220/0006123102020207

In Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2017), pages 202-207

ISBN: 978-989-758-223-3

respectively.

Recently, a necessary and sufﬁcient condition has

been established that guarantee that a proposed matrix

represents a genuine CSDM (Mart

ınez-Herrero and

Mej

ıas, 2009). This condition is an extension of the

previously derived superposition rule (Gori and San-

tarsiero, 2007; Mart

ınez-Herrero et al., 2009a) that

guarantee the nonnegativeness condition for being a

genuine cross-spectral density in the scalar treatment

(Mandel and Wolf, 1995).

In order to evaluate the coherence properties of a

electromagnetic source, we will use the scalar func-

tion g (r

) deﬁned as (Gori et al., 2007; Mart

ınez-

Herrero and Mej

ıas, 2007a; Mart

ınez-Herrero and

Mej

ıas, 2007b)

g(r

) = µ

ST F

(1)



det

W (r

)



W (r

)

W (r

)

where µ

ST F

is the electromagnetic degree of coher-

ence (Tervo et al., 2003; Set

a et al., 2004), and ”tr”

and ”det” denote the trace and determinant of a ma-

trix, respectively.

From physical point of view, this quantity can be

understood as the intimate capability of the ﬁeld to

improve their fringe visibility, under unitary transfor-

mation, in a suitable Young interference.

On the other hand, the polarization characteristics

of the ﬁeld can be described by its polarization matrix

resulting from the evaluation of its CSDM at the same

point r = r

= r

(Mandel and Wolf, 1995).

A useful tool to describe the state of polarization

of the ﬁeld is the Stokes vector S = (S

)

(Born and Wolf, 1980; Goldstein, 2003), where su-

perscript T denotes transpose. For non uniformly po-

larized beams, S is a point dependent vector and it

can be derived from the polarization matrix as (Man-

del and Wolf, 1995)

(r) = tr

W (r,r)

, (2)

where

are the 2 ×2 identity matrix together with

the three Pauli matrices (Mandel and Wolf, 1995)



1 0

0 1



, (3)



1 0

0 −1



, (4)



0 1

1 0



, (5)



0 −i

i 0



. (6)

An important parameter describing the polariza-

tion properties of the ﬁeld is the degree of polariza-

tion, P, that gives the ratio of the polarized part of the

ﬁeld to the total irradiance (Mandel and Wolf, 1995).

It can be obtained from the polarization matrix as

P =

1 −

4det

W (r,r)



W (r,r)

o

. (7)

For linearly polarized light the azimuth, ψ(r), can

be related to the Stokes parameters by (Born and

Wolf, 1980; Goldstein, 2003)

tan2ψ(r) =

(r)

. (8)

In order to get an insight of the polarization

characteristics of this source, global parameters

(Mart

ınez-Herrero et al., 2008) as the radial and az-

imuthal polarized content of the ﬁeld can be analyzed.

The irradiance ratio of the radial (or azimuthal) com-

ponent of the ﬁeld to the total irradiance are related

to the Stokes parameters of the ﬁeld as (Mart

ınez-

Herrero et al., 2008)

(r) =

cos2θ

(r)

sin2θ

(r)

(9)

and

(r) =

−

cos2θ

(r)

−

sin2θ

(r)

. (10)

Note that 0 ≤ ρ

(r) ≤ 1 (0 ≤ ρ

(r) ≤ 1), 0 mean-

ing that the radial (azimuthal) component is null and

1 that the ﬁeld is radially (azimuthally) polarized. It

can be observed that ρ

(r) + ρ

(r) = 1 so they carry

complementary information. They are point depen-

dent parameters for non uniformly polarized ﬁelds.

Their average over the region where the ﬁeld irra-

diance is signiﬁcant can be obtained as (Mart

ınez-

Herrero et al., 2008)

(r)tr

W (r,r)

, (11)

and

(r)tr

W (r,r)

. (12)

3 PROPOSED SOURCE

In the present work, we introduce an new class of

electromagnetic sources whose CSDM is given by

W (r

) =

∗

)

V (r

) . (13)

Partially Coherent Linearly Polarized Sources with Inhomogeneous Azimuth

203

being

V (r) the following deterministic matrix

V (r) =



(r) cos β

0 f

(r) cos β



, (14)

where m and n are integers, β

= mθ −α with α an

arbitrary constant angle, and f

(r) are real functions

of the radial coordinate that must be zero at the ori-

gin in order to avoid singularities. On the other hand,

) matrix is of the form

) = τ

∗

)τ(r

)G(r

−r

)

A, (15)

where the function τ(r) is an arbitrary complex func-

tion and

A is a constant 2 ×2 matrix that satisfy

det

= 0 so the proposed source is totally polar-

ized. Finally, the function G (r

−r

) is deﬁned as

G(r

−r

) =

(ρ)exp[ikρ ·(r

−r

)]dρ (16)

being h(ρ) a real function and k the wavenumber.

From a physical point of view,

) can be

interpreted as the CSDM of a partially coherent Schell

type source.

It can be proven that the matrix given in Eq. (13)

with the chosen

V (r) and

) (Eqs. (14) and

(15)) is a genuine CSDM (Gori and Santarsiero, 2007;

Mart

ınez-Herrero et al., 2009a; Mart

ınez-Herrero and

Mej

ıas, 2009). Then, the proposed source described

by Eq. (13) is physically realizable.

Figure 1 shows a schematics of a proposal for an

experimental set-up in order to obtain the proposed

source. A TEM

He-Ne laser linearly polarized at

π/4 is expanded by microscope objective (MO) and,

after a distance d, a rotating ground glass generates an

incoherent beam with Gaussian irradiance proﬁle and

transverse width w

. Note that the size of the incoher-

ent source can be tuned by changing the distance d.

After freely propagating a distance D, from the van

Cittert-Zernike theorem follows that the transverse

coherent length is (Mart

ınez-Herrero et al., 2009b)

µ =

√

πw

, (17)

where λ is the wavelength, thus, we can control the

degree of coherence of the source on varying the dis-

tance D. Afterwards, the L

lens with focal length D

collimates the incoherent beam and a Gaussian ﬁlter

(GF) performs its irradiance proﬁle.

In order to synthesize the non uniformly polarized

ﬁeld, we transform the source given by Eq. (15) by

means of a set-up based on a modiﬁed Mach-Zehnder

interferometer where x− and y−component of the

beam are independently manipulated by a spatial light

modulator (SLM) in each arm of the interferometer

(Maluenda et al., 2013). The complex transmittance

introduced with the SLM can be described by a point

dependent 2 ×2 matrix, in this case this matrix is

V (r), so the resulting CSDM given by Eq. (13) is

implemented in the source plane.

4 CHARACTERISTICS OF THE

PROPOSED SOURCE

To characterize the coherence properties, we analyze

the behavior of parameter g (r

) given by Eq. (1).

For our source this parameter reads

g(r

) =

G(r

−r

)

G(0)

. (18)

Then, we have that g(r

) is independent of m,

n and α parameters. However, it can be controlled

by modifying the transverse coherence length of the

source that impinges on the modiﬁed Mach-Zender

interferometer (see ﬁgure 1 and Eq. (17)).

In this work, we consider the matrix

A correspond-

ing to a linearly polarized ﬁeld at π/4, that is

A = a



1 1



. (19)

In this case, the following polarization matrix is ob-

tained

W (r,r) =

∗

(r)

(r,r)

V (r) (20)

τ(r)

G(0)

∗

(r)

V (r).

The resulting source is partially coherent and to-

tally polarized because det

W (r,r) = 0. However the

state of polarization changes from point to point in a

way determined by the spatial dependence of the ma-

trix

V (r). In fact, evaluation of Eq. (20) results in the

following polarization matrix

W (r,r) = a

τ(r)

G(0) (21)



(r, θ) p

(r, θ)

(r, θ) p

(r, θ)



where the values for the p

i j

elements are

(r, θ) = f

(r) cos

, (22)

(r, θ) = f

(r) f

(r) cos β

sinβ

, (23)

(r, θ) = p

(r, θ) . (24)

and

(r, θ) = f

(r) sin

. (25)

The Stokes parameters result

(r, θ) = a

τ(r)

G(0) (26)



(r) cos

+ f

(r) sin



PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

204

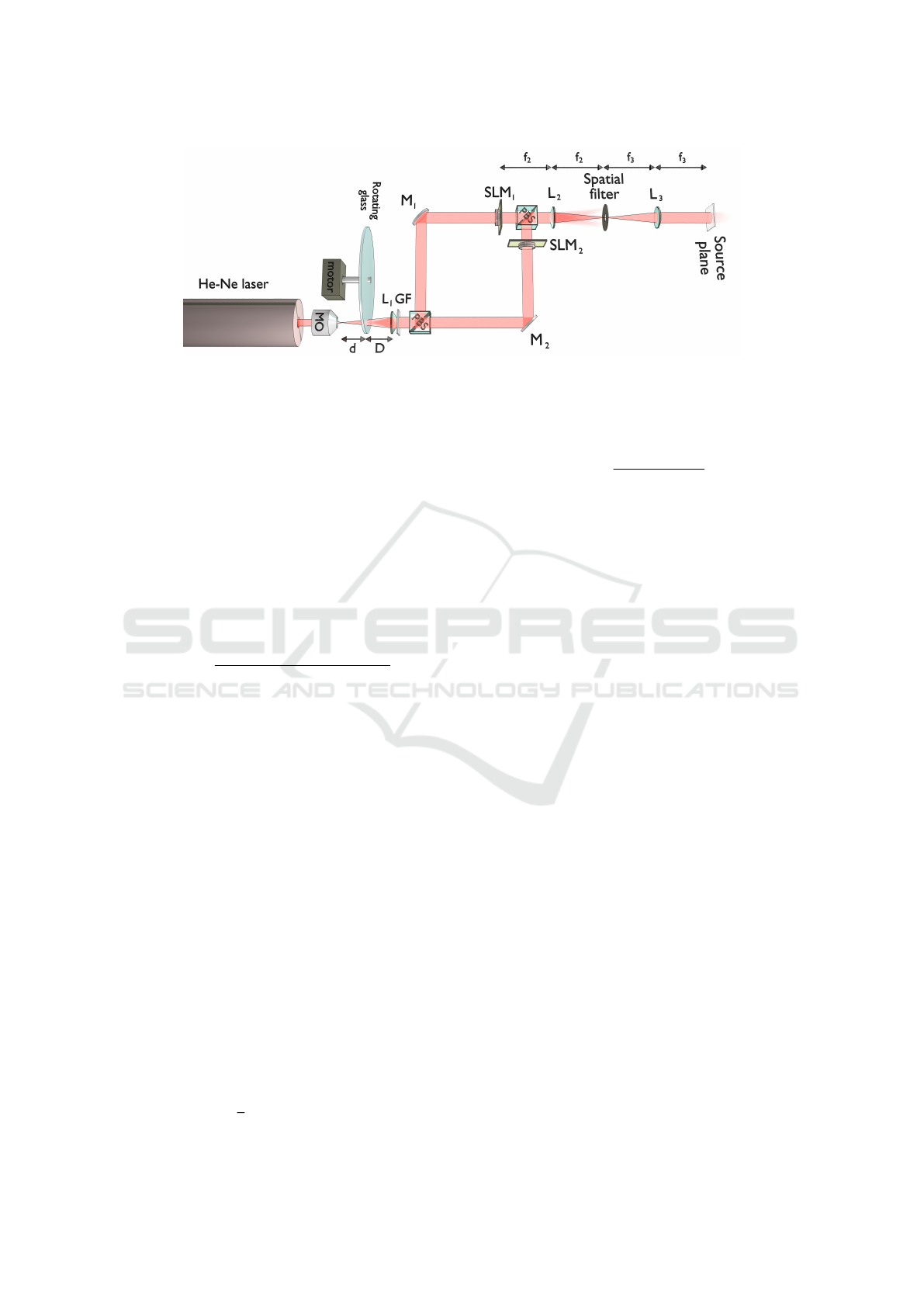
Figure 1: Experimental set-up for obtaining the proposed source.

(r, θ) = a

τ(r)

G(0) (27)



(r) cos

− f

(r) sin



(r, θ) = a

τ(r)

G(0) (28)

× 2 f

(r) f

(r) cos β

sinβ

and

(r, θ) = 0 , (29)

that is a linearly polarized ﬁeld at any point of the

source cross section (S

(r, θ) = 0).

The azimuth results

tan2ψ(r) =

2 f

(r) f

(r) cos β

sinβ

(r) cos

− f

(r) sin

. (30)

Note that this ψ (r) is a point dependent function that

varies in a different way depending on the source pa-

rameters.

For the particular selection of m = n, the Stokes

parameters take the simple form

(r, θ) = a

τ(r)

G(0) f

(r) , (31)

(r, θ) = a

τ(r)

G(0) f

(r) cos 2β

, (32)

(r, θ) = a

τ(r)

G(0) f

(r) sin 2β

, (33)

and

(r, θ) = 0 . (34)

In this case the azimuth only depends on the an-

gular coordinate as ψ(θ) = β

= mθ −α, i.e., the az-

imuth rotates continuously at different rates depend-

ing on m value.

The resulting radial polarization content only de-

pends on the azimuth θ as

(θ) =

[1 + cos (2θ −2β

)] . (35)

When averaging this value according to Eq. (11)

the following value is obtained

1 + δ

m,1

cos2α

, (36)

being δ

i, j

the Kronecker delta function. Then, the

ﬁeld shows a spirally polarized pattern for m = n = 1

(Gori, 2001; P

akk

onen et al., 2002), i. e., spirally

polarized beams are a particular case included in the

proposed class of sources.

It is known that spirally polarized beams show

a polarization map where the azimuth rotates at the

same rate than the angular coordinate θ and in the

same sense (counterclockwise).

In the more general case m = n 6= 1, the average

of radial and azimuthal content are equal to 1/2, in-

dependently of the parameter α. Figure 2 shows the

polarization map obtained for m = n = 2 and α = 0.

For drawing this ﬁgure and the all ﬁgures below, the

family of functions f

(r) = br

has been chosen. It

can be observed that the azimuth of the linearly po-

larized states rotates twice faster than for spirally po-

larized beams (see Figure 2). In general, the rotation

rate of the azimuth is |m| times faster than in the case

of spirally polarized beams. The sense of rotation is

counterclockwise for positive m values and clockwise

for negative m values. For example, ﬁgure 3 shows

the case m = n = −1.

5 CONCLUSIONS

A new class of electromagnetic sources is proposed.

They present the property of being partially coherent

non uniformly totally polarized sources. Once the pa-

rameters of the source have been selected, this source

can be experimentally generated by means of a mod-

iﬁed Mach-Zender interferometer where two spatial

light modulators control the polarization properties of

each interferometer arm. The coherence area of the

Partially Coherent Linearly Polarized Sources with Inhomogeneous Azimuth

205

Figure 2: Polarization map for m = n = 2 and α = 0. Colors

indicate irradiance level: red for high irradiance and violet

for low irradiance. Arrows indicate the electric ﬁeld.

Figure 3: Same that ﬁgure 2 for m = n = −1.

source can be easily modiﬁed by simply varying a dis-

tance in the proposed experimental setup. The state

of polarization is always linearly polarized and its az-

imuth varies in different ways depending on the cho-

sen values for the characteristic parameters deﬁning

the source. In the particular case of selecting m = n,

for any concentric ring to the source axis, the azimuth

of the polarized light rotates periodically in the whole

circle and the number of periods correspond to 2|m|

in a complete circle. The sense of rotation changes

with the sign of the m value.

ACKNOWLEDGEMENTS

This work has been supported by Spanish Minis-

terio de Econom

ıa y Competitividad under projects

FIS2013-46475 and FIS2016-75147.

REFERENCES

Ambrosini, D., Bagini, V., Gori, F., and Santarsiero, M.

(1994). Twisted Gaussian Schell-model beams: A

superposition model. Journal of Modern Optics,

41(7):1391–1399.

Borghi, R., Gori, F., Guattari, G., and Santarsiero, M.

(2015). Twisted Schell-model beams with axial sym-

metry. Opt. Lett., 40(19):4504–4507.

Born, M. and Wolf, E. (1980). Principles of Optics. Cam-

bridge University Press, sixth (corrected) edition.

Brown, T. G. and Zhan, Q. (2010). Focus issue: Uncon-

ventional polarization states of light. Opt. Express,

18(10):10775–10776.

de Sande, J. C. G., Santarsiero, M., Piquero, G., and Gori,

F. (2012). Longitudinal polarization periodicity of un-

polarized light passing through a double wedge depo-

larizer. Opt. Express, 20(25):27348–27360.

Friberg, A. T. and Sudol, R. J. (1982). Propagation param-

eters of Gaussian Schell-model beams. Optics Com-

munications, 41(6):383 – 387.

Friberg, A. T. and Turunen, J. (1988). Imaging of Gaussian

Schell-model sources. J. Opt. Soc. Am. A, 5(5):713–

720.

Goldstein, D. H. (2003). Polarized Light. Marcel Dekker,

Inc., second (revised and expanded) edition.

Gori, F. (2001). Polarization basis for vortex beams. J. Opt.

Soc. Am. A, 18(7):1612–1617.

Gori, F., Ram

ırez-S

anchez, V., Santarsiero, M., and Shirai,

T. (2009). On genuine cross-spectral density matri-

ces. Journal of Optics A: Pure and Applied Optics,

11(8):085706.

Gori, F. and Santarsiero, M. (2007). Devising genuine spa-

tial correlation functions. Opt. Lett., 32(24):3531–

3533.

Gori, F., Santarsiero, M., and Borghi, R. (2007). Maximiz-

ing Young’s fringe visibility through reversible optical

transformations. Opt. Lett., 32(6):588–590.

Gori, F., Santarsiero, M., Borghi, R., and Piquero, G.

(2000). Use of the van Cittert–Zernike theorem for

partially polarized sources. Opt. Lett., 25(17):1291–

1293.

Gori, F., Santarsiero, M., Borghi, R., and Ram

ırez-S

anchez,

V. (2008). Realizability condition for electromagnetic

Schell-model sources. J. Opt. Soc. Am. A, 25(5):1016–

1021.

Gori, F., Santarsiero, M., Borghi, R., and Vicalvi, S.

(1998). Partially coherent sources with helicoidal

modes. Journal of Modern Optics, 45(3):539–554.

Gori, F., Santarsiero, M., Piquero, G., Borghi, R., Mondello,

A., and Simon, R. (2001). Partially polarized Gaus-

sian Schell-model beams. Journal of Optics A: Pure

and Applied Optics, 3(1):1.

Liang, C., Wang, F., Liu, X., Cai, Y., and Korotkova, O.

(2014). Experimental generation of cosine-Gaussian-

correlated Schell-model beams with rectangular sym-

metry. Opt. Lett., 39(4):769–772.

Maluenda, D., Juvells, I., Mart

ınez-Herrero, R., and Car-

nicer, A. (2013). Reconﬁgurable beams with arbitrary

polarization and shape distributions at a given plane.

Opt. Express, 21(5):5432–5439.

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

206

Mandel, L. and Wolf, E. (1995). Optical Coherence and

Quantum Optics. Cambridge University Press.

Mart

ınez-Herrero, R., Mej

ıas, P., Piquero, G., and Ram

ırez-

anchez, V. (2008). Global parameters for charac-

terizing the radial and azimuthal polarization content

of totally polarized beams. Optics Communications,

281(8):1976 – 1980.

Mart

ınez-Herrero, R. and Mej

ıas, P. M. (2007a). Maxi-

mum visibility under unitary transformations in two-

pinhole interference for electromagnetic ﬁelds. Opt.

Lett., 32(11):1471–1473.

Mart

ınez-Herrero, R. and Mej

ıas, P. M. (2007b). Rela-

tion between degrees of coherence for electromag-

netic ﬁelds. Opt. Lett., 32(11):1504–1506.

Mart

ınez-Herrero, R. and Mej

ıas, P. M. (2008). Propaga-

tion of light ﬁelds with radial or azimuthal polariza-

tion distribution at a transverse plane. Opt. Express,

16(12):9021–9033.

Mart

ınez-Herrero, R. and Mej

ıas, P. M. (2009).

Elementary-ﬁeld expansions of genuine cross-spectral

density matrices. Opt. Lett., 34(15):2303–2305.

Mart

ınez-Herrero, R., Mej

ıas, P. M., and Gori, F. (2009a).

Genuine cross-spectral densities and pseudo-modal

expansions. Opt. Lett., 34(9):1399–1401.

Mart

ınez-Herrero, R., Mej

ıas, P. M., and Piquero, G.

(2009b). Characterization of Partially Polarized Light

Fields. Springer Series in Optical Science. Springer.

Mei, Z. and Korotkova, O. (2016). Electromagnetic

Schell-model sources generating far ﬁelds with stable

and ﬂexible concentric rings proﬁles. Opt. Express,

24(5):5572–5583.

akk

onen, P., Tervo, J., Vahimaa, P., Turunen, J.,

and Gori, F. (2002). General vectorial decompo-

sition of electromagnetic ﬁelds with application to

propagation-invariant and rotating ﬁelds. Opt. Ex-

press, 10(18):949–959.

Piquero, G., Gori, F., Romanini, P., Santarsiero, M., Borghi,

R., and Mondello, A. (2002). Synthesis of par-

tially polarized Gaussian Schell-model sources. Op-

tics Communications, 208(13):9 – 16.

Ram

ırez-S

anchez, V., Piquero, G., and Santarsiero, M.

(2010). Synthesis and characterization of partially

coherent beams with propagation-invariant trans-

verse polarization pattern. Optics Communications,

283(22):4484 – 4489. Electromagnetic Coherence and

Polarization.

Rodrigo, J. A. and Alieva, T. (2015). Evolution of coher-

ence singularities of Schell-model beams. Opt. Lett.,

40(15):3635–3638.

Santarsiero, M., Borghi, R., and Ram

ırez-S

anchez, V.

(2009). Synthesis of electromagnetic Schell-model

sources. J. Opt. Soc. Am. A, 26(6):1437–1443.

Santarsiero, M., Gori, F., Borghi, R., Cincotti, G., and Vahi-

maa, P. (1999). Spreading properties of beams radi-

ated by partially coherent schell-model sources. J.

Opt. Soc. Am. A, 16(1):106–112.

Serna, J., Mej

ıas, P., and Mart

ınez-Herrero, R. (1992).

Beam quality dependence on the coherence length

of Gaussian Schell-model ﬁelds propagating through

ABCD optical systems. Journal of Modern Optics,

39(3):625–635.

Seshadri, S. R. (1999). Partially coherent gaussian schell-

model electromagnetic beams. J. Opt. Soc. Am. A,

16(6):1373–1380.

Set

a, T., Tervo, J., and Friberg, A. T. (2004). Complete

electromagnetic coherence in the space–frequency do-

main. Opt. Lett., 29(4):328–330.

Shirai, T., Korotkova, O., and Wolf, E. (2005). A method

of generating electromagnetic Gaussian Schell-model

beams. Journal of Optics A: Pure and Applied Optics,

7(5):232.

Tervo, J., Set

a, T., and Friberg, A. T. (2003). Degree of

coherence for electromagnetic ﬁelds. Opt. Express,

11(10):1137–1143.

Wang, F. and Korotkova, O. (2016). Random sources for

beams with azimuthally varying polarization proper-

ties. Opt. Express, 24(14):15446–15455.

Zhan, Q. (2009). Cylindrical vector beams: from mathe-

matical concepts to applications. Adv. Opt. Photon.,

1(1):1–57.

Partially Coherent Linearly Polarized Sources with Inhomogeneous Azimuth

207