
A Novel 2.5D Feature Descriptor Compensating for Depth Rotation
Frederik Hagelskjær, Norbert Kr
¨
uger and Anders Glent Buch
Maersk Mc-Kinney Moller Institute, University of Southern Denmark, Odense, Denmark
Keywords:
Gabor Filter, Descriptor, Depth Rotation Compensation, 2.5D.
Abstract:
We introduce a novel type of local image descriptor based on Gabor filter responses. Our method operates
on RGB-D images. We use the depth information to compensate for perspective distortions caused by out-of-
plane rotations. The descriptor contains the responses of a multi-resolution Gabor bank. Contrary to existing
methods that rely on a dominant orientation estimate to achieve rotation invariance, we utilize the orientation
information in the Gabor bank to achieve rotation invariance during the matching stage. Compared to SIFT
and a recent also projective distortion compensating descriptor proposed for RGB-D data, our method achieves
a significant increase in accuracy when tested on a wide-baseline RGB-D matching dataset.
1 INTRODUCTION
In this paper, we introduce a novel 2.5D descriptor,
which exploits the expressiveness of Gabor filters in
combination with a perspective distortion compen-
sation mechanism, which is based on the underly-
ing depth data provided by RGB-D sensors.
1
Clas-
sical appearance descriptors, e.g. (Schmid and Mohr,
1997; Lowe, 2004), do not utilize any 3D information
that comes with RGB-D sensors and rely on RGB data
for representing local image patches in an invariant
manner.
In this work we use the 3D surface data to increase
invariance, all based on 3D frame defined around the
local surface normal. This information can facilitate
the matching process, since local image patches can
be transformed to a canonical and therefore better
comparable coordinate system. Only the in-plane ro-
tation stays as an unknown property in our method;
however, we also show how to utilize the orientation
information in the Gabor filter responses to actively
compensate for in-plane rotations during matching,
leading to an accurate method for matching local im-
age structures.
The general idea of the descriptor is outlined in
Fig. 1. Our method relies on an external interest point
detector for finding candidate regions for description
and subsequent matching. Then, using the under-
lying depth information, we introduce a compensa-
tion method for transforming the image region into
1
The descriptor is available in the Cognitive Vision li-
brary https://gitlab.com/caro-sdu/covis
a fronto-parallel virtual plane at a fixed distance. Ap-
plying this technique to regions in different images al-
lows for an invariant description of local image struc-
tures, even under large out-of-plane rotations. Finally,
we apply a Gabor filter bank with 24 rotations to the
patch at 4 scales. We compute both the mean and stan-
dard deviation of the response at every rotation and
scale, which are placed in the final 192-dimensional
descriptor. The result is a multi-model and multi-
scale description of the interest point, which pro-
vides very accurate region matches. Specifically, we
show superior performance over 2D descriptors such
as SIFT (Lowe, 2004) and SURF (Bay et al., 2008) as
well as over a recent 2.5D descriptor (Gossow et al.,
2012), which also compensates for perspective distor-
tions using depth information.
The paper is structured as follows. In the follow-
ing section, we provide an overview of state of the art
for local image features. In Sect. 3 we describe our
contribution in detail. In Sect. 4 we present results on
an external wide-baseline matching dataset. Finally,
we draw conclusions and outline directions for future
works in Sect. 5.
2 STATE OF THE ART
Local feature descriptors were popularized by the
seminal work on the SIFT descriptor (Lowe, 2004),
which drew inspiration from local grayvalue invari-
ants introduced in (Schmid and Mohr, 1997). The use
of local features based on the description of local gra-
158
HagelskjÃ˛er F., KrÃijger N. and Buch A.
A Novel 2.5D Feature Descriptor Compensating for Depth Rotation.
DOI: 10.5220/0006123201580166
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 158-166
ISBN: 978-989-758-225-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Visualization of the construction of our descriptor in two different views, one with a frontal view of the object
(leftmost), and one with the object in a cluttered scene (rightmost). The two local image patches (green), found by an external
interest point detector, are normalized by our compensation method, leading to the corrected patches. The Gabor filter bank
is shown in the bottom left, and the jets representing the filter responses are shown for the two corresponding patches before
correction immediately below the two input images and after correction in the bottom right. Comparing the jets before and
after correction clearly shows the increased invariance achieved by our compensation method.
dients became popular in the following years, leading
to the introduction of PCA-SIFT (Ke and Sukthankar,
2004), HOG (Dalal and Triggs, 2005), SURF (Bay
et al., 2008) and many others. Additionally, some
works focused exclusively on the interest point de-
tection step. Examples hereof are (Mikolajczyk and
Schmid, 2004). Comprehensive evaluation of both
interest point detectors and local feature descriptors
were performed in (Mikolajczyk et al., 2005) and
(Mikolajczyk and Schmid, 2005), respectively, pro-
viding researchers a common framework for bench-
marking their performances.
More recently, a new class of binary descriptors
were introduced. Instead of describing image con-
tents by gradient histograms, binary strings are used.
Examples hereof are LBP (Ojala et al., 2002), BRIEF
(Calonder et al., 2012), ORB (Rublee et al., 2011),
BRISK (Leutenegger et al., 2011) and FREAK (Alahi
et al., 2012). The latter uses a retinotopic sampling
pattern building a discriminative descriptor. Our de-
scriptor, being based on Gabor filter responses, also
has a biological motivation, but from a later stage in
the visual system. This stems from the fact that Ga-
bor filter responses have been shown to model simple
cells appearing in the early stages of the visual corti-
cal stream of the primate (Hubel and Wiesel, 1959).
Mostly related to our work is a recent local de-
scriptor, called DAFT (Gossow et al., 2012), which
generalizes the SIFT interest point detector to RGB-
D data, followed by a local description using SURF
histograms. The depth channel allows for good nor-
malization of local interest points, even in the pres-
ence of large depth or out-of-plane rotations. Our
method does not include an interest point detector,
which allows us to apply any type of detector. Ad-
ditionally, we use a fundamentally different strategy
for compensating for depth rotations, and we use a
Gabor filter bank to compute a compact, yet highly
discriminative descriptor for matching image regions
under large viewpoint changes.
3 METHOD
In this article the focus is on the development of a
feature descriptor that uses Gabor filter responses for
description of local image regions. Many previous
works use various kinds of detectors based on dif-
ferent local operators for finding good interest points
for description. Examples hereof are the difference-
of-Gaussian used by SIFT (Lowe, 2004), the fast-
Hessian used by SURF (Bay et al., 2008) and many
others. Building upon these works, we have chosen to
rely on existing detectors for interest point or keypoint
detection. As we will show in Sect. 4, we achieve sig-
nificant improvement in matching performance on the
same interest points over competing descriptors.
Our local feature descriptor is computed in two
main steps (see Fig. 1). Before computing the de-
scriptor a depth compensation is performed. This
step compensates for perspective distortions caused
by depth rotations of an interest point using the local
surface normal. The description is now performed us-
ing a Gabor filter bank on the corrected image patch
around the interest point. Fig. 1 shows the method for
comparing an interest point in an object and a scene.
A Novel 2.5D Feature Descriptor Compensating for Depth Rotation
159

The patch in the scene is corrected by a transforma-
tion into a frontal view, whereupon it is subjected
to the Gabor filters and a matching of the descrip-
tors or jets can be performed. The following sections
describe how our depth compensation method works
(Sect. 3.1), the details of our descriptor (Sect. 3.2)
and how we use this for matching local image regions
(Sect. 3.3). For an overview of all parameters men-
tioned in the following sections, we refer the reader
to Tab. 1.
3.1 Depth Compensation
The depth compensation method removes the ef-
fects of depth rotations, which causes perspective
distortions. After this correction, there will still be
an unknown in-plane rotation and quantization arti-
facts. Many other methods achieve rotation invari-
ance by estimating the dominant orientation in the
patch (Lowe, 2004; Bay et al., 2008; Rublee et al.,
2011) before computing the descriptor. We have
tested this approach, but have found better results
when we exploited the rotation information in the Ga-
bor jet during matching. We will elaborate on this
particular aspect in Sect. 3.3.
Similar to earlier works (e.g. (Gossow et al.,
2012)), our method utilizes depth information to com-
pensate for depth rotations. Our method is tested on a
dataset captured by a commodity Kinect RGB-D sen-
sor, which provides an aligned depth map along with
the captured image. This allows us to apply the al-
gorithm of (Holzer et al., 2012) for fast extraction of
local surface normals at each surface point. This is
the first step of our algorithm. We include all sur-
face points in a neighborhood of radius r to estimate
the normal. We denote such an oriented surface point
(p, n), where p captures the point information and
n the surface normal. As mentioned previously, we
only consider interest points identified by an external
detector, which constitute a small subset of the total
RGB-D image.
For each interest point, for which we also have a
precomputed normal orientation, we now project the
camera axes x = [1 0 0]
T
and y = [0 1 0]
T
onto the
plane spanned by (p, n). Denote these projections x
n
and y
n
, respectively. These vectors along with the
vector n are then concatenated to provide the full ro-
tation frame R ∈ SO(3) between the actual view and
a virtual frontal view of the local image patch:
R = [x
n
y
n
n] (1)
We now wish to normalize the local depth rotated
patch to a frontal view. We start by defining a fronto-
parallel 3D planar patch by four anchor points. These
are placed at ±r
anchor
in the x and y directions and
c
depth
· d
avg
in the z direction, where d
avg
is computed
as the average depth of all interest points in a scene
(see also Tab. 1).
2
Denote these four points P
planar
.
Using the rotation matrix, R, and the interest points
position, p, each of these points can be placed around
the interest point in the current scene:
P
scene,i
= R · P
planar,i
+ p i ∈ {1, . . . , 4} (2)
We now use the camera matrix K to project both
the frontal anchor points and the anchor points around
the interest point to the image:
p
planar,i
= K · P
planar,i
(3)
p
scene,i
= K · P
scene,i
(4)
The final step of the normalization procedure now
amounts to simply estimating the homography be-
tween the 2D point sets p
planar
and p
scene
. This ho-
mography is applied to the full patch around the inter-
est point in the scene and provides a frontal normal-
ization, which is suitable for description. An example
is shown in the green frames in Fig. 1.
3.2 Descriptor
The descriptor employed in this work is based on Ga-
bor filter responses. Gabor filters (Granlund, 1978;
Daugman, 1985) have a long history in computer vi-
sion, where they have been used for e.g. face recog-
nition tasks (Wiskott et al., 1997). By modulating the
filter parameters, a bank of several Gabor filters can
be realized, providing a ”complete” coverage of the
frequency content of an image. We believe that this
makes Gabor filters very tractable for local feature
matching where the task is to capture the local con-
tent of a patch in a discriminative manner. The con-
crete Gabor filter bank used in this work is inspired
by (Ilonen et al., 2007), giving the function for the 2D
Gabor filter as follows:
G(x, y; θ) =
f
2
0
πσ
2
exp(
− f
2
0
σ
2
(x
02
+ y
02
))exp
i2π f
0
x
0
(5)
x
0
= x cos θ − y sinθ y
0
= x sin θ + y cosθ (6)
where x
0
, y
0
are the x and y coordinates rotated by an
angle of θ, f
0
is the normalized base frequency and σ
represents the standard deviation of the Gaussian en-
velope. The parameter values were chosen with (Ilo-
nen et al., 2007) as a basis with further adjustments
2
The dimensions and distance of this 3D patch are cho-
sen by experimentation, but varying them has little impact
on the performance of our descriptor.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
160

Table 1: List of parameters used by our method. The aver-
age depth of all interest points d
avg
is computed online from
the input scene.
Description Symbol Value
Normal radius r 5 cm
3D patch width r
anchor
10 cm
Computed avg. keypoint depth d
avg
-
3D patch avg. depth multipler c
depth
1.4
Normalized base frequency f
0
0.2
Filter standard deviation σ 0.795
Number of scales - 4
Number of rotations - 24
to improve the effectiveness for local feature match-
ing. Notice also that since we can assume normal-
ized patches when applying our filter, we use a cir-
cular (non-elliptical) filter, which only requires one
parameter (σ) for specifying the shape of the Gaus-
sian envelope. The chosen values for all parameters
are shown in Tab. 1.
As mentioned, these parameters are based on the
initial implementation and further optimized by thor-
ough experimentation on our side. For further details
of the parameters, the reader is referenced to (Ilonen
et al., 2007). When modulating the scale, our imple-
mentation keeps the filter size fixed, while downscal-
ing the image patch instead. This allows for a faster
computation of the responses. The specific filter bank
we use is shown in the bottom left corner of Fig. 1.
The result of applying the filter bank at all four
scales is a 96-dimensional magnitude response at each
pixel within the local image patch. We now take the
inscribed circle of the rectangular image patch and
only consider filter responses in this circular region.
This helps achieving rotation invariance, as described
below. For each rotation and scale we compute the
mean and the standard deviation of the magnitude re-
sponses in the circular region and stack the two 96-
dimensional response statistics, arriving at a final de-
scriptor of dimension 192. The bottom right corner of
Fig. 1 shows the resulting output in red frames when
applying the filters and computing the mean and stan-
dard deviation of the responses the corrected patches.
3.3 Matching
As the correction does not compensate for in-plane
rotations, the descriptor is not rotationally invariant
in itself. However, the descriptor can be matched in
a rotationally invariant manner by circularly shifting
the columns and matching all 24 rotated versions of
the bank. When matching a single interest point pair
between two scenes, we thus compute all 24 rotations
of our descriptor for the first image and then match the
descriptor in the second image against all 24 descrip-
tors and return the match which resulted in the small-
est Euclidean distance. This effectively removes the
need for a dominant orientation estimate employed by
many existing descriptors, but at the expense of in-
creased matching time.
4 RESULTS
We evaluate our proposed descriptor on two differ-
ent RGB-D datasets to test the matching performance
of the descriptor. Our descriptor is compared against
SIFT and SURF, two descriptors which still stand as
competing methods for local image content descrip-
tion as well as two newer and free to use methods
FREAK and ORB. As FREAK does not have a detec-
tor we use the BRISK detector for interest points. Ad-
ditionally we compare our results with the DAFT de-
scriptor (Gossow et al., 2012), as this is also a method
which compensates for depth and has shown better
performance than SIFT for RGB-D data, as seen in
(Gossow et al., 2012). As any interest point detec-
tor can be used for our descriptor, we have tested it in
combination with the detectors of all five comparative
algorithms.
The performance of a descriptor is measured by its
precision-recall (PR), as introduced in (Mikolajczyk
and Schmid, 2005). Similar to this work, we match
descriptors only at interest points which pass an over-
lap test with a less than 50 % error. The PR curve
for a single image pair is generated by ordering the
matches by their nearest neighbor matching distance
in feature space (Lowe, 2004) and varying the thresh-
old for accepting matches, while monitoring the abso-
lute and relative number of correct matches under the
current threshold value. A single performance mea-
sure for a PR curve can be computed by calculating
the area under the PR curve (AUC).
4.1 DAFT Dataset
The DAFT dataset is a recently introduced wide-
baseline matching benchmark on RGB-D data (Gos-
sow et al., 2012). The dataset contains six image se-
quences with different types of camera movements
with a total of 66 images. For the tests on this dataset,
the first image in each sequence is matched against all
other images in the same sequence.
In Fig. 2 on p. 6 we show PR curves for match-
ing the first image with the middle image in each
sequence as well as the AUC for matching with all
images in the sequence. From the AUC curves,
we observe state of the art performances, except for
A Novel 2.5D Feature Descriptor Compensating for Depth Rotation
161

Table 2: Summed area under precision recall curves for the tested detector+descriptor pairs on the DAFT dataset. Best result
for each row is shown in bold.
Detector SIFT SURF BRISK ORB DAFT DAFT SIFT SURF BRISK ORB DAFT
Descriptor SIFT SURF FREAK ORB DAFT Gabor Gabor Gabor Gabor Gabor Gabor
no-ori
Frosties 3.527 3.330 3.227 3.309 5.048 5.820 4.255 3.752 4.476 1.248 5.823
Granada 40
◦
4.188 3.559 3.640 4.515 7.356 1.482 4.385 4.442 6.361 2.059 6.961
Granada 60
◦
2.818 2.938 2.772 3.002 10.30 2.207 3.146 3.231 4.347 1.982 10.28
Worldmap Viewpoint 2.805 2.452 2.647 4.146 5.335 4.174 3.031 2.947 5.084 1.069 6.456
Worldmap Rotate 4.729 5.821 4.370 9.451 6.744 1.308 6.755 6.649 9.255 1.794 6.890
Worldmap Scaled 3.947 2.026 2.735 5.385 4.193 5.338 4.447 4.264 4.607 2.794 5.094
sum 22.02 20.13 19.39 29.81 38.99 20.33 26.02 25.29 34.13 10.95 41.51
# interest points 84553 80861 16992 15464 58566 57741 84330 80570 16970 15308 58529
the Worldmap sequence where one descriptor (ORB)
shows the best results.
To summarize all results, we report the sum of
all AUCs for each sequence in Tab. 2. As an ad-
ditional test, we included results for the combina-
tions of all other detectors and our descriptor, and fi-
nally a no-orientation version of our matching scheme
when combined with the highest-peforming detector
(DAFT). It is clearly seen that the Gabor descriptor
provides the best results using the DAFT detector.
The performance of our descriptor outperforms SIFT
clearly and is also significantly higher than that of
DAFT. The exceptions are the sequences where very
large depth rotations occur, e.g. the Granada images
which appear in the second and third row of Fig. 2.
This is possibly due to quantization errors, where the
areas of corresponding patches become very small.
As the descriptor does not use the scale that the in-
terest point is found at, but multiple scales, any quan-
tization errors effect the descriptor more directly. In
the remaining cases of pure in-plane rotation, pure
depth rotation, scaling and arbitrary movements, our
descriptor outperforms both SIFT and DAFT. Look-
ing at the summed AUC from Tab. 2, the overall per-
formance is approximately 88 % better than SIFT,
106 % better than SURF and 6.4 % better than DAFT.
ORB is the highest-performing pure 2D descriptor,
still being 39 % worse than our Gabor-based descrip-
tor. Additionally, good performance is only ensured
at small viewpoint angles. This can be seen in Fig. 2,
e.g. for the Granada 60
◦
sequence, where the AUC
completely drops. The FREAK descriptor generally
performs a bit worse, as seen in Tab. 2.
4.2 Homography Estimation
In another experiment using the DAFT dataset, we
test the use of our descriptor for a higher-level task,
namely homography estimation for finding the rela-
tive camera movement between two scenes. We use a
simple RANSAC (Fischler and Bolles, 1981) estima-
Table 3: Frobenius distances between ground truth and esti-
mated homographies for the tested detector+descriptor pairs
on the DAFT dataset.
Detector SIFT SURF DAFT DAFT
Descriptor SIFT SURF DAFT Gabor
Frosties 439.2 658.5 483.7 599.2
Granada 40
◦
66.38 53.00 64.83 68.43
Granada 60
◦
7042 7047 314.4 243.0
Rotate 42.44 32.17 87.31 66.23
Viewpoint 155.2 195.0 289.8 179.4
Scaled 16.25 15.47 1095 247.5
tor and input the correspondences produced by match-
ing the different descriptors. For an example, we refer
to Fig. 3. The dataset provides a ground truth homog-
raphy H between the first frame and all subsequent
frames in a sequence and we verify each estimated
homography
ˆ
H using the matrix norm of the differ-
ence:
v
u
u
t
3
∑
i=1
3
∑
j=1
H
i j
−
ˆ
H
i j
2
(7)
where subscripts enumerate the matrix elements of
the homographies.
The results of the homography estimation experi-
ment are shown in Tab. 3. For this test, we took again
the best detector (DAFT) for our descriptor and com-
pared it with DAFT—being the competing RGB-D
descriptor—and SIFT and SURF. The better matches
for this RGB-D data provided by our descriptor and
DAFT clearly lead to superior results over SIFT and
SURF. Especially the Grenada 60
◦
sequence poses
problems for SIFT and SURF due to the large depth
rotations that occur in this sequence. The Worldmap
Scaled sequences poses some problems to both DAFT
and our descriptor, and in this sequence our descriptor
produced one failure. But apart from this, our descrip-
tor provides generally good performance.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
162

(a) Frosties (b) Image # 5
(c) Granada
40
◦
(d) Image # 6
(e) Granada
60
◦
(f) Image # 9
(g) Worldmap
Viewpoint
(h) Image # 6
(i) Worldmap
Rotated
(j) Image # 7
(k) Worldmap
Scaled
(l) Image # 5
Figure 2: Results of the testing. To the left is shown the first and middle image of the six sequences in the DAFT test image
dataset. The results of precision-recall on the middle image is shown in the first graph and the AUC of each image sequence
is shown to the right. In the Frosties sequence, the curves for our Gabor-based descriptors both with and without rotation
invariant matching overlap.
4.3 RGB-D Scenes
For further testing, we have also considered the RGB-
D Scenes dataset (Lai et al., 2011), which consists of
thousands of RGB-D frames from 7 indoor scenarios,
captured by a moving Kinect camera. For these se-
quences, full 6 DoF camera poses relative to the first
A Novel 2.5D Feature Descriptor Compensating for Depth Rotation
163

(a) SIFT
(b) SURF
(c) DAFT
(d) Gabor
Figure 3: Homography estimation example for the
Grenada 60
◦
sequence (1st and 11th frame). We mark a
region of interest in the left frame with green and apply the
estimated homography to it to visualize the quality of the
estimate. Also, correspondences from the feature matching
stage are shown by colored lines. In this example, DAFT
and our descriptor provide accurate results, while SIFT and
SURF fail due to many spurious matches.
frame are given for each frame. An example of four
consecutive frames from the RGB-D Scenes is show
in figure Fig. 4. In contrast to the DAFT scenes tested
in the previous section, the RGB-D Scenes dataset
contains non-planar, general 3D structures. Using the
depth image, the camera pose and the internal cam-
era parameters, each detected keypoint in an RGB-D
frame can be reprojected to 3D, transformed to an-
other camera pose and then projected into the 2D im-
age of any other frame. This allows us to perform the
usual overlap test, as was done for the DAFT dataset,
where ground truth homographies were used for the
overlap test. We considered every fifth frame over
all sequences, giving a total of 286 test images for
143 pairwise tests. The PR curves over all 143 wide-
baseline image pairs can be seen in Fig. 5. Although
DAFT starts with a high precision (moving left on the
horizontal axis), it slowly decreases as the recall in-
creases, giving a fading curve which ends at 0.41.
Surprisingly, SIFT and SURF both perform better
than DAFT, with a stable precision until a sharp de-
cline ending at 0.52 and 0.48, respectively, with SIFT
having a higher precision than SURF at all times. The
FREAK descriptor performs quite well with a very
high precision in the beginning, although it ends at a
recall around 0.51, clost to SIFT. The ORB descrip-
tor performs very poorly for this data with a recall
of 0.39. The curve for our Gabor-based descriptor
is quite different. Although it starts with a smaller
precision than DAFT and SIFT, no sharp decline ever
occurs. As the recall rises, the precision also remains
significantly higher than the others (again moving left
on the horizontal axis). Looking at the AUC for the
descriptors the results are for SIFT, SURF, FREAK,
ORB, DAFT and Gabor: 0.337, 0.277, 0.341, 0.198,
0.238 and 0.444, respectively.
To further investigate the details of the descriptor
performances, the AUC is calculated individually for
each of the 143 image pairs and a histogram is calcu-
lated. This histogram can be seen in Fig. 6, thus show-
ing the variation in accuracy for the descriptors. From
the histogram it is evident that DAFT shows poor per-
formance whereas the Gabor-based descriptor clearly
gives the best results.
5 CONCLUSIONS AND FUTURE
WORK
A novel method for matching local features in RGB-
D images has been proposed. We first introduced a
method for compensating for arbitrary out-of-plane
rotations of local patches using surface information
provided by the depth channel. The result of this
is a normalized image patch, which we then de-
scribe using a series of Gabor filters, providing a
192-dimensional compact, local image descriptor. We
achieve in-plane rotation invariance by using the ori-
entation information inherent in the Gabor filter dur-
ing the feature matching stage. Our results show,
when measured on an external wide-baseline RGB-
D matching dataset, that our descriptor outperforms
both SIFT, ORB and the DAFT RGB-D descriptor by
88 %, 39 % and 6.4 %, respectively, when using the
Area Under Curve as a performance measure.
The RGB-D Scene dataset is even further proof
of the effectiveness of the Depth Oriented Gabor fil-
ter compared to DAFT. Looking at the AUC Gabor
performs 30 % better than the second best, ORB,
and 86 % betten than DAFT. This is a dataset for
which the DAFT descriptor wasn’t trained for and
here the DAFT completely underperforms compared
to the other dataset. SIFT and SURF still performs
reliably which shows the reason that even after more
than ten years they are still in use.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
164
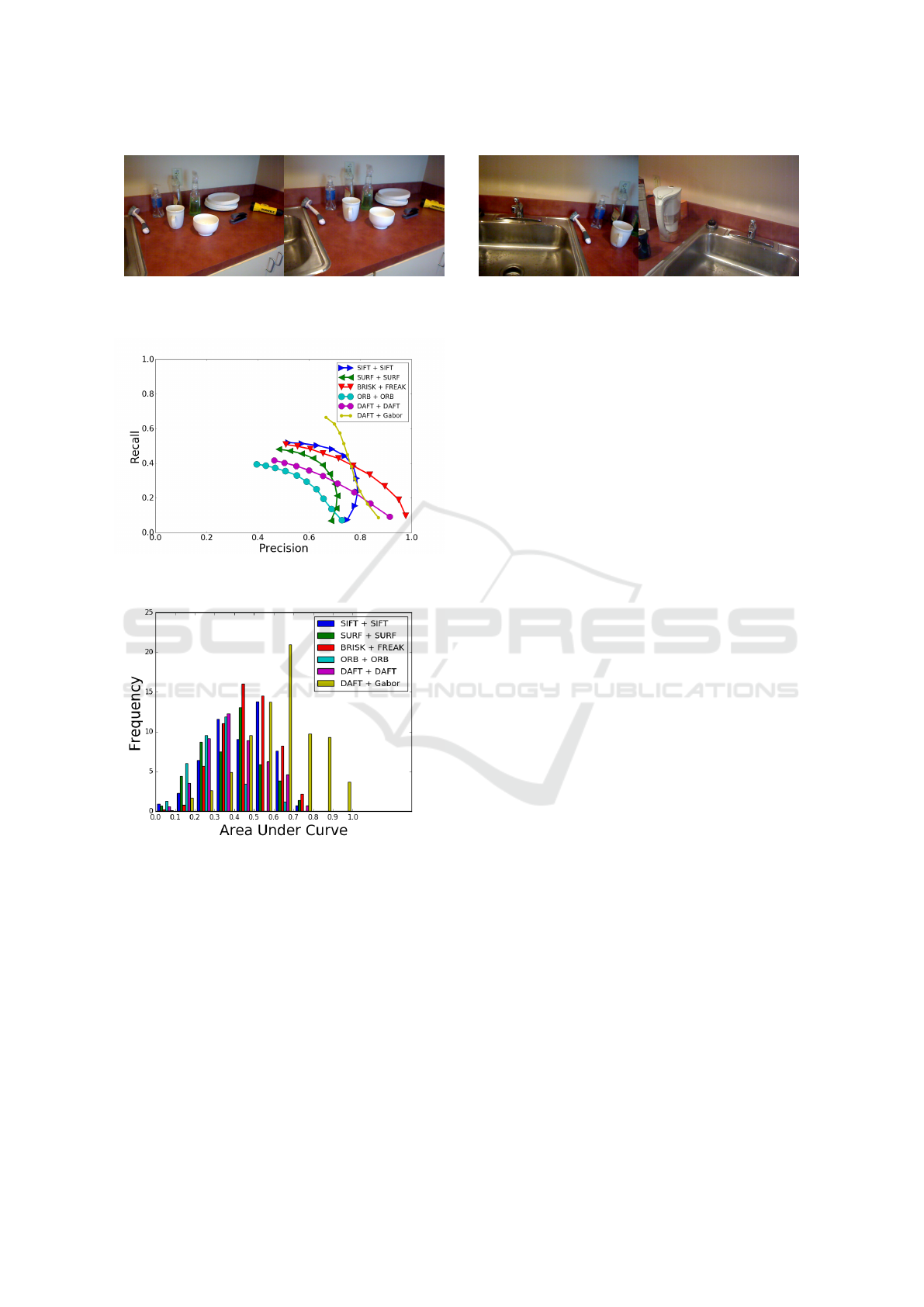
Figure 4: An example of four consecutive frames in the RGB-D dataset. Features are matched between the two first images
and the last two.
Figure 5: PR curve for all matches between all image pairs
in the RGB-D Scene dataset.
Figure 6: Histogram of Area Under Curve for each individ-
ual image pair of the RGB-D dataset.
We believe it to be possible to also use the Gabor
filter responses to locate stable interest points. This
will require a suitable local operator on top of the
low-level responses, which by themselves are good
indicators of edge structures. We wish to pursue this
in the future, such that we will be able to provide a
full Gabor-based matching system consisting of both
a detector and a descriptor. Finally, we also see it as
an immediate extension to include the depth channel
not only in the compensation method, but also dur-
ing the description stage, at which we currently only
use the RGB data. This enhancement will most likely
require a dedicated Gabor filter bank, which is more
suited for smooth depth data.
ACKNOWLEDGMENT
The research leading to these results has received
funding from the European Communitys Seventh
Framework Programme FP7/2007-2013 (Programme
and Theme: ICT-2011.2.1, Cognitive Systems and
Robotics) under grant agreement no. 600578, ACAT
and by Danish Agency for Science, Technology and
Innovation, project CARMEN.
REFERENCES
Alahi, A., Ortiz, R., and Vandergheynst, P. (2012). Freak:
Fast retina keypoint. In Computer Vision and Pat-
tern Recognition (CVPR), 2012 IEEE Conference on,
pages 510–517. Ieee.
Bay, H., Ess, A., Tuytelaars, T., and Van Gool, L. (2008).
Speeded-up robust features (surf). Computer vision
and image understanding, 110(3):346–359.
Calonder, M., Lepetit, V., Ozuysal, M., Trzcinski, T.,
Strecha, C., and Fua, P. (2012). Brief: Computing
a local binary descriptor very fast. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
34(7):1281–1298.
Dalal, N. and Triggs, B. (2005). Histograms of oriented gra-
dients for human detection. In Computer Vision and
Pattern Recognition, 2005. CVPR 2005. IEEE Com-
puter Society Conference on, volume 1, pages 886–
893. IEEE.
Daugman, J. G. (1985). Uncertainty relation for resolution
in space, spatial frequency, and orientation optimized
by two-dimensional visual cortical filters. JOSA A,
2(7):1160–1169.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: a paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM, 24(6):381–395.
Gossow, D., Weikersdorfer, D., and Beetz, M. (2012).
Distinctive texture features from perspective-invariant
keypoints. In Pattern Recognition (ICPR), 2012
21st International Conference on, pages 2764–2767.
IEEE.
A Novel 2.5D Feature Descriptor Compensating for Depth Rotation
165

Granlund, G. (1978). In search of a general picture process-
ing operator. Computer Graphics and Image Process-
ing, 8:155–173.
Holzer, S., Rusu, R. B., Dixon, M., Gedikli, S., and Navab,
N. (2012). Adaptive neighborhood selection for real-
time surface normal estimation from organized point
cloud data using integral images. In Intelligent Robots
and Systems (IROS), 2012 IEEE/RSJ International
Conference on, pages 2684–2689. IEEE.
Hubel, D. H. and Wiesel, T. N. (1959). Receptive fields of
single neurones in the cat’s striate cortex. The Journal
of physiology, 148(3):574–591.
Ilonen, J., Kamarainen, J.-K., and Kalviainen, H. (2007).
Fast extraction of multi-resolution gabor features. In
Image Analysis and Processing, 2007. ICIAP 2007.
14th International Conference on, pages 481–486.
IEEE.
Ke, Y. and Sukthankar, R. (2004). Pca-sift: A more
distinctive representation for local image descriptors.
In Computer Vision and Pattern Recognition, 2004.
CVPR 2004. Proceedings of the 2004 IEEE Computer
Society Conference on, volume 2, pages II–506. IEEE.
Lai, K., Bo, L., Ren, X., and Fox, D. (2011). A large-
scale hierarchical multi-view rgb-d object dataset. In
Robotics and Automation (ICRA), 2011 IEEE Interna-
tional Conference on, pages 1817–1824. IEEE.
Leutenegger, S., Chli, M., and Siegwart, R. Y. (2011).
Brisk: Binary robust invariant scalable keypoints. In
Computer Vision (ICCV), 2011 IEEE International
Conference on, pages 2548–2555. IEEE.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International journal of computer
vision, 60(2):91–110.
Mikolajczyk, K. and Schmid, C. (2004). Scale & affine in-
variant interest point detectors. International journal
of computer vision, 60(1):63–86.
Mikolajczyk, K. and Schmid, C. (2005). A perfor-
mance evaluation of local descriptors. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
27(10):1615–1630.
Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,
Matas, J., Schaffalitzky, F., Kadir, T., and Van Gool,
L. (2005). A comparison of affine region detectors.
International journal of computer vision, 65(1-2):43–
72.
Ojala, T., Pietik
¨
ainen, M., and M
¨
aenp
¨
a
¨
a, T. (2002). Mul-
tiresolution gray-scale and rotation invariant texture
classification with local binary patterns. Pattern Anal-
ysis and Machine Intelligence, IEEE Transactions on,
24(7):971–987.
Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.
(2011). Orb: an efficient alternative to sift or surf.
In Computer Vision (ICCV), 2011 IEEE International
Conference on, pages 2564–2571. IEEE.
Schmid, C. and Mohr, R. (1997). Local grayvalue invari-
ants for image retrieval. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 19(5):530–534.
Wiskott, L., Fellous, J.-M., Kuiger, N., and Von Der Mals-
burg, C. (1997). Face recognition by elastic bunch
graph matching. Pattern Analysis and Machine Intel-
ligence, IEEE Transactions on, 19(7):775–779.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
166
