
LiDAR-based 2D Localization and Mapping System using Elliptical
Distance Correction Models for UAV Wind Turbine Blade Inspection
Ivan Nikolov and Claus Madsen
Department of Architecture, Design, and Media Technology, Aalborg University, Rendsburggade 14, Aalborg, Denmark
{iani, cbm}@create.aau.dk
Keywords:
Localization, Mapping, Scanning, LiDAR, IMU, UAV, SLAM, Wind Turbine Blades Inspection.
Abstract:
The wind energy sector faces a constant need for annual inspections of wind turbine blades for damage, erosion
and cracks. These inspections are an important part of the wind turbine life cycle and can be very costly and
hazardous to specialists. This has led to the use of automated drone inspections and the need for accurate,
robust and inexpensive systems for localization of drones relative to the wing. Due to the lack of visual
and geometrical features on the wind turbine blade, conventional SLAM algorithms have a limited use. We
propose a cost-effective, easy to implement and extend system for on-site outdoor localization and mapping in
low feature environment using the inexpensive RPLIDAR and an 9-DOF IMU. Our algorithm geometrically
simplifies the wind turbine blade 2D cross-section to an elliptical model and uses it for distance and shape
correction. We show that the proposed algorithm gives localization error between 1 and 20 cm depending on
the position of the LiDAR compared to the blade and a maximum mapping error of 4 cm at distances between
1.5 and 3 meters from the blade. These results are satisfactory for positioning and capturing the overall shape
of the blade.
1 INTRODUCTION
As robots and drones become widely used in different
branches of the industry, a need for localization and
mapping systems, which are able to work in non-ideal
conditions, arises. The state of the art for drone simul-
taneous localization and mapping (SLAM) is most
widely used both from monocular (Mur-Artal et al.,
2015), stereo camera (Endres et al., 2012), LiDAR
and laser scanners (Berger, 2013) (Zlot and Bosse,
2014) . A lot of SLAM algorithms for the outdoors
are used together with GPS positioning and orienta-
tion from an inertial measurement unit (IMU) (Else-
berg et al., 2012) (Shepard and Humphreys, 2014).
SLAM algorithms work best in environments, which
are rich in geometric features and vary significantly.
The precision of these algorithms significantly suffers
when the environment is too featureless or when there
are insufficient number of points of interest, which
requires the introduction of algorithm modifications,
such as visual feature clustering (Negre et al., 2016)
or combining camera and laser scanner depth data
(Oh et al., 2015). When the number of points ex-
tracted from laser scanner is too low, due to sharp cor-
ners or thin surfaces, these modification cannot sus-
tain a high enough performance. Similar problems
are present when using drones in the wind energy sec-
tor for inspection of wind turbine blades. Wind tur-
bine blades are normally located at over 100 meter
heights and do not have any other landmarks around
them. This, combined with the monochrome color of
the blades and the lack of corners and other geometric
features, makes autonomous localization of the drone
and mapping the environment, hard.
We propose a cost-effective and easy to imple-
ment solution for localization and mapping the over-
Figure 1: Our proposed localization and mapping solution
using elliptical distance correction models.
418
Nikolov I. and Madsen C.
LiDAR-based 2D Localization and Mapping System using Elliptical Distance Correction Models for UAV Wind Turbine Blade Inspection.
DOI: 10.5220/0006124304180425
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 418-425
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

all shape of the blade (Figure 1), designed to work in
feature-poor wind turbine blade environments, with
minimum prior information. Our system consists of
the RPLIDAR scanner and the BNO055 9-DOF IMU
for orientation. Our algorithm is based on the assump-
tion that a blade is stopped in a vertical position, at
either the top or bottom and is the only thing that is
visible for the LiDAR. The algorithm uses prior in-
formation for the cross-section width and depth and
it models the blade using primitive elliptical shapes,
providing drone positioning relative to the blade in
a much simpler way than conventional SLAM algo-
rithms. The initial angle between the LiDAR and
blade is found by using a 2D iterative closest point
(ICP) algorithm and the angle heading is monitored
and maintained using an IMU. Additionally we model
the distance measurement and sampling errors of the
RPLIDAR to boost the accuracy of the localization.
We address the sunlight noise problem of the RPL-
IDAR with a hybrid hardware and software filtering
solution. We perform initial ground-based tests on
the system to determine its accuracy and error rate
by comparing with ground truth manually measured
positions. Additionally we estimate to what extent
the algorithm can capture the overall shape of the 2D
cross-section of the blade, using a ground truth cross-
section. Both tests demonstrate that the system per-
forms well even with a small number of points present
from the scanned area and can be used for drone local-
ization relative to the blade and generation of initial
sparse 2D point clouds of the shape of the blade.
2 STATE OF THE ART
Drone inspection of wind turbine blades is a hot
topic for the computer vision, automaton and robotics
fields. The limited number of points of interest, the
featureless and monochrome shape of the wind tur-
bine blades and the required operational height, to-
gether with environment hazards like gusts of wind,
blade swaying and weather changes make localiza-
tion and mapping non-trivial problems. The research
from (Morgenthal and Hallermann, 2014) shows that
inspection by images can suffer significantly if the
drone’s localization and stabilization systems cannot
compensate for environmental and weather changes.
One way to tackle these problems is to have an initial
fly-through, through which an occupancy map of the
blade is created and which is then used for planning
a flightpath, as suggested by (Sch
¨
afer et al., 2016).
Another solution proposed by (Jung et al., 2015) can
come not only from relying on a flying drone, but
creating a hybrid flying and climbing vehicle, which
(a) (b)
Figure 2: The hardware used for the proposed system - the
RPLIDAR and the BNO055 9-DOF IMU.
uses a combination of sonar, IMU and LiDAR system
to orient itself. Using a dynamic flightpath planning
from a camera feed is a another strategy employed by
(Galleguillos et al., 2015) and (Cordero et al., 2014),
combining it together with navigation sensors like an
IMU, GPS, barometer, etc.
We propose a localization and shape mapping sys-
tem, which uses a LiDAR scanner and an IMU, plus a
simplification of the wind turbine blade cross-section
to a elliptical model for distance and shape correc-
tion. Our algorithm is based on the assumption that
only the blade is visible at any time and works even
when as little as 2 or 3 points are obtained from the
scanned surface.
3 METHODOLOGY
3.1 Algorithm Overview
The proposed system, given in Figure 3, relies on
prior shape information for a proper positioning. The
prior information in our case, comes in the form of
a model of the shape of the blade cross-section. Be-
cause finding a real world 3D model for each piece of
the cross-section of the different kinds of blades in a
problematic task, a simplified elliptical model is pro-
posed. The elliptical model requires much less prior
information and it gives centimeter precision results
as shown in Section 4. Stray sunlight in the sensor
causes detection noise, which is filtered away using a
combination of hardware polarization and software k-
nearest neighbors and line filters, before the LiDAR’s
raw data is used.
As an initial step, before the main localization al-
gorithm is started, the angle between the blade and
drone is calculated using readings from a low-cost Li-
DAR from (Slamtec, 2010), shown in Figure 2a and
an 2D iterative closest point algorithm, as described
in Subsection 3.4. The angle is used to rotate the el-
liptical model in the same direction as the blade and is
then maintained with the readings from the IMU from
(Adafruit, 2012), shown in Figure 2b. It is observed
LiDAR-based 2D Localization and Mapping System using Elliptical Distance Correction Models for UAV Wind Turbine Blade Inspection
419

Figure 3: Algorithm and work pipeline overview. From raw
LiDAR data and IMU orientation, to localization of the Li-
DAR compared to the blade and mapping the points of the
blade cross-section.
that the LiDAR exhibits errors in its readings, which
change with the distance from the measured surface.
To compensate for this error, we compare the mea-
surements from the LiDAR and ground truth readings
from a DISTO laser distance scanner. The differences
are calculated, interpolated and smoothed out using a
cubic spline and used as distance corrections.
Once the data is clear of noise, corrected from
the distance errors and properly rotated, the ellipti-
cal distance correction model (EDC model) as seen
in Subsection 3.3, together with the angle correction
from the IMU, are applied. The localized drone po-
sition is filtered to remove false movement readings
using a covariance ellipse error filtering, as proposed
by (Friendly, 1991) and the blade points are mapped
accordingly.
3.2 From Corrected LiDAR Data to
Initial Drone Localization
The corrected output data from the RPLIDAR comes
in polar coordinates. To position the data for each Li-
DAR reading in a unified coordinate system, the data
is first transformed to Cartesian coordinates. We as-
sume that only the wind turbine blade is seen by the
LiDAR at any given time, so the origin of the new
Cartesian coordinate system is chosen to be the cen-
ter of the scanned blade. We then wish to map ev-
erything to this coordinate system - both drone po-
sitions and blade surface points. Formula 1 is used
for transforming the coordinates. Lets for a moment
also assume that the centroid of the measured points
from the LiDAR is a good approximation for the cen-
ter of te blade, independent of where the LiDAR is
compared to the blade. Naturally the are problems
with that assumption and we will demonstrate how to
compensate for that error in the next sections.
x
d
= 0 − D
mean
· sin(α
mean
)
y
d
= 0 − D
mean
· cos(α
mean
)
(1)
Where the x
d
and y
d
are the drone coordinates in
the new coordinate system, D
mean
and α
mean
are the
mean distance and angle calculated from all detected
points in a 360 degree reading. Once the LiDAR is
self localized, compared to the blade, the LiDAR’s
position is used as a new center of a polar coordinate
system to find the blade’s previously detected points.
The points are calculated in a Cartesian coordinate
system using Formula 2.
x
i
= x
d
+ D
i
· sin(α
i
)
y
i
= y
d
+ D
i
· cos(α
i
)
(2)
Here x
i
and y
i
, are the coordinates of each of the
data points in one reading and D
i
and α
i
are respec-
tively their distances and angles. The center for calcu-
lating the blade points positions is the LiDAR’s coor-
dinates x
d
and y
d
, calculated in Formula 1. The whole
process is visualized in Figure 4. The initial naive ap-
proach to localization and mapping yields some prob-
lems, such that the whole cross-section needs to be
opened up. Additional processing is required to get
the correct cross-section mapping and position local-
ization. This is why we introduce the elllipse distance
correction model (EDC model).
3.3 Elliptical Distance Correction
Model (EDC Model)
In real life the LiDAR does not measure the distance
from the drone to the blade center, but to the exterior
shell/body of the blade. The distance from the cen-
ter of the blade to the exterior points that the LiDAR
measures is not known to the LiDAR. This discrep-
ancy leads to improper modeling of the surface shape
of the blade and incorrect drone position calculation.
To be able to capture the proper shape of the blade
profile and the proper LiDAR positions, an initial
guess of the blade form is needed. The wing of a
wind turbine has a very specific and hard to model
shape, which changes with height. Each blade man-
ufacturer has different specifications, numbering and
shape mold and this information is not readily avail-
able. Therefore, an approximate simplified model is
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
420
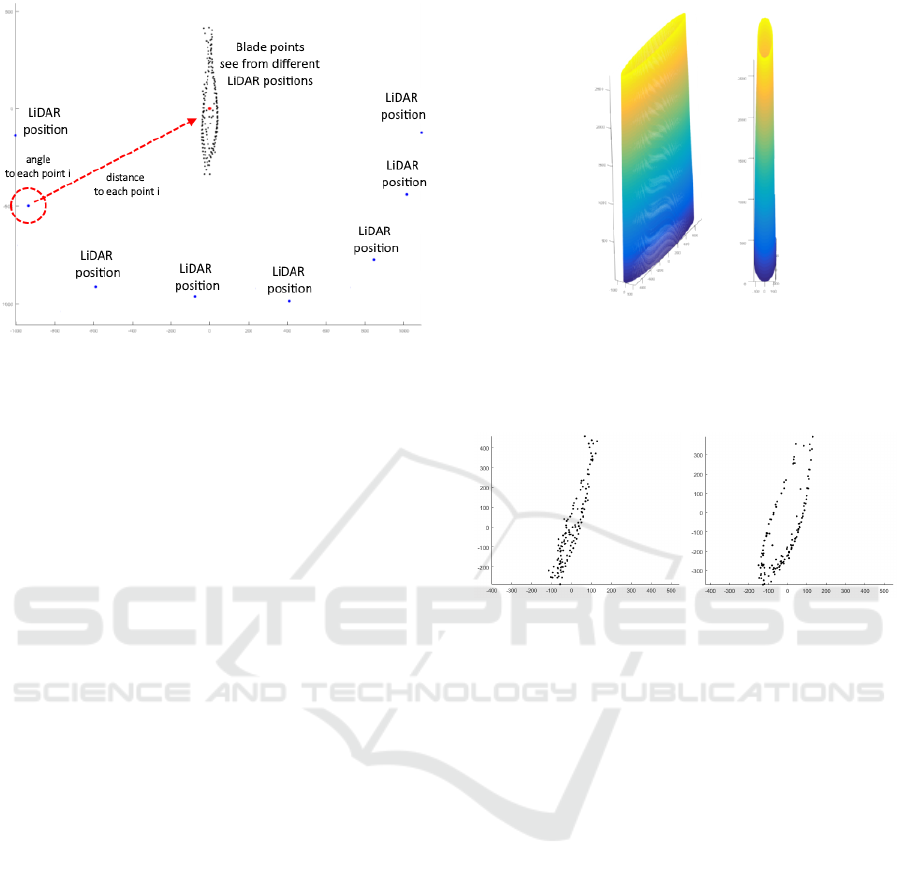
Figure 4: Initial drone localization. The corrected LiDAR
data is transformed into a Cartesian coordinate system and
the mean angle and distance are used to self-position the
LiDAR compared to the blade. Once these positions are
found they are used to find the blade points’ positions. Eight
LiDAR positions and the visible blade points are plotted in
the Figure.
required as a substitute of the blade shape. The model
can be further adjusted using known blade shapes.
This requires making some assumptions:
• The LiDAR sees only the wind turbine blade;
• The wind turbine blade is stopped;
• The blade’s cross-section width and depth are
known;
• The vertical position of the drone is known.
An ellipse is suggested as such a simple geometri-
cal shape, as it closely resembles the the blade cross-
section, especially in the leading edge. To model
properly the blade’s size for the different heights, an
ellipse shape is calculated for each height slice of the
blade. The ellipse points are calculated using the For-
mula 3, where r
1
and r
2
are the two radii of the ellipse,
which are selected based on the width and depth of
the cross-section at the particular blade height and the
angle β ∈ [0 : 2π] .
x
e
= 0 − r
1
· sin(β)
y
e
= 0 − r
2
· cos(β)
(3)
A full model of the blade is created and is saved in
a table, for an easy access depending on the height of
the drone, compared to the blade. Multiple elliptical
models can be created for different blade dimensions
and manufacturer models. A full 3D model can be
seen in Figure 5.
For each point on the ellipse, the radius from the
center to the point is calculated, as well as the angle
on a circle with a center in (0,0). Each point on the
Figure 5: Elliptical model for correcting the LiDAR’s po-
sition. The 3D model is created with interpolation of the
two radii of the ellipse cross-section in Z direction, follow-
ing the notion that wind turbine blades become smaller with
height.
(a) Without EDC model (b) With EDC model
Figure 6: Example mapping of the blade before and after
the EDC model. The points’ positions are corrected and the
whole profile is opened up, especially the blade edge points.
ellipse is positioned in the same coordinate system as
the points from the LiDAR. This way when the Li-
DAR position is calculated using the mean distance,
the distance of the point on the ellipse with the closest
angle to the mean angle of the LiDAR is added to it.
This effectively pushes outwards the mean points and
gives an initial guess on the shape of the blade. The
difference can be seen when plotting the blade sur-
face points before and after the elliptical correction,
as seen in Figure 6. The correction is most notice-
able on the points on the leading edge of the blade.
The whole profile is opened up, representing the blade
cross-section more closely.
Another problem becomes evident when using the
EDC model - the ellipse needs to be initially oriented
the same way as the blade profile. The rotation of the
blade is initially unknown and needs to be determined
before the correction can be applied to the localization
and mapping.
LiDAR-based 2D Localization and Mapping System using Elliptical Distance Correction Models for UAV Wind Turbine Blade Inspection
421

3.4 Calculating Initial Angle between
Drone and Blade
The drone’s yaw orientation is taken from the IMU
unit. The angle between the detected blade profile
from the LiDAR and the IMU connected to the drone
is calculated. The initial angle is used to first orient
the ellipse compared to the blade’s orientation for the
EDC model and also for keeping the mapped posi-
tions at the same heading. The change in the orien-
tation of the wind turbine blade, while the LiDAR is
scanning, is deemed too small, as it will be stopped
from moving or rotating for the duration of the drone
flight.
The angle between the blade and LiDAR can be
calculated using ICP. Heuristically it is determined
that at least 8 points are required in one reading for
the ICP registration to be successful. The sides of
the blade are better for registration than the edge,
as they contain more points, which are spread more
evenly. Because the success of the ICP depends on
the quantity and quality of the registration points, a
cubic spline is approximated to the scanned points.
This way the scanned points are interpolated and any
small noise position errors are smoothed over. A 2D
ICP algorithm by (Bergstr
¨
om and Edlund, 2014) is
used to register the LiDAR points to the prior ellip-
tical model. A rigid registration is performed with
only rotation and translation, as the ellipse is properly
sized beforehand, using the initial information for the
width and depth of the blade profile. The process can
be seen in Figure 7.
Once the registration is completed, the rotation an-
gle is used to rotate the EDC model. The angle is also
added to the yaw angle measured by the IMU for use
with the drone’s yaw holding.
Figure 7: Initial ICP orientation of the EDC model. Blue
points show the LiDAR’s reading, red points are the approx-
imated cubic spline and the green ellipse is the correction
model.
4 SYSTEM TESTS AND RESULTS
4.1 Localization Test
The first test aims to measure the localization accu-
racy of finding the position of the LiDAR compared
to the blade. As the system is still in the prototyping
stages, the measurements are done on the ground. A
number of ground truth points are measured around
the blade profile, ranging from 0.5m to 3.5m in dis-
tance from LiDAR to the blade leading edge. Two
sets of fifteen positions are selected. The first set is
with positions arranged in a circle and the second -
in a line. These are selected, to demonstrate the sys-
tem’s performance with different scan patterns. Both
sets contain outliers positions to verify the accuracy of
the system in harder localization points, such as those
far away or too close to the blade. The LiDAR is posi-
tioned on each of the ground truth points and the mea-
sured position is computed. Fifty readings are taken
so any noisy measurements can be filtered away using
the covariance ellipse error filtering. The Euclidean
distance between each of the ground truth positions
and measured LiDAR self positioning is computed,
both with and without the elliptical distance correc-
tion model. The resultant error values from the first
and second position datasets are given in Table 1 and
the plotted LiDAR and blade points are given in Fig-
ure 8.
Table 1: Results from the first and second set of posi-
tions around the blade. The distance error(mm) between the
ground truth position and the one measured by the LiDAR
with the correction algorithm E
algorithm
and with only the
raw data E
raw
.
Dataset 1 Dataset 2
Pos E
raw
E
algorithm
E
raw
E
algorithm
1 88.36 76.01 213.10 119.22
2 259.96 210.01 183.81 79.88
3 187.54 119.01 221.20 111.19
4 221.32 118.63 199.42 88.59
5 228.45 104.67 221.51 75.40
6 386.52 81.49 372.17 153.79
7 263.29 64.54 333.90 64.49
8 152.99 16.18 306.11 41.51
9 84.32 12.20 276.03 43.08
10 47.17 18.26 150.44 66.08
11 138.62 42.21 136.81 18.49
12 341.87 51.91 110.82 45.54
13 183.16 135.09 75.77 34.39
14 180.57 110.27 131.25 36.79
15 285.28 84.67 248.22 4.59
Avg 203.30 83.01 212.04 65.54
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
422

(a) Dataset 1 without EDC model (b) Dataset 1 with EDC model
(c) Dataset 2 without EDC model (d) Dataset 2 with EDC model
Figure 8: Localization test using the first (8a and 8b) and second(8c and 8d) position datasets. The ground truth data is
shown with red dots and the LiDAR calculated positions with blue dots. The mapped blade points are also plotted, for easier
orientation.
The results show that the system can provide a
stable position estimate for where the drone is com-
pared to the blade. The biggest differences between
the measured and ground truth points come from po-
sitions where just a small amount of points from the
surface can be seen in the Dataset 1 distances between
ground truth and measurements in positions 3, 4, 5
and 13. In addition positions which are too far away
from the blade surface exhibit both lower precision
and accuracy, because insufficient points are sampled
by the LiDAR, which makes faraway point angle and
distance estimation jump around too much, as seen in
the measurement in position 14 and 15 in Dataset 1.
Some larger distances are observed in the first dataset,
which can also be explained by problems with the
yaw hold and small changes in the rotation of the Li-
DAR, as seen in position 2. In all positions, the intro-
duction of the EDC model is shown to dramatically
increase the accuracy of the localization, compared to
just using the raw data. This is especially evident in
the measurements 5 to 9 from Dataset 2.
4.2 Mapping Test
For testing the mapping capabilities of the LiDAR
system, the blade profile is scanned with a Faro laser
scanner and a high quality point cloud is created.
A 2D cross-cut of the point cloud is then used as a
ground truth, when comparing with the mapped blade
point positions. In this test the LiDAR is placed in
positions, forming a semicircle around the blade with
three radii - 1.5 m, 2 m and 3 m, for testing the map-
ping capabilities from different distances. Addition-
ally a post-processed mapping from 1.5 m, which has
been registered to the elliptical prior model using the
ICP algorithm is given, to demonstrate one way that
the proposed algorithm can be extended to boost ac-
curacy. The signed distances between each point of
the two 2D point clouds is calculated. This is done
using the free open source software CloudCompare
(Girardeau-Montaut, 2003). From the distances, the
mean and standard deviation of the distance distribu-
tion are calculated. The mean and standard deviation
are given in Table 2 and the mapped blade surface
points are given in Figure 9
The difference between the elliptical correction
model and the blade cross-section becomes larger the
farther away from the edge it goes, because the scan-
ning is done only in a 180 degree semi-circle around
the blade and details of the back of the blade are
sparse. The front of the blade in the LiDAR scans
shows a higher standard deviation and some noisy
LiDAR-based 2D Localization and Mapping System using Elliptical Distance Correction Models for UAV Wind Turbine Blade Inspection
423

Table 2: Mean value (µ) in mm, standard deviation (σ) in
mm
2
, minimum (d
min
) and maximum (d
max
) in mm of the
absolute distance metrics between the ground truth and the
LiDAR mapped points from three distances to the blade
(D
b
) - 1.5, 2 and 3 meters.
D
b
µ σ d
min
d
max
1.5 10.93 7.32 0.36 38.13
1.5 + ICP 9.32 6.92 0.24 31.038
2 14.89 9.19 0.62 38.40
3 15.65 9.23 1.31 39.30
(a)
Ground
truth
(b) 1.5
meters
(c) 1.5
meters
+ ICP
(d) 2
meters
(e) 3
meters
Figure 9: Mapped blade surface from the LiDAR, using the
EDC model, together with the ground truth Faro scan and
the post-processed 1.5 meter mapping using the ICP algo-
rithm together with the elliptical prior model. The 2D point
clouds get sparser and noisier the further away the LiDAR
is.
points, because of the small amount of points seen
from those angles. Even with these problems and the
relatively small sampling density of the RPLIDAR,
the proposed algorithm manages to restore the shape
of the blade with centimeter accuracy. If a registra-
tion is done, the results get closer to the ground truth
shape. This shows that the algorithm can be used as a
proper substitute to SLAM.
5 CONCLUSION AND FUTURE
WORK
We propose a low-cost, easy to implement drone
localization and mapping system for wind turbine
blades, using a cheap commercial LiDAR and an off-
the-shelf IMU. Our system uses prior shape infor-
mation in the form of elliptical distance correction
model. It requires minimum prior information; it is
computationally fast; simpler to implement than con-
ventional SLAM; it can easily be extended and refined
with additional training and provides satisfactory re-
sults. We demonstrate through ground based localiza-
tion and a mapping tests that the system can self po-
sition and obtain mapping of the blade cross-cut with
centimeter accuracy. In addition we propose a filter
for removing noisy position information. Our algo-
rithm also removes distance measurement errors and
direct sunlight noise, so it can be used both outdoors
and indoors.
As an extension of our work we propose an in-
depth test of our system and algorithm against the
state of the art SLAM algorithms performed on blade
profiles, to verify the calculated accuracy of the sys-
tem. Testing the algorithm using a ”default” blade
shape, which will better resemble the scanned blades,
as a distance correction model is also suggested, as
well as further adjusting it using training sets.
REFERENCES
Adafruit (2012). Adafruit bno055 9-dof imu. https://learn.
adafruit.com/adafruit-bno055-absolute-orientation-
sensor. Accessed: 2016-09-15.
Berger, C. (2013). Toward rich geometric map for slam:
Online detection of planes in 2d lidar. Journal of Au-
tomation Mobile Robotics and Intelligent Systems, 7.
Bergstr
¨
om, P. and Edlund, O. (2014). Robust registra-
tion of point sets using iteratively reweighted least
squares. Computational Optimization and Applica-
tions, 58(3):543–561.
Cordero, M., Trujillo, M., Ruiz, J., Jimenez, A., Diaz,
L., and Viguria, A. (2014). Flexible framework for
the development of versatile mav systems for multi-
disciplinary applications. In IMAV 2014: Interna-
tional Micro Air Vehicle Conference and Competition
2014, Delft, The Netherlands, August 12-15, 2014.
Delft University of Technology.
Elseberg, J., Borrmann, D., and N
¨
uchter, A. (2012).
6dof semi-rigid slam for mobile scanning. In 2012
IEEE/RSJ International Conference on Intelligent
Robots and Systems, pages 1865–1870. IEEE.
Endres, F., Hess, J., Engelhard, N., Sturm, J., Cremers, D.,
and Burgard, W. (2012). An evaluation of the rgb-
d slam system. In Robotics and Automation (ICRA),
2012 IEEE International Conference on, pages 1691–
1696. IEEE.
Friendly, M. (1991). SAS system for statistical graphics.
SAS Publishing.
Galleguillos, C., Zorrilla, A., Jimenez, A., Diaz, L., Mon-
tiano,
´
A., Barroso, M., Viguria, A., and Lasagni, F.
(2015). Thermographic non-destructive inspection of
wind turbine blades using unmanned aerial systems.
Plastics, Rubber and Composites.
Girardeau-Montaut, D. (2003). Cloudcompare. http://
www.cloudcompare.org/. Accessed: 2016-09-15.
Jung, S., Shin, J.-U., Myeong, W., and Myung, H. (2015).
Mechanism and system design of mav (micro aerial
vehicle)-type wall-climbing robot for inspection of
wind blades and non-flat surfaces. In Control, Au-
tomation and Systems (ICCAS), 2015 15th Interna-
tional Conference on, pages 1757–1761. IEEE.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
424

Morgenthal, G. and Hallermann, N. (2014). Quality assess-
ment of unmanned aerial vehicle (uav) based visual
inspection of structures. Advances in Structural Engi-
neering, 17(3):289–302.
Mur-Artal, R., Montiel, J., and Tard
´
os, J. D. (2015). Orb-
slam: a versatile and accurate monocular slam system.
IEEE Transactions on Robotics, 31(5):1147–1163.
Negre, P. L., Bonin-Font, F., and Oliver, G. (2016).
Cluster-based loop closing detection for underwater
slam in feature-poor regions. In 2016 IEEE In-
ternational Conference on Robotics and Automation
(ICRA), pages 2589–2595. IEEE.
Oh, T., Kim, H., Jung, K., and Myung, H. (2015). Graph-
based slam approach for environments with laser scan
ambiguity. In Ubiquitous Robots and Ambient Intel-
ligence (URAI), 2015 12th International Conference
on, pages 139–141. IEEE.
Sch
¨
afer, B. E., Picchi, D., Engelhardt, T., and Abel, D.
(2016). Multicopter unmanned aerial vehicle for au-
tomated inspection of wind turbines. In 2016 24th
Mediterranean Conference on Control and Automa-
tion (MED), pages 244–249. IEEE.
Shepard, D. P. and Humphreys, T. E. (2014). High-precision
globally-referenced position and attitude via a fusion
of visual slam, carrier-phase-based gps, and inertial
measurements. In 2014 IEEE/ION Position, Loca-
tion and Navigation Symposium-PLANS 2014, pages
1309–1328. IEEE.
Slamtec (2010). Slamtec rplidar. http://
www.slamtec.com/en. Accessed: 2016-09-15.
Zlot, R. and Bosse, M. (2014). Efficient large-scale 3d
mobile mapping and surface reconstruction of an un-
derground mine. In Field and service robotics, pages
479–493. Springer.
LiDAR-based 2D Localization and Mapping System using Elliptical Distance Correction Models for UAV Wind Turbine Blade Inspection
425
