An Integrated System based on Binocular Learned Receptive Fields for
Saccade-vergence on Visually Salient Targets
Daniele Re
1
, Agostino Gibaldi
1
, Silvio P. Sabatini
1
and Michael W. Spratling
2
1
Department of Informatics, Bioengineering, Robotics and System Engineering, University of Genoa, Genoa, Italy
2
Department of Informatics, King’s College London, London, U.K.
Keywords:
Disparity, Binocular Vision, Stereopsis, Vergence, Saccade, Attention, Basis Function Networks, Neural
Networks, Sensory-sensory Transformations, Sensory-motor Control, Learning, V1 Area, Receptive Field
Learning.
Abstract:
The human visual system uses saccadic and vergence eyes movements to foveate interesting objects with both
eyes, and thus exploring the visual scene. To mimic this biological behavior in active vision, we proposed a
bio-inspired integrated system able to learn a functional sensory representation of the environment, together
with the motor commands for binocular eye coordination, directly by interacting with the environment itself.
The proposed architecture, rather than sequentially combining different functionalities, is a robust integration
of different modules that rely on a front-end of learned binocular receptive fields to specialize on different
sub-tasks. The resulting modular architecture is able to detect salient targets in the scene and perform precise
binocular saccadic and vergence movement on it. The performances of the proposed approach has been tested
on the iCub Simulator, providing a quantitative evaluation of the computational potentiality of the learned
sensory and motor resources.
1 INTRODUCTION
An intelligent perceptual system must be able to in-
teract with its environment through sensing, process-
ing and interpreting information about the external
world at different levels of representation, and eventu-
ally solve complex problems in contingent situations.
Conceiving such an intelligent system, a number of
abilities are required, such as: to attain online re-
source allocation; to generate and execute complex
plans; to deal with problems as they arise in real-
time; and to reason with incomplete information and
unpredictable events. To fulfill all these tasks, con-
siderable computational resources are required, that
might exceed those available. In active machine vi-
sion, it has been demonstrated that both perceptual
and action processes can rely on the same computa-
tional resources (Antonelli et al., 2014; Ognibene and
Baldassare, 2015), at an early level that mimics the lo-
calized, oriented and band-pass receptive fields avail-
able in the primary visual cortex (V1 area) of mam-
mals (Daugman, 1985a). Notably, learning such re-
sources (Olshausen et al., 1996; Olshausen and Field,
1997) has become a popular approach, for a num-
ber of advantages. In fact, it allows the emergence
of spatial competences that can be exploited by the
system to self-calibrate both to the working space
and to the geometric features of its own body schema
(Gibaldi et al., 2015c), and ultimately specialize task-
dependent representations (Ballard et al., 1997). Con-
sidering visual exploration of the three-dimensional
(3D) environment, this behaviour is composed of a
sequential cascade of operations. First, the visual in-
formation impinging on the two retinas has to be en-
coded and interpreted, in order to gather the salient
features in the visual scene. Next, a binocular coordi-
nation of the eyes is necessary to perform a saccadic
movement to foveate a visual target in the 3D space.
Finally, a vergence refinement precisely aligns the op-
tical axes on the object of interest, allowing for a bet-
ter interpretation of disparity information.
From this perspective, the control of such com-
pounded operations in active vision, requires not just
the implementation of different complementary mod-
ules, each capable of solving one of these single ac-
tions, but their joint integration in a structured frame-
work that allows us to obtain the complex behaviours
required for a natural interaction with the surrounding
environment. Here we present an integrated frame-
work for autonomous saccade-vergence control of a
204
Re D., Gibaldi A., P. Sabatini S. and W. Spratling M.
An Integrated System based on Binocular Learned Receptive Fields for Saccade-vergence on Visually Salient Targets.
DOI: 10.5220/0006124702040215
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 204-215
ISBN: 978-989-758-227-1
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

binocular visual system. The proposed framework is
able learn an efficient internal representation of 3D vi-
sual scene, both for the perceptual and motor space, in
order to perform accurate binocular foveation towards
salient visual targets. In the proposed approach, both
the perceptual and motor capabilities are learned by
a direct interaction with the working environment, in
a concurrent process that closes the loop between ac-
tion and perception at system level. Moreover, the
distributed approach, used both for the perceptual and
motor aspects of the framework, allows for a simple
and straightforward communication among the differ-
ent integrated modules, since they rely on similar neu-
ral codes for representing sensory and motor informa-
tion.
The remaining of the paper is organized as fol-
lows: Section 2 reviews the state of the art; Section 3
presents the different modules and their integration in
the proposed framework; the capabilities of the ap-
proach within the iCub simulator are evaluated in Sec-
tion 4; in Section 5 we draw the conclusions.
2 STATE OF ART
Encoding Visual Information - In the early visual sys-
tem, the sensory pathway is commonly considered
a communication channel that performs an efficient
coding of the sensory signals, i.e. it is able to repre-
sent the sensory information with the minimal amount
of resources, while preserving the coded informa-
tion. Over the last two decades, researchers have pro-
posed different unsupervised learning algorithms to
model a range of neural processes at the early sen-
sory stages. Imposing a sparseness constraint, it is
possible to learn basis functions that resemble V1 re-
ceptive fields (Olshausen et al., 1996; Olshausen and
Field, 1997), forming an efficient image representa-
tions (Daugman, 1985b). The approach can be also
extended to stereoscopic information (Hyv¨arinen and
Hoyer, 2000; Okajima, 2004; Hyv¨arinen et al., 2009),
exploiting the natural disparity distribution (Hunter
and Hibbard, 2015) to obtain ideal disparity detectors
(Hunter and Hibbard, 2016).
The monocular and binocular visual information
encoded by this early sensory stage, can thus be ex-
ploited by subsequent processing stages with different
decoding strategies, depending on the task at hand:
the monocular responses can be interpreted as fea-
ture map, and used as input to an bottom-up attention
module, whereas the binocular responses can be used
to drive the disparity-vergence control.
Attention Model - Attention is considered the process
of selecting and gating visual information, and has a
fundamental role in perceiving the surrounding envi-
ronment and driving the eye movements. In humans
and primates, this process is mediated by two com-
petitive mechanisms: a bottom-up interpretation of
the visual information to obtain a saliency map of the
visual features, and a top-down interpretation of the
scene based on a prior knowledge about the scene.
From this perspective, it is worth considering that
during the early development of the visual system,
visual attention relies on bottom-up process mainly,
since it is not yet supported by a sufficient cognitive
development (see (Gerhardstein and Rovee-Collier,
2002), as review). Being our integrative model fo-
cused on modeling the early functionalities of the vi-
sual system, we adopt a bottom-up attentive behavior,
which is more suited to that purpose. To this aim,
visual search models can be designed by integrating
different visual features from the image (orientation,
color, direction of movement), on the top of which
the most salient parts in a scene pop out. The seminal
work of of Itti and Koch (Itti et al., 1998) paved the
way to different approaches saliency-based attention
(Houghton and Tipper, 1994; Ma and Zhang, 2003;
Hu et al., 2004). In our model, we adopted the ap-
proach proposed by (Bruce and Tsotsos, 2005), for its
deep biological inspiration. The authors related spa-
tial visual saliency to regions characterized by large
differences between the monocular response of sim-
ple cells within a local region, and the response of
the cells with similar tuning in a surrounding region.
Such an antagonist organization of the input mimics
the lateral inhibition strategy present in area V1 (Rao
and Ballard, 1999). The resulting saliency map is
used to define the target position in visual space, in
order to drive the ocular gaze through saccadic eyes
movements.
Saccadic Control - In order to effectively direct the
gaze toward an interesting visual target, the brain
must transform the sensory coordinates of the stim-
ulus into headcentric motor coordinates, so to gener-
ate an effective motor command in joint coordinates
(Crawford and Guitton, 1997) How does the brain
perform such sensorimotor transformations? In the
past, several neural networks have been proposed to
convert input information, i.e. eye position and reti-
nal target position, into an output, e.g. the targets lo-
cations in head coordinates (Pouget and Sejnowski,
1997; Chinellato et al., 2011; Antonelli et al., 2014;
Muhammad and Spratling, 2015). Typically, this
mapping occurs by developing a distributed represen-
tation in a ”hidden layer” interposed between the in-
put and output layers. In our work, we adopted a
basis function network (Muhammad and Spratling,
2015) able to perform both sensory-sensory mapping
An Integrated System based on Binocular Learned Receptive Fields for Saccade-vergence on Visually Salient Targets
205

(retinotopic-headcentered coordinates) and sensory-
motor mapping (headcentered-joint coordinates).
Disparity-Vergence Control - During vergence eye
movements, the eyes rotate in opposite direction in
order to reduce and eventually nullify the binocular
disparity of the fixated object. Disparity-vergence
eye movements were first modeled using a simple
feedback control system (Rashbass and Westheimer,
1961). Classical models of vergence control can gen-
erally be classified into three basic configurations:
continuous feedback, feedback with pre-programmed
control (Hung et al., 1986) and switched-channelwith
feedback (Pobuda and Erkelens, 1993). The primary
limitation of these models is that they first require the
computation of the disparity map for the extraction
of the control signals, thus limiting the functional-
ity of the vergence system within the range of where
the system is able to solve the stereo correspondence
problem. Subsequent approaches, gathering inspira-
tion form the primates visual system, are based on
a distributed representation of binocular information
(Gibaldi et al., 2010; Wang and Shi, 2011; Lonini
et al., 2013; Gibaldi et al., 2016), overcoming this
limitation. On this basis, we exploited a neural net-
work model that directly interprets the population re-
sponse into a vergence control, to nullify the disparity
in fovea (Gibaldi et al., 2010).
System integration - Here, we review the studies
that are relevant to the proposed integrative model,
with a particular care for those integrating active
perceptual approach with bottom-up biologically in-
spired attention modules. Since our approach fo-
cuses on the interplay between oculomotor control
and early visual processing, we will not take into
account those works including higher cognitive pro-
cesses (Borji et al., 2010), as they would deserve a
dedicated consideration (Orquin and Loose, 2013).
Bottom-up attentive module are important to select
objects of interest (Serre et al., 2007) in order to di-
rect the gaze across the scene (Wang and Shi, 2011).
The former work, starting from a standard model of
visual cortex (Serre et al., 2005), designed a 4-layers
neural network able to learn a vocabulary of visual
features from images and to use it for the recogni-
tion of real-world object-categories. The latter work,
proposed a saccade model that integrates three driv-
ing factors of human attention reflected by eye move-
ments: reference sensory responses, fovea periphery
resolution discrepancy, and visual working memory.
These capabilities are required also for the control of
humanoid robots (Ruesch et al., 2008). In fact, the
recent developments of artificial intelligence require
humanoid robots able to cope with variable and un-
predictable problems, similar to those tackled by the
human perceptual system. On this common ground,
efficient biologically inspired solutions are an effec-
tive approach (Pfeifer et al., 2007).
Specifically, in our integrative model, attention
acts as a front-end module in acquiring the target of
interest, for a subsequent oculomotor control, that is
composed of a binocular coordinated saccade and a
vergence movement. Specifically, we are interested in
employing a computational approach derived by bio-
inspired models of primates’ visual cortex. Accord-
ingly, while the saccadic control is based on a network
of radial basis functions (Muhammad and Spratling,
2015), the latter relies on a substrate of binocular
receptive fields (Gibaldi et al., 2010; Gibaldi et al.,
2016).
3 THE INTEGRATED SYSTEM
The system we designed integrates different modules
(see Fig. 1) to provide an active stereo head with au-
tonomous exploration capabilities: 1) a front-end for
the encoding of the visual information, 2) a bottom-up
attentive model to obtain salient features in the visual
scene, 3) a saccadic control module to fixate the ob-
ject of interest, and 4) a vergence control module to
refine the vergence posture. At the root of the percep-
tion process, we implemented a set of binocular ba-
sis functions (receptive fields), directly learned from
the images captured by the cameras, that provide a
distributed coding of monocular and binocular visual
information. The information from each monocular
channel is exploited by an attentive process in order
to derive a bottom-up saliency map of the visual fea-
tures. The relationship between the selected target in
retinotopic coordinates and the required eye move-
ment to binocularly foveate it, is learned through a
basis function network, that eventually drives coordi-
nated binocular saccadic movements in the 3D space.
Finally, a closed-loop vergence control decodes the
binocular disparity information to refine the binocular
alignment on the object of interest. In the following,
we will describe each single module and its imple-
mentation on the iCub Simulator.
3.1 Learning Binocular Receptive
Fields
For binocular receptive field learning, we exploited a
pre-existing algorithm proposed by (Olshausen et al.,
1996; Olshausen and Field, 1997), which relies on an
unsupervised strategy. Specifically, an image I(x) can
be locally represented in terms of a linear combina-
tion of basis functions φ
i
(x), where x = (x,y) are the
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
206

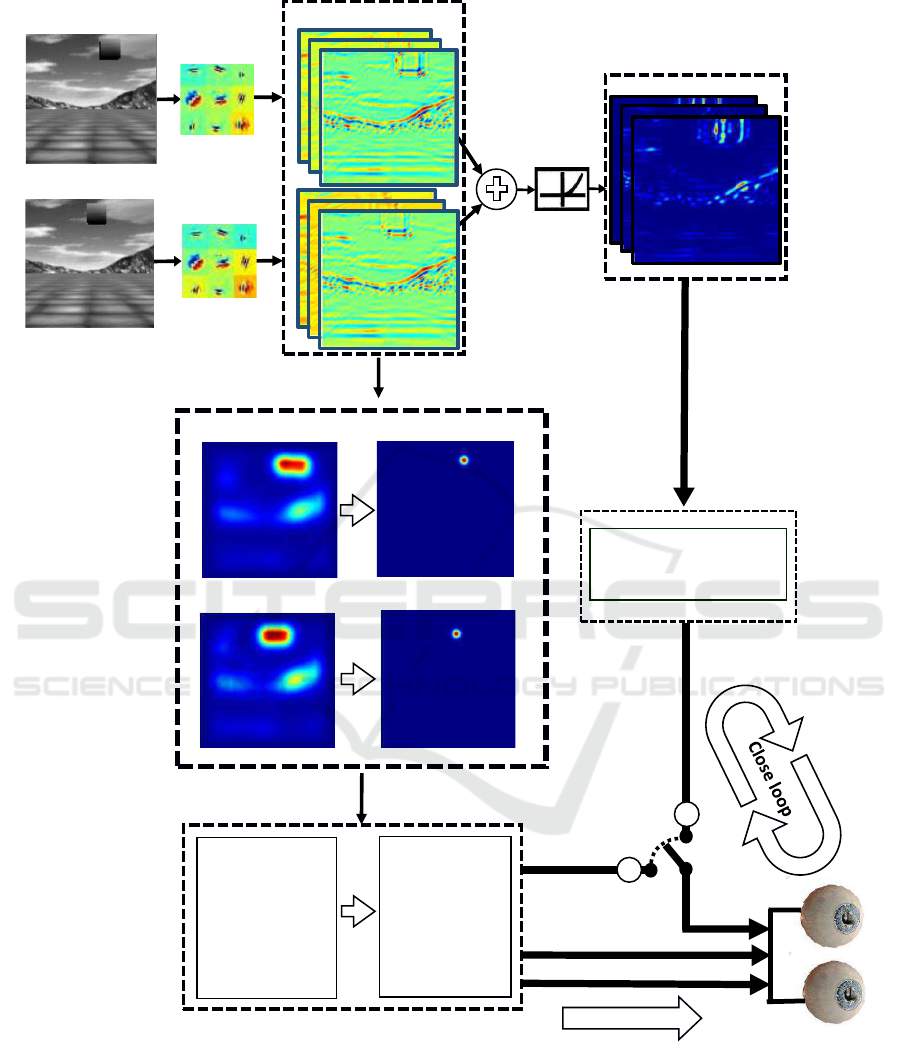
Image left
Image right
Binocular response
Monocular response
Sensory-
sensory
mapping
Sensory-
motor
mapping
Pan
Tilt
Verg
Verg
Basis left
Basis right
Vergence
actuators
Saliency left
Saliency right
Open loop
1
2
Saccadic/vergence
model
Attentive
model
Disparity-vergen
ce
model
Figure 1: Schematic diagram of the integrated attentive-saccadic-vergence model. The monocular and binocular information
obtained by filtering with the over-complete set of basis function is processed separately by the bottom-up attentive model and
the disparity vergence control. The attentive model locates the most salient object on which to plan an open-loop binocular
saccadic movement (verg,
1
). At a subsequent stage, a closed-loop vergence refinement is guided by disparity information
(verg,
2
).
retinal coordinates. In order to learn the basis func-
tions with the associated weights, the algorithm uses
a set of patches extracted from natural scenes images,
and seeks to maximize the sparseness of the encoded
visual information. The basis functions that emerge,
are a complete set that strongly resembles the recep-
An Integrated System based on Binocular Learned Receptive Fields for Saccade-vergence on Visually Salient Targets
207

tive fields found in the primary visual cortex, and
provide an efficient image representations (Daugman,
1985a).
In our implementation, we extended the approach
to stereoscopic vision, in order to obtain binocular
V1-like RFs. The image patches were taken from a
set of twenty stereo images directly acquired from the
iCub Simulator. A textured panel is placed at different
depths in front of the iCub head, so as to obtain left
and right patches with different binocular disparities.
The monocular patches are then vertically concate-
nated to form a binocular patch [p
L
k
(x), p
R
k
(x)]
T
. Ac-
cording to (Lonini et al., 2013), these stereo patches
can be approximated by:

ˆp
L
k
(x)
ˆp
R
k
(x)

=
N
∑
i
a
ik

φ
L
i
(x)
φ
R
i
(x)

(1)
where N is the number of basis functions. In the
implemented binocular approach, the resulting basis
functions (e.g. Fig 2) are composed of a left, φ
L
i
(x)
and a right, φ
R
i
(x) part. In order to characterize the
properties of such functions, we can fit them as a bank
of Gabor-like stereo receptive field pairs:
φ
L/R
i
(x) ≃ η ·exp

−
(x−x
L/R
0
)
T
(x−x
L/R
0
)
2σ
2

· (2)
cos(k
T
0
x+ ψ
L/R
)
where the following quantities are approximately
equal in the left and right RFs: σ is the variance of the
Gaussian spatial support and defines the RF size, η
is a proper normalization constant, k
0
= (k
0
sin(θ) −
k
0
cos(θ))
T
is the spatial frequency of the RF, k
0
is
the radial peak frequency orthogonal to the RF ori-
entation θ. The learned binocular RF profile is char-
acterized by a difference between the phases (ψ
L
and
ψ
R
) of the monocular RFs and their positions (x
L
0
and
x
R
0
) on the image plane. Hence, the linear monocular
response of a layer of simple cells is given by:
r
L/R
i
(x) =
Z
I
L/R
(x
′
)φ
L/R
i
(x
′
−x)dx
′
(3)
with i = 1,..., N. It is worth noting that r(x)
L/R
i
also
define the feature map associated to the i-th feature.
The response of a corresponding layer of binocular
simple cells can be modeled as the cascade of the
binocular linear response and a static non-linearity:
r
B
i
(x) = (r
L
i
(x) + r
i
(x)
R
)
2
. (4)
By pooling the responses of simple cells with differ-
ent monocular phase symmetries, but the same inte-
rocular phase and/or position shift, we obtain binocu-
lar complex cells with a specific disparity tuning, in-
dependent of the stimulus phase (Qian, 1994). Ac-
cordingly, the binocular cell is sensitive to a vector
Figure 2: (Top) Examples of 50 learned basis functions, dis-
played pairing the left and right receptive field. Despite the
similar size, orientation and frequency, each pair exhibits
both a phase and a position shift in their profile (see Sec. 4).
(Middle) An example of a learned binocular receptive field
together with its fitting. The blue ellipses represent the size
of the envelope and its horizontal and vertical meridians
along the orientation of the receptive field. (Bottom) The
2D tuning curve of the binocular cell to horizontal and verti-
cal retinal disparity, together with its horizontal and vertical
cross sections. The tuning curve is derived as squared sum
of the response of the two monocular receptive fields. (Ta-
ble): the table shows the values of the spatial frequency(k
0
),
phase shift(∆ψ), location shift (s) and orientation(θ) of the
above-mentioned basis.
disparity (δ
H
,δ
V
), oriented along the direction or-
thogonal to its spatial orientation θ, which depends
on the characteristics of the binocular receptive fields,
and specifically on the frequency k
0
, the phase shift
∆ψ = ψ
L
−ψ
R
and the position shift s = x
L
0
−x
R
0
:
r
B
i
(δ
H
,δ
V
) = r
B
i
(x;k
0
,s, ∆ψ) ∝ cos(1+ k
T
0
(δ−s) + ∆ψ)
(5)
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
208

that defines the tuning of the complex cell to a specific
disparity value.
In the next stages, the monocular cell responses
are fed to the attentive model to obtain the saccadic
target, while the binocular responses are used to ob-
tain the disparity-vergence control.
3.2 The Bottom-Up Attentive Module
This module is used to define interesting targets
within the visual scene, to autonomously drive the
saccadic eye control. Specifically, we exploited the
Attention based on Information Maximization (AIM)
algorithm (Bruce and Tsotsos, 2005). The authors de-
fine visual saliency as the relationship between the
monocular response (r
L/R
) of simple cells within a
local region (C
i
), and the response of the cells with
similar tuning in a surrounding region (S
i
). For each
image location, the response value of each monocular
basis can be interpreted as a local match between the
frequency and orientation content of the image, and
the tuning properties of that basis. Since visual fea-
tures can be considered salient when they stand out
the background (Bruce and Tsotsos, 2005), a classi-
cal center-surround function is used to process each
feature map to obtain a saliency map S
i
for each of
the basis functions considered:
S
L/R
i
(x) =
1
√
2πσ
V
∑
x∈Γ
G(x,σ
S
) · (6)
exp[(r
L/R
C
i
(x) −r
L/R
S
i
(x))
2
/(2σ
2
V
)]
where and r
L/R
C
i
and r
L/R
S
i
are the monocular response
for the local region and surround region for the i-th
basis function, σ
V
is the variance of the Gaussian ker-
nel used for spatial averaging over a neighborhood
Γ (Bruce and Tsotsos, 2005),
1
√
2πσ
V
is a normaliz-
ing factor, and G(x,σ
S
) indicates the contribution of
neighboring elements to the local estimate. The value
of S
L/R
i
(x) returns a saliency density where the uni-
tary value suggests a redundancy between local and
surround region, i.e. no saliency, and a value close to
zero indicates a substantial content difference. The
density information can be used to predict at each
retinal location the saliency l(x) of the monocular re-
sponse over the whole set of visual features encoded:
l
L/R
(x) =
N
∑
i=1
−log(S
L/R
i
(x)) (7)
thus returning large values for salient features in the
image and vice-versa.
This attentive model is thus exploited to define
salient locations within the visual scene as targets of
gaze-shifts. In order to make the saccadic vergence
control able to foveate on a generic salient object in-
dependently of its specific shape, a Mexican hat re-
current filtering is applied on the l
L/R
in order to re-
duce the saliency map to a blurred spot centered on
the most salient object (see attentive block in Fig.
1), mimicking a winner-takes-all strategy (Itti et al.,
1998). In the next section we will describe the imple-
mented model for saccadic eye movements.
3.3 The Saccadic Module
In order to shift the gaze to a desired target, we imple-
mented a sensory-sensory and a sensory-motor trans-
formation. The goal is to transform visual informa-
tion about the target location on the retinas and propri-
oceptive information about the positions of both eyes
in the head, to obtain the necessary motor control to
foveate the target with both eyes. To this purpose,
we used the Predictive Coding/Bias Competition-
Divisive Input Modulation (PC/BC-DIM) neural net-
work (Muhammadand Spratling, 2015). PC/BC-DIM
is a basis function network that performs a mapping
between an input layer i and a reconstruction layer
ρ (see Fig 3). The range of possible mappings are
encoded by connection weights (W and V) and are
mediated by a hidden layer of prediction nodes π that
encodes the distinct causes that can underlie the input:





ρ = Vπ
ε = i⊘(c
2
+ ρ)
π ← (c
1
+ π) ⊗Wε.
(8)
Where ε is the error between the input and the net-
work’s reconstruction of the input (ρ); c
1
and c
2
are
constants; and ⊘ and ⊗ indicate element-wise divi-
sion and multiplication, respectively. Both i and ρ
are partitioned into four parts representing the visual
target position in retinotopic coordinates, the eye pan
value, the eye tilt, and the head-centered location of
the target.
The model employs the connection weights V and
W as a “dictionary” containing all the possible com-
binations among the stimulus location in retinal coor-
dinates, the eye position (pan and tilt values), and the
head-centered bearing of the visual target. Their val-
ues are determined by a training process in which a
stationary visual target is presented to the iCub Sim-
ulator while the cameras move, generating distinct
combinations of eye pan/tilt and retinal inputs. After
an exhaustive number of eye movements are realized
for a specific position of the target, the process is re-
peated for a different stimulus position, thus defining
a new head-centered position. After the training pro-
cess, the model is able to return the pan and tilt values
An Integrated System based on Binocular Learned Receptive Fields for Saccade-vergence on Visually Salient Targets
209

PC/BC-DIM
PC/BC-DIM
?
?
?
W V
input
recontruction
input
recontruction
sensory-sensory mapping
sensory-motor mapping
W V
actual
desired
Figure 3: The figure shows the PC/BC-DIM model being used to calculate the eye pan and tilt values necessary to foveate
the target (for a single eye). In the first step, the network is provided with the saliency map showing the visual target in
retinotopic coordinates (1
st
partition) and pan and tilt eye position values (2
nd
and 3
rd
partitions). The network calculates
the head-centered coordinates of the visual target (4
th
partition of the reconstruction array). In the second step, the network
takes as new input the head-centered coordinates from the previous step and a reference signal showing the desired position
of the target at the center of the retina. The network calculates, in the reconstruction array, the pan and tilt values necessary to
foveate the target.
necessary to move the fovea onto the desired target
position, as described in Fig. 3.
This process of planning eye movements was per-
formed for the left and right eye separately. The
iCub Simulator has a single actuator for conjugate tilt
movement, a single actuator for conjugate pan move-
ment, and a separate control for vergence. These val-
ues were determined by combining the separate left
and right eye pan and tilt values calculated by PC/BC-
DIM as follows:





Pan = (Pan
L
+ Pan
R
)/2
Tilt = (Tilt
L
+ Tilt
R
)/2
Vergence = Pan
L
−Pan
R
.
(9)
It is worth considering that the saccadic module
works in a ballistic open-loop manner: after the com-
mand there is no visual feedback to correct the result-
ing vergence movement in order to fixate the target
in depth. A visually-driven closed-loop refinement is
thus required to correctly align the eyes on the ob-
ject of interest. To this aim, we used the disparity-
vergence module described in the following section.
3.4 Disparity-Vergence Module
To obtain an effective disparity-vergence control, we
used the disparity tuning properties of the binocu-
lar complex cells described in Section 3.1. The de-
sired vergence control is an odd symmetric signal that
evokes a convergent movement for crossed dispar-
ity and a divergent movement for uncrossed dispar-
ity. In this way, the vergence control can be applied
in closed-loop until the disparity on the target is null,
i.e. until the complex cell population response is max-
imum (Gibaldi et al., 2015b)).
The response of a vergence neuron r
V
, that drives
the convergent and divergent movements of the robot
eyes, is obtained through a weighted sum of the
binocular responses over a spatial neighborhood Ω:
r
V
=
∑
x∈Ω
N
∑
i
w
i
r
B
i
(x) (10)
The connection weights w
i
are learned by minimizing
the following cost function:
argmin
w
i




∑
N
i=1
r
B
i
(δ
H
,0)w
i
−v
H




2
+ (11)
+λ




∑
N
i=1
r
B
i
(0,δ
V
)(w
i
−1)




2
where v
H
is the desired control profile, δ
H
is the hor-
izontal disparity and δ
V
is vertical disparity, whereas
r
B
i
(δ
H
) and r
B
i
(δ
V
) are the binocular tuning curves
for horizontal and vertical disparity, respectively, and
λ > 0 is a factor that balances the relevance of the
second term over the first.
3.5 Implementation and Learning
The integrated system has been implemented within
the iCub Simulator (Tikhanoff et al., 2008), which is
an open-source computer simulator for the humanoid
robot iCub, developed to be a test-bed for robotic con-
trol algorithms. Specifically, we used this environ-
ment since the iCub stereo head has the necessary
characteristics for binocular active vision (Beira et al.,
2006).
Binocular Receptive Fields - The iCub robot gazes at
a textured panel with different vergence angles in or-
der to produce a disparity approximately in the range
[−2,2] pixels. The images are captured from the left
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
210

and right cameras at a resolution of 128×128 pixels,
covering ≈ 24
◦
of visual field. From those images,
we randomly extracted sets of 300 stereoscopic im-
age patches, of size 15×15 pixel, i.e. covering ≈ 3
◦
of visual field. The stereoscopic patches are then are
fed to the algorithm described in section 3.1, in order
to learn the set of basis functions. The procedure is it-
erated for ≈ 300 sets of patches, before the receptive
field learning converges to a stable solution.
Attentive Model - Each of the 150 learned basis is
used to generate a feature maps of the same size of the
input image (128×128). Each feature map is trans-
formed in a saliency map through a comparison be-
tween a center (single pixels) and surround (39 ×39
pixels) values in a local region of the feature map (see
Eq. 7). Thereafter, an overall likelihood for all co-
efficients corresponding to a single location is given
by the product of the likelihoods associated with each
individual basis type (see Eq. 7). The final output re-
turn a map, again of the same size of the input image
(128 ×128), with high coefficients associated to the
less expected values. In order to select the highest
salient regions only, the map is filtered by an iterative
Difference of Gaussian function (30 ×30, σ
C
= 4.5,
σ
S
= 6 pixels), in order to obtain the target for the
subsequent saccadic control.
Learning Oculo-Motor Transformation - In order
to learn the W and V matrices required by the the
PC/BC-DIM network, the visual space is sequentially
explored. A visual target (a box of 0.05 m
3
) is placed
on a 3×3 grid of 3D points ranging from -0.2 m to
0.2 m at steps of 0.2 m along the x-axis, and from
-0.2 m to 0.2 m at steps of 0.2 m along the y-axis.
The grid is placed at a distance of 0.5 m from the
robot head (z-axis). For each position of the visual
target, the eyes perform a set of movements toward
the box, starting from a grid of 31 ×41 points in a
range [−20
◦
,20
◦
] pan and [−15
◦
,15
◦
] tilt, at steps of
1
◦
. For each iteration, the images (128 ×128 pizels)
is filtered with a 91 Gaussian filter bank (σ = 7 pixel)
that covers all the image locations. The obtained
1×91 vector is concatenated with a 1 ×11 array for
pan movement, a 1×7 array for tilt movement and a
value for the headcentered position of the box. Once
all the ocular movements are performed for that spe-
cific box position, the location is changed and a new
learning set is implemented adding a new vector ele-
ment corresponding to the new headcentric location.
This procedure allows us to obtain the W and V ma-
trices with the learned combination from which the
PC/BC-DIM network can obtain headcentric informa-
tion (sensory-sensory mapping) or joints information
(sensory-motor mapping). During the saccadic con-
trol, the attentive output will be used as retinal input
to the saccadic model.
Vergence Control - Subsequently, the obtained ba-
sis functions are used to learn the weights for the
disparity-vergence control (as described in section
3.4). The disparity tuning curves, used to compute
the weights w, as in Eq.11, have been obtained by
random dot stereograms with retinal disparity varying
between [−6,6] pixels, both for its horizontal and ver-
tical component. The obtained control is able to pro-
duce the correct vergence movement while the stim-
ulus disparity is approximately in a range three times
larger than the one used to learn the basis function
(i.e. [−2, 2] pixels).
4 RESULTS
The following results show the accuracy and robust-
ness of the integrated system starting from a reduced
set of high informative resources. The implemented
algorithm is indeed effective in achieving its main
goal of moving the fixation point of a simulated stereo
head towards salient locations at different depths.
Testing the basis functions - As a preliminary as-
sessment of our approach, we evaluated if the learned
resources are able to provide an efficient coding of
binocular information. To this purpose, we fit the
learned monocular basis functions with Gabor func-
tions (see Fig. 2) in order to characterize the resources
by the hybrid position-phase-based model (Ohzawa
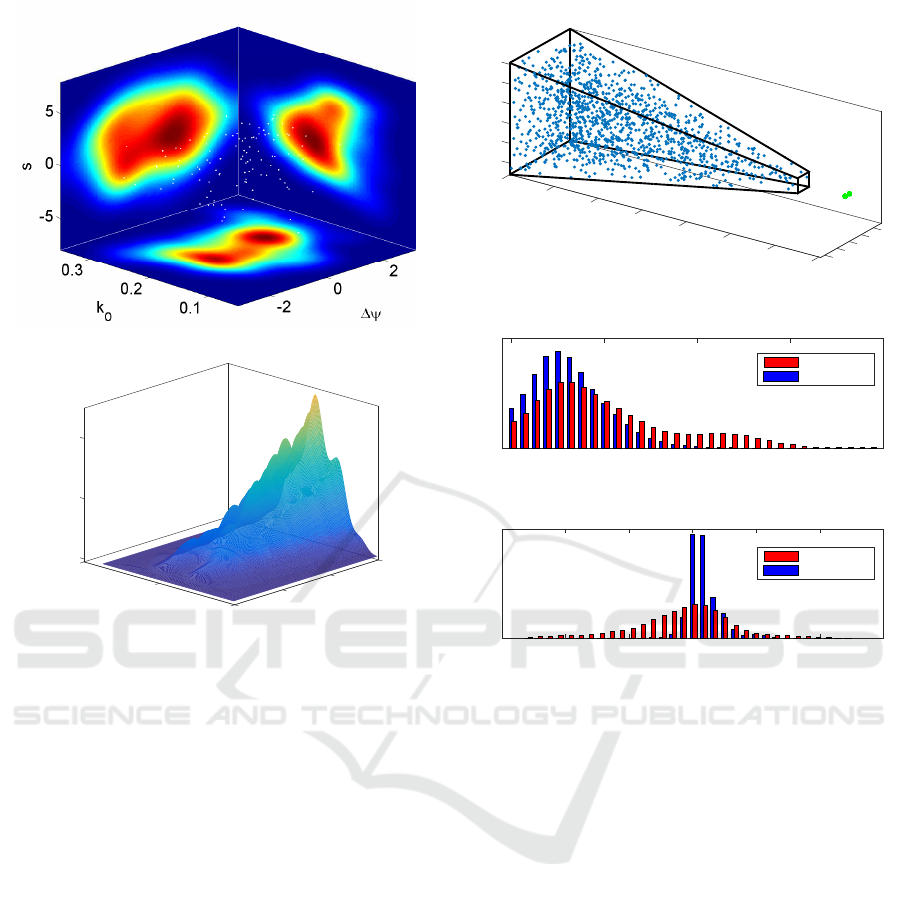
et al., 1990). Fig. 4a shows the distribution of the fit-
ted parameters of frequency tuning k
o
, phase ∆ψ and
position shift s. It is interesting to notice how the
binocular computational resources properly tile the
parameter space, with a distribution that qualitatively
resembles the actual distribution of V1 complex cells
of area V1 (Prince et al., 2002; Gibaldi et al., 2015a).
In order to characterize the effectiveness of the
sensory coding performed by the learned binocular
resources, we used the Fisher information (Ralf and
Bethge, 2010). To this purpose, we derived the dis-
parity tuning curves in response to random dot stere-
ograms in which the disparity is varied in the range
of [−6, 6] pixels Fig. 4b shows the trend of Fisher in-
formation over the iterations. It is evident how at the
first iteration, i.e. when the basis functions are ran-
domly initialized, the population carries no informa-
tion about retinal disparity. Along the learning, the
binocular information coding improves at each itera-
tion over the disparity range, and, more particularly,
it is peaked at zero disparity which is specifically in-
formative for guiding vergence behavior.
Testing the integrated model - In order to test
An Integrated System based on Binocular Learned Receptive Fields for Saccade-vergence on Visually Salient Targets
211

(a)
0
300
-6
0.02
Distribution
200
0.04
Iteration
Disparity
0
100
0
6
(b)
Figure 4: (a) Representation of learned binocular cells with
respect to frequency k
0
, phase difference ∆ψ and position
shift s (white dots), together with the joint distributions. (b)
Fisher information carried by the binocular cells (Ralf and
Bethge, 2010) for each disparity value; plotted against the
iterations of the basis functions learning process.
the integrated behaviour of the system, we used the
iCub Simulator to implement a simple environment
suited to the task at hand: a “salient” object is placed
at random positions against a textured background
(see Fig. 5a). The system firstly uses the bottom-up
attentive model to find the salient object. The target
is brought in the fovea through a coordinate saccadic-
vergence movement implemented by the PC/BC-DIM
model. Then, the disparity-vergence control is iter-
ated until the binocular disparity of the target reaches
a threshold value close to zero. Once a proper fix-
ation is reached, the salient object is displaced to a
new random position. The target object is a square
box of 0.038 m, presented at 500 random positions
within a portion of space represented by the frustum
shown in Fig.5a. For each target position the iCub-
simulator executes an open-loop saccadic movement,
followed by a closed loop vergence movement. The
performance of the integrated system, has been eval-
uated by computing the saccadic error and the ver-
0.6
0.8
3.5
1
1.2
1.4
1.6
3
2.5
2
Z
1.5
0.4
0.2
1
X
0
0.5
-0.2
-0.4
0
(a)
0 5 10 15 20
Euclidean distance from target [pixel]
Target disparity [pixel]
Distribution
SACCADIC ERROR
-15 -10 -5 0 5 10 15
Distribution
VERGENCE ERROR
Post-saccade
Post-vergence
Post-saccade
Post-vergence
(b)
Figure 5: (a) Random locations (500) in which the target is
placed during the test. Specifically, the positions fall in the
visual field of the robot, within a frustum defined by a range
of [−15+ 15] degrees of pan and [−10 + 10] degree of tilt
covering a depth ranging from 0.5 to 3.5m. (b) Distribution
of the saccadic (top) and vergence error (bottom) at target
location, after the 3D saccadic movement (red) and after
applying the disparity-vergence control (blue).
gence error. In order to evidence the positive ef-
fect of the vergence control on the fixation posture,
we computed these two quantities after the binocular
saccade (Post-saccade) and after the vergence refine-
ment (Post-vergence). The saccadic error is computed
as the mean distance between the center of mass of
the object’s image and the “foveas” of the cameras
(see Fig. 5b, top), and quantifies the accuracy of the
performed saccadic movement in foveating the target
(mean error < 3.5 pixels). The vergence error is com-
puted as the residual retinal disparity (absolute value)
over a foveal sub-window corresponding to the target
area (see Fig. 5b, bottom). After the 3D saccadic con-
trol, the residual disparity is ≈ 3.2 pixels and it drops
to ≈ 1.2 pixels after the action of the vergence con-
trol. This result demonstrates the efficacy of the im-
plemented algorithm to properly fixate the visual tar-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
212

get in depth. Moreover,the vergencecontrol, bringing
the object of interest into the foveas, is also helpful to
reduce the post saccadic error (see Fig. 5b, top).
For a demonstration of the overall capa-
bilities of the proposed model, see the video
https://www.youtube.com/watch?v=EFsEu25-nR4&
feature=youtu.be. The video represents a sequential
series of tasks performed by the iCub robot, simulated
within the iCub Simulator:
1. Receptive fields learning: the proposed algorithm
for binocular receptive field learning is fed with
stereo images acquired from the iCub head. The
vergence angle is randomly changed in order to
obtain stereo images with variable binocular dis-
parity, and thus to obtain receptive fields with dif-
ferent disparity sensitivities.
2. Disparity vergence control: the performance of
the vergence control is shown with a step stimulus
(Hung et al., 1986; Gibaldi et al., 2010; Gibaldi
et al., 2016). A frontoparallel textured plane sud-
denly changes depth, generating binocular dispar-
ities in the foveal area of the stereo images, and
consequently triggering the closed-loop vergence
control to nullify the binocular disparity.
3. The integrated model: the proposed approach
is tested with a sequence of attention, saccadic
movement and vergence refinement. The bottom-
up attentive module firstly selects the most salient
image region within the scene, then a binocular
saccade is performed to bring this region in the
foveae of both the eyes, finally the closed-loop
vergence control refines the eye position on the
selected area, in order to nullify the binocular dis-
parity.
5 CONCLUSIONS
In this paper, we proposed an integrated bio-inspired
architecture able to learn functional sensory and mo-
tor competences directly from the interaction with
the 3D environment. The visual front-end of learned
V1-like computational resources provides an efficient
coding of the binocular visual information, instru-
mental to different complementary tasks. The flex-
ibility and adaptability of the distributed coding al-
lows us to exploit the population response at different
levels of complexity, from disparity-vergence control
in closed-loop, to visual saliency on which to learn,
plan and perform open-loop saccadic and vergence
movements in the 3D environment. The resulting sys-
tem’s performance goes well beyond those obtained
by the previous work on saccade (Muhammad and
Spratling, 2015) and vergence (Gibaldi et al., 2010;
Gibaldi et al., 2016) control considered in isolation.
Advantages have been observed in terms of both ac-
curacy and generalization capability.
Summarizing, the proposed bio-inspired ap-
proach, rather than sequentially combining different
functionalities, defines an integrated and coherent ar-
chitecture where each module relies on the same
source of information and applies it to specialized
sub-tasks. This would allow us not just to solve the
single separate tasks, but also to develop complex be-
haviours for an active natural interaction of a robot
agent with the environment.
A future extension of the present work will be ded-
icated to include in the network a top-down module
for visual attention, in order to provide the robot with
a higher level behavior, possibly endowed by cogni-
tive capabilities. Moreover, the proposed approach
will be tested on a real robot system (e.g. the iCub
stereo head (Beira et al., 2006)).
REFERENCES
Antonelli, M., Gibaldi, A., Beuth, F., et al. (2014). A hi-
erarchical system for a distributed representation of
the peripersonal space of a humanoid robot. Au-
tonomous Mental Development, IEEE Transactions
on, 6(4):259–273.
Ballard, D. H., Hayhoe, M. M., Pook, P. K., and Rao, R. P.
(1997). Deictic codes for the embodiment of cogni-
tion. Behavioral and Brain Sciences, 20(04):723–742.
Beira, R., Lopes, M., Prac¸a, M., Santos-Victor, J.,
Bernardino, A., Metta, G., Becchi, F., and Saltar´en,
R. (2006). Design of the Robot-Cub (iCub) head. In
Proceedings 2006 IEEE International Conference on
Robotics and Automation, 2006. ICRA 2006., pages
94–100. IEEE.
Borji, A., Ahmadabadi, M. N., Araabi, B. N., and Hamidi,
M. (2010). Online learning of task-driven object-
based visual attention control. Image and Vision Com-
puting, 28(7):1130–1145.
Bruce, N. and Tsotsos, J. (2005). Saliency based on infor-
mation maximization. In Advances in neural informa-
tion processing systems, pages 155–162.
Chinellato, E., Antonelli, M., Grzyb, B. J., and Del Po-
bil, A. P. (2011). Implicit sensorimotor mapping of
the peripersonal space by gazing and reaching. IEEE
Trans. on Autonomous Mental Development, 3:43–53.
Crawford, J. D. and Guitton, D. (1997). Visual-motor
transformations required for accurate and kinemati-
cally correct saccades. Journal of Neurophysiology,
78(3):1447–1467.
Daugman, J. G. (1985a). Uncertainty relation for resolution
in space, spatial frequency, and orientation optimized
by two-dimensional visual cortical filters. JOSA A,
2(7):1160–1169.
An Integrated System based on Binocular Learned Receptive Fields for Saccade-vergence on Visually Salient Targets
213

Daugman, J. G. (1985b). Uncertainty relation for resolution
in space, spatial frequency, and orientation optimized
by two-dimensional visual cortical filters. JOSA A,
2(7):1160–1169.
Gerhardstein, P. and Rovee-Collier, C. (2002). The de-
velopment of visual search in infants and very young
children. Journal of Experimental Child Psychology,
81(2):194–215.
Gibaldi, A., Canessa, A., and Sabatini, S. (2015a). Ver-
gence control learning through real V1 disparity tun-
ing curves. In Neural Engineering (NER), 2015 7th In-
ternational IEEE/EMBS Conference, pages 332–335.
Gibaldi, A., Canessa, A., Solari, F., and Sabatini, S.
(2015b). Autonomous learning of disparity–vergence
behavior through distributed coding and population
reward: Basic mechanisms and real-world condition-
ing on a robot stereo head. RAS, 71:23–34.
Gibaldi, A., Chessa, M., Canessa, A., Sabatini, S., and So-
lari, F. (2010). A cortical model for binocular ver-
gence control without explicit calculation of disparity.
Neurocomputing, 73(7):1065–1073.
Gibaldi, A., Sabatini, S. P., Argentieri, S., and Ji, Z.
(2015c). Emerging spatial competences: From
machine perception to sensorimotor intelligence.
Robotics and Autonomous Systems, (71):1–2.
Gibaldi, A., Vanegas, M., Canessa, A., and Sabatini, S. P.
(2016). A portable bio-inspired architecture for effi-
cient robotic vergence control. International Journal
of Computer Vision, pages 1–22.
Houghton, G. and Tipper, S. P. (1994). A model of in-
hibitory mechanisms in selective attention.
Hu, Y., Xie, X., Ma, W.-Y., Chia, L.-T., and Rajan, D.
(2004). Salient region detection using weighted fea-
ture maps based on the human visual attention model.
In Pacific-Rim Conference on Multimedia, pages 993–
1000. Springer.
Hung, G. K., Semmlow, J. L., and Ciufferda, K. J. (1986). A
dual-mode dynamic model of the vergence eye move-
ment system. IEEE Transactions on Biomedical En-
gineering, (11):1021–1028.
Hunter, D. W. and Hibbard, P. B. (2015). Distribution of
independent components of binocular natural images.
Journal of vision, 15(13):6–6.
Hunter, D. W. and Hibbard, P. B. (2016). Ideal binocu-
lar disparity detectors learned using independent sub-
space analysis on binocular natural image pairs. PloS
one, 11(3):e0150117.
Hyv¨arinen, A. and Hoyer, P. (2000). Emergence of phase-
and shift-invariant features by decomposition of natu-
ral images into independent feature subspaces. Neural
computation, 12(7):1705–1720.
Hyv¨arinen, A., Hurri, J., and Hoyer, P. O. (2009). Natural
Image Statistics: A Probabilistic Approach to Early
Computational Vision., volume 39. Springer Science
& Business Media.
Itti, L., Koch, C., and Niebur, E. (1998). A model of
saliency-based visual attention for rapid scene anal-
ysis. IEEE Transactions on Pattern Analysis & Ma-
chine Intelligence, (11):1254–1259.
Lonini, L., Zhao, Y., Chandrashekhariah, P., Shi, B. E.,
and Triesch, J. (2013). Autonomous learning of ac-
tive multi-scale binocular vision. In Development and
Learning and Epigenetic Robotics (ICDL), 2013 IEEE
Third Joint International Conference on, pages 1–6.
Ma, Y.-F. and Zhang, H.-J. (2003). Contrast-based image at-
tention analysis by using fuzzy growing. In Proceed-
ings of the eleventh ACM international conference on
Multimedia, pages 374–381. ACM.
Muhammad, W. and Spratling, M. (2015). A neural model
of binocular saccade planning and vergence control.
Adaptive Behavior, 23(5):265–282.
Ognibene, D. and Baldassare, G. (2015). Ecological ac-
tive vision: Four bioinspired principles to integrate
bottom-up and adaptive top-down attention tested
with a simple camera-arm robot. Autonomous Men-
tal Development, IEEE Transactions on, 7(1):3–25.
Ohzawa, I., DeAngelis, G., and Freeman, R. (1990). Stereo-
scopic depth discrimination in the visual cortex: neu-
rons ideally suited as disparity detectors. Science,
249(4972):1037–1041.
Okajima, K. (2004). Binocular disparity encoding cells gen-
erated through an infomax based learning algorithm.
Neural Networks, 17(7):953–962.
Olshausen, B. A. et al. (1996). Emergence of simple-cell
receptive field properties by learning a sparse code for
natural images. Nature, 381(6583):607–609.
Olshausen, B. A. and Field, D. J. (1997). Sparse coding
with an overcomplete basis set: A strategy employed
by V1? Vision research, 37(23):3311–3325.
Orquin, J. L. and Loose, S. M. (2013). Attention and choice:
A review on eye movements in decision making. Acta
psychologica, 144(1):190–206.
Pfeifer, R., Lungarella, M., and Iida, F. (2007). Self-
organization, embodiment, and biologically inspired
robotics. science, 318(5853):1088–1093.
Pobuda, M. and Erkelens, C. J. (1993). The relationship
between absolute disparity and ocular vergence. Bio-
logical Cybernetics, 68(3):221–228.
Pouget, A. and Sejnowski, T. J. (1997). Spatial transfor-
mations in the parietal cortex using basis functions.
Journal of cognitive neuroscience, 9(2):222–237.
Prince, S., Pointon, A., Cumming, B., and Parker, A.
(2002). Quantitative analysis of the responses
of V1 neurons to horizontal disparity in dynamic
random-dot stereograms. Journal of Neurophysiology,
87(1):191–208.
Qian, N. (1994). Computing stereo disparity and motion
with known binocular cell properties. Neural Compu-
tation, 6(3):390–404.
Ralf, H. and Bethge, M. (2010). Evaluating neuronal codes
for inference using fisher information. In Advances in
neural information processing systems.
Rao, R. and Ballard, D. (1999). Predictive coding in
the visual cortex: a functional interpretation of some
extra-classical receptive-field effects. Nat. Neurosci.,
2(1):79–87.
Rashbass, C. and Westheimer, G. (1961). Disjunctive eye
movements. The Journal of Physiology, 159(2):339.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
214

Ruesch, J., Lopes, M., Bernardino, A., Hornstein, J.,
Santos-Victor, J., and Pfeifer, R. (2008). Multimodal
saliency-based bottom-up attention a framework for
the humanoid robot icub. In Robotics and Automation,
2008. ICRA 2008. IEEE International Conference on,
pages 962–967. IEEE.
Serre, T., Kouh, M., Cadieu, C., Knoblich, U., Kreiman, G.,
and Poggio, T. (2005). A theory of object recognition:
computations and circuits in the feedforward path of
the ventral stream in primate visual cortex. Technical
report, DTIC Document.
Serre, T., Wolf, L., Bileschi, S., Riesenhuber, M., and Pog-
gio, T. (2007). Robust object recognition with cortex-
like mechanisms. IEEE transactions on pattern anal-
ysis and machine intelligence, 29(3):411–426.
Tikhanoff, V., Cangelosi, A., Fitzpatrick, P., et al. (2008).
An open-source simulator for cognitive robotics re-
search: the prototype of the iCub humanoid robot sim-
ulator. In Proc. of the 8th workshop on performance
metrics for intelligent systems, pages 57–61. ACM.
Wang, Y. and Shi, B. E. (2011). Improved binocular ver-
gence control via a neural network that maximizes an
internally defined reward. IEEE Transactions on Au-
tonomous Mental Development, 3(3):247–256.
An Integrated System based on Binocular Learned Receptive Fields for Saccade-vergence on Visually Salient Targets
215