On using Support Vector Machines for the Detection and Quantiﬁcation

of Hand Eczema

Stefan Schn

urle

, Marc Pouly

, Tim vor der Br

uck

, Alexander Navarini

and Thomas Koller

Lucerne University of Applied Sciences and Arts, Rotkreuz, Switzerland

Department of Dermatology, University Hospital of Zurich, Zurich, Switzerland

Keywords:

Machine Learning, Support Vector Machines, Classiﬁcation, Eczema Detection and Quantiﬁcation.

Abstract:

Hand eczema is one of the most frequent skin diseases affecting up to 14% of the population. Early detec-

tion and continuous observation of eczemas allows for efﬁcient treatment and can therefore relieve symptoms.

However, purely manual skin control is tedious and often error prone. Thus, an automatic approach that can

assist the dermatologist with his work is desirable. Together with our industry partner swiss4ward, we devised

an image processing method for hand eczema segmentation based on support vector machines and conducted

several experiments with different feature sets. Our implementation is planned to be integrated into a clinical

information system for operational use at the University Hospital Zurich. Instead of focusing on a high accu-

racy like most existing state-of-the-art approaches, we selected F

score as our primary measure. This decision

had several implications regarding the design of our segmentation method, since all popular implementations

of support vector machines aim for optimizing accuracy. Finally, we evaluated our system and achieved an F

score of 58.6% for front sides of hands and 43.8% for back sides, which outperforms several state-of-the-art

methods that were tested on our gold standard data set as well.

1 INTRODUCTION

Hand eczema is one of the most frequent dermatoses,

affecting up to 14% of the population, and more than

20% have moderate-to-severe disease requiring inten-

sive treatment (Hald et al., 2008). It can occur in all

ages, commonly follows a chronic course and persists

10-15 years after onset (Meding et al., 2005). Hand

eczema manifests by redness of the skin, scaling,

ﬁssures, pain, itching, papules and blisters, as well

as clear discharge and sometimes bacterial infection

with subsequent pustules. Although the area it usually

affects is small, it still can have grave consequences

for the patient, leading to impairment or disability to

work in many professions. Hand eczema ranks among

the most prevalent occupational diseases (Diepgen,

2003) and can be caused by e.g. exposure to con-

tact allergens and irritants (Hald et al., 2008). Costs

caused by such occupational contact diseases (OCD)

consist of direct medical costs and indirect costs as-

sociated with lost workdays and loss of productiv-

ity. Data on the economic impact of OCD reveals

that in the US alone, annual direct costs for physi-

cians, clinic services and prescription drugs were as

high as USD 1.6 billion, with indirect costs of ap-

proximately USD 566 million for lost productivity

(Meding et al., 2005). In Europe, OCD constitute up

to 30% of all occupational diseases, for which com-

pensation is payable with an average incidence rate

of 0.5 to 1.9 cases per 1000 full-time workers per

year (Diepgen, 2003). Since these ﬁgures originate

from registries, they may even underestimate the ac-

tual number of cases as registries are known to be in-

complete due to under-diagnosis and under-reporting

of diseases (Diepgen, 2003). British studies reported

an estimate of approximately 4 million working days

to be lost every year resulting from work related skin

diseases. The costs for these lost days were estimated

to be approximately GBP 200 million per year (En-

glish, 2016).

If hand eczema cannot be prevented, e.g., by

changing profession, early detection of exacerbation

is key to an effective treatment (Diepgen, 2003).

Moisturizers and gloves are often used as secondary

prevention to avoid relapses. However, these have

weak adherence rates by affected patients. More se-

vere cases require the application of topical steroids

or other drugs for a few days to reduce disease activ-

ity. In this process, dermatitis patients rely on their

own perception whether their skin condition is sta-

SchnÃijrle S., Pouly M., vor der BrÃijck T., Navarini A. and Koller T.

On using Support Vector Machines for the Detection and Quantiﬁcation of Hand Eczema.

DOI: 10.5220/0006125000750084

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 75-84

ISBN: 978-989-758-220-2

ble or worsening and therefore they often miss the

point in time when early treatment of a relapse would

be efﬁcacious to prevent full-edged eczema. Active

drugs against eczema cannot be used indeﬁnitely due

to costs and side-effects such as skin thinning, ten-

dency to bruising, local suppression of the immune

system resulting in danger of cancer and infection, as

well as systemic side effects.

Eczema of the hand is a well-deﬁned disease that

can be driven by allergic and toxic-irritative effects on

the skin, most often by both. The ability to measure

eczema severity in a reproducible manner is crucial

for management of treatment. Hence, much effort has

gone into creating and validating scores for eczema

(Johansen et al., 2011). Once physicians are trained

to use scores, studies have shown good agreement in

the assessment of the overall extent of eczema. How-

ever, these scores need to take into account the many

clinical subtypes, namely chronic dry ﬁssured hand

eczema, palmar hyperkeratotic hand eczema, vesicu-

lar hand eczema, nummular hand eczema and pulpitis

(Johansen et al., 2011). Thus, grading of hand eczema

currently still is a time-consuming manual process

and in urgent need of improvement. As an example,

the most widely used Hand Eczema Severity Index

(HECSI) takes a dermatologist about 10 minutes to

ﬁll in. Considering this situation, establishing a (semi-

) automatic way to objectively quantify eczematous

skin changes to support diagnostic and therapeutic de-

cisions by physicians as well as patients is of utmost

importance.

Our ultimate project goal consists of an objective

detection and quantiﬁcation of hand eczema for auto-

mated computation of clinical scores, monitoring and

documentation of the disease process. When brought

to mobile devices, the same application further allows

patients to react early on worsening disease states and

physicians to use tele-dermatology on a novel level. In

(Suter et al., 2014), we presented ﬁrst results from a

supervised statistical learning algorithm built on tex-

tons and nearest neighbor classiﬁcation. In this paper,

we show that Support Vector Machines (SVMs) using

a revised and extended feature set and preceding com-

plex data cleaning yields superior results in compari-

son to our previous work and the current literature.

2 LITERATURE

The following literature review is limited to ap-

proaches that either segment eczema affected skin re-

gions from healthy skin or categorize skin diseases

into several classes including eczema. (Nisar et al.,

2013) determine eczema affected areas by clustering

the image with features from different color models.

Besides the analysis of color distributions, the use of

texture recognition methods has proven very useful.

(Mittra and Parekh, 2011) introduce an approach for

image categorization that detects several skin diseases

by means of gray level co-occurrence matrices over

speciﬁc image areas, whose entries are taken as tex-

ture features. (Malik et al., 2001) describe a system

for segmenting image regions by contour and texture

properties built on ﬁlter responses. (Cula et al., 2004)

extend this approach using a series of special lighting

conditions to derive a so-called bidirectional feature

histogram. They have applied this technique to de-

tect psoriasis, carcinoma, cases of urticarial vasculi-

tis and other skin defects. (Varma and Zisserman,

2005) claim superior results in texture classiﬁcation

using a texture method from single images using ro-

tationally invariant ﬁlters. In this method, a texture

is represented by a histogram of textons, and a tex-

ton is represented by the centroid of a cluster of ﬁl-

ter bank responses over all pixels of the current input

image patch. Based on this approach we derived a

classiﬁer for eczema quantiﬁcation based on textons

(Suter et al., 2014). (Varma and Zisserman, 2009)

modiﬁed their previous approach for material classi-

ﬁcation from 2005 to use pixel neighborhood patches

instead of ﬁlters. They conclude that this can outper-

form ﬁlter bank based classiﬁcation. Another statis-

tical approach presented by (Sparavigna and Maraz-

zato, 2010) quantitatively evaluates color and coarse-

ness differences in skin. Using a concept called co-

herence length, they can detect skin defects and also

compare changes over time. In addition to image fea-

tures, (Yasir et al., 2014) incorporate data from pa-

tients and medical investigations such as liquid type,

liquid color, elevation, feeling, sex and age.

In several approaches, image ﬁlters are applied

prior to classiﬁcation or segmentation or as a post

processing step to reﬁne the results. (Amarathunga

et al., 2015) increase the contrast of the image and

additionally employ a median and Gauss ﬁlter to re-

duce the effect of noise or small hairs. After all fea-

ture values are determined, they are typically com-

bined by a supervised machine learning approach to a

single outcome. (Yasir et al., 2014) as well as (Abdul-

Rahman et al., 2012) use an artiﬁcial neural network

for classiﬁcation. (Amarathunga et al., 2015) tested

several different machine learning approaches, in par-

ticular AdaBoost, Bayes Networks, decision trees,

multilayer perceptrons and Naive Bayes, where multi-

layered perceptrons performed best in their study.

(Nisar et al., 2013) employ an unsupervised ap-

proach (i.e. k-means clustering) for lesion segmenta-

tion. The texton-based eczema recognition approach

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

(Suter et al., 2014) exploits nearest neighbor search

to determine the feature vector (and its associated

class label) most correlated to the input feature vec-

tor measured in terms of chi-square. (van der Maaten

and Postma, 2007) describe several generally usable

advanced texture recognition approaches, which are

presumably useful for eczema recognition, in particu-

lar frequency histograms, complex wavelet transform,

spin images and polar Fourier features. Finally, (Liu

and Fieguth, 2012) employed random projections of

the high dimensional texture patch vectors with the

goal to compress data without losing the ability to dis-

tinguish between texture classes.

The reported evaluation results of the individual

approaches are summarized in Table 1.

Table 1: Reported evaluation results for eczema categoriza-

tion (C) and segmentation (S).

Method Measure Goal Value

(Mittra and Parekh, 2011) Accuracy C 96.6%

(Yasir et al., 2014) Success Rate C 88.0%

(Amarathunga et al., 2015) Accuracy C 85.0%

(Suter et al., 2014) Accuracy S 78.0%

(Nisar et al., 2013) Accuracy S 76.6%

3 TRAINING DATA

In our previous work, we had access to photographs

of hands showing eczema patches of different size and

degrees of severity labeled by a single dermatologist

who created an overlay bit-mask for every image to

point out eczema regions, see Figure 1. Training and

evaluation was done on a per-pixel basis, being fully

aware that manual labeling can never be done with

such precision. In fact, some issues with data qual-

ity, such as labeled areas beyond the edges of hands,

could be sorted out algorithmically, and some ma-

chine learning algorithms are known to cope with a

certain degree of noise in training data. However, ret-

rospectively this issue was largely underestimated.

Picture of Hands

Position of the ecema

Figure 1: Image with eczema overlay mask.

In daily routine, dermatologists use to focus on the

most expressive and thus clinically relevant eczema

patches. Not surprisingly, small patches were there-

fore considered clinically relevant on some images

but not on others, and false positive diagnoses of clas-

siﬁers were later assessed to correctly show eczema

patches that, in comparison to other areas on the same

image, were just not expressive enough for the la-

beling dermatologist. This made statistical evaluation

of classiﬁers nearly impossible. In order to weaken

this human bias in our data, we strived for obtaining

labeled images that represent a consensus diagnosis

among a group of experts. For this purpose we devel-

oped an online platform, where each invited dermatol-

ogist was asked to label a random sample of images

from our corpus, and derived a consensus diagnosis

per image through majority voting, see Figure 2.

Table 2: Performance of baseline classiﬁers on front-side

hand images; area error is reported in percentage points.

Classiﬁer

Accuracy (%)

Recall (%)

Precision (%)

Speciﬁcity (%)

score (%)

Area error (pp)

Coin Flip 50.00 49.99 12.73 50.00 20.30 37.26

Majority Class 87.26 0.00 n/a 100.00 n/a 12.74

Minority Class 12.74 100.00 12.74 0.00 22.60 87.26

Table 3: Performance of baseline classiﬁers on back side

hand images; area error is reported in percentage points.

Classiﬁer

Accuracy (%)

Recall (%)

Precision (%)

Speciﬁcity (%)

score (%)

Area error (pp)

Coin Flip 49.99 49.99 7.07 49.99 12.39 42.94

Majority Class 92.93 0.00 n/a 100.00 n/a 7.07

Minority Class 7.07 100.00 7.07 0.00 13.21 92.93

A second important observation regarding train-

ing and evaluation data concerns the intrinsic class

imbalance of eczema detection. Our available data ex-

poses an average ratio of 1:8 on front side and 1:15 on

back side hand images between eczema and healthy

skin pixels. As shows in Tables 2 and 3, a trivial

classiﬁer that always outputs the majority class label

(i.e. healthy skin) would reach an accuracy of 87% or

93%, respectively. Classiﬁer optimization and evalu-

ation based on accuracy (and similar measures) as re-

ported by the competing approaches in the literature

(see Table 1) is therefore not an option. Instead, we

subsequently report F

score measurements for clas-

On using Support Vector Machines for the Detection and Quantiﬁcation of Hand Eczema

Figure 2: Consolidated diagnosis of at least 30%, 50%, 70% and 99% of the involved experts.

siﬁers (see Section 5). High recall is reached when

most, ideally all, eczema pixels are correctly pre-

dicted; high precision, on the other hand, is reached

when most, ideally all, healthy skin pixels are cor-

rectly predicted. The F

score as the harmonic mean

between recall and precision takes these two often

contradictory goals into account.

4 METHODS

A Support Vector Machine (SVM) is used for classi-

ﬁcation with a variety of different input features. The

features are described in this section followed by the

different combinations employed in our experiments.

In contrast to the state-of-the-art eczema detection

and segmentation methods, we strive to reach a high

score and not necessarily the best possible accu-

racy. Optimizing for F

score presents a challenge,

since almost all SVM implementations target accu-

racy. One of the rare systems actually able to opti-

mize for the F

score, SVMPerf (Joachims, 2005) per-

formed very slowly on our dataset and therefore had

to be ruled out. Instead, we opted to use the (accuracy

optimizing) SVM implementation LIBSVM (Chang

and Lin, 2011) and boosted the F

score by the fol-

lowing measures:

• We oversampled our training data and removed

Tomek links, see Section 4.2. Oversampling nor-

mally improves the F

-Score obtained for imbal-

anced data sets for the following reason: Since the

SVM model reﬂects the distribution of the data,

the majority class will usually be predicted more

often by the SVM than the minority class. How-

ever, the F

-Score usually focuses on the minority

class (this is also the case in our scenario). So the

precision will be quite high but the recall poor.

Strongly deviating precision and recall values re-

sult in a low F

-Score (harmonic mean of preci-

sion and recall). By oversampling the values in

the minority class, the values of recall and pre-

cision draw closer together and therefore the F

Score increases (see also (Liu, 2004)).

• False positives and false negatives were weighted

differently inside the quadratic optimization pro-

cess conducted by the SVM. For determining the

optimal weights, we applied a grid search to the

training set and chose the combination of weights

and regularization parameters that led to the high-

est F

score on a held out set, see Section 4.3.

4.1 Features

We masked out the image background and calculated

all features from pixels showing skin only. To calcu-

late the features, a pixel’s neighborhood of 41 ×41

pixels is considered. Figure 3 highlights some dif-

ferences between textures of eczematous and healthy

skin; the red square shows an eczematous region, the

green squares two healthy regions (the lower shows

smooth skin, the upper skin with hand lines, respec-

tively), and their magniﬁcation.

(a) Grayscale image. (b) Gradient magnitude

from grayscale image

(Sobel operator).

Figure 3: Difference between eczematous and healthy skin.

4.1.1 Filters and Textons

Filter sets have a long history in image processing and

were inspired by models of processing in the early

stages of the primate visual system. Often they are

modeled using radially symmetric and odd- and even-

symmetric ﬁlters at different resolution (Malik et al.,

2001). In (Varma and Zisserman, 2005) a set of 38

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

ﬁlters is used, which are combined into 8 ﬁlter re-

sponses (MR8) by calculating the maximum across

multiple orientations. The ﬁlters include a Gaussian,

a Laplacian of a Gaussian and ﬁrst and second deriva-

tive ﬁlters at six orientations and three scales. More

recently (Mellor et al., 2008) uses combinations of

ﬁlters to achieve more invariance with respect to con-

trast, rotation and scale. While ﬁlter responses contain

a rich detail of the pixel neighborhood, they might not

be a very efﬁcient representation of the relevant fea-

tures of a class. Therefore, they are often aggregated

from all the responses of a single class and clustered.

The resulting cluster centers called textons form a dic-

tionary. In this work, the MR8 ﬁlter set is used to-

gether with other features, see Section 4.1.4.

4.1.2 Gray Level Co-occurrence Matrix

Another popular approach to capture the texture prop-

erties of a patch is the gray level co-occurrence matrix

(GLCM) introduced by (Haralick et al., 1973). The

GLCM measures how often a speciﬁc combination of

a pixel value and the value of a neighboring pixel in a

speciﬁc direction occurs in the patch. All channels of

all color spaces take values between 0 and 255, thus

resulting in GLCMs of dimension 256×256. The ma-

trix can be calculated using different spacings to the

neighboring pixel, often called stride, and in differ-

ent directions. For this work, we use a stride of one

and average over the 4 principle directions to yield a

rotational invariant description. Moreover, we calcu-

late the GLCMs once on the grayscale images, once

on the CIE Lab L* channel, as suggested by (Gebejes

and Huertas, 2013), and once on the magnitude of the

gradient of the grayscale images to accentuate certain

eczema structures like ﬁssures. Following (Haralick

et al., 1973) and (Gebejes and Huertas, 2013), we cal-

culate several features from the GLCM, namely en-

tropy, energy, homogeneity, contrast and dissimilar-

ity, see Equations (1). p(i, j) ∈ R denotes the (i, j)

component in the GLCM.

Entropy = −

∑

i, j

p(i, j)log p(i, j)

Energy =

∑

i, j

p(i, j)

Homogeneity =

∑

i, j

p(i, j)

1+|i−j|

Contrast =

∑

i, j

(i − j)

p(i, j)

Dissimilarity =

∑

i, j

|i − j|p(i, j)

(1)

According to (Gebejes and Huertas, 2013), these fea-

tures are connected to each other; they emphasize the

following aspects:

• Entropy aims to capture spatial disorder. Ran-

dom distributions would gain high entropy,

whereas solid tone images result in zero entropy.

• Energy is a measure of local homogeneity, thus

constituting the opposite of entropy. More homo-

geneous images correspond to high energy, con-

stant images expose an energy of 1.

• Homogeneity measures the uniformity of the

non-zero entries and is equal to 1 when the image

exposes no variation.

• Contrast captures the variation in the GLCM. If

neighboring pixels are similar in their value, con-

trast is low. Constant images correspond to a con-

trast of zero.

• Dissimilarity measures variation of gray level

pairs, similarly to contrast, but contrast grows

quadratically. Constant images expose a dissim-

ilarity of zero.

4.1.3 Color

Images tend to be available in the RGB color space.

However, this space is not optimal for image process-

ing as the channels are highly correlated, are psycho-

logically non-intuitive and non-uniform in respect to

the perceived differences between colors. As the train-

ing data is labeled by experts who might rely on color

differences, this cannot be neglected. Our calcula-

tion are performed in the CIE Lab color space, which

has the advantage of being an absolute color space

that uses perceptual uniformity. Additionally we use

the HSI (Hue, Saturation, Intensity) color space for

a more intuitive description of color and better sep-

aration of the color tone values as for example red-

ness might be an inﬂuential property for distinguish-

ing eczema.

For the detection of eczema it seem to be a valid

hypothesis that color provides additional information,

and thus several texture properties should be calcu-

lated using color. In order to describe the neighbor-

hood of a pixel, we calculate several color moments

(Stricker and Orengo, 1995), namely the mean, the

empirical standard deviation, the skewness and the

kurtosis on each channel of the RGB, the CIE Lab

and the HSI color spaces, see Equations (2). p( j) ∈ R

denotes the color channel value of the j

pixel in the

considered neighborhood of N ∈N pixels.

Mean (µ) =

∑

j=1

p( j)

Standard Dev. =

∑

j=1

(p( j) −µ)

Skewness =

∑

j=1

(p( j) −µ)

Kurtosis =

∑

j=1

(p( j) −µ)

(2)

On using Support Vector Machines for the Detection and Quantiﬁcation of Hand Eczema

Table 4: Correlation coefﬁcients of selected features with

class label.

Feature PCC

GLCM grayscale dissimilarity 0.30

GLCM grayscale+Sobel entropy 0.29

CM CIELab std. dev. 0.24

CM RGB kurtosis 0.21

MR8 T40 texton #9 0.18

MR8 T40 texton #17 -0.14

CM HSI mean -0.18

GLCM Sobel homogeneity -0.27

4.1.4 Feature Combinations

We conduct several experiments with different feature

sets, of which the most interesting results were ob-

tained by the following settings:

• T40: Histograms of 40 textons calculated from the

ﬁlter responses of the MR8 ﬁlter bank. No color

moments or GLCMs are used.

• CM1/GLCM1: Color moments in RGB space

and GLCM on grayscale image.

• T40/CM1/GLCM2: 40 textons, color moments

on CIE Lab space, GLCM on CIE Lab L* chan-

nel, GLCM on grayscale images with Sobel oper-

ator.

• T40/CM3/GLCM3: Like T40/CM1/GLCM2 but

with additional color moments on RGB and HSI

space, and an additional GLCM calculated on the

grayscale image.

• T40/CM3/GLCM3/TL/S: T40/CM3/GLCM3

with the removal of Tomek links with subsequent

oversampling via SMOTE (see Section 4.2).

• CM3/GLCM3/TL/S: T40/CM3/GLCM3/TL/S

but without the texton features.

We calculate the Pearson product-moment cor-

relation coefﬁcient (PCC) for all features with re-

spect to the corresponding class for each example and

found that features from the GLCMs show the high-

est |PCC|, followed by the color moments, followed

by the texton histogram features. A high PCC magni-

tude indicates (linearly) discriminating features. Ta-

ble 4 shows a selection of features from one image

with their PCC value.

4.2 Data Preprocessing

Since the available data is imbalanced, in our most

successful experiments, the minority (i.e. positive)

class is oversampled by applying the Synthetic Mi-

nority Oversampling Technique (SMOTE) algorithm

developed in (Chawla et al., 2002). For each example

of the positive class, SMOTE determines its K nearest

positive neighbors with respect to the Euclidean dis-

tance. Then, one of those neighbors is selected ran-

domly, and a new data instance is created at a ran-

domly chosen position on the line segment between

the original data example and the selected neighbor.

We set K = 5 and repeatedly apply SMOTE until the

minority are majority classes are of similar size.

There are some potential issues when applying

SMOTE, e.g., its application might amplify existing

problems such as outliers or noise, and it assumes the

neighborhood of a positive example is also positive

(Batuwita and Palade, 2013; Wu and Chang, 2003).

One strategy to mitigate these issues is the application

of data cleaning techniques such as the removal of

Tomek links. Given two examples E

and E

belonging

to different classes with distance d(E

, E

) between E

and E

: A pair (E

, E

) is called a Tomek link if there

is not an example E

, such that d(E

, E

) < d(E

, E

)

or d(E

, E

) < d(E

, E

) (Batista et al., 2004)

. We

search the data examples for Tomek links and remove

their negative class example only to not further dimin-

ish the positive class examples. This is repeated until

no further Tomek links exist.

For the features x barely correlated to the class

(|PCC| < 0.1), we calculate a number of transforma-

tions like

√

x or ln|x|. If the |PCC| of the transformed

feature is increased, we provide the transformed fea-

ture instead of the original to the SVM.

Due to runtime considerations, a subset of up to

1 ‰ (about 10

examples) is sampled in a random-

ized, stratiﬁed fashion from the available training data

and used to train the SVM.

4.3 Evaluation

The available image material consists of a total of

48 hand photographs of a size of 1-2 megapixels, of

which 24 show front sides, and the other 24 show

back sides of hands. For each photography, there are

between 1 and 11 associated expert labels which are

consolidated to the ﬁnal label, the experts’ consensus

diagnoses. The hands are separated from the back-

ground and only pixels displaying skin are used as

data examples. We evaluate our approach for images

of front and back sides separately. This accounts for

the presumed differences in the skin’s structure (e.g.

wrinkles) as well as in speciﬁc skin features (e.g. hair

density) between the front and back sides of hands,

Please note that in the literature there exist several non-

equivalent deﬁnitions of Tomek links.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

as previous work suggests (Suter et al., 2014). Since

our corpus is comparatively small, we evaluate using

a 9-fold cross-validation. From the 24 images, those

6 with the least number of expert’s labels are held

out to serve as test set for the SVM’s hyperparame-

ter search for each fold, leaving 18 images, of which

for each fold 2 are evaluated. A single confusion ma-

trix is calculated on all folds’ results. From this ma-

trix, we report accuracy, precision, recall, the F

score

and an absolute area error, see Equations (3) (T/F =

true/false, P/N = positives/negatives). The area error

is reported because it is a contributing factor for the

HECSI score as mentioned in Section 1.

Accuracy =

T P+T N

T P+FN+T N+F P

Precision =

T P

T P+FP

Recall =

T P

T P+FN

Speciﬁcity =

T N

T N+FP

Score = 2 ·

Precision·Recall

Precision+Recall

Area Error = |

(T P+FN)−(T P+FP)

T P+FN+T N+F P

(3)

For all our experiments, we utilize the LIBSVM

implementation (Chang and Lin, 2011) of an SVM,

together with the Gaussian radial based function

(RBF) kernel and different error costs for the two

classes (reﬂecting the ratio of the number of negative

to positive training examples as proposed by (Ben-

Hur and Weston, 2010)). For each fold, we conduct

a grid search over the SVM’s hyperparameters C (the

weight of the optimization objective’s regularization

term, i.e. the misclassiﬁcation cost) and γ (the free pa-

rameter of the RBF kernel, γ = (2σ

)

−1

), using the

fold’s training examples to train the SVM and the

held out examples to evaluate its performance. The

SVM with the hyperparameters yielding the highest

score is retained and the fold’s 2 unseen images

are predicted.

5 RESULTS

In this section, we present the results of the exper-

iments selected and described in Section 4.1.4. The

keys to the visualizations are provided in Figure 4 in-

dicating the colors and symbols used in the plots.

Figure 5 shows the best results obtained over all

experiments for the front and back sides sets, respec-

tively. Their individual F

scores reach a satisfac-

tory level. This objective measurement corresponds

to the intuitive impression conveyed by the images.

From the visualization, it is obvious that the predicted

(a) Colors key. (b) Experiments key.

Figure 4: Keys to visualizations in this section.

classes form connected regions, and not e.g. scattered

pixels all across the image. We conclude that the fea-

tures chosen capture the differences between eczema-

tous and healthy skin quite well.

(a) Best front side image with F

= 91.97%.

(b) Best back side image with F

= 86.75%.

Figure 5: Results with highest F

score of all experiments.

Tables 5 and 6 show the results of the experiments

for front and back sides of hands, respectively. All ex-

periments clearly outperform the baseline classiﬁers

introduced in Section 3 with respect to the F

score –

not necessarily with respect to accuracy, area error

or other metrics, which again puts emphasis on the

On using Support Vector Machines for the Detection and Quantiﬁcation of Hand Eczema

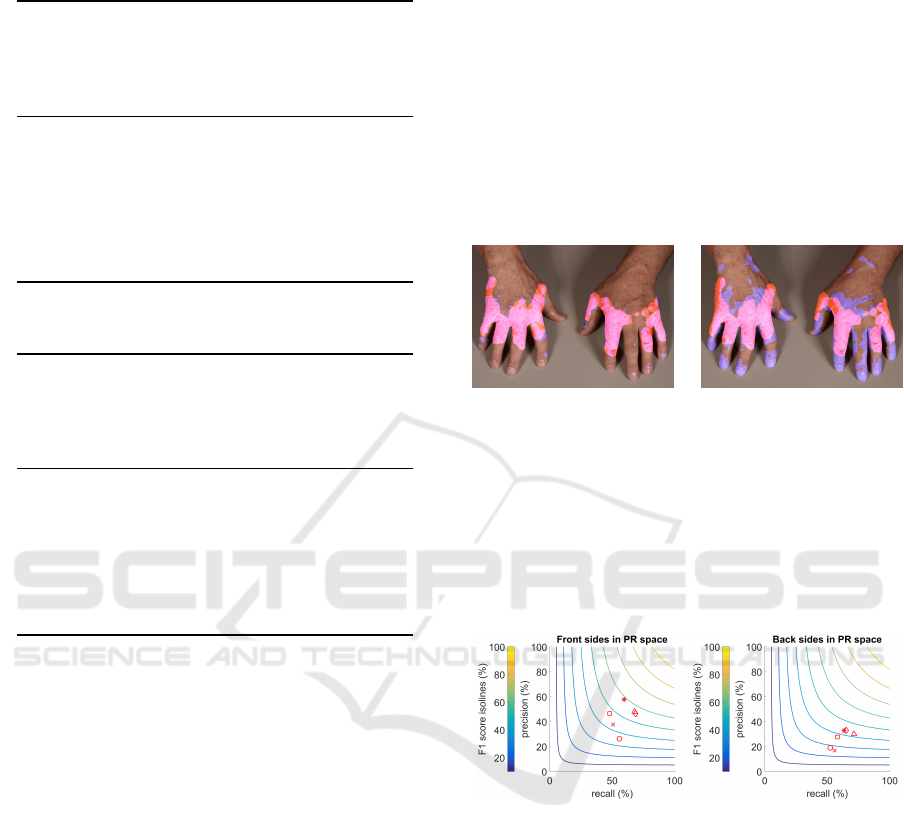
Table 5: Summary of experiments: front sides of hands.

Experiment

Accuracy (%)

Recall (%)

Precision (%)

Speciﬁcity (%)

score (%)

Area error (pp)

T40 74.50 55.73 26.33 77.24 35.77 14.83

CM1/GLCM1 83.01 50.69 37.61 87.73 43.18 7.77

T40/CM1/GLCM2 86.33 48.00 46.46 91.92 47.22 8.15

T40/CM3/GLCM3 85.88 68.69 46.33 88.38 55.34 6.68

T40/CM3/GLCM3/TL/S 86.53 67.92 47.97 89.25 56.23 7.39

CM3/GLCM3/TL/S 89.29 59.54 57.69 93.63 58.60 4.60

Table 6: Summary of experiments: back sides of hands.

Experiment

Accuracy (%)

Recall (%)

Precision (%)

Speciﬁcity (%)

score (%)

Area error (pp)

T40 80.71 52.49 18.90 82.86 27.80 13.31

CM1/GLCM1 77.39 55.90 16.86 79.02 25.91 18.04

T40/CM1/GLCM2 86.27 58.13 27.63 88.41 37.46 9.97

T40/CM3/GLCM3 88.20 65.14 33.04 89.95 43.84 8.38

T40/CM3/GLCM3/TL/S 86.22 71.43 30.06 87.35 42.32 10.55

CM3/GLCM3/TL/S 88.17 63.48 32.68 90.05 43.15 8.26

necessity to focus on metrics like the F

score when

evaluating classiﬁcation performance on imbalanced

data.

The T40 experiment, conducted by utilizing tex-

ton frequencies as features for the SVM only, shows

the worst results with respect to all measurements ex-

cept recall on the front sides. The results are compa-

rable to previous work (Suter et al., 2014) with a sim-

pler classiﬁer, which suggests that texton frequencies

alone are not sufﬁcient to provide satisfactory results

for detecting hand eczema.

When enriching the texton features with color mo-

ments and features calculated from GLCMs, even

when abstaining from using texton features at all, the

classiﬁcation performance improves considerably. Ta-

ble 5 shows continuous improvements with respect to

the F

score the more features are used, culminating in

the best performance when additionally oversampling

of the training examples and data cleaning is con-

ducted. Clearly, improvements in precision allowed

for improvements in the F

score as well. For the back

sides of hands shown in Table 6, similar observations

hold. However, here the ﬁnal CM3/GLCM3/TL/S ex-

periment lead to a slightly worse precision. This can

be caused by differences with respect to skin fea-

tures (e.g. hair density), or the different ratio between

eczema and healthy skin pixels as observed in Sec-

tion 3. Further research will be necessary to deﬁni-

tively isolate this effect.

For a particular image, Figure 6 opposes the

best result (experiment CM3/GLCM3/TL/S from Fig-

ure 5) to the worst (experiment T40). Observe in par-

ticular the big difference in precision. Moreover, Fig-

ure 6b provides several insights on difﬁculties for the

classiﬁer, e.g., ﬁngernails are often detected as false

positives, and wrinkles pose another challenge.

(a) F

= 86.75%. (b) F

= 65.56%.

Figure 6: Same image in different experiments.

In Figure 7, we plot the F

score of the discussed

experiments for front and back sides separately into

precision-recall (PR)space. The hyperbolic isolines of

the F

score are plotted in steps of 10 percentage

points to provide for a better intuition of the PR space.

This emphasizes another challenge for almost all clas-

siﬁers, which is to reach a satisfactory precision level.

(a) Front sides. (b) Back sides.

Figure 7: F

score in PR space with a number of isolines.

In Figure 8, we display the area error reached by

our classiﬁer. The visualization consists of a box plot

of each expert’s absolute area error (or deviation) with

respect to the consensus diagnoses. We suggest to in-

terpret this box plot as the baseline that should be

reached by the predictions of a trained classiﬁer. The

arithmetic mean is plotted as a blue dot and the area

errors of the experiments are displayed in the same

ﬁgure, right to the central axis the box plot is aligned

on. Disregarding outliers, human experts seem to dif-

fer from the consensus diagnoses by about 0 to 10 per-

centage points. Our best classiﬁer for the front side of

hands performs as well as the median of the experts’

labels, which is a very satisfactory result with respect

to the area error metric. The best classiﬁers for the

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

back sides of hands do not reach the median, but at

least would not be considered outliers (like the worst

classiﬁers) compared to the box plot. Again, this indi-

cates that eczema detection on the back sides of hands

is more challenging than on the front sides.

(a) Front sides. (b) Back sides.

Figure 8: Area error as box plots.

For comparison, we have implemented the ap-

proach of (Varma and Zisserman, 2009) for eczema

detection and obtained an accuracy of 81.2% for front

and 86.63% for back sides of hands, while observing

a surprisingly low F

score on our data set: 30.48%

for front sides, 14.79% for back sides, respectively.

In addition, we evaluated the unsupervised clustering-

based segmentation of (Nisar et al., 2013), see Sec-

tion 2. The highest F

score was achieved by cluster-

ing on the red channel of the RGB color space model

(selecting adapt light compensate as preprocessing),

i.e. F

score of 15.04% for front sides and 14.47% for

back sides of hand.

6 CONCLUSION AND OUTLOOK

Our results demonstrate that a combination of differ-

ent families of features enhanced with extensive data

cleaning before being fed into a standard SVM clas-

siﬁer leads to superior results for distinguishing be-

tween healthy and eczematous skin as compared to

several state-of-the-art techniques. We previously at-

tempted (Suter et al., 2014) to integrate color with

the MR8 features directly as suggested in (Varma

and Zisserman, 2005), but were not able to reach a

signiﬁcant improvement compared to pure MR8 fea-

tures without color information. We now show a much

more successful integration of color features giving a

major improvement over the previous results.

Results on the back side of the hand are cur-

rently not as good as on the front, presumably due

to e.g. more hairs, other structures with ﬁnger nails

and more prominent wrinkles on the joints. So, fur-

ther challenges remain to still improve on the features

or maybe use different learning strategies for different

parts of the hand.

One of the most crucial elements of any success-

ful supervised learning approach is the quality of the

input data. In our project, we have seen large differ-

ences between the labelling of the data from different

dermatologists and have shown a way to mitigate this

problem using a consensus diagnosis. Nonetheless,

we aim to provide dermatologists with better tools for

the labelling in order to get more homogeneous data.

Recently, deep learning has been very success-

ful in image classiﬁcation (Krizhevsky et al., 2012;

Szegedy et al., 2015) and object detection (Szegedy

et al., 2013; Ren et al., 2015). As Neural Networks

aim to learn the complete image processing pipeline,

the feature selection is done by the network, mak-

ing it unnecessary to specify the feature combina-

tions beforehand. We are going to investigate these

approaches for eczema detection as well as some re-

cent techniques that use neural networks either only

for feature selection or only as a classiﬁer.

ACKNOWLEDGEMENTS

We would like to thank CTI

for funding this re-

search and swiss4ward

and the University Hospital

of Zurich

for the productive collaboration.

REFERENCES

Abdul-Rahman, S., Norhan, A. K., Yusoff, M., Mohamed,

A., and Mutalib, S. (2012). Dermatology diagno-

sis with feature selection methods and artiﬁcial neu-

ral network. In Proceedings of the IEEE EMBS

Conference on Biomedical Engineering and Sciences

(IECBES), pages 371–376. IEEE.

Amarathunga, A., Ellawala, E., Abeysekara, G., and Amal-

raj, C. (2015). Expert system for diagnosis of skin

diseases. International Journal of Scientiﬁc and Tech-

nology Research, 4(1).

Batista, G. E. A. P. A., Prati, R. C., and Monard, M. C.

(2004). A study of the behavior of several methods

for balancing machine learning training data. ACM

SIGKDD Explorations Newsletter, 6(1):20–29.

Batuwita, R. and Palade, V. (2013). Class imbalance learn-

ing methods for support vector machines. In He, H.

and Ma, Y., editors, Imbalanced learning, pages 83–

99. John Wiley & Sons, Inc, Hoboken, New Jersey.

Ben-Hur, A. and Weston, J. (2010). A user’s guide to sup-

port vector machines. Methods in molecular biology

(Clifton, N.J.), 609:223–239.

Commission for Technology and Innovation, CTI,

http://www.kti.admin.ch/

http://swiss4ward.com/

http://www.en.usz.ch/

On using Support Vector Machines for the Detection and Quantiﬁcation of Hand Eczema

Chang, C.-C. and Lin, C.-J. (2011). LIBSVM:

A library for support vector machines. ACM

Transactions on Intelligent Systems and Tech-

nology, 2:27:1–27:27. Software available at

http://www.csie.ntu.edu.tw/ cjlin/libsvm.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,

W. P. (2002). Smote: synthetic minority over-

sampling technique. Journal of Artiﬁcial Intelligence

Research, 16(1):321–357.

Cula, O. G., Dana, K. J., Murphy, F. P., and Rao, B. K.

(2004). Bidirectional imaging and modeling of skin

texture. IEEE Transactions on Biomedical Engineer-

ing, 51(12):2148–2159.

Diepgen, T. L. (2003). Occupational skin-disease data in

europe. International Archives of Occupational and

Environmental Health, 76(5):331–338.

English, J. (2016). Current concepts of irritant contact der-

matitis. Occupational and Environmental Medicine,

61:722726.

Gebejes, A. and Huertas, R. (2013). Texture characteriza-

tion based on grey-level co-occurrence matrix. In Pro-

ceedings of the Conference of Informatics and Man-

agement Sciences, volume 2, pages 375–378. EDIS -

Publishing Institution of the University of Zilina.

Hald, M., Berg, N., Elberling, J., and Johansen, J. (2008).

Medical consultations in relation to severity of hand

eczema in the general population. The British Journal

of Dermatology, 158:773–777.

Haralick, R. M., Shanmugam, K., and Dinstein, I. (1973).

Textural features for image classiﬁcation. IEEE

Transactions on Systems, Man, and Cybernetics,

SMC-3(6):610–621.

Joachims, T. (2005). A support vector method for multi-

variate performance measures. In Proceedings of the

22nd International Conference on Machine Learning

(ICML), Bonn, Germany.

Johansen, J. et al. (2011). Classiﬁcation of hand eczema:

clinical and aetiological types. Based on the guideline

of the Danish Contact Dermatitis Group. Contact Der-

matitis, 65(1):13–21.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In Proceedings of the Conference on Neural

Information Processing Systems (NIPS), pages 1097–

1105.

Liu, A. Y. (2004). The effect of oversampling and un-

dersampling on classifying imbalanced text datasets.

Master’s Thesis, University of Texas.

Liu, L. and Fieguth, P. (2012). Texture classiﬁcation from

random features. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, 34(3):574–586.

Malik, J., Belongie, S., Leung, T., and Shi, J. (2001). Con-

tour and texture analysis for image segmentation. In-

ternational journal of computer vision, 43(1):7–27.

Meding, B., Wrangsj

o, K., and J

arvholm, B. (2005).

Fifteen-year follow-up of hand eczema: persistence

and consequences. The British Journal of Dermatol-

ogy, 152:975–980.

Mellor, M., Hong, B.-W., and Brady, M. (2008). Locally

rotation, contrast, and scale invariant descriptors for

texture analysis. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, 30(1):52–61.

Mittra, A. K. and Parekh, D. R. (2011). Automated detec-

tion of skin diseases using texture. International Jour-

nal of Engineering Science and Technology, 3:4801–

4808.

Nisar, H., Ch’ng, Y. K., Chew, T. Y., Tang, J., Yap, V.,

and Yeap, K. (2013). A color space study for skin

lesion segmentation. In Proceedings of the Interna-

tional Conference on Circuits and Systems (ICCAS),

pages 172–176. IEEE.

Ren, S., He, K., Girshick, R., and Sun, J. (2015). Faster

r-cnn: Towards real-time object detection with region

proposal networks. In Proceedings of the Conference

on Neural Information Processing Systems (NIPS),

pages 91–99.

Sparavigna, A. and Marazzato, R. (2010). An image-

processing analysis of skin textures. Skin research and

technology, 16(2):161–167.

Stricker, M. A. and Orengo, M. (1995). Similarity of

color images. In Niblack, W. and Jain, R. C., edi-

tors, Proceedings of the IS&T/SPIE’s Symposium on

Electronic Imaging: Science & Technology, SPIE Pro-

ceedings, page 381. SPIE.

Suter, C., Navarini, A., Pouly, M., Arnold, R., Gutzwiller,

F. S., Meier, R., and Koller, T. (2014). Detection

and quantiﬁcation of hand eczema by visible spectrum

skin pattern analysis. In Schaub, T., Friedrich, G., and

O’Sullivan, B., editors, ECAI 2014, volume volume

263 of Frontiers in Artiﬁcial Intelligence and Appli-

cations, pages 1101–1102. IOS Press, Amsterdam.

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S.,

Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-

novich, A. (2015). Going deeper with convolutions.

In Proceedings of the IEEE Conference on Computer

Vision and Pattern Recognition, pages 1–9.

Szegedy, C., Toshev, A., and Erhan, D. (2013). Deep neural

networks for object detection. In Proceedings of the

Conference on Neural Information Processing Sys-

tems (NIPS), pages 2553–2561.

van der Maaten, L. and Postma, E. (2007). Texton-based

texture classiﬁcation. In Proceedings of Belgium-

Netherlands Artiﬁcial Intelligence Conference.

Varma, M. and Zisserman, A. (2005). A statistical approach

to texture classiﬁcation from single images. Interna-

tional Journal of Computer Vision, 62(1-2):61–81.

Varma, M. and Zisserman, A. (2009). A statistical ap-

proach to material classiﬁcation using image patch ex-

emplars. IEEE transactions on pattern analysis and

machine intelligence, 31(11):2032–2047.

Wu, G. and Chang, E. Y. (2003). Class-boundary alignment

for imbalanced dataset learning. In Proceedings of the

ICML 2003 workshop on learning from imbalanced

data sets II, Washington, DC, pages 49–56.

Yasir, R., Rahman, M. A., and Ahmed, N. (2014). Der-

matological disease detection using image processing

and artiﬁcial neural network. In Proceedings of the

International Conference on Electrical and Computer

Engineering (ICECE), pages 687–690.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence