Pattern Width Description through Disk Cover

Application to Digital Font Recognition

Nikita Lomov and Leonid Mestetskiy

Moscow State University, Faculty of Computational Mathematics and Cybernetics, Moscow, Russia

{nikita-lomov, mestlm}@mail.ru

Keywords: Disk Cover, Morphological Width, Polygonal Figure, Medial Representation, Skeleton, Radial Function,

Bicircle, Font Comparing.

Abstract: We consider the concept of "the width of a figure" for objects of complex shapes in order to use it as an

integral morphological descriptor in image recognition tasks. In this article we propose a new approach to

the description of this concept on the basis of the figures covering by disks of a certain size. The area of the

disk cover as a function of the covering disc size is a shape descriptor. Original method for analytical

calculation the area of disk cover of polygonal shapes is presented. The method is universal because there is

always the possibility of polygonal approximating of complex digital binary images and geometric objects

with nonlinear boundary. The method is based on the medial representation of the polygonal figure as a

skeleton and a radial function. Our approach ensures high accuracy and computational efficiency calculate

the area of disk cover. The effectiveness of the proposed approach is demonstrated for applications in

computer font’s recognition problem.

1 INTRODUCTION

The width of the objects is an important feature of

image shape. This feature cannot be well described

by a scalar value, such as "average" width, for the

objects of complex shape, in which the different

parts have different width and length. Therefore, the

description of width “distribution” that characterizes

the whole range of its values is required to be used

as width descriptor.

Local description of the width can be based on

the size of the primitive, which can be inscribed in

the object. The larger width of the object, the larger

the size of the primitive. If we inscribe in the object

the primitives of a given size, such as disks of a

certain diameter, the part of the object covered by

the primitives can be considered as a region of a

given width. Then the function describing the

dependence of the region area from the primitive

size can be regarded as an integral description of the

object width. This article proposes an approach to

the construction of the image width descriptor,

which is based on the area of the disk cover of the

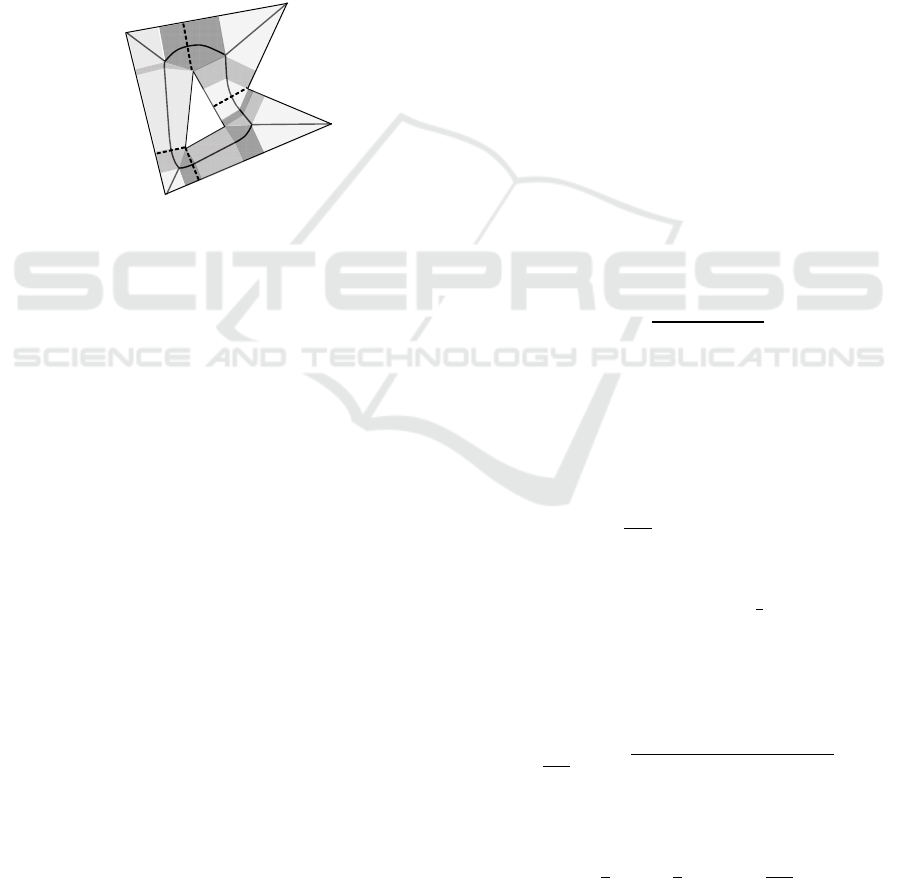
object (Fig.1). Selecting a disk as primitive provides

invariance of the descriptor to the shift, rotation and

scaling of images.

The object width descriptor is a diagram

representing the dependency of the cover area from

the size of covering disks (Fig.2).

Figure 1: Disk covers of the “lizard” figure (on the right

the examples of covering disks are shown).

484

Lomov N. and Mestetskiy L.

Pattern Width Description through Disk Cover - Application to Digital Font Recognition.

DOI: 10.5220/0006128804840492

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 484-492

ISBN: 978-989-758-225-7

Figure 2: Diagram of the dependency of disk cover area of

the “lizard” figure from the size (radius) of covering disks.

To compute the cover area, the method of pattern

spectrum (Maragos, 1989), based on a discrete

mathematical morphology (Serra, 1982), can be

applied. In this case, the object width descriptor is

the pattern spectrum diagram, constructed on the

base of morphological opening operation using a

disc structuring element. An example of this

approach is described in (Ramirez-Cortes et al.,

2008). Pattern spectrum method allows a simple

software implementation, however, it has a high

computational complexity, especially when working

with large high-resolution images. To cope with this

problem in (Vizilter and Sidyakin, 2012, 2014) a

combined discrete-continuous approach to the

calculation of the pattern spectrum was proposed,

which allowed significantly reduce the computation

time, but not so much. The task cannot be solved in

real-time of the computer vision systems.

Our approach is aimed at drastically reducing the

computation time of the cover area through the use

of a continuous model of an image shape.

Continuous model is a polygonal shape

approximating a digital image. Selecting a polygonal

shape (a polygon with polygonal holes) as a model

of the object shape is due to two reasons. On the one

hand, polygonal shapes can accurately approximate

the boundary of complex objects represented by

discrete raster images. On the other hand, for the

polygonal figure the regions of a given width can be

described using the medial representation – the

skeleton and the radial function. A medial

representation of a polygonal shape can be obtained

with high-performance computational geometry

algorithms (Mestetskiy, 2008).

(a) (b)

Figure 3: Continuous model of the disk cover for binary

image: a) binary image, b) approximating polygonal figure

c) its skeleton, d) example of r-cover.

Our method of the calculation of the disk cover

area for objects on bitmap images includes the

following steps:

1. Approximation of a binary image by a

polygonal shape.

2. Medial representation of a polygonal shape in

the form of the skeleton and the radial

function based on Voronoi diagrams of line

segments that constitute the shape boundary.

3. Representation of a complex-shaped

polygonal figure as a union of bicircles –

elementary geometric shapes corresponding

to the edges of the skeleton.

4. Representation of the figure disk cover as the

union of a subset of bicircles and calculating

the cover area through bicircles' areas.

5. Construction of the distribution function of

the disk cover area as a function of the disk

size.

2 DISK COVER AND FIGURE

SKELETON

Definition 1. A figure is a closed region in the plane

bounded by a finite number of disjoint closed Jordan

curves.

Definition 2. A circle is considered to be empty

if it is located entirely in the figure.

Definition 3. Disk -cover of the figure is the

union of all empty circles of the radius . Examples

of disk -cover for different values of  are shown in

Fig.1.

Definition 4. -area of the figure is the area of its

disk -cover.

According to this definition, the area of the entire

figure is its 0-area.

Definition 5. Morphological width  of the

figure is its -area as a function of . Morphological

width is a non-increasing function of the .

Morphological width could be calculated by

using pattern spectrum (Maragos, 1989) through the

Pattern Width Description through Disk Cover - Application to Digital Font Recognition

485

opening operation of a discrete mathematical

morphology (Serra, 1982). The disk is used as a

primitive. This approach requires a lot of

computation time, and may be applied only to

discrete images. Our method is much faster and is

more universal because it allows you to work with

discrete and continuous images through

approximation by polygonal figure.

Definition 6. An inscribed circle of the figure is

an empty circle, which is the maximum, i.e., is not

contained in any other empty circle.

Definition 7. A skeleton of a figure is the set of

all points that are centers of inscribed circles.

Definition 8. The radial function is defined in

the skeleton points and assigns to the skeleton point

the radius of the inscribed circle centered at this

point.

Obviously, each empty circle of radius more than

 can be represented as the union of empty circles of

radius . Therefore, any inscribed circle with radius

 or more is contained in the disk -cover.

Consequently, the disk -cover of the figure

coincides with the union of all the inscribed circles

of radius at least . The centers of the inscribed

circles constitute a subset of the skeleton points.

Thus, for calculating the morphological width of the

figure it is sufficient to consider only the circles

whose centers lie on the skeleton. The challenge is

to obtain for given values of argument  the

corresponding values of figure -area. The solution

to this problem for the polygonal shapes will be

obtained in an explicit form.

3 POLYGONAL FIGURES AND

BICIRCLES

Definition 9. A polygonal figure is a figure whose

boundary consists of closed polylines.

The boundary of a polygonal figure can be

represented as the union of a finite number of

subsets, called sites: point-sites (vertices of the

figure) and segment-sites (sides of the figure without

end points).

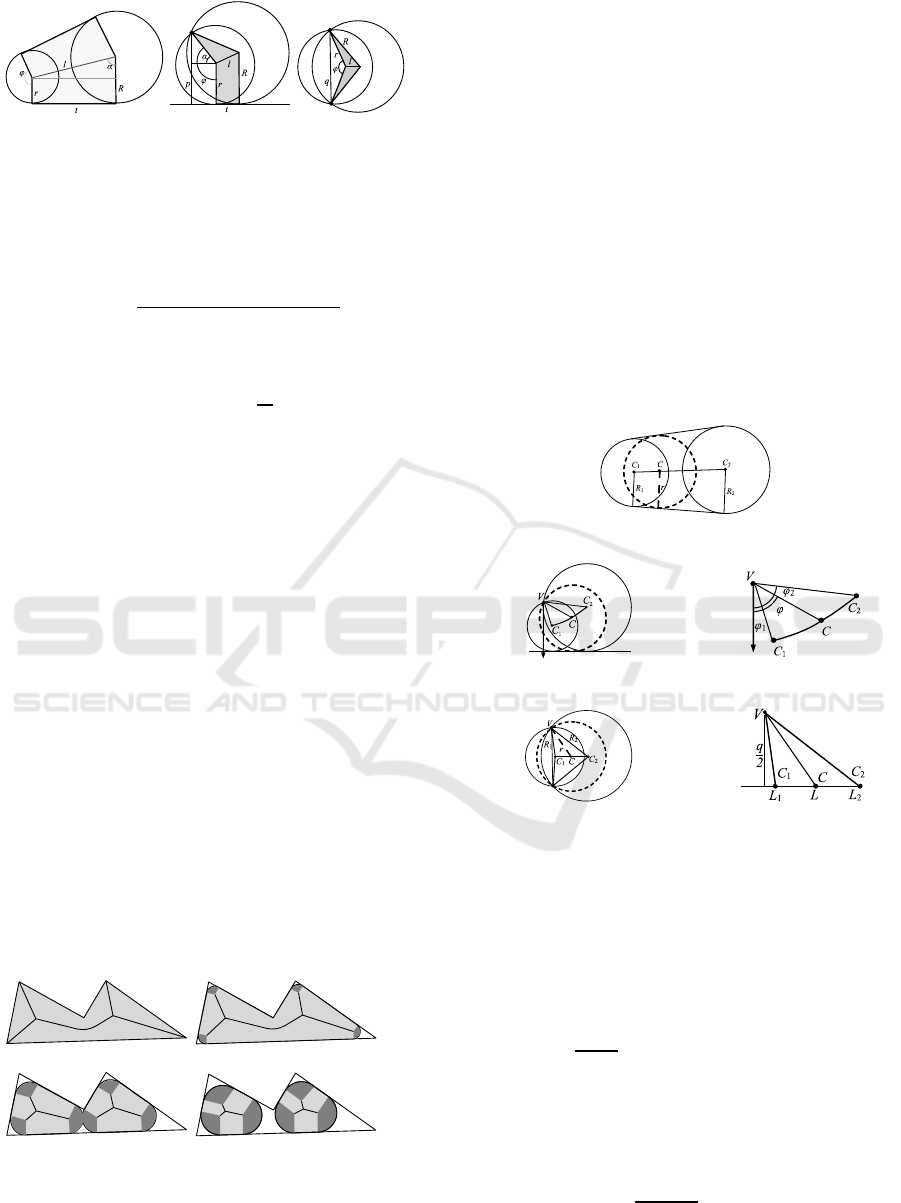
A skeleton of a polygonal figure (Fig.4) looks

like geometric graph whose edges are segments of

straight lines and quadratic parabolas, and the

vertices are the endpoints of edges. Each edge is a

connected set of points that are centers of inscribed

circles having the same incident pair of sites, called

site-generators of the edge. If both site-generators

are of the same type (two point-sites or two

segment-sites) then the edge is a straight line

segment. If site-generators are of different types

(point-site and segment-site) then the edge is a

segment of a quadratic parabola.

Figure 4: Polygonal figure and its skeleton.

Polygonal approximation of the digital binary

image and the construction of the continuous

skeleton and radial function are performed by

means of high-performance algorithms

(Mestetskiy, 2008). The proposed method for

calculating -area, using the special properties of a

skeleton of a polygonal shape, is based on the

decomposition of the figure on the constituent

elements – bicircles.

Definition 10. A bicircle is the union of all

inscribed circles centered on one edge of the

skeleton. The edge line is called the axis of the

bicircle.

Three types of bicircles are distinguished

depending on the pair of their site-generators: linear

(two segment-sites – Fig.5a-b), parabolic (segment-

site and point-site – Fig.5c) and hyperbolic (two

point-sites – Fig.5d). This terminology is caused by

the dependency of the radial function on the position

of a point on the axis of the bicircle.

Circles with centers at the vertices of the

skeleton are called the end circles of the bicircle.

The boundary of the bicircle is the envelope of the

family of its constituent circles. The boundaries of

linear and parabolic bicircles include, fully or

partially, their generating segment-sites (Fig.5a-c).

In addition, the boundaries of all kind of bicircles

contain arcs of end circles.

(a) (b) (c) (d)

Figure 5: Bicircles: axes, proper regions, external sectors

of end circles.

Definition 11. The sector of end circle relied on

the arc of the bicircle boundary is called an external

sector of a bicircle.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

486

Definition 12. A spoke is a line segment

connecting the skeleton point with the nearest point

of figure boundary.

Definition 13. A proper region of a bicycle is the

union of all spokes of the bicircle incident to points

of its axis.

The bicircle is the union of its proper region and

the pair of external sectors. The shape of the proper

area depends on the type of bicircle (Fig.5). For a

linear bicycle it is the union of two triangles (Fig.5a)

or two trapezoids (Fig.5b). In the parabolic bicircle

it is a “house-shaped” figure, which can be regarded

as the union of a trapezoid and a triangle (Fig.5c), in

the hyperbolic one it is the union of two triangles

(Fig.5d).

Figure 6: Coverage of the polygonal figure by proper

regions of bicircles.

Let  is a polygonal figure, 



is a subset of the

figure formed by the union of all spokes of length 

and more. It is obvious that 



is entirely contained

in -cover. Proper areas of bicircles form the cover

of the whole polygonal figure, the cover coincides

with the union of all spokes, i.e. 



 (Fig.6).

Definition 14. Bicircle is called monotonic if the

radial function monotonically decreases or increases

along its axis.

It is clear that a linear bicircle is monotonic,

because the linear radial function is monotonic on

the axis. A linear bicircle of constant width

considered to be monotonic by definition.

In the parabolic bicircle, if the vertex of the

parabola is an interior point of the bicircle axis,

when passing through the vertex the behavior of the

radial function changes from the decreasing to the

increasing (Fig.5c). The vertex of the parabola is a

point of local minimum of the radial function and

the bicycle at this time is not monotonic. In other

cases, when the vertex of the parabola lies outside

the axis or coincides with the end point of the axis,

the parabolic bicircle is monotonic.

In the hyperbolic bicircle, the monotonic

property is determined by the position of the centers

of end circles with respect to the site line (the line

passing through the point-sites). If the centers are on

different sides of this line, the point of intersection

of this line with the bicircle axis is inside the axis

and the minimum of radial function is achieved in

this point – therefore, the bicircle is not monotonic

(Fig. 5d). In other cases, the hyperbolic bicircle is

monotonic.

Calculation of morphological width for

monotonic bicircles involves a simpler problem than

for non-monotonic ones. Therefore each non-

monotonic bicircle can be replaced with a pair of

monotonic ones. So its axis can be divided into two

monotonic segments by adding vertices in the

bicircles’ minimal points and splitting the respective

edges into two parts. In the example (Fig.6) four

extreme bicircles are divided into monotonic pairs.

The dotted line shows the corresponding proper

areas of the bicircles.

4 PROPER REGIONS AND

EXTERNAL SECTORS

Figure 6 presents the monotonic bicircles of all three

types. Here,  and  are the radii of the small and

the large end circles,  is the distance between their

centers. If the bicircle is linear or parabolic, it has

the generating segment-site, and then  is the length

of the projection of the bicycle axis at this site:



















In the parabolic bicircle  is the distance between

the point-site and a line of the segment-site (the

focal parameter of the parabola). In the hyperbolic

bicircle  is the distance between point-sites.

For the linear bicircle (Fig.7a) the proper region

area is determined as the sum of the areas of two

trapezoids, with the bases  and  and the height :





2∙





∙







∙.

(1)

The angular size of the external sector of the

small end circle is





22∙





(2)

For parabolic bicircle (Fig.7b) the proper region

area is composed of the area of the same trapezoid

and the area of the triangle with vertices at the

centers of end circles and at the point-site. The area

of the triangle is calculated by Heron's formula:











∙



, (3)

where /2.

The angular size of the external sector of the

small end circle of parabolic bicircle is























(4)

Pattern Width Description through Disk Cover - Application to Digital Font Recognition

487

(a) (b) (c)

Figure 7: Proper regions and external sectors of bicircles:

(a) linear, (b) parabolic, (c) hyperbolic.

Proper region area of the hyperbolic bicircle

(Fig.7c) is the sum of the areas of the two triangles,

calculated according to Heron's formula:





2



.

(5)

The angular size of the external sector of the

small end circle is





2





(6)

5 TRUNCATED BICIRCLES

Disk -cover of the polygonal figure at 0

coincides with the polygonal figure. As  increases,

the cover shrinks and the part of the figure, covered

with disks, diminishes (Fig.8). This cover is a figure

whose boundary consists of line segments and arcs.

Disk -cover is the union of circles with a radius

greater than or equal to , inscribed in the polygonal

figure. We call the set of the centers of these circles

the axis of the -cover. Obviously, the axis of the -

cover is the subset of the polygonal figure skeleton.

This subset is connected at small values of , but as

 increses it can split into several connected

components (Fig.8).

Therefore, the polygonal figure skeleton is

divided into two parts: -cover axis – the subset

where the radial function is equal to  or more, and

the rest – the subset where the radial function is less

than . Both of these subsets can be considered as

geometric graphs.

(a) (b)

Figure 8: Changing of disk -cover with increasing disk

radius.

For 0, all bicircles of the polygonal figure

are broken down into three groups: wide (all the

circles of the bicircle belongs to the -cover

completely), narrow (no circle belongs completely),

and truncated (part of the circles belong completely).

Let 



and 



are the minimum and the

maximum radii of circles in the monotonic bicircle.

Than 



 in the wide bicircle, and 



 in the

narrow bicircle.

If 







, then the -cover includes only

those circles of the bicircle, whose radius is not less

than . We define the truncation operation of such

bicircle, which is to remove the circles with a radius

smaller than . The resulting new bicircle will be

called truncated. The minimum circle of the

truncated bicycle changes to the circle of radius r,

and the maximum one remains the circle with a

radius 



(a)

(b)

(c)

Figure 9: Correction of truncated bicircles.

Let 



,



are the centers of the small and the

great end circles. We determine the new position of

the small end circle. Let the point  is the desired

center of the circle with radius  (Fig.9).

For the linear bicircle (Fig.9a), we have













∙,

where 













. In the particular case when









, we suppose 0.

For the parabolic bicircle (Fig.9b) choose a polar

coordinate system , with the origin at the point-

site  of the bicircle and the axis orthogonal to the

segment-site. The equation of the parabola in these

coordinates is 





, where  is the focal

parameter of the parabola. The end circles centers

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

488

have coordinates 









,





and 









,





, where













1, 











1. The

required point is ,,  





1

Without loss of generality, we assume 







Vector 



is obtained through rotating 





by angle





and multiplying by factor







. Then the

desired center of the circle is 







∙∙



where  is the rotation matrix by angle :



cos sin

sin cos

.

In the hyperbolic bicircle (Fig.9c) the point 

lies between 



and 



. Let q is the distance between

point-sites. If  is a point-site, the projections of the

vectors 



, 





, 





on the bicircle axis have

lengths























































































Then 











∙, where 













These formulas allow us to find a new position

of the small end circle, then the calculation of the

area of the bicircle and the angular sizes of the

external sectors is carried out by the same formulas

(1)‒(6), as for wide bicircles.

Therefore, the disk -cover is the union of two

sets of bicircles: full bicircles, where 



, and

truncated bicircles, where 







. This

cover is composed from proper regions of these

bicircles and external sectors of small circles of the

truncated bicircles.

At Figure 8 proper regions are highlighted in

light gray, and the external sectors – in dark gray.

The total area of the union of the proper regions is

the sum of areas of bicircles’ proper regions.

End circles of truncated bicircles in the -cover

have a radius . The area of the external sector with

an angle  is 









∙



. But the sectors can have

a nontrivial intersection (Fig.8c).

6 BICIRCLES' INTERSECTIONS

Define those of the bicircles, which can have

significant intersections with each other. When

calculating -area it is only necessary to find the

intersections of adjacent bicircles, i.e. those between

which gaps are formed by removing narrow bicircles

having a width smaller than .

We are interested in only the external sectors of

the small end circles of the bicircles. In the

monotonic bicircle the angular size of the external

sectors of the small end circle .

Definition 15. Two truncated bicircles in the -

cover called adjacent if there is a route in the

skeleton connecting the centers of the end circles,

such that the radial function at all points of the route

is less than .

The external sector of the truncated bicircle may

have the intersection not only with the external

sector of another bicycle, but also with its proper

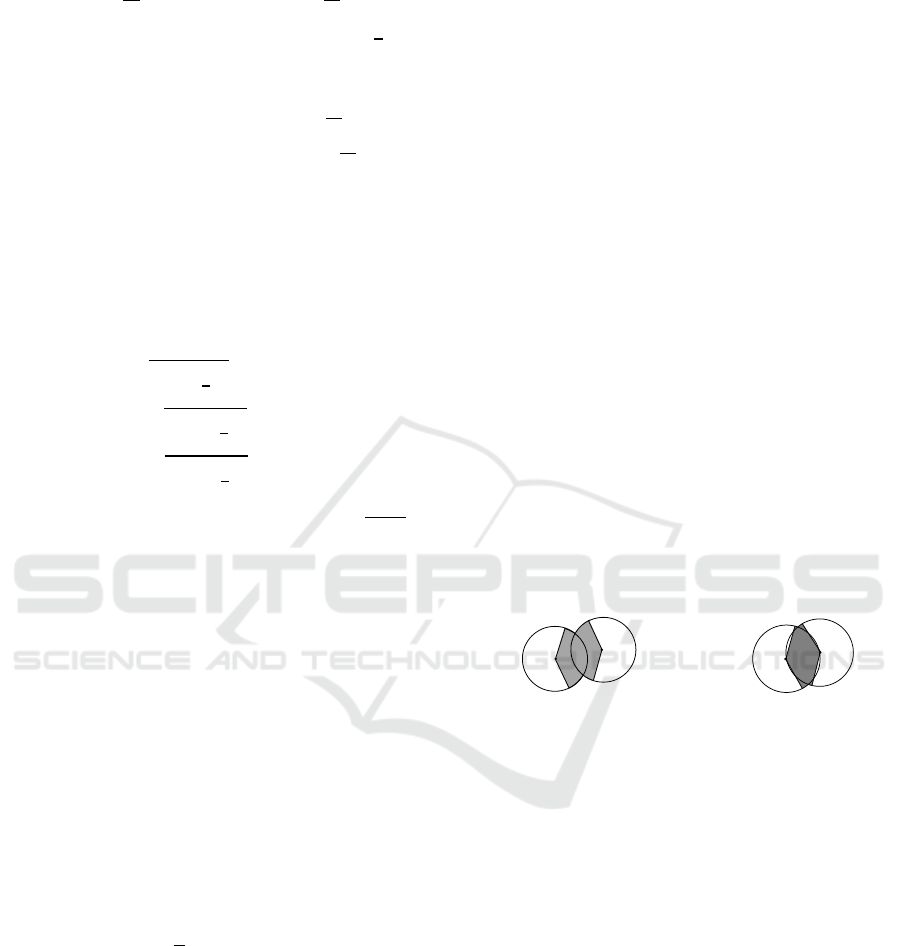
region. Figure 9 shows examples of possible mutual

arrangements of the external sectors of the two

truncated bicircles. In the first case (Fig.10a) in the

intersection of two sectors the “lens” figure, the

boundary of which consists of two equal circular

arcs, is formed. In the second case (Fig.10b) the

intersection of the sectors is a more complex figure

whose boundary includes straight-line segments of

the spokes and the circular arcs. The gray

highlighted areas in Figure 10 are formed by the

union of the external sectors except for the

intersection of them with the proper areas of the

bicircles. Such areas will be called the outer zone of

the bicircle pair.

(a) (b)

Figure 10: Mutual arrangement of the pair of crossing

external sectors of truncated bicircles.

We denote:





is the area of the end circles of the

bicircles;





is the area of the lens formed by the

intersection of the end circles;







, 





are the areas of the bicircles’

external sectors;







, 





are the areas of internal sectors of

the end circles.

Internal sector is the addition of the external

sector in the end circle. Internal sectors of two

adjacent truncated bicircles do not intersect each

other. Since the angular size of the external sector

does not exceed , it turns out that the internal sector

size is not less than .

The area of the outer zone formed by a pair of

external sectors of the two intersecting truncated

Pattern Width Description through Disk Cover - Application to Digital Font Recognition

489

bicircles is the sum of the areas of these sectors less

the area of the lens formed by the intersection of the

end circles:

























(7)

Indeed, the total area of the union of two

intersecting end circles is equal to

2







Since internal sectors of the circles do not

intersect:





2





























.

Obviously,





























Taking this into account, we obtain the desired

relation to the area of the outer zone:



























































Let 



,



are the angular sizes of two

intersecting external sectors. Then













∙





, 











∙





The angular size of the lens formed by the two

circles of radius , with centers located at a distance

2 of each other, is

  





The area of this lens is











sin



Thus, the area (7) of the outer zone of the pair of

intersecting bicircles is equal to







∙











∙











sin



(8)

The case of three or more intersecting external

sectors seems more difficult. Possible options for the

intersection of three equal circles are depicted in

Figure 11.

(a) (b) (c)

Figure 11: Intersections of three end circles of the

truncated bicircles.

However, as shown in (Lomov and Mestetskiy,

2016), in the case of the intersection of three

truncated bicircles options shown in Figure 11a,b

are impossible. The only possible option for the

intersection of three truncated bicircles is pairwise

intersections as in the example on Figure 11c.

Consequently, the area of the outer zone formed

by the external sectors of three pairwise

intersecting truncated bicircles, is the sum of the

areas of these sectors minus the areas of lenses

formed by the intersection of end circles. The area

of the disk cover is the sum of areas of proper

regions of all bicircles and areas of external sectors

of the truncated bicircles minus the areas of

intersections of adjacent truncated bicircles.

Search for the pairs of adjacent truncated

bicircles is performed on the base of the polygonal

figure skeleton, starting from the minimum points

of the radial function. As a result of the sequential

analysis of width of these bicircles, we find all

truncated bicircles, bordering the narrow

component of the skeleton, adjacent to the given

minimum point of the radial function.

7 STRUCTURE OF THE

ALGORITHM

Thus, to calculate the -area we can use the

representation of the disk -cover as the union of

bicircles. To do this, take the following steps:

1. Build the medial representation of a

polygonal figure in the form of a skeleton and

a radial function. The algorithm described in

(Mestetskiy, 2008).

2. Find the edges, in which the minimum points

of the radial function are located, and divide

them down into monotonic parts (Section 3).

Build the set of monotonic bicircles covering

the polygonal figure.

3. For a given value of  find the set of

truncated bicircles and calculate the positions

of their small end circles (Section 5).

4. For complete and truncated bicircles calculate

the areas of proper regions and take their sum

(Section 4).

5. For truncated bicircles determine their

external sectors and find their total area

(Section 5).

6. Find all the lenses in the intersections of the

external sectors and calculate their total area

(Section 6).

7. Find the -area as the sum of areas of proper

regions and end sectors of the bicircles minus

the total area of the lens.

8 COMPUTER FONT

RECOGNITION

As an example of the proposed method of

morphological image analysis we consider the

problem of computer font recognition by some

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

490

context. Currently, thousands of computer fonts

developed.The need to identify what font is used in

the text arises for designers, font developers and

experiment is to evaluate the possibilities of using

the proposed method for solving these problems.

Example (Fig.12a) demonstrates width

diagrams for 5 letters of the Times New Roman

font, belonging to the word HORSE. The example

shows that the font characters have clearly

distinguishable individual portraits.

(a)

(b)

Figure 12: Width diagrams of different characters of the

same font (a) and the same character in different fonts (b).

Differences between the portraits of the same

letter H, typed by different fonts (Times New

Roman, Aria, Garamond, Britannic Bold,

Rockwell) are shown in next example (Fig.12b).

These diagrams are obtained for high-resolution

images, which are considered as reference samples.

To conduct the experiment under more realistic

conditions, reference images of 52 characters of the

Latin alphabet (26 uppercase and 26 lowercase

letters) for 1848 typefaces ParaType digital font

collection (Yakupov et al., 2015) have been

constructed. For the reference images the width

diagrams were obtained by the method described in

this article. To do this, each character was drawn

on a binary raster image on such a scale that the

height of a capital letter H was 1000 pixels. For

these images continuous skeletons were

constructed and their basis width histograms were

calculated with the radius step of 0.5 pixel.

For the same fonts the images of the characters

were obtained in a lower resolution, so that the

height of letter H was 100 and 70 pixels. For these

characters, width diagrams also were built. Step

radius in the calculation was 0.05 and 0.035 pixels,

respectively. These diagrams were normalized so

that they could be compared with the diagrams of

reference font characters. Normalization was done

by stretching the diagrams 10 times along the -

axis and 100 times along the -axis and 14.29

times along the -axis and 204.08 times along the

-axis for low resolutions of 100 and 70 pixels

respectively. As a result, all the normalized

diagrams used the same set of radius values.

Creating of the skeletons and the calculation of

width diagrams (for 52 glyphs of 1848 fonts) took

in total less than 4 minutes on the computer with

Intel® Core i5

processor and 6GB of RAM

Further, for each font images of the 1000

common English words, random 30% of which were

converted to upper case, were composed from the

letters in low resolution. These images were used as

the test set. Next, the diagrams of the letters on test

images were compared with the diagrams of

reference images in 



metric. As an integral font

similarity metric we use a linear combination of

distances between all characters present in the

word. The coefficients of the linear form for each

word were obtained by training on the entire set of

test fonts. In the experiment, we calculated the

distances for 52 letters between all pairs of 1848

typefaces, which took 18 minutes, and 1000 times

trained the linear form, which took 32 minutes.

This means that the time of the request – checking

the typeface in the basis of the references – is 2

seconds and most of this time is spent to training of

the linear form.

The experimental results showed that the font

recognition accuracy by one word at the resolution

of 100 was 91%, and at a resolution of 70 – more

than 81%. Using the imaginary word containing all

52 characters we achieved the accuracy of 97% and

95% respectively.

Thus, the experiment confirmed the efficiency

of the proposed method and showed its efficiency

on the practical task of comparing a large number

of images (1848184852) with a fairly high

recognition quality.

9 CONCLUSION

The proposed approach opens up new possibilities

for the use of highly efficient computational

geometry algorithms in image analysis and shape

recognition. The continuous model of width of

polygonal figures on the basis of the disk cover

allowed to make the decomposition of the original

Pattern Width Description through Disk Cover - Application to Digital Font Recognition

491

problem and reduce the computation to simple

geometric calculations.

The developed algorithm is the first to provide

accurate analytical representation of the width

distribution function of a polygonal figure. Raster

objects approximation with polygonal figures makes

it possible to use the method in the analysis and

recognition of images. The high efficiency of the

proposed method allows to compare and measure the

similarity of figures by their width in real-time

computer vision systems.

ACKNOWLEDGEMENTS

The work was funded by Russian Foundation of

Basic Research grant No. 14-01-00716.

REFERENCES

Maragos P., 1989. Pattern Spectrum and Multiscale Shape

Representation. In IEEE Trans. On Pattern Analysis

and Machine Intelligence, Vol. 11, №7, pp. 701–716.

Serra J., 1982. Image Analysis and Mathematical

Morphology, London: Academic Press.

Ramirez-Cortes, J.M., Gomez-Gil, P., Sanchez-Perez, G.,

Baez-Lopez, D., 2008. A Feature extraction method

based on the pattern spectrum for hand shape

biometry. In Proc. World Congress on Engineering

and Computer Science.

Vizilter Yu.V., Sidyakin S.V., 2012. Morphological

spectra [in Russian]. In Computer vision in control

systems 2012. Proceedings of the scientific-technical

conference, Moscow, 14–16 March, 2012. Pp. 234–

241.

Vizilter Yu.V., Sidyakin S.V., 2015. Comparison of

shapes of two-dimensional figures with the use of

morphological spectra and EMD metrics. In Pattern

Recognition and Image Analysis, Vol. 25, No. 3, pp.

365–372.

Lomov N.A, Mestetskiy L.M, 2016. Area of the disk cover

as an image shape descriptor. In Computer Optics, vol.

40(1), pp. 516-525.

Mestetskiy, L., Semenov, 2008. Binary image skeleton

continuous approach. VISAPP 2008 - 3rd

International Conference on Computer Vision Theory

and Applications, Proceedings 1, pp. 251-258.

Yakupov E., Petrova I., Fridman G., Korolkova A., Levin

B., 2015. PARATYPE Originals – Digital Typefaces.

Moscow, 2015.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

492