Edge based Blind Single Image Deblurring with Sparse Priors
Khouloud Guemri
1
, Fadoua Drira
1
, Rim Walha
1
, Adel M. Alimi
1
and Frank LeBourgeois
2
1
ReGIM-lab, University of Sfax, ENIS, BP 1173, Sfax, 3038, Tunisia
2
LIRIS, University of Lyon, INSA-Lyon, CNRS, UMR5205, F-69621, Lyon, France
Keywords:
Blind Image Deblurring, Sparse Representation, Edge based Information, Kernel Estimation, Deconvolution.
Abstract:
Blind image deblurring is the estimation of the blur kernel and the latent sharp image from a blurry image.
This makes it a significant ill-posed problem with various investigations looking for adequate solutions. The
recourse to image priors have been noticed in recent approaches to improve final results. One of the most
interesting results are based on data priors. This has been the starting point to the proposed blind image
deblurring system. In particular, this study explores the potential of the sparse representation widely known
for its efficiency in several reconstruction tasks. In fact, we propose a sparse representation based iterative
deblurring method that exploits sparse constraints of edge based image patches. This process includes the K-
SVD algorithm useful for the dictionary definition. Our main contributions are (1) the application of a shock
filter as a pre-processing step followed by filter sub-bands applications for an effective contour detection, (2)
the use of an online training data-sets with elementary patterns to describe edge-based information and (3)
the recourse to an adaptative dictionary training. The experimental study illustrates promising results of the
proposed deblurring method compared to the well-known state-of-the-art methods.
1 INTRODUCTION
1.1 Background
Blind image deblurring, similarly known in the litera-
ture as blind deconvolution or shape estimation from
defocus or motion blur, is the estimation of the blur
kernel and the latent sharp image from a blurry image.
Mathematically, the problem is generally modeled as
follows:
Y = K ⊗ X + n; (1)
where Y is the blurry degraded image, K is the blur
kernel, X is the latent image, n is noise, and ⊗ is the
convolution operator. The given deblurring problem
is a significant ill-posed problem. Its solution consists
in recovering both X and K from Y . Various investi-
gations looking for adequate solutions are presented.
The recourse to image priors have been noticed in re-
cent approaches to improve final results.
1.2 Related Works
One of the most interesting deblurring results are
based on data priors and, in particularly, the priors
that are deeply related to edge preserving properties.
Tensor driven approaches are among important solu-
tions that offer promising issues due to their efficiency
in edge preservation (Guemri and Drira, 2014); nev-
ertheless, they do not exploit the images similarities
which are very useful in improving the overall perfor-
mance. In fact, the redundancy of the image features
is very noticeable and argued the success of the non-
local means defined as the estimation of a pixel value
by the weighted average of the similar structure pixels
(Buades et al., 2005). Different image deblurring so-
lutions based on this concept are later proposed. Fur-
thermore, other existing solutions of blind deconvolu-
tion algorithms encompass explicitly edges for kernel
estimation. For instance, the methods of Joshi et al.
(Joshi et al., 2008) and Cho et al. (Cho et al., 2011)
extract blurry edges to estimate the blur kernel use-
ful for the overall deblurring process. These methods
efficient in the case of small scale blur remain very
limited in the case of large blur kernels. As a solution
to this limitation, Cho and Lee (Cho and Lee, 2009)
method incorporates a coarse to-fine fashion process
to restore sharp edges and to estimate the blur ker-
nel. A further extension of this method was proposed
by Xu and Jia (Xu and Jia, 2010) who introduced a
measure of the usefulness of the image edges via gra-
dient image selection. Another category of methods
174
Guemri K., Drira F., Walha R., Alimi A. and LeBourgeois F.
Edge based Blind Single Image Deblurring with Sparse Priors.
DOI: 10.5220/0006129001740181
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 174-181
ISBN: 978-989-758-225-7
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

exploit patch priors on edges of the latent image. For
instance, Sun et al. (Sun et al., 2013) employed patch-
based priors to focus on the image regions that are
more informative for blur kernel estimation. Michaeli
and Irani (Michaeli and Irani, 2014) adopted the in-
ternal patch recurrence property for estimation of the
exploited blur kernel. Wei-Sheng et al. (Lai et al.,
2015) utilized the normalized color-line prior to re-
store sharp edges without altering edge structures or
enhancing noise.
The study of the state-of-the-art reveals that the
promising solution to deal successfully with patch pri-
ors is the use of the sparse representation (Aharon
et al., 2006; Elad et al., 2010). Especially, this rep-
resentation exploits an over-complete dictionary from
which few elements are linearly combined to describe
an image patch. Among the existing sparse coding
based deblurring methods, we can give as examples
the methods of Lou et al. (Lou et al., 2011), Hu et al.
(Hu et al., 2010), Liu et al. (Liu et al., 2013) and Yu
et al. (Yu et al., 2010).
1.3 Contributions
Attracted by the simplicity and the efficiency of the
Hu et al. method (Hu et al., 2010), we propose in this
study to investigate the properties of this sparse repre-
sentation based method by adding specific constraints
on the edge based information inspired from the Sun
et al. approach (Sun et al., 2013). In particular,
the proposed edge based method exploits sparse rep-
resentation using a dictionary learned directly from
edges’ patches of the blurred image. Indeed, the de-
tection of these patches is with a binary mask that
indicates the location of pixels with largest filter re-
sponses from a filter bank. The proposed method re-
quires only the blurred image itself and utilizes spar-
sity constraints to iteratively estimate the deblur ker-
nel and then applies a standard non-blind deconvolu-
tion algorithm to recover the deblurred image.
The rest of the paper is organized as follows. Sec-
tion 2 gives an overview of the Hu et al. (Hu et al.,
2010) method that represents an Adaptive Dictionary
learning (ADL) based blind Deblurring method. A
modified variant of this method via the introduction
of edges-based constraints represents the underlying
idea of our proposition detailed in Section 3. Section
4 gives numerical experiments to demonstrate the ef-
ficiency of the proposed method within a comparative
study. Section 5 presents a conclusion including an
overview of our contributions and a presentation of
further investigations to deal with, looking especially
for improving the proposed method.
2 BLIND SINGLE IMAGE
DEBLURRING WITH SPARSE
PRIORS
2.1 Numerical Formulation of the
Sparse Coding for Image
Deblurring
Sparse coding has been successfully used in image
representation tasks mainly for addressing inverse
problems like resolution enhancement (Walha et al.,
2015b) and denoising (Walha et al., 2015a). Thus, it
becomes a widely known approach in computer vi-
sion to learn dictionaries of image patches. In partic-
ular, the key idea of the sparse coding algorithm is to
represent an input signal as a linear combination of
a small number of elements, called atoms, selected
from an over-complete dictionary. Mathematically,
given an over-complete dictionary D ∈ ℜ
n×m
;n, m ∈
ℜ with m atoms and n ≺ m, an image X ∈ ℜ
n
could be
sparsely represented by D as follows (Aharon et al.,
2006):
X = Dα; (2)
where the representation cœfficient α ∈ ℜ
m
is sparse.
This problem is formulated as the given optimization
problem (P0)
(P0) : min
α
k
α
k
0
s.t.
k
X − Dα
k
2
2
≤ ρ; (3)
where
k
α
k
0
= card
{
k α
k
6= 0
}
is the l
0
pseudo-norm
of α (i.e. number of non-zero elements in α) and
ρ characterizing an allowable error reconstruction.
Looking for a simplification of the NP-hard problem
(P0), the l
0
pseudo-norm is substituted by the l
1
-norm
as follows:
(P1) : min
α
k
α
k
1
s.t.
k
X − Dα
k
2
2
≤ ρ. (4)
Moreover, the learning of a dictionary D from the
training data Y according to the sparse coding prin-
ciple is defined by
D = argmin
D,α
k
Y − Dα
k
2
2
+ λ
k
α
k
1
; (5)
where α is the sparse representation of the training
samples Y over the dictionary D, and the constant λ is
a regularization parameter used for balancing sparsity
of the solution and fidelity of the approximation to Y .
Faced with the deblurring problem and given the lin-
earity of the convolution operator, the blurred image
could be formulated as follows:
Y = K ⊗ X = K ⊗ (Dα) = (K ⊗ D)α = D
b
α. (6)
By adapting equation 5 in the context of deblur-
ring, the reconstruction of an image patch y
i
could be
Edge based Blind Single Image Deblurring with Sparse Priors
175

addressed by solving the following optimization prob-
lem:
(P1) :
ˆ
α
i
= argmin
α
i
k
α
i
k
1
s.t.
k
y
i
− D
b
α
i
k
2
2
≤ ρ. (7)
We must notice that the input blurry image Y ∈ ℜ
n
is considered as an arranged set of image patches and
the restoration is performed on each image patch y
i
.
After that, the optimal solution to (P1) is thus applied
to recover the deblurred image patch x
i
based on a
deblurred version of the dictionary D
b
as follows:
x
i
= D
ˆ
α
i
. (8)
2.2 Case Study of the Adaptive
Dictionary Learning based Method
The Adaptive Dictionary learning (ADL) based blind
Deblurring method is able to estimate blur kernels and
thereby deblurred images (Hu et al., 2010). In fact,
the main steps of this method could be summarized
as follows: (1) an iterative process to encode each im-
age patch with sparse coefficients and using an over-
complete dictionary in order to converge to the latent
image, (2) estimation of the blur kernel, (3) Dictio-
nary update without any additional information. The
deblurred image is finally recovered once the deblur
kernel is estimated.
In spite of the efficiency and the simplicity of the
Adaptive Dictionary learning based blind Deblurring
method, the deblurred output image still contain ring-
ing artifacts around edges. Looking for improving its
efficiency, a possible solution to overcome this limita-
tion is mainly the exploitation of an edge patch based
dictionary. This represents the core idea of our propo-
sition further detailed in the next section.
3 PROPOSED BLIND IMAGE
DEBLURRING METHOD
3.1 Motivation
Recently, edge based information has been exploited
as a useful solution for the high-quality kernel esti-
mation. This is due to their specificity compared to
other image regions like flat or textured areas. Indeed,
the blur tends around the edge image to attenuate its
peaks and to smooth it in directions depending on the
blur itself. Consequently, restoring the edge image
could provide reliable edge information for kernel es-
timation. However, according to (Xu and Jia, 2010),
not all the salient edges are useful in the process of
kernel estimation since strong edges could degrade it
under certain circumstances. That’s why we propose
to exploit sparse representation for an edge based dic-
tionary learned online or in other words directly from
the patch edges of the blurred image. Next sections
detail the different steps of the proposed blind deblur-
ring method.
3.2 Description of the Proposed Method
Algorithm 1 summarizes the main steps of the pro-
posed algorithm. In fact, the specificity of our propo-
sition remains in the definition of the dictionary. The
latter has a specific structure characterized by edge
patches with a fixed size 12 ∗ 12; the same value has
been already defined in the ADL based method and
the overall process is described in the work of Pan et
al. (Pan et al., 2014). These patches are extracted
from the deconvoluted image. The edge patches are
extracted with the help of a binary mask that indicates
the location of the pixels with largest filter responses
from a filter bank. This filter consists of the deriva-
tives of elongated Gaussians in eight orientations. It
keeps the top of 2% of pixels locations.
For instance, Figure 1 shows that the edge de-
tected by this mask are spanning all orientations and
the number of detected edges increase from iteration
to other. Consequently, the blurred and the latent im-
age contain enough information to estimate the pro-
file of blur kernel. As illustration, Figure 2 gives an
idea about the main difference between the dictionary
taken into account in ADL based method and the pro-
posed method.
It is obvious from the given description in the Al-
gorithm 1 that the proposed algorithm iteratively opti-
mizes at once the kernel K, the edge dictionary D
edge
and the sparse coefficient α
i
to converge to the deblur-
ring blur kernel K using the Tikhonov regularization
method. At each iteration, the recovered latent im-
age X is the weighted sum of the overlapping image
patches. Indeed, each image block x
i
of the recov-
ered image is the result of the multiplication of the
updated edge dictionary D
edge
and the sparse coeffi-
cient (Equation8).
4 EXPERIMENTAL STUDY
In this section, we present results of the proposed
edge based blind image deblurring method and we
compare it to some state-of-the-art approaches (Xu
and Jia, 2010; Hu et al., 2010; Sun et al., 2013; Shan
et al., 2008) which utilize prior information on im-
age edges. Indeed, we examine the performance of
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
176

Algorithm 1: The proposed deblurring algorithm.
Input: Blurry image Y ,Kernel size, Patch size, Number of iteration
Output: Latent image X and Blur kernel K
Initialization : K= Gaussian kernel, Dictionary D
edge
=DCT cœfficient
for each iteration do
1. Deconvolute the input image with the estimated kernel K.
2. Apply shock filter on the deconvoluted image.
3. Build edge mask from the enhanced image using directional filters.
4. Extract edge patches from the deconvoluted image.
5. Update the dictionary D
edge
via KSVD algorithm using edge patches.
6. Generate the blurred version D
b
of the dictionary D
edge
.
for each image patch y
i
o f Y do
7. Find the sparse representation
ˆ
α
i
of y
i
according to D
b
by solving the (P1) problem (Eq.7)
8. Compute the corresponding version x
i
of the image patch y
i
using the dictionary D
edge
via Eq.8
end for
9. Merge overlapping patches to construct the deblurred image.
10. Estimate the deblur kernel K using Tikhonov regularization method.
end for
11. Deconvolute the input image with the estimated kernel.
Figure 1: The increase of the number of edge detection by the binary mask .(a)the blurred image,(b) the edge detection in the
first iteration, (c) the edge detection in the second iteration.
the proposed method via both qualitative and quan-
titative comparisons. Experimental studies are per-
formed on various blurred images synthesized with
different motion blurs as: fluff of the koala, and four
test images from levin’s database (Levin et al., 2011)
of size 256*256.
A first experiment concerns the recovery of a
blurred image (Figure 3 (a)) using the proposed
method and different other methods such as (Hu et al.,
2010; Shan et al., 2008; Xu and Jia, 2010). Figure 3
presents visual results of the restored images. After
visual inspection, we can observe that only our re-
sult and the result of Hu et al. are the most similar to
the ground-truth image, especially in the face region.
For a deeper evaluation, Table 1 compares quantita-
tively the RMSE, PSNR, and SSIM results of the re-
stored images. According to this table, we can see
that the image reconstructed by the proposed sparse
prior based deblurring method achieves the best mea-
surement values than the other methods involved in
this study.
A second experiment is performed to restore
blurred images from Levin et al.’s database (Levin
et al., 2011). Figure 4 provides examples of these
Edge based Blind Single Image Deblurring with Sparse Priors
177

Figure 2: Illustration of the difference between the dictionary of the ADL based method and the the dictionary of our proposed
method.
Figure 3: Visual comparative study between different methods for the reconstruction of an input blurred image.(a) The input
image.(b) The result of Shan et al. (Shan et al., 2008) . (c) The result of Hu et al.(Hu et al., 2010).(d) The result of Xu et
al.(Xu and Jia, 2010). (e )Our result.(f) The ground-truth image.
tested images which are blurred with various ker-
nels (Figure 4(a), Figure4(d), Figure 4(g)and Fig-
ure 4(m)). In this experiment, we compare the per-
formance of the proposed method with Hu et al.’s
method. According to Figure 4, we observe that our
method conserves the structure of the objects and the
texture region does not contain ringing artifacts but
the blur still exist in the deblurred results. Conse-
quently, the visual comparison is difficult to deter-
mine the best result. That is why the quantitative anal-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
178

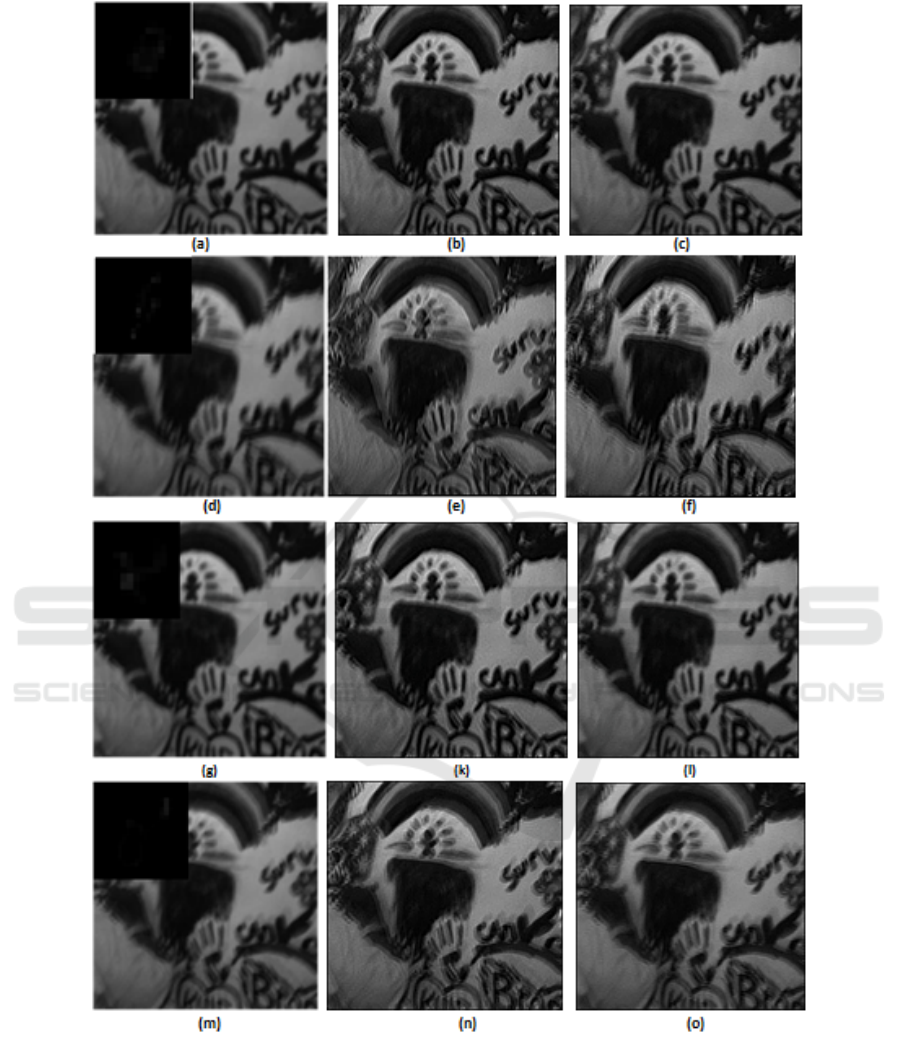
Figure 4: Qualitative comparison between images degraded with various motion blur and reconstructed using Hu et al.’s
method((b),(e),(k),(n)) and our method ( (c), (f), (l),(o)).
ysis using the image metrics is important in this stage.
Table 2 presents the results which are evaluated by
calculating the PSNR and the SSIM values. Exper-
imental results reported in this table clearly demon-
strate the effectiveness of the proposed method.
In a third experiment, we evaluate the perfor-
mance of the proposed sparse prior based blind
deblurring method against a non-blind deblurring
method that requires the kernel motion blur as an in-
put parameter. For instance, the non-blind deconvo-
lution of the Lucy image is involved in this study.
Results of this experiment are presented in Figure 5
Edge based Blind Single Image Deblurring with Sparse Priors
179

Table 1: Quantitative comparison based on PSNR, SSIM and RMSE results of images recovered by different deblurring
methods.
Image quality Result of Result of Result of Result of
metrics (Hu et al., 2010) (Shan et al., 2008) (Xu and Jia, 2010) the proposed method
PSNR 23.943 24.235 26.747 27.965
SSIM 0.602 0.652 0.756 0.806
RMSE 16.1937 15.659 11.727 10.192
Table 2: Comparative study between the proposed method and Hu et al.’s method for the deblurring for different motion blur
kernels.
Input images Image quality metrics Results of (Hu et al., 2010) Our results
Image(a) PSNR 21.694 24.595
SSIM 0.669 0.844
Image(d) PSNR 21.321 22.581
SSIM 0.617 0.731
Image(g) PSNR 21.635 23.276
SSIM 0.690 0.768
Image (m) PSNR 22.007 22.169
SSIM 0.641 0.680
Table 3: Quantitative evaluation between blind and non-
blind deblurring methods.
Result of the Result of the
non-blind deblurring proposed blind
Lucy’s method deblurring method
PSNR 19.541 23.276
SSIM 0.556 0.768
and Table 3. Quantitative and qualitative evaluations
prove the efficiency of the proposed method that out-
performs the non-blind deblurring method involved in
this study.
5 CONCLUSIONS
In this paper, a novel edge based blind image deblur-
ring method is proposed. This method exploits itera-
tively sparse priors using an online learned dictionary
that adaptatively includes only edge patches extracted
from the intermediate latent images. Indeed, the de-
tection of these patches is successfully performed us-
ing shock and directional filters. This adaptative edge
based-dictionary is useful for a more accurate estima-
tion of blur kernels and hence improving deblurring
images. The impact of the given contribution is stud-
ied visually and quantitatively on different test images
and interesting results have been achieved. Further
investigations, currently in progress, test the perfor-
mance of the proposition with the help of two dic-
tionaries; one devoted to patch based edges where as
the other to the patch-based texture synthesis. Further
tests would study the impact of various directional fil-
ters.
Figure 5: Qualitative evaluation between blind and non-
blind image deblurring methods.(a) The blurred image,(b)
the result of Lucy method,(c) Our result,(d)The groundtruth
image.
REFERENCES
Aharon, M., Elad, M., and Bruckstein, A. (2006). The k-
svd: an algorithm for designing of overcomplete dic-
tionaries for sparse representation. IEEE Transactions
on Signal Processing, page 43114322.
Buades, A., Coll, B., and Morel, J. (2005). review of im-
age denoising algorithms, with a new one. Multiscale
Modeling and Simulation: A SIAM Interdisciplinary
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
180

Journal, 4:490530.
Cho, S. and Lee, S. (2009). Fast motion deblurring. ACM
Transaction on Graphics, 28(5):145:1145:8.
Cho, T. S., Paris, S., Horn, B. K. P., and Freeman, W. T.
(2011). Blur kernel estimation using the radon trans-
form. In Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition.
Elad, M., Figueiredo, M., and Ma, Y. (2010). On the role
of sparse and redundant representations in image pro-
cessing. Proceedings of the IEEE, 98(6):972982.
Guemri, K. and Drira, F. (2014). Adaptative shock filter
for image characters enhancement and denoising. In-
ternational Conference of Soft Computing and Pattern
Recognition (SoCPaR), 7(3):279–283.
Hu, Z., Huang, J., and Yang, M. (2010). Single image de-
blurring with adaptive dictionary learning. Interna-
tional Conference on Image Processing (ICIP), page
11691172.
Joshi, N., Szeliski, R., and Kriegman, D. (2008). Psf esti-
mation using sharp edge prediction. In Proceedings of
the IEEE Conference on Computer Vision and Pattern
Recognition.
Lai, W., Ding, J., Lin, Y., and Chuang, Y. (2015). Blur
kernel estimation using normalized color-line priors.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, page 783798.
Levin, A., Weiss, Y., Durand, F., and Freeman, W. T. (2011).
Understanding blind deconvolution algorithms. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence (PAMI), 33(12):23542367.
Liu, Q., Liang, D., Song, Y., Luo, J., Zhu, Y., and Li,
W. (2013). Augmented lagrangian-based sparse rep-
resentation method with dictionary updating for im-
age deblurring. SIAM Journal Imaging Science, page
1689C1718.
Lou, Y., Bertozzi, A., and Soatto, S. (2011). Direct sparse
deblurring. Journal of Mathematical Imaging and Vi-
sion, page 112.
Michaeli, T. and Irani, M. (2014). Blind deblurring using
internal patch recurrence. In Proceedings of the Euro-
pean Conference on Computer Vision, page 783798.
Pan, J., Hu, Z., Su, Z., and Yang, M. (2014). Deblurring text
images via l0-regularizedintensityandgradientprior.
IEEE Conference on Computer Vision and Pattern
Recognition.
Shan, Q., Jia, J., and Agarwala, A. (2008). High-quality
motion deblurring from a single image. ACM Special
Interest Group on Computer Graphics (SIGGRAPH).
Sun, L., Cho, S., Wang, J., and Hays, J. (2013). Edge-based
blur kernel estimation using patch priors. in Proceed-
ings of the IEEE International Conference on Compu-
tational Photography.
Walha, R., Drira, F., Lebourgeois, F., Garcia, C., and Al-
imi, A. (2015a). Joint denoising and magnification
of noisy low-resolution textual images. International
Conference on Document Analysis and Recognition
(ICDAR), pages 871–875.
Walha, R., Drira, F., Lebourgeois, F., Garcia, C., and Al-
imi, A. (2015b). Resolution enhancement of textual
images via multiple coupled dictionaries and adaptive
sparse representation selection. International Jour-
nal on Document Analysis and Recognition (IJDAR),
18(1):87–107.
Xu, L. and Jia, J. (2010). Two-phase kernel estimation for
robust motion deblurring. European Conference on
Computer Vision (ECCV), 28(5):145:1145:8.
Yu, G., Sapiro, G., and Mallat, S. (2010). Image modeling
and enhancement via structured sparse model selec-
tion. International Conference on Image Processing
(ICIP), page 16411644.
Edge based Blind Single Image Deblurring with Sparse Priors
181