Image Segmentation using Local Probabilistic Atlases Coupled with
Topological Information
Gaetan Galisot
1
, Thierry Brouard
1
, Jean-Yves Ramel
1
and Elodie Chaillou
2
1
LI Tours, Universit
´
e Francois Rabelais, 64 avenue Jean Portalis, 37000, Tours, France
2
PRC, INRA, CNRS, IFCE, Universit
´
e de Tours, 37380, Nouzilly, France
Keywords:
Atlas-based Segmentation, 3D Brain Images, Topological Information, Markov Random Field.
Abstract:
Atlas-based segmentation is a widely used method for Magnetic Resonance Imaging (MRI) segmentation. It
is also a very efficient method for the automatic segmentation of brain structures. In this paper, we propose
a more adaptive and interactive atlas-based method. The proposed model allows to combine several local
probabilistic atlases with a topological graph. Local atlases can provide more precise information about the
structure’s shape and the spatial relationships between each of these atlases are learned and stored inside a
graph representation. In this way, local registrations need less computational time and image segmentation
can be guided by the user in an incremental way. Pixel classification is achieved with the help of a hidden
Markov random field that is able to integrate the a priori information with the intensities coming from different
modalities. The proposed method was tested on the OASIS dataset, used in the MICCAI’12 challenge for
multi-atlas labeling.
1 INTRODUCTION
In this paper, the segmentation of the subcortical brain
structures in MRI is considered (as described in (Dolz
et al., 2014)). We propose a new method based on a
more local modeling of the different structures that
need to be segmented and that increases the interac-
tivity in order to be robust when some structures have
an unexpected position or shape. This new modeling
has first been designed for the case of 3D brain im-
ages, but it can be easily generalized for several oth-
ers applications of image segmentation using a priori
knowledge of shape and position of the regions.
In medical imaging, an atlas is a type of a pri-
ori spatial information which helps the localization of
anatomical structures. The methods using this kind
of atlases for the automatic segmentation of brain
images have become very popular (Cabezas et al.,
2011). However, these methods also suffer from sev-
eral drawbacks. The segmentation of only one region
needs the registration of the whole brain and can re-
quire an important computational time on 3D images
with a high resolution. The second problem comes
from the inter-individual variability; the atlas should
be generic enough to describe effectively the whole
population with a large anatomical variation but it
should also be specific enough in order to give sig-
nificant information about each region. One of the
solution to obtain better segmentation results can be a
selection of the information inside the different train-
ing images depending on the position in the brain im-
age. For example, some multi-atlas methods use lo-
cal information to improve the segmentation quality.
(Shi et al., 2010; van Rikxoort et al., 2010). Note that
the information provided by the user is rarely com-
bined with this kind of atlas-based methods which are
typically automatic. Another type of popular tech-
niques is based on a graph representation of the brain
to help and drive the segmentation. In (Colliot et al.,
2006; Nempont et al., 2008; Al-Shaikhli et al., 2014),
the authors use topological and spatial information to
drive edges segmentation.
In this article, we proposed a new way to represent
and use the a priori information during the segmen-
tation. Brain structures are modeled by a graph in
which the nodes represent the regions and the edges
represent spatial relationships between regions. For
each region, a specific probabilistic atlas is created
and stored as attributes of the nodes. These atlases,
composed of a probability map associated to a tem-
plate image, are defined locally on a partial part of
the image (not on the whole image such as the usual
case). We call these atlases local atlases. Spatial rela-
tionships between each region of interest are extracted
Galisot G., Brouard T., Ramel J. and Chaillou E.
Image Segmentation using Local Probabilistic Atlases Coupled with Topological Information.
DOI: 10.5220/0006130605010508
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 501-508
ISBN: 978-989-758-225-7
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
501

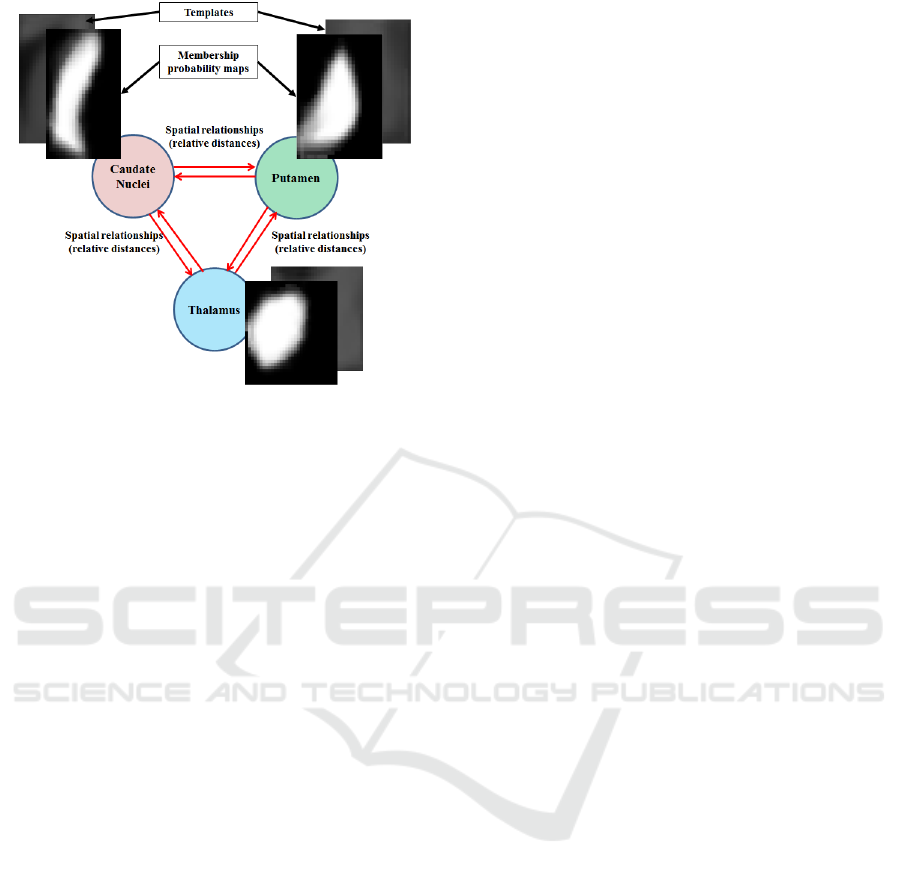
Figure 1: Schematic representation of a priori graph with
3 anatomical structures. Each node embeds a local atlas: a
template and a membership probability map.
with the help of a training dataset and stored as at-
tributes on the edges. The position and relative size of
the regions (encoded in the edges) constitute the spa-
tial relationships and are partially separated from the
shape information encoded in the nodes of the graph.
This a priori information is used during a sequential
segmentation which is done through a Markov ran-
dom field (MRF) classification.
2 CREATION OF THE
TOPOLOGICAL GRAPH
The proposed method uses a graph in order to model
and store the needed a priori information for segmen-
tation. This graph is a complete one because spa-
tial relationships exist between each region. Figure
1 shows an example of a priori graph that represents
a structure containing three different regions.
2.1 Creation of Local Probabilistic
Atlas
The atlas encodes the a priori knowledge about the
shape of the region and the associated intensities in
the different modalities. The local atlas is created in
several steps (cf. Figure 2) starting from training data
composed of N couples of MRI images and associated
labeled images.
• Region delineation
The process of atlas creation is initialized by the
delineation of the bounding box associated to each re-
gion represented in training dataset. Based on the N
labeled available images and for each region r, the
volume inside the bounding box of r and the vol-
ume associated in the MRI image are extracted and
denoted L
r
and B
r
, respectively. A margin is added
around each bounding box in order to better tolerate
the possible variability (i.e, smoothing the edges in-
side the local atlas). This margin is a percentage of
the real size of the bounding box. Throughout this
paper, the bounding box will refer to this extended
bounding box.
• Normalization
In order to correct the intensity of MRI images
which can be different between one acquisitions and
another, a normalization is performed for each region
on the N images B
r
. The method described in (Nyul
et al., 2000) is applied in this case. This intensity nor-
malization is local and achieved separately for each
region r available in the training dataset.
• Reference image selection
A reference image is also needed for each region
r. This reference has to be chosen from the images B
r
.
The image selected as a reference is the one minimiz-
ing the euclidean distance with all the other images
inside the training set. The couple of reference im-
ages of the region r is denoted as L
0
r
and B
0
r
. L
0
r
allows
to compute the first iteration of the probability map of
membership of voxels to r denoted by P
0
r
(if the voxel
of L
0
r
is labeled region, the probability is fixed to 1, 0
otherwise). B
0
r
is the first iteration of local template
of r. The template is denoted by T
0
r
.
• Probability map and template construction
The template T and the probability map P are
build incrementally. The transformations are done re-
gion by region and image by image considering all the
available images in the training set. Considering the
image whose number is I, a registration is performed
from the image I to the current template. For that,
the same process as before is followed, the volumes
inside the bounding box of the region previously ex-
tracted (on the MRI and the labeled images) are de-
noted by as L
I
r
and B
I
r
, respectively. B
I
r
is registered to
the current template (T
0
r
for the first image) in two
steps: a linear transformation (for a dimension ad-
justement) followed by a nonlinear registration is per-
formed using Bsplines (Fornefett et al., 2001). The
metric minimized by the transformation is the mean
square error. This transformation is noted τ
2
.
The template T and the probability map P are up-
dated by averaging the current value with the regis-
tered information as follows:
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
502

Figure 2: Outline of the local atlas construction.



T
I
r
=
(T
I−1
r
∗I+τ
2
(τ
1
(B
I
r
))
(I+1)
)
P
I
r
=
(P
I−1
r
∗I+τ
2
(τ
1
(L
I
r
))
(I+1)
)
(1)
The registered region are parallelepipeds where
the voxels intensities around the brain can be different
from zero (unlike the complete brain image). A voxel
V of the target image T
I−1
r
can be linked to no voxel
on the image to be registered B
I
r
. In this case, the
voxel V of the template keeps its value from the pre-
vious iteration and the voxel V of the probability map
is updated considering the membership probability of
the registered image as 0. For this kind of voxels V ,
P
I
r
[V ] and T
I
r
[V ] are updated as follows:
(
P
I
r
[V ] =
(P
I−1
r
[V ]∗I)
(I+1)
)
T
I
r
[V ] = T
I−1
r
[V ]
(2)
At the end of the process, each couple of images
{T
r
, P
r
} describes the local atlas of the considered re-
gion r and is stored inside the node of the graph cor-
responding to that region.
2.2 Creation of the Topological
Relationships
The local atlas does not provide information about the
position (of the bounding box) and the size (scale) of
the region. In order to store this information, spatial
relationships between each region are learned and in-
corporated into the edges of the so-called topological
Figure 3: Distance relationships (8 relationships instead of
12 in 3D) from the structure R1 to the structure R2.
graph. It becomes then possible to deduce the posi-
tion of a target region from the position of one or sev-
eral source regions previously localized. Fuzzy spa-
tial relationships have already been established in the
past (Bloch et al., 2003) allowing to create a member-
ship probability map compared to a reference struc-
ture. In our case, the problem is to automatically de-
cide, as precise as possible, the position of the local
atlas. The fuzzy membership information will be pro-
vided afterward by the local atlas.
Twelve distances between the two structures to be
linked have to be learned and stored in the graph in
order to be able to deduce the position of a box from
the position of another one (cf. Figure 3). The dis-
tance values are relative to the size of the source re-
gion, allowing to make the relation independent on
the dimensions of the used images (and also the res-
olution of the image). For each of the 12 spatial re-
lationships, the minimum and maximum relative dis-
tances, observed in the training set, are stored as an
interval. The minimum and maximum relative dis-
tance between the side edge i of the region r
1
and the
side edge j of the region r
2
are denoted by Min
E
i
r1
E
j
r
2
and Max
E
i
r
1
E
j
r
2
, respectively. In 3D, the side edges i
and j can take 6 different values but the distance rela-
tionships Min and Max are defined only if i and j are
in the same plane.
3 INCREMENTAL
SEGMENTATION
3.1 Outline of the Segmentation
The segmentation (of a brain) uses all the information
which is encoded inside the learned topological graph
but in an incremental way. The desired regions have
to be extracted one by one according to the decision
Image Segmentation using Local Probabilistic Atlases Coupled with Topological Information
503

of an expert (i.e, a user) or by using a heuristic. The
segmentation of a region is composed of several steps.
First, the selection of the region to be segmented. Sec-
ond, the positioning of its bounding box. Third, the
registration of the local atlas inside the bounding box.
Last but not least, the pixel classification with a MRF.
The position of the bounding box can be pro-
ceeded automatically or manually. In some cases, it
can be interesting to let the user define or refine the
position of the bounding box of a region in order to
have an efficient segmentation inside it. The user
can also let the algorithm use the spatial relationships
learned previously (cf. Section 3.2) in order to auto-
matically compute the position of the bounding box of
the desired region; knowing that the user always has
the possibility to correct the wrong positioning. When
the bounding box is positioned, the box is inflated of
several voxels in each direction in order to define the
extended volume Be
R
for the region R. This number
of voxels is the same as during the atlas creation (10
% of the size of the bounding box). The margin de-
creases the impact of errors which could occur during
the manual or automatic positioning.
From the nodes, the graph provides information
about the region R: the probability map and the as-
sociated template. The template is registered to Be
R
in the same way as during the atlas construction (cf.
Section 2.1 ). The transformations τ
1
and τ
2
defining
the registration is also applied to the probability map
associated to the template. The result of this transfor-
mation initializes the process of voxel classification
included inside Be
R
giving a membership probability
to the region for each voxel. The segmentation pro-
cess, using a MRF, is described in Section 3.3.
3.2 Region Positioning
When at least one region has already been segmented,
the spatial relationships stored in the edges of the
graph can be used to determine the position of the
new region to be segmented. All the regions already
segmented are used as references to determine the po-
sition of the new bounding box. The set of regions
already localized is denoted by R and the region we
are looking for is denoted by r
new
. The side-edges
of the bounding box of r
new
are positioned indepen-
dently the ones with respect to the others. Six posi-
tions should be determined (two in each direction X,
Y , Z defining the width, the height and the depth of
the bounding box, respectively). The interval of min-
imum and maximum values [min, max] are provided
for each side edge by each region that is already posi-
tioned. Each region r include in R provides its infor-
mation about the position of the region.
The first step is the transformation of the relative
distances into real position in the image we want to
segment. If we consider one direction on the image
(X) and we search one of the two edges of r
new
. The
position of the edges of r, the size of the bounding
box of r and the intervals of relative distance between
r and r
new
, provide two intervals of position denoted
as [Xmin
E
1
r
, Xmax
E
1
r
] (from the first edge of r) and
[Xmin
E
2
r
, Xmax
E
2
r
] (from the second edge of r).
We use the rectangular function Π(x) with x ∈ X:
Π
1
r
(x) =

1 if x ∈ [Xmin
E
1
r
, Xmax
E
1
r
]
0 otherwise.
(3)
In order to weight the different a priori informa-
tion coming from each segmented region, a weight W
is assigned to each interval ([Xmin
E
1
r
, Xmax
E
1
r
]) which
is inversely proportional to its length. Thereby, the
more precise the relation, the more it will have im-
portance compared to the other intervals.
W
E
1
r
=
1
Xmax
E
1
r
− Xmin
E
1
r
+ α
(4)
where α is a parameter strictly positive, fixed to
0.1 in our case allowing to have a finite value for the
weights.
All the intervals are combined together to obtain
the final position of the edge of the region using the
expected value of the sum of the intervals.
E
1
rnew
= Expected(
∑
r∈R
W
E
1
r
Π
1
r
(x) +
∑
r∈R
W
E
2
r
Π
2
r
(x))
(5)
3.3 Voxel Classification
The hidden Markov random field is often used for im-
age segmentation especially for the segmentation of
MRI brain images. It provides satisfactory results not
only for the segmentation of matters (Zhang et al.,
2001) but also for the anatomical structures (brain nu-
cleus) of the brain (Fischl et al., 2002). The HMRF
performs the classification of the voxels in K distinct
classes. The initialization is done with a Kmeans
algorithm where the number of class K is fixed by
the user. In the end, the voxels should be classified
into two classes: region and non-region. However,
the complexity of the tissues (in case of brain MRI
images) cannot often be modeled by only 2 classes.
Nevertheless, we make the hypothesis that the region
we want to segment is composed of only one tissue
and its intensity is homogeneous. One class is re-
quired to model the region intensity and 2 or 3 classes
are needed to model the intensity outside the region.
In practice, the results are similar if the number of
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
504

classes of the outside region is fixed to 2 or 3 inde-
pendent of the region. At the end of the Kmeans al-
gorithm, the class which has the highest number of
voxels whose membership probability to the region R
is important is labeled as region. All the other classes
are referred to as non-region. The atlas information is
provided by an external field. For the class defined as
region, the external field is equal to -log(atlas
i
) and
equal to -log(1 − atlas
i
) for the other classes defined
as non-region.
Then, the MRF has to classify the voxels inside
the bounding box. The optimization problem is per-
formed as in (Scherrer et al., 2009). The Expectation
Maximization (EM) algorithm allows to optimize the
Gaussian parameters that models the voxel intensities
of each class. After the optimization, the voxels are
classified into the most likely class. If the class’s label
is non-region, the voxel is not classified and could be
classified during a future segmentation. If the class’s
label is region, the voxel is definitively assigned to the
region R.
A parameter (α
i
) supporting the atlas information
and (β) supporting the neighborhood influence can
modulate the energy function and were chosen empir-
ically during experiments. So, the chosen values are
β = 0.05 and α
i
= 0.75 + 2 ∗ H
i
with H
i
the entropy
link to the a posteriori probability.
4 EXPERIMENTS
4.1 Dataset Description and Method
Validation
The experiments were carried out on a dataset used in
the Workshop MICCAI’12 (Landman et al., 2012) for
the segmentation of cortical and subcortical regions
with multi-atlas segmentation. This dataset is com-
posed of T1 3D MRI images and of the associated
ground truth (cortical and subcortical structures are
available). Fifteen images are used to learn the a pri-
ori information and twenty images are used as test im-
ages where 13 subcortical regions have been chosen
to test our method. The quality of the segmentation
is evaluated by the Dice similarity coefficient defined
as:
Dice =
2∗TruePositives
2∗TruePositives+FalsePositives+FalseNegatives
The proposed method needs first the choice of the
segmentation order given by the user in an interac-
tively way and second the manual positioning of the
first bounding box. In our study, the order of seg-
mentation is fixed and same for all the segmentation.
(a) E1-Image1003 (b) E2-Image1003
(c) E1-Image1128 (d) E2-Image1128
(e)
Figure 4: Results of a segmentation on an image close to
images inside the training dataset, for the experiment E1 (a)
and for the experiment E2 (b). Results of a segmentation
on an image different from the images inside the training
dataset, for the experiment E1 (c) and for the experiment
E2 (d). The red pixels describe the pixels where the ground
truth and the segmentation are not compatible.
The order was chosen arbitrarily while trying to se-
lect structures in both hemispheres. Two experiments
were conducted:
- Experiment E1: the spatial relationships are not
used and the bounding box are manually positioned
with the ground truth for all the structures. In this ex-
periment, the performance of the learning of the local
atlas and MRF are evaluated.
- Experiment E2: The first 5 structures (left cau-
date nuclei, right pallidum, left putamen, right thala-
mus, right ventricle) are positioned perfectly accord-
ing to the ground truth. The next structures are au-
tomatically positioned with the spatial relationships
learned and stored in the graph.
4.1.1 Qualitative Results
The image (cf. Figure 4) demonstrates the results ob-
tained on two brain images. The images (4a, 4b) rep-
resent the experiments E1 and E2 from a brain of a
young person which is similar to the images inside
Image Segmentation using Local Probabilistic Atlases Coupled with Topological Information
505

the training dataset of young people. The images
(4c, 4d) represent the experiments E1 and E2 from
a brain of an old person where the anatomical struc-
tures can be different from the structures inside the
training dataset.
In both images, the experiments E2 give results
with a similar quality than the experiments E1. The
learned spatial relationships seem to be robust enough
to not cause additional segmentation errors. The
images (4c, 4d) shows some limits of the proposed
method. Indeed, the differences between the training
and test images are responsible of more errors; espe-
cially for the ventricle and caudate nuclei where the
difference between old and young brains are impor-
tant.
4.1.2 Quantitative Results
Table 1 describes the results obtained in experiments
E1 and E2. Two methods used during the MICCAI’12
challenge are included. The method PICSL BC ex-
plained in (Wang and Yushkevich, 2013) (the best
one in the multi-atlas labeling challenge) and the
CRL STAPLE technique in (Avants et al., 2010).
When the structures are perfectly positioned with
the ground truth information, the results of our
method are similar to the state-of-the-art’s method for
the subcortical regions with an important size and rel-
atively stable like the putamens, thalamus, brain stem
and pallidums (around 2 or 3 lower than PICSL BC).
The detection of the hippocampus and caudate nu-
clei are a little bit under the state-of-the-art’s results.
However, they are close to the other methods. The
quality of the segmentation of the ventricle is lower
than the both methods described here. The lower re-
sults, shown in Table 1, can be explained by the uti-
lization of probabilistic atlases. In contrary to multi-
atlas, probabilistic atlas lose some information during
the process of template creation.
When the brain structures (bounding boxes) are
positioned in an automatic way, the obtained results
are slightly lower than when the structures are po-
sitioned with the ground truth. The difference is
around 3 points for most of the anatomical structures.
Only the caudate nuclei is more different compared to
the segmentation quality of experiment E1 (6 points).
The margin of the bounding box is one of the reason
explaining the results similar between E1 and E2.
Our method is coded in C++/Cli without any par-
ticular optimization. The computation time (on a PC,
2.70 Ghz and 16 Go Ram) is included between 20
seconds and 2 minutes 20 seconds for each region
to be segmented, according to the size of the region
and the parameters used for the registration. Further-
more, we can obtain suitable results (i.e, Dice coef-
ficient average of experiment E1 is equal to 0.851
instead of 0.853), for the segmentation presented in
the table, with a lower computation time (i.e, 22 sec-
onds in average by region). Our method provides
very fast results when we want to segment only some
regions of the brain. This capability (computational
time) is a strong advantage compared to the methods
designed to deal with the whole segmentation of the
brain. Such methods need around one hour of compu-
tational time as mentioned in (Wang and Yushkevich,
2013).
4.1.3 Segmentation of Sheep Brain Images
This work is part of a collaboration with the INRA
(french national institute - http://www.inra.fr/). The
goal is to create an adaptive segmentation tool that
could be used on different types of brains (animal
species). To demonstrate the flexibility of our method,
the algorithm presented here has been applied on
sheep brain 3D MRI images. Tests were performed
on 3D T2 MRI images of sheep brains provided by the
NeuroSpin platform
1
. These images were done on ex
vivo brain in order to have better resolution (0.3 x 0.3
x 0.3 mm). Seven regions were labeled inside 4 im-
ages of the brain. Five regions are internal structures
of the brain (caudate nuclei, hippocampus and peri-
aqueductal gray), and 2 regions are cortical structures
(olfactory bulb). A segmentation has been achieved
on a fifth image in order to have a qualitative study.
In spite of the small number of images in the train-
ing dataset, an accurate segmentation can be obtained
with the method when the bounding boxes are posi-
tioned manually (Figure 5). The segmentation of cau-
date nuclei, hippocampus and periaqueductal gray
seem accurate. The olfactory bulb is more difficult
to localize because of the variation between subjects
in the cortical area. When we try to use the learned
spatial relationships, the segmentation quality is more
variable depending on the desired regions. In these
first experiments, the caudate nuclei and periaque-
ductal gray needs to be manually positioned to ob-
tain a correct segmentation. The hippocampus and
olfactory bulb can be automatically localized depend-
ing on the previously segmented regions. The error in
the positioning of the bounding boxes can be linked to
the fact that brains are slightly deformed with ex vivo
imaging, the distance relationships are then more vari-
able. These results are promising for future works on
animal brain images. The method could be tested on
a higher number of brain structures and on different
types of images like T1 in vivo images.
1
NeuroSpin, CEA, Saclay, http://i2bm.cea.fr/drf/i2bm/
Pages/NeuroSpin.aspx
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
506

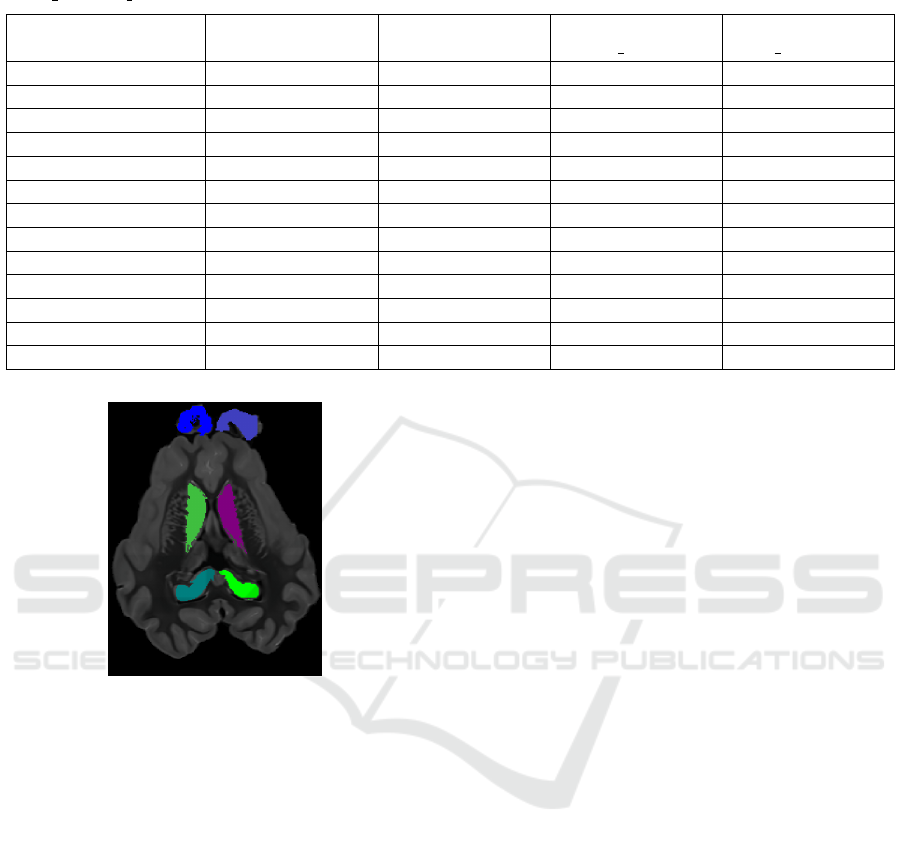
Table 1: Similarity ratios of the segmentation of 13 subcortical regions on the MICCAI’12 dataset, for the methods E1, E2,
PICSL BC, CRL STAPLE. The five first regions positioned with the ground truth are denoted by ’*’.
Region E1 E2 Method
PICSL BC
Method
CRL STAPLE
Caudate nuclei (left) 0.78 ∓ 0.25 0.78∓0.07 * 0.89 ∓0.07 0.84∓0.11
Caudate nuclei (right) 0.80 ∓ 0.06 0.74∓0.08 0.89∓ 0.07 0.82∓0.09
Pallidum (left) 0.83∓ 0.08 0.81∓0.19 0.87∓ 0.03 0.88∓0.02
Pallidum (right) 0.85∓ 0.07 0.85∓0.19 * 0.87∓ 0.05 0.88∓ 0.05
Thalamus (left) 0.87∓ 0.03 0.84∓0.04 0.91∓ 0.04 0.92∓0.03
Thalamus (right) 0.87∓ 0.03 0.87∓0.05 * 0.91∓ 0.05 0.91∓0.03
Putamen (left) 0.89∓ 0.05 0.89∓0.03 * 0.92∓ 0.01 0.91∓0.02
Putamen (right) 0.90∓ 0.04 0.88∓0.02 0.92∓ 0.01 0.91∓0.02
Ventricle (left) 0.81∓ 0.07 0.80∓0.09 0.93∓ 0.03 0.88∓0.05
Ventricle (right) 0.80∓ 0.07 0.80∓0.05 * 0.94∓ 0.03 0.87∓0.04
Hippocampus (left) 0.81∓ 0.03 0.78∓0.19 0.87 ∓ 0.02 0.84∓0.04
Hippocampus (right) 0.82∓ 0.03 0.82∓0.26 0.87∓ 0.02 0.84∓0.04
Brainstem 0.90∓ 0.01 0.89 ∓0.13 0.94∓ 0.01 0.93∓0.01
Figure 5: 2D image of a sheep brain with 6 regions seg-
mented : caudate nuclei, hippocampus and olfactory bulb.
5 CONCLUSION
In this paper, we presented a method which can pro-
vide satisfactory results (compared to state-of-the-
art methods designed specifically for the challenge)
for the segmentation of several subcortical regions of
the human brains. It is noticable that the proposed
method can perform a fast partial segmentation as
each region extraction is independent from the other.
Furthermore, an expert user can decide the adequate
order for the segmentation of the different structures
we want to extract. The segmentation order can have
an impact on the results. This method provides more
precise information than usual atlas constructed with
the same registration properties. Finally, thanks to the
local characteristic of the a priori information, each
local atlas can be learned separately. That is, the train-
ing set can be different for each region. Only the spa-
tial relationships need some full images with several
segmented regions inside. The flexibility of the pro-
posed method has also been demonstrated by provid-
ing some qualitative results on sheep brains processed
base on very few training samples. In our future work,
several points in the method could be improved. First,
the influence of the segmentation order or an incre-
mental segmentation correction should be studied in
order to limit the impact of the definitive segmenta-
tion. Second, the creation of the local atlases could be
based on techniques less influenced by the selected
reference image. Finally, it could be interesting to
store more precise statistical information rather than
only the minimum and maximum distances between
the region borders.
ACKNOWLEDGEMENTS
This work has been partially supported by the Neu-
roGeo project funded by the Region Centre - Val de
Loire. We would like to thank, Cyril Poupon for the
acquisition of the ex vivo brain images perform in
NeuroSpine and Oph
´
elie Menant for the manual seg-
mentation of the sheep brain images.
REFERENCES
Al-Shaikhli, S. D. S., Yang, M. Y., and Rosenhahn, B.
(2014). Multi-region labeling and segmentation using
a graph topology prior and atlas information in brain
images. Computerized Medical Imaging and Graph-
ics, 38(8):725–734.
Avants, B. B., Yushkevich, P., Pluta, J., Minkoff, D., Kor-
czykowski, M., Detre, J., and Gee, J. C. (2010). The
Image Segmentation using Local Probabilistic Atlases Coupled with Topological Information
507

optimal template effect in hippocampus studies of dis-
eased populations. NeuroImage, 49(3):2457–2466.
Bloch, I., G
´
eraud, T., and Ma
ˆ
ıtre, H. (2003). Representation
and fusion of heterogeneous fuzzy information in the
3D space for model-based structural recognition - Ap-
plication to 3D brain imaging. Artificial Intelligence,
148(1-2):141–175.
Cabezas, M., Oliver, A., Llad
´
o, X., Freixenet, J., and
Bach Cuadra, M. (2011). A review of atlas-based seg-
mentation for magnetic resonance brain images. Com-
put. Methods Prog. Biomed., 104(3):e158–e177.
Colliot, O., Camara, O., and Bloch, I. (2006). Integration of
fuzzy spatial relations in deformable modelsApplica-
tion to brain MRI segmentation. Pattern Recognition,
39(8):1401–1414.
Dolz, J., Massoptier, L., and Vermandel, M. (2014). Seg-
mentation algorithms of subcortical brain structures
on MRI : a review. Journal of Neuroimage, page
200/212.
Fischl, B., Salat, D. H., Busa, E., Albert, M., Dieterich,
M., Haselgrove, C., Van Der Kouwe, A., Killiany,
R., Kennedy, D., Klaveness, S., Montillo, A., Makris,
N., Rosen, B., and Dale, A. M. (2002). Whole brain
segmentation: Automated labeling of neuroanatomi-
cal structures in the human brain. Neuron, 33(3):341–
355.
Fornefett, M., Rohr, K., and Stiehl, H. (2001). Radial ba-
sis functions with compact support for elastic registra-
tion of medical images. Image and Vision Computing,
19(1-2):87–96.
Landman, B. A., Warfield, S. K., Hammers, A., Akhondi-
asl, A., Asman, A. J., Ribbens, A., Lucas, B., Avants,
B. B., Ledig, C., Ma, D., Rueckert, D., Vandermeulen,
D., Maes, F., Holmes, H., Wang, H., Wang, J., Doshi,
J., Kornegay, J., Hajnal, J. V., Gray, K., Collins, L.,
Cardoso, M. J., Lythgoe, M., Styner, M., Armand, M.,
Miller, M., Aljabar, P., Suetens, P., Yushkevich, P. A.,
Coupe, P., Wolz, R., and Heckemann, R. A. (2012).
MICCAI 2012 Workshop on Multi-Atlas Labeling.
Nempont, O., Atif, J., Angelini, E., and Bloch, I. (2008).
Structure Segmentation and Recognition in Images
Guided by Structural Constraint Propagation. Eu-
ropean Conference on Artificial Intelligence ECAI,
pages 621–625.
Nyul, L. G., Udupa, J. K., and Zhang, X. (2000). New vari-
ants of a method of MRI scale standardization. IEEE
Transactions on Medical Imaging, 19(2):143–150.
Scherrer, B., Forbes, F., Garbay, C., and Dojat, M. (2009).
Distributed Local MRF Models for Tissue and Struc-
ture Brain Segmentation. IEEE Transactions on Med-
ical Imaging, 28(8):1278–1295.
Shi, F., Yap, P.-T., Fan, Y., Gilmore, J. H., Lin, W., and
Shen, D. (2010). Construction of multi-region-multi-
reference atlases for neonatal brain MRI segmenta-
tion. NeuroImage, 51(2):684–93.
van Rikxoort, E. M., Isgum, I., Arzhaeva, Y., Staring, M.,
Klein, S., Viergever, M. a., Pluim, J. P. W., and van
Ginneken, B. (2010). Adaptive local multi-atlas seg-
mentation: application to the heart and the caudate nu-
cleus. Medical image analysis, 14(1):39–49.
Wang, H. and Yushkevich, P. A. (2013). Groupwise seg-
mentation with multi-atlas joint label fusion. Lecture
Notes in Computer Science (including subseries Lec-
ture Notes in Artificial Intelligence and Lecture Notes
in Bioinformatics), 8149 LNCS(PART 1):711–718.
Zhang, Y., Brady, M., and Smith, S. (2001). Segmenta-
tion of brain MR images through a hidden Markov
random field model and the expectation-maximization
algorithm. IEEE Trans Med Imag, 20(1):45–57.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
508