
Automatic Generation and Detection of Visually Faultless Facial
Morphs
Andrey Makrushin, Tom Neubert and Jana Dittmann
Otto-von-Guericke University of Magdeburg, Universitaetsplatz 2, Magdeburg, Germany
andrey.makrushin@ovgu.de, {tom.neubert, jana.dittmann}@iti.cs.uni-magdeburg.de
Keywords: Face Morph, Morphing Attack, Automatic Face Recognition, Morph Detection, Digital Image Forensics.
Abstract: This paper introduces an approach to automatic generation of visually faultless facial morphs along with a
proposal on how such morphs can be automatically detected. It is endeavored that the created morphs
cannot be recognized as such with the naked eye and a reference automatic face recognition (AFR) system
produces high similarity scores while matching a morph against faces of persons who participated in
morphing. Automatic generation of morphs allows for creating abundant experimental data, which is
essential (i) for evaluating the performance of AFR systems to reject morphs and (ii) for training forensic
systems to detect morphs. Our first experiment shows that human performance to distinguish between
morphed and genuine face images is close to random guessing. In our second experiment, the reference
AFR system has verified 11.78% of morphs against any of genuine images at the decision threshold of 1%
false acceptance rate. These results indicate that facial morphing is a serious threat to access control systems
aided by AFR and establish the need for morph detection approaches. Our third experiment shows that the
distribution of Benford features extracted from quantized DCT coefficients of JPEG-compressed morphs is
substantially different from that of genuine images enabling the automatic detection of morphs.
1 INTRODUCTION
Face as a biometric modality is a widely accepted
means of personal identity verification. For many
years, a printed facial image has been an important
part of identification documents. Recently, printed
face images have been supplemented by digital face
images stored on a chip integrated in the document.
On the one hand, issuing machine-readable
documents with digital photographs opens up new
horizons for applying Automatic Face Recognition
(AFR) systems to identity verification which saves
expensive manpower. On the other hand, the risk of
criminal intent to overcome AFR systems arises.
One of the possible attacks is brought to the
forefront by Ferrara et al. (Ferrara, 2014). This so-
called morphing attack is based on blending digital
face images of a criminal and his accomplice
resulting in a morphed face image (morph), which is
visually similar to both faces: the accomplice’s face
and the criminal’s face. As a result, two persons can
share one document.
In order to confirm the severity of this attack,
Ferrara et al. (Ferrara, 2016) evaluated the human
performance to match faces in original and morphed
images as well as the performance of three
commercial AFR systems to reject morphs. The
conclusions raise a major concern because, in many
cases, testees said that genuine and morphed face
images depict the same person and the experts were
not better in performing this task than laymen. Even
worse results came from AFR systems. The Morph
Acceptance Rate (MAR) at the decision thresholds
of 1% and 0.1% False Acceptance Rate (FAR) is
confirmed to be very high, indicating that the tested
systems are not able to distinguish between morphed
and genuine face images.
All in all, the systematic analysis of the
morphing attack has to be performed including the
study on morphing generation approaches as well as
the development of approaches to automatic morph
detection.
The morphs in (Ferrara, 2016) include a manual
retouch, which makes morph generation very time
consuming. There have only been 80 morphs
generated resulting in 160 morph verification
attempts for computing MAR. To the best of our
knowledge, there are currently no large publicly
available datasets of facial morphs. Therefore, we
propose an algorithm for automatic generation of
morphs enabling fast creation of thousands of
Makrushin A., Neubert T. and Dittmann J.
Automatic Generation and Detection of Visually Faultless Facial Morphs.
DOI: 10.5220/0006131100390050
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 39-50
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
39

realistic morphs. Possessing a large database of
multifarious morphs allows (i) for statistically
significant estimation of MAR, thus establishing the
resistance of AFR systems against the morphing
attack and (ii) for training and evaluation of forensic
morph detection algorithms.
For our experiments, we generated 3940 halfway
facial morphs from the Utrecht ECVP face dataset
(http://pics.psych.stir.ac.uk/2D_face_sets.htm) and
500 morphs from FEI Face Database (http://fei.edu.
br/~cet/facedatabase.html).
The visual quality of our morphs is proven in the
experiment on human perception of morphs. In
contrast to (Ferrara, 2016), in our experiment, a
testee decides for each single image whether it is a
morph or not. Human failure to reveal a morph
indicates its visual faultlessness. The MAR of
humans is 44.60% while the False Rejection Rate
(FRR) is 43.64%.
Next, we tested our morphs with the Luxand
Face SDK 6.1 (https://www.luxand.com/facesdk/)
which is taken as a reference COTS AFR system. At
the thresholds of 1% and 0.1% FAR, the MAR
yields 60.59% and 53.77% correspondingly.
Nonetheless, only 11.78% of morphs have been
verified against any of genuine images at 1% FAR
and 3.21% of morphs at 0.1% FAR.
The poor performance of AFR systems to reject
morphs motivates us to work on automatic morph
detection. Our detector is based on Benford features
calculated from quantized Discrete Cosine
Transformation (DCT) coefficients of JPEG-
compressed images. Classification of feature vectors
is performed using a linear Support Vector Machine
(SVM). We state and experimentally show that the
distributions of Benford features are substantially
different for morphed and genuine images. The
MAR of our morph detector does not exceed 13%.
Our contributions can be summarized as follows:
we introduce a splicing-based approach to
automatic generation of visually faultless facial
morphs (Section 4.1) and evaluate the quality of
the morphs experimentally in a human test
(Section 5.4) and with a COTS AFR system
(Section 5.5);
we introduce an automatic morph detection
approach based on Benford features and linear
SVM classifier (Section 4.2) and evaluate its
classification performance (Section 5.6).
Hereafter, the paper is organized as follows.
Related work is summarized in Section 2 including
recent advances in automation of facial morphing
and standard approaches of digital image forensics.
Section 3 encompasses the theoretical background of
facial morphing and tampering detection based on
JPEG compression artifacts. In Section 4, our
approaches to automatic morph generation and
detection are introduced. Our experiments are
presented in Section 5. Section 6 concludes the
paper with the results and future work.
2 RELATED WORK
2.1 Facial Morphing
Morphing or “Metamorphosis” is a well-studied
topic in computer graphics. A brief survey on
morphing approaches is given in (Wolberg, 1998).
Generally, morphing can be seen as a combination
of image warping and a cross-dissolve of image
elements. Wolberg in (Wolberg, 1990) summarizes
the fundamentals of image warping focusing on the
mesh warping technique. The most frequently
referenced morphing technique is, however, feature-
based warping introduced in (Beier, 1992). The
authors suggest locating pairs of corresponding line
segments and designing the mapping function for
each point based on the distance to each line. Further
techniques suggest locating pairs of corresponding
key points and applying the same mapping functions
to local neighborhoods around these points (Arad,
1994; Lee, 1996).
Early morphing approaches, mostly applied in
the film industry as a computer animation tool, have
always required human assistance to specify image
features. Modern morphing approaches evolve
towards automatic establishing of structural
similarity between objects in source and target
images (Liao, 2014).
A human face seems to be a favorite object for
morphing, because it is very intuitive and impressive
to visualize aging or a metamorphosis of one human
to another.
Blanz and Vetter (Blanz, 1999) introduce a
technique for face and face pose morphing
comprised of fitting the morphable 3D model to a
2D face image and modifying the resulting
individual 3D face towards another individual or
another pose exploiting principal component
analysis. However, this approach requires manual
assistance to obtain an accurate alignment between
the morphable model and a face in the image.
The efforts towards automatic generation of
facial morphs start with locating facial features in a
fully automated way. Cootes et al. (Cootes, 2000)
propose the concept of Active Shape Models to
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
40

locate key points using local template matching
employing constraints of the shape models. This
concept is effectively used to locate facial landmarks
and to modify face appearance easily, representing
another way of face morphing. ASM is applied in
(Zanella, 2009) to face images in a frontal view to
perform morphing automatically. A comprehensive
survey on locating facial landmarks is presented in
(Celiktutan, 2013).
In spite of recent advances in facial morphing,
the automatic generation of visually faultless facial
morphs is still a very challenging task. The diversity
of facial images including different poses, skin
colors, hair styles and illumination conditions
drastically influences the appearance of automati-
cally generated morphs making them look less
realistic. One way to visually improve morphs is
retouching photographs to remove unrealistic hair
and spurious shadows caused by cross-dissolving of
images. An automatic interpolation of hair for
portrait morphing is addressed in (Weng, 2013).
Another way to achieve a realistic appearance is to
cut facial regions, warp them, blend them to a
mutual face, and seamlessly stitch it back into one of
the input images. We refer to the result of this
strategy as a splicing morph. A splicing morph is
taken as an opposite of a complete morph that could
be seen as a result of warping and blending of
complete facial images including hair, torso and
background. We focus on generation of the former,
because the visual inaccuracies created by splicing
are easier to conceal. A relatively simple and
straight-forward way to achieve seamless stitching
during generation of splicing morphs is automatic
selection of similar input images as suggested in
(Bitouk, 2008) for swapping faces or in (Vyas,
2015) for morphing.
2.2 Detection of Face Morphs
Since facial morphing can be seen as a special case
of tampering with image content, well-established
approaches to tampering detection from the field of
digital image forensics can be adopted. Indeed, a
morphing process along with a subsequent retouch,
on the one hand, creates specific artifacts in the
image and, on the other hand, destroys a camera-
specific fingerprint. Standard techniques of digital
image forensics are summarized in (Farid, 2009).
Notice that different morphing approaches create
different inconsistencies. For instance, the afore-
mentioned splicing morphs represent a special case
of image insertion or image splicing also referred to
as a cut-and-paste attack (Piva, 2013).
In (Schetinger, 2016) the “indirect arms race”
between image tampering and image forensics is
discussed. The authors assign image morphing to the
group “Image Enhancement/Tweaking” and state:
“Even though image insertion and manipulation can
create visually convincing results, they should not
pose a problem for modern forensic techniques.”
Dealing with morphed images created by an
attacker, a forensic expert is limited to so-called
“blind” approaches, implying that no other
information except for the probe image is presented
for analysis. The most complete bibliography on
blind tampering detection is gathered in (Mahdian,
2010). Image splicing detection is a substantial part
in this review.
There are three basic clues to detect splicing
independently from the image content. These are:
noise distribution (Lyu, 2014), demosaicing
inconsistencies (Dirik, 2009; Ferrara, 2012) and
compression artifacts (Lukas, 2003; Bianchi, 2012;
Milani, 2014).
Camera Noise is also referred to as Photo
Response Non-Uniformity (PRNU) of the camera
sensor and considered to be unique for each camera
(Fridrich, 2009). However, splicing detection from
PRNU is traditionally performed in the presence of
camera reference images. An alternative approach to
exposing spliced regions by means of noise
estimation is presented in (Lyu, 2014).
Demosaicing, also referred to as Color Filter
Array (CFA) interpolation, arises in color images
because standard sensors capture only a single color
value at each pixel location and the missing colors
are interpolated from the adjacent pixels. Tampering
detection (Dirik, 2009) as well as fine-grained
splicing detection (Ferrara, 2012) by analyzing
demosaicing inconsistencies has been proven an
effective technique so long as fragile CFA traces
have not been destroyed by legitimate image editing.
It is mentioned in (Schetinger, 2016) that even a
simple median or Gaussian filter is able to remove
CFA traces. Nonetheless, CFA analysis is effective
to distinguish native and non-native images, and
therefore can be applied to detection of splicing
morphs generated from raw images. Image
morphing detection by analyzing CFA traces is
addressed in (Ghatol, 2013).
Compression Artifacts arise in images after lossy
compression performed by a camera or by a
photographer after editing a raw image. After
tampering with image content, images are often re-
compressed. The vast majority of tampering
detection approaches deal with JPEG as the most
common compression standard. In order to detect
Automatic Generation and Detection of Visually Faultless Facial Morphs
41

double JPEG compression, most of the algorithms
rely on the analysis of the histogram of DCT
coefficients (Piva, 2013). A recent study utilizing
this idea (Bianchi, 2012) performs block-grained
localization of tampered regions in the presence of
aligned and non-aligned double JPEG compression.
Milani et al. (Milani, 2014) advocate the idea of
using first digit features also referred to as Benford
features to identify a level of compression.
Analysis of JPEG compression inconsistency is
especially promising for detection of splicing
morphs. Since the original images used for morph
generation are often JPEG-compressed, a morphed
image contains the original background blocks with
compression artifacts and synthetic face blocks with
destroyed compression artifacts due to interpolation
and cross-dissolve. Hence, the compressed splicing
morphs should contain blocks with different levels
of compression.
In (Schetinger, 2016), CFA and double JPEG
compression artifacts are asserted to be plausible
traces for morphing detection and noise to be an
identifiable trace.
The most recent effort to withstand the attack
from (Ferrara, 2014) is reported in (Ramachandra,
2016) introducing a morph detection approach based
on binarized statistical image features used in
conjunction with a linear SVM.
3 GENERAL DEFINITIONS OF
MORPHING AND BENFORD
FEATURES
3.1 Facial Morphing
Morphing is defined as a process of fluid transfor-
mation of one digital image (source) into another
(target). Generation of intermediate images is
realized by image warping supplemented by color
interpolation. Warping is a geometric transformation
applied to one or both images aiming at alignment
between important image features. We rely on the
mesh warping technique setting mesh elements to
triangles. Color interpolation can be understood as
alpha-blending of intensity values of both images for
each color layer separately. The parameter alpha
defines the proportion of pixel intensity values
obtained from source and target images.
In the case of facial morphing, the features are
defined by key points depicting eyes, nose, mouth
and face contour. The warping functions are defined
for the triangles built by the triplets of the key
points. Mapping of triangles is known to be the
standard affine transformation whose coefficients
can be easily and efficiently found. Any kind of
triangulation is theoretically possible. Practically, it
is shown that Delaunay triangulation yields
convincing results (Wu, 2011). We further use the
term facial landmarks to refer to the key points.
There are two ways to warp images: forward and
reverse mapping. Forward mapping starts with a
pixel within the source image and transfers it into
the corresponding location in the destination image.
Reverse mapping starts with a pixel within the
destination image and looks for its color in the
source image at the corresponding location. Forward
mapping might lead to unpainted pixels in the
destination image. Contrary to this, reverse mapping
ensures that every pixel in the destination image
obtains a value.
For the source (
I
s
) and target (I
t
) input face
images, the procedure of generation of intermediate
frames
I
α
can be formally described as follows:
1. define α from the interval [0,1]
2. find facial landmarks L
s
= {l
s
j
,
j=1..n} and L
t
= {l
t
j
, j=1..n}
3. create blended landmarks L
m
= {l
m
j
:
l
m
j
= (1-α)·l
s
j
+ α·l
t
j
, j=1..n}
4. create set of triangles T = {t
i
:
t
i
=(a,b,c), a,b,c L
m
, i=1..k}
5. initialize warped images I
sw
and I
tw
6. for each t
i
I
i
denotes the set of pixels in I
enclosed in the triangle t
i
(e.g.
I
s
i
, I
t
i
, I
sw
i
and I
tw
i
)
6.1 create mapping functions:
f
s
i
:
+2
→
+2
and f
t
i
:
+2
→
+2
6.2 apply these:
I
sw
i
= f
s
i
(I
s
i
) and I
tw
i
= f
t
i
(I
t
i
)
7. I
sw
= {I
sw
i
, i=1..k} and I
tw
= {I
tw
i
,
i=1..k}
8. I
α
= (1-α)·I
sw
+ α·I
tw
where n is the number of landmarks and k is the
number of triangles.
3.2 Morph Detection by Analyzing
JPEG Compression Artifacts
Facing the diversity of morphing techniques, the
creation of a general morph detection algorithm is
extremely challenging. Quite to the contrary, the
algorithms for detection of particular types of facial
morphs can be developed with far less effort.
However, detection of morphs requires the thorough
understanding of the morph generation process and
possible image artifacts resulting from it.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
42

We believe that splicing morphs can be efficiently
detected by analyzing JPEG compression artifacts.
Our hypothesis is that a morphed image contains
blocks from the original image that have already
undergone a JPEG compression as well as synthetic
blocks generated by the morphing process. These
blocks are uncompressed. If the morphed image
undergoes JPEG compression, the original blocks
become double-compressed and the synthetic blocks
are single-compressed.
In order to comprehend the features that we use
for morph detection, let us look at the process of
JPEG compression which is comprised of three basic
steps: DCT, quantization and entropy coding.
Firstly, the color space of an image is
transformed from RGB to YCbCr. Notice that the
color levels are processed independently. Each layer
is divided into non-overlapping blocks of 8x8 pixels
and the DCT is applied to these blocks resulting in
64 DCT coefficients. Each coefficient represents the
contribution (amplitude) of a certain cosine function
to the linear combination of cosine functions
oscillating at different frequencies. This linear
combination represents the original signal. In other
words, the DCT coefficients give us an idea which
frequencies reside in an image.
Secondly, the DCT coefficients are quantized
according to a quantization table. The table, which is
not specified by the standard, describes the
correspondence between compression levels and
quantization factors. Formally, the quantized value
is calculated from the original one by dividing it by
a quantization factor and rounding to the nearest
integer. Quantization is an irreversible transforma-
tion leading to lossy data compression.
Thirdly, the quantized DCT coefficients are
coded without loss of information applying Huffman
coding.
Application of Benford features (first digits of
the quantized DCT coefficients) is suggested in (Fu,
2007; Milani, 2014) for tampering detection in
JPEG-compressed images. The hypothesis behind
applying Benford features is that the naturally
generated data follow Benford’s law and the
manipulated data violates it.
Benford’s law states that the distribution of the
first digits in a set of natural numbers is logarithmic.
A set of numbers satisfies the generalized Benford
law if the first digit x (x=1,2,…,9) occurs with a
probability p(x):
10
1
() log 1px n
x
(1)
where n is the normalization factor and α, β are the
parameters specifying the distribution.
Fu et al. (Fu, 2007) show that the quantized DCT
coefficients of single-compressed JPEG images
follow the generalized Benford law while the
quantized DCT coefficients of double-compressed
JPEG images violate it, which is reflected in the fact
that the distribution of Benford features deviates
from the logarithmic distribution.
Moreover, it is shown in (Milani, 2014) that the
distribution of Benford features is specific for
further levels of JPEG compression making the
features a powerful instrument for revealing the
image compression history.
Let Y
i
denote the i-th quantized DCT coefficient,
and N the number of DCT coefficients, then the first
digits fd are computed as follows:
NiYfd
i
Y
ii
...,2,1,10
10
log
(2)
and the Benford features as follows:
9...,2,1,
0
1
,
1
1
j
jfd
jfd
N
Benf
i
i
i
N
i
ij
(3)
4 OUR APPROACH TO
GENERATION AND
DETECTION OF MORPHS
4.1 Automatic Generation of Morphs
Our approach to automatic generation of face
morphs follows the general morphing procedure
described in Section 3.1. Aiming at creating a morph
appearing similar to both persons, we generate only
halfway morphs (α=0.5) where both images
contribute equally. Hence, alpha-blending is nothing
else but averaging. The mapping of triangles is done
in the reverse way making use of bilinear
interpolation. The discontinuities between triangles
are concealed applying the 2x2 median filter.
There are 68 facial landmarks localized using the
class
shape_predictor from the dlib program-
ming library (http://dlib.net/). Three landmarks
depicting the lower contour of the upper lip are
replaced by two landmarks at the lower lip. This
adjustment is important because ID photographs
require a closed mouth. Given that, the lower
contour of the upper lip might overlap with the
upper contour of the lower lip causing the triangles
with collinear corners that are inappropriate for
warping. Moreover, the set of landmarks is extended
by two landmarks at the pupils and seven landmarks
at the forehead (see Figure 1a).
Automatic Generation and Detection of Visually Faultless Facial Morphs
43

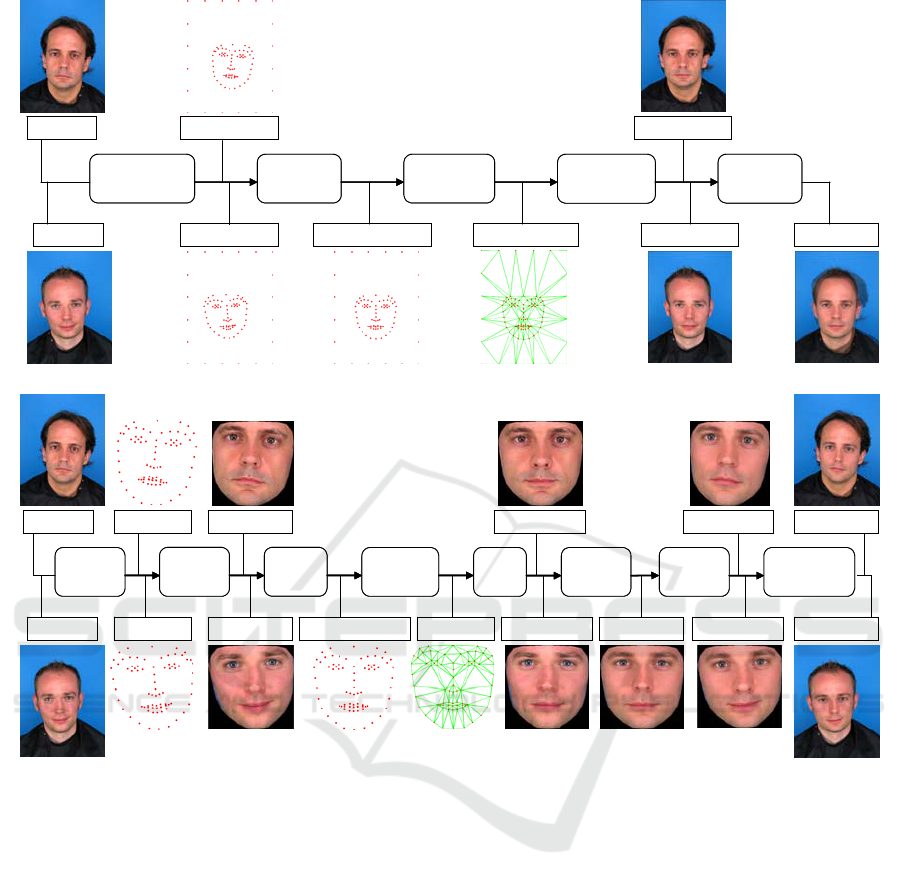
(a) (b)
Figure 1: (a) Facial landmarks localized by dlib (green,
blue), removed landmarks (blue) and our additional
landmarks (red); (b) mask to apply smoothing filter.
Figure 2a depicts the generation of complete
morphs. The workflow starts with extraction of
facial landmarks which are extended by 20
landmarks on the image borders. Then the landmark
coordinates are averaged. The blended landmarks
are used for triangulation. The triangles from the
first input image are warped to the average position
resulting in the first warped image. Likewise, the
second warped image is generated from the second
input image. Finally, the warped images are
averaged. Hence, a complete morph has mutual face
geometry and texture. However, spurious shadows
and strong visual inconsistencies in the hair region
resulting from blending are the visual flaws that can
hardly be concealed automatically. Therefore, we
consider complete morphs to be inappropriate for the
morphing attack, unless they have undergone a
manual retouch.
Splicing Morphs are designed to overcome the
visual flaws encountered in complete morphs. Figure
2b visualizes the morph generation process. After
extracting facial landmarks, the convex hull
representing a face is cut from the input images. The
landmark coordinates are averaged and the blended
landmarks are used for triangulation. The triangles
from the first face are warped to the average position
resulting in the first warped face. The same is done
to obtain the second warped face. The warped faces
are averaged in the frontal position similar to how is
suggested in (Lee, 1998). This scheme allows for
morphing three and more faces. The blended frontal
face is warped back twice, namely to the face
positions in the first and in the second input images.
The result is two morphed faces. The final step is the
splicing of the morphed faces into the corresponding
original images. In order to make the transmission
between the original and blended regions appear
natural, all pixels in the mask in Figure 1b are
smoothed by applying a Gaussian filter. The width
of the mask and the parameters of the Gaussian filter
are defined as relative values in accordance with the
interpupillary distance.
The advantage of the proposed splicing approach
is that a morph looks realistic because the seams of
the blended region match the original face contour.
The disadvantage is that, after inverse warping, the
blended face has the same geometry as the face it is
warped into. Therefore, the morph has a mutual
texture, but the geometry is adopted from one of the
input faces. Consequently, the splicing morphs are
expected to match well with one subject. In order to
match with another subject, both faces should have a
similar geometry.
For perfectly frontal faces, inverse warping can
be replaced by scaling and the blended face can be
directly inserted into the one or other image. In this
case, the blended face has an average geometry and
an average texture, but the average geometry may
differ from the original face geometry making
seamless splicing extremely difficult.
Further factors impeding morphs from appearing
realistic are different skin color and occlusion of
face parts by hair e.g. abundant hair at the forehead
region in input images. A straight-forward approach
to control the quality of morphs is an automatic
selection of input face images in regard to skin and
hair. Analyzing and mitigating these factors will be a
part of our future work.
The morph generation algorithm is implemented
in Matlab.
4.2 Automatic Detection of Morphs
Based on the nine Benford features described in
Section 3.2, we train the linear SVM classifier from
two sets of images. The first one is comprised of
splicing morphs and the second one encompasses
original images as well as images after legitimate
editing usually performed by photographers. This
includes in-plane rotation, scaling and cropping.
Notice that, after in-plane rotation, images are
always cropped to get rid of blank corners.
The parameters for image editing operations are
randomly chosen from the following ranges:
cropping: from 60 to 80 pixels at every side (left,
right, top, bottom);
scaling factor: from 0.8 to 1.2;
rotation angle: from -3° to 3°.
The set of “positive” samples contains 524
morphs that have been randomly selected from the
whole set of 2614 splicing morphs. The set of
“negative” samples contains 131 original, 131
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
44
Blended Keypoints
Triangulation
Blend
geometry
Warping
Warped Image2
Cross
dissolve
Image2
Extract
landmarks
Keypoints2
Image1
Keypoints1
Triangles
Final Morph
Warped Image1
Blended Keypoints
Triangulation
Blend
geometry
Warping
Warped Image2
Cross
dissolve
Image2
Extract
landmarks
Keypoints2
Image1
Keypoints1
Triangles
Final Morph
Warped Image1
(a)
Image2
Extract
landmarks
Warping
Blended Face
Cross
dissolve
Face2
Keypoints2
Triangulation
Insert blended
face into image
Cut convex
hull
Triangles
Image1 Face1 Final Morph1
Blend
geometry
Keypoints1
Blended Keypoints
Inverse
warping
Warped Face2 Morphed Face2 Final Morph2
Warped Face1 Morphed Face1
Image2
Extract
landmarks
Warping
Blended Face
Cross
dissolve
Face2
Keypoints2
Triangulation
Insert blended
face into image
Cut convex
hull
Triangles
Image1 Face1 Final Morph1
Blend
geometry
Keypoints1
Blended Keypoints
Inverse
warping
Warped Face2 Morphed Face2 Final Morph2
Warped Face1 Morphed Face1
(b)
Figure 2: The workflow for the automatic generation of (a) complete morphs and (b) splicing morphs.
scaled, 131 cropped, and 131 rotated and cropped
images, 524 samples in total. The equal number of
positive and negative samples designates a balanced
training set leading to the unbiased classifier. All
training images are decompressed and then
compressed in a JPEG format with 100% quality.
For each test sample, the classifier makes a decision
on which of two classes the sample belongs to.
Before classification, all test images undergo re-
compression similar to that which is done for
training images. Training of the linear SVM
classifier as well as classification of test samples is
carried out with WEKA data mining software 3.8.0
(Hall, 2009) using default parameterization.
5 EXPERIMENTS
5.1 Evaluation Goals
The evaluation addresses the morph generation and
morph detection approaches introduced in Sections
4.1 and 4.2 correspondingly. The quality of splicing
morphs generated by the former is tested in two
experiments on how well humans can recognize
morphs as such (Exp1) and how many morphs
would be accepted by a COTS AFR (Exp2). The
classification performance of the latter is evaluated
in the experiment (Exp3) with complete and splicing
morphs from the Utrecht ECVP face dataset as well
as with the original images and splicing morphs
from the FEI Face Database.
Automatic Generation and Detection of Visually Faultless Facial Morphs
45

5.2 Evaluation Dataset
The morphing attack is usually performed on ID
photographs that are compliant with the ISO/IEC
19794-5 standard (ISO, 2011). In other words, a face
pose in a photograph is frontal with the face parts
located at particular regions. Facial expression is
neutral and occlusions of eyes, nose or mouth do not
occur. The interpupillary distance exceeds 120
pixels. Lighting is equally distributed on a face.
From among the publicly available face datasets,
we have selected Utrecht ECVP face dataset as the
one that best fits the ISO/IEC 19794-5 standard. It
contains 131 images of 67 different individuals (20
women, 47 men). The image resolution yields
900x1200 pixels with the average interpupillary
distance of 200 pixels. The majority of individuals
are shot with neutral and smiling facial expressions.
Morphs are generated from all possible image
pairs of 52 individuals (17 women, 35 men) utilizing
only the images with neutral expressions. For each
pair of images one complete morph and two splicing
morphs are possible. Hence, 1326 complete morphs
and 2614 splicing morphs were generated. Our
algorithm failed to generate the remaining 38
splicing morphs because some triangles had
collinear corners disabling warping. Finally, we
manually selected 183 visually pleasing splicing
morphs for evaluating human ability to distinguish
between morphs and genuine images.
5.3 Performance Measures
In order to obtain uniform performance measures in
all our experiments, we extend the standard
performance measures of biometric systems
expressed in terms of FAR/FRR by the MAR, which
is used, on the one hand, for evaluation of AFR
performance to reject morphs and, on the other hand,
for humans and our morph detector to designate the
relative number of morphs falsely classified as
genuine images.
Assuming the matching score of an AFR system
expresses the similarity between a probe and a
gallery sample, the FAR is estimated by the relative
number of impostor attempts with matching scores
exceeding or equal to a decision threshold, while the
FRR is estimated by the relative number of genuine
attempts with matching scores lower than the
threshold. Similarly, we estimate the MAR of an
AFR system by the relative number of morph
attempts with matching scores exceeding or equal to
the threshold. Since a morph attempt is a special
case of an impostor attempt, the MAR can be seen as
a substitute for the FAR and the performance of an
AFR system to reject morphs is expressed by the
combination of MAR and FRR.
For biometric systems FAR and FRR are not
equally important because the FAR is considered the
security measure and the FRR the convenience
measure. Therefore, the decision threshold is usually
defined so that the FAR does not exceed a certain
value and the FRR is then calculated at this
threshold. Typical values for the FAR are 1% and
0.1%. It is common to denote the FRR at the
decision threshold of 1% FAR as FRR
100
and at the
decision threshold of 0.1% FAR as FRR
1000
.
Following the same logic, MAR
100
and MAR
1000
are
defined in (Ferrara, 2016).
The estimated MAR values give a pessimistic
impression of the success of a morphing attack.
Indeed, if a face image of person A is only slightly
modified toward person B, an AFR system would
still verify the morphed image against images of
person A and would fail to verify the morphed
image against images of person B. The MAR with
such morphs would yield 50% implying that 50% of
morph attempts have been falsely accepted. In
reality, these morphs are useless because person B
cannot use them to deceive an AFR system.
We propose to count the number of successful
morphs instead of accepted morph attempts. A
morph is successful if it has been verified against all
gallery images of both persons. We call this
performance measure the realistic MAR (rMAR).
For morph detection, no matter whether it is
performed by humans or by an automated morph
detection system, the "positive" decision is that an
image is a morph and the "negative" decision is that
an image is genuine. The MAR is, therefore, equal
to the False Negative Rate (FNR) because a morph
falsely accepted by an AFR system means a morph
falsely missed by a morph detection system. The
FRR is equal to the False Positive Rate (FPR),
because a genuine image falsely rejected (as a
morph) by an AFR system means a false alarm of a
morph detection system. FNR and FPR completely
describe detection performance. We also report the
classification accuracy as the relative number of
correct decisions in the total number of decisions.
Since, for morph detection systems, each morph is
associated with exactly one morphing attempt, the
MAR equals the rMAR.
5.4 Evaluation of Morphs by Humans
The first experiment (Exp1) on the human capability
to distinguish between morphs and genuine images
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
46
has two goals:
evaluating the visual quality of our splicing
morphs;
obtaining clues on how humans recognize
anomalies in portrait images to utilize this
knowledge for developing algorithms for
automatic morph detection.
For the experiment, we take 23 out of 183 pre-
selected splicing morphs and 7 out of 15 genuine
face images that have not been used for creating
morphs. In total, there are 30 images in the test. The
images are printed with standard photo quality on
photo paper having the passport dimensions of
35x45 mm. Morphs and genuine photographs are
mixed and presented sequentially to 42 participants
under “thinking aloud test” conditions. Testees were
asked to say whatever they think about the images
and what pushes them to make one or another
decision while performing morph detection.
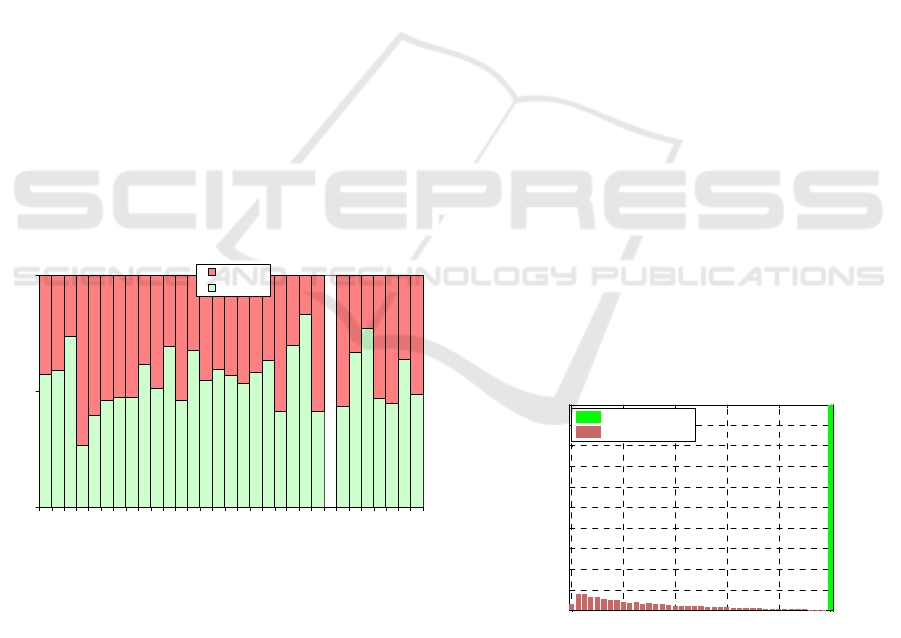
The results are visualized in Figure 3. The
classification accuracy of humans yields 55.62%
with the MAR of 44.6% and the FRR of 43.64%. As
can be seen in the diagram, 8 out of 23 morphs have
been falsely recognized as genuine images by 50 and
more percent of testees and only 3 morphs have been
correctly detected by 70 and more percent of testees.
Even worse is the situation with genuine images, 4
out of 7 genuine images have been falsely detected
as morphs by 50 and more percent of testees.
57,50%
58,97%
73,68%
26,83%
40,00%
46,15%
47,22%
47,62%
61,54%
51,22%
69,23%
46,15%
67,50%
54,76%
59,46%
57,14%
53,66%
57,89%
63,41%
41,46%
70,00%
82,93%
41,46%
43,59%
66,67%
77,50%
47,06%
45,00%
64,10%
48,78%
42,50%
41,03%
26,32%
73,17%
60,00%
53,85%
52,78%
52,38%
38,46%
48,78%
30,77%
53,85%
32,50%
45,24%
40,54%
42,86%
46,34%
42,11%
36,59%
58,54%
30,00%
17,07%
58,54%
56,41%
33,33%
22,50%
52,94%
55,00%
35,90%
51,22%
0% 50% 100%
M1
M2
M3
M4
M5
M6
M7
M8
M9
M10
M11
M12
M13
M14
M15
M16
M17
M18
M19
M20
M21
M22
M23
G1
G2
G3
G4
G5
G6
G7
False
Correct
Figure 3: Results of the experiment on human capability to
distinguish morphs (M1-23) from genuine images (G1-7).
Evaluating the morph detection performance of the
testees separately, we see that the performance
strongly fluctuates from one person to another. Only
9 out of 42 testees have correctly classified more
than two thirds of test images. Six of them have
mentioned blurring in the face region as a clue for
indicating morphs and five of them also pointed to
slight color differences in the face and the forehead
regions.
All in all, this detection performance can be
considered as close to random guessing enabling us
to conclude that humans are not able to distinguish
between splicing morphs and genuine images. This
justifies the visual faultlessness of our automatically
generated splicing morphs.
5.5 Evaluation of Morphs with the
Reference AFR System
The second experiment (Exp2) aims at testing how
many of our splicing morphs can deceive a COTS
AFR system. Matching of face images is done with
the Luxand FaceSDK 6.1 later referred to as “the
matcher”. The matcher produces similarity scores in
the interval [0,1]. Based on the internal experiments,
the SDK provides decision thresholds to obtain a
given level of the FAR. The thresholds, at which the
FAR yields 1% and 0.1%, are 0.99 and 0.999
correspondingly.
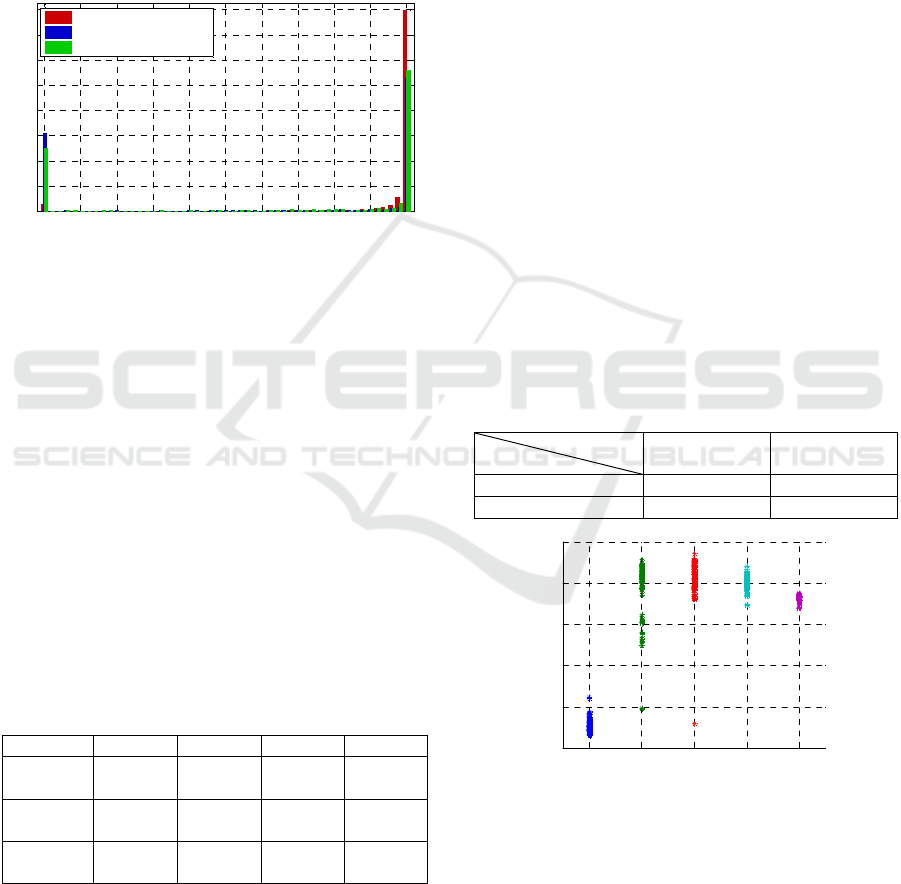
First, the matcher is evaluated with the complete
Utrecht ECVP face dataset to get an idea about the
distributions of genuine and impostor matching
scores. 69 genuine scores result from the comparison
of neutral and smiling faces (or two neutral faces) of
the same person. 8446 impostor scores result from
the pair-wise comparison of all images of different
persons in the database. The distributions of genuine
and impostor scores are depicted in Figure 4. All
genuine scores are located in the interval [0.999, 1].
The mean value of the impostor scores yields 0.2645
while the maximum impostor score is 0.9751. In
other words, the matcher shows the perfect result
making no mistakes at both thresholds 0.99 and
0.999.
0 0.2 0.4 0.6 0.8 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Matching score
Density
Genuine Scores
Impostor Scores
Figure 4: Distributions of genuine and impostor matching
scores resulting from the cross-matching of original
images in the Utrecht ECVP face dataset using the Luxand
FaceSDK 6.1.
Second, 1326 complete and 2614 splicing morphs
are matched against all images of the persons who
participated in these particular morphs. Normally,
Automatic Generation and Detection of Visually Faultless Facial Morphs
47
there are four morph attempts for each morphed
image: two images with neutral faces (source images
for morph generation) and two images with smiling
faces. Notice that some persons do not have a
smiling photograph and some persons have more
than one neutral photograph. The distributions of
matching scores for complete, splicing and manually
selected splicing morphs are depicted in Figure 5.
The corresponding values of MAR and rMAR are
given in Table 1.
0.95 0.955 0.96 0.965 0.97 0.975 0.98 0.985 0.99 0.995 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Matching score
Density
Complete morphs
Splicing morphs
Selected splicing morphs
Figure 5: Distributions of matching scores resulting from
matching of morphs against original images; the histogram
bin yields 0.001; the left-most column shows the relative
number of matching scores in the interval [0, 0.9501).
Despite their visual imperfection, most of the
complete morphs are able to deceive the matcher.
83.27% of complete morph attempts are accepted at
0.1% FAR and 55.20% are verified against any of
the genuine images in the test at the same threshold.
The scores with splicing morphs are substantially
lower. Only 53.77% of splicing morph attempts are
accepted at 0.1% FAR and only 3.21% are verified
against any of the genuine images. These 84 out of
2614 morphs (3.21%) can be considered perfect,
having the characteristic that these would neither be
detected by humans nor rejected by the reference
AFR system.
Table 1: Pessimistic and realistic MAR at the decision
thresholds of 1% and 0.1% of FAR.
MAR
100
MAR
1000
rMAR
100
rMAR
1000
Complete
morphs
93.34% 83.27% 80.39% 55.20%
Splicing
morphs
60.59% 53.77% 11.78% 3.21%
Selected
spl.morphs
65.43% 57.30% 16.94% 5.46%
In order to check whether the visually pleasing
splicing morphs can better deceive the reference
AFR, we have selected 183 out of 2614 and
calculated MAR
100
and MAR
1000
for them. As can be
seen in Table 1, the MAR values become slightly
higher (see also Figure 5) but the difference in MAR
values is still too low to assert that the realistic
appearance of the face in a morphed image
correlates with the performance of AFR to reject
morphs.
5.6 Evaluation of Our Morph Detector
In the third experiment (Exp3), the performance of
our morph detector is evaluated in two tests. In the
first one, the 10-fold cross-validation is performed
on the training dataset. In the second one, the morph
detector is tested with four test datasets (T):
T
1
: the remaining 2090 splicing morphs from the
Utrecht ECVP face dataset;
T
2
: 1326 complete morphs from the Utrecht
ECVP face dataset;
T
3
: 400 original images from the FEI Face
Database;
T
4
: 500 splicing morphs from the FEI Face
Database.
The confusion matrix of the first test is depicted
in Table 2. The classification accuracy yields
98.09% (1028/1048). Only 20 genuine images have
been misclassified as morphs and none of the
morphs has been misclassified as a genuine image.
Table 2: Confusion matrix of the 10-fold cross-validation
of our morph detector.
Classified as
Ground truth
Genuine Splicing
morphs
Genuine
504 (96.18%)
20 (3.82%)
Splicing morphs 0
524 (100%)
original cropped rotated scaled morphs
0.1
0
.15
0.2
0
.25
0.3
0
.35
Figure 6: Distribution of samples for the feature Benf
1
.
This result signifies that original and legitimately
edited images have substantially different feature
distribution compared to that of splicing morphs
which is shown in the example of feature Benf
1
in
Figure 6. The distribution of the feature values for
splicing morphs is narrow with a small variation.
The distributions of original and legitimately edited
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
48

images are broader with means significantly
different from that of splicing morphs. Based on this
diagram, we assert that the utilized features are not
suitable to differentiate between the types of
legitimate image editing but are highly suitable for
distinguishing between splicing morphs and
remaining images.
The results of the second test are depicted in
Table 3. The MAR values of morphs created from
Utrecht ECVP face dataset (T
1
and T
2
) yield 12.11%
for splicing morphs and 12.97% for complete
morphs, indicating superior morph detection
performance regarding humans. The classification
accuracy of 98.44% (886/900) in the test with the
FEI Face Database (T
3
+T
4
) indicates that the
proposed classifier is capable of correctly classifying
test images that are significantly different from
images used for training.
Table 3: Classification results with four test datasets.
Classified as
Ground truth
Genuine Morph
T
1
(morph) 253 (12.11%)
1837 (87.89%)
T
2
(morph) 172 (12.97%)
1154 (87.03%)
T
3
(genuine)
386 (96.50%)
14 (3.50%)
T
4
(morph) 0
500 (100%)
Nevertheless, the conducted test does not enable us
to make conclusions about the general suitability of
our proposed classifier. We realize that the
distribution of Benford features can be different if
morphs are generated from random face images
using morphing techniques which are different from
image warping with a subsequent cross-dissolve.
Moreover, it is possible to create face images with
the similar distributions of Benford features using
legitimate image processing techniques. For
instance, it is shown in (Wang, 2011) that the
application of Benford's law to image tampering
detection is vulnerable to the histogram
manipulation attack.
6 CONCLUSIONS
In this paper, we have proposed (i) the approach to
automatic generation of visually faultless facial
morphs, (ii) the approach to morph detection by
utilizing Benford features calculated from quantized
DCT coefficients of JPEG-compressed images and
(iii) evaluated both in three experiments.
The visual faultlessness of our splicing morphs is
confirmed in the experiment with humans. The
MAR of humans yields 44.60% with the FRR of
43.64% which is close to random guessing (see
Exp1).
The suitability of our splicing morphs to deceive
an AFR system has been tested in Exp2. Considering
all verification attempts, the MAR
100
is 60.59% and
the MAR
1000
is 53.77%. 11.78% of morphs have
been verified against any of the genuine images at
1% FAR and 3.21% at 0.1% FAR.
Our morph detector yields 12.11% MAR with
splicing and 12.97% MAR with complete morphs
clearly outperforming humans. The classification
accuracy of 98.44% with the alternative face
database indicates that our morph detector is capable
of correctly classifing test images that are fairly
different from images used for training (see Exp3).
In our future work, we are going to visually
improve morphs that will achieve higher matching
scores with the reference AFR system. To this end,
we plan an automatic selection of facial images with
similar skin color, hair and head geometry along
with automatic image editing including re-coloring
and a hair retouch. We also plan engaging an
alternative AFR system to the morph generation
process for morph quality control by straight-away
matching of just generated morphs against genuine
images.
Our morph detector will be improved by
considering the local features derived from blocks
located at the face contour and in the face region.
Following clues from the “thinking aloud test”, the
local analysis of skin texture will be performed to
detect excessive blurriness in the face region and
color inconsistencies.
Due to the severity of the morphing attack and
the limited capability of AFR systems to reject
morphs, we believe that much attention should be
paid to adoption of tampering detection approaches
from digital image forensics to facial morphing,
potentially making automatic morphing detection an
indispensable component of AFR systems.
ACKNOWLEDGEMENTS
The work in this paper has been funded in part by
the German Federal Ministry of Education and
Science (BMBF) through the research programme
under the contract no. FKZ: 13KIS0509K.
REFERENCES
Arad, N., et al., 1994. Image Warping by Radial Basis
Functions: Applications to Facial Expressions. In
Automatic Generation and Detection of Visually Faultless Facial Morphs
49

CVGIP:Graph Models Image Proc.56(2), pp. 161-172.
Beier, T., Neely, S., 1992. Feature-based image
metamorphosis. In Comp. Graphics. 26(2), pp. 35-42.
Bianchi, T., Piva, A., 2012. Image Forgery Localization
via Block-Grained Analysis of JPEG Artifacts. In
IEEE Trans. on Information Forensics and Security
7(3), pp. 1003-1017.
Bitouk, D., et al., 2008. Face Swapping: Automatically
Replacing Faces in Photographs, In ACM Trans. on
Graphics 27(3), 39.
Blanz V., Vetter, T., 1999. A morphable model for the
synthesis of 3D faces. In Proc. Conf. on Computer
Graphics and Interactive Techniques, pp. 187-194.
Celiktutan, O., et al., B., 2013. A comparative study of
face landmarking techniques. In EURASIP Journal on
Image and Video Processing 2013 (1), 1.
Cootes, T.F., Taylor, C.J., 2000. Statistical Models of
Appearance for Computer Vision. Technical Report,
University of Manchester.
Dirik, A.E., Memon, N., 2009. Image tamper detection
based on demosaicing artifacts. In Proc. IEEE Int.
Conf. on Image Processing, pp. 1497-1500.
Farid, H., 2009. Image forgery detection. In IEEE Signal
Processing Magazine 26(2), pp.16-25.
Ferrara, M., Franco, A., Maltoni, D., 2014. The magic
passport. In Proc. IEEE Int. Joint Conf. on Biometrics,
Clearwater, Florida, pp. 1-7.
Ferrara, M., Franco, A., Maltoni, D., 2016. On the Effects
of Image Alterations on Face Recognition Accuracy.
In Bourlai, T. (ed.) Face Recognition Across the
Electromagnetic Spectrum, Springer, pp. 195-222.
Ferrara, P., Bianchi, T., De Rosa, A., Piva, A., 2012.
Image Forgery Localization via Fine-Grained Analysis
of CFA Artifacts. In IEEE Trans. on Information
Forensics and Security 7(5), pp. 1566-1577.
Fridrich, J., 2009. Digital image forensic using sensor
noise. In IEEE Sig. Proc. Magazine 26(2), pp.26-37.
Fu, D., Shi, Y.Q., Su, W., 2007. A generalized Benford’s
law for JPEG coefficients and its applications in image
forensics. In Proc. SPIE EI 6505, San Jose, CA.
Ghatol, N., et al., 2013. Image Morphing Detection by
Locating Tampered Pixels with Demosaicing
Algorithms, In Int.J.of Computer App.66(8), pp.23-26.
Hall, M., et al., 2009. The WEKA data mining software:
An update. In SIGKDD Explorations 11(1), pp. 10-18.
ISO, 2011. ISO/IEC 19794-5:2011, Information
technology - Biometric data interchange formats, Part
5: Face image data.
Lee, S., et al., 1996. Image Metamorphosis with Scattered
Feature Constraints. In IEEE Trans. on Visualization
and Computer Graphics 2(4), pp 337-354.
Lee, S., Wolberg, G., Shin, S.Y., 1998. Polymorph:
Morphing Among Multiple Images. In IEEE
Computer Graphics and Applications 18(1)
, pp. 58-71.
Liao, J., et al., 2014. Automating Image Morphing using
Structural Similarity on a Halfway Domain. In ACM
Transactions on Graphics 33(5), 168.
Lukáš, J., Fridrich, J., 2003. Estimation of primary
quantization matrix in double compressed JPEG
images. In Proc. Digital Forensics Research
Conference (DFRWS’03).
Lyu, S., Pan, X., Zhang, X., 2014. Exposing Region
Splicing Forgeries with Blind Local Noise Estimation.
In Journal of Computer Vision 110(2), pp. 202-221.
Mahdian, B., Saic, S., 2010. A bibliography on blind
methods for identifying image forgery. In Signal
Processing: Image Communication 25, pp. 389-399.
Milani, S., et al, 2014. Discriminating multiple JPEG
compressions using first digit features. In APSIPA
Trans. on Signal and Inf. Processing 3(e19), pp. 1-10.
Piva, A., 2013. An Overview on Image Forensics., In
ISRN Signal Processing, Article ID 496701, 22 p.
Ramachandra, R., Raja, K., Busch, C., 2016.
Demystifying Magical Passport: A Robust Morphed
Face Image Detection Scheme. In Proc. IEEE Int.
Conf. on Biometrics: Theory, Appl., and Systems.
Schetinger, V., Iuliani, M., Piva, A., Oliveira, M. M.,
2016. Digital Image Forensics vs. Image Composition:
An Indirect Arms Race. In CoRR abs/1601.03239.
Vyas, J.P., Joshi, M.V., Raval., M.S., 2015. Automatic
target image detection for morphing. In Journal of
Visual Comm. and Image Represent. 27, pp. 28-43.
Wang, J., et al., 2009. Understanding Benford’s law and
its vulnerability in image forensics. In Proc. IEEE Int.
Conf. on Multimedia and Expo, pp. 1568-1571.
Weng, Y., et al., 2013. Hair interpolation for portrait
morphing, In Comp.Graph. Forum 32(7), pp. 79-84.
Wolberg, G., 1998. Image morphing: a survey, In Visual
Computer 14(8), pp. 360-372.
Wolberg, G., 1990. Digital Image Warping, IEEE
Computer Society Press, Los Alamitos CA.
Wu, J., 2011. Face Recognition Jammer using Image
Morphing. Tech.Rep. No. ECE-2011-03, Boston Uni.
Zanella, V., Ramirez, G., Vargas, H., Rosas, L.V., 2009.
Automatic Morphing of Face Images. Adaptive and
Natural Computing Alg., LNCS 5495, pp 600-608.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
50
