
Transposition Based Blendshape Direct Manipulation
Ozan Cetinaslan
1
, John Lewis
2
and Ver
´
onica Orvalho
1
1
Instituto de Telecomunicac¸
˜
oes & Faculdade de Ci
ˆ
encias, Universidade do Porto, Porto, Portugal
2
Victoria University, Wellington, New Zealand
Keywords:
Blendshape, Facial Expression, Deformation, 3D Mesh, Facial Animation.
Abstract:
The blendshape approach is a predominant technique for creating high quality facial animation. Facial poses
are generated by altering the corresponding weight parameters manually for each key-frame by using tradi-
tional slider interfaces. However, authoring a production quality facial animation with this process requires
time-consuming, labor intensive and iterative work the artists. Direct manipulation interfaces address this
problem with a “pin-and-drag” operation inspired by the inverse kinematics approaches. The mathematical
frameworks of the direct manipulation techniques are mostly based on pseudo-inverse of the blendshape ma-
trices which include all target shape’s vertex positions. However, the pseudo-inverse approaches often give
unexpected results during the facial pose editing process because of its unstable behavior. To this end, we
propose the transposition approach to enhance the direct manipulation by reducing unexpected movements
during weight editing. Our approach extracts the deformation directions from the blendshape matrix, and di-
rectly maps the sparse constrained point movements to the extracted directions. Our experiments show that,
instead of psuedo-inverse based formulations, transposition based framework gives more smooth and reliable
facial poses during the weight editing process. The proposed approach improves the fidelity of the generated
facial expressions by keeping the hazardous movements in a minimum level. It is robust, efficient, easy to
implement and operate on any blendshape model.
1 INTRODUCTION
Computer generated characters have recently become
ubiquitous in movies, cartoons, advertisements and
computer games. With the advances of technology
and computer graphics techniques, it is currently pos-
sible to create lifelike characters. During the pro-
cess of creating character animation, facial animation
plays a key role to carry emotions and personality
to the spectators. Especially, the increasing demand
of the entertainment industry for high quality results
drives the researchers to investigate new techniques
to automate the animation workflow for realistic 3D
characters. Despite the extensive use of 3D facial
animation, the evolution in animation packages and
workflows have been rather slow, because the adap-
tation of advanced methods to the current animation
pipelines requires a long time period. As a result, cre-
ating high-quality facial animation is still a labor in-
tensive and time-consuming process.
Blendshape is a widely adopted technique for
high-quality facial rigging (Lewis et al., 2014). The
blendshape model forms a specific facial expression
as a sum of linear combination of target faces. These
target faces are obtained either by a skilled artist man-
ually sculpts from a neutral facial mesh, or by scan-
ning a human face with various expressions. Most
commercial animation and modeling software pack-
ages support blendshape models with their weight
editing interfaces. These interfaces, nevertheless, al-
low the animators to perform the pose editing process
only on external modules, where each pose is repre-
sented by a slider. However, creating facial anima-
tion using blendshapes requires a significant effort in
production environment for realistic models that may
consist of 100 or more target shapes.
Direct manipulation methods address the diffi-
culty of the pose editing process by offering a mathe-
matical framework with a practical pin-and-drag op-
eration (Lewis and Anjyo, 2010). The user simply
selects arbitrary points on the surface of the 3D fa-
cial model, and freely drags them until the desired
facial pose is obtained for each animation frame. Be-
neath the direct manipulation interface, the mathemat-
ical framework solves an inverse problem of weight
determination for the arbitrary selected point move-
ments. However, solving the inverse problem is gen-
erally a challenging task, because of the problem’s
Cetinaslan O., Lewis J. and Orvalho V.
Transposition Based Blendshape Direct Manipulation.
DOI: 10.5220/0006131901050115
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 105-115
ISBN: 978-989-758-224-0
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
105

Figure 1: Face posing with our novel transposition based blendshape direct manipulation method. Unlike the pseudo-inverse
based techniques, our method generates the facial poses without any artifact or unexpected movements. Our method provides
the artistic editing with a simple, efficient and easy-to-implement mathematical framework which is inspired by Jacobian
Transpose method.
excessive under-constrained behavior. Besides, in-
verse kinematics algorithms perform similar to direct
manipulation, nevertheless constraints and number of
unknowns are notably less than the direct manipula-
tion approaches. For example, human arm movement
can be expressed roughly 7 degrees of freedom for
the joint angles (Tolani and Badler, 1996), but in a
production quality blendshape model, the number of
unknown for weights can exceed 100.
A discrete function has to be defined to satisfy all
constraints to solve the inverse problem for direct ma-
nipulation. According to blendshape direct manipula-
tion (Lewis and Anjyo, 2010), moved points deter-
mine the resultant face as a simple linear combination
of predefined target shapes,
m ≈ Bw (1)
where m is the vector of resulting vertex positions
that are already moved, w is the corresponding weight
vector and B is the blendshape matrix which includes
vertex coordinates of all target shapes at its columns.
The solution of Equation (1) shows that there is an ob-
vious pseudo-inverse relationship between the blend-
shape weights and manipulated points. The general
pseudo-inverse approach gives the best possible ap-
proximated solution to w by minimizing the moved
point to its correspondent target shapes (min
w
kBw −
mk
2
). However, pseudo-inverse based mathematical
frameworks are known with their unstable and unin-
tuitive results. Altering an arbitrary side of the face
model causes unexpected little changes in the remain-
ing parts of the model. The reason for this insta-
bility is the fact that pseudo-inverse tends to assign
many non-zero values to its columns which cause un-
intended moved point projections for the irrelevant
weights.
To prevent these unexpected movements during
weight editing, we introduce a new direct manipula-
tion algorithm. Our approach is inspired from the Ja-
cobian Transpose method (Welman, 1993) and pro-
vides the direct projection of the moved points onto
B which avoids the instability of the pseudo-inverse
approach. During the drag operation, employing the
transpose of B instead of its pseudo-inverse allows
the user to manipulate desired part of the face with-
out any little alterations in the remaining parts of the
3D model (see Figure 1). In terms of computing
the weight updates directly using the transpose of B,
we analyzed the deformation (vertex displacements)
directions to prove that our transposition based di-
rect manipulation is a modified version of the classic
pseudo-inverse approach. By considering each col-
umn of B is a deformation vector for the base neu-
tral pose, we extract the deformation directions from
the columns of B by using Gram-Schmidt process
and store these columns as a new orthonormal ma-
trix, which shares the same deformation directions
as B. After applying the pseudo-inverse algorithm to
the new matrix, the resultant mathematical framework
has appeared similar to the proposed transposition
based framework with an additional step-size matrix.
In our experiments, we compare the proposed ap-
proach with two different pseudo-inverse based al-
gorithms for blendshape weight updates. The first
version is the classic pseudo-inverse method, and
the other is the commonly used pseudo-inverse with
Tikhonov regularization (Lewis and Anjyo, 2010).
Against both methods, our approach produces more
intuitive and reliable posing results. Further, we
discuss the advantages and disadvantages of both
approaches and present a hybrid approximation by
combining only the powerful sides of pseudo-inverse
based approach and our transposition based approach.
Finally, the resulting approach is simple to imple-
ment, efficient (based on solving only linear systems),
and can be adapted easily to the existing blendshape
deformation frameworks.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
106

2 RELATED WORK
Blendshape is a commonly used rigging technique
to create realistic facial animation for over many
years, (Orvalho et al., 2012). Performance capture or
keyframe animation techniques have been employed
for obtaining blendshape animation. After its practi-
cal usage in industry, (Pighin et al., 1998) explored
blendshapes as a research topic. They offered a set
of techniques which allows to create the textured tar-
get shapes rapidly from pictures of a human face with
a painterly interface to blend the parts of the morph
targets. After this prior research, blendshape was in-
tegrated nicely to other fields of facial animation such
as modeling (Pighin et al., 1998), facial performance
capture (Joshi et al., 2003), facial animation retarget-
ing (Deng et al., 2006), and facial rigging (Li et al.,
2010).
Several techniques exist for character animation
and facial deformation based on Inverse Kinemat-
ics approach. Some significant techniques include
pose-space deformation (Lewis et al., 2000), shape
by example (Sloan et al., 2001), style-based inverse
kinematics (Grochow et al., 2004), mesh-based in-
verse kinematics (Sumner et al., 2005), differential
inverse kinematics (Lewis and Dragosavac, 2010),
and partial differential equations based animation
(Gonz
´
alez Castro et al., 2010). Besides, robotics re-
search often employs inverse kinematics approaches
such as (Nakamura and Hanafusa, 1986), (Nakamura
et al., 1987), (Chan and Lawrence, 1988).
Direct manipulation methods allow to create de-
formations by directly selecting and moving points
on the surface of the 3D models. This type of ap-
proach has been common in inverse kinematics meth-
ods for character animation, and recently got popu-
lar for facial animation. Blendshape direct manipu-
lation methods solve an inverse problem to find the
beneath weights that are most appropriate for the de-
sired movement. (Joshi et al., 2003) proposed an au-
tomatic segmentation for localized blendshapes with
a direct manipulation technique. (Zhang et al., 2004)
offered a method that obtains the target shapes from
a high quality stereoscopic data on a template mesh,
and provides direct editing by using adaptive local ra-
dial basis blends.
For the first time, (Lewis and Anjyo, 2010) solved
the problem of direct manipulation for blendshape
models. They developed a novel solution by formu-
lating direct manipulation as a soft constrained in-
verse problem of finding the underlying weights for
the selected point movements. The solution includes
Tikhonov regularization parameter (Tikhonov and Ar-
senin, 1977) for the optimum results during interac-
tive editing. (Seo et al., 2011) improved the regu-
larization term of the inverse problem, and offered a
new matrix compression scheme for complex mod-
els based on hierarchically semi-separable representa-
tions with an interactive GPU-based animation. (Tena
et al., 2011) proposed to control more local modifi-
cation by dividing the PCA based facial models into
independently trained regions which share the bound-
aries with each other. This method allows the user
to directly interact with the model using the pin-and-
drag operation. (Anjyo et al., 2012) presented an al-
gorithm, which provides rapid and better edits that
learned from the previous animation.
Recently, (Neumann et al., 2013) introduced
sparse localized deformation method, which decom-
poses the global deformations to localized compo-
nents from the performance capture data using a vari-
ant of sparse PCA. (Holden et al., 2015) developed
a real-time solution to the inverse problem of rig
function, which enables mapping of the animation
data from character rig to the skeleton of the char-
acter. That method can be applicable to whole char-
acter animation as well as bone based facial anima-
tion. (Cetinaslan et al., 2015) proposed an approach
to locate the manipulators onto the facial model in-
tuitively by using a sketch-based interface, and apply
the drag operation after the sketching procedure. (Yu
and Liu, 2014) proposed a method to reproduce the
facial poses based on blendshape regression, which
uses an optimization procedure to improve the quality
of the facial expressions. We refer to (Lewis et al.,
2014) as a comprehensive report about practical and
theoretical aspects of blendshape facial models.
In the proposed approach, we have taken advan-
tage of the listed prior work. However, pseudo-
inverse solutions dominated the final mathematical
frameworks of the prior works. In contrast to the pre-
vious research, we provide a transposition based so-
lution to direct manipulation for more robust and in-
tuitive results.
3 METHOD
In this section, we first explain the algebraic perspec-
tive of blendshape models and their pseudo-inverse
relation. After, we describe the details of the proposed
transposition based direct manipulation.
3.1 Blendshape Direct Manipulation
and Pseudo-inverses
Blendshape model can be defined as a linear vector
sum of predefined target shapes as illustrated in Equa-
Transposition Based Blendshape Direct Manipulation
107

tion 2:
f =
∑
k
b
k
w
k
(2)
where f is the produced final face in a vector form
which includes all vector positions of the mesh in the
order of xyzxyz..., b
k
are the blendshape targets in a
vector form, and w
k
are the corresponding weights.
Equation 2 can also be denoted as f = Bw. However,
one particular target shape, which is the neutral face,
can be considered different than the other shapes. Be-
cause, all other targets are the offsets from the neutral
target shape ( f
0
). Therefore, it is added to Equation
2, ( f = Bw + f
0
). This new formulation is called delta
form of blendshape model, and provides many zero
or almost zero entries to each target vector. Current
commercial modeling and animation software pack-
ages most often use the delta form for blendshape ap-
plications.
According to direct manipulation scheme, the ma-
nipulators (or pins) are located on the surface of the
model by selecting some arbitrary vertices. After
moving these pins on the surface of the face, math-
ematically the resultant face can be explained as f =
m+ f
0
, where m denotes for the moved pins. The delta
form and the new face form with moved pins direct us
to Equation 1.
By using the aforementioned mathematical
model, the weight updates can be simply approxi-
mated as in Equation 3:
w = B
+
m (3)
where B
+
denotes for the pseudo inverse of B, (B
+
is
also defined as (B
T
B)
−1
B
T
). However, in some cases
the inverse operation in Equation 3 may fail because
of the singularity of B
T
B. In these cases, blendshape
matrix may not provide a full rank.
(Lewis and Anjyo, 2010) addressed this problem
with the Tikhonov regularization term to update the
weights with the most optimal fit to the point move-
ments. Another advantage of applying regularization
term is keeping the equilibrium of the system by fit-
ting the new weight values according to the desired
pose during point movements. Equation 4 shows the
weight update from (Lewis and Anjyo, 2010) after ap-
plying regularization to the system defined in Equa-
tion 3
w = (B
T
B + αI)
−1
(B
T
m + αw
0
) (4)
where α is the regularization term which is defined by
user, and w
0
are the previous weights. α term is added
to the diagonals of B
T
B matrix, and forces the system
to obtain the most close weight values with the corre-
sponding pin drags. In general, α is chosen as a small
value, such as 0.001 or 0.0001, therefore it can not
dominate B
T
B matrix with a significant change. After
setting the α term to such a small number, the term
αw
0
of Equation 4 has an almost zero effect to deter-
mine the final weights. If α is selected as zero, Equa-
tion 4 transforms to the classic pseudo-inverse form,
which is shown in Equation 3. While dragging the
constraint points on the surface of the model, Equa-
tion 3 or 4 constantly updates the weight values for
each coordinate unit.
3.2 Transposition Approach
Direct manipulation formulation is based on pseudo-
inverse of B with or without regulation term. How-
ever, pseudo-inverse approaches have a well-known
instability problem, by which unexpected and unintu-
itive movements can be observed during the pin-and-
drag operation. For example, while the user drags a
pin in the mouth region of the face, eye brows may
move slightly. The problem can be understood intu-
itively as follows: Denote the rows of Equation 2 cor-
responding to the moved pin as m =
¯
Bw. Expanding
¯
B with an SVD, we have m = USV
T
w. We see that
the largest entries of S are those that (when rotated
by U) are most effective for reaching the moved pin
m. But in forming the corresponding pseudo-inverse
(Equation 3), w = V S
+
U
T
m, the singular values are
inverted, so the directions that are least effective in
reaching m are scaled by the largest values. In prac-
tice this means that distant blendshape targets that
have little effect on a particular pinned point will tend
to move more than is desirable.
Inspired from the Jacobian transpose approach
of differential inverse kinematics (Lewis and
Dragosavac, 2010), we reformulate the blendshape
direct manipulation in a more stable and efficient
perspective. The inverse kinematics problem is
explained as min
q
kp − f (q)|
2
which was solved by
(Zhao and Badler, 1994) with a general nonlinear
programming. According to their approach, nonlin-
ear f () turns into a linear function about the current
position with an update equation:
˙p = J ˙q (5)
where ˙p is the vector from the point on the inverse
kinematics handle to the target point, J is the Jacobian
of f (). Equation 5 has to be solved for the parameter
update ˙q with the most optimal approximation. The
resultant system is nothing but ˙q = J
+
˙p. The problem
in Equations 1 and 5 nicely fits to each other. How-
ever, Welman (Welman, 1993) offers the Jacobian
Transpose algorithm for differential inverse kinemat-
ics to avoid the unstable behavior of pseudo-inverse
approach. According to this algorithm, the parameter
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
108

Figure 2: (a) Neutral pose of the model with the located pin.
(b) Pin moved down and right by using our Transposition
Approach. (c) Pin moved to the same position as (b) by
using the Pseudo-Inverse Approach.
update is defined as ˙q = J
T
˙p instead of ˙q = J
+
˙p. In
our transposition approach, we adapt Jacobian Trans-
pose algorithm to the blendshape direct manipulation
in an elegant way to reduce the global deformation
impact to a minimal level. Therefore, the weight up-
dates are defined as:
w = B
T
m (6)
The transition from pseudo-inverse based weight
updates to our transposition based approach is given
in Appendix section. From an intuitive perspective,
Equation 6 provides a direct projection of the point
movements onto the B. Therefore, point displace-
ments directly determine the exact deformation with
the correcting rows of B
T
. This type of approach pre-
vents the unexpected and unintuitive deformation ef-
fects on the facial model during the artistic pose edit-
ing. We accomplish this by appending the constrained
points to m, and corresponding rows to B. Thereby,
each pinned points adds three columns to B
T
and rows
to m. For example, while n arbitrary number of pins
are located on the 3D facial model with k blendshape
targets, the system described in Equation 6 can be rep-
resented in the matrix form in Equation 7:
w
1
w
2
w
3
.
.
.
w
k
=
x y z ··· z
x y z ··· z
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
b
T
1
b
T
2
b
T
3
··· b
T
3n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
m
1x
m
1y
m
1z
m
2x
m
2y
m
2z
.
.
.
m
3nz
(7)
It should be noted that in Equation 7, B
T
is k × 3n
matrix that consists of the coordinates of blendshape
targets over the selected vertex, and w vector includes
all weight values to form the resultant face. It is clear
that each weight value is computed as the inner prod-
uct of the relevant B vector and the constraint points
vector (w
i
= b
i
· m). Therefore, this statement reveals
that each pin displacement is only projected on its
Figure 3: The screen-shots of the slider interface according
to the pin movements that is shown in Figure 2. (a) is for
our Transposition Approach. (b) is for the Pseudo-Inverse
Approach.
corresponding blendshape targets, and this behavior
keeps the system stable, intuitive and prevents the un-
expected movements.
Strictly speaking Equation 6 gives the same an-
swer as Equation 3 in the case where the problem
is linear and Equation 6 is iterated to convergence.
However, in interactive use, the pin m is constantly
moving, and Equation 6 is not iterated to convergence.
In this case the Jacobian transpose approach natu-
rally moves each weight in proportion to the amount
that the corresponding blendshape target is useful in
reaching the goal, and there is no need to rigidly
threshold the singular values to separate what direc-
tions are part of the nullspace.
3.3 Pseudo-inverse with Transposition
Approach
The pseudo-inverse and the proposed transpose ap-
proaches have their own complementary advantages
and disadvantages. Therefore, it would be desirable to
combine them for obtaining a smooth and promising
hybrid approach. The instability problem of pseudo-
inverse approaches is already mentioned in the pre-
vious section. However, this negativity can be used
as an advantage during the pose editing. Because in
some particular cases, the movement of target shapes
naturally requires the movement of other shapes. For
example, the specific movement of inner eyebrow for
the “anger expression” is only possible with the slight
movement of the mouth. During pose editing, this
type of coupling may seem unexpected but not neces-
sarily unrealistic. Besides, in rare cases, the gross pin
movements may overshoot the pose with the trans-
position approach. By taking these possibilities into
account, we define a simple parametric representation
for the weight updates that is shown in Equation 8:
w = (γB
+
+ (1 − γ)B
T
)m (8)
where γ is an arbitrary scalar which keeps the balance
of the system. The value of γ would vary between
[0,1] where error stays in a minimal state. Unfortu-
nately, in this context there is no exact definition of
Transposition Based Blendshape Direct Manipulation
109
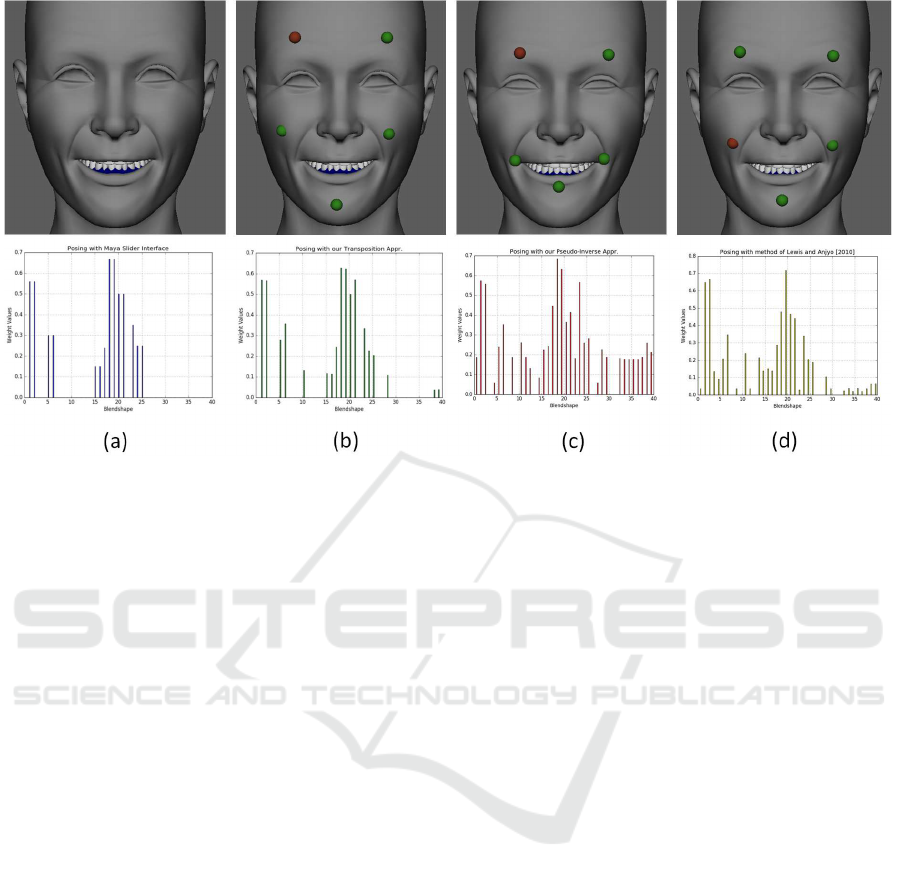
Figure 4: Blendshape direct manipulation comparison example on a model with 40 blendshape targets. (a) is the target
pose which was created using Maya’s slider interface. An experienced user tried to generate the closest pose to (a) by using
our transposition approach in (b), classic pseudo-inverse approach in (c) and the method of (Lewis and Anjyo, 2010) in (d).
Below, the weight values are reported for each above corresponded pose. Our transposition based approach clearly gives the
most close approximation to the target pose.
error, since pseudo-inverse part of Equation 8 already
produces a slight error. However, this error can be
considered as the unexpected movements of the face
that are within the tolerable limits. The further details
of Equation 8, and the γ value will be discussed in the
next section.
4 EXPERIMENTAL RESULTS
AND ANALYSIS
Our approach and its interface have been imple-
mented as a plugin for Maya 2016 using Python.
Numpy package has been used for matrix calcula-
tions. We demonstrate the comparison of our trans-
position approach with the other existing techniques
on the various blendshape facial models. All direct
manipulation techniques including our transposition
approach respond in real time, and rapidly produce
the interactive visual feedback to the user. Our main
motivation has been keeping the user away from the
technical aspects of the method during the implemen-
tation. For that reason except the mouse, the interface
does not include any control components. All the tests
were performed on 4-core Intel Core i7-2600 3.4 GHz
machine with 8 GB of RAM and an nVidia GTX 570
GPU.
Comparison to Pseudo-inverse based
Approaches
Despite the instability problem of pseudo-inverse
based approaches, over the years they have dominated
the research on direct manipulation. However, our ex-
periments show that our transposition approach de-
forms the desired area of the face with a more smooth
blending. Besides, the unexpected movements are al-
most completely eliminated. Figure 2 visually com-
pares our approach with the pseudo-inverse technique
under the single pin editing scenario. The model
consists of 18 blendshape targets, and the same pin
movements produce thoroughly different facial poses.
The slider interface of Figure 2 is shown in Figure 3.
The pseudo-inverse approach clearly updates the least
corresponding weights more than it should be, and
the resultant pose stays far away from the expected
pose. On the other hand, our transposition approach
directly maps the displacement of the pin movement
onto the corresponding blendshape targets. The resul-
tant pose is in the direction of the expectations. Be-
sides, it should be noted that both approaches operate
in the deformation space defined by the preconfigured
blendshape targets. Therefore, it is not possible to ex-
press poses beyond the limits of what blendshapes al-
low to the user.
Further, we created an experimental pose (Figure
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
110

Figure 5: Comparison of our proposed approach with other pseudo-inverse based techniques on a production quality blend-
shape model with more than 100 target shapes. Our transposition based approach in (a) generates visually plausible and
desired results with same pin drag direction. The other methods (in b and c) produce unintuitive results with many unexpected
global deformations.
4a) for an experienced user, and asked briefly produce
the same pose using our transposition based approach,
pseudo-inverse based approach and the method of
(Lewis and Anjyo, 2010). The test model consists
of 40 blendshape targets and we measured each tar-
get shape value as shown in Figure 4 below. The most
correct pose was intuitively obtained by our transposi-
tion approach. However, all three approaches produce
errors, which are reported using the root mean square
deviation per weight:
E
RMS
=
s
1
N
N
∑
i=1
|w
i
− ¯w
i
|
2
(9)
where N is the number of target shapes, w
i
is the
weight value of the i
th
target shape, and ¯w
i
is the cor-
responding weight value of the i
th
target shape of the
experimental pose (Figure 4a). The error values for
each target shape is compared in Figure 6. According
to the error analysis, the pseudo-inverse approach and
the method of (Lewis and Anjyo, 2010) produce sev-
eral irrelevant weight values during the pose genera-
tion. Besides, both approaches generate error values
on the relevant weights which cause unintuitive end
results. On the other hand, our transposition based ap-
proach produce very few error values, which mostly
occur on the relevant weight values. This difference
is due to the precise mouse movements, and is almost
not observable on the model. Figure 6 demonstrates
these error differences in scatter and line graph styles.
We compare all three approaches for posing with a
production quality model (number of blendshapes >
100) in Figure 5, which is a more realistic scenario for
the artists to create facial expressions during the an-
imation process. We observe that method of (Lewis
and Anjyo, 2010) (Figure 5c) produces visually more
plausible poses than the classic pseudo-inverse ap-
proach (Figure 5b), nevertheless they both produce
unexpected movements on the regions that are other
Transposition Based Blendshape Direct Manipulation
111
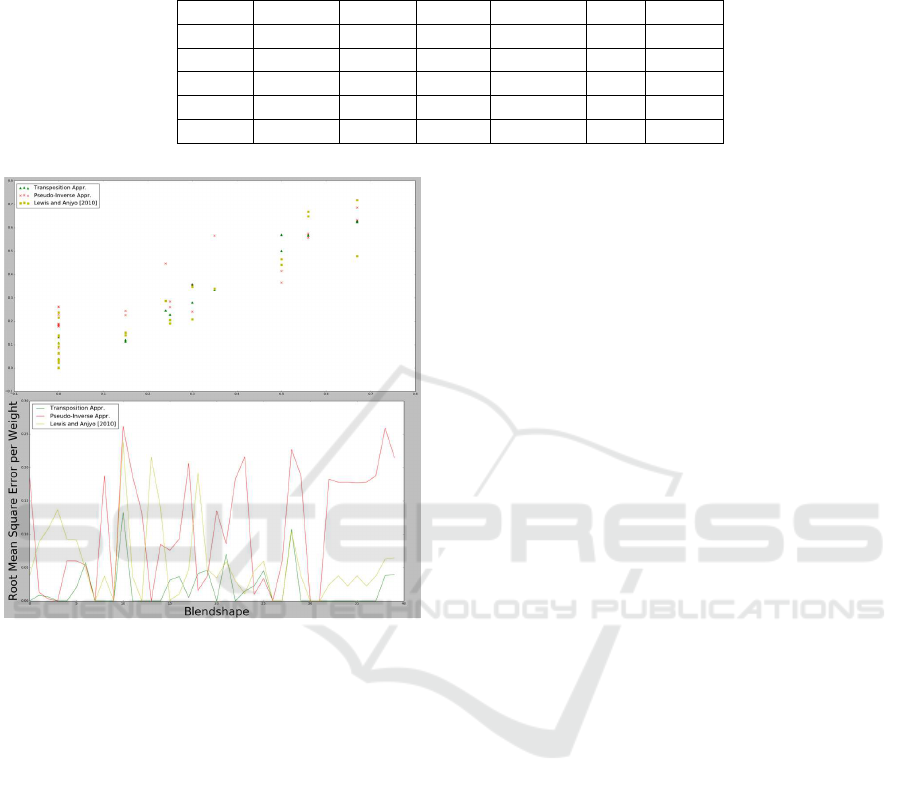
Table 1: Summary of the processed datasets. The face model order follows the order in Figure 1 (from left to right). For
example, Face 1 is the left most model, Face 3 is the cartoon model in the middle, Face 5 is the right most model. From left to
right, columns show in order, the model used, number of vertices, number of edges, number of faces, number of blendshape
targets, T
pin
is average timing for pin generation, T
edit
is exact timing for pose editing. All computation times are in seconds.
Model #Vertex #Edge #Face #Targets T
pin
T
edit
Face 1 6720 19984 13264 40 0.15 0.0099
Face 2 9562 28416 18848 18 0.03 0.0099
Face 3 11926 35576 23648 36 0.13 0.0099
Face 4 5692 11282 5584 127 1.75 0.015
Face 5 5792 11625 5834 136 1.46 0.019
Figure 6: The error analysis of the weight deviation from
Figure 4. The error values are calculated by using Equa-
tion 9. The scatter plot of error values are presented in the
top graph, and the comparison of error values are shown in
the bottom graph. Our transposition approach produces the
minimum error during the pose generation.
than the desired deformation region of the face. Our
transposition based approach (Figure 5a) provides al-
most fully local deformation which allows the artists
to edit only the desired manipulation area without any
visible global deformation impact. It should be noted
that in Figure 5, all sub-figures are intended to pro-
duce the same pose with the same number of pins.
Figure 8 illustrates the application of our transpo-
sition based approach on different facial models. Ta-
ble 1 summarizes the processed data, model details,
and computation timings for the proposed approach.
Parametrization of the Hybrid Approach
Assigning a fixed parameter value to γ value in Equa-
tion 8 can be considered as the most straightforward
approach. In that case, it would be most likely to
choose a small heuristic value (such as 0.1) and al-
low the transposition approach to dominate Equation
8. Instead, we apply the singular value decomposi-
tion to B
T
where B
T
= V SU
T
and choose the smallest
singular value σ
1
for γ. The singular values smoothly
approach to zero when the number of pins increase.
On the other hand, since B
+
= V S
+
U
T
, the singular
values of pseudo-inverses grow toward infinity.
As the user applies few number of pins to the
model (such as 1 or 2), the pseudo-inverse side of
Equation 8 will be intrinsically effective. Besides,
by intuition few number of pins denotes that the user
does not fully constrain the model, and execute only
a simple weight update. Another possibility can be an
unstable pose needed for a particular case. Neverthe-
less, the general practice is based on applying the high
number of pins to the model (such as 5 to 15), and
controlling all of them without any artifact. In these
cases, our transposition approach dominates Equation
8, and provides smooth results. Figure 7 demonstrates
an example case to the usage of Equation 8. Some
poses are necessary for irregular expressions, and it
is possible to create with 1 or 2 pins that can be seen
in the first and second columns of Figure 7. In these
cases, pseudo-inverse approach can be considered to
generate the desired irregular pose. However, when
the number of pins increase on the model, transposi-
tion based approach dominates Equation 8 (last col-
umn of Figure 7).
Limitations. Our transposition approach works
without any limitation. However, there exists one lim-
itation in our hybrid approach which comes from the
fact that the γ value in Equation 8 is computed ac-
cording to the located number of pins on the model.
Therefore, it is ideal to locate the desired number of
pins on the model before applying the posing opera-
tion.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
112

Figure 7: While the transposition approach generally pro-
duces good results, in certain cases the hybrid approach
from Equation 8 is superior. The parametrization in Equa-
tion 8 is calculated according to singular values of SVD.
When the user locates few number of pins on the model,
SVD produces a high value for the gamma parameter and
pseudo-inverse side of Equation 8 dominates. On the other
hand, with high number of pins on the model, SVD pro-
duces a very small number and transposition part of Equa-
tion 8 dominates.
5 CONCLUSIONS
In this paper, we develop a practical transposition
based blendshape direct manipulation for 3D facial
animation. Our approach has focused on the precise
projection of the pin displacements onto the corre-
sponding deformation vectors. Unlike the previous
pseudo-inverse based methods, our approach provides
a direct control of the deformation space by purely
sticking its dimensions. This behavior reduces the un-
expected movements during the artistic editing, and
almost completely reduces the deformation influence
area to the local geometry where the pins are located.
While the artifacts of the pseudo-inverse approach
can be reduced with regularizers, our new approach
is more stable intrinsically. The difference between
the two approaches is particularly noticeable while
dragging the mouse, and when the matrix B
+
in (3)
has a large nullspace. In addition, we offer a hybrid
approach, which incorporates our proposed transpo-
sition approach with the pseudo-inverse solution. In
the results, we demonstrate how our approach pro-
vides intuitive and stable artistic edits on blendshape
models almost without any artifacts. Our approach is
an original, simple, and powerful direction that can
be easily adapted to the existing direct manipulation
frameworks.
Hybrid combination of transposition and pseudo-
inverse approaches, as offered by our method, is
a promising direction that we would like to pur-
sue in the future. Applying an arbitrary number
of pins within the blendshape deformation space
is parametrized by employing the smallest singular
value in our current form. We plan to extend this
approach to formulate a balanced form that reduces
the differences between pseudo-inverse and transpo-
sition in the final result. Another promising research
direction is to explore a step-size formulation for the
proposed transposition approach to prevent possible
overshooting during the gross pin movements.
ACKNOWLEDGEMENTS
This article is a result of the project NanoS-
TIMA, NORTE-01-0145-FEDER-000016, sup-
ported by Norte Portugal Regional Operational
Programme (NORTE 2020), through Portugal
2020 and the European Regional Development
Fund. This work also had the collaboration
of the Fundac¸
˜
ao para a Ci
ˆ
encia e Tecnolo-
gia/FCT (SFRH/BD/82477/2011), POPH/FSE
program and Instituto de Telecomunicac¸
˜
oes
(UID/EEA/50008/2013). We thank Faceware
Technologies, Jason Baskin, Xenxo Alvarez and
Hiroki Itokazu for the models.
REFERENCES
Anjyo, K., Todo, H., and Lewis, J. P. (2012). A practical
approach to direct manipulation blendshapes. Journal
of Graphics Tools, 16(3):160–176.
Cetinaslan, O., Orvalho, V., and Lewis, J. (2015). Sketch-
based controllers for blendshape facial animation. In
Eurographics 2015 - Short Papers.
Chan, S. K. and Lawrence, P. D. (1988). General inverse
kinematics with the error damped pseudoinverse. In
Robotics and Automation, 1988. Proceedings., IEEE
International Conference on, pages 834–839 vol.2.
Cheney, W. and Kincaid, D. (2009). Linear algebra: The-
ory and applications. Jones and Barlett Publishers,
Sudbury, Massachusetts.
Deng, Z., Chiang, P.-Y., Fox, P., and Neumann, U. (2006).
Animating blendshape faces by cross-mapping mo-
tion capture data. In Proceedings of the 2006 Sym-
posium on Interactive 3D Graphics and Games, I3D
’06, pages 43–48, New York, NY, USA. ACM.
Gonz
´
alez Castro, G., Athanasopoulos, M., and Ugail, H.
(2010). Cyclic animation using partial differential
equations. The Visual Computer, 26(5):325–338.
Grochow, K., Martin, S. L., Hertzmann, A., and Popovi
´
c, Z.
(2004). Style-based inverse kinematics. ACM Trans.
Graph., 23(3):522–531.
Holden, D., Saito, J., and Komura, T. (2015). Learning an
inverse rig mapping for character animation. In Pro-
Transposition Based Blendshape Direct Manipulation
113

ceedings of the 14th ACM SIGGRAPH / Eurographics
Symposium on Computer Animation.
Joshi, P., Tien, W. C., Desbrun, M., and Pighin, F. (2003).
Learning controls for blend shape based realistic fa-
cial animation. In Proceedings of the 2003 ACM SIG-
GRAPH/Eurographics Symposium on Computer Ani-
mation, SCA ’03, pages 187–192.
Lewis, J. P. and Anjyo, K. (2010). Direct manipulation
blendshapes. IEEE Comput. Graph. Appl., 30(4):42–
50.
Lewis, J. P., Anjyo, K., Rhee, T., Zhang, M., Pighin, F., and
Deng, Z. (2014). Practice and theory of blendshape
facial models. In Eurographics STAR, pages 199–218.
Lewis, J. P., Cordner, M., and Fong, N. (2000). Pose space
deformation: A unified approach to shape interpola-
tion and skeleton-driven deformation. In Proceedings
of the 27th Annual Conference on Computer Graphics
and Interactive Techniques, SIGGRAPH ’00, pages
165–172, New York, NY, USA. ACM Press/Addison-
Wesley Publishing Co.
Lewis, J. P. and Dragosavac, N. (2010). Stable and efficient
differential inverse kinematics. In ACM SIGGRAPH
ASIA 2010 Sketches, SA ’10, pages 1–2.
Li, H., Weise, T., and Pauly, M. (2010). Example-based
facial rigging. ACM Trans. Graph., 29(4):1–6.
Nakamura, Y. and Hanafusa, H. (1986). Inverse kinematic
solutions with singularity robustness for robot manip-
ulator control. Journal of Dynamic Systems, Measure-
ment and Control, 108:163–171.
Nakamura, Y., Hanafusa, H., and Yoshikawa, T. (1987).
Task-priority based redundancy control of robot ma-
nipulators. Int. J. Rob. Res., 6(2):3–15.
Neumann, T., Varanasi, K., Wenger, S., Wacker, M., Mag-
nor, M., and Theobalt, C. (2013). Sparse local-
ized deformation components. ACM Trans. Graph.,
32(6):179:1–179:10.
Orvalho, V., Bastos, P., Parke, F., Oliveira, B., and X., A.
(2012). A facial rigging survey. In in Proc. of the
33rd Annual Conference of the European Association
for Computer Graphics - Eurographics, pages 10–32.
Pighin, F., Hecker, J., Lischinski, D., Szeliski, R., and
Salesin, D. H. (1998). Synthesizing realistic facial
expressions from photographs. In Proc. 25th Annual
Conference on Computer Graphics and Interactive
Techniques, SIGGRAPH ’98, pages 75–84.
Seo, J., Irving, G., Lewis, J. P., and Noh, J. (2011). Com-
pression and direct manipulation of complex blend-
shape models. In Proceedings of the 2011 SIGGRAPH
Asia Conference, SA ’11, pages 164:1–164:10.
Sloan, P.-P. J., Rose, III, C. F., and Cohen, M. F. (2001).
Shape by example. In Proceedings of the 2001 Sym-
posium on Interactive 3D Graphics, I3D ’01, pages
135–143, New York, NY, USA. ACM.
Sumner, R. W., Zwicker, M., Gotsman, C., and Popovi
´
c, J.
(2005). Mesh-based inverse kinematics. ACM Trans.
Graph., 24(3):488–495.
Tena, J. R., De la Torre, F., and Matthews, I. (2011). In-
teractive region-based linear 3d face models. In ACM
SIGGRAPH 2011 Papers, pages 76:1–76:10.
Tikhonov, A. and Arsenin, V. (1977). Solutions of ill-posed
problems. Wiley, New York.
Tolani, D. and Badler, N. (1996). Real-time inverse kine-
matics of the human arm. Presence, 5(4):393–401.
Welman, C. (1993). Inverse kinematics and geometric con-
straints for articulated figure animation. Master The-
sis, Simon Fraser University.
Yu, H. and Liu, H. (2014). Regression-based facial ex-
pression optimization. IEEE Transactions on Human-
Machine Systems, 44(3):386–394.
Zhang, L., Snavely, N., Curless, B., and Seitz, S. M. (2004).
Spacetime faces: High resolution capture for model-
ing and animation. ACM Trans. Graph., 23(3):548–
558.
Zhao, J. and Badler, N. I. (1994). Inverse kinematics posi-
tioning using nonlinear programming for highly artic-
ulated figures. ACM Trans. Graph., 13(4):313–336.
APPENDIX: Transition from
Pseudo-inverse to Transposition
The transposition algorithm can be motivated by ex-
pressing the pseudoinverse in terms of an orthonor-
malized basis. We orthonormalize the B
T
matrix,
and extract the deformation directions from the blend-
shape matrix, because both share the same vector
spans. Therefore, we apply the Gram-Schmidt pro-
cess (Cheney and Kincaid, 2009), and store the ex-
tracted orthonormal matrix in Q. After, we substitute
the new Q matrix instead of B
T
in Equation 3 with a
scaling step-size matrix R for the point movements.
The new pseudoinverse equation becomes:
w = (QQ
T
)
−1
Q(Rm) (10)
In Equation 10, Q is an orthonormal matrix.
Thereby, QQ
T
becomes an identity matrix. The new
update function turns into w = Q(Rm). According to
Jacobian Transpose suggestion, weight update can be
represented as w = B
T
m. To minimize the scaling
step-size of the point movements we apply the fol-
lowing minimization:
min
R
kB
T
− QRk
2
(11)
The solution of Equation 11 shows us R = Q
T
B
T
.
Alternatively, least square process can be replaced
with a simple qr factorization. Then, R is substituted
to Equation 10 and the final weight update function
becomes:
w = B
T
m (12)
Reviewing these steps, we see that when the basis
is orthogonal, the pseudoinverse can be reduced to the
transposition approach. In turn, the bad behavior of
the pseudoinverse can be understood in terms of the
lack of orthogonality of the basis.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
114

Figure 8: Sequential posing using our transposition based blendshape direct manipulation approach. Our approach can
be applicable to all blendshape models without any pre-configuration, and it takes less than 3 minutes to create the final
expression from the neutral pose. The details of the models are reported in Table 1.
Transposition Based Blendshape Direct Manipulation
115
