Video-based Feedback for Assisting Physical Activity
Renato Baptista, Michel Antunes, Djamila Aouada and Bj
¨
orn Ottersten
Interdisciplinary Centre for Security, Reliability and Trust (SnT), University of Luxembourg, Luxembourg, Luxembourg
Keywords:
Template Action, Temporal Alignment, Feedback, Stroke.
Abstract:
In this paper, we explore the concept of providing feedback to a user moving in front of a depth camera so
that he is able to replicate a specific template action. This can be used as a home based rehabilitation system
for stroke survivors, where the objective is for patients to practice and improve their daily life activities.
Patients are guided in how to correctly perform an action by following feedback proposals. These proposals
are presented in a human interpretable way. In order to align an action that was performed with the template
action, we explore two different approaches, namely, Subsequence Dynamic Time Warping and Temporal
Commonality Discovery. The first method aims to find the temporal alignment and the second one discovers
the interval of the subsequence that shares similar content, after which standard Dynamic Time Warping can
be used for the temporal alignment. Then, feedback proposals can be provided in order to correct the user with
respect to the template action. Experimental results show that both methods have similar accuracy rate and the
computational time is a decisive factor, where Subsequence Dynamic Time Warping achieves faster results.
1 INTRODUCTION
It is essential for elderly people to keep a good level
of physical activity in order to prevent diseases, to
maintain their independence and to improve the qual-
ity of their life (Sun et al., 2013). Physical activity
is also important for stroke survivors in order to re-
cover some level of autonomy in daily life activities
(Kwakkel et al., 2007). Post-stroke patients are ini-
tially submitted to physical therapy in rehabilitation
centres under the supervision of a health professional,
which mainly consists of recovering and maintain-
ing daily life activities (Veerbeek et al., 2014). Usu-
ally, the supervised therapy session is done within a
short period of time mainly due to economical rea-
sons. In order to support and maintain the rehabilita-
tion of stroke survivors, continuous home based ther-
apy systems are being investigated (Langhorne et al.,
2005; Zhou and Hu, 2008; Sucar et al., 2010; Hon-
dori et al., 2013; Mousavi Hondori and Khademi,
2014; Chaaraoui et al., 2012; Ofli et al., 2016). Hav-
ing these systems at home and easily accessible, the
patients keep a good level of motivation to do more
exercise. An affordable technology to support these
home based systems are RGB-D sensors, more specif-
ically, the Microsoft Kinect
1
sensor. Generally, these
systems combine exercises with video games (Kato,
1
https://developer.microsoft.com/en-us/windows/kinect
2010; Burke et al., 2009) or emulate a physical ther-
apy session (Ofli et al., 2016; Sucar et al., 2010).
Existing works usually focus on detection, recog-
nition and posterior analysis of performed actions
(Kato, 2010; Burke et al., 2009; Sucar et al., 2010;
Ofli et al., 2016). Recent works have explored ap-
proaches for measuring how well an action is per-
formed (Pirsiavash et al., 2014; Tao et al., 2016; Wang
et al., 2013; Ofli et al., 2016), which can be used as a
home based rehabilitation application. Ofli et al. (Ofli
et al., 2016) presented an interactive coaching system
using the Kinect sensor. Their system provides feed-
back during the performance of exercises. For that,
they have defined some physical constraints on the
movement such as keeping the hands close to each
other or keeping the feet on the floor, etc. Pirsiavash
et al. (Pirsiavash et al., 2014) proposed a framework
which analyses how well people perform an action
in videos. Their work is based on a learning-based
framework for assessing the quality of human actions
using spatio-temporal pose features. In addition, they
provide feedback on how the performer can improve
his action.
Recently, Antunes et al. (Antunes et al., 2016b)
introduced a system able to provide feedback in the
form of visual information and human-interpretable
messages in order to support a user in improving a
movement being performed. The motivation is to sup-
274
Baptista R., Antunes M., Aouada D. and Ottersten B.
Video-based Feedback for Assisting Physical Activity.
DOI: 10.5220/0006132302740280
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 274-280
ISBN: 978-989-758-226-4
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

port the physical activity of post-stroke patients at
home, where they are guided in how to correctly per-
form an action.
In this work, we explore the concept of a template
action, which is a video that represents a specific ac-
tion or movement, in order to provide feedback to a
user performing an action, ideally in an online man-
ner. For example, a template action can be a video
created by a physiotherapist with a specific movement
for the patient to reproduce. We propose to extend
the framework of (Antunes et al., 2016b) in order to
provide real-time feedback with respect to the tem-
plate action instead of a single pose or presegmented
video clips as (Antunes et al., 2016b). To that end, an
important alignment problem needs to be solved be-
tween the performed action and the template action.
The main challenge is that classical alignment meth-
ods, such as Dynamic Time Warping (DTW), require
the first and the last frame of the two sequences to
be in correspondence. This information is not avail-
able in our problem, since the action of interest is not
presegmented, and the feedback provided ideally in
an online manner. Two approaches from the liter-
ature are suitable for solving this problem, namely,
Subsequence-DTW (SS-DTW) (M
¨
uller, 2007) and
Temporal Commonality Discovery (TCD) (Chu et al.,
2012). In this paper, we propose to adapt both SS-
DTW and TCD for the feedback system in (Antunes
et al., 2016b) and evaluate the performance of both
alignment methods and the corresponding feedback.
This paper is organized as follows: Section 2 in-
troduces the problem formulation of the feedback sys-
tem proposed in (Antunes et al., 2016b). Section 3
provides a brief introduction of temporal alignment
and proposes to adapt SS-DTW and TCD for the feed-
back system. Experimental results, comparing the
performance of SS-DTW and TCD, are shown and
discussed in Section 4, and Section 5 concludes the
paper.
2 PROBLEM FORMULATION
A human action video is represented using the spa-
tial position of the body joints, e.g. (Vemulapalli
et al., 2014; Antunes et al., 2016a). Let us define S =
[j
1
, ··· , j
N
] as a skeleton with N joints, where each
joint is defined by its 3D coordinates j = [ j
x
, j
y
, j
z
]
T
.
An action M = {S
1
, ··· , S
F
} is a skeleton sequence,
where F is the total number of frames. The objective
is to provide feedback proposals in order to improve
the conformity between the action M that was per-
formed and the template action
ˆ
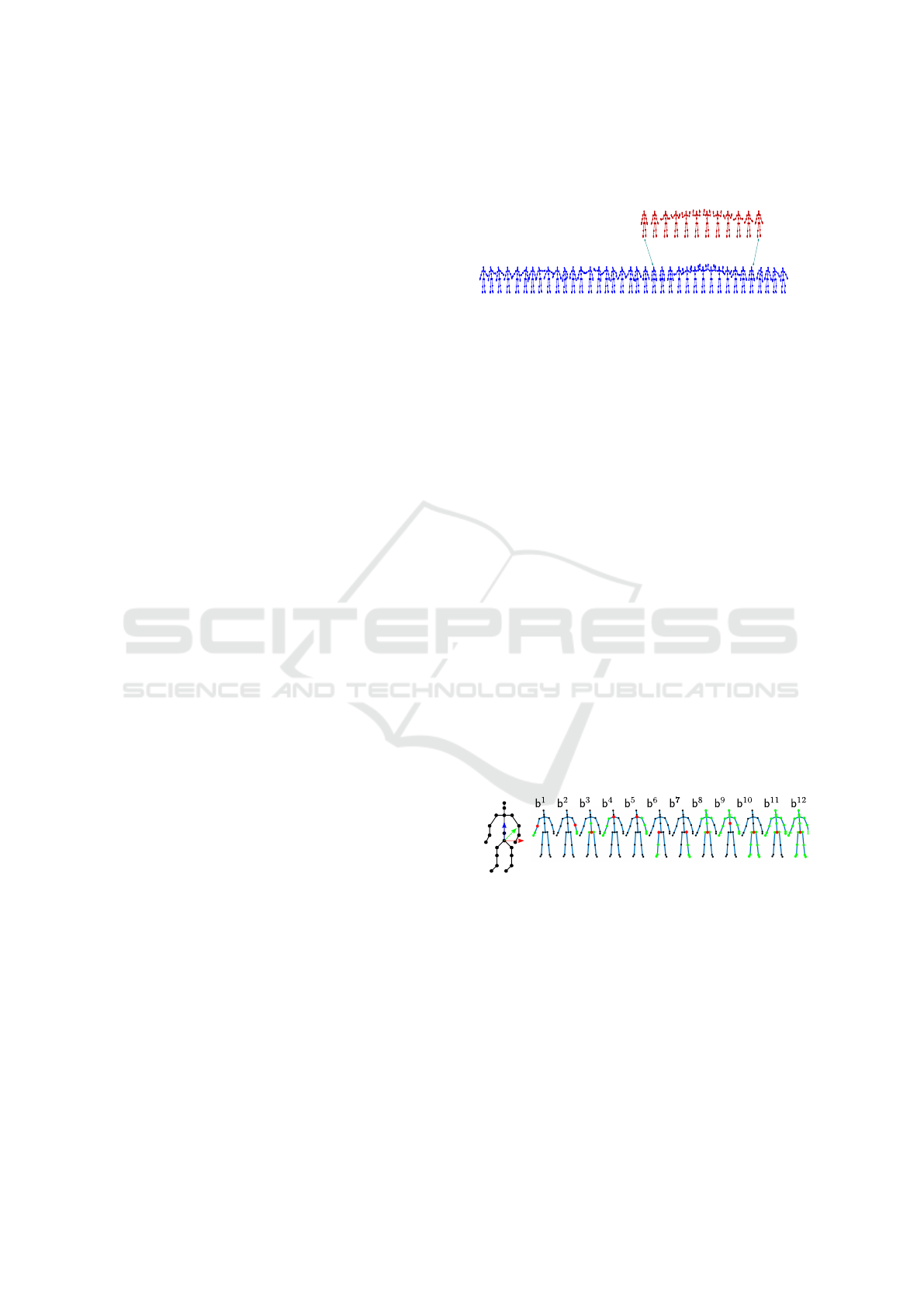
M. Figure 1 shows
an example of the data used in this work. The first
row shows a template action and the sequence in the
second row represents the action that was performed.
M
^
M
Figure 1: An illustration of the alignment between the tem-
plate action (top row, red) and the performed action (bottom
row, blue).
In order to compare two different actions, the
skeleton sequences must be spatially and temporally
aligned (Vemulapalli et al., 2014). The spatial reg-
istration is achieved by transforming each skeleton S
such that the world coordinate system is placed at the
hip center. In addition, the skeleton is rotated in a
manner that the projection of the vector from the left
hip to the right hip is parallel to the x-axis (refer to
Figure 2(a)). In order to handle variations in the body
part sizes of different subjects, the skeletons in M are
normalized such that each body part length matches
the corresponding part length of the template action
skeletons in
ˆ
M. Remark that this is done without
changing the joint angles. The temporal alignment
of skeleton sequences is the main goal of this paper.
This will be discussed in Section 3.
As proposed in (Antunes et al., 2016b), we rep-
resent a skeleton S by a set of body parts B =
{b
1
, ··· , b
P
}, where P is the number of body parts
and each body part b
k
is defined by n
k
joints b
k
=
[b
k
1
, ··· , b
k
n
k
]. Each body part has its own local ref-
erence system defined by the joint b
k
r
(refer to Fig-
ure 2(b)).
x
y
z
(a)
R
Forearm
L
Forearm
Back
R
Arm
L
Arm
R
Leg
L
Leg
Torso
Upper
Body
Lower
Body
Full
Body
Full
Upper Body
(b)
Figure 2: 2(a) Centered and aligned skeleton; 2(b) Repre-
sentation of 12 body parts. The set of joints for each body
part is highlighted in green and its local origin is the red
colored joint (R=Right, L=Left).
Given two corresponding skeletons S
i
of M and
ˆ
S
ˆ
i
of
ˆ
M, the goal of the physical activity assistance sys-
tem proposed in (Antunes et al., 2016b) is to compute
the motion that each body part of S
i
needs to undergo
to better match
ˆ
S
ˆ
i
. This is achieved by computing for
each body part b
k
the rigid motion that increases the
similarity between its corresponding body parts
ˆ
b
k
.
This is performed iteratively, where at each iteration,
Video-based Feedback for Assisting Physical Activity
275

the body part motion which ensures the highest im-
provement is selected. Finally, the previous corrective
motion is presented to the patient in the form of visual
feedback and human interpretable messages (refer to
Figure 5).
3 TEMPORAL ALIGNMENT
In this section, we propose to adapt and apply SS-
DTW and TCD to the physical activity assistance sys-
tem of (Antunes et al., 2016b). An interval measure-
ment is also proposed in order to quantitatively eval-
uate performance of the two methods. A brief intro-
duction of how two sequences are aligned using DTW
(M
¨
uller, 2007) is provided, and the boundary con-
straint assumed by DTW is discussed. This constraint
can be removed using recent methods, of which two
were selected and are presented bellow.
DTW (M
¨
uller, 2007) is a widely known tech-
nique to find the optimal alignment between two tem-
poral sequences which may vary in speed. Let us
assume two skeleton sequences M = {S
1
, ··· , S
F
}
and
ˆ
M = {
ˆ
S
1
, ··· ,
ˆ
S
ˆ
F
}, where F and
ˆ
F are the number
of frames of each sequence, respectively. A warping
path φ = [φ
1
, ··· , φ
L
] with length L, defines an align-
ment between the two sequences. The warping path
instance φ
i
= (m
i
, ˆm
i
) assigns the skeleton S
m
i
of M to
the skeleton
ˆ
S
ˆm
i
of
ˆ
M. The total cost C of the warping
path φ between sequences M and
ˆ
M is defined as
C
φ
(M,
ˆ
M) =
L
∑
i=1
c(S
m
i
,
ˆ
S
ˆm
i
), (1)
where c is a local cost measure. Following (1), the
DTW distance between the sequences M and
ˆ
M is
represented by DTW(M,
ˆ
M) and is defined as
DTW(M,
ˆ
M) = min{C
φ
(M,
ˆ
M)}. (2)
As discussed in (M
¨
uller, 2007), DTW assumes
three constraints regarding the warping path: the
boundary, the monotonicity and the step size con-
straints. We aim at analysing approaches that lever-
age the boundary constraints, and we refer the reader
to (M
¨
uller, 2007) for a thorough description of the re-
maining constraints.
The boundary constraint in DTW assumes that the
first and the last frames of both sequences are in cor-
respondence. This is mathematically expressed as
φ
1
= (1, 1) and φ
L
= (F,
ˆ
F). (3)
Figure 3(a) illustrates the boundary constraint of
DTW. As it requires the alignment of the first and
the last frames, this method is not suitable for our
problem, because the template action will be in many
cases a sub-interval of the action that was performed.
There are some recent methods for suppressing
the boundary constraint (Gupta et al., 2016; Kulka-
rni et al., 2015; Zhou and Torre, 2009; ?). We se-
lected two of them based on the following: SS-DTW
(M
¨
uller, 2007) is a simple and natural extension of
DTW, and TCD (Chu et al., 2012) was recently shown
to work well for human motion analysis. These ap-
proaches are described next.
3.1 SS-DTW
SS-DTW (M
¨
uller, 2007) is a variant of the DTW that
removes the boundary constraint. Referring to our
problem, this method does not align both sequences
globally, but instead the objective is to find a subse-
quence within the performed action that best fits the
template action.
Given
ˆ
M and M the objective is to find the subse-
quence {S
s
: S
e
} of M with 1 ≤ s ≤ e ≤ F, that best
matches
ˆ
M, where s is the starting and e is the ending
point of the interval. This is achieved by minimizing
the DTW distance in (2) as follows:
{S
s
∗
: S
e
∗
} = argmin
(s,e)
(DTW(
ˆ
M, {S
s
: S
e
})), (4)
where {S
s
∗
: S
e
∗
} is the optimal alignment interval.
Figure 3(b) illustrates the result of the SS-DTW algo-
rithm between two sequences, where it is able to find
a good alignment in a long sequence M.
3.2 Unsupervised TCD
The TCD algorithm (Chu et al., 2012) discovers the
subsequence that shares similar content between two
or more video sequences in an unsupervised manner.
Given two skeleton sequences M and
ˆ
M, where M
contains at least one similar action as the template ac-
tion
ˆ
M. The objective is to find the subsequence {S
s
:
S
e
} of M that better matches the subsequence {
ˆ
S
ˆs
:
ˆ
S
ˆe
} of
ˆ
M. Referring to our problem, the objective is
to find the best subsequence {S
s
: S
e
} that better fits
the template action
ˆ
M. This can be achieved by mini-
mizing the distance d between two feature vectors ψ
ˆ
M
and ψ
{S
s
:S
e
}
defined as
min
s,e
d(ψ
ˆ
M
, ψ
{S
s
:S
e
}
), (5)
such that e − s ≥ l, where l is the minimal length to
avoid the case of an empty set. Assuming A as a se-
quence of skeletons, where each skeleton is expressed
by the 3D coordinates of the human body joints. The
feature vector ψ
A
is represented as the histogram of
temporal words (Chu et al., 2012). In order to find
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
276

the optimal solution to (5), TCD uses a Branch and
Bound (B&B) algorithm. Figure 3(c) shows an exam-
ple of TCD, where the result is the interval of each
sequence that shares similar pattern. After the detec-
tion of the matching intervals, the standard DTW can
be applied to align the obtained subsequence {S
s
: S
e
}
of M with the template action
ˆ
M.
Time
Sequence M
Sequence M
^
(a) Alignment between two temporal sequences using DTW.
Time
Sequence M
^
Sequence M
s
e
(b) Alignment between
ˆ
M and the sequence M using SS-
DTW.
Sequence M
^
Sequence M
ŝ ê
s
e
(c) Discovered common content between two sequences us-
ing TCD.
Figure 3: Described methods of temporal alignment and
similar content detection. Sub-figures 3(a) and 3(b) show
that the SS-DTW is capable to remove the boundary con-
straint of DTW. The blue rectangles highlight the removal
of this constraint. Sub-figure 3(c) illustrates the intervals
obtained from TCD algorithm, where both sequences share
similar triangles.
3.3 Proposed Interval Measure
In order to evaluate the performance of the interval
detection using the temporal alignment methods de-
scribed previously, we first use standard DTW to align
the template action
ˆ
M with the same action performed
by a different subject M
1
, where F
1
is the number
of frames of M
1
. Let us assume the alignment be-
tween
ˆ
M and M
1
using φ = [φ
1
, ··· , φ
L
]. After the
alignment, the action M
1
is divided in 3 different sub-
sequences with different lengths:
1. Complete sequence, M
L
1
= M
1
- the whole warp-
ing path φ = [φ
1
, ··· , φ
L
], Figure 4(a);
2.
3
4
L of the sequence, M
L
0
1
, where L
0
=
3
4
L - warping
path φ = [φ
1
, ··· , φ
L
0
], Figure 4(b);
3.
1
2
L of the sequence, M
L
00
1
, where L
00
=
1
2
L - warp-
ing path φ = [φ
1
, ··· , φ
L
00
], Figure 4(c);
M1
M
^
(a) M
L
1
.
M1
M
^
(b) M
L
0
1
.
M1
M
^
(c) M
L
00
1
.
Figure 4: Temporal alignment between the sequences
ˆ
M
and M
1
using DTW. The blue sequence represents the se-
quence
ˆ
M and the green sequence is the sequence M
1
. The
red color corresponds to the subsequences with 3 different
lengths.
Then, for evaluating the performance of the align-
ment methods, we generate new sequences M using
the resulting 3 subsequences from M
1
. Considering
this, the objective is to evaluate the accuracy in the
detection of the start, s, and end point, e, of the inter-
val obtained from SS-DTW and TCD. To compute the
accuracy, we use s and e from the subsequence of M
1
(introduced in M) to calculate the difference with the
results from both methods. If the difference between
the corresponding points is higher than a pre-defined
threshold ε, then it is considered as an outlier. Other-
wise, the accuracy is defined as
Acc = 1 −
|di f f (s
M
1
,s)|
F
1
, (6)
where di f f (s
M
1
, s) is the the difference between
ground-truth start points s
M
1
from M
1
and s from the
alignment methods (same for the end points).
4 EXPERIMENTS
We validate SS-DTW and TCD quantitatively using
a public dataset UTKinect (Xia et al., 2012) and also
qualitatively using data captured by the Kinect v2 sen-
sor.
4.1 Quantitative Evaluation
The UTKinect dataset consists of 10 actions per-
formed by 10 subjects. We select an action from the
Video-based Feedback for Assisting Physical Activity
277

dataset to be the template action
ˆ
M (e.g. wave hands).
An action to be aligned M is generated by concate-
nating random actions from the dataset before and af-
ter the action of interest, which is divided in 3 subse-
quences with different lengths as described before.
According to Table 1 and Table 2, both methods
have better results when detecting the start point of
the performed action, and also, the more information
existing in the performed action (the greater the length
of the introduced subsequence), the better the results.
The accuracy and the outlier rate for both methods
are very similar. Considering that TCD requires more
computational effort and posterior alignment using
standard DTW, SS-DTW is recommended in the case
where the computational time is an important factor.
Comparing the runtime of each method, the SS-DTW
achieves faster results than TCD, where the time for
SS-DTW is on average 0.021s and for TCD is 0.073s.
Table 1: Accuracy and outlier rate of the start point using
SS-DTW and TCD for the 3 different lengths of the align-
ment. In this evaluation, we used ε = 6 frames. All reported
accuracies are computed using (6) and provided in %.
M
L
1
M
L
00
1
M
L
00
1
Accuracy Outliers Accuracy Outliers Accuracy Outliers
SS-DTW 91.58 31.43 85.35 24.29 79.27 20.00
TCD 90.13 30.00 80.64 33.57 75.58 55.00
Table 2: Accuracy and outlier rate of the end point using
SS-DTW and TCD for the same experiments as in Table 1.
M
L
1
M
L
0
1
M
L
00
1
Accuracy Outliers Accuracy Outliers Accuracy Outliers
SS-DTW 80.77 42.14 81.91 25.71 67.97 25.00
TCD 82.21 45.71 82.58 30.71 84.47 45.00
Given an optimal alignment between the template
action
ˆ
M and the performed action M, feedback pro-
posals are provided for each instance and they are pre-
sented in the form of visual arrows and also as hu-
man interpretable messages. The feedback proposals
are achieved by reproducing the method presented in
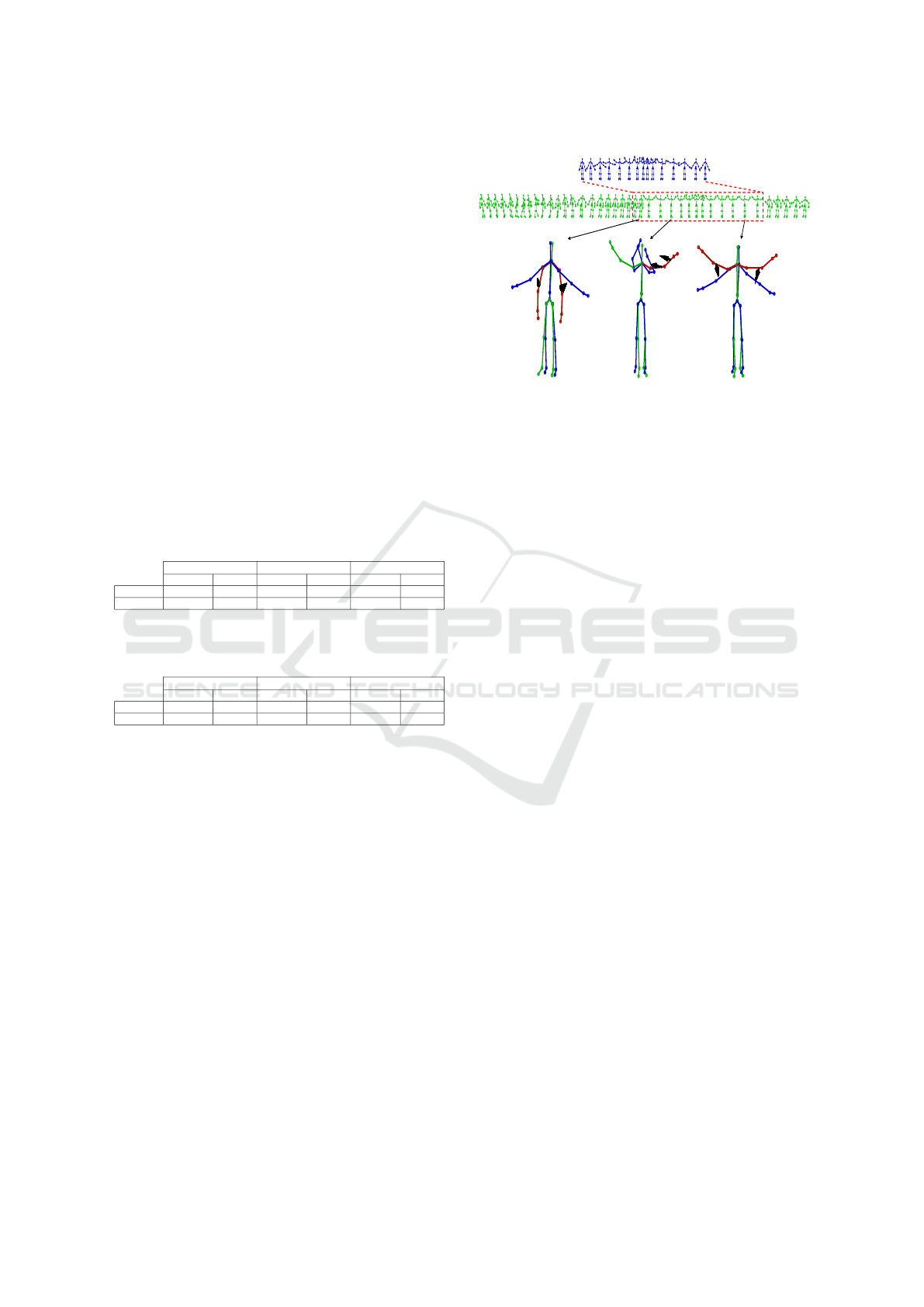
(Antunes et al., 2016b). Figure 5 shows an example
of the alignment and the feedback proposals. The first
row (blue) is the template action
ˆ
M (wave hands), the
second row (green) is the generated action M and the
aligned subsequence {S
s
: S
e
} of M is represented by
the red rectangle. In addition, for each instance, feed-
back proposals are provided to the highlighted body
parts (red) that need to be improved in order to match
the template action at the corresponding instance.
4.2 Qualitative Evaluation
The data was captured using the Kinect v2 sensor (ex-
ample of the captured data is shown in Figure 7(a)).
The main idea of this dataset is to simulate a specific
Right Arm BACK
Left Arm RIGHT
Right Arm BACK
Left Arm DOWN
Left Arm FORWARD
Left Forearm LEFT
Figure 5: The first row represents the template action
ˆ
M
(blue), the second row (green) is the generated action M and
the subsequence {S
s
: S
e
} inside the red rectangle is the re-
sult from SS-DTW. Then, feedback proposals are presented
for the body parts that need to be improved to best match the
template action for that instance. These body parts are col-
ored in red to help the user to understand which body part
he should move following the arrows and the text messages.
scenario considering post-stroke patients with the ob-
jective of helping the patients in such a way that they
keep to regularly practice the proposed movements.
In order to simulate the difficulty in the movements
of a post-stroke patient, we use a “bosu” balance ball
to introduce the problem of the body balance and also
used a kettle-bell to simulate possible arm paralysis.
Figure 6 illustrates the equipment used to simulate the
post-stroke patient. The scenario consists of the fol-
lowing: first, a template action is shown; then, the pa-
tient tries to reproduce the same action after a starting
sign and within a fixed time (refer to Figure 7(a)).
Given two sequences, a template action
ˆ
M and a
simulated post-stroke patient action M, we applied
both methods (SS-DTW and TCD) and then com-
puted feedback proposals in order to support the pa-
tient to improve and correct the action. Note that, the
template action can be a video created by a physio-
therapist with a specific movement, then the patient
can understand, practice and improve the movement
by following the feedback proposals. This can be seen
as a motivation for the patient to maintain the continu-
ity of the rehabilitation at home. Figure 7 shows the
results of the temporal alignment methods (SS-DTW
and TCD) and the feedback proposals are provided to
correct the user.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
278

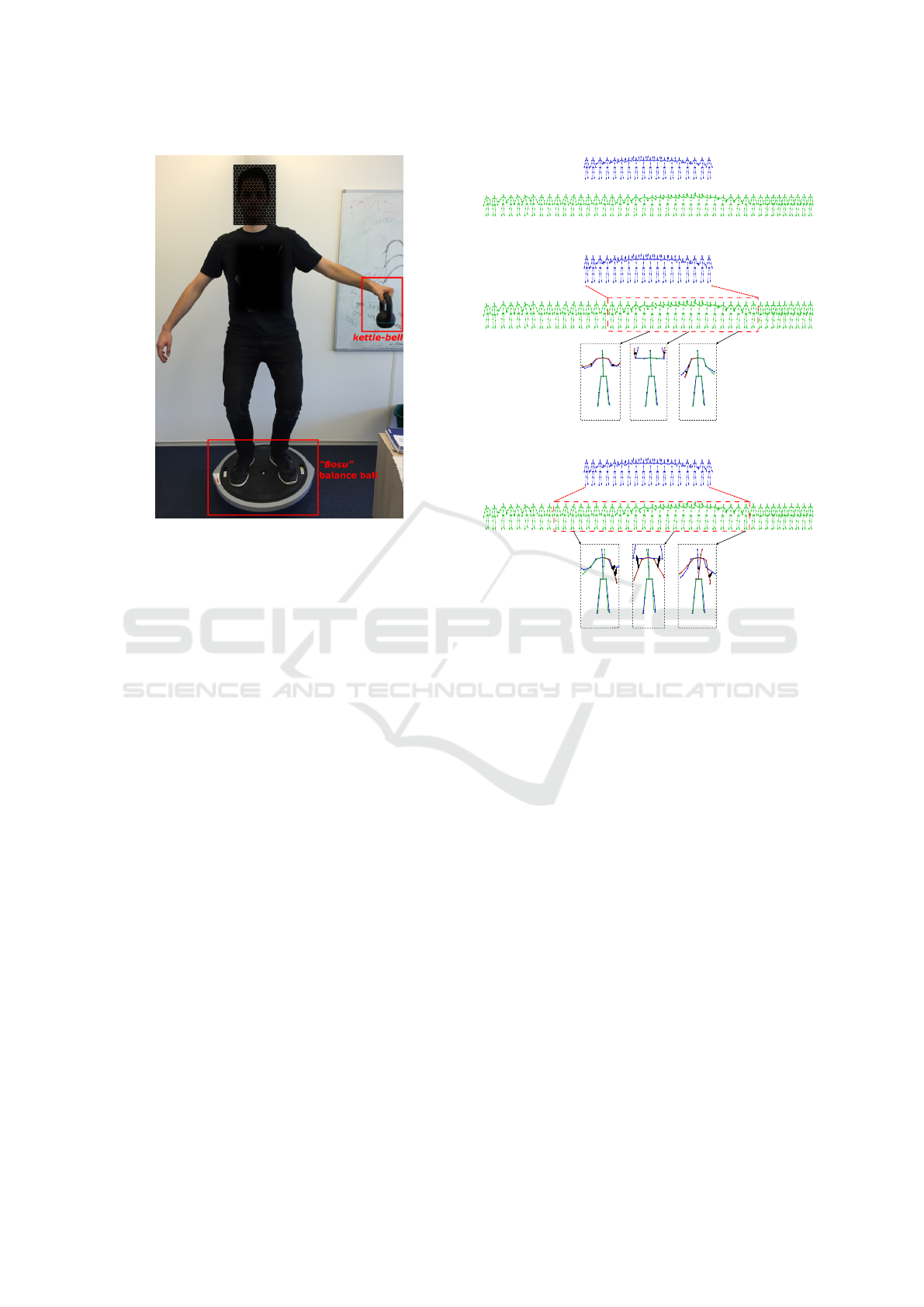
Figure 6: Simulation of a post-stroke patient. The balance
problem is simulated by using a “bosu” balance ball and to
simulate the problem related to the arm paralysis, a kettle-
bell is used.
5 CONCLUSION
In this paper, we propose a system to guide a user in
how to correctly perform a specific movement. This is
achieved by applying appropriate temporal alignment
methods, namely, SS-DTW and TCD, and then using
the feedback system of (Antunes et al., 2016b). Both
of these methods can leverage the “static” physical
activity assistance system proposed in (Antunes et al.,
2016b).
The accuracy and the outlier rate of SS-DTW and
TCD, as can be seen in Table 1 and Table 2, are very
similar. Since TCD involves complex computations,
such as the representation of the skeleton information
in a new descriptor space, and also requires the poste-
rior alignment using standard DTW, we recommend
the use of SS-DTW in the case where the computa-
tional time is an important factor.
Nevertheless, both methods were not specifically
designed for working in an online manner. This
means that every time that a new frame is captured,
the complete pipeline needs to be run again. An ap-
propriate approach that iteratively rejects irrelevant
data would certainly increase the efficiency of the
temporal alignment.
(a) Proposed scenario.
Right Arm BACK
Left Arm DOWN
Left Forearm RIGHT
Right Forearm LEFT
Left Forearm LEFT
Left Arm UP
(b) Alignment from SS-DTW.
Right Forearm UP
Right Arm UP
Left Arm UP
Right Arm UP
Lean LEFT
Right Forearm UP
(c) Discovered interval from TCD and then DTW alignment
with the template action.
Figure 7: Temporal alignment using SS-DTW and TCD,
and computed feedback proposals. The template action
ˆ
M
is the top sequence (blue) of each sub-figure, and the bottom
sequence (green) is the performed action M. The interval re-
trieved from both methods ({S
s
: S
e
}) is represented by the
red rectangle. Feedback proposals are shown for the same
instance for both methods in order to correct the position
with respect to the template action.
ACKNOWLEDGEMENTS
This work has been partially funded by the Euro-
pean Union‘s Horizon 2020 research and innovation
project STARR under grant agreement No.689947.
This work was also supported by the National Re-
search Fund (FNR), Luxembourg, under the CORE
project C15/IS 10415355/3D-ACT/Bj
¨
orn Ottersten.
REFERENCES
Antunes, M., Aouada, D., and Ottersten, B. (2016a). A
revisit to human action recognition from depth se-
quences: Guided svm-sampling for joint selection.
Video-based Feedback for Assisting Physical Activity
279

In 2016 IEEE Winter Conference on Applications of
Computer Vision (WACV), pages 1–8.
Antunes, M., Baptista, R., Demisse, G., Aouada, D., and
Ottersten, B. (2016b). Visual and human-interpretable
feedback for assisting physical activity. In European
Conference on Computer Vision (ECCV) Workshop on
Assistive Computer Vision and Robotics Amsterdam,.
Burke, J. W., McNeill, M., Charles, D., Morrow, P., Cros-
bie, J., and McDonough, S. (2009). Serious games
for upper limb rehabilitation following stroke. In Pro-
ceedings of the 2009 Conference in Games and Virtual
Worlds for Serious Applications, VS-GAMES ’09,
pages 103–110, Washington, DC, USA. IEEE Com-
puter Society.
Chaaraoui, A. A., Climent-P
´
erez, P., and Fl
´
orez-Revuelta,
F. (2012). A review on vision techniques applied to
human behaviour analysis for ambient-assisted living.
Expert Systems with Applications.
Chu, W.-S., Zhou, F., and De la Torre, F. (2012). Unsuper-
vised temporal commonality discovery. In ECCV.
Gupta, A., He, J., Martinez, J., Little, J. J., and Woodham,
R. J. (2016). Efficient video-based retrieval of human
motion with flexible alignment. In 2016 IEEE Win-
ter Conference on Applications of Computer Vision
(WACV).
Hondori, H. M., Khademi, M., Dodakian, L., Cramer, S. C.,
and Lopes, C. V. (2013). A spatial augmented reality
rehab system for post-stroke hand rehabilitation. In
MMVR.
Kato, P. M. (2010). Video Games in Health Care: Closing
the Gap. Review of General Psychology, 14:113–121.
Kulkarni, K., Evangelidis, G., Cech, J., and Horaud, R.
(2015). Continuous action recognition based on se-
quence alignment. International Journal of Computer
Vision, 112(1):90–114.
Kwakkel, G., Kollen, B. J., and Krebs, H. I. (2007). Effects
of robot-assisted therapy on upper limb recovery after
stroke: a systematic review. Neurorehabilitation and
neural repair.
Langhorne, P., Taylor, G., Murray, G., Dennis, M., An-
derson, C., Bautz-Holter, E., Dey, P., Indredavik, B.,
Mayo, N., Power, M., et al. (2005). Early supported
discharge services for stroke patients: a meta-analysis
of individual patients’ data. The Lancet.
Mousavi Hondori, H. and Khademi, M. (2014). A review
on technical and clinical impact of microsoft kinect on
physical therapy and rehabilitation. Journal of Medi-
cal Engineering, 2014.
M
¨
uller, M. (2007). Dynamic Time Warping. Springer.
Ofli, F., Kurillo, G., Obdrz
´
alek, S., Bajcsy, R., Jimison,
H. B., and Pavel, M. (2016). Design and evaluation
of an interactive exercise coaching system for older
adults: Lessons learned. IEEE J. Biomedical and
Health Informatics.
Pirsiavash, H., Vondrick, C., and Torralba, A. (2014). As-
sessing the quality of actions. In Computer Vision–
ECCV 2014, pages 556–571. Springer.
Rakthanmanon, T., Campana, B., Mueen, A., Batista, G.,
Westover, B., Zhu, Q., Zakaria, J., and Keogh, E.
(2012). Searching and mining trillions of time se-
ries subsequences under dynamic time warping. In
Proceedings of the 18th ACM SIGKDD International
Conference on Knowledge Discovery and Data Min-
ing, KDD ’12, pages 262–270, New York, NY, USA.
ACM.
Sucar, L. E., Luis, R., Leder, R., Hernandez, J., and
Sanchez, I. (2010). Gesture therapy: a vision-
based system for upper extremity stroke rehabilita-
tion. In Engineering in Medicine and Biology Soci-
ety (EMBC), 2010 Annual International Conference
of the IEEE.
Sun, F., Norman, I. J., and While, A. E. (2013). Physical
activity in older people: a systematic review. BMC
Public Health.
Tao, L., Paiement, A., Damen, D., Mirmehdi, M., Han-
nuna, S., Camplani, M., Burghardt, T., and Craddock,
I. (2016). A comparative study of pose representation
and dynamics modelling for online motion quality as-
sessment. Computer Vision and Image Understand-
ing.
Veerbeek, J. M., van Wegen, E., van Peppen, R., van der
Wees, P. J., Hendriks, E., Rietberg, M., and Kwakkel,
G. (2014). What is the evidence for physical therapy
poststroke? a systematic review and meta-analysis.
PloS one.
Vemulapalli, R., Arrate, F., and Chellappa, R. (2014). Hu-
man action recognition by representing 3d skeletons
as points in a lie group. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion.
Wang, R., Medioni, G., Winstein, C., and Blanco, C.
(2013). Home monitoring musculo-skeletal disorders
with a single 3d sensor. In Proceedings of the IEEE
Conference on Computer Vision and Pattern Recogni-
tion Workshops, pages 521–528.
Xia, L., Chen, C., and Aggarwal, J. (2012). View invari-
ant human action recognition using histograms of 3d
joints. In Computer Vision and Pattern Recognition
Workshops (CVPRW), 2012 IEEE Computer Society
Conference on, pages 20–27. IEEE.
Zhou, F. and Torre, F. (2009). Canonical time warping for
alignment of human behavior. In Bengio, Y., Schu-
urmans, D., Lafferty, J. D., Williams, C. K. I., and
Culotta, A., editors, Advances in Neural Information
Processing Systems 22, pages 2286–2294. Curran As-
sociates, Inc.
Zhou, H. and Hu, H. (2008). Human motion tracking for
rehabilitationa survey. Biomedical Signal Processing
and Control, 3(1):1–18.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
280