Probabilistic Background Modelling for Sports Video Segmentation

Nikolas Ladas

, Paris Kaimakis

and Yiorgos Chrysanthou

Department of Computer Science, University of Cyprus, Nicosia, Cyprus

Department of Computing, University of Central Lancashire Cyprus, Larnaca, Cyprus

{nladas, yiorgos}@cs.ucy.ac.cy, pkaimakis@uclan.ac.uk

Keywords:

Segmentation, Background Modelling, Shadow Detection, Visibility Decomposition.

Abstract:

This paper introduces a segmentation algorithm based on the probabilistic modelling of the background color

using a Lambertian formulation of the scene’s appearance. Central in our formulation is the computation of

the degree of light visibility at the scene location depicted by each pixel. Because our approach speciﬁcally

models the formation of shadows, segmentation results are of high accuracy. The quality of our results is

further boosted by utilizing key observations about scene appearance. A qualitative and quantitative evaluation

indicates that the proposed method performs better than commonly used segmentation algorithms, both for

sports as well as for generic datasets.

1 INTRODUCTION AND

RELATED WORK

Accurately tracking players in sports games allows

for the generation of statistics, such as ball posses-

sion, player speed, distance travelled and more. These

statistics are useful for professionals, such as coaches,

and add entertainment value to viewers (Graham,

2012). Prior to tracking, it is often desirable to seg-

ment each frame from the input video such that only

the objects of interest are visible. Seen as a prepro-

cessing stage onto which other higher-order vision

tasks depend, it is paramount for segmentation algo-

rithms to ensure above real time processing speeds,

and low misclassiﬁcation rates.

The problem of automatic segmentation of images

has been the subject of intensive research in the last

two decades, and a number of surveys attempt to pro-

vide a taxonomy on the algorithms proposed thus far

(Wang and Cohen, 2007), (Sanin et al., 2012), (Dun-

can and Sarkar, 2012).

Accurate results can be obtained by alpha mat-

ting. Using user-speciﬁed labels, (Levin et al., 2008)

and (Shahrian et al., 2013) determine, at the pixel

level, the alpha matte which controls the opacity of

the foreground and the background. Alpha-matting

algorithms are particularly useful for translucent ob-

jects such as a person’s hair, but require user inter-

vention and have not be made to run in real time as

yet.

Another class of algorithms attempts to identify

Figure 1: Example of a segmentation result obtained with

our method.

salient regions within the image, which are likely to

be of interest to a human observer. To this end, the au-

thors of (Perazzi et al., 2012) and (Yan et al., 2013) di-

vide the image into superpixels, each of which is asso-

ciated with a measure of dissimilarity against the rest.

Then, superpixels of large dissimilarity are classiﬁed

as foreground. By formulation, saliency algorithms

Ladas N., Kaimakis P. and Chrysanthou Y.

Probabilistic Background Modelling for Sports Video Segmentation.

DOI: 10.5220/0006135505170525

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 517-525

ISBN: 978-989-758-225-7

517

Figure 2: Video frame (above) and computed visibility (be-

low) according to Equation (6). Red indicates visibility val-

ues greater than one.

are restricted to perform well only when background

and foreground classes are chromatically distinct and

are computationally expensive, making them inappli-

cable to real-time applications.

Good segmentation results have been achieved by

using a priori information about the scene’s fore-

ground objects. In (Hsieh et al., 2003) and (Chen

and Aggarwal, 2010) for example, the shape and ori-

entation of pedestrians was used. Such techniques

can indeed achieve convincing results, but are re-

stricted to speciﬁc domains when the nature of fore-

ground objects is previously known. Furthermore, we

take the position that accurate segmentation should be

achieved prior to scene understanding.

The most populous class of segmentation algo-

rithms attempts to model the scene’s background.

This is commonly achieved by gathering statistics

about image features, such as color and texture, from

a sequence of images or from a video stream. Then,

for each new image or video frame the background in-

formation is used to classify each pixel as either fore-

ground or background. Within the background mod-

elling literature two categories stand out: (a) local al-

gorithms, which operate on the pixel level, and (b)

non-local algorithms which operate on image regions

or employ global (i.e. image-wide) statistics.

Non-local algorithms include methods based on

texture, such as (Leone and Distante, 2007), (Sanin

et al., 2010) which operate on scene regions, under

the assumption that textures remain unaffected even

in shadow. Other techniques have combined multiple

image cues. In (Huerta et al., 2013), color, edge, and

intensity cues are used, whereas (Khan et al., 2014)

uses a convolutional neural network to learn useful

255

2550

col(A)

= v

= 1

Figure 3: Relationship between the column space of A,

hereby denoted as col(A), the observed value b, the visi-

bility solution x

= v and the error e. For the sake of clar-

ity, the ﬁgure only shows the red and green color channels

and the background color is assumed gray. The color rep-

resented by b corresponds to a visibility solution that falls

ouside the allowed range [v

, v

] while at the same time pro-

ducing a large error e.

cues from the whole image automatically. Generally,

non-local algorithms are more accurate than local al-

gorithms but this comes at the expense of lower per-

formance and increased implementation complexity,

both of which hinder their widespread adoption.

Finally, local algorithms rely solely on spectral in-

formation at the pixel level. The authors of (Zivkovic,

2004), (Barnich and Van Droogenbroeck, 2011),

(Godbehere and Goldberg, 2014) and (Kaimakis and

Tsapatsoulis, 2013) learn the distribution of the back-

ground color for each pixel and then use probabilis-

tic models, such as mixtures of Gaussians (MOG) or

histograms in order to classify pixels as either fore-

ground or background. Because they do not rely on

extensive assumptions, these algorithms perform well

on a broad range of scenes, and as a result they have

been widely adopted. Additionally, because they op-

erate on the pixel level, they can be implemented ef-

ﬁciently by exploiting parallelism. For example the

OpenCV implementation of (Zivkovic, 2004) is ac-

celerated on the GPU using OpenCL (Stone et al.,

2010). Nevertheless, the quality of their results is of-

ten limited, with examples of misclassiﬁcation arising

particularly at the presence of shadows.

In this paper we present a background modelling

algorithm which operates on the pixel level. Our

method’s robustness stems from an explicit account

of the formation of shadows in the scene, which im-

proves segmentation quality without sacriﬁcing gen-

erality.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

518

col(A)

p(e|BG)

(a)

col(A)

p(v|BG)

(b)

col(A)

p(e, v|BG)

(c)

Figure 4: Likelihood functions for e and v according to the background model.

2 METHODOLOGY

Our method is based on a Lambertian formulation of

scene appearance which accounts for shadows specif-

ically by means of a visibility term (Section 2.1). We

solve for the visibility on a per-pixel basis using linear

least squares (Section 2.2). Using the least squares

solution for the visibility and the error associated to

it, we derive a probabilistic model that computes the

likelihood of each pixel’s color (Section 2.3). This is

thresholded to give the ﬁnal output (see Figure 1).

2.1 Formulation of Scene Appearance

The basis of our formulation is the common assump-

tion of a Lambertian scene. Under this assumption, a

fully lit location x = [x, y, z]

of the scene reﬂects light

I given by

I(x) = R(x) L

(x) (1)

where R is the diffuse reﬂectance of the scene at x,

and L

is the maximum incoming illumination

at the

same location.

By contrast, for locations x immersed in shadow,

the incident illumination is only a fraction of L

. In

order to account for both, fully lit as well as shadowed

locations, Equation (1) is adapted as follows:

I(x) = v(x) R(x) L

(x) (2)

where v(x) ∈ [0, 1] is the visibility factor determining

the proportion of maximum illuminance L

arriving at

x. Hence, v = 1 for fully lit locations, and v < 1 for

locations in shadow.

Under the Lambertian assumption, a camera pixel

m = [u, v]

observing scene location x will have the

same value irrespective of camera position and orien-

tation. Therefore, Equation (2) holds for pixels m as

well as scene locations x. For the remainder of this

paper all operations will be performed on the pixel

i.e. the illumination when x is fully lit.

level and references to scene and pixel locations will

be omitted for the sake of clarity.

2.2 Visibility Decomposition

The scene formulation of (2) contains multiple un-

knowns that we remove using a background image

which does not contain foreground objects. For ex-

ample, in a sports video the background image would

depict the playing ﬁeld without any players present.

We estimate a background image by averaging a

sequence of frames from the input video. This re-

quires the camera to be static or for the camera move-

ments to be registered correctly. For simplicity, in this

paper we assume a static camera and leave camera

movement calibration as future work.

We assume the background image I

to be

shadow-free and so v = 1 in (2) for every pixel in the

image. With v out of the way, we can express the re-

ﬂectance of the background at every pixel to be:

(3)

Given the background image, we now wish to de-

termine the visibility, at each pixel, for every frame of

the input video.

As noted in Section 2.1, Equation (2) is true for

each pixel of the input video frame. However, both

the visibility v and reﬂectance are unknown. We ob-

serve that most of the input video will closely match

the background image. Noticeable differences will

come from the players on the ﬁeld and any shadows

they cast on the ground.

The key observation that enables our method is

that regions in shadow have the same reﬂectance as

the background but different visibility. The players

themselves will likely have different reﬂectance and

the mismatch can be used to classify the players as

foreground. Following this observation, we proceed

by substituting the background reﬂectance of (3) into

Probabilistic Background Modelling for Sports Video Segmentation

519

Figure 5: Top-left: Input frame, top-right: foreground objects identiﬁed due to high system error, bottom-left: foreground

objects identiﬁed due to abnormally low (red) or high(magenta) visibility values, bottom-right: ﬁnal result. A player from

each team is shown magniﬁed in the bottom-left of each sub-image.

(2) yielding:

I = I

v (4)

The substitution removes the unknown reﬂectance

term and also the constant illumination term L

which

leaves v as the only unknown. Equation (4) holds si-

multaneously for all color channels within the pixel,

with the visibility remaining the same for all three.

This leads to an overdetermined system,

Ax = b (5)

where A is a 3×1 matrix that contains the RGB chan-

nel values of I

, b contains the RGB values of I and

x is the solution to v that we are looking for. We solve

this system using least squares (LS):

= (A

−1

b (6)

which can be solved efﬁciently for a 3 × 1 system.

The relationship between x

, b and the column space

of A is illustrated in Figure 3.

The result of solving Equation (6) for each pixel

within a video frame can be seen in Figure 2 which il-

lustrates that well lit parts have visibility values close

to 1. Furthermore, since we used the background’s

reﬂectance in our formulation, some of the pixels

that represent the payers whose reﬂectance does not

match the background, have visibility values outside

the range [0, 1] which are invalid (marked red on Fig-

ure 2).

The error e of the LS solution for the visibility,

deﬁned as

e = kb −Ax

k (7)

is an indication of the overall quality of the least

squares solution (smaller is better). As illustrated in

Figure 3, the error e is the distance of solution v from

the column space of A, hereby denoted as col(A),

which represents the chromaticity of the background.

For a pixel to belong to the background, v must

have valid values and the error e should be small. This

is formalized in the following section which describes

our background model.

Table 1: Conﬁgurations tested for each algorithm. The best performing conﬁgurations for each algorithm and each dataset

are shown in bold.

Method Metric Football Toscana

MOG2 Mahalanobis distance 64 96 128 160 192 96 128 160 192

GMG Decision threshold .7 .8 .9 .95 .99 .8 .9 .95 .99

ViBe Matching threshold 30 40 50 60 70 15 20 25 30

Ours Decision threshold .1 .2 .3 .4 .5 .01 .05 .1 .15

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

520

Figure 6: Comparison of MOG2, GMG, ViBe and our method for the football data. A zoomed-in view of the highlighted

region of the second frame can be seen in Figure 7.

2.3 Background Model

Our background model utilizes, at each pixel, the vis-

ibility v obtained using the solution of Equation (6)

and the error e given by (7) in order to estimate the

likelihood for the pixel’s color.

We begin by interpreting e as a measure of dissim-

ilarity between the frame pixel and the background

(e.g. a red-wearing player on a green football ﬁeld),

Then, the likelihood function:

p(e|BG) = exp



−

2σ



(8)

where σ

is a model parameter, describes the fact that

background pixels are rarely associated with large

values of e. We have used variance σ

= 25 for all ex-

periments, meaning that p(e|BG) signiﬁcantly drops

when e ≥ 25 units of pixel intensity. A plot of (8)

can be seen in Figure 4a. The top-right image in Fig-

ure 5 shows the result of calculating (8) for each pixel

within a video frame.

It is possible for a foreground object to obtain a

visibility solution with low error e even if it clearly

does not belong to the background. For example, a

player wearing bright green colors on a grass ﬁeld will

Probabilistic Background Modelling for Sports Video Segmentation

521

Figure 7: Zoomed-in view of the results of the second frame of Figure 6.

have low e since bright green is chromatically close to

grass. To handle such problems, we incorporate the

visibility v in our background model.

Visibility values must, by deﬁnition, reside in the

[0, 1] range. It follows that visibility values greater

than 1 are indicative of foreground objects (for exam-

ple players wearing bright colors). Additionally, we

observe that typical sports stadiums are well lit and so

zero illumination areas are unlikely. As a result, very

small visibility values are more likely caused by dark

objects, such as players with dark clothing, rather than

very strong shadows. Based on these observations we

model the likelihood of a pixel’s visibility based on

the background model to be:

p(v|BG) =











exp



−

2σ

(v − v

)



if v < v

1 if v

≤ v ≤ v

exp



−

2σ

(v − v

)



otherwise

(9)

where v

, v

are lower and upper thresholds for the

visibility. Figure 4b illustrates a plot of (9) and Fig-

ure 5 (bottom-left) shows the result of calculating (9)

for each pixel within a video frame. We set v

= 0.2,

= 1 and σ

= 1.5 for all experiments that follow.

Further to the above, a foreground object may

have a visibility value that is within the allowed range

(v ∈ [v

, v

]) but have a different color than the back-

ground (e  0). It is also possible for a foreground

object to be chromatically similar to the background

(e ≈ 0) but have abnormal visibility values. Thus,

to model the pixel color’s likelihood given the back-

ground model, equations (8) and (9) are combined to:

p(e, v|BG) = p(e|BG)p(v|BG) (10)

where conditional independence between v and e

stems from the orthogonality between them (see Fig-

ure 3). Figure 4c illustrates the resulting likelihood

function and an application of (10) on each pixel

within a video frame is illustrated in Figure 5 (bottom-

right).

Finally, having obtained the likelihood as per (10),

our algorithm’s ﬁnal segmentation result is obtained

by thresholding.

3 EVALUATION

For the evaluation of our method we used data from

two football matches (Pettersen et al., 2014) and the

Toscana dataset featuring pedestrians (Maddalena and

Petrosino, 2015). We performed a qualitative and

quantitative comparison against the MOG2 (Zivkovic,

2004) and GMG (Godbehere and Goldberg, 2014)

background segmentation methods as implemented in

OpenCV and the ViBe algorithm (Barnich and Van

Droogenbroeck, 2011) using the implementation pro-

vided by the authors.

We experimented with the decision threshold (or

equivalent) parameter in each algorithm in order to

ﬁnd a high performing conﬁguration. Additionally,

we investigated other parameters such as the shadow

threshold parameter for the OpenCV implementation

of (Zivkovic, 2004), and found that the default set-

tings produced good results. The images shown in

this paper are those produced by the best-performing

conﬁguration of each algorithm, the parameters of

which are listed in Table 1.

Figure 5 shows a frame from the football video

data and the partial results our method uses to achieve

the the ﬁnal segmentation. The top-right image shows

foreground objects identiﬁed due to high system er-

ror using Equation (8). This metric is able to de-

tect foreground objects that are signiﬁcantly different,

chromatically, than the background but has problems

with dark objects. The bottom-left image shows fore-

ground objects identiﬁed by erroneous visibility val-

ues as given by Equation (9). Red segments indicate

low visibility values and are useful for identifying the

players wearing dark uniforms. The magenta seg-

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

522

Figure 8: Comparison of MOG2, GMG, ViBe and our method for a scene with pedestrians.

ments indicate visibility values greater than one and

mostly identify the players wearing bright uniforms.

Combining all metrics using Equation (10) gives a

high quality segmentation (bottom-right). It is noted

that the error metric complements the visibility metric

in some cases, such as the red sleeves on the uniforms,

where the visibility happens to be valid (0.2 ≤ v ≤ 1)

but the color does not match the background thus giv-

ing high error values.

Figure 6 compares our method against the MOG2,

GMG and ViBe background subtractors. A ground

truth segmentation is also shown for reference. In

general, our method is able to correctly identify the

players as foreground while also correctly labelling

shadows as background. By contrast other methods

either mislabel shadows as foreground or mislabel

Probabilistic Background Modelling for Sports Video Segmentation

523

1 2 3 4 5 6 7 8 9 10

0.2

0.3

0.4

0.5

0.6

0.7

128

160

MOG2

1 2 3 4 5 6 7 8 9 10

0.2

0.3

0.4

0.5

0.6

0.7

128

160

MOG2

1 2 3 4 5 6 7 8 9 10

0.2

0.3

0.4

0.5

0.6

0.7

128

160

MOG2

1 2 3 4 5 6 7 8 9 10

0.2

0.3

0.4

0.5

0.6

0.7

128

160

MOG2

Figure 9: F

scores for different conﬁgurations of each algorithm for 10 images of the football dataset. The best conﬁguration

is in bold green.

parts of the players as background. This is highlighted

in more detail in Figure 7. MOG2 misidentiﬁes parts

of the player’s pixels (speciﬁcally the player on the

top) as background. GMG correctly labels the players

but mislabels parts of shadows as foreground. ViBe

behaves similarly to MOG2 but since it is optimized

for speed instead of accuracy much of the players are

mislabelled. Comparably, our method performs bet-

ter because it captures most of the player silhouettes

while avoiding misidentiﬁcation of shadows.

Although our method was implemented with the

speciﬁc domain of sports in mind, Figure 8 shows

that we obtain good results in more general scenes and

outperform the other methods when dark foreground

objects are present.

Our empirical observations are backed by a quan-

titative evaluation. We manually segmented 5 frames

from each football match (using a 150-frame inter-

val between each frame) and the 6 images from the

Toscana dataset and computed their F

scores (Rijs-

bergen, 1979) for various conﬁgurations of each algo-

rithm (Table 1). Figure 9 shows the F

score for each

conﬁguration running on the football dataset. Our

method consistently outperforms the other methods

for most conﬁgurations tested. A similar comparison

was performed to determine the best conﬁguration for

each algorithm for the Toscana dataset (we omit the

graphs due to space constraints). When comparing

the best conﬁguration of each algorithm (Figure 11)

our method outperforms the second-best method by as

much as 10% (5% on average) on the football dataset

and 24% (9% on average) on the Toscana images.

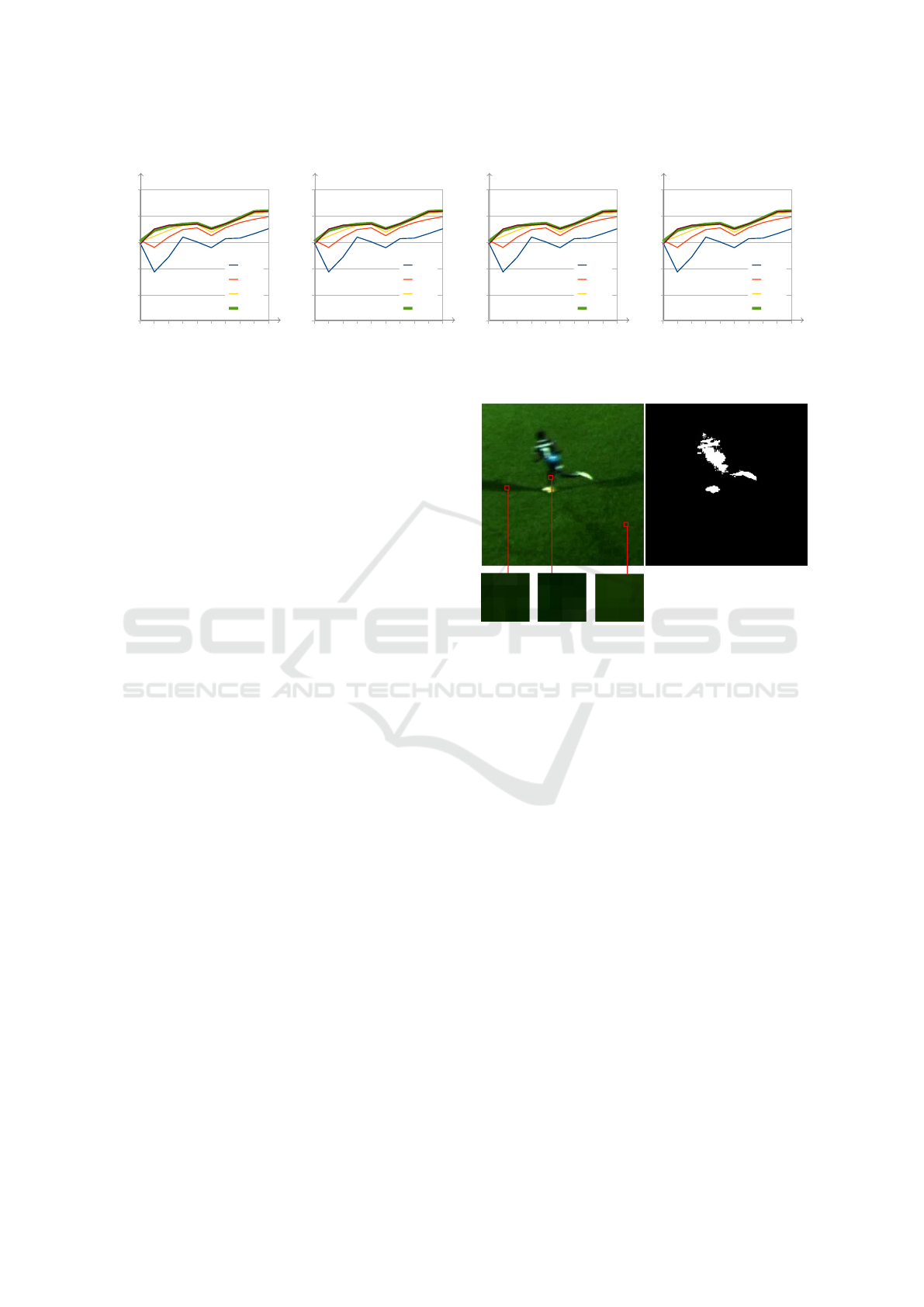
A downside of our model is that it can some-

times misidentify small parts on the players as back-

ground. One such case can be seen in Figure 10.

Because the player is moving quickly, motion blur

blends the color of the player’s leg and the grass turf

behind it producing a dark green color which closely

matches the background when in shadow. As a re-

sult, the algorithm treats that region as shadow and

Figure 10: A failure case. Motion blur causes parts of the

player to match regions in shadow which causes misidenti-

ﬁcation.

assigns low foreground probability. Similar problems

appear when applying the MOG2, GMG and ViBe al-

gorithms indicating that a correct decision may not be

possible based on spectral information alone, and that

additional information may be necessary.

4 CONCLUSIONS AND FUTURE

WORK

We have presented a probabilistic background sub-

traction method based on a Lambertian scene model

for the purpose of segmenting sports video data. We

have shown, both through visual comparison and

quantitative measurements, that our method outper-

forms other commonly used background subtraction

methods for two football matches and a more general

scene with pedestrians.

Our algorithm operates on the pixel level making

it amenable to parallelization. In the future, we would

like to optimize and parellelize our implementation

(possibly on the GPU) and compare timings against

other techniques. Some problems remain when deal-

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

524

1 2 3 4 5 6 7 8 9 10

0.2

0.3

0.4

0.5

0.6

0.7

MOG2 GMG

ViBe Ours

image

1 2 3 4 5 6

0.2

0.4

0.6

0.8

MOG2 GMG

ViBe Ours

image

Figure 11: Comparison of the best conﬁguration of each

algorithm for the football and Toscana data. Our algorithm

consistently outperforms the other methods for the football

dataset and is better for most images of the Toscana dataset.

ing with fast-moving objects that blend with the back-

ground. We plan to explore solutions to these prob-

lems using texture and geometric information. An-

other direction would be to experiment with color

spaces other than RGB whose channels are less cor-

related as it could increase the quality of our least

squares solution. Lastly, we plan to extend the pro-

posed method to operate under variable illumina-

tion conditions, dynamic backgrounds, and non-static

cameras.

REFERENCES

Barnich, O. and Van Droogenbroeck, M. (2011). ViBe:

A Universal Background Subtraction Algorithm for

Video Sequences. IEEE Transactions on Image Pro-

cessing, 20(6):1709–1724.

Chen, C.-C. and Aggarwal, J. (2010). Human Shadow Re-

moval with Unknown Light Source. In 20th Interna-

tional Conference on Pattern Recognition, volume 27,

pages 2407–2410, Istanbul, Turkey.

Duncan, K. and Sarkar, S. (2012). Saliency in images and

video: a brief survey. IET Computer Vision, 6(6):514–

523.

Godbehere, A. B. and Goldberg, K. (2014). Algorithms for

Visual Tracking of Visitors Under Variable-Lighting

Conditions for a Responsive Audio Art Installation.

In Controls and Art, pages 181–204. Springer Inter-

national Publishing, Cham.

Graham, T. (2012). Sports tv applications of computer

vision. BBC Research & Development White Paper

WHP220.

Hsieh, J.-W., Hu, W.-F., Chang, C.-J., and Chen, Y.-

S. (2003). Shadow elimination for effective moving

object detection by Gaussian shadow modeling. Im-

age and Vision Computing, 21(6):505–516.

Huerta, I., Amato, A., Roca, X., and Gonz

alez, J. (2013).

Exploiting multiple cues in motion segmentation

based on background subtraction. Neurocomputing,

100:183–196.

Kaimakis, P. and Tsapatsoulis, N. (2013). Background

Modeling Methods for Visual Detection of Maritime

Targets. In In Proc. Int. Workshop on Analysis and

Retrieval of Tracked Events and Motion in Imagery

Stream, pages 67–76, Barcelona, Spain.

Khan, S. H., Bennamoun, M., Sohel, F., and Togneri,

R. (2014). Automatic Feature Learning for Robust

Shadow Detection. In Proc. Conf. Comp. Vision and

Pattern Recognition, pages 1939–1946, Columbus,

Ohio, USA.

Leone, A. and Distante, C. (2007). Shadow detection for

moving objects based on texture analysis. Pattern

Recognition, 40(4):1222–1233.

Levin, A., Lischinski, D., and Weiss, Y. (2008). A Closed-

Form Solution to Natural Image Matting. Trans. Pat-

tern Analysis and Machine Intelligence, 30(2):228–

242.

Maddalena, L. and Petrosino, A. (2015). Towards Bench-

marking Scene Background Initialization. In Proc

Int. Conf. Image Analysis and Processing, volume

9281, pages 469–476.

Perazzi, F., Krahenbuhl, P., Pritch, Y., and Hornung,

A. (2012). Saliency ﬁlters: Contrast based ﬁltering

for salient region detection. In Proc. Conf. Comp. Vi-

sion and Pattern Recognition, pages 733–740.

Pettersen, S. A., Halvorsen, P., Johansen, D., Johansen,

H., Berg-Johansen, V., Gaddam, V. R., Mortensen,

A., Langseth, R., Griwodz, C., and Stensland, H. K.

(2014). Soccer video and player position dataset. In

Proc. Multimedia Systems Conf., pages 18–23, New

York, USA.

Rijsbergen, C. J. V. (1979). Information Retrieval.

Butterworth-Heinemann, Newton, MA, USA, 2nd

edition.

Sanin, A., Sanderson, C., and Lovell, B. C. (2010). Im-

proved Shadow Removal for Robust Person Tracking

in Surveillance Scenarios. In Proc. Int. Conf. on Pat-

tern Recognition, pages 141–144.

Sanin, A., Sanderson, C., and Lovell, B. C. (2012). Shadow

detection: A survey and comparative evaluation of re-

cent methods. Pattern Recognition, 45(4):1684–1695.

Shahrian, E., Rajan, D., Price, B., and Cohen, S. (2013). Im-

proving Image Matting Using Comprehensive Sam-

pling Sets. In Proc. Conf. Computer Vision and Pat-

tern Recognition, pages 636–643.

Stone, J. E., Gohara, D., and Shi, G. (2010). OpenCL:

A Parallel Programming Standard for Heterogeneous

Computing Systems. Computing in Science & Engi-

neering, 12(3):66–73.

Wang, J. and Cohen, M. F. (2007). Image and Video Mat-

ting: A Survey. Foundations and Trends in Computer

Graphics and Vision, 3(2):97–175.

Yan, Q., Xu, L., Shi, J., and Jia, J. (2013). Hierarchical

saliency detection. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 1155–1162.

Zivkovic, Z. (2004). Improved adaptive Gaussian mixture

model for background subtraction. In Proc. 17th In-

ternational Conf. on Pattern Recognition, volume 2,

pages 28–31 Vol.2, Washington, DC, USA.

Probabilistic Background Modelling for Sports Video Segmentation

525