CSG Ray Tracing Revisited: Interactive Rendering of Massive Models

Made of Non-planar Higher Order Primitives

Seyedmorteza Mostajabodaveh

1,2

, Andreas Dietrich

1,2

, Thomas Gierlinger

1,2

, Frank Michel

1,2

and Andr

e Strok

1,2

Fraunhofer IGD, Darmstadt, Germany

Technische Universit

at Darmstadt, Darmstadt, Germany

Keywords:

Real-time Rendering, Rendering Algorithms, Image-based Rendering.

Abstract:

In many scientiﬁc and engineering areas, CAD models are constructed by combining simple primitives using

Boolean set operations. Rendering such a dataset usually requires a preprocess, where the surface of the CAD

model is approximated by an often highly complex triangle mesh.

Real-time ray tracing provides an alternative to triangle rasterization as it allows for the direct visualization

of (higher-order) solid and planar primitives without having to triangulate them. Additionally, Boolean com-

positing operations can be performed implicitly per ray, primitives have low storage requirements, and curved

surfaces appear pixel-accurate. In this paper we demonstrate these properties using massive real-world CAD

models.

1 INTRODUCTION

Although constructive solid geometry (CSG) is one

of the oldest techniques for modeling solid objects,

it is still found in CAD packages due to its intuitive

concept. Complicated solid objects are constructed

by combining simple solid primitives using Boolean

set operators (typically union, intersection, and differ-

ence). While CSG is often applied to model solids, it

is rarely found in rendering systems. Rather than di-

rectly rendering CSG primitives and composites, such

models are usually preprocessed and converted into a

surface representation, most often a triangle mesh, as

it can be efﬁciently rendered on current graphics hard-

ware. This is a viable approach for small and mid-size

scenes. However, for complex datasets, preprocessing

can become prohibitively time consuming, moreover

it can result in a huge number of triangles, potentially

too many to ﬁt into GPU memory.

An alternative is to directly ray trace complex

CSG models (Glassner, 1989). With the public avail-

ability of real-time ray tracing frameworks, such

as NVIDIA’s OptiX (Parker et al., 2010) or Intel’s

Embree (Wald et al., 2014), it has become feasible to

ray trace even huge CAD models at interactive frame

rates. Additionally, these frameworks scale to multi-

ple GPUs (NVIDIA Optix) or CPUs (Intel Embree)

which is a big advantage compared to rasterization

frameworks. Our CSG ray tracing approach has a

number of attractive beneﬁts:

On-the-ﬂy Compositing. Boolean set operations are

performed on a per-ray basis immediately during

rendering. It is therefore not necessary to ap-

ply them in a preprocess, which enables the user

to change the set operators while inspecting the

scene.

Low Storage Requirement. Since no a priori trian-

gulation of primitives is necessary, they can be

described by a small set of parameters. For ex-

ample, for a cylinder only height and radius need

to be stored. (Additionally a transformation ma-

trix may be needed, but it is not always required

to store a full 4 × 4 matrix as we will see further

below.) This enables holding scenes in memory,

which would not ﬁt in a triangulated form (see

Figure 1).

Pixel-accurate Higher Order Surfaces. Higher or-

der primitives, such as cylinders or tori, can be

directly tested for intersection with a ray by solv-

ing the appropriate equations without having to

triangulate ﬁrst. Consequently, no discretization

artifacts are visible, and curved surfaces appear

perfectly smooth (see Figure 5).

The main contribution of this paper is to present a

method to apply CSG operations in real-time during

258

Mostajabodaveh S., Dietrich A., Gierlinger T., Michel F. and Stork A.

CSG Ray Tracing Revisited: Interactive Rendering of Massive Models Made of Non-planar Higher Order Primitives.

DOI: 10.5220/0006136402580265

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 258-265

ISBN: 978-989-758-224-0

Figure 1: A complex CAD scene built out of 8,000 individual plant models. In total, the scene consists of more than

100,000,000 non-planar second-order (cylinders, cones, etc.) and forth-order (tori) primitives, ray traced at more than

10 frames per second on 16 CPU cores, including pixel-accurate shadows.

ray tracing while keeping the memory overhead low.

Additionally, we have evaluated this method in com-

parison to two well-known rasterization-based CSG

operation techniques: (Goldfeather et al., 1986) and

(Stewart et al., 2002).

Structure of the Paper. In chapter 2, related work

to our approach is described. In chapter 3, our CSG

ray tracing approach and its implementation using

NVIDIA Optix (Parker et al., 2010) is described.

In chapter 4, the proposed ray tracing approach is

compared to rasterization-based CSG rendering ap-

proaches (Goldfeather (Goldfeather et al., 1986) and

SCS (Stewart et al., 2002)). Additionally, we describe

our experiences of applying real-time CSG ray tracing

to models from two different domains. The ﬁrst one

is a complex IC package of a Cell Broadband Engine

chip. The second one is a collection of plant mod-

els described in the AVEVA PDMS 3D model for-

mat (RVM). Conclusions of the paper are presented

in chapter 5.

2 RELATED WORK

An early algorithm for directly ray tracing CSG ob-

jects without extracting a surface mesh was presented

by Roth (Roth, 1982). It computes ray–object inter-

section intervals and combines them using Boolean

operations. Our approach is similar to this paper.

However, we beneﬁt from state-of-the-art ray tracing

techniques and utilize today’s modern parallel graph-

ics and central processors. Later (Goldfeather et al.,

1986) demonstrated how to directly render CSG mod-

els using a depth-layering Z-buffer approach. The

number of render passes required in this method is

of O(n

) complexity where n is the number of prim-

itives. The required number of draw calls for this

method is similarly of subquadratic order. (Wiegand,

1996) implements a GPU accelerated version of this

algorithm. (Stewart et al., 2002) introduces an image-

based Sequence Convex Subtraction(SCS) algorithm

utilizing depth and stencil buffer to render CSG mod-

els. While this approach only supports convex primi-

tives, it can render the CSG model in a constant num-

ber of passes. The drawback of this method is its

large number of required draw calls to achieve the cor-

rect stencil and depth buffer values which is of sub-

quadratic order w.r.t the number of primitives. (Guha

et al., 2003) devised an algorithm which uses depth

and stencil buffers to perform depth peeling (Everitt,

2001) which peels off the model layers and perform

CSG operations on the ﬂy. For every peeled layer,

it tests if the pixels belong to the ﬁnal result. If a

result pixel was found, the pixel is masked for the

next peeling steps to reduce the computation load.

The number of passes for this method is still de-

pendent on the number of primitives which causes

a performance drop when being applied to massive

CSG models. (Hable and Rossignac, 2005) combines

depth peeling and a linear formulation of Boolean ex-

pressions to render CSG models. It depth peels the

scene while performing CSG operations from front-

to-back. The objects need to be drawn in k stages,

where k is the scene’s number of depth-layers. As

massive and complex scenes are made of a tremen-

dous number of layers (e.g. for doing CSG opera-

tions on a PCB board made of many different lay-

ers), this method will have a signiﬁcant performance

drop. More recently, Romeiro et al. (Romeiro et al.,

2006) used a combination of spatial subdivision and

ray tracing methods to render massive CSG models.

They tried to construct a simple Octree containing the

CSG tree which can be used for rendering the model

correctly. As this method ends up with a huge number

of draw calls, it can distribute the workload properly

on CPU and GPU for small enough models. How-

ever, the CPU will limits the GPU rendering for han-

CSG Ray Tracing Revisited: Interactive Rendering of Massive Models Made of Non-planar Higher Order Primitives

259

dling massive models. In 2010 Hijazi et al. (Hijazi

et al., 2010) interactively ray traced CSG objects de-

ﬁned as implicit functions using interval arithmetic.

(Engel, 2014) presents a two stage procedure to ren-

der deformable meshes made by CSG operations. In

the ﬁrst stage, the fragments are collected into a big

enough constantly allocated buffer, and in the second

stage, they are sorted by depth and CSG operations

are applied per-pixel. This method requires a huge

amount of memory to store the whole fragments in

the ﬁrst stage. The size of buffer can exceed the avail-

able GPU memory, e.g. for PCB board models which

contain a lot of different levels of primitives overlap-

ping each other.

3 CSG RAY TRACING

When modeling a scene with CSG techniques, sim-

ple objects, such as boxes, cylinders, tori, etc., form

more complex objects by applying Boolean set opera-

tions, where the basic operators are union, difference,

and intersection. (Although we will here use solids

the concept is also applicable to the combination of

2D objects.) A compound object can be described by

means of a binary tree, where the leaves correspond

to primitives and the inner nodes to set operations.

3.1 Interval Evaluation

Ray tracing such a structure can be done in a straight-

forward way. For each ray all the intersection points

of the ray with the primitives of the scene are calcu-

lated. This leads to a set of intervals that determine the

ranges where a ray runs inside or outside of a prim-

itive. These intervals can be grouped in a so-called

Roth diagram (Roth, 1982). Here, for each primitive

that was pierced by the ray, all entry and exit points

are recorded in a sorted order. For each two primitives

that are to be combined, the intervals in the Roth di-

agram are merged according to the relevant Boolean

operation. The resulting Roth diagram, i.e, the result-

ing intervals, represent the entry and exit points of the

composite object. The entry point with the closest dis-

tance to the ray origin represents the eventual hitpoint

(i.e., the nearest surface point which is visible).

3.2 Optimized Hitpoint Calculation

Obviously, for scenes with millions of primitives this

can result in a high number of intervals. While the

amount of memory required to store these intervals

may be negligible for a single ray, it can become pro-

hibitive on GPUs (or many-core architectures in gen-

eral) where hundreds of thousands of rays may be

traced in parallel.

In order to avoid having to compute and store all

intersection intervals along a ray, we take advantage

of the structure of our scenes. Similar to depth peel-

ing, from the camera perspective the CSG model is or-

ganized into a number of layers L

(i = 1, ..., l). Each

layer is composed of a number of positive solids P

i, j

( j = 1,..., p

) and negative solids N

i,k

(k = 1, ..., n

We will refer to the negative solids as cutouts in the

following. Thus, the CSG operations for a scene S can

be described as

S =

∑

i=1

with L

∑

j=1

i, j

−

∑

k=1

i,k

where + and − denote union and difference set op-

erations, respectively. Basically, a layer can be seen

as the difference of two compound (positive and neg-

ative) objects. Because of this, CSG ray tracing a sin-

gle layer can be done by tracking when a ray runs

within a positive or negative medium. To this end, we

employ two counters (posDepth and negDepth) that

are attached as custom parameters to each ray. When-

ever the ray tracer ﬁnds the closest intersection of a

ray with the primitives of a layer, a hit program is

called which is illustrated in algorithm 1.

Algorithm 1: RayTraceLayer(ray).

ray: current ray hitting a primitive

1: if entering primitive then

2: delta := +1;

3: else

4: delta := −1;

5: end if

7: if positive primitive hit then

8: ray.posDepth += delta;

9: else

10: ray.negDepth += delta;

11: end if

12:

13: if (ray.posDepth > 0) && (ray.negDepth <= 0)

then

14: ReportHit(); // ﬁnal hit in layer found

15: else

16: ContinueRay(ray); // still inside a negative

medium

17: end if

Each time a ray enters or leaves a positive or nega-

tive primitive, the counters are increased or decreased,

respectively. In case we are inside a positive medium,

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

260

but not inside a negative medium, we found the cor-

rect hitpoint corresponding to a layer. Otherwise ray

traversal continues using the updated counters.

To ﬁnd the ﬁnal global hitpoint in the scene, a pri-

mary ray is sequentially tested against all layers, and

from the set of layer hitpoints the nearest one is ac-

cepted as ﬁnal position for shading. In the scene graph

used by the ray tracing engines, the layers of a scene

can be stored as independent sub-trees, which can be

intersected separately.

3.3 Implementation

The heart of a ray tracer is its acceleration struc-

ture. We have used the Bounding Volume Hierar-

chy (BVH) (MacDonald and Booth, 1990) accelera-

tion structure as it provides better performance for our

CSG models than other available acceleration struc-

tures. To exploit multi-threaded acceleration structure

construction in NVIDIA Optix (Parker et al., 2010),

its scenegraph is constructed in correspondence to the

binary tree description of the CSG operations. As we

described in the last section, the ray deﬁnition needs

to be extended to store depth of positive and negative

primitives intersections. Nvidia Optix (Parker et al.,

2010) provides a rtcDeclare macro to attach addi-

tional information to a ray deﬁnition. When a ray–

primitive intersection is reported, the shading func-

tion is executed. The shader is implemented accord-

ing to algorithm 1. The primitives supported by our

implementation are shown in ﬁgure 4.

The ray–primitive intersection test is calculated

with 32-bit ﬂoating point operations for all primi-

tives robustly except the circular torus where inter-

section test equation is quartic; while this equation

type can be solved in constant time (Abramowitz,

1974), achieving a robust solution demands double-

precision calculation. Furthermore, the accumulation

buffer (Haeberli and Akeley, 1990) is used to remove

artifacts from the ﬁnal result image when the camera

is ﬁxed.

4 RESULTS

Our original motivation for applying CSG ray trac-

ing to CAD data stems from two massive models:

A complex electronic circuit that is contained in an

IC package of a Cell Broadband Engine chip (Gjonaj

et al., 2006), and a collection of plant models. To

compare the performance of the CSG ray tracer, we

have proposed three test cases to compare the ray

tracing approach to well-known rasterization image-

based CSG rendering techniques (Goldfeather et al.,

1986) and (Stewart et al., 2002). OpenCSG (Kirsch

and D

ollner, 2005) is a library for image-based CSG

rendering which provides optimized implementations

of these two methods. OpenCSG 1.4 (which is re-

leased September 2014) is used for implementing and

evaluating the test cases. For the sake of simplic-

ity, the primitives rendered with OpenCSG are tessel-

lated with ﬁxed number of triangles which result in

not pixel-accurate images in most of cases; especially

when the primitives are close to the camera.

4.1 Comparison with

Rasterization-based Approaches

To clarify our approach’s beneﬁts, it is necessary to

compare it against state-of-the-art real-time CSG ren-

dering algorithms. Goldfeather (Goldfeather et al.,

1986) and SCS (Stewart et al., 2002) are two of the

well-known CSG rendering methods. OpenCSG as a

library for CSG model rendering provides optimized

implementations of these two methods. Three differ-

ent test cases are deﬁned to compare performance of

our proposed approach in comparison to (Goldfeather

et al., 1986) and SCS (Stewart et al., 2002). The test

cases are deﬁned as follows:

• Unions test model: Consists of a box with n

spheres placed on top of it (Figure 2a).

• Subtraction test model: Consists of a box with

n spheres placed on top of it which are reduced

from the supporting box (Figure 2b).

• Overlapping subtraction test model: The model

consists of a cubic box from which a cubic grid of

spheres is subtracted (Figure 2c).

The test system used for comparison has an Intel

Core i5-6400 CPU, one NVIDIA Geforce GTX 960,

and 16 GB of memory.

The rasterization-based and ray tracing based

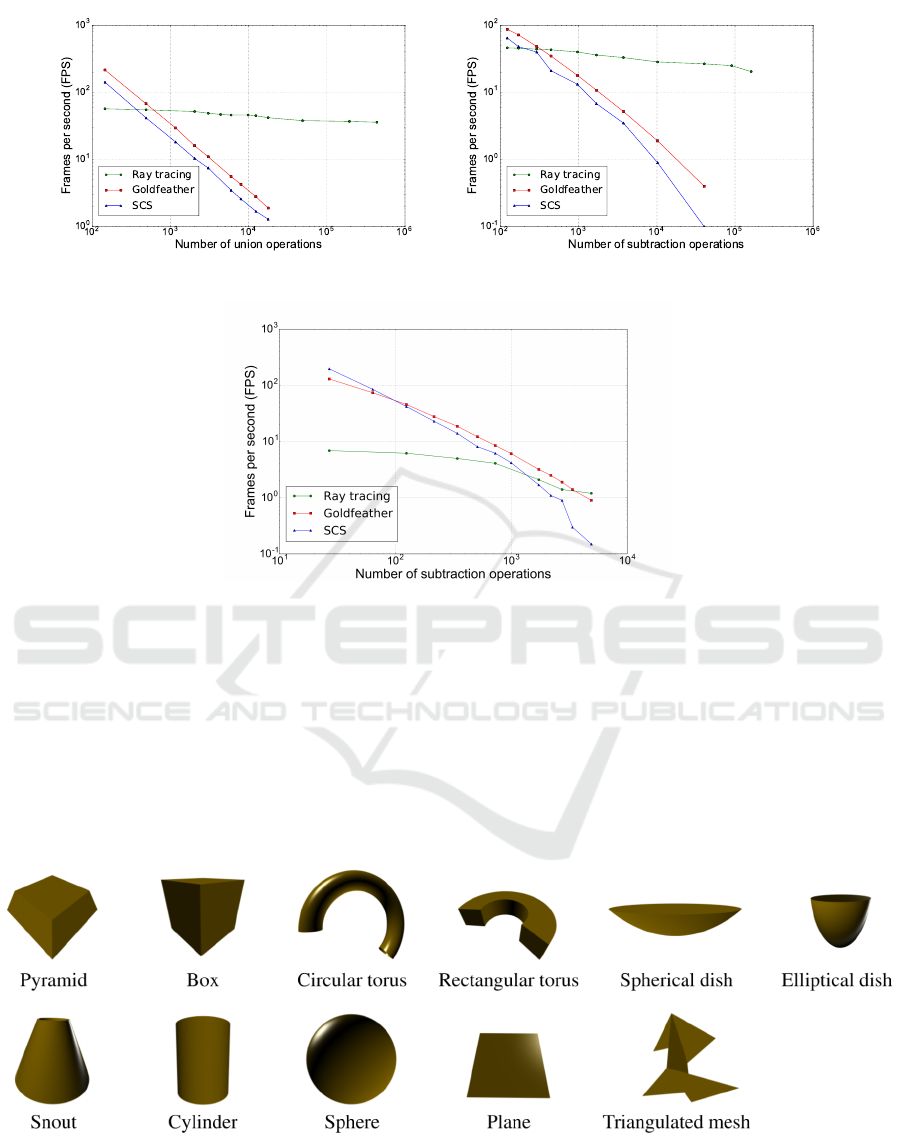
evaluation results are shown in ﬁgure 3. Figure 3a

shows the number of union operations and resulting

frames per second for rendering the union test case.

It shows that the rasterization-based rendering meth-

ods are faster for few number of primitives. However,

their performance vanishes with increasing number of

union operations. The ray tracing approach’s perfor-

mance is reducing with lower rate in comparison to

the rasterization-based approaches w.r.t. the number

of CSG operations. Furthermore, It can be seen that

the ray tracing approach keeps 40 frames per second

while rendering 1 million pixel-accurate spheres.

Figure 3b shows the rendering performance curve

(frames per second) of different rendering approaches

for models with different number of subtraction oper-

ations. Similar to the union test case, for a small num-

CSG Ray Tracing Revisited: Interactive Rendering of Massive Models Made of Non-planar Higher Order Primitives

261

(a) model made by union operations (b) model made by subtraction opera-

tions

tion operations

Figure 2: Evaluation of CSG models. Three CSG models were designed to compare the proposed CSG ray tracing approach

against (Goldfeather et al., 1986) and (Stewart et al., 2002) rasterization-based CSG rendering algorithms. The ﬁrst model

(left ﬁgure) is the union of a number of spheres and a supporting box underneath. The second model (middle ﬁgure) is similar

to the ﬁrst model but the spheres are subtracted from the supporting box. The last model (right ﬁgure) is constructed by

subtracting a 3d grid of spheres from a box. These cases are used to evaluate every aspect of CSG operations. The ﬁrst one

is used to evaluate rendering of unions of primitives, the second one evaluates rendering of subtracted primitives, and the last

one is used to evaluate rendering of overlapping subtracted primitives. The evaluation results are shown in ﬁgure 3.

ber of subtractions the performance of rasterization-

based rendering approaches is higher than ray tracing.

Similarly it is abruptly dropping by increasing num-

ber of subtraction operations. A box with 200,000

holes inside can be ray traced approximately 20 times

per second.

Figure 3c shows the rendering performance for

the model made by subtracting different number of

overlapping holes. Since a lot of overlapping primi-

tives exist in this case, enabling hardware occlusion

query (Bittner et al., 2004) can have a signiﬁcant im-

pact on the Goldfeather and SCS rendering modes be-

cause the primitives which do not contribute to the

ﬁnal frame buffer will be removed from CSG render-

ing draw calls. Our measurements show that the oc-

clusion query improves the performance by factor of

2-10 for Goldfeather and 2-30 for SCS.

In this case ray tracing performance curve is

much lower than rasterization-based methods. On

our test machine ray tracing performance outperforms

the rasterization-based methods when more than 5

thousand CSG operations are performed. Although

number of frames per second is still larger than for

rasterization-based methods beyond 5k operations,

the absolute performance is not interactive anymore

(below 1 frames per second). The ray tracing per-

formance drops because a lot of subtracted primitives

are overlapping, the rays stop at every ray–primitive

intersection and a new ray is shot against the next sub-

tracted primitive. The acceleration structure has to be

traversed from root for every new ray shot which will

decreases the performance signiﬁcantly.

4.2 Electric Circuit Model

A more practically relevant example, is an electric

circuit model consists of a number of stacked circuit

layers that are interconnected. In order to describe

the circuits, the model makes use of three different

primitives: extruded polygons, oriented boxes, and

cylinders (no triangles were used). Boxes are typi-

cally used for conductive circuit paths, while cylin-

ders model so-called vias, which connect circuit lay-

ers. Essentially, each model layer is an extruded 2D

design. This allows for storing the geometry data in a

very efﬁcient way. For example, cylinders are always

oriented perpendicular to the layers, and only require

a center, vertical extrusion and radius as parameters.

Likewise, an extruded polygon is described by a set

of 2D points, plus its vertical position and extrusion

length. The extrusion vector is always perpendicular

to the 2D area.

Figure 5 shows two layers of the circuit model. It

can be seen how circular cutouts cut holes into an ex-

truded polygon. Conductive traces are formed with

boxes and cylinders. Since for all primitives the inter-

section with a ray is directly calculated, all curved sur-

faces are pixel-accurately displayed without the need

to use explicitly deﬁned triangles.

For this scene we implemented all functions for

intersecting, shading, and traversal as custom pro-

grams in NVIDIA’s OptiX (Parker et al., 2010) frame-

work. The test scene shown in Figure 5 consists

of more than 88,000 primitives. On an NVIDIA

GeForce GTX 980 it can be rendered at more than

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

262

(a) Evaluation of union CSG operations (b) Evaluation of subtraction CSG operations

Figure 3: Evaluation of CSG model rendering using different algorithms. The proposed ray tracing approach, and two

other rasterization-based CSG rendering methods (Goldfeather (Goldfeather et al., 1986) and SCS (Stewart et al., 2002))

are compared for rendering the models shown in Figure 2. Figure 3a evaluates the performance of rendering unions of

primitives. The performance of the rasterization-based rendering methods reduced signiﬁcantly with increasing number of

CSG operations while the ray tracing approach performance is reducing slowly. The evaluation shows that the ray tracing

approach is well-ﬁt to massive model rendering. Figure 3b evaluates the performance of primitive subtraction rendering. It

similarly shows that the ray tracing approach has signiﬁcantly better performance for rendering a large number of subtracting

primitives. Figure 3c diagram evaluates rendering of CSG models having overlapping subtraction primitives. Calculating

pixel color covering a lot of overlapping subtracting primitives result in a lot of ray–primitive intersections which requires

traversing the ray tracer’s acceleration structure multiple times per pixel. Therefore the performance of the ray tracer drops

signiﬁcantly while the impact on the stencil-buffer approaches is more moderate.

Figure 4: RVM primitives used in the plant model.

50 frames per second at full HD resolution. 4.3 Plant Model

This model (see Figure 1) was exported from the

AVEVA PDMS 3D CAD software, which is tailored

CSG Ray Tracing Revisited: Interactive Rendering of Massive Models Made of Non-planar Higher Order Primitives

263

Figure 5: Two views of a Cell IC package. Top: Overview

of the layers. Bottom: Closeup view showing some cutouts.

Note the pixel-exact curved surfaces.

to the design of plant projects. The resulting data

is stored in RVM format (AVEVA, 2001). RVM de-

scribes geometry as a tree of named groups contain-

ing 11 types of primitives (including solids and pla-

nar primitives). Figure 4 shows the different RVM

primitives used to describe the plant model. In this

version of the model only positive primitives are in-

cluded, therefore only union operations need to be

performed, i.e., simply the closest ray intersection of

all primitives has to be determined.

The provided CAD data contains four different

plant datasets of varying size. As a stress test we

replicated them randomly 8,000 times. This resulted

in a scene consisting of more than 100,000,000 non-

planar primitives. Including acceleration structures

the whole scene amounts to more than 50 GB in

size. As this amount of data is too big to ﬁt into

GPU memory, we ported our routines over to Intel’s

Embree (Wald et al., 2014) CPU ray tracing frame-

work. On a PC ﬁtted with 64 GB of main memory and

two Intel Xeon E5-2650 v2 eight-core CPUs (clocked

at 2.60 GHz) the complete scene can be visualized at

10–20 frames per second including shadows.

Figure 6 presents two views illustrating the high

amount of detail found in the scene. Notice the intri-

cate structure of the pipes and tubes. Again, curved

Figure 6: Close up view of the plant model. The intri-

cate structure is modeled with the primitives described in

the AVEVA RVM CAD format.

surfaces appear pixel-exact.

5 CONCLUSIONS

In this paper, we demonstrated the application of real-

time ray tracing of massive CSG models made of

(higher-order) primitives using available state-of-the-

art ray tracing engines. This approach is of high prac-

tical relevance since in many scientiﬁc and engineer-

ing disciplines CAD models are designed which con-

sist of simple (solid or planar) primitives that can

be directly displayed by a ray tracer without hav-

ing to resort to triangulation. Apart from a straight-

forward implementation, real-time CSG ray tracing

has the advantage of on-the-ﬂy compositing (with-

out any pre-processing), low storage requirements,

and pixel-accurate curved surfaces. Our results show

that our approach which is beneﬁting from today’s ad-

vanced rendering techniques has higher performance

for rendering massive CSG model compared to well-

known approaches e.g. Goldfeather (Goldfeather

et al., 1986) and SCS (Stewart et al., 2002). Addition-

ally, we applied our approach to two practical models:

PCB board, and factory which are made by CSG oper-

ations. We showed that 100 Mio of non-planar higher

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

264

order primitives (second-order and forth-order) can be

ray traced on 16 cores CPU at 10 frames per second.

ACKNOWLEDGEMENTS

The work of the authors has been supported by the

European Union’s Seventh Framework Programme

(FP7/2007-2013) under grant agreement no 619439.

REFERENCES

Abramowitz, M. (1974). Handbook of Mathematical Func-

tions, With Formulas, Graphs, and Mathematical Ta-

bles,. Dover Publications, Incorporated.

AVEVA (2001). PDMS DESIGN Reference

Manual Part 3: Elements and Attributes.

http://www.scribd.com/doc/23187647/Pdms-Design.

Bittner, J., Wimmer, M., Piringer, H., and Purgathofer, W.

(2004). Coherent hierarchical culling: Hardware oc-

clusion queries made useful. Computer Graphics Fo-

rum, 23(3):615–624.

Engel, W. (2014). GPU Pro 5: Advanced Rendering Tech-

niques. CRC Press.

Everitt, C. (2001). Interactive order-independent trans-

parency.

Gjonaj, E., Perotoni, M., and Weiland, T. (2006). Large

Scale Simulation of an Integrated Circuit Package.

In Proceedings of the 15th Conference on Electrical

Performance of Electronic Packaging (EPEP), pages

291–294.

Glassner, A. (1989). An Introduction to Ray Tracing. Mor-

gan Kaufmann.

Goldfeather, J., Hultquist, J. P., and Fuchs, H. (1986). Fast

Constructive-Solid Geometry Display in the Pixel-

Powers Graphics System. In Computer Graphics

(Proceedings of ACM SIGGRAPH), pages 107–116.

Guha, S., Krishnan, S., Munagala, K., and Venkatasubra-

manian, S. (2003). Application of the two-sided depth

test to csg rendering. In Proceedings of the 2003 Sym-

posium on Interactive 3D Graphics, I3D ’03, pages

177–180, New York, NY, USA. ACM.

Hable, J. and Rossignac, J. (2005). Blister: Gpu-based ren-

dering of boolean combinations of free-form triangu-

lated shapes. ACM Trans. Graph., 24(3):1024–1031.

Haeberli, P. and Akeley, K. (1990). The accumulation

buffer: Hardware support for high-quality rendering.

In Proceedings of the 17th Annual Conference on

Computer Graphics and Interactive Techniques, SIG-

GRAPH ’90, pages 309–318, New York, NY, USA.

ACM.

Hijazi, Y., Knoll, A., Schott, M., Kensler, A. E., Hansen,

C. D., and Hagen, H. (2010). CSG Operations of Ar-

bitrary Primitives with Interval Arithmetic and Real-

Time Ray Casting. In Scientiﬁc Visualization: Ad-

vanced Concepts, pages 78–89.

Kirsch, F. and D

ollner, J. (2005). Opencsg: A library for

image-based csg rendering. In Proceedings of the An-

nual Conference on USENIX Annual Technical Con-

ference, ATEC ’05, pages 49–49, Berkeley, CA, USA.

USENIX Association.

MacDonald, D. J. and Booth, K. S. (1990). Heuristics for

ray tracing using space subdivision. Vis. Comput.,

6(3):153–166.

Parker, S. G., Bigler, J., Dietrich, A., Friedrich, H., Hobe-

rock, J., Luebke, D., McAllister, D., McGuire, M.,

Morley, K., Robison, A., and Stich, M. (2010). OptiX:

A General Purpose Ray Tracing Engine. In ACM

Transactions on Graphics (Proceedings of ACM SIG-

GRAPH), pages 66:1–66:13.

Romeiro, F., Velho, L., and de Figueiredo, L. H. (2006).

Hardware-assisted Rendering of CSG Models. In Pro-

ceedings of XIX Brazilian Symposium on Computer

Graphics and Image Processing (SIBGRAPI), pages

139–146.

Roth, S. D. (1982). Ray Casting for Modeling Solids. Com-

puter Graphics and Image Processing, 18(2):109–

144.

Stewart, N., Leach, G., and John, S. (2002). Linear-time

csg rendering of intersected convex objects. In In 10th

International Conference in Central Europe on Com-

puter Graphics, Visualization and Computer Vision -

WSCG 2002 (2002, pages 437–444.

Wald, I., Woop, S., Benthin, C., Johnson, G. S., and Ernst,

M. (2014). Embree: A Kernel Framework for Efﬁcient

CPU Ray Tracing. In ACM Transactions on Graph-

ics (Proceedings of ACM SIGGRAPH), pages 143:1–

143:8.

Wiegand, T. E. (1996). Interactive rendering of csg models.

Computer Graphics Forum, 15(4):249–261.

CSG Ray Tracing Revisited: Interactive Rendering of Massive Models Made of Non-planar Higher Order Primitives

265