Cost-efﬁcient Localisation System for Agricultural Use Cases

abor Paller

, S

ebastien Aubin

, G

abor

and Olivier Camp

echenyi Istv

an University, Information Society Research & Education Group, Egyetem t

er 1. Gy

or, Hungary

ESEO, 10 Boulevard Jean Jeanneteau, Angers, France

Keywords:

Agriculture, Low-cost Localisation, Trilateration Simulation.

Abstract:

Connected agricultural applications often depend on exact localisation solutions. Often the term “precision

agriculture” implies a technology that identiﬁes the location of the livestock, crop, ﬁeld of agricultural ma-

chinery with more or less of precision. While precision requirements vary, the localisation often has to be

quite precise like sub-meter or even decimeter precision. Dual-band GPS solutions are able to satisfy these

high-precision requirements but these equipments are quite costly and their purchase is often regulated. This

paper presents two agricultural use cases and the combination of low-cost GPS and short-range localisation

systems that are able to satisfy high-precision requirements for fraction of the costs of dual-band GPS.

1 INTRODUCTION

Connected sensor applications in the agriculture do-

main often require precise localisation functionality.

The state-of-the art solution is high-precision dual-

frequency GPS receiver with Real-Time Kinematic

(RTK) support. Typically these receivers cost 3-

4000 USDs and have strict control of purchase which

makes them suitable for a costly agricultural machine

like a combine-harvester but are prohibitively expen-

sive for localising less valuable moving objects. Pre-

cise localisation requirements have arisen in two sep-

arate projects run by the institutions collaborating in

the research described in this paper. At ESEO, the

task is to localise dairy cows with a precision of less

than 1 meter. At Sz

echenyi University our task was

to mobilize the agricultural camera sensor (Paller and

o, 2016) by mounting it onto a robot vehicle that

traverses a predetermined trajectory. For this use case,

precise localisation is needed to keep the robot on

the tracks (typically dirt roads) used by agricultural

machines. We targeted the precision requirement of

better than 1 meter in this case too. In both cases,

the value of the objects to be tracked does not justify

expensive GPS receivers that are also hard to protect

against theft on the ﬁeld.

Even though the requirements seem to be similar,

they are not the same. The robot localisation task may

allow a limited number of ﬁxed stations while for the

cow localisation, the use of such ﬁxed stations is dis-

couraged. The robot’s movement is under our control,

e.g. it is possible to stop the robot to allow for more

precise localisation. For the cows, such “stopping” is

not possible.

The paper shall be organised as follows.

• Section 2 presents our ﬁndings with regards to the

precision of low-cost standalone and differential

GPS solutions.

• Section 3 evaluates a low-cost differential solu-

tion.

• Section 4 presents behavioural analysis of dairy

cows based on publicly available measurement

data that supports our proposal for a localisation

solution using RTK GPS and short-range localiza-

tion technologies.

• Section 5 presents our proposal for distance-based

short-range localisation technique.

• Section 6 presents our proposal for an angle-based

short-range localisation technique.

2 EVALUATION OF LOW-COST

STANDALONE AND

DIFFERENTIAL GPS

GPS measurements are subject to satellite and re-

ceiver clock errors, ionosphere and troposphere prop-

agation delays, multipath and random noise er-

rors. The most interesting factor of standalone (non-

differential) GPS receivers is the ionospheric delay.

142

Paller G., Aubin S., ÃL’lÅ

S G. and Camp O.

Cost-efﬁcient Localisation System for Agricultural Use Cases.

DOI: 10.5220/0006137501420149

In Proceedings of the 6th International Conference on Sensor Networks (SENSORNETS 2017), pages 142-149

ISBN: 421065/17

The electromagnetic property of the ionosphere inﬂu-

ences the electromagnetic signals’ propagation speed,

including that of GPS signals. As the signal propaga-

tion speed is used in the pseudorange calculation (the

satellite’s distance from the receiver deduced from the

signal delay between the satellite and the receiver),

changes in the real propagation speed introduce errors

into pseudorange calculations. This error ranges from

1 meter to up to 50 meters in case of satellites with

low elevation and even higher in case of increased so-

lar activity.

Ionospheric delay is complicated from the error

correction point of view because it introduces system-

atic (non-random) location measurement error. Even-

tually the mean value of this error is close to zero but

that needs very long observation period, in the range

of several hours (Langley, 1991). Dual-frequency

GPS receivers can ﬁlter out this error but these re-

ceivers are very costly. Space-Based Augmentation

Systems (SBAS) is a differential GPS technology that

transfers corrections over satellites that are distinct

from GPS satellites, still transmit data on GPS fre-

quencies. SBAS signals are often problematic to re-

ceive on ground level. We made measurements with

SBAS-equipped GPS receivers to ﬁgure out, what

precision can be achieved with this technology in our

use cases. The SBAS receiver was MediaTek 3339,

equipped with ceramic patch antenna or external ac-

tive antenna. As reference, Ashtech Z-Xtreme high-

precision dual-band receiver was used in static sur-

vey (non-differential) mode. The measurements were

made in the Angers area, France. We also made mea-

surements at a geodetic reference site (Ecouﬂant I)

whose coordinates have been established with high

precision by the National Institute of Geographic and

Forestry Information (IGN) of France.

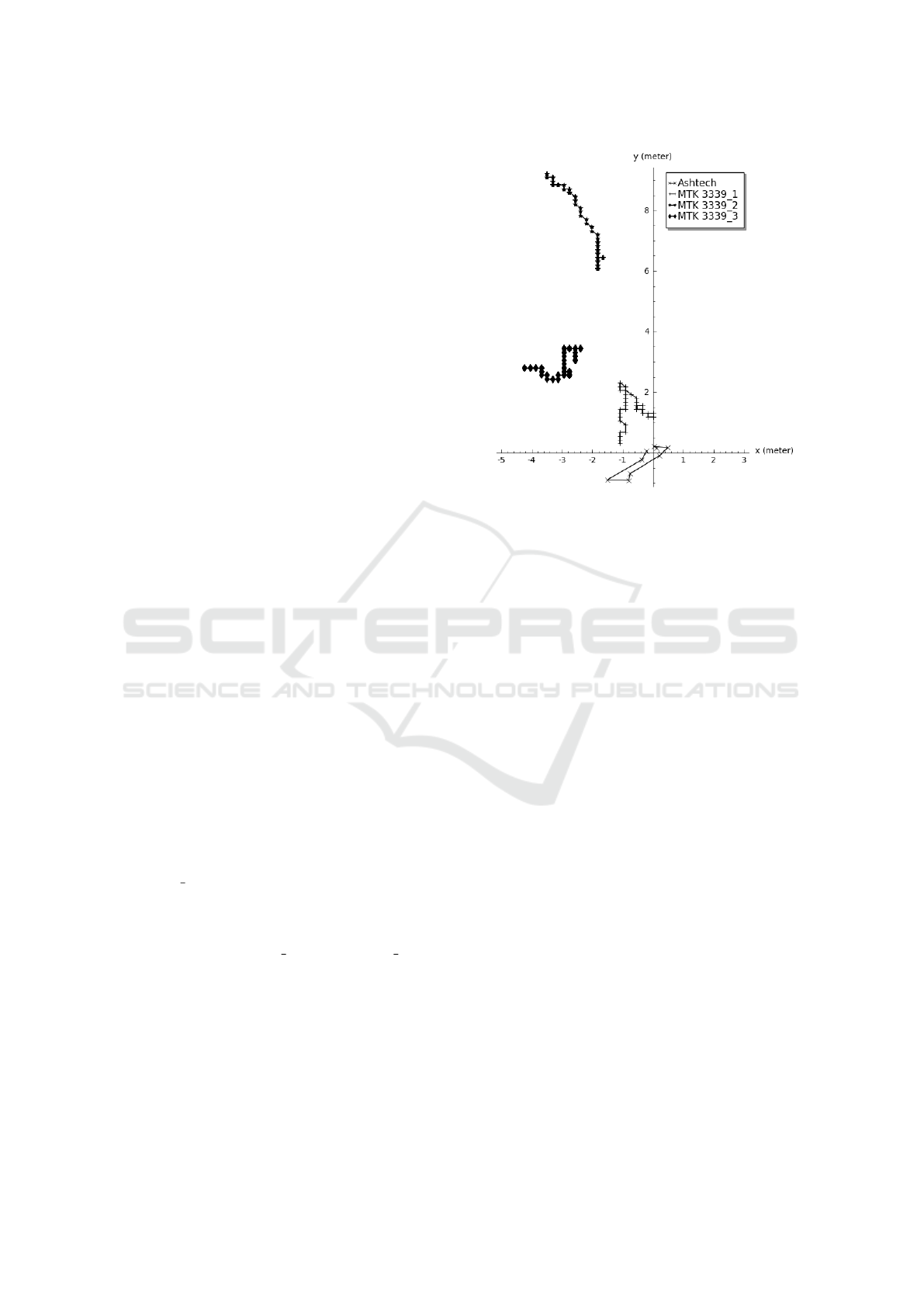
Figure 1 shows the results of a typical mea-

surement at the reference site. The origo of the

graph is the IGN reference coordinate for the site,

deviation from the origo means measurement error.

MTK3339 2 was not able to lock on the SBAS sig-

nal (even though the other two modules in its vicinity

were eventually able to receive SBAS corrections),

this fact is reﬂected in its much less precise mea-

surements than MTK3339 1 and MTK3339 3. The

two modules that did lock on SBAS produced much

less precise locations than the 1 meter error required.

Even the advanced Ashtech reference receiver had a

maximum error that was larger than 1 meter.

The maximum error relative to the reference point

measured with the MTK3339 was in the 2.22-11.51

meters range. All the measurements were made in

an environment that models agricultural conditions:

mostly ﬂat area with minor depressions, low vegeta-

Figure 1: Results of one measurement at Ecouﬂant I site.

tion with occassional trees. The reference coordinates

were either taken from the Ashtech receiver (when

the measurement was not performed at the geodetic

reference point) or were the coordinates speciﬁed by

IGN for the reference point. The measurement ses-

sions lasted 10 minutes, measured from the moment

when all the 3 SBAS receivers locked on the SBAS

signal. This could take quite a long time depending

on the location and time of the day, it was quite com-

mon that 10-15 minutes needed from the ﬁrst GPS

location ﬁx to the ﬁrst SBAS ﬁx and there were mea-

surements when one module could not even obtain

SBAS ﬁx, in spite of the fact that the SBAS receivers

were placed very near to each other (3 centimeters).

When the SBAS signal was not acquired, the maxi-

mum error was 30.89 meters. Our conclusion based

on the ﬁeld measurements is that low-cost GPS re-

ceivers even with SBAS differential corrections are

not able to satisfy our requirement of 1 meter accu-

racy. In addition, SBAS signal cannot be reliably ac-

quired on ground level.

3 EVALUATION OF LOW-COST

DIFFERENTIAL GPS

Our measurements presented in section 2 convinced

us that a low-cost GPS receiver supporting only the

L1 band is only able to support our accuracy re-

quirements if it is used in differential mode. The

goGPS software (Herrera et al., 2016) was created

to support exactly these kinds of receivers with dif-

Cost-efﬁcient Localisation System for Agricultural Use Cases

143

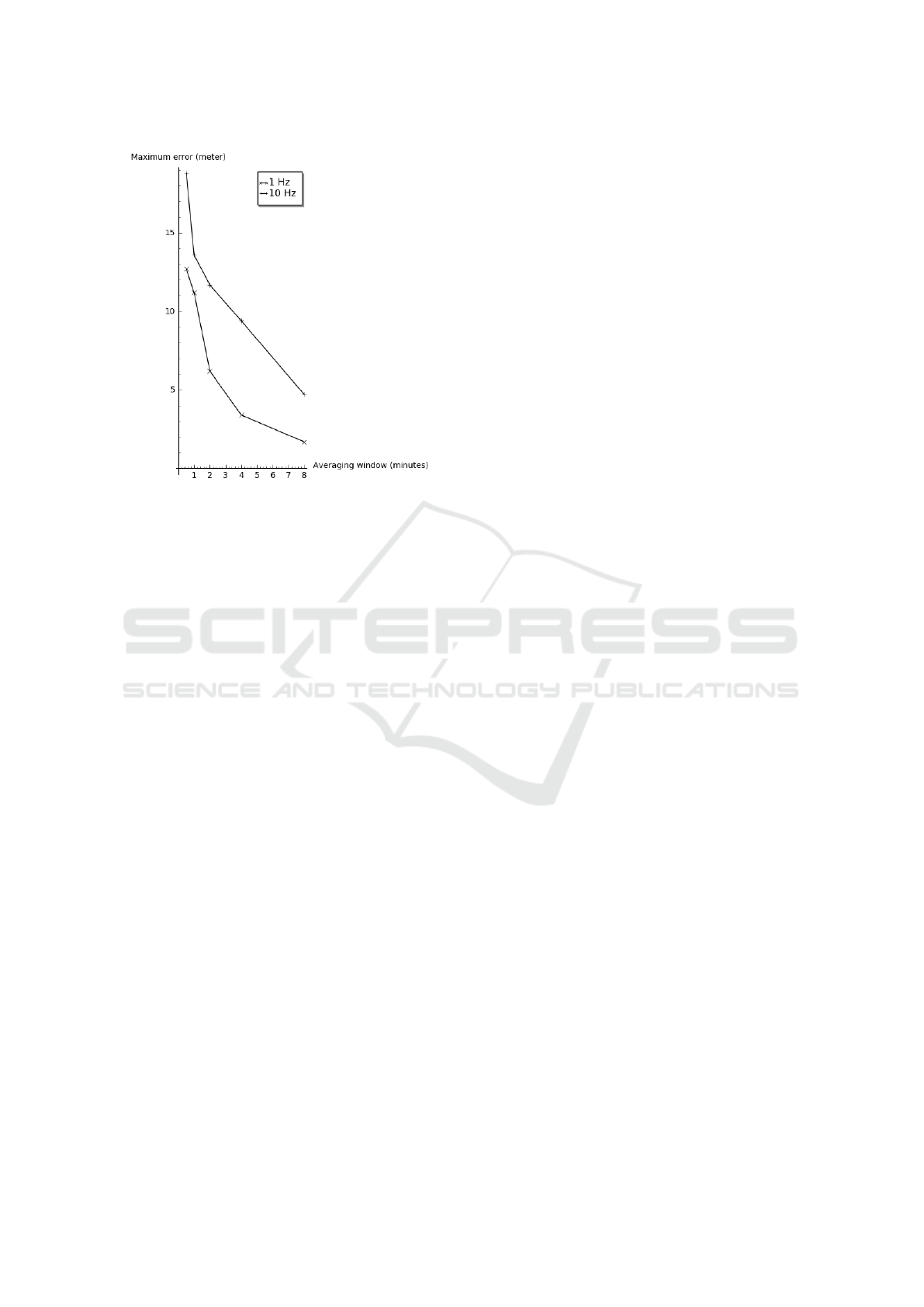
Figure 2: Maximum position error as a function of sampling

frequency and averaging time.

ferential support. Readers interested in the details

of goGPS should consult the cited references, only a

brief overview is presented here.

In order to enhance the baseline accuracy of low-

cost receivers, goGPS relies on raw observation data

(pseudorange, carrier phase) from the GPS receiver,

provided by the u-blox LEA-6T receiver in our case.

We used goGPS in off-line mode when the rover and

the master are not connected during the measure-

ments. It is possible to set up the system with two

low-cost receivers (one in master role located at a

well-known coordinate and one in rover role) or with

one professional reference station in master role (we

used IGN’s NGER reference station which is about 10

km from the location where the measurements were

made) and a low-cost receiver in rover mode.

Double differencing in differential GPS mode

eliminates efﬁciently the effect of ionospheric delay

but other error terms like random noise, multipath ef-

fects and receiver clock errors still affect the locations

calculated by the goGPS software. Figure 2 shows

the maximum position error when the GPS receiver

sampling frequency was 1 Hz and 10 Hz as a func-

tion of sliding averaging window length. The window

length was between 0.5 min and 8 min. The ﬁgure

demonstrates that the residual position error can be

efﬁciently decreased with low-pass ﬁltering but this

affects the temporal sensitivity of the system which

cannot be compensated by increasing the receiver’s

sampling frequency.

The effect of high-quality reference station mas-

ter vs. using a low-cost receiver as master was also

evaluated. High-quality reference station decreases

the noise of at least the master receiver. On the other

hand, the IGN reference station had a sampling pe-

riod of 30 seconds. The goGPS software assumes a

1:1 relationship between rover and master samples,

discarding rover samples if there is no corresponding

master sample. The outcome is a signiﬁcant reduc-

tion of effective sampling frequency which reduces

the averaging window size to achieve the same tem-

poral sensitivity. We evaluated the effect in two mea-

surements and we found that the maximum error with

low-cost master station was 1.3 meters while the max-

imum error with IGN master was 3.31 meters. While

this measurement cannot be considered extensive, it

indicates that high-quality master may improve the

accuracy only if its sampling frequency is compara-

ble with that of the rover.

We conclude that goGPS is indeed capable of pro-

ducing location measurements using data from low-

cost receivers if the target is stationary for at least 8-

10 minutes. In case of moving targets (in particular in

case of targets moving unpredictably like the cows)

its error quickly increases so that trajectory tracking

becomes impossible.

4 BEHAVIOURAL ANALYSIS OF

DAIRY COWS

In this section we analyse whether it is possible to

measure cow location in spite of the restriction im-

posed by goGPS’ deﬁciency in tracking moving tar-

gets. The other use case is simpler as we control the

movement of the robot entirely so if there is a need of

a precise location ﬁx, we can stop the movement for

the required period. Cows, however, move according

to their will and if they do not stay stationary for long

enough, the low-cost rover will not be able to acquire

the target’s accurate position even occasionally. This

phase of the research was accomplished based on data

sets acquired by earlier research projects. (Wietrzyk

and Radenkovic, 2007) (from now called Notting-

ham measurement) tracked 6 dairy cows for 2 days

using GPS collars. Based on our experiences about

GPS accuracy (see section 2), we consider the target

stationary if its location does not change more than

3 meters from the baseline position acquired when

the assumed stationary period started for 10 minutes.

(De Weerd et al., 2015) (from now called Weerd mea-

surement) tracked 9 cows for 11 days and added hu-

man observations to high-frequency GPS data. Hu-

man observations attach 7 labels to high-frequency

GPS data of which we considered 5 (“Drinking”,“Dry

forage”,“Foraging”,“Standing”, “Grooming”) as sta-

tionary. If the animals stayed for at least 10 minutes

SENSORNETS 2017 - 6th International Conference on Sensor Networks

144

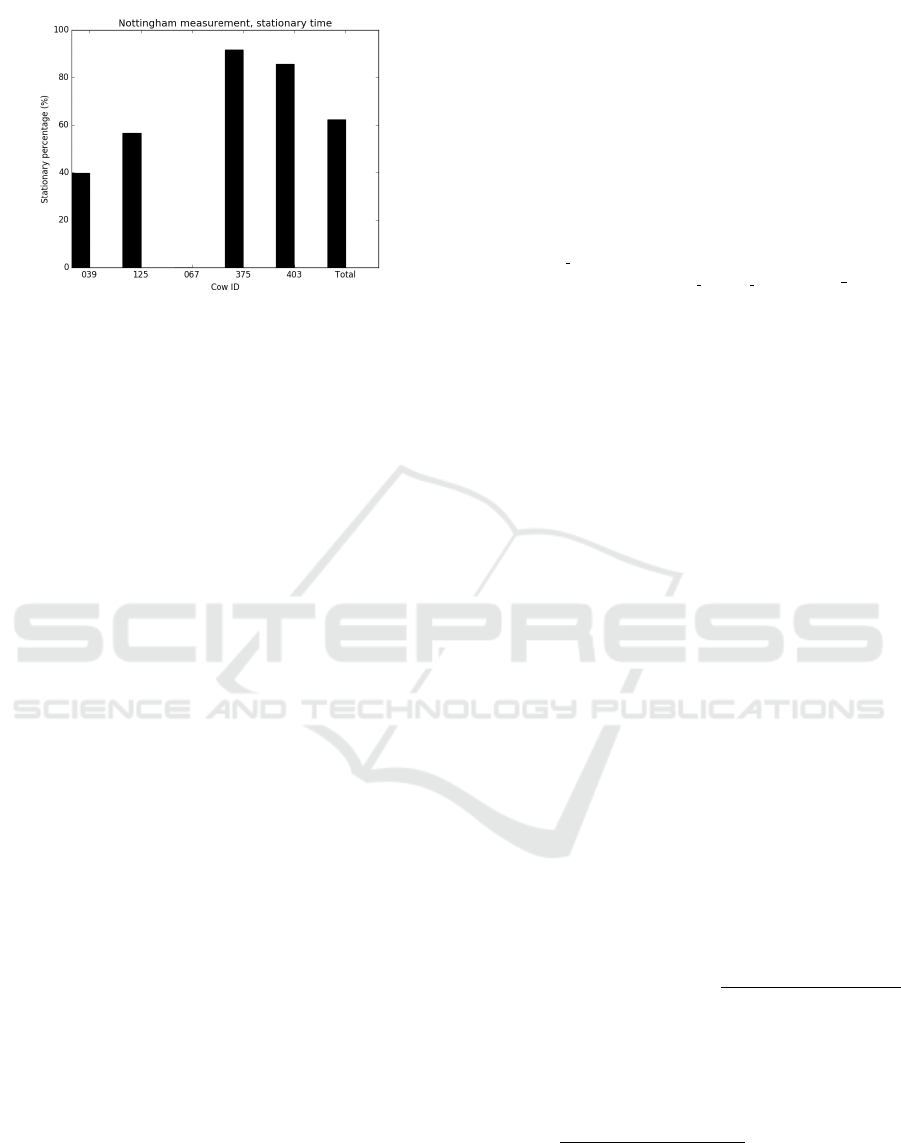
Figure 3: Stationary time per cow, Nottingham measure-

ment.

in a stationary state, then the time spent in the state

was added to the stationary time. The total stationary

time was derived in this case entirely from human-

observed labels. We processed only open-ﬁeld (as op-

posed to forest) measurement in this paper.

Figure 3 presents the stationary time for the Not-

tingham measurement, by cow. One cow was found

to be stationary all the time and its data has been elim-

inated from this chart. In general, the cows spend 40-

90% of their time stationary even though the one with

ID of ”067” was constantly moving. Eventually on

average the 5 cows were stationary for 62.3% of their

time.

The Weerd measurement presented much more

uniform picture. All the 9 cows were found to be sta-

tionary between 79.5 %-89.8 % of the time with an

average of 80.9 %. We therefore concluded that even

though the movement pattern of the animals depends

on the particular cow, it can be assumed with high

probability that at least some animals in the group stay

stationary for the time period needed for an accurate

GPS measurement. These animals can be used as ref-

erence points to locate the animals that were found

to be moving with short-range distance or angle mea-

surement methods.

5 DISTANCE-BASED

SHORT-RANGE

LOCALISATION

The problem of the distance-based short-range lo-

calisation is the following. We intend to localise a

point with unknown position on a 2D map based on

distance measured from reference points with well-

known positions. We can then calculate the position

of the unknown point with a trilateration algorithm

(Cheung et al., 2006). We assume that the cows are

equipped with an Ultra-Wideband (UWB) range mea-

suring system and a GPS. There are competing UWB

technologies on the market that we are still evaluat-

ing. UWB system is for the relative distance estima-

tion among the animals and the GPS is for absolute

positions. We have to understand how the errors of

each system affect the unknown position’s estimation

error. Trilateration studies often omit the error to sim-

plify the equations’ resolution.

The ﬁrst part of our simulation is a simple problem

with N well-known ﬁxed points. If we measure all the

distances r

n wpt/u

between the well-known points with

the following coordinate [x

n wpt

] with n wpt =

1,...,N and the unknown point [x

], we can ﬁnd the

unique point, only if all the well-known points are not

aligned. a system with simple circles equations give

this results.

5.1 The Effect of Distance

Measurement Error

In the ﬁrst simulation we tried to ﬁnd how an error

on distance measurement could affect the reconstruc-

tion of the unknown point. The aim of this simu-

lation is to verify if we can reconstruct the position

of an unknown point and to determine what is the

error of the unknown point estimation in the pres-

ence of distance measurement error. We have tried

N = {4,5,6,10,20}. We chose the location of these

well-known points according to real grazing situa-

tion. In (Dumont et al., 2005), the domestic herbi-

vores used to graze in group. Few animals are alone.

The selected plot is an area of maximum 300 meters

× 300 meters. As example, this is the coordinate for

10 ﬁxed points: [0,0] ; [0, 5] ; [−10,10] ; [−10,−6] ;

[100,100] ; [10,−8] ; [70,−40] ; [80,−45] ; [75,−35]

; [−5,90]. A random point is picked in the area. The

exact radius could be calculated with the knowledge

of the ﬁxed points and random point coordinates. A

different random error of ε meters is added to each ra-

dius to reﬂect the error. Finally this overdetermined

system is described in the following equation:











− x

)

+ (y

− y

)

− (

− x

)

+ (y

− y

)

+ ε

)

= 0

− x

)

+ (y

− y

)

−

(

− x

)

+ (y

− y

)

+ ε

)

= 0

(1)

This system in this form is a non-linear least-squares

problem. We use iterative non-linear least-squares al-

gorithm to solve these equations due to distance mea-

Cost-efﬁcient Localisation System for Agricultural Use Cases

145

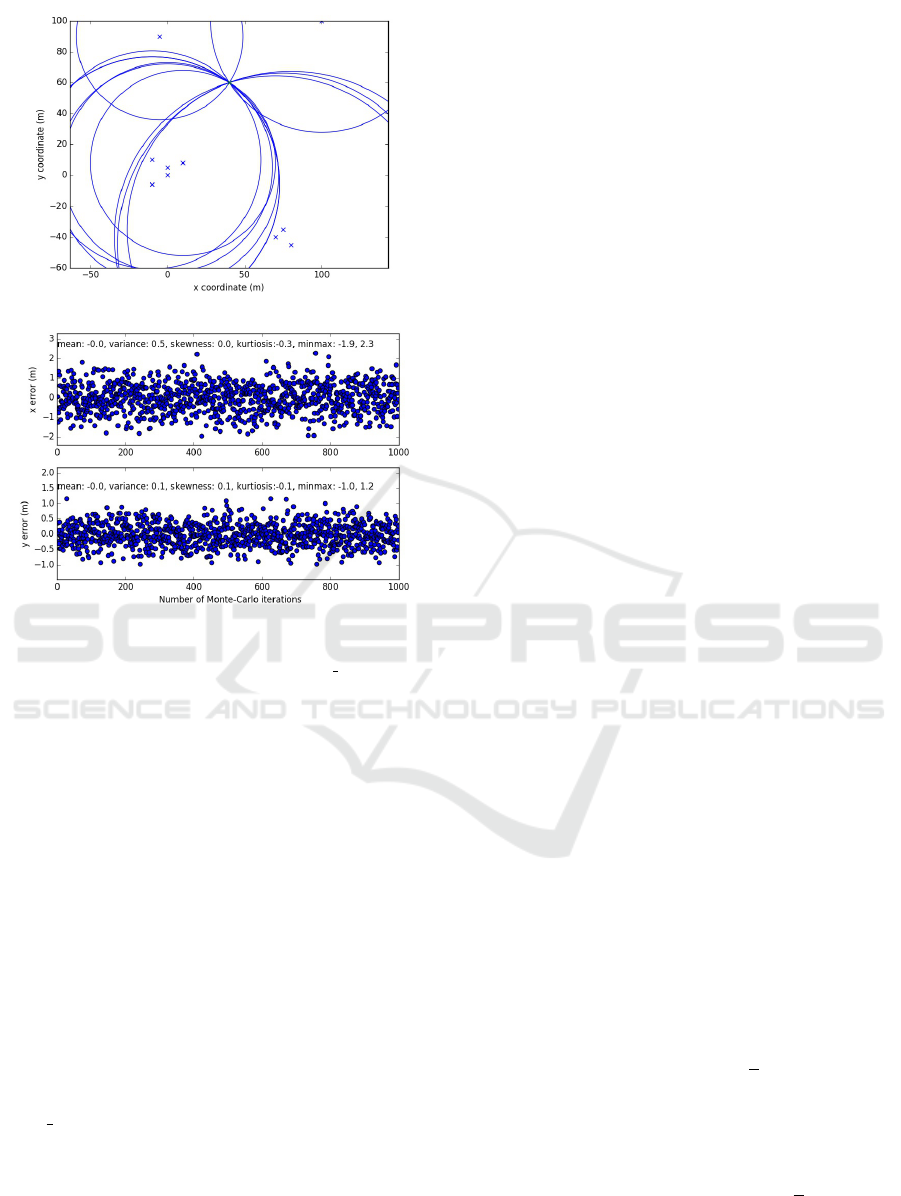
Figure 4: Optimal situation for 10 ﬁxed points.

Figure 5: Example of the error repartition on x and y.

surement errors. In our simulation each ε

n wpt

is a ran-

dom value between ±2 meters. Using Python’s scipy

package, we iterate the process 1 000 times to act as a

Monte-Carlo test and we repeat the process with 100

random and unknown points. Figure 4 represents the

ideal situation with 10 well-known points. Figure 5

represents the error after 1 000 iterations for a given

list of well-known points.

The results are presented in table 1 with regards

to different number of ﬁxed points. ∆

max

is the dif-

ference between the maximum error and the mini-

mum error for all the situations. So it is the upper

bound of the error for all the situations (and itera-

tions). ∆

mean(ε

)

represent the upper bound of the

mean of errors on one axis. max(σ

) is the maxi-

mum of the variance in all the situations. [

;

] is a

N × 2 matrix size of all the estimation results of the

unknown point.

We have started the iterative algorithm

(least squares() from the scipy Python library)

from the same initial point and we experienced that

the results were slightly different after the end of

each iterative process. Therefore we executed the

iterative process several times and we took the mean

of the results. Our experience is that this mean value

is of better quality than any of the standalone results.

In the following simulations, however, we considered

that each distance measurement has a different

measurement error. We consider that we only have

one chance to calculate the unknown position to save

power in the real case.

The main problem of this simulation is to help

the algorithm to ﬁnd the correct minimal solution.

Optimisation functions are very susceptible to initial

state. When the number of well-known points is not

enough, a good solution is hard to ﬁnd. That why the

variances are very high for 4 and 5 ﬁxed well-known

points. Moreover, in 4 and 5 ﬁxed points, we try to

model a real grazing situation, so animals are really

close. A group of reference points that are close to

each other could behave as if they were one point.

This situation is not suitable to estimate the position

if no reference points are available that are far away

from this group. The reason of this phenomenon is the

small distance between the ﬁrst points, the large dis-

tance to the last point, and the addition of a random

error.

In conclusion, our simulation shows it is impor-

tant to have at least 3 ﬁxed points which are far away

to be sure of the good problem resolution. This result

is interesting to minimise the calculation load in an

embedded system and to help us to evaluate the num-

ber of UWB anchors. Moreover, if a group of cows

is close to each other, it is possible to activate only a

part of the GPS receivers in the group to save power.

5.2 Effect of Reference Point Position

Error

We consider using GPS to obtain the coordinates of

the ﬁxed points and to use UWB to measure the dis-

tance between the ﬁxed points and the unknown point.

In that case, the GPS error may introduce a more sig-

niﬁcant error source. We made a second simulation

to understand the consequence of a GPS localisation

error in the reconstruction of the unknown point. In

this situation, we consider no distance measurement

error.

The aim is to reduce the system to linear equa-

tions. The new system can be written as:











− x

) · x

+ (y

− y

) · y

− r

+ x

− x

+ y

− y

)

− x

N−1

) · x

+ (y

− y

N−1

) · y

N−1

− r

+ x

− x

N−1

+ y

− y

N−1

))

(2)

SENSORNETS 2017 - 6th International Conference on Sensor Networks

146

Table 1: Statistics on all the unknown point estimation in distance error situation in meter.

n wpt x (meter) y (meter)

pts ∆

max

mean(ε

) ∆

mean(ε

)

max(σ

) ∆

max

mean(ε

) max(σ

) ∆

mean(ε

)

4 23.6 -0.1 39 2.4 24.6 0.1 43.9 2.4

5 24.32 -0.1 37.8 3.8 23.6 0.0 43.0 4.0

6 12.5 0.0 5.5 0.3 14.8 0.0 7.8 0.3

10 9.7 0.0 2.9 0.2 9.9 0.0 2.7 0.1

20 6.2 0.0 1.2 0.1 6.4 0.0 1.0 0.1

This could be put in a matrix form (equation 3).

Subtracting the last equation from the other equations

is arbitrary.

Gβ = F (3)

where G =







− x

− y

− x

N−1

− y

N−1







, β =





, F =







− r

+ x

− x

+ y

− y

N−1

− r

+ x

− x

N−1

+ y

− y

N−1







The localisation estimation could be found with this

linear equation using the standard linear least-squares

method (eq. 4).

β = (G

−1

F (4)

β is the estimated coordinate.

To visualize the problem, the ﬁgure 6 represents

10 ﬁxed points with 1 000 different simulated errors

added to them and the estimation of the unknown

point. One larger patch in this ﬁgure represents a ref-

erence point with a set of error values added.

The results of this simulation are presented in ta-

ble 2. For 10 ﬁxed points in this conﬁguration, the

results are good. In some cases with few ﬁxed points,

this table show some variance problem. Sometime the

simple resolution does not work and the result of the

least-squares solution exhibits a large error. A low-

pass ﬁlter that we did not implement could be used to

control the problem.

The calculation takes approximately 20 to 50 sec-

onds with the linear least-square method and 520 sec-

onds to 715 seconds with the iterative non-linear al-

gorithm proportion to the number of ﬁxed points de-

pending on the number of ﬁxed points. The processor

used is an Intel i7-4700MQ, 2.4 GHz and the com-

puter is equipped with 16 GBytes of volatile memory.

We can conclude that linear least-square algorithm

could be used if we have enough separate ﬁxed points.

If we have enough computation resources and not

enough separate ﬁxed points, we could use non-linear

least-square techniques to ﬁnd the correct unknown

Figure 6: Representation of 10 ﬁxed points with simulated

error added to them and the effect of the error of the locali-

sation of the unknown point.

point. We can see that for a same measurement error,

in our case ±2 meters, with enough separated ﬁxed

points, the estimation is better if we assume that the

measurement error is introduced into the ﬁxed points’

positions. In our real study, the distance measurement

could be given by UWB which have, theoretically, a

better accuracy than ±2m. Finally the error position

could only depend on the effect of reference point po-

sition error. But we have to do other simulation and

try.

6 ANGLE-BASED SHORT-RANGE

LOCALISATION

Beside distance-based short-range localisation, we in-

vestigated whether we can build an in-house angle-of-

arrival (AOA) short range localization system. This

localisation method depends on a direction-sensitive

antenna. The antenna rotates and ﬁnds out the angle

of signals from stations with known locations. These

stations can either be ﬁxed to the ground or mounted

to a moving platform which stops for long enough

time periods so that it can be localised accurately (see

section 3).

Our AOA localisation method is based on the prin-

Cost-efﬁcient Localisation System for Agricultural Use Cases

147

Table 2: Statistics on all the unknown point estimation in ﬁxed points error situation in meters.

linear least-squares solution

n wpt x (meter) y (meter)

pts ∆

max

mean(ε

) ∆

mean(ε

)

max(σ

) ∆

max

mean(ε

) ∆

mean(ε

)

max(σ

)

4 4·10

49.1 4341 15·10

4·10

-50.9 4473 16·10

5 128.3 0.0 1.7 223.6 134.6 0.0 1.9 269.1

6 19.7 0.0 0.3 9.6 18.4 0.0 0.5 10.5

10 19.9 0.0 0.4 10.0 20.0 0.0 0.5 12.6

20 12.7 0.0 0.4 5.0 12.3 0.0 0.3 5.6

non-linear least-squares solution

n wpt x (meter) y (meter)

pts ∆

max

mean(ε

) ∆

mean(ε

)

max(σ

) ∆

max

mean(ε

) ∆

mean(ε

)

max(σ

)

4 338 -0.1 5.9 178 370 0.1 189

5 344.8 0.1 5.6 169.4 368.5 0.1 6.3 167.0

6 13.8 0.0 0.2 5.8 15.6 0.0 0.3 9.2

10 9.4 0.0 0.2 2.6 10.0 0.0 0.2 2.8

20 7.2 0.0 0.1 1.4 6.4 0.0 0.1 0.9

ciples described in (Cheung et al., 2006). We assume,

however, that instead of the ﬁxed stations measuring

the angle of the mobile station’s beacon signal, it is

the mobile station that measures the angle of the ﬁxed

stations’ beacon signal. So equation (47) in (Cheung

et al., 2006) changes to equation 5.

tan(r

AOA,i

) =

sin(r

AOA,i

)

cos(r

AOA,i

)

− y

− x

(5)

where r

AOA,i

is the angle of the ith ﬁxed station as

measured by the mobile station, x

is the known

position of the ith ﬁxed station, and β =





is the

unknown position of the mobile station. By bringing

this set of equations to a linear matrix form, we get

H =







−sin(r

AOA,1

) cos(r

AOA,1

)

−sin(r

AOA,N

) cos(r

AOA,N

)







(6)

k =







−x

sin(r

AOA,1

) + y

cos(r

AOA,1

)

−x

sin(r

AOA,N

) + y

cos(r

AOA,N

)







(7)

where N is the number of the ﬁxed stations whose

angle is measured. N is at least 3 but the measure-

ment may be overdetermined where N > 3 hence lin-

ear least-square solution is calculated.

β = (H

−1

k (8)

We have made simulations to estimate the localisation

accuracy. Figure 7 shows the localisation error mea-

sured in a simulation with varying angle measurement

error and distance between the mobile station and the

Figure 7: AOA localisation accuracy as a function of the

distance to the ﬁxed stations and angle measurement error.

ﬁxed stations. The 4 ﬁxed stations were arranged in

a square, the mobile station was from equal distance

from all the ﬁxed stations. The distance shown in the

ﬁgure is the distance between the mobile station and

any of the ﬁxed stations. We assumed that there is a

ﬁxed measurement error (x axis). The angle measure-

ment error was added to the exact angles so that the

distance between

β and β is maximal and this maxi-

mum error is shown in the ﬁgure.

With the distance of 50 meters, the required lo-

calisation precision can be achieved only if the an-

gle measurement error is less than 1 degree. We

built a simple prototype to verify how easily these

requirements can be implemented based on Atmel

ATmega328P MCU (Arduino Pro Mini) and Nordic

nRF24L01P RF module, operating in the 2.4 GHz

SENSORNETS 2017 - 6th International Conference on Sensor Networks

148

band. The sender unit was equipped with a simple

omnidirectional stick antenna and the receiver unit

was equipped with a 9 dBm PCB Yagi antenna. By

turning around the Yagi antenna, the angle range (0

degree being the direction of the sender) was iden-

tiﬁed where the sender’s data can be received. Un-

fortunately the nRF24L01P module has no Received

Signal Strength Indicator (RSSI) feature, the signal is

either present or not. This means that there is a min-

imum distance to the sender because if the receiver

is closer to the sender than the minimal distance, the

signal can be received independently of the angle of

the receiver’s antenna. This restriction can be miti-

gated by a receiver that provides RSSI along with the

received data packets.

The measurements were made on an agricultural

ﬁeld that serves as a pasture. The sender’s trans-

mission power was set to one of the 3 levels the

nRF24L01P supports. The receiver was located at

a speciﬁed distance from the sender and the antenna

was rotated. The angle when the signal appeared and

when the signal disappeared was recorded. With this

simple method the direction of the sender was iden-

tiﬁable with 1 degree precision. The minimum and

maximum distances with different power levels were

the following: PA MIN: 4-20 meters, PA LOW: 22-

41 meters, PA HIGH: 31-70 meters.

7 CONCLUSIONS

Low-cost, accurate localisation is often required in

agricultural applications. We found that low-cost GPS

modules are inadequate but in differential setup cer-

tain low-cost modules are able to produce the required

accuracy if the target is stationary for at least 8-10

minutes. Certain cows (but not all of them) were

found to satisfy the criteria for being stationary for

40-80 % of their grazing time. Movements have to

be tracked by an auxiliary technology. We made sim-

ulations for two of such technologies: distance- and

angle-based short-range localisation technology. In

case of distance-based, the effect of distance mea-

surement error results in worse position estimation

than the effect of reference point measurement error.

Angle-based short-range localisation turned out to be

more cost-efﬁcient but also more problematic, due to

the rapidly growing localisation error as the distance

between the mobile and the ﬁxed station grows.

ACKNOWLEDGEMENTS

The Hungarian side of the research is supported by

the AgroDat.hu project (project code: VKSZ 12-1-

2013-0024), ﬁnanced by the Government of Hungary.

I thank ESEO for co-ﬁnancing my research stay in

Angers, France where part of the research was done.

The French side of the research is ﬁnanced by the re-

gion of ”Pays de la Loire” (Vagabond project).

REFERENCES

Cheung, K. W., So, H. C., Ma, W.-K., and Chan,

Y. T. (2006). A constrained least squares approach

to mobile positioning: Algorithms and optimality.

EURASIP J. Appl. Signal Process., 2006:150–150.

De Weerd, N., van Langevelde F., and van Oeveren H.,

e. a. (2015). Deriving animal behaviour from high-

frequency gps: Tracking cows in open and forested

habitat. PLoS ONE. 2015;10(6):e0129030.

Dumont, B., Boissy, A., Achard, C., Sibbald, A., and Er-

hard, H. (2005). Consistency of animal order in spon-

taneous group movements allows the measurement of

leadership in a group of grazing heifers. Applied Ani-

mal Behaviour Science, 95(1–2):55–66.

Herrera, A. M., Suhandri, H. F., Realini, E., Reguzzoni, M.,

and Lacy, M. C. (2016). goGPS: Open-source MAT-

LAB software. GPS Solut., 20(3):595–603.

Langley, R. B. (1991). The mathematics of gps. GPS World,

pages 45 – 50.

Paller, G. and

o, G. (2016). Power consumption con-

siderations of an agricultural camera sensor with

image processing capability. In 2nd International

Conference on Sensors and Electronic Instrumen-

tal Advances (SEIA’ 2016), 22-23 September 2016,

Barcelona, Castelldefels, Spain.

Wietrzyk, B. and Radenkovic, M. (2007). CRAWDAD

dataset nottingham/cattle (v. 2007-12-20). Down-

loaded from http://crawdad.org/nottingham/cattle/

20071220.

Cost-efﬁcient Localisation System for Agricultural Use Cases

149