Biologically-Inspired Neural Network for Walking Stabilization of

Humanoid Robots

Guilherme Barros Castro

, Kazuya Tamura

, Atsuo Kawamura

and André Riyuiti Hirakawa

Department of Computer Engineering and Digital Systems, University of São Paulo, São Paulo, Brazil

Department of Electrical and Computer Engineering, Yokohama National University, Yokohama, Japan

Keywords: Biologically-Inspired Neural Network, Humanoid Robots, Computational Intelligence, Walking

Stabilization.

Abstract: In order to accomplish desired tasks, humanoid robots may have to deal with unpredicted disturbances,

generated by objects, people and even ground imperfections. In some of these cases, foot placement is

critical and cannot be changed. Furthermore, the robot has to conduct the actions planned meanwhile

stabilizing its walking motion. Therefore, we propose a Biologically-inspired Neural Network (BiNN) to

stabilize the walking motion of humanoid robots by ankle joint control, which minimally affects the current

movements of the robot. In contrast to other neural networks, which only generate walking patterns, the

BiNN is adaptive, as it compensates disturbances during the robot motion. Moreover, the BiNN has a low

computational time and can be used as a module of other control methods. This approach was evaluated

with Webots simulator, presenting improvements in the compensation of an external force in regard to its

magnitude and duration.

1 INTRODUCTION

Humanoid robots are expected not only to act in the

same environment and to perform similar tasks as

humans, but also to act in dangerous environments,

such as those present in catastrophe or rescue scena-

rios, and to perform tasks that humans are not able

to, such as lifting heavy weights. In these situations,

humanoid robots may need to avoid objects and

people and deal with irregular ground, all of which

may generate disturbances and affect its balance.

There are two main alternatives to compensate

external disturbances and stabilize robot motion:

stepping (Stephens and Atkeson, 2010; Luo et al.,

2015), and postural control (Sano and Furusho,

1990; Stephens, 2007; Lee and Goswami, 2012;

Lober, Padois and Sigaud, 2014; Maalouf et al.,

2015). Stephens and Atkeson (2010) state that

humanoid robots are able to sustain larger

disturbances by stepping. However, in some

situations the robot may have to perform specific

foot placements due to environment constraints. In

these cases, postural control is the best alternative to

guarantee stability without violating any constraints.

Different strategies were proposed to achieve

postural control, which can be classified into two

categories: whole body control (Lee and Goswami,

2012; Lober, Padois and Sigaud, 2014) and ankle

joint control (Sano and Furusho, 1990; Stephens,

2007; Maalouf et al., 2015). Whilst in the whole

body control strategy all actuators can be used to

balance the robot motion, strategies based on ankle

joint control stabilize the motion only with ankle

actuators. In spite of the effectiveness of the former

control method against more severe disturbances, as

shown in (Stephens, 2007), this research focuses on

ankle joint control, for its simplicity and efficiency.

By controlling only the ankle joints it is possible

to compensate significant disturbances without

changes to other joint trajectories, not interfering

with the upper limb actions currently being executed

or previously planned by the robot. Moreover, ankle

joint control can be used with other control

approaches, being activated in the cases that external

disturbances are moderate.

Sano and Furusho (1990) achieved natural

dynamic walking by controlling the ankle torque of

the supporting leg and, thus, manipulating the robot

angular momentum. Stephens (2007) analyses the

disturbance compensation capacity based on the

current state of humanoid robots which adopt the

ankle stabilization strategy. Maalouf et al. (2015)

proposed a model-free approach for humanoid robot

Castro G., Tamura K., Kawamura A. and Hirakawa A.

Biologically-Inspired Neural Network for Walking Stabilization of Humanoid Robots.

DOI: 10.5220/0006138700960104

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 96-104

ISBN: 978-989-758-220-2

stabilization, showing improved results in

comparison to the model-based approach presented

in (Stephens, 2007). Nevertheless, the authors only

investigated push recovery situations in which the

robot was standing still, and their control objective

was to maintain an upright position. Both aspects do

not allow the direct application of the approach to

stabilize a walking motion.

In this paper, we propose a Biologically-inspired

Neural Network (BiNN) to stabilize the walking

motion of humanoid robots. The approach proposed

is modular, i.e., can be used in conjunction with

walking pattern generation and stepping approaches,

and has a low computation time, which is relevant to

ensure real-time control. We investigate here the

stability of NAO humanoid robot in regard to lateral

disturbances (y-direction) during a walking motion,

evaluating with simulations the BiNN capacity of

stabilizing different external forces as well as the

computation time of each control step.

In contrast to Artificial Neural Networks

(ANNs), whose focus is on the learning aspect of

biological neural networks, the BiNN focuses on

determining its structure and parameters in order to

achieve a desired behaviour. Whereas ANNs with

different training methods were proposed to estimate

humanoid robot models for control purposes (Liu

and Li, 2003; Rai et al., 2012; Sun et al., 2016), the

BiNN proposed does not adopt previous training and

does not have a convergence period.

However, other characteristics of the BiNN

proposed resemble biological neural networks, such

as: inhibitory synapses, which represent negative

influences between neurons; sensorial inputs, which

resemble biological sensorial receptors; and different

activation functions, as in the different types of

biological neurons (Kandel et al., 2012).

Works related to BiNNs were proposed to

control different types of robots, as surveyed by Yu

et al. (2014). In addition to the robots presented in

(Yu et al., 2014), which adopt BiNNs with an

oscillatory behaviour inspired by the biological

Central Pattern Generator (CPG) of humans,

Nichols, Mcdaid and Siddique (2013) and

Helgadóttir et al. (2013) proposed other BiNNs to

control the motion of wheeled robots. Different

BiNNs have different network structures, neuron

models, which comprise membrane potential

(activation) and neuron output determination, types

of synapses and neural adaptation mechanisms.

BiNNs for humanoid robot control, such as those

proposed by Taga, Yamaguchi and Shimizu (1991),

Cao and Kawamura (1998), Endo et al. (2008) and

Saputra et al. (2016), focus on the walking pattern

generation part of the robot motion, not being able to

adaptively compensate external disturbances.

Contrary to these approaches, the BiNN proposed

does not focus on the walking pattern generation, but

on the walking stabilization.

2 HUMANOID ROBOT WALKING

STABILIZATION

Stable walking of a humanoid robot can be defined

as the realization of any walking motion in which

the humanoid robot achieves the final position

desired without falling down. In order to guarantee

the dynamical balance of the walking motion, the

Zero Moment Point (ZMP) of the robot must remain

inside its support polygon during its entire motion

(Vukobratović, Borovac and Potkonjak, 2006).

Thereby, ZMP is the point at which the resultant

ground reaction force acts, whereas the support

polygon is the projected area beneath the robot’s feet

which is formed by the convex hull of its footprints

(Vukobratović and Stepanenko, 1972). Equation (1)

represents this stability criterion for the y-direction,

which is the focus of this paper. In the equation,





represents the current ZMP, and 



and 



represent the upper and lower bounds of the support

polygon in the y-direction.













(1)

The grey area in Fig. 1a corresponds to the

support polygon of NAO robot – used in this

research – when both feet are on the ground. In the

figure, the labels (LFsrFL, LFsrFR, etc.) indicate the

position of eight Force Sensitive Resistors (FSR),

which measure resistance changes according to the

variation of the pressure applied. When only one

foot is on the ground, the support polygon

corresponds to the footprint area of that foot.

To determine the current ZMP in the y-direction,

the ZMP equation rewritten by Kajita et al. (2003)

from (Vukobratović and Stepanenko, 1972) is

Figure 1: (a) Support polygon of NAO robot. (b) Ankle

joint control.

Biologically-Inspired Neural Network for Walking Stabilization of Humanoid Robots

adopted, as represented by (2). In the equation, 



and 



represent the center of mass position in y-

and z-directions, g represents the gravitational

acceleration, and 



represents the center of mass

acceleration in y-direction.





=



−











(2)

The approach presented in this paper controls the

robot ankle motors in order to control the ZMP,

guaranteeing a stable walking by satisfying the

stability criterion even in scenarios with external

disturbances. Thus, the BiNN influences the centre

of mass position and acceleration by determining the

ankle angular position 



(and angular velocity







), as illustrated in Fig. 1b. The hip motors are

also controlled, but only to maintain the robot torso

vertical, reducing the overall motion range and

increasing its stability.

The control cycle of the method proposed is

illustrated by a block diagram in Fig. 2. The first

block, ‘Walking pattern generation’, has as inputs

the walking parameters that determine the motion

desired, such as step height, step length and walking

speed. The robot joint angles compose the outputs of

this block. The second block is the control cycle

plant, i.e., the robot. To accomplish closed loop

control, FSR measurements, such as the ZMP, are

sent as a feedback to the BiNN, which is the main

contribution of this paper. The neural network

processes this information and produces an output

with two components, one positive (Out1) and one

negative (Out2), altering the ankle and hip angles

sent as references to the robot.

3 WALKING PATTERN

GENERATION

The walking pattern generation approach adopted in

this research is based on three fundamental

movements (transfer, lift and extend), illustrated in

Fig. 3, and does not have as an objective the robot

stabilization during its entire motion. These

fundamental movements are sequential and may

overlap, depending on the walking speed desired.

Despite the disadvantage of not considering the

robot stability to generate its joint trajectories, this

approach has an advantage: its simplicity, which

provides low design and computation times.

The equations that describe the fundamental

movements, presented in this section, are derived

from geometrical relationships between their

variables. These equations are shown in their final

Figure 2: Control cycle.

form, as they are not the main focus of this paper.

The first fundamental movement is ‘transfer’. Its

objective is to transfer the centre of mass position to

the next support foot of the walking motion by

changing the ankle roll angle of both legs. Equation

(3) determines the ankle roll angles 

,

based on the

desired centre of mass shift ∆



and on the

current support leg length 



. The support leg

length, calculated by (4), is the actual length of the

support leg, which considers changes in the ankle

and knee pitch angles (

,

and 

,

). Constants 



and 



correspond to the lower and upper leg

lengths, respectively. Fig. 4 illustrates all leg

parameters, as well as the maximum angle values in

each direction. In order to maintain the torso

vertical, the hip roll angles 

,

are equal to the

opposite value of the ankle roll angles 

,

, as

represented in (5).



,

=asin

∆







 (3)





=





,





(

,



.

) (4)



,

=−

,

(5)

Figure 3: Fundamental movements: ‘transfer’, ‘lift’ and

‘extend’.

The second and third fundamental movements

(lift and extend) are based on the same equations,

(6)-(10). These movements change hip and knee

pitch angles (

,

and 

,

) of the moving leg

according to (6) and (7) to achieve the foot height

desired (∆). Whilst in the second fundamental

movement (‘lift’), the foot height has a positive

value, in the third fundamental movement (‘extend’)

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

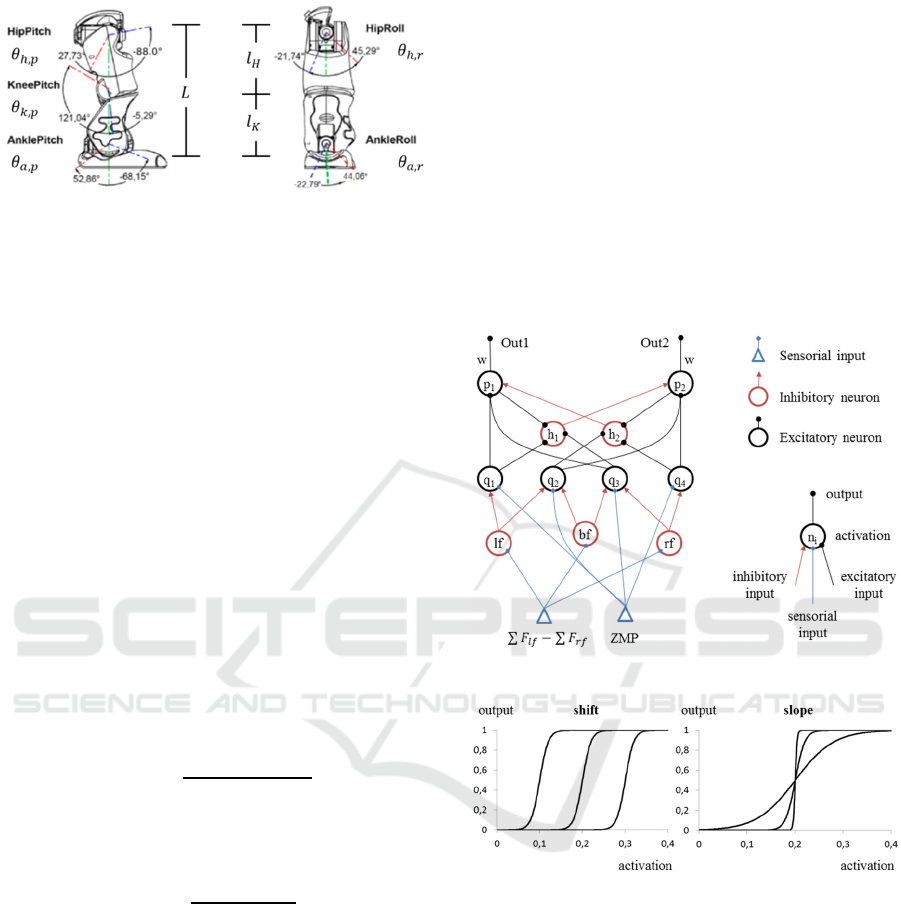
Figure 4: Leg parameters of NAO robot.

it is equal to 0, so that the foot touches the ground.

Simultaneously, the ankle pitch angle 

,

of the

moving leg is adjusted by (10) to maintain the

moving foot parallel to the ground.

In (6), the hip pitch angle is adjusted by the torso

pitch angle 

,

, defined by (8) as the sum of the hip,

knee and ankle pitch angles of the supporting leg,

because the torso inclination directly affects the hip

pitch angle of the moving leg. The current moving

leg length is determined by (9) based on the current

support leg length and on the desired foot height.

The roll angles are used in the equation to account

for the lateral inclination of both legs.

Free parameter α is used to simplify (6). α

defines the relationship between hip and knee pitch

angles, as shown in (7), and may have different

values in ‘lift’ and ‘extend’, with a higher value in

‘extend’ to produce a more natural motion. The

more negative α is, the straighter the moving leg is

and the larger the step will be (until α is equal to 

,

and 

,

reaches 0).



,

= −acos









(

,

)







,

(6)



,

=−

,

(7)



,

=

,,



,,



,,

(8)









(

.

)∆

(

,

)

(9)



,

=

,

−

,



,

 (10)

4 BIOLOGICALLY-INSPIRED

NEURAL NETWORK

4.1 Fundamentals

A general neuron model, represented in the right-

hand side of Fig. 5, may have different types of

inputs, which determine the neuron activation and,

consequently, its output. Whilst inhibitory inputs

have only negative values and excitatory inputs have

only positive values, sensorial inputs can have either

negative or positive values. Activation A

of a neuron

i is determined by the weighted sum of its n inputs

, as shown in (11). Output O

of a neuron i is a

function of its activation A

. In this research, a

sigmoid function is adopted as the activation

function, as represented in (12). Parameters s and m

determine the activation function shift and slope,

respectively, and the effects of their modification are

shown in Fig. 6.







∑













(11)







=1 1















 (12)

Figure 5: Biologically-inspired Neural Network.

Figure 6: Activation functions of neurons.

4.2 Network Structure and Parameter

Determination

The left-hand side of Fig. 5 illustrates the BiNN

structure proposed to stabilize the humanoid robot

walking motion. This research focuses on stabilizing

the humanoid robot from lateral disturbances (y-

direction). Hence, two BiNNs with this structure

would be necessary in order to stabilize the robot in

both x- and y-directions. The sensorial inputs of this

network are: the difference between the sums of all

FSR values of the left foot

∑





and of all FSR

values of the right foot

∑





; and the ZMP,

calculated with the measurements and positions of

Biologically-Inspired Neural Network for Walking Stabilization of Humanoid Robots

FSR sensors by the method detailed in (Tamura,

Nozaki and Kawamura, 2015).

The former sensorial input is processed by the

first layer of inhibitory interneurons (lf, bf and rf),

which determine whether each foot is on the ground

or not. Thereby, the slope coefficient modulus of

their activation function (m) is high (500) to

originate a steep threshold function. The slope

coefficient of lf is positive and its shift coefficient is

0.1, causing an input higher than 0.1 to produce an

output, which indicates that the left foot is on the

ground. In contrast, the slope coefficient of rf is

negative and its shift coefficient is -0.1, causing

inputs lower than -0.1 to produce outputs. The

activation function of bf is a combination of the

activation functions of lf and rf, causing values

between -0.1 and 0.1 to produce outputs.

The first layer of excitatory neurons (q

, q

and q

) has the ZMP as one of its inputs and

represents the support polygon boundaries in the y-

direction, producing outputs if these boundaries are

violated. Therefore, their shift coefficients exactly

match the values of the boundaries. However, only

the neurons that represent the boundaries of the

current support polygon do not have their outputs

inhibited by the inhibitory interneurons.

Whilst q

represents the right boundary of the

support polygon when either only the right foot or

both feet are on the ground, q

represents the left

boundary when only the right foot is on the ground,

represents the right boundary when only the left

foot is on the ground and q

represents the left

boundary when either only the left foot or both feet

are on the ground. The slope coefficient modulus of

these neurons is 100 so that outputs are produced

before the ZMP approaches the boundaries, creating

a safety margin.

The second layer of inhibitory interneurons (h

and h

) also have a steep activation function (m

equal to 500) and a low threshold value (s equal to

0.1). Their purpose is to inhibit the activity of the

opposite p neuron with lateral inhibition dynamics,

which allows only one p neuron to become active at

a time. These neurons receive inputs from p neurons,

generating feedback inhibition, as well as from q

neurons, generating feedforward inhibition. Whilst

feedback inhibition reflects the current state of p

neurons, feedforward inhibition anticipates

variations in their inputs.

The second layer of excitatory neurons (p

and

) produces the neural network outputs (Out1 and

Out2). Their activation functions have a low slope

coefficient (10) and a shift coefficient of 0.5,

providing a varying output in the input range of 0 to

1.0. These neurons receive inputs based on the

distance of the ZMP to the support polygon

boundaries and produce outputs with values from 0

to 1.0, which are transformed into angle increments

by the synaptic weight w.

The synaptic weights of all connections between

neurons are set to 1 in order to simplify the

parameter determination. However, the synaptic

weight w of the outputs (Out1 and Out2) is a free

parameter. w determines the angle increment Δθ

generated by the BiNN, which alters the ankle joint

angles provided by the ‘Walking pattern generation’

block to stabilize the robot motion. Hence, w has a

direct influence on the centre of mass position,

generating a shift in the y-direction Δy

CoM

with Δθ.

From (2), and assuming that the centre of mass

variation in the z-direction is negligible, as in [6],

there are two possibilities to control the ZMP in the

y-direction: by 



or by 



. But, in the case of

the NAO robot, the maximum value of the second

part of (2) is 0.0014m, due to a low centre of mass

height (0.27m) and a low stall torque (73.44mNm),

which affects the maximum 



generated

according to (13). In the equation, m is the robot

mass (5.18kg) and F is the force generated by the

torque T.













(



)



(13)

In contrast, the maximum value of 



0.06m, due to an ankle angle limitation (22

). The

first part of (2) influences the ZMP position 42 times

more than the second part and, therefore, generating

a Δy

CoM

by choosing the appropriate value of w is

the stabilization method proposed herein.

The ankle angle increment generated by the

BiNN is represented by (14). As the maximum

BiNN output is equal to 1, the maximum ankle

increment is equal to w, as stated in (15). Hence, the

synaptic weight w required to generate a centre of

mass shift Δy

CoM

is determined by (17), which is

derived from (16) and (15).

∆ = 

(

1−2

)



(14)

∆



=



(15)

∆



=

(

∆

)





(16)

=asin

∆









 (17)

To guarantee the compensation of an external

disturbance with short duration (less than one

second), the centre of mass variation generated by

the ankle motors 



must be higher than the

center of mass variation caused by the external force

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

100





, as stated in (18). Thereby, a safety factor γ (e.g.

1.1) can be used to transform the inequality into an

equality, as shown in (19). In the equation, the

center of mass velocity caused by the external force

is considered to be equal to the centre of mass

acceleration caused by the external force 



multiplied by its duration ∆t. Subsequently, the

center of mass acceleration caused by the external

force is assumed to be equal to the external force





divided by the robot mass.





>





(18)





=



=∆



∆





(19)

Assuming the centre of mass variation to be

equal to the centre of mass shift divided by the

iteration step value, as in (20), the synaptic weight w

required to compensate an external force 



given by (21). This equation allows tuning w

according to the maximum value of the expected

external disturbance. Whilst a higher value of w

compensates higher external forces and causes a

more aggressive behaviour, a lower value of w

causes a smoother behaviour, but cannot compensate

higher external forces.





∆







(20)

=asin

∆











 (21)

Fig. 7 shows (21) for γ equal to 1.01, ∆t equal to

0.2s, 



equal to 0.01s and 



equal to 0.27m,

showing the stable and unstable regions that the

equation originates. Force duration of 0.2s was

chosen so that the force acts for a sufficient time so

as not to be considered an impulse. In the figure, the

maximum force that the robot is physically able to

sustain is also shown. This value can be obtained by

substituting the centre of mass acceleration 



the external force 



divided by the robot mass m

in (2), and rearranging the equation as shown in

(22).





(







)





(22)

Thereby, substituting the constants m, g and 



in the equation and assigning to 



the value of

the support polygon boundary (-0.06m) and to 



its best feasible position (0.06m), the maximum

external force of 22.48N is obtained. External forces

higher than 22.48N cause a center of mass

acceleration that drives the ZMP out of the support

polygon regardless of the center of mass position

(among its feasible values). In this case, a stepping

approach would be necessary to avoid falling.

5 SIMULATION RESULTS

In this section the BiNN performance for stabilizing

the walking motion of the humanoid robot NAO is

evaluated in two manners. The first regards the

computation time of the BiNN for each iteration

step, whereas the second evaluates the BiNN

capacity of compensating external forces with

different magnitudes and durations. Two software

were used to conduct the simulations: Choregraphe

(v. 2.1.4) and Webots (v. 8.4.0).

Figure 7: Synaptic weight w as a function of the external

force Fext.

5.1 Computation Time

The personal computer used to perform the

simulations has an Intel Core i7-3517U processor

with 1.9GHz and 8GB of random access memory

(RAM). Twenty runs, with 106 iteration steps each,

were conducted to obtain the results. The average

computation time of the BiNN for each iteration step

was 0.0027ms and its coefficient of variation was

0.62%. This computation time corresponds to the

calculation of (11) and (12) for each neuron of the

BiNN.

As an iteration step of 10ms was adopted for

robot control, the BiNN computation time

corresponds to less than 0.1% of the complete

iteration step. Moreover, the low computation time

obtained allows the combination of the BiNN with

other control methods, which have average

computation times of 20ms (Ishihara and Morimoto,

2015), 40ms (Carpentier et al., 2016) and 300ms

(Tedrake et al., 2015) for each iteration step.

Figure 8 illustrates the computation times of

these control methods, showing that the BiNN

computation time is negligible in comparison to

Biologically-Inspired Neural Network for Walking Stabilization of Humanoid Robots

101

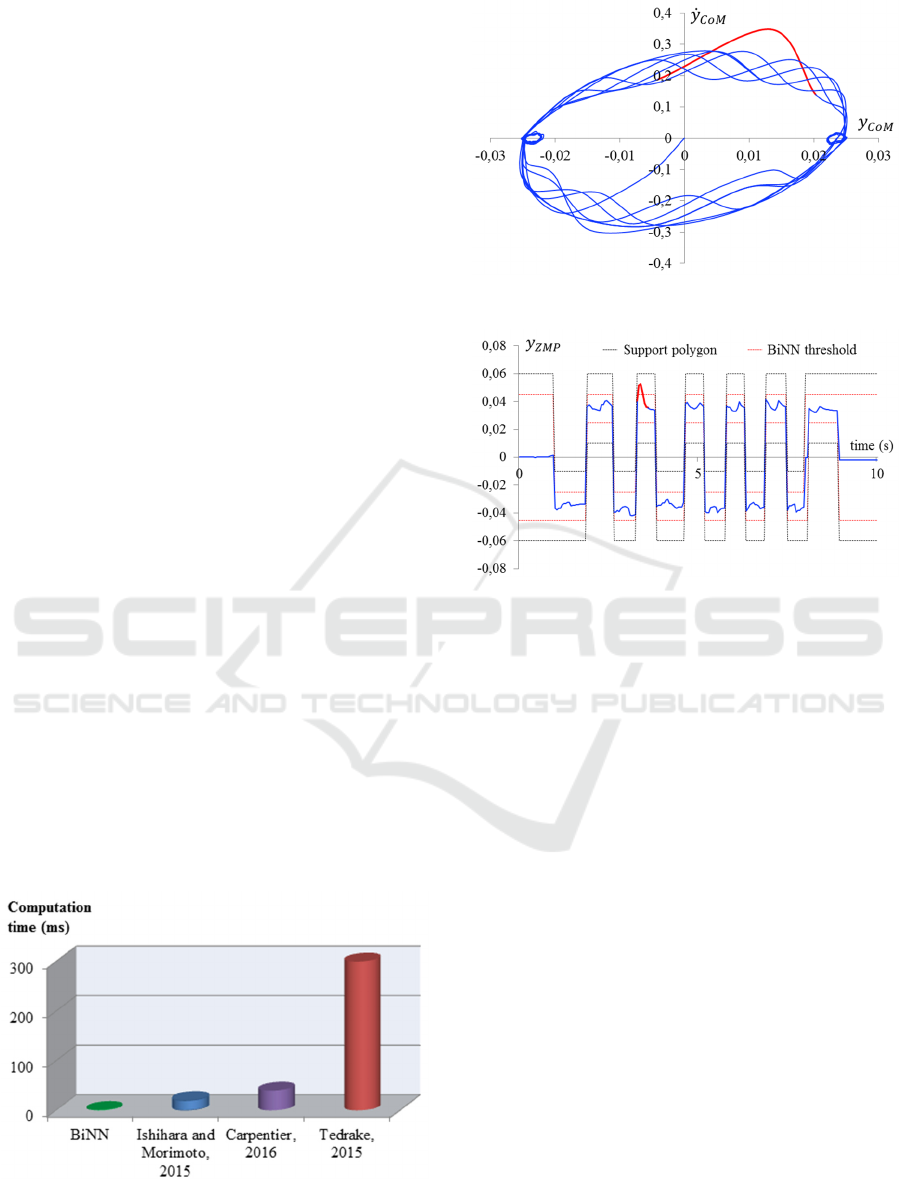
them. This occurs because the BiNN only computes

the current activation and output of its neurons,

whilst predictive approaches are recurrent, i.e., they

compute a sequence of iteration steps in the future in

order to make a decision in the present.

5.2 Walking Stabilization

In order to evaluate the BiNN capacity of

compensating external forces during a walking

motion, the ‘Walking pattern generation’ block and

the BiNN were programmed in Choregraphe

platform. The walking pattern generated had an

average duration of 0.05s for the double standing

phase and of 0.5s for the single standing phase. The

BiNN was evaluated in two simulation studies.

In the first simulation study, a force of 20N in

the y-direction was applied to NAO for 0.2s during

the single standing phase in Webots simulator with a

physics plugin. This force is sufficient to knock the

robot down in the cases in which it is being

controlled either by the default Model Predictive

Control (MPC) method of Choregraphe (Wieber,

2006) or by the open loop version of the control

method proposed (i.e., without the BiNN feedback).

In this simulation, w was set to 1.63, according to

(21). The centre of mass trajectory and the ZMP in

the y-direction, illustrated in Fig. 9 and Fig. 10,

respectively, show that the BiNN was able to

compensate the applied force and that the robot was

able to continue its walking motion. Moreover, the

results also prove that the parameter determination

method proposed is adequate.

Fig. 9 shows the centre of mass position in the y-

direction 



as well as its derivative 



, whose

combined trajectory present a limit-cycle behaviour.

This trajectory is highlighted in red from the

moment in which the external force was applied.

Figure 8: Computation time comparison.

Figure 9: Centre of mass trajectory.

Figure 10: ZMP as a function of time.

The figure shows that the BiNN stabilizes the robot

when the centre of mass trajectory deviates from its

limit-cycle, bringing the trajectory back to it and

allowing the robot to continue its walking motion

without interruption.

The walking stabilization is also showed in Fig.

10, in which the ZMP, the support polygon

boundaries and the BiNN threshold are plotted as

functions of time. The BiNN threshold represents

the ZMP values from which the q neurons start

generating outputs, which originates a safety margin

that prevents the ZMP from approaching the support

polygon boundaries. In this figure, the ZMP is also

highlighted in red from the moment the external

force was applied. After crossing the BiNN

threshold, the ZMP returned to the stable region in

0.084s, showing a fast response of the BiNN.

The second simulation study regards the

evaluation of the BiNN capacity of compensating

forces with different magnitudes and durations. In

each simulation a force in the y-direction was

applied to NAO in the exact same moment during

the ‘lift’ movement of the single standing phase. The

BiNN performance was compared to the

performance of the default MPC used by

Choregraphe (Wieber, 2006).

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

102

Fig. 11 illustrates the simulation results, showing

that the BiNN was able to compensate a higher force

magnitude for every force duration tested. Each

combination of force magnitude and duration was

evaluated 20 times for each control method. The

lines plotted in the figure correspond to force

magnitudes and durations which the robot was able

to withstand in all 20 simulated experiments.

The BiNN was on average 52.55% better than

the MPC, having higher improvements for shorter

force durations. This occurs due to the BiNN fast

response, which becomes less relevant for longer

force durations. The maximum force compensated

by the BiNN was 22N, applied for 0.1s,

corroborating the theoretical result obtained with

(22) by a margin of 2.14%.

Figure 11: External force compensation.

These results reaffirm that the use of a simpler

stabilization strategy, i.e. to control the ankle joint

with the BiNN, is not only possible due to its low

computation time, but also more effective than the

standard stepping approach of NAO robot. Thereby,

in the cases that the disturbance is moderate (10N-

22N), the ankle joint control proposed would be

active, whereas for stronger disturbances the robot

could use a supplementary stepping approach, such

as those proposed by Stephens and Atkeson (2010)

and Luo et al. (2015).

6 CONCLUSION

This paper presented a Biologically-inspired Neural

Network (BiNN) to stabilize the walking motion of

humanoid robots. The approach proposed considers

scenarios in which foot placement cannot be

changed. Thus, the BiNN uses the Zero Moment

Point (ZMP) as input and alters ankle joint angles to

stabilize the robot.

Simulation studies evaluated the BiNN perfor-

mance in compensating lateral forces with different

magnitudes and durations, which were applied

during the walking motion. The BiNN presented a

fast response to disturbances and had a performance,

on average, 52.55% better than a MPC proposal. The

simplicity and low computation time of the BiNN

(0.0027ms) allows its combination with other

control methods, such as reactive stepping

approaches.

Future research directions encompass using two

BiNNs with the proposed structure to compensate

external forces contained in the x-y plane and three

BiNNs to compensate omnidirectional external

forces. Moreover, experiments will also be planned

in order to evaluate the BiNN performance in

compensating external forces with different

magnitudes and durations applied to the actual NAO

robot.

ACKNOWLEDGEMENTS

This work was supported by CNPq, Conselho

Nacional de Desenvolvimento Científico e

Tecnológico – Brasil / Brazilian National Council of

Scientific and Technological Development.

REFERENCES

Cao, M. and Kawamura, A. (1998). A Design Method of

Neural Oscillatory Networks for Generation of

Humanoid Biped Walking Patterns. In Proceedings of

the International Conference on Robotics and

Automation, pp. 2357-2362.

Carpentier, J., Tonneau, S., Naveau, M., Stasse, O. and

Mansard, N. (2016). A Versatile and Efficient Pattern

Generator for Generalized Legged Locomotion. In

Proceedings of the IEEE International Conference on

Robotics and Automation, pp. 3555–3561.

Endo, G., Morimoto, J., Matsubara, T., Nakanishi, J. and

Cheng, G. (2008). Learning CPG-based Biped Loco-

motion with a Policy Gradient Method: Application to

a Humanoid Robot. International Journal of Robotics

Research, 27(2), pp. 213-228.

Helgadóttir, L. I., Haenicke, J., Landgraf, T., Rojas, R. and

Nawrot, M. P. (2013). Conditioned behavior in a robot

controlled by a spiking neural network. In Proceedings

of the International IEEE/EMBS Conference on

Neural Engineering, pp. 891–894.

Ishihara, K. and Morimoto, J. (2015). Real-time Model

Predictive Control with Two-step Optimization based

on Singularly Perturbed System. In Proceedings of the

IEEE-RAS International Conference. on Humanoid

Robots, pp. 173–180.

Kajita, S., Kanehiro, F., Kaneko, K., Fujiwara, K., Harada,

K., Yokoi, K. and Hirukawa, H. (2003). Biped

Biologically-Inspired Neural Network for Walking Stabilization of Humanoid Robots

103

Walking Pattern Generation by using Preview Control

of Zero-Moment Point. In Proceedings of the IEEE

International Conference on Robotics and

Automation, pp. 1620–1626.

Kandel, E. R., Schwartz, J. H., Jessell, T. M., Siegelbaum,

S. A. and Hudspeth, A. J. (2012). Principles of Neural

Science. McGraw-Hill Education.

Lee, S. H. and Goswami, A. (2012). A momentum-based

balance controller for humanoid robots on non-level

and non-stationary ground. Autonomous Robots, 33(4),

pp. 399–414.

Liu, Z. and Li, C. (2003). Fuzzy neural network quadratic

stabilization output feedback control for biped robots

via H∞ approach. IEEE Transactions on Systems,

Man, and Cybernetics, Part B, 33(1), pp. 67–84.

Lober, R., Padois, V. and Sigaud, O. (2014). Multiple task

optimization using dynamical movement primitives

for whole-body reactive control. In Proceedings of the

IEEE-RAS International Conference. on Humanoid

Robots, pp. 193–198.

Luo, D., Han, X., Ding, Y., Ma, Y., Liu, Z. and Wu, X.

(2015). Learning push recovery for a bipedal

humanoid robot with Dynamical Movement

Primitives. In Proceedings of the IEEE-RAS

International Conference. on Humanoid Robots, pp.

1013–1019.

Maalouf, N., Elhajj, I. H., Asmar, D. and Shammas, E.

(2015). Model-Free Human-Like Humanoid Push

Recovery. In Proceedings of the IEEE International

Conference on Robotics and Biomimetics, pp. 1560–

1565.

Nichols, E., Mcdaid, L. J. and Siddique, N. (2013).

Biologically inspired SNN for robot control. IEEE

Transactions on Cybernetics, 43(1), pp. 115–128.

Rai, J. K., Singh, V. P., Tewari, R. P. and Chandra, D.

(2012). Artificial neural network controllers for biped

robot. In Proceedings of the International Conference

on Power, Control and Embedded Systems, pp. 625-

630.

Sano, A. and Furusho, J. (1990). Realization of natural

dynamic walking using the angular momentum

information. In Proceedings of the IEEE International

Conference on Robotics and Automation, pp. 1476–

1481.

Saputra, A. A., Botzheim, J., Sulistijono, I. A. and Kubota,

N. (2016). Biologically Inspired Control System for 3-

D Locomotion of a Humanoid Biped Robot. IEEE

Transactions on Systems, Man, and Cybernetics:

Systems, 46(7), pp. 898-911.

Stephens, B. J. (2007). Humanoid push recovery. In

Proceedings of the IEEE-RAS International Conferen-

ce. on Humanoid Robots, pp. 589–595.

Stephens, B. J. and Atkeson, C. G. (2010). Push recovery

by stepping for humanoid robots with force controlled

joints. In Proceedings of the IEEE-RAS International

Conference. on Humanoid Robots, pp. 52–59.

Sun, C., He, W., Ge, W. and Chang, C. (2016). Adaptive

Neural Network Control of Biped Robots. IEEE

Transactions on Systems, Man, and Cybernetics:

Systems, PP(99), pp. 1-12.

Taga, G., Yamaguchi, Y. and Shimizu, H. (1991). Self-

organized control of bipedal locomotion by neural

oscillators in unpredictable environment. Biological

Cybernetics, 65(3), pp. 147-159.

Tamura, K., Nozaki, T. and Kawamura, A. (2015). Visual

Servo System for Ball Dribbling by Using Bipedal

Robot Nao. In Proc. Annual Conference of IEEE

Industrial Electronics Society, pp. 3461–3466.

Tedrake, R., Kuindersma, S., Deits, R. and Miura, K.

(2015). A closed-form solution for real-time ZMP gait

generation and feedback stabilization. In IEEE-RAS

International Conference. on Humanoid Robots, pp.

936–940.

Vukobratović, M. and Stepanenko, J. (1972). On the

stability of anthropomorphic systems. Mathematical

Biosciences, 15(1–2), pp. 1–37.

Vukobratović, M., Borovac, B. and Potkonjak, V. (2006).

ZMP: a review of some basic misunderstandings.

International Journal of Humanoid Robotics, 3(2), pp.

153–175.

Wieber, P. B. (2006). Trajectory Free Linear Model

Predictive Control for Stable Walking in the Presence

of Strong Perturbations. In IEEE-RAS International

Conference. on Humanoid Robots, pp. 137 – 142.

Yu, J., Tan, M., Chen, J. and Zhang, J. (2014). A survey

on CPG-inspired control models and system

implementation. IEEE Transactions on Neural

Networks and Learning Systems, 25(3), pp. 441-456.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

104