
A Minimally Invasive Method for Beat-by-Beat Estimation of
Cardiac Pressure-Volume Loops
Shaun Davidson
1
, Chris Pretty
1
, Shun Kamoi
1
, Thomas Desaive
2
and J. Geoffrey Chase
1
1
Department of Mechanical Engineering, University of Canterbury, Christchurch, New Zealand
2
GIGA-Cardiovascular Sciences, University of Liège, Liège, Belgium
Keywords: Pressure-Volume Loops, Cardiovascular Signals, Clinical Monitoring, Stroke Work.
Abstract: This paper develops a minimally invasive means of estimating a patient-specific cardiac pressure-volume
loop beat-to-beat. This method involves estimating the left ventricular pressure and volume waveforms using
clinically available information including heart rate and aortic pressure, supported by a baseline
echocardiography reading. Validation of the method was performed across an experimental data set spanning
5 Piétrain pigs, 46,318 heartbeats and a diverse clinical protocol. The method was able to accurately locate a
pressure-volume loop, identifying the end-diastolic volume, end-systolic volume, mean-diastolic pressure and
mean-systolic pressure of the ventricle with reasonable accuracy. While there were larger percentage errors
associated with stroke work derived from the estimated pressure-volume loops, there was a strong correlation
(average R value of 0.83) between the estimated and measured stroke work values. These results provide
support for the potential of the method to track patient condition, in real-time, in a clinical environment. This
method has the potential to yield additional information from readily available waveforms to aid in clinical
decision making.
1 INTRODUCTION
Cardiovascular disease and dysfunction (CVD) was
responsible for 31% of global deaths in 2013
(Mozaffarian et al., 2015), and continues to be a
leading worldwide cause of Intensive Care Unit
(ICU) admission and mortality. The global cost of
CVD was an estimated $863 billion USD in 2010,
equivalent to 1.39% of gross world product
(Mozaffarian et al., 2015). Incorrect or inadequate
diagnosis of cardiac dysfunction contributes to these
statistics, potentially increasing ICU length of stay,
cost and mortality (Angus et al., 2001, Pineda et al.,
2001). With these figures expected to rise with aging
populations, there is a clear need for optimised,
patient-specific cardiovascular care to mitigate the
social and economic burden.
Management of cardiac patients in the ICU often
utilises information from catheters placed in the
arteries and veins around the heart. Despite their
information rich nature, the use of such catheters is
not necessarily associated with improved clinical
outcomes (Frazier and Skinner, 2008, Chatterjee,
2009). There is thus potential for new methods to
more effectively extract cardiac information from
these catheter signals, yielding further value from
readily available data that has potentially been under-
utilised to date.
The Pressure-Volume (PV) loop is one of the
fundamental means of expressing internal cardiac
dynamics and function (Hall, 2010). A PV loop is
formed by plotting ventricular pressure and volume
for a heartbeat. The area within the PV loop is
equivalent to stroke work, the work done by the heart
to eject blood into the aorta (Suga, 1990, Burkhoff
and Sagawa, 1986). Stroke work is an important
metric that changes in response to cardiac
dysfunction. Further, the location of the PV loop
provides information about contractility (Suga et al.,
1973, Broscheit et al., 2006), which is similarly
sensitive to changes in cardiac state and function.
Unfortunately, PV loops cannot be directly
measured in clinical practice, as this would require
placing catheters directly into the heart chambers.
Hence, the use of PV loops is mainly limited to
experimental and conceptual work. Clinically, there
has been interest in curves and metrics derived from
the PV loop, such as the End-Systolic Pressure-
Volume Relation (ESPVR) (Suga et al., 1973), the
Stroke Work to End-Diastolic Volume Relation
54
Davidson S., Pretty C., Kamoi S., Desaive T. and Chase J.
A Minimally Invasive Method for Beat-by-Beat Estimation of Cardiac Pressure-Volume Loops.
DOI: 10.5220/0006140200540063
In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 54-63
ISBN: 978-989-758-212-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(Little et al., 1989) and the dP/dt
max
to End-Diastolic
Volume Relation (Little, 1985).
Accordingly, there has been various work towards
clinically estimating these relationships and their
associated properties. However, these methods
typically focus on individual components such as
ESPVR (Senzaki et al., 1996, Chen et al., 2001), End-
Diastolic Pressure Volume Relation (EDPVR) (Klotz
et al., 2006) or Preload Recruitable Stroke Work
(PRSW) (Karunanithi and Feneley, 2000, Lee et al.,
2003), as such they fail to provide the comprehensive
and unified set of information about cardiac dynamics
provided by a PV loop. Further, these methods
typically rely on continuous echocardiography, which
is not practical for ICU wide implementation due to
the current cost of these systems (Ferrandis et al.,
2013). There has been little work associated with non-
invasive estimation the PV loop itself to date.
This paper presents a novel method of non-
invasively estimating the beat-by-beat PV loop. The
method combines simple physiological assumptions
with clinically available catheter waveforms to
individually estimate the pressure and volume
components of the PV loop. Clinically feasible
measurements mean the method has the potential for
real-time implementation at the bedside, without
additional invasive instrumentation. These PV loops
could be used to provide additional, patient specific
information on intra-beat behaviour and inter-beat
variation in the functioning of the heart.
2 METHODS AND ANALYSIS
2.1 Proposed Method
The left ventricular PV loop is generated from two
waveforms, the left ventricular pressure (P
lv
) and left
ventricular volume (V
lv
). Both waveforms can be
directly measured, but doing so is not clinically
feasible (Kastrup et al., 2007). The proposed method
approximates these two waveforms (P
lv
, V
lv
) using
three inputs, as shown in Fig. 1 Two of these inputs,
a continuously sampled aortic pressure waveform
(P
ao
) and heart rate (HR), are typically available in a
modern ICU. The third input, baseline End-Systolic
(V
es
) and End-Diastolic (V
ed
) Volume, may be
clinically obtained from a brief echocardiography
reading, which is increasingly clinically available
(Vieillard-Baron et al., 2008). The continuous
pressure measurement (P
ao
), situated directly
downstream from the ventricle, is an effective basis
to estimate P
lv
. However, there is no similar
measurable volume waveform from which to estimate
V
lv
, resulting in the relative complexity of the shaded
region in Fig. 1.
Figure 1: Summary flowchart of the proposed method.
This method encompasses the estimation of two
output waveforms (V
lv
, P
lv
) using one input waveform
(P
ao
). It is important to note that this goal can only be
effectively accomplished because all three
waveforms (P
lv
, V
lv
, P
ao
) consist of different regions
of behaviour governed by different physiological
phenomena, and have been extensively characterised
(Hall, 2010). More specifically, these three
waveforms are both rich in information and heavily
interconnected.
2.1.1 Estimating P
lv
from P
ao
The aortic valve separates the left ventricle
(upstream) from the aorta (downstream). The valve
opens during systole, as blood is ejected from the
ventricle into the aorta, and closes during diastole,
while the ventricle fills. Provided aortic valve
resistance is negligible, P
lv
can be assumed to be
equivalent to P
ao
while the aortic valve is open
(Section P.1, Fig 2), subject to a slight phase lag (δ).
Figure 2: Estimating left ventricular pressure, note P
ao
has
been shifted left by δ.
Cont.:
P
ao
Baseline:
V
ed
and V
es
Kamoi et
al.: SV
Cont.:
HR
Eqs. 1, 2:
P
lv
Eqs. 3, 8:
V
lv
Eq. 7:
E
C
Eq. 9:
V
es
Eq. 10:
V
ed
Measured:
Output:
P
DN
0 0.2 0.4 0.6 0.8 1 1.2
0
10
20
30
40
50
60
70
80
t
1
t
2
t
3
t
4
P1 P2 P3
Time (Seconds)
Pressure (mmHg)
Measured P
lv
Simulated P
lv
Measured P
ao
A Minimally Invasive Method for Beat-by-Beat Estimation of Cardiac Pressure-Volume Loops
55
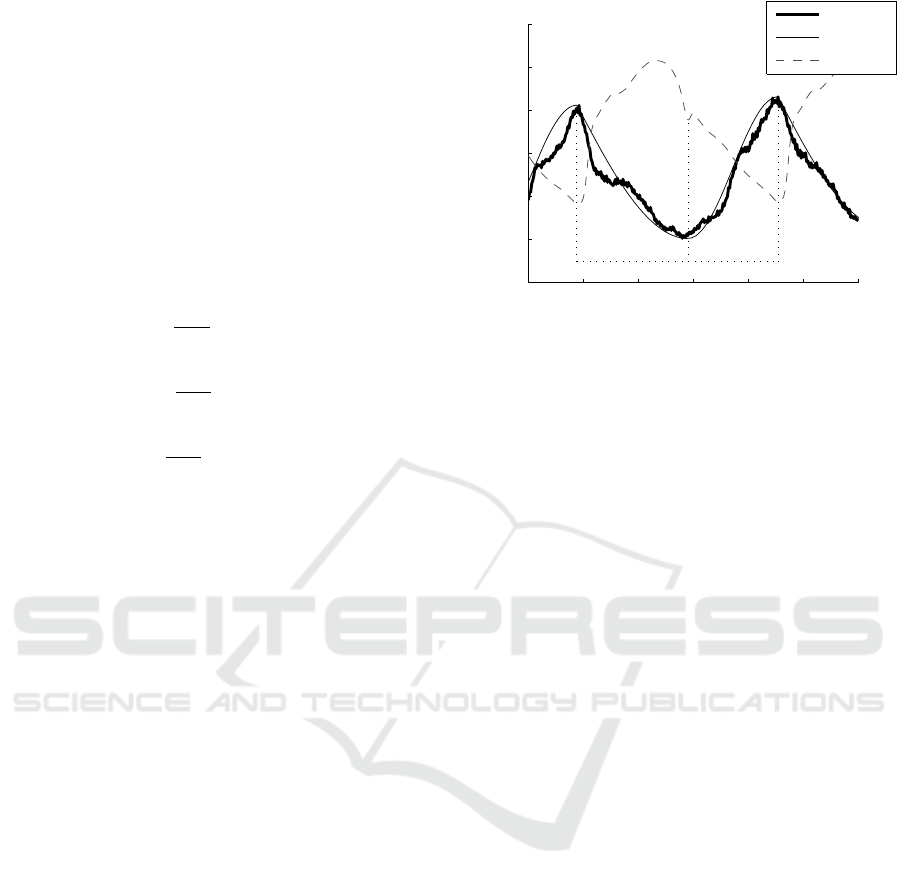
When the aortic valve is closed during diastole, P
ao
and P
lv
diverge significantly. However, as the
ventricle relaxes and fills during diastole, its
behaviour in this region is largely passive (Hall,
2010). Diastolic P
lv
was thus approximated using a
pair of generic exponential functions. The first
simulates ventricular relaxation during early diastole
(Section P. 2, Fig. 2) to a fixed baseline pressure. The
second captures the beginning of ventricular
contraction in late diastole-early systole (Section P. 3,
Fig. 2). Atrial behaviour is neglected in this model.
Per Fig. 2, P
lv
for the n
th
heartbeat is thus defined:
(1a)
(1b)
(1c)
0.62
0.38
(1d)
6
6
.
.
(2)
where: 0.008s
2.1.2 Estimating V
lv
from P
ao
and HR
Estimating V
lv
is significantly more complicated than
P
lv
due to the lack of volume or flow information
readily available from typical clinical
instrumentation. V
lv
was estimated by selecting a
generic waveform and then locating the timing and
magnitude of the peaks and troughs of this waveform
on a beat-by-beat basis. The generic waveform
consisted of a piecewise sine wave broken down into
two sections: systole (Section V. 1, Fig. 3) and
diastole (Section V. 2, Fig. 3), with a 90° phase shift
at the beginning of systole. While the underlying
behaviour of the ventricle might be better represented
by a series of exponentials (Hall, 2010), the use of
sine waves achieves a similar results in Fig. 3, while
requiring considerably fewer variables.
To locate the waveform peaks and troughs, six
points per heartbeat are required (t
1
, t
2
, t
3
and (V
ed
)
n
,
(V
es
)
n
, (V
ed
)
n+1
). The timing associated with systole
start (t
1
), systole end (t
2
), and diastole end (t
3
) are
readily determined from the aortic pressure waveform
(Fig. 3):
Figure 3: Estimating left ventricular volume.
(3a)
(3b)
(3c)
Finding the magnitude of these peaks and troughs is
more involved. For a given heartbeat, stroke volume
(SV) can be approximated from the aortic waveform
per (Kamoi et al., 2014), relating V
es
and V
ed
. The
End-Systolic PV Relation (ESPVR) can be used to
find V
es
(Sagawa, 1981):
(4)
where E
es
is the end-systolic elastance and V
0
is the
ventricular volume at zero pressure. Eq. 4 can be
rewritten:
(5)
where this change is justified by:
The pressures in the ventricle and aorta, as
previously mentioned, can be assumed to be
similar while the aortic valve is open, thus P
DN
can
be used a surrogate for P
es
V
d
and V
0
have similar physiological
definitions and values, and the two are frequently
used interchangeably (Sagawa, 1981, Stevenson
et al., 2012b, Stevenson et al., 2012a). It is
possible to approximate baseline V
d
as a fixed
percentage of baseline V
es
(Davidson et al., 2016),
which is available during the initial
echocardiographic reading. V
d
is known to change
with condition, but such changes cannot be
captured without additional echocardiography
readings. While such intermittent measures are
feasible, V
d
is fixed at its baseline value in this
study.
0.48
(6)
0 0.2 0.4 0.6 0.8 1 1.2
50
60
70
80
90
100
110
V1 V2
t
1
t
2
t
3
Time (Seconds)
Volume (mL)
Measured V
lv
Simulated V
lv
Measured P
ao
BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing
56

Finally, it is necessary to account for E
es
, which
changes in response to loading conditions (Burkhoff
et al., 1993, Baan and Van Der Velde, 1988) and
contractility (Suga et al., 1973). To approximate these
changes, Eq. 5 is modified:
(7)
where E
es
is approximated as a function of heart rate
(HR) and a coefficient (E
C
). A single term power
relation was selected as it can be explicitly defined
during the echocardiography calibration, and
provides reasonable effective tracking for the data set
presented here. Changes in both E
es
and HR are staple
cardiovascular system responses to most changes in
conditions (Hall, 2010). As heart rate is continuously
monitored in most modern ICUs, it provides an easily
obtained, but only partial, indication of
cardiovascular system response to inform an
approximated elastance. Further supporting evidence
is provided in the validation and discussion of results.
During the echocardiography calibration,
measurements for P
DN
, HR and V
es
are available
(Lang et al., 2015). Thus, a constant value for E
C
can
be defined (Eq. 7), enabling beat-by-beat
approximation of E
es
and thus V
es
. The beat-to-beat
ventricular volume can thus be estimated:
sin
2
1
2
cos
1
2
(8)
where:
(9)
(10)
2.1.3 Summary of Proposed Method
The overall derivation of the driver function, also in
Fig. 1, can be summarised:
Initially or Intermittently:
1. Calculate V
d
using Eq. 6 and baseline V
es
2. Calculate E
C
using Eq. 7, P
DN
, HR and baseline V
es
Every heartbeat:
1. Simulate P
lv
using Eq. 1, Eq. 2 and P
ao
2. Determine V
es
using Eq. 9, P
DN
, HR and E
C
3. Determine SV using (Kamoi et al., 2014) and P
ao
4. Determine V
ed
using Eq. 10, V
es
and
5. Simulate V
lv
using Eq. 3, Eq. 8, P
ao
, V
es
and V
ed
6. Use P
lv
and V
lv
to generate the PV loop
2.2 Analysis and Validation
The performance of the proposed method was
evaluated over an experimentally gathered data set,
consisting of continuously measured method inputs
(P
ao
) and outputs (V
lv
, P
lv
). This data set allowed
validation of the ability of the method to individually
estimate P
lv
and V
lv
, as well as validation of the
overall method through comparisons between
estimated and directly measured PV loops. The data
set includes a total of 46,318 heartbeats across 5
Piétrain pigs, measured across a clinical protocol
designed to provide diverse cardiac conditions.
2.2.1 Experimental Procedure
Five male, pure Piétrain pigs weighing between 18.5
and 29 kg were subject to a protocol approved by the
Ethics Commission for the Use of Animals at the
University of Liège, Belgium. The pigs were sedated,
anaesthetised and mechanically ventilated (GE
Engstrom CareStation) with a baseline positive end-
expiratory pressure (PEEP) of 5 cmH
2
O. The heart
was accessed via a median sternotomy, and an
admittance PV catheter (Transonic, NY, USA) with a
sampling rate of 250 Hz inserted into the left
ventricle. Proximal aortic pressure was continually
sampled using a pressure catheter (Transonic, NY,
USA) with a sampling rate of 250 Hz.
To ensure a diverse range of cardiac states was
exhibited, several procedures were performed:
A single infusion of endotoxin
(lipopolysaccharide from E. Coli, 0.5 mg/kg
injected over 30 minutes) to induce septic shock,
which drives a change in afterload conditions and
is associated with a large variety of effects
including an inflammatory response and capillary
leakage that may lead to hypovolemia, global
tissue hypoxia and cardiac failure (Nguyen et al.,
2006).
Several PEEP driven recruitment manoeuvres
(RMs), both pre- and post- endotoxin infusion,
which drive a change in preload conditions and
are typically associated with a decrease in mean
blood pressure and cardiac output (Jardin et al.,
1981).
1 – 4 infusions of 500 mL saline solution over 30
minute periods, pre- and post- endotoxin infusion,
simulating fluid resuscitation therapy, a key
component of hemodynamic resuscitation in
patients with severe sepsis, which itself results in
a change in circulatory volume (Vincent and
Gerlach, 2004).
A Minimally Invasive Method for Beat-by-Beat Estimation of Cardiac Pressure-Volume Loops
57

2.2.2 Model Validation
The overall method presented here is designed to
simulate the left ventricular PV loop beat-by-beat,
without requiring additionally invasive
instrumentation of the heart or continuous real-time
image-based monitoring, neither of which is
clinically or ethically feasible in care. As such,
validation of the method relies on comparison of the
simulated PV loop to the invasively measured, ‘true’
PV loop.
The important information contained in a PV loop
can be broadly broken down into its shape and
enclosed area, as well as the absolute (P, V) position
of the loop. Comparison of the estimated and
measured PV loops thus encompasses several
metrics:
Mean Pressures: A comparison between
measured and estimated mean systolic and
diastolic pressures for each heartbeat (P
sys
, P
dia
).
Volumes: A comparison between the
measured and estimated end-systolic volume (V
es
)
and end-diastolic volume (V
ed
) for each heartbeat.
Stroke Work: A comparison of the area
enclosed within a given pressure volume loop.
Each comparison involves an evaluation of the
beat-by-beat percentage errors between the measured
and estimated values of the relevant metric. Estimated
stroke work values were also compared to stroke
work approximated by equation:
(11)
where MSP is the mean systolic pressure in the aorta
and SV the stroke volume of a given heartbeat. Eq. 11
is a lumped approximation of stroke work (Klabunde,
2011). Finally, the linear correlation between the
measured and simulated stroke work was evaluated
using Pearson’s correlation coefficients.
3 RESULTS
3.1 Pressure and Volume
Per Eq. 2, the systolic pressure is primarily a function
of phase shifted P
ao
, while the diastolic pressure is
primarily a function of fixed waveforms. Thus, the
errors presented in Table 1 provide a means to
validate both the performance of the overall method,
as well as the specific assumptions involved with
estimating the different regions of P
lv
. The extremely
low errors for P
sys
, with medians of 1.5-12.1%
suggest that, as would be physiologically expected,
P
ao
provides an effective estimate for systolic
ventricular pressure. The errors associated with P
dia
are somewhat higher, but it should be noted that these
are percentage errors and values for P
dia
are often an
order of magnitude smaller than those of P
sys
. As
such, median errors ranging from 6.4-23.8% for
generic exponential functions still imply the method
is functioning reasonably effectively.
Table 1: Percentage errors associated with pressure
estimation, median (25
th
percentile – 75
th
percentile).
Pig
Abs. Error: Mean-
Diastolic Pressure (P
dia
)
Abs. Error: Mean-
Systolic Pressure (P
sys
)
Pig 1 23.3% (8.5 – 30.7) 7.1% (4.8 – 10.4)
Pig 2 6.4% (2.9 – 12.9) 1.5% (0.6 – 2.6)
Pig 3 13.4% (5.8 – 19.8) 1.7% (1.1 – 2.6)
Pig 4 17.4% (12.8 – 26.2) 12.1% (10.1 – 13.7)
Pig 5 23.8% (14.9 – 31.2) 2.2% (1.3 – 4.2)
Average 16.9% (9.0 – 24.2) 4.9% (3.6 – 6.7)
Per Eq. 8, the end-systolic volume is a function of a
variety of assumptions made in deriving a modified
ESPVR (Eq. 7). Thus the errors presented in Table 2
serve as an excellent means of validating this body of
assumptions. The end-diastolic volume, per Eq. 10,
combines the assumptions made in deriving V
es
with
those made in deriving SV as in (Kamoi et al., 2014).
The results in Table 2 thus provide a means of
approximating the contribution to error of the various
assumptions and equations involved in estimating V
lv
.
The errors associated with V
es
are low, with median
values ranging from 2.0-6.6%. This result implies that
the assumptions concerning simulating E
es
using HR
and V
d
using baseline V
es
are, at least, effective over
the data set evaluated. The errors for V
ed
are slightly
greater, with medians ranging from 4.5-13.2%. This
error is still within a very acceptable level, especially
when one considers it combines error contributions
from estimation of both V
es
and SV. Overall, the
results in Tables 1 and 2 suggest the method is able to
effectively locate a PV loop.
Table 2: Percentage errors associated with pressure
estimation, median (25
th
percentile – 75
th
percentile).
Pig
Abs. Error: End-
Systolic Volume (V
es
)
Abs. Error: End-
Diastolic Volume (V
ed
)
Pig 1 2.0% (1.0 – 3.3) 4.5% (1.5 – 8.8)
Pig 2 6.6% (4.4 – 9.9) 13.2% (4.9 – 17.5)
Pig 3 4.5% (2.6 – 7.6) 6.2% (2.9 – 12.0)
Pig 4 4.7% (2.2 – 8.1) 5.6% (3.1 – 11.0)
Pig 5 4.3% (2.5 – 8.1) 5.3% (3.0 – 9.9)
Average 4.4% (2.5 – 7.4) 7.0% (3.1 – 11.8)
3.2 Stroke Work
Table 3 presents the percentage errors in stroke work
BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing
58

for different approximations compared to stroke work
derived from the directly measured V
lv
and P
lv
waveforms. Estimated stroke work represents stroke
work derived from the estimated PV loop, while
simplified stroke work uses Eq. 11. As highlighted by
the bolded values, the estimated method produced
lower percentage errors in 11 of the 15 metrics
assessed, and lower overall average error values.
However, the estimated method did produce mildly
higher 25
th
percentile and median errors for Pig 2, and
significantly higher (though still relatively low) 25
th
percentile and median errors for Pig 4.
Table 3: Percentage errors associated with stroke work
estimation, median (25
th
percentile – 75
th
percentile).
Pig
Abs. Error: Estimated
Stroke Work (SW
E
)
Abs. Error: Simplified
Stroke Work (SW
S
)
Pig 1 15.6% (5.3
–
21.3) 30.6% (7.5 – 39.1)
Pig 2 16.4% (10.4 – 20.7) 14.3% (7.6 – 24.0)
Pig 3 24.6% (12.4
–
42.9) 43.1% (22.5 – 67.6)
Pig 4
41.2% (14.2 – 61.1)
57.4% (25.0 – 74.8)
Pig 5 20.8% (17.5 – 55.6) 8.9% (4.7 – 96.4)
Average
23.6% (12.0 – 40.3)
30.9% (13.5 – 60.4)
Figure 4: Correlation plots for estimated and measured
stroke work.
Fig. 4 presents correlation plots between the
estimated and directly measured stroke work. The
correlation coefficients are generally high, with an
average of R = 0.83. The exception to this is Pig 2,
with a correlation coefficient of just R = 0.58.
Regardless, these results show a generally strong link
in trends between simulated and measured stroke
work values, combined with the improvement in
percentage error values over a current approximation
method in Table 3, provide support for the
applicability of this method.
Fig. 5 presents a set of example measured and
estimated PV loops for each of the 5 pigs. The three
PV loops presented for each pig are designed to
provide examples representative of 25
th
percentile,
median and 75
th
percentile error for that pig. As can
be seen from these example PV loops, the method
does a reasonable job of capturing the range of
distinct shapes the PV loop assumes as condition and
subject changes. Additionally, in support of the
results in Tables 1 and 2, the method locates the PV
loops with relative accuracy, even when stroke work
errors are relatively high.
4 DISCUSSION
4.1 Pressure and Volume
The pressure and volume results summarised in
Tables 1 and 2 provide both a means of validating the
ability of the method to correctly locate the PV loop,
as well as a means of validating various model
assumptions and evaluating their contribution to
error. The low errors for P
sys
in Table 1 suggest the
phase shifted P
ao
effectively simulates systolic
ventricular pressure, and this ‘edge’ of the PV loop is
effectively captured. The higher errors for P
dia
in
Table 1 are expected due to the generic nature of the
exponentials used to simulate systolic ventricular
pressure. However, given the relatively low
magnitude of these values, the 6.4-23.8% median
errors observed do not correspond to a significant
absolute deviation in this ‘edge’ of the PV loop.
Estimation of V
lv
was significantly more
challenging. However, the errors in Table 3 are very
comparable to those presented in Tables 1 – 2. Errors
associated with V
es
are relatively low, with medians
of 2.0-6.6%. These low values are important, because
V
es
is a product of both the assumption that V
d
can be
approximated from baseline V
es
(Eq. 6) and that
elastance can be approximated as a function of HR
(Eq. 7), both of which are significant assumptions.
0 500 1000 1500 2000 2500
0
500
1000
1500
2000
2500
Pig 1
R = 0.95
Measured Work
Estimated Work
0 1000 2000 3000 4000 500
0
0
1000
2000
3000
4000
5000
Pig 2
R = 0.58
Measured Work
Estimated Work
0 1000 2000 3000 4000 5000
0
1000
2000
3000
4000
5000
Pig 3
R = 0.88
Measured Work
Estimated Work
0 500 1000 1500 2000 250
0
0
500
1000
1500
2000
2500
Pig 4
R = 0.84
Measured Work
Estimated Work
0 500 1000 1500 2000 2500
0
500
1000
1500
2000
2500
Pig 5
R = 0.92
Measured Work
Estimated Work
1−1 Line
A Minimally Invasive Method for Beat-by-Beat Estimation of Cardiac Pressure-Volume Loops
59

Figure 5: Example measured and estimated PV loops for different error quartiles from all 5 pigs.
Errors associated with V
ed
are slightly larger, with
medians 4.5-13.2%. These results are very acceptable
considering they combine the error contributions
from the method of deriving V
es
with the error
contributions from estimating SV per (Kamoi et al.,
2014). Regardless, all of the specified errors appear
well within acceptable margins, suggesting the
method should be able to accurately locate the PV
loop.
0 50 100
0
50
100
ε: 5.3%
Pig 1 − Low
Vent. Vol., mL
Vent. Pres., mmHg
0 50 100
0
50
100
ε: 15.2%
Pig 1 − Med
Vent. Vol., mL
Vent. Pres., mmHg
0 50 10
0
0
50
100
ε: 22.7%
Pig 1 − High
Vent. Vol., mL
Vent. Pres., mmHg
0 50 100
0
50
100
ε: 10.4%
Pig 2 − Low
Vent. Vol., mL
Vent. Pres., mmHg
0 50 100
0
50
100
ε: 16.4%
Pig 2 − Med
Vent. Vol., mL
Vent. Pres., mmHg
0 50 10
0
0
50
100
ε: 20.2%
Pig 2 − High
Vent. Vol., mL
Vent. Pres., mmHg
0 50 100
0
50
100
Pig 3 − Low
ε: 12.1%
Vent. Vol., mL
Vent. Pres., mmHg
0 50 100
0
50
100
Pig 3 − Med
ε: 23.3%
Vent. Vol., mL
Vent. Pres., mmHg
0 50 10
0
0
50
100
Pig 3 − Hig
h
ε: 45.5%
Vent. Vol., mL
Vent. Pres., mmHg
0 50 100
0
50
100
ε: 14.1%
Pig 4 − Low
Vent. Vol., mL
Vent. Pres., mmHg
0 50 100
0
50
100
ε: 41.1%
Pig 4 − Med
Vent. Vol., mL
Vent. Pres., mmHg
0 50 10
0
0
50
100
ε: 61.1%
Pig 4 − High
Vent. Vol., mL
Vent. Pres., mmHg
0 50 100
0
50
100
ε: 17.2%
Pig 5 − Low
Vent. Vol., mL
Vent. Pres., mmHg
0 50 100
0
50
100
ε: 20.8%
Pig 5 − Med
Vent. Vol., mL
Vent. Pres., mmHg
0 50 10
0
0
50
100
ε: 55.3%
Pig 5 − High
Vent. Vol., mL
Vent. Pres., mmHg
Measured Estimated
BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing
60

It is still important to note the assumptions made,
specifically in Eq. 7, represent a significant
simplification of actual cardiac behaviour. The power
function used to estimate E
es
from HR attempts to
capture the sympathetic component of cardiac system
response. Inevitably, though this sympathetic
relationship varies between individuals, accounted
for here by calibration, and with changes in condition
and time. While this approximation has been shown
to remain effective across the progression of sepsis in
the data set presented, further validation is desired.
Existing work has been performed on estimating
the ESPVR (Chen et al., 2001) and EDPVR (Klotz et
al., 2006) using single-beat methods and
echocardiography. However, these methods broadly
require continuous echocardiography, relying on
continuous stroke volume and ejection fraction
information, which is cost prohibitive for
implementation ICU wide (Ferrandis et al., 2013). In
contrast, the method presented here utilises only a
short echocardiography calibration, allowing sharing
of equipment, and is independent of continuous
stroke volume or ejection fraction measurements.
Other supplementary measurements are also
frequently required such as arm cuff pressures (Chen
et al., 2001). Finally, these methods focus on
presenting a single relationship rather than the unified
set of cardiac dynamic information provided by a PV
loop.
4.2 Stroke Work
The stroke work percentage errors in Table 3 compare
two methods of approximating stroke work to directly
measured stroke work. Estimated stroke work, from
the estimated PV loop, exhibited notable errors, with
medians of 15.6-41.2%. These errors, while non-
negligible, still represent an improvement over the
errors associated with a simplified stroke work metric
in Eq. 11 in 11 of 15 quartiles evaluated. Overall, the
average 25
th
percentile, median and 75
th
percentile
errors were also reduced.
The correlation plots in Fig. 4 show estimated
stroke work effectively captured trends in the
measured stroke work. The average R value was 0.83,
representing a strong correlation. These strong
correlation coefficients, which are sustained over a
variety of significant changes in subject condition,
suggest the method can effectively be used to track
changes in stroke work. This outcome is of major
importance when monitoring patients.
There is some discrepancy between the low error
values in Tables 1 – 2 and high correlation
coefficients in Fig. 4, which imply the method is
effectively simulating PV loops, and the relatively
high error values in Table 3, suggesting the opposite.
The most likely explanation is that while points are
located correctly, the generic waveforms do not
always effectively match the contours of the
measured waveforms. This outcome is somewhat
expected due to the simplicity of the method and its
minimal data input requirements
The example PV loops provided in Fig. 5 show
that the method is able to capture the general shape
and position of the driver function relatively
effectively. The examples in Fig. 5 cover 25
th
percentile, median and 75
th
percentile absolute
percentage error in stroke work estimation. As such,
they show that, even at relatively high percentage
errors, the method is still able to provide a relatively
effective approximation of the shape and position of
the PV loop. This, combined with the high R values
in Fig. 4 suggest the method can consistently provide
an indicator of relative if not necessarily absolute
patient condition.
The positive bias in some cases (Pig 2) and
negative bias in others (Pigs 3 and 4) suggests the
approximation does an overall reasonable job of
estimating central behaviour, but is unable to capture
the variety of subject-specific cardiac waveforms that
can occur. That this bias seems clustered suggests it
is due to each individual having a waveform shape
that does not necessarily change significantly over
their time monitored, but also does not conform to a
sine wave. It may be possible to capture this baseline
ventricular waveform during the echocardiography
calibration, and use it instead of sine waves to
simulate V
lv
continuously. This approach would
capture of this ‘characteristic’ subject-specific
behaviour and add more detail to the method inputs
to overcome this issue.
There exist single-beat methods to estimate
Preload Recruitable Stroke Work (PRSW), which has
been shown to have a strong correlation with
measured stroke work, using non-invasive
measurements and echocardiography (Karunanithi
and Feneley, 2000). This approach was shown to
perform well using invasive measurements in dogs
(Karunanithi and Feneley, 2000). Invasive validation
on humans showed similarly strong performance, but
use of non-invasive measurements resulted in a fall in
correlations between the estimated and measured
PRSW to R = 0.66 (associated percentage errors
aren’t reported) (Lee et al., 2003), lower than the
method presented here (R = 0.83). Further, this
method requires more expensive, continuous
echocardiography (Ferrandis et al., 2013), as opposed
a short echocardiography calibration. Finally, this
A Minimally Invasive Method for Beat-by-Beat Estimation of Cardiac Pressure-Volume Loops
61

method does not provide the unified set of absolute
pressure, volume and P-V contour information
provided by the method presented here.
Overall the errors in Tables 1 – 2 suggest the
method can be used to correctly locate a PV loop. The
high correlation coefficients in Fig. 4 suggest the
method can be used to effectively track changes in
patient stroke work, and thus patient condition.
Further, the method provides a reduction in errors
associated with approximating stroke work in 11 of
15 assessed quartiles compared to a current method.
It also provides an additional detailed plot, as opposed
to a single lumped metric value. These overall
outcomes provide a body of support for the validity
and utility of the method.
4.3 Limitations
There are several limitations to this study that should
be considered. First, it relies on a short initial
calibration period of approximately 100 beats, during
which echocardiography or similar is required. While
echocardiography equipment is becoming more
available in the modern ICU (Vieillard-Baron et al.,
2008), and this process is non-invasive, this
requirement still prevents full implementation of the
method without a modest additional clinical workload
using normal ICU instrumentation.
It addition, the data presented in this study is the
product of a single protocol, which involved a single,
but complex and varied (Nguyen et al., 2006),
condition (sepsis), and several standardised
interventions. This data set encompasses a range of
subjects and behaviour, covering the full progression
a healthy cardiac system to cardiac failure, including
clinically standard ventilation and fluid interventions.
However, there are a much larger range of possible
cardiac conditions. The method would thus benefit
from testing using different protocols involving
different cardiac conditions. However, the overall
physiology and assumptions used to develop this
method would be largely expected to generalise to
other cardiac conditions, as no condition or
intervention specific assumptions are made.
Finally, the method requires validation in human
subjects. However, a number of similar studies on
single-beat approximations of cardiac dynamics have
compared human and animal dynamics and found
strong similarities between them (Karunanithi and
Feneley, 2000, Lee et al., 2003, Klotz et al., 2006).
This suggests the method, which is built on similar
principles and encompasses the same physical
system, should transfer effectively to human
physiology.
5 CONCLUSIONS
A minimally invasive method for estimating PV loops
beat-to-beat was developed. This method was
validated over a cohort of 5 pure Piétrain pigs, which
were subject to a protocol designed to exhibit a
diverse range of cardiac states and levels of health.
The method demonstrated the ability to effectively
locate the four ‘edges’ of the PV loop, with low
overall median errors for End-Systolic Volume
(4.4%), End-Diastolic Volume (7.0%), Mean-
Systolic Pressure (16.9%) and Mean-Diastolic
Pressure (4.9%). While the method was able to
accurately capture trends in stroke work (average R
value of 0.83), there were notable errors when
directly estimating stroke work values (median of
23.6%). While the method requires validation in
human subjects, it has promise as a means of
providing additional real time insight into cardiac
behaviour at a patient bedside, without requiring
additionally invasive instrumentation.
REFERENCES
Angus, D. C., Linde-Zwirble, W. T., Lidicker, J., Clermont,
G., Carcillo, J. & Pinsky, M. R. 2001. Epidemiology of
Severe Sepsis in the United States: Analysis of
Incidence, Outcome, and Associated Costs Of Care.
Critical Care Medicine, 29, 1303-1310.
Baan, J. & Van Der Velde, E. T. 1988. Sensitivity of Left
Ventricular End-Systolic Pressure-Volume Relation to
Type of Loading Intervention in Dogs. Circulation
Research, 62, 1247-1258.
Broscheit, J.-A., Weidemann, F., Strotmann, J., Steendijk,
P., Karle, H., Roewer, N. & Greim, C.-A. 2006. Time-
Varying Elastance Concept Applied To The Relation
Of Carotid Arterial Flow Velocity And Ventricular
Area. Journal of Cardiothoracic and Vascular
Anesthesia, 20, 340-346.
Burkhoff, D., De Tombe, P. P. & Hunter, W. C. 1993.
Impact of Ejection on Magnitude and Time Course of
Ventricular Pressure-Generating Capacity. American
Journal of Physiology-Heart and Circulatory
Physiology, 265, H899-H909.
Burkhoff, D. & Sagawa, K. 1986. Ventricular Efficiency
Predicted By an Analytical Model. American Journal
of Physiology-Regulatory, Integrative and
Comparative Physiology, 250, R1021-R1027.
Chatterjee, K. 2009. The Swan-Ganz Catheters: Past,
Present, and Future A Viewpoint. Circulation, 119,
147-152.
Chen, C.-H., Fetics, B., Nevo, E., Rochitte, C. E., Chiou,
K.-R., Ding, P.-A., Kawaguchi, M. & Kass, D. A. 2001.
Noninvasive Single-Beat Determination of Left
Ventricular End-Systolic Elastance in Humans. Journal
of the American College of Cardiology, 38, 2028-2034.
BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing
62

Davidson, S., Pretty, C., Pironet, A., Desaive, T., Jannsen,
N., Lambermont, B., Morimont, P. & Chase, J. G. 2016.
Estimation of Ventricular Dead Space Volume through
Use of Frank-Starling Curves. Journal of Physiology
(London) (In Review).
Ferrandis, M.-J., Ryden, I., Lindahl, T. L. & Larsson, A.
2013. Ruling out Cardiac Failure: Cost-Benefit
Analysis of a Sequential Testing Strategy with Nt-
Probnp before Echocardiography. Upsala Journal of
Medical Sciences, 118, 75-79.
Frazier, S. K. & Skinner, G. J. 2008. Pulmonary Artery
Catheters: State of the Controversy. Journal of
Cardiovascular Nursing, 23, 113-121.
Hall, J. E. 2010. Guyton and Hall Textbook of Medical
Physiology, Elsevier Health Sciences.
Jardin, F., Farcot, J.-C., Boisante, L., Curien, N., Margairaz,
A. & Bourdarias, J.-P. 1981. Influence of Positive End-
Expiratory Pressure on Left Ventricular Performance.
New England Journal of Medicine, 304, 387-392.
Kamoi, S., Pretty, C., Docherty, P., Squire, D., Revie, J.,
Chiew, Y. S., Desaive, T., Shaw, G. M. & Chase, J. G.
2014. Continuous Stroke Volume Estimation from
Aortic Pressure Using Zero Dimensional
Cardiovascular Model: Proof of Concept Study from
Porcine Experiments.
Karunanithi, M. K. & Feneley, M. P. 2000. Single-Beat
Determination of Preload Recruitable Stroke Work
Relationship: Derivation and Evaluation in Conscious
Dogs. Journal of the American College of Cardiology,
35, 502-513.
Kastrup, M., Markewitz, A., Spies, C., Carl, M., Erb, J.,
Grosse, J. & Schirmer, U. 2007. Current Practice of
Hemodynamic Monitoring and Vasopressor and
Inotropic Therapy in PostOperative Cardiac Surgery
Patients in Germany: Results from a Postal Survey.
Acta Anaesthesiologica Scandinavica, 51, 347-358.
Klabunde, R. 2011. Cardiovascular Physiology Concepts,
Lippincott Williams & Wilkins.
Klotz, S., Hay, I., Dickstein, M. L., Yi, G.-H., Wang, J.,
Maurer, M. S., Kass, D. A. & Burkhoff, D. 2006.
Single-Beat Estimation of End-Diastolic Pressure-
Volume Relationship: A Novel Method with Potential
for Noninvasive Application. American Journal of
Physiology-Heart and Circulatory Physiology, 291,
H403-H412.
Lang, R. M., Badano, L. P., Mor-Avi, V., Afilalo, J.,
Armstrong, A., Ernande, L., Flachskampf, F. A., Foster,
E., Goldstein, S. A. & Kuznetsova, T. 2015.
Recommendations For Cardiac Chamber
Quantification By Echocardiography In Adults: An
Update From The American Society Of
Echocardiography And The European Association Of
Cardiovascular Imaging. Journal of the American
Society of Echocardiography, 28, 1-39. E14.
Lee, W.-S., Huang, W.-P., Yu, W.-C., Chiou, K.-R., Ding,
P. Y.-A. & Chen, C.-H. 2003. Estimation of Preload
Recruitable Stroke Work Relationship by a Single-Beat
Technique in Humans. American Journal of
Physiology-Heart and Circulatory Physiology, 284,
H744-H750.
Little, W., Cheng, C., Mumma, M., Igarashi, Y., Vinten-
Johansen, J. & Johnston, W. 1989. Comparison Of
Measures Of Left Ventricular Contractile Performance
Derived From Pressure-Volume Loops In Conscious
Dogs. Circulation, 80, 1378-1387.
Little, W. C. 1985. The Left Ventricular Dp/Dtmax-End-
Diastolic Volume Relation in Closed-Chest Dogs.
Circulation Research, 56, 808-815.
Mozaffarian, D., Benjamin, E. J., Go, A. S., Arnett, D. K.,
Blaha, M. J., Cushman, M., Das, S. R., De Ferranti, S.,
Després, J.-P. & Fullerton, H. J. 2015. Heart Disease
and Stroke Statistics—2016 Update A Report from The
American Heart Association. Circulation, Cir.
0000000000000350.
Nguyen, H. B., Rivers, E. P., Abrahamian, F. M., Moran,
G. J., Abraham, E., Trzeciak, S., Huang, D. T., Osborn,
T., Stevens, D. & Talan, D. A. 2006. Severe Sepsis and
Septic Shock: Review of the Literature and Emergency
Department Management Guidelines. Annals of
Emergency Medicine, 48, 54. E1.
Pineda, L. A., Hathwar, V. S. & Grant, B. J. 2001. Clinical
Suspicion of Fatal Pulmonary Embolism. Chest
Journal, 120, 791-795.
Sagawa, K. 1981. Editorial: The End-Systolic Pressure-
Volume Relation Of The Ventricle: Definition,
Modifications And Clinical Use. Circulation, 63.
Senzaki, H., Chen, C.-H. & Kass, D. A. 1996. Single-Beat
Estimation of End-Systolic Pressure-Volume Relation
in Humans A New Method with the Potential for
Noninvasive Application. Circulation, 94, 2497-2506.
Stevenson, D., Revie, J., Chase, J. G., Hann, C. E., Shaw,
G. M., Lambermont, B., Ghuysen, A., Kolh, P. &
Desaive, T. 2012a. Algorithmic Processing Of Pressure
Waveforms to Facilitate Estimation of Cardiac
Elastance. Biomedical Engineering Online, 11, 1-16.
Stevenson, D., Revie, J., Chase, J. G., Hann, C. E., Shaw,
G. M., Lambermont, B., Ghuysen, A., Kolh, P. &
Desaive, T. 2012b. Beat-To-Beat Estimation of the
Continuous Left and Right Cardiac Elastance from
Metrics Commonly Available In Clinical Settings.
Biomedical Engineering Online, 11, 73.
Suga, H. 1990. Ventricular Energetics. Physiological
Reviews, 70,
247-277.
Suga, H., Sagawa, K. & Shoukas, A. A. 1973. Load
Independence of the Instantaneous Pressure-Volume
Ratio of the Canine Left Ventricle and Effects of
Epinephrine and Heart Rate on the Ratio. Circulation
Research, 32, 314-322.
Vieillard-Baron, A., Slama, M., Cholley, B., Janvier, G. &
Vignon, P. 2008. Echocardiography in the Intensive
Care Unit: From Evolution to Revolution? Intensive
Care Medicine, 34, 243-249.
Vincent, J.-L. & Gerlach, H. 2004. Fluid Resuscitation in
Severe Sepsis and Septic Shock: An Evidence-based
Review. Critical Care Medicine, 32, S451-S454.
A Minimally Invasive Method for Beat-by-Beat Estimation of Cardiac Pressure-Volume Loops
63
