A Comparison of Statistical Linkage Keys with Bloom Filter-based

Encryptions for Privacy-preserving Record Linkage using Real-world

Mammography Data

Rainer Schnell

, Anke Richter

and Christian Borgs

City, University of London, Northampton Square, London EC1V 0HB, U.K.

Institute for Cancer Epidemiology, Ratzeburger Allee 160, 23538 L

ubeck, Germany

University of Duisburg-Essen, German Record Linkage Center, Lotharstr. 65, 47057 Duisburg, Germany

Keywords:

Medical Record Linkage, Patient Identiﬁcation Codes, Pseudonyms.

Abstract:

New EU regulations on the need to encrypt personal identiﬁers for linking data will increase the importance of

Privacy-Preserving Record Linkage (PPRL) techniques over the course of the next years. Currently, the use of

Anonymous Linkage Codes (ALCs) is the standard procedure for PPRL of medical databases. Recently, Bloom

ﬁlter-based encodings of pseudo-identiﬁers such as names have received increasing attention for PPRL tasks. In

contrast to most previous research in PPRL, which is based on simulated data, we compare the performance

of ALCs and Bloom ﬁlter-based linkage keys using real data from a large regional breast cancer screening

program. This large regional mammography data base contains nearly 200.000 records. We compare precision

and recall for linking the data set existing at point

with new incident cases occuring after

using different

encoding and matching strategies for the personal identiﬁers. Enhancing ALCs with an additional identiﬁer

(place of birth) yields better recall than standard ALCs. Using the same information for Bloom ﬁlters with

recommended parameter settings exceeds ALCs in recall, while preserving precision.

1 INTRODUCTION

Many medical studies link different databases contain-

ing information on the same patient (Jutte et al., 2010).

If unique common identiﬁers are available, linking is

trivial. However, in many situations in practice such

unique identiﬁcation numbers are not available. If pri-

vacy is not an issue, probabilistic record linkage based

on pseudo-identiﬁers such as surname, ﬁrst name, date

of birth and address information can be used (Herzog

et al., 2010). Under legal constraints demanding pri-

vacy for pseudo-identiﬁers, privacy-preserving record

linkage (PPRL, for an overview see (Vatsalan et al.,

2013)) is required.

In general, jurisdictions for linking patient data dif-

fer widely. Therefore, the technical details to comply

with national legal requirements vary between coun-

tries. In the US, the HIPAA rules require the removal

of nearly all information used for record linkage. The

current legal situation in Europe has made pseudomy-

sation of record linkage identiﬁers factually mandatory:

Due to increasing privacy concerns of the population,

the European Council, Parliament and Commission

agreed on a new “General Data Protection Regula-

tion” (Council of European Union, 2016), which will

be part of the national jurisdictions in all 28 member

states of the European Union by May 2018. The regu-

lation clearly demands pseudonymisation techniques

able to withstand re-identiﬁcation attacks, but does

not require absolute anonymization.Given this recent

development, the demand for PPRL solutions will in-

crease sharply.

Currently, due to the regional and organisational

fragmentation of medical health care, the standard set-

ting for medical record linkage is based on a one-time-

exchange between otherwise computationally sepa-

rated organizational units. This constraint restricts the

number of potential PPRL solutions to a small sub-

set of the many different PPRL approaches which

have been suggested (for a review, see (Vatsalan et al.,

2013)). Nearly all applied PPRL protocols use three

types of actors: Two or more data holders, one linkage

unit and a research group. In general, in such settings,

all units interact only once. Most protocols assume

that all partners act according to the protocol (but may

keep track of all local computations). This assumption

is called ‘honest, but curious’ or ‘semi-honest’ model

(Goldreich, 2004).

276

Schnell R., Richter A. and Borgs C.

A Comparison of Statistical Linkage Keys with Bloom Filter-based Encryptions for Privacy-preserving Record Linkage using Real-world Mammography Data.

DOI: 10.5220/0006140302760283

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 276-283

ISBN: 978-989-758-213-4

For such scenarios, only three approaches for link-

ing medical data have been used repeatedly for real-

word applications of large medical databases (Schnell,

2015): Using a third-party trustee, using encrypted

identiﬁers

and using Bloom-ﬁlters.

If a third-party data trustee (Kelman et al., 2002) is

used, unencrypted patient pseudo-identiﬁers are trans-

ferred to a trusted third party, which links the pseudo-

identiﬁers and assigns a new identiﬁcation number to

the linked records. These newly constructed IDs are

then used for linkage by a research group.

By far the most common approach in practical set-

tings is the use of encrypted pseudo-identiﬁers. Here,

the identiﬁers are concatenated into a single string

which is then encrypted. The resulting encrypted string

is called an anonymous linking code (ALC, (Herzog

et al., 2007)).

Many of the more recent PPRL approaches (see

(Vatsalan et al., 2013; Karapiperis et al., 2016) for

reviews) have limited scalability, so they can not be

used with large datasets. For example, although techni-

cally interesting, all homomorphic encryption methods

are computationally expensive and do not scale well

(Karakasidis et al., 2015). An exception are Bloom ﬁl-

ter approaches. (Schnell et al., 2009) ﬁrst suggested the

use of Bloom ﬁlters for privacy-preserving record link-

age. The approach is based on splitting each identiﬁer

into a set of substrings of length 2 (bigrams), which

are mapped into a binary vector for each identiﬁer with

a linear combination of different cryptographic hash

functions such as SHA-1 and MD-5. The similarity

of these binary vectors (Bloom ﬁlters) approximates

the similarity of the pseudo-identiﬁers, which makes

Bloom ﬁlters attractive for error-tolerant PPRL.

Although using separate Bloom ﬁlters for each

pseudo-identiﬁer is the most common approach, the

use of one common binary vector is harder to attack.

The use of a single Bloom ﬁlter for all identiﬁers

has been ﬁrst proposed in (Schnell et al., 2011) and

has been explored further by (Durham, 2012). The

resulting composite Bloom ﬁlter is called a Crypto-

graphic Long-term Key (CLK) in the original publica-

tion or ‘record based Bloom ﬁlter’ (RBF) by (Durham,

2012). CLKs have been used on real world data exten-

sively (Randall et al., 2014; Schnell and Borgs, 2015;

Schmidlin et al., 2015).

Although data sets without direct personal identiﬁers,

but containing indirect identifying information such as date

of hospital admission and discharge are occasionally sug-

gested (Karmel and Gibson, 2007) for record linkage, they

rarely contain enough discriminating information for unique

linkage pairs.

Our Contribution.

No previous publication com-

pared the performance of CLKs with the performance

of the more traditional ALCs using real-world data.

Therefore, we report on a new study assessing the per-

formance of different variations of CLKs and ALC

variants using real-world data from a large regional

breast cancer screening program (Katalinic et al.,

2007). Furthermore, for the ﬁrst time, we compare

the effect of including additional identiﬁers to linkage

keys and Bloom ﬁlter encodings.

2 PREVIOUS WORK

Currently, only two different versions of encoding iden-

tiﬁers seem to be in practical use for PPRL: Anony-

mous Linkage Codes (ALCs) and Bloom ﬁlters. Both

will be described shortly.

2.1 ALC Variants

ALCs are an encrypted single string formed by con-

catenating substrings or functions of different pseudo-

identiﬁers. These pseudo-identiﬁers should be stable

over time and free of errors. Most often, ﬁrst name,

surname, date of birth and sex are used for construct-

ing ALCs. The resulting combination of identiﬁers

is encrypted using cryptographic hash functions. The

resulting hashed string is used as the linkage key. If

two ALCs match exactly, the corresponding records

are classiﬁed as representations of the same real-world

entity. Due to the cryptographic hash function, it is

nearly impossible to decrypt the identiﬁers directly.

The most simple and widely-used ALC is con-

structed in three steps (Herzog et al., 2007): all identi-

ﬁers are preprocessed using a set of rules (for example,

removal of non-alphabetical characters from names,

removal of non-digits from dates, and capitalization

of all characters). The resulting preprocessed identi-

ﬁers are then concatenated to form one single string,

which is ﬁnally encrypted with a cryptographic hash

function. Examples of applications of Basic ALCs are

described by (Kijsanayotin et al., 2007; Sch

ulter et al.,

2007; Johnson et al., 2010; Tessmer et al., 2011).

The design of the Basic ALC is not error-tolerant,

since even the replacement of a single letter will result

in an entirely different hash code. As spelling and ty-

pographical errors in patient identiﬁers are common,

many true record pairs will not be classiﬁed as matches.

Hence patients with variations in their respective iden-

tiﬁers might have different characteristics than patients

with agreeing identiﬁers. Ignoring this problem can

result in biased estimates (Ridder and Mofﬁtt, 2007).

A Comparison of Statistical Linkage Keys with Bloom Filter-based Encryptions for Privacy-preserving Record Linkage using Real-world

Mammography Data

277

Different approaches to constructing ALCs allow

for some errors in identiﬁers. The Swiss Federal Of-

ﬁce for Statistics asked the Cryptological Unit of the

Swiss Military to develop a privacy-preserving link-

age method for medical patient data (Ofﬁce f

eral de

la statistique, 1997).To construct this ALC variation,

the Soundex code of surname and ﬁrst name are cre-

ated after some preprocessing. The Soundex codes are

concatenated with the date of birth and sex. The re-

sulting string is encrypted using a cryptographic hash

function (Ofﬁce f

eral de la statistique, 1997). Appli-

cations and reviews of the Swiss ALC are discussed

in (Borst et al., 2001; Holly et al., 2005; Eggli et al.,

2006; El Kalam et al., 2011).

Another approach to construct more error-tolerant

ALCs was invented by the Australian Institute of

Health and Welfare (AIHW). Their solution uses sub-

strings of ﬁrst and last names instead of the full string.

(Ryan et al., 1999) tested several variations and con-

cluded that the second, third, and ﬁfth character of the

surname combined with the characters at the second

and third position of the ﬁrst name concatenated with

sex and date of birth performed best. The resulting

string forms the Statistical Linkage Key (SLK) which is

often included in data published by the AIHW (Karmel

et al., 2010). After applying a cryptographic hash func-

tion to the SLK, the Encrypted SLK, sometimes also

denoted as 581-Key is the ALC variant that is widely

used in Australian data linkage (Taylor et al., 2014).

(Karmel et al., 2010) tested the effect of adding dif-

ferent versions of state and postcode to the 581-Keys.

In general, 581-Keys don’t seem to be considered as

state-of-the-art any longer (Randall et al., 2016).

2.2 Simple Bloom Filters

Bloom ﬁlters have been used for calculating string

similarities in privacy-preserving probabilistic record

linkage (Schnell et al., 2009). A Bloom ﬁlter is an

array of data proposed by Howard (Bloom, 1970) for

checking the set membership of records efﬁciently

(Broder and Mitzenmacher, 2003). It is represented

by a bit array with a length of

bits initially set to

zero. For the mapping,

independent hash functions

h ∈ {h

, . . . , h

}

are used.To store the set of entities

S =

{

, x

, . . . , x

}

in the Bloom ﬁlter, each element

∈ S

is hashed using the

independent hash functions.

The bit positions given by the hash functions are set to

1. If a bit was already set to 1, nothing is changed.

To store all elements of a set in Bloom ﬁlters, we

apply the double hashing scheme proposed by (Kirsch

and Mitzenmacher, 2006). They show that using two

independent hash functions is sufﬁcient to implement a

Bloom ﬁlter with

hash functions without an increase

in the asymptotic false positive probability (Kirsch and

Mitzenmacher, 2006). Therefore, the positional values

of the

hash functions are computed with the function

(x) = (h

(x) + i · h

(x)) mod l (1)

where

i ∈ {0, . . . , k − 1}

and

is the length of the bit

array. We use two different keyed hash message au-

thentication codes (HMACs), namely, HMAC-SHA1

(

) and HMAC-MD5 (

) (Krawczyk et al., 1997) to

create the Bloom ﬁlters.

2.3 Composite Bloom Filters

For some applications, a single linkage key has to be

used. If separate Bloom ﬁlters are used, for these ap-

plications, the set of Bloom ﬁlters has to be combined

in a composite Bloom ﬁlter. Storing all of the identi-

ﬁers used in a single Bloom ﬁlter was ﬁrst proposed by

(Schnell et al., 2011). This is called a Cryptographic

Long-term Key (CLK), since they were intended for

use in a longitudinal study of offenders.

For the construction of a CLK, each identiﬁer is

split into a set of

-grams. Each set is stored using

hash functions using the same Bloom ﬁlter of the

length

for all

-gram sets of all identiﬁers used. This

additive Bloom ﬁlter represents the CLK.

After preprocessing, ﬁrst name and surname are

split into bigrams, birth year into unigrams. In the

second step, the ﬁrst

-gram set (e.g. ﬁrst name) is

stored in the Bloom ﬁlter. Each bigram is hashed

times. Bits having indices corresponding to the hash

values are set to one. In the third step, the second

gram set (e.g. surname) is mapped to the same Bloom

ﬁlter. Finally, unigrams are mapped to the same bit

array.

2.4 Cryptographic Attacks on ALCs

Frequency attacks on standard ALCs have not been

reported in the literature so far. Discussions about the

security of ALCs and 581-Keys up to now are hypo-

thetical, not empirical (Randall et al., 2016).

However, since the same password is used for all

records, within a combination of sex and date of birth,

the most frequent name/surname combination will

also yield the most frequent ALC. Therefore, given a

large random sample, the most frequent name/surname

combinations have a high risk of re-identiﬁcation.

Under the (unrealistic) assumption of uniformly dis-

tributed dates of birth, age and sexes, there are about

365 ∗ 100 ∗ 2 = 73.000

combinations possible. This

way, in a database of

10.000.000

records, about 137

records per combination are expected. If the frequency

HEALTHINF 2017 - 10th International Conference on Health Informatics

278

distribution of names is skewed, aligning the most fre-

quent name subsets could identify a large proportion

of the records using this simple frequency alignment.

2.5 Cryptographic Attacks on Bloom

Filters

Bloom ﬁlter-based PPRL has been attacked by two

different techniques: by applying a Constrained Satis-

faction Solver (CSS) on frequencies of entire Bloom

ﬁlters (Kuzu et al., 2011; Kuzu et al., 2013) and by a in-

terpreting the Bloom ﬁlter bit patterns as a substitution

cipher (Niedermeyer et al., 2014).

The ﬁrst attack is a variant of a simple rank swap-

ping attack (Domingo-Ferrer and Muralidhar, 2016)

which used the estimated length of the encrypted

strings as additional information. (Kuzu et al., 2011)

consider their attack on separate Bloom ﬁlters as suc-

cessful, but not their attack on composite Bloom ﬁlters

(Kuzu et al., 2013). It should be noted that this CSS

attack is based on the entire data set of Bloom ﬁlters,

therefore it is no decoding, but an alignment. This

way of attack is impossible if many groups of similar

cases generates a new bit pattern, for example by us-

ing salted encodings (Niedermeyer et al., 2014). In a

salted encoding, a stable identiﬁer such as date of birth,

year of birth or place of birth is added to the password

determining the hash functions.

The second attack attempted the actual revealing

of all identiﬁers as clear text by a cryptanalysis of

individual bit patterns within the Bloom ﬁlters (Nie-

dermeyer et al., 2014). This attack is based on the

limited number of bit patterns generated by the lin-

ear combination of two hash functions in the double-

hashing scheme (Kirsch and Mitzenmacher, 2006)

of the initial proposal. Exploiting this speciﬁc con-

struction of the hash functions, (Niedermeyer et al.,

2014) were successful with basic Bloom ﬁlters and

(Kroll and Steinmetzer, 2015) with CLKs/composite

Bloom ﬁlters. Therefore, replacing the double-hashing

scheme by random hashing should prevent the suc-

cess of this attack on Bloom ﬁlters (Niedermeyer et al.,

2014). Random hashing is based on the idea of using

bigrams as seeds for random number streams. This

could be implemented by a linear-congruential pseudo-

random number generator (LCG, (Stallings, 2014)),

to generate a sequence

with the length

for each

-gram.Random hashing increases the number of pos-

sible bit patterns (

l = 1000, k = 15

) for a given

gram from less than

to more than

6.8 · 10

. There-

fore, the Niedermeyer-attack should fail for randomly

hashed Bloom ﬁlters. This theoretical expectation has

been empirically veriﬁed by (Schnell and Borgs, 2016).

In conclusion, for salted Bloom ﬁlter encodings

using random hashing, no successful attack method

is known. Of course, the number of records using the

same salt should not exceed the minimum required

for a frequency attack either on the whole pattern or

the individual attributes mapped to the Bloom ﬁlter.

Based on experiments reported by (Schnell and Borgs,

2016), this minimum number seems to be about 300

records. In most medical applications, this number is

only exceeded in national databases. For this, an ad-

ditional salt has to be used. Given this condition, we

consider Bloom ﬁlter-based encodings as meeting the

requirements of the EU Protection Regulation (Coun-

cil of European Union, 2016) for a pseudonymisation

method.

3 METHODS

Using real data from a German state-wide breast can-

cer screening program (Katalinic et al., 2007), we com-

pared the CLK encryption with the Basic and Swiss

ALCs and the encrypted SLK (581-Key).

The test data consists of mammography records of

patients in a German state, covering about 3.4% of the

total German population. File A consists of cases until

the end of 2011 (with one record for each case) with

n = 138.131

records, ﬁle B encompasses cases after

2011 (more than one record per case was possible)

with n = 73.004 cases in 198.475 records.

The standard CLK is set up with a length of

l = 1000

. First name and Surname were padded with

spaces before being split into bigrams (Robertson

and Willett, 1998). The other identiﬁers were split

into unigrams. Each set of

-grams is hashed using

k = 10

HMACs (Hash functions) and a different cryp-

tographic key. Since CLKs allow for matching strate-

gies other than exact matching (Schnell et al., 2011),

following (Schnell, 2014), Multibit Trees with various

Tanimoto-thresholds were used. The statistical linkage

keys were evaluated using exact matching.

The set of identiﬁers used consisted of ﬁrst name,

surname, date of birth and sex. According to recent

studies, including more stable identiﬁers is desirable

(Schnell and Borgs, 2015). Address information is very

volatile, since places of residence may change during

the course of a lifetime. Therefore, (Schnell and Borgs,

2015) suggested using places of birth as an additional

identiﬁer for Bloom ﬁlter-based PPRL. In the second

experiment, we did this by adding place of birth to the

set of identiﬁers for the CLKs and 581-Keys.

Since the real-world data sets used here contained

only current places of residence, we simulated the

place of birth according to German administrative pop-

ulation counts. We introduced artiﬁcial 10% address

A Comparison of Statistical Linkage Keys with Bloom Filter-based Encryptions for Privacy-preserving Record Linkage using Real-world

Mammography Data

279

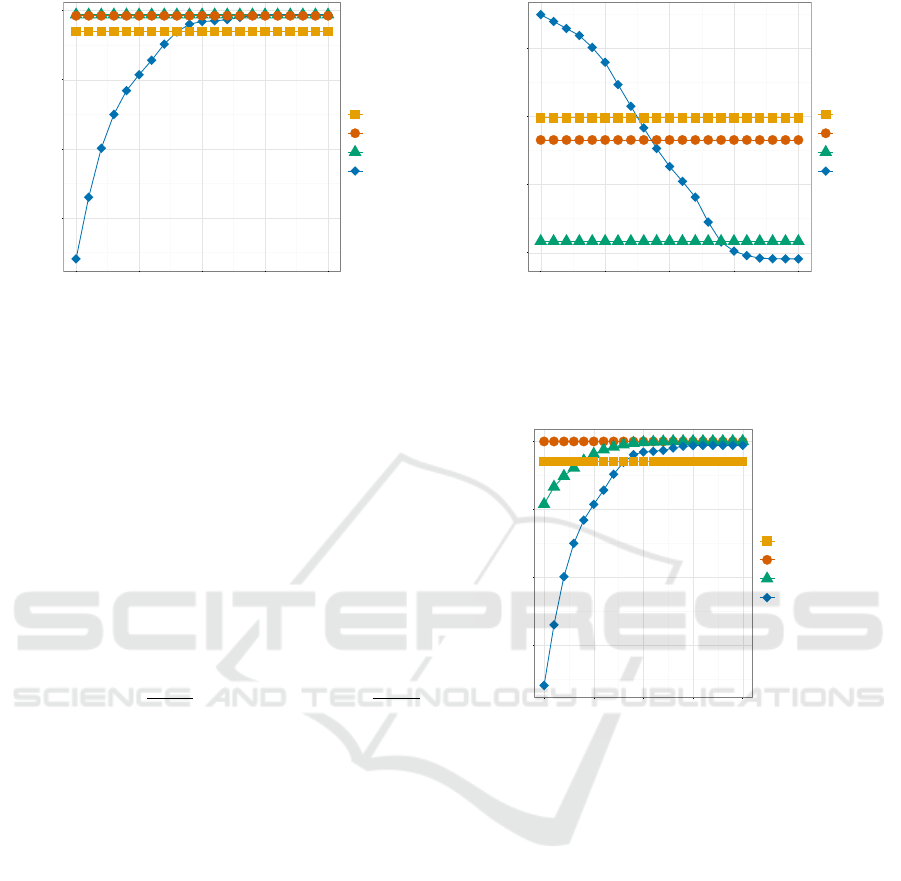
0.925

0.950

0.975

1.000

0.80 0.85 0.90 0.95 1.00

Tanimoto-Threshold

Precision

Encryption

581-Key

Swiss ALC

Basic ALC

CLK k=10

Figure 1: Precision of the CLK and encrypted statistical

linkage key variants. Since the ALCs were matched exactly,

their values are shown as constants, while several similarity

thresholds were used for CLKs.

changes to the simulated data. As the two linked ﬁles

refer to different years, this percentage should reﬂect a

worst-case scenario for the amount of regional mobility

in the population.

The current gold standard in use at the cancer

screening program is considered as reﬂecting the true

matching status. Based on this classiﬁcation, the com-

pared methods will yield true positive (TP), false posi-

tive (FP), true negative (TN) and false negative (FN)

classiﬁcations of record pairs.

This way, we can compare the methods using preci-

sion (

Precision =

TP+FP

) and recall (

Recall =

TP+FN

)

(Baeza-Yates and Ribeiro-Neto, 1999).

According to legal requirements, unencrypted iden-

tiﬁers were processed only at the ofﬁce of the data

holder. ALCs, 581-Key and CLKs were generated with

Python 3, while R (R Core Team, 2016) was used for

the matching and statistical computation.

4 RESULTS

Figures 1 and 2 show the results of the standard CLK

(

k = 10

hash functions) against the encrypted linkage

keys in terms of precision and recall. Lowering the

threshold improves the recall. Precision is stable until

the threshold approaches 0.88. Above this threshold,

precision drops considerably. Given this set of iden-

tiﬁers, CLK does not exceed the performance of the

Swiss ALC and the 581-Key.

All in all, ALCs offer higher precision (less false

positives) compared to the CLK. However, the CLK

outperforms the ALCs in terms of recall as the simi-

larity threshold is lowered below 0.88. At the recom-

mended Tanimoto-threshold of 0.85 (Schnell, 2015),

0.95

0.96

0.97

0.98

0.80 0.85 0.90 0.95 1.00

Tanimoto-Threshold

Recall

Encryption

581-Key

Swiss ALC

Basic ALC

CLK k=10

Figure 2: Recall of the CLK and encrypted statistical link-

age key variants. Since the ALCs were matched exactly,

their values are shown as constants, while several similarity

thresholds were used for CLKs.

0.925

0.950

0.975

1.000

0.80 0.85 0.90 0.95 1.00

Tanimoto-Threshold

Precision

Encryption

581-Key

581-Key + Birthplace

CLK k=10 + Birthplace

CLK k=10

Figure 3: Precision of the 581-Key and CLK with and with-

out inclusion of places of birth.

CLKs show more (0.7% – 2.8%) true positives than

both standard ALC variants (see table 1), even out-

performing the 581-Key. However, given this set of

identiﬁers, the amount of false positives is consider-

ably higher. Since CLKs should perform better if more

(stable) identiﬁers are included. Therefore, for the sec-

ond set of experiments, we included place of birth and

hashed it into the original CLKs. We did the same with

the 581-Key, concatenating place of birth to the 581-

Key before hashing it again. Figures

and 4 show

that the performance now exceeds the standard ALCs

in terms of recall while showing improved precision

values.

Table 1 lists the detailed classiﬁcations in terms of

true (TP) and false positive (FP) record pairs, as well

as missed record pairs (false negatives (FN)) along

with recall and precision at a Tanimoto-threshold of

0.85 for all ALCs, the 581-Key and the CLKs. Details

on the results for adding the simulated place of birth

HEALTHINF 2017 - 10th International Conference on Health Informatics

280

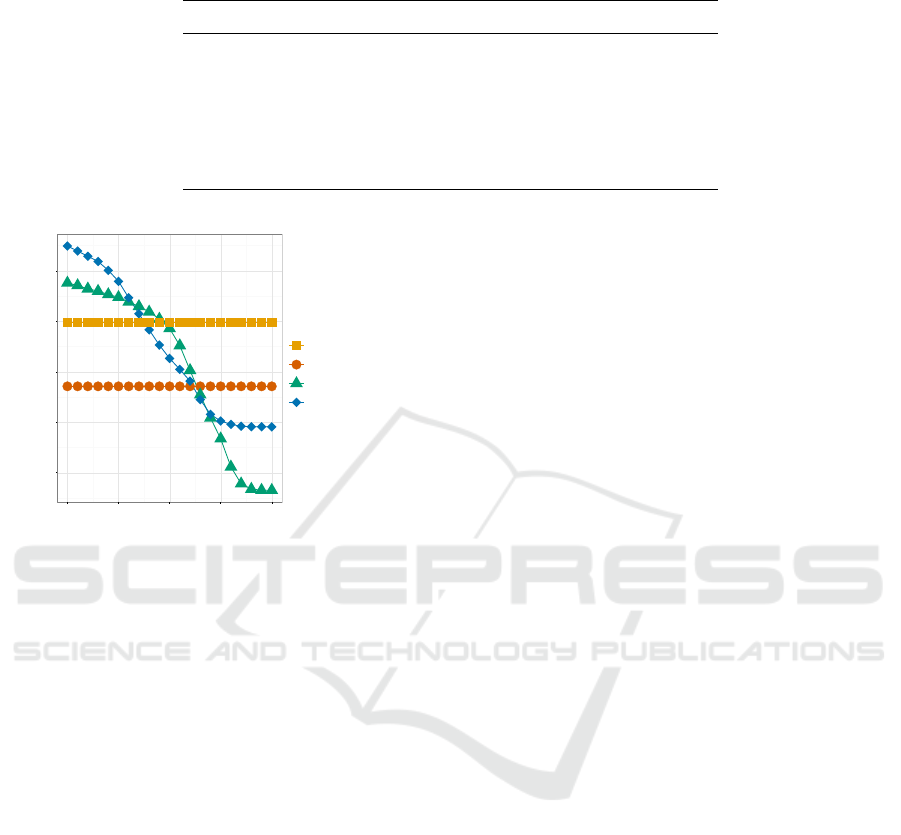
Table 1: Classiﬁcation results for all methods presented. CLK results are based on a Tanimoto-threshold of 0.85 using Multibit

Trees.

Variant TP FP FN Prec. Rec.

Basic ALC 51.587 79 2.620 0.998 0.952

Swiss ALC 52.454 101 1.816 0.998 0.967

581-Key 52.633 400 1.640 0.992 0.970

CLK

k10

53.012 1.260 1.196 0.977 0.978

581-Key

+place of birth

51.945 5 2.328 0.999 0.957

CLK

k10+place of birth

52.840 251 1.368 0.995 0.975

0.94

0.95

0.96

0.97

0.98

0.80 0.85 0.90 0.95 1.00

Tanimoto-Threshold

Recall

Encryption

581-Key

581-Key + Birthplace

CLK k=10 + Birthplace

CLK k=10

Figure 4: Recall of the 581-Key and CLK with and without

inclusion of places of birth.

are shown as well. The CLKs consistently show more

true positive classiﬁcations, while the ALCs and 581-

Key perform better in terms of precision (fewer false

positives).

It has to be noted that adding the place of birth to

the set of identiﬁers improves the precision for both

the 581-Key and the CLKs, while only decreasing re-

call marginally (likely due to the 10% errors simulated

for the birth places). A CLK with birthplace informa-

tion stored in it outperforms all standard ALC variants

and the 581-Key without additional identiﬁers in both

recall and precision.

Since the simulated birth places assumed a worst-

case setting of 10% errors in the data, real-world ap-

plications using CLKs will beneﬁt from including ad-

ditional stable identiﬁers. These results show the po-

tential of using Bloom ﬁlters for real-world privacy-

preserving record linkage applications, especially if

additional stable information is available.

5 DISCUSSION

In this paper, we showed a real-world application of

the Cryptographic Long-term Key. Previously, ALCs

were built by encrypting hashed or sampled identiﬁers.

The CLK, representing an array of bits allows for simi-

larity comparisons using Multibit Trees. The presented

simulation results show better recall, but lower preci-

sion than best-performing ALCs. Since CLKs can be

easily ﬁne-tuned by selecting different thresholds, the

impact of linkage errors on substantial results can be

easily studied. Therefore, we consider the impact of

increased false positives as not limiting the application

of CLKs.

Precision and recall of CLKs will exceed ALCs

and 581-Keys if more stable identiﬁers can be used.

Recently, (Brown et al., 2016) showed that the optimal

choice of identiﬁers and parameters is critical for the

performance of Bloom ﬁlter-based PPRL. Their results

vary, depending on the set of identiﬁers used. They also

showed the need for stable identiﬁers, as errors and

missing values (for example, in recent addresses) will

reduce recall.

After ﬁne-tuning parameters and identiﬁer sets,

PPRL linkage quality comparable to clear text link-

age can be achieved with CLKs. Furthermore, using

Multibit Trees as suggested by (Schnell, 2014), PPRL

using CLKs can be done (without additional blocking)

on standard hardware with two ﬁles containing 5 mil-

lion records each in a little over 4 days (Brown et al.,

2016). If additional blocks such as date of birth are

used, linkage can be done in less than an hour (Schnell,

2015).

Bloom ﬁlters can be used to represent other data

than strings: (Vatsalan and Christen, 2016) demon-

strated the use of numerical and date information, (Far-

row and Schnell, 2017) tested the inclusion of distance-

preserving locational data. Both techniques will extend

the number of possible applications for PPRL.

Currently, there is no known way of attacking

CLKs and state-of-the-art variants of single Bloom ﬁl-

ters (Schnell and Borgs, 2016). Therefore, they might

be used to link ﬁles using personal identiﬁers accord-

ing to the de-facto anonymity standard required by the

new EU regulation on data protection.

A Comparison of Statistical Linkage Keys with Bloom Filter-based Encryptions for Privacy-preserving Record Linkage using Real-world

Mammography Data

281

ACKNOWLEDGEMENTS

The study was supported by German Research Founda-

tion (DFG) research grant SCHN 586/17-2 awarded to

the ﬁrst author. The ﬁrst author would like to thank the

Isaac Newton Institute for Mathematical Sciences for

support and hospitality during the programme ‘Data

Linkage and Anonymisation’ (which was supported by

the EPSRC grant Number EP/K032208/1) when work

on this paper was undertaken.

REFERENCES

Baeza-Yates, R. and Ribeiro-Neto, B. d. A. (1999). Modern

Information Retrieval. Addison-Wesley, Harlow.

Bloom, B. H. (1970). Space/time trade-offs in hash coding

with allowable errors. Communications of the ACM,

13(7):422–426.

Borst, F., Allaert, F.-A., and Quantin, C. (2001). The Swiss

solution for anonymous chaining patient ﬁles. In Patel,

V., Rogers, R., and Haux, R., editors, Proceedings of

the 10th World Congress on Medical Informatics: 2–5

September 2001; London, pages 1239–1241, Amster-

dam. IOS Press.

Broder, A. and Mitzenmacher, M. (2003). Network applica-

tions of Bloom ﬁlters: a survey. Internet Mathematics,

1(4):485–509.

Brown, A., Borgs, C., Randall, S., and Schnell, R. (2016).

High quality linkage using multibit trees for privacy-

preserving blocking. International Population Data

Linkage Conference (IPDLN2016): 24.08-26.08.2016;

Swansea.

Council of European Union (2016). Council regulation (EU)

no 679/2016.

Domingo-Ferrer, J. and Muralidhar, K. (2016). New direc-

tions in anonymization: Permutation paradigm, veriﬁa-

bility by subjects and intruders, transparency to users.

Information Sciences, 337–338:11–24.

Durham, E. A. (2012). A framework for accurate, efﬁcient

private record linkage. Dissertation. Vanderbilt Univer-

sity.

Eggli, Y., Halfon, P., Chikhi, M., and Bandi, T. (2006). Am-

bulatory healthcare information system: A conceptual

framework. Health Policy, 78:26–38.

El Kalam, A., Melchor, C., Berthold, S., Camenisch, J.,

Clauss, S., Deswarte, Y., Kohlweiss, M., Panchenko,

A., Pimenidis, L., and Roy, M. (2011). Further pri-

vacy mechanisms. In Camenisch, J., Leenes, R., and

Sommer, D., editors, Digital Privacy, pages 485–555.

Springer, Berlin.

Farrow, J. and Schnell, R. (2017). Locational privacy pre-

serving distance computations with intersecting sets of

randomly labelled grid points. Journal of the Royal

Statistical Society, Series A, Under review.

Goldreich, O. (2004). Foundations of Cryptography. Volume

2, Basic Applications. Cambridge University Press,

Cambridge.

Herzog, T. N., Scheuren, F. J., and Winkler, W. E.

(2007). Data Quality and Record Linkage Techniques.

Springer, New York.

Herzog, T. N., Scheuren, F. J., and Winkler, W. E. (2010).

Record linkage. Wiley Interdisciplinary Reviews: Com-

putational Statistics, 2(5):535–543.

Holly, A., Gardiol, L., Eggli, Y., Yalcin, T., and Ribeiro, T.

(2005). Ein neues gesundheitsbasiertes Risikoaus-

gleichssystem f

ur die Schweiz. G+G Wissenschaft,

5(2):16–31.

Johnson, S. B., Whitney, G., McAuliffe, M., Wang, H., Mc-

Creedy, E., Rozenblit, L., and Evans, C. C. (2010). Us-

ing global unique identiﬁers to link autism collections.

Journal of the American Medical Informatics Associa-

tion, 17(6):689–695.

Jutte, D. P., Roos, L. L., and Brownell, M. D. (2010). Ad-

ministrative record linkage as a tool for public health.

Annual Review of Public Health, 31:91–108.

Karakasidis, A., Koloniari, G., and Verykios, V. S. (2015).

Scalable blocking for privacy preserving record linkage.

In Proceedings of the 21th ACM SIGKDD International

Conference on Knowledge Discovery and Data Mining,

KDD ’15, pages 527–536, New York, NY, USA. ACM.

Karapiperis, D., Verykios, V. S., Katsiri, E., and Delis, A.

(2016). A tutorial on blocking methods for privacy-

preserving record linkage. In Karydis, I., Sioutas,

S., Triantaﬁllou, P., and Tsoumakos, D., editors, Algo-

rithmic Aspects of Cloud Computing: First Interna-

tional Workshop, ALGOCLOUD 2015, Patras, Greece,

September 14-15, 2015. Revised Selected Papers, pages

3–15. Springer International Publishing, Cham.

Karmel, R., Anderson, P., Gibson, D., Peut, A., Duckett, S.,

and Wells, Y. (2010). Empirical aspects of record link-

age across multiple data sets using statistical linkage

keys: the experience of the PIAC cohort study. BMC

Health Services Research, 10(41).

Karmel, R. and Gibson, D. (2007). Event-based record link-

age in health and aged care services data: a method-

ological innovation. BMC Health Services Research,

7:154.

Katalinic, A., Bartel, C., Raspe, H., and Schreer, I. (2007).

Beyond mammography screening: quality assurance in

breast cancer diagnosis (the quamadi project). British

Journal of Cancer, 96(1):157–161.

Kelman, C. W., Bass, A. J., and Holman, C. D. J. (2002).

Research use of linked health data: a best practice pro-

tocol. Australian and New Zealand Journal of Public

Health, 26(3):251–255.

Kijsanayotin, B., Speedie, S. M., and Connelly, D. P. (2007).

Linking patients’ records across organizations while

maintaining anonymity. Proceedings of the 2007 Amer-

ican Medical Informatics Association Annual Sympo-

sium, page 1008.

Kirsch, A. and Mitzenmacher, M. (2006). Less hashing same

performance: building a better Bloom ﬁlter. In Azar, Y.

and Erlebach, T., editors, Algorithms-ESA 2006. Pro-

ceedings of the 14th Annual European Symposium: 11-

13 September 2006; Z

urich, Switzerland, pages 456–

467, Berlin. Springer.

Krawczyk, H., Bellare, M., and Canetti, R. (1997). HMAC:

keyed-hashing for message authentication. Internet

RFC 2104.

HEALTHINF 2017 - 10th International Conference on Health Informatics

282

Kroll, M. and Steinmetzer, S. (2015). Who Is

1011011111...1110110010? Automated Cryptanalysis

of Bloom Filter Encryptions of Databases with Several

Personal Identiﬁers. In Biomedical Engineering Sys-

tems and Technologies 2015, pages 341–356. Springer.

Kuzu, M., Kantarcioglu, M., Durham, E., and Malin, B.

(2011). A constraint satisfaction cryptanalysis of

Bloom ﬁlters in private record linkage. In The 11th

Privacy Enhancing Technologies Symposium: 27–29

July 2011; Waterloo, Canada.

Kuzu, M., Kantarcioglu, M., Durham, E. A., Toth, C., and

Malin, B. (2013). A practical approach to achieve pri-

vate medical record linkage in light of public resources.

Journal of the American Medical Informatics Associa-

tion, 20(2):285–292.

Niedermeyer, F., Steinmetzer, S., Kroll, M., and Schnell, R.

(2014). Cryptanalysis of basic bloom ﬁlters used for

privacy preserving record linkage. Journal of Privacy

and Conﬁdentiality, 6(2):59–69.

Ofﬁce f

eral de la statistique (1997). La protection des

donn

ees dans la statistique m

edicale. Technical report,

Neuchatel.

R Core Team (2016). R: A Language and Environment for

Statistical Computing. R Foundation for Statistical

Computing, Vienna, Austria.

Randall, S., Ferrante, A., Boyd, J., Brown, A., and Semmens,

J. (2016). Limited privacy protection and poor sensi-

tivity: Is it time to move on from the statistical linkage

key-581? Health Information Management Journal,

45(2):71–79.

Randall, S. M., Ferrante, A. M., Boyd, J. H., Bauer, J. K., and

Semmens, J. B. (2014). Privacy-preserving record link-

age on large real world datasets. Journal of Biomedical

Informatics, 50:205–212.

Ridder, G. and Mofﬁtt, R. (2007). The econometrics of data

combination. In Heckman, J. J. and Leamer, E. E.,

editors, Handbook of Econometrics, volume 6B, pages

5469–5547. Elsevier, Amsterdam.

Robertson, A. M. and Willett, P. (1998). Applications of

n-grams in textual information systems. Journal of

Documentation, 54(1):48–67.

Ryan, T., Holmes, B., and Gibson, D. (1999). A national min-

imum data set for home and community care. Canberra,

AIHW.

Schmidlin, K., Clough-Gorr, K. M., Spoerri, A., and SNC

study group (2015). Privacy preserving probabilistic

record linkage (P3rl): a novel method for linking ex-

isting health-related data and maintaining participant

conﬁdentiality. BMC medical research methodology,

15:46.

Schnell, R. (2014). An efﬁcient privacy-preserving record

linkage technique for administrative data and censuses.

Journal of the International Association for Ofﬁcial

Statistics, 30(3):263–270.

Schnell, R. (2015). Privacy preserving record linkage. In Har-

ron, K., Goldstein, H., and Dibben, C., editors, Method-

ological Developments in Data Linkage, pages 201–

225. Wiley, Chichester.

Schnell, R., Bachteler, T., and Reiher, J. (2009). Privacy-

preserving record linkage using Bloom ﬁlters. BMC

Medical Informatics and Decision Making, 9(41).

Schnell, R., Bachteler, T., and Reiher, J. (2011). A novel

error-tolerant anonymous linking code. Working Paper

WP-GRLC-2011-02, German Record Linkage Center,

Duisburg.

Schnell, R. and Borgs, C. (2015). Building a national peri-

natal database without the use of unique personal iden-

tiﬁers. In 2015 IEEE 15th International Conference

on Data Mining Workshops (ICDM 2015), pages 232–

239., Atlantic City, NJ, USA. IEEE Publishing.

Schnell, R. and Borgs, C. (2016). Randomized response and

balanced bloom ﬁlters for privacy preserving record

linkage. In 2016 IEEE 16th International Conference

on Data Mining Workshops (ICDM 2016), Barcelona,

Dec 12, 2016 - Dec 15, 2016. IEEE Publishing.

Sch

ulter, E., Kaiser, R., Oette, M., M

uller, C., Schmeisser,

N., Selbig, J., Beerenwinkel, N., Lengauer, T., D

aumer,

M., and Hoffmann, D. (2007). Arevir: A database to

support the analysis of resistance mutations of human

immunodeﬁciency. European Journal of Medical Re-

search, 12(Supplememt III):10–11.

Stallings, W. (2014). Cryptography and Network Security:

Principles and Practice. Pearson, New Jersey, 6 edi-

tion.

Taylor, L. K., Irvine, K., Iannotti, R., Harchak, T., and Lim,

K. (2014). Optimal strategy for linkage of datasets

containing a statistical linkage key and datasets with

full personal identiﬁers. BMC Medical Informatics and

Decision Making, 14:85.

Tessmer, A., Welte, T., Schmidt-Ott, R., Eberle, S., Barten, G.,

Suttorp, N., and Schaberg, T. (2011). Inﬂuenza vaccina-

tion is associated with reduced severity of community-

acquired pneumonia. European Respiratory Journal,

38(1):147–153.

Vatsalan, D. and Christen, P. (2016). Privacy-preserving

matching of similar patients. Journal of Biomedical

Informatics, 59:285–298.

Vatsalan, D., Christen, P., and Verykios, V. S. (2013). A tax-

onomy of privacy-preserving record linkage techniques.

Information Systems, 38(6):946–969.

A Comparison of Statistical Linkage Keys with Bloom Filter-based Encryptions for Privacy-preserving Record Linkage using Real-world

Mammography Data

283