
Performance Analysis of Spatial Laser Speckle Contrast
Implementations
Pedro G. Vaz
1,2
, Anne Humeau-Heurtier
2
, Edite Figueiras
3
, Carlos Correia
1
and Jo
˜
ao Cardoso
1
1
LIBPhys-UC, Department of Physics, University of Coimbra, R. Larga, 3004-516 Coimbra, Portugal
2
University of Angers, LARIS - Laboratoire Angevin de Recherche en Ing
´
enierie des Syst
`
emes,
62 avenue Notre-Dame du Lac, 49000 Angers, France
3
International Iberian Nanotechnology Laboratory, Ultrafast Bio and Nanophotonics Group, Braga, Portugal
Keywords:
Laser Speckle Imaging, Spatial Contrast, Algorithm Implementation, MATLAB, Convolution.
Abstract:
This work presents an analysis of the performances for four different implementations used to compute laser
speckle contrast on images. Laser speckle contrast is a widely used imaging technique for biomedical appli-
cations. These implementations were tested using synthetic laser speckle patterns with different resolutions,
speckle sizes, and contrasts. From the applied methods, three implementations are already known in the
literature. A new alternative is proposed herein, which relies on two-dimensional convolutions, in order to
improve the image processing time without compromising the contrast assessment. The proposed implemen-
tation achieves a processing time two orders of magnitude lower than the analytical evaluation. The goal of
this technical manuscript is to help the developers and researchers in computing laser speckle contrast images.
1 INTRODUCTION
Laser speckle is an interference phenomenon that oc-
curs when coherent light is used to illuminate a sam-
ple. This interference is characterized by the visu-
alization of bright and dark spots which are called
speckles (Briers et al., 2013). Figure 1 shows an
example of a laser speckle image. The bright and
dark spots can vary in size and shape, depending on
the used sample, coherent light source and imaging
system. This image has been sensitized using the
algorithm detailed in (Kirkpatrick et al., 2007) and
presents a situation with a speckle size of 8 pixels per
speckle.
The laser speckle effect is widely used in biomed-
ical applications as a tool to assess the blood perfu-
sion (Briers et al., 2013). Its utilization fall from the
idea that, when a moving scatterer is presented in the
analysed sample, the speckle pattern will change over
time. The temporal speckle variations encode infor-
mation that can be related with the velocity of the dy-
namic scatterers. The analysis of laser speckle pat-
terns over time is called dynamic laser speckle (Vaz
et al., 2016a).
Normally, a two-dimensional imaging system,
with finite exposure time, is used to record these
speckle patterns along time resulting in a video struc-
ture. This information can be analysed by different
ways. On one hand, these changes can be identi-
fied by comparing two consecutive speckle patterns.
On the other hand, the speckle pattern can be anal-
ysed by computing its contrast using a method often
called Laser Speckle Contrast Imaging (LSCI) (Drai-
jer et al., 2009). The pattern contrast is related with
the movement of the scatterers present in the sam-
ple. Faster scatterers mean faster image decorrelation
leading to lower contrast (Briers and Webster, 1996).
When this technique is applied to biomedical sam-
ples, like cerebral tissue, the moving scatterers are
mainly the red blood cells. As a consequence of the
speckle behaviour, the contrast of the laser speckle
pattern can be related with the tissue blood perfusion
(Vaz et al., 2016b). The speckle contrast is usually
computed in smaller regions of interest (ROI’s) in or-
der to achieve a two-dimensional contrast map. Laser
speckle is able to produce two-dimensional perfusion
maps in real-time (Humeau-Heurtier et al., 2013) and
with frame rates above 100 frames per second (Tom
et al., 2008) at a fair cost.
Speckle contrast can be computed using three dif-
ferent algorithms (Vaz et al., 2016b): the first one uses
a spatial-based contrast computation, the second one
uses a temporal-based computation and, finally, the
last one combines the two previous families.
148
Vaz P., Humeau-Heurtier A., Figueiras E., Correia C. and Cardoso J.
Performance Analysis of Spatial Laser Speckle Contrast Implementations.
DOI: 10.5220/0006141101480153
In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 148-153
ISBN: 978-989-758-214-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Synthetic laser speckle image with resolution of
320 × 240 pixels and a spot size of 8 pixels per speckle.
LSCI is used as a clinical and research tool in
many different types of tissues and diseases. Most
of the blood flow analyses performed with LSCI are
related with highly vascularized tissues, like cerebral
tissues (Kazmi et al., 2015), retinal tissues (Cheng
and Duong, 2007) and hepatic tissues (Sturesson
et al., 2013). However, more recently, the assess-
ment of low vascularized tissues, like the skin, be-
came also a major field of the application of LSCI
(Humeau-Heurtier et al., 2013; Roustit et al., 2010).
In this type of samples, studies on disorders like sys-
temic sclerosis (Ruaro et al., 2013), port wine stains
(Huang et al., 2009) and wound healing (Rege et al.,
2012) have been performed using laser speckle imag-
ing methods.
In this work, we propose to test the performance
of a set of spatial-based contrast implementations. We
will focus on this family because it is the most often
used. When computing the contrast spatially a small
two-dimensional ROI is used on the raw images. This
ROI is translated along the laser speckle image (LS
image) in the horizontal and vertical directions, gen-
erally without overlapping. Figure 2 presents an illus-
tration of the spatial contrast algorithm.
The ROI is usually defined as a square of 3×3
(Pericam PSI documentation (Perimed AB, 2015)),
5×5 or 7×7 pixels (Draijer et al., 2009). The con-
trast is computed using the fundamental equation K =
σ(I)/hIi where σ(I) represents the standard deviation
of the intensity and hIi the mean intensity within the
ROI (Briers and Webster, 1996).
When online applications are necessary, or large
images are analysed, computational speed is a key
factor. The goal of this work is to explore different
spatial contrast implementations in order to determine
which one can achieve the best performance. This
paper will aid researchers to select the suitable im-
plementation depending on their requirements and to
i
i-1
i+1
j-1
j
j+1
Figure 2: Schematic of spatial contrast algorithm. The blue
square symbolizes a 3×3 ROI. Its contrast value is asso-
ciated with the raw image pixel (i,j). This ROI is trans-
lated along the lines and columns of the speckle image.
The red lines correspond to boundary regions where con-
trast determination requires padding. Adapted from (Vaz
et al., 2016b) with authors permission.
enlarge their implementations possibilities.
MATLAB
R
has been selected as a tool to test the
different algorithm implementations. MATLAB
R
is
a mathematical computing software, widely used in
research for signal processing due to its rapid learn-
ing curve and large range of pre-implemented func-
tions. The selected implementations, used to compute
speckle contrast, correspond to methods presented in
the literature (Steimers et al., 2016). Some implemen-
tations correspond to works previously performed
(Duncan and Kirkpatrick, 2008; Steimers et al., 2016)
and one corresponds to a novel implementation (sub-
section 2.4).
The performance results should be taken as spe-
cific for these experimental conditions, however these
conclusions might be applied for other software and
hardware platforms. The different implementations
were tested using synthetic LS images produced us-
ing the method presented by Kirkpatrick et al. (Kirk-
patrick et al., 2007).
2 METHODS
Four different implementations were developed in
MATLAB R2016a-64 bits. The first one corresponds
to an analytical evaluation of the contrast equation
and was used as a reference. The second one is based
on image filtering (Duncan and Kirkpatrick, 2008).
The third one relies on a moving sums (Steimers et al.,
2016). The fourth one uses convolution. The process-
ing time of each implementation was analysed using
different LS images and different ROI sizes.
Performance Analysis of Spatial Laser Speckle Contrast Implementations
149

LS images were synthesized with resolutions
of 320×240, 640×480, and 1024×768 pixels and
speckle sizes of 4, 8, 16, and 32 pixels. The applied
ROI’s have been defined as squares of 3×3, 5×5 or
7×7 pixels. For each resolution, 200 different random
generated images were used, 50 for each speckle size,
and the computation time was determined as mean ±
standard deviation. The FLoating-point Operations
Per Second (FLOPS) were not computed because this
command is no longer available in MATLAB after
version R13SP2.
These images were filtered with an average filter
in order to uniform their contrast. Figure 3 shows
the global contrast distribution of the 600 images that
were analysed in this work. This contrast exceeds the
maximum theoretical laser speckle contrast due to the
nature of the synthesis algorithm (Duncan and Kirk-
patrick, 2008). None attempt has been made to cor-
rect this contrast overshoot in order to allow for other
authors to follow the same protocol.
The first implementation (section 2.1) is based on
the application of the contrast formula K = σ(I)/hIi
to compute the output data. The other three (sec-
tions 2.2, 2.3, and 2.4) are based on a modified for-
mula which replaces the standard deviation by inten-
sity sums (Steimers et al., 2016):
K =
v
u
u
t
N
2
N − 1
×
∑
I
2
∑
I
2
−
N
N − 1
, (1)
where N is the number of summed points. While the
standard equation requires to compute both the mean
and standard deviation of the ROI, equation (1) only
requires to sum the pixels of the LS image and of its
square. With this new equation, the spatial-contrast
algorithm can be implemented in an optimized way.
The use of the modified contrast equation (Eq.
(1)) presents a practical issue that should be discussed
before its application. The square root operation can
lead to imaginary values when its radicand is lower
than 0. Rearranging the square root radicand we ob-
tain that this equation is only valid if
∑
I
2
/(
∑
I)
2
≥
1/N. This condition must be checked before the ap-
plication of this equation.
2.1 Analytical Computation
The analytical computation corresponds to the direct
application of the contrast equation in each ROI. The
mean intensity and standard deviation in each ROI
were computed using the functions std2 and mean2.
The ROI was applied to the entire LS image with-
out overlapping, by using two For cycles (one for the
rows and the other for the columns). The application
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1
Contrast
0
20
40
60
80
100
120
140
Number of Images
Figure 3: Distribution of the average contrast values of all
the tested images. Total number of images: 600 frames.
of this process results in a reduction of the original
image resolution depending on the ROI size. This im-
plementation was not optimized and has been used as
the reference method.
Algorithm 1: Analytical computation.
Input: LS raw image (LSimage) and element size
(ROIsize)
Output: Contrast image (cImage)
for ii ← 1 to # of LSimage lines with ROIsize steps
do
for jj ← 1 to # of LSimage columns with ROI-
size steps do
ROI ← cut subimage with input size and the
pixel center in the position (ii,jj)
mean ← mean2(ROI)
std ← std2(ROI)
contrast ← std/mean
cImage ← contrast is stored in the correct po-
sition of the cImage
end for
end for
return cImage
2.2 Filtering Implementation
The filtering implementation consists in the applica-
tion of two images filters to the LS image. A regu-
lar filter, imfilter, with a kernel equal to the ROI
was applied in order to compute the LS image sum
and LS image squared sum. These data were then
used to evaluate Eq. (1). The original implementation
has been performed using MATLAB
R
(Duncan and
Kirkpatrick, 2008). This implementation is detailed
in pseudo-code in algorithm 2.
BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms
150

Algorithm 2: FILTERING.
Input: LS raw image (LSimage) and element size
(ROIsize)
Output: Contrast image (cImage)
Kernel ← all-ones matrix with the ROIsize
Sum ← imfilter(LSimage, Kernel)
Sum2 ← imfilter(LSimage
2
, Kernel)
cImage ← application of the sums equation for each
point (Eq. 1)
return cImage
2.3 Moving Sum Implementation
The moving sum implementation has been described
in (Steimers et al., 2016) and (Tom et al., 2008). The
original algorithms were implemented in CUDA and
C programming languages. Hence, an adaptation of
this algorithm was implemented in MATLAB
R
. This
implementation aims at computing the sums of Eq.
(1) by performing a moving sum within the lines of
the LS image and a moving sum in the columns of
the resultant matrix. The moving sum was achieved
by using the movsum function. This implementation
is described in pseudo-code in algorithm 3.
Algorithm 3: MOVING SUM.
Input: LS raw image (LSimage) and element size
(ROIsize)
Output: Contrast image (cImage)
SumLines ← movsum(LSimage, ROIsize) for each
line
SumLines2 ← movsum(LSimage.∗ LSimage) for each
line
Sum ← movsum(movSumLines, ROIsize) for each
column
Sum2 ← movsum(movSumLines2, ROIsize) for each
column
cImage ← application of the sums equation for each
point (Eq. 1)
return cImage
2.4 Convolution Implementation
The two-dimensional convolution has been computed
using conv2 MATLAB
R
function. With this method,
equation (1) can easily be computed. Both sums were
computed by performing a convolution of the LS raw
image with a all-ones matrix with size equal to the
ROI. conv2 uses the algorithm presented in equa-
tion (2). This MATLAB
R
function has also been
tested against an equivalent method (convolution by
fast Fourier transform) and presented the best results.
This implementation is described in pseudo-code in
algorithm 4.
c(n1,n2) =
∞
∑
k1=−∞
∞
∑
k2=−∞
I
1
(k1, k2)I
2
(n1−k1,n2−k2) (2)
Algorithm 4: CONVOLUTION.
Input: LS raw image (LSimage) and element size
(ROIsize)
Output: Contrast image (cImage)
Kernel ← all-ones matrix with size equals to ROIsize
Sum ← conv2(LSimage, Kernel)
Sum2 ← conv2(LSimage. ∗ LSimage, Kernel)
cImage ← application of the sums equation for each
point (Eq. 1)
return cImage
3 PERFORMANCE RESULTS
The results were analysed in terms of image reso-
lution and ROI size. All the tests were performed
in a computer Toshiba Tecra S11-11G - i7 M620 @
2.67GHz with 4GB RAM with Windows 10 Pro as
operating system. The results (figure 4) show that the
convolution implementation achieves the best perfor-
mance in all the cases, followed by the filtering algo-
rithm.
The results are summarized in figure 4. This fig-
ure shows the computation time needed to process a
single laser speckle frame in different conditions and
with different implementations. Figure 4(a) presents
the processing time as function of the image resolu-
tion and implementation. Figure 4(b) represents the
processing time as function of the selected ROI size
and implementation.
In general, the computation time decreases when
the image resolution decreases. Regarding the ROI
size, the computation time decreases for the analyti-
cal implementation but slightly increases for the other
methods when the ROI size increases. The analyti-
cal computation presents the poorest performance, for
a long margin, in all the tested cases. This was an
expected result because this implementation have not
been optimized in any form while the other have.
The moving sum (section 2.3) achieved the worst
performance among the optimized implementations
followed by the filtering implementation (section 2.2).
Finally, the convolution implementation has achieved
the best results.
The convolution implementation achieved a com-
putational time which is approximately 50% lower
than the one of the moving sum algorithm and two
Performance Analysis of Spatial Laser Speckle Contrast Implementations
151
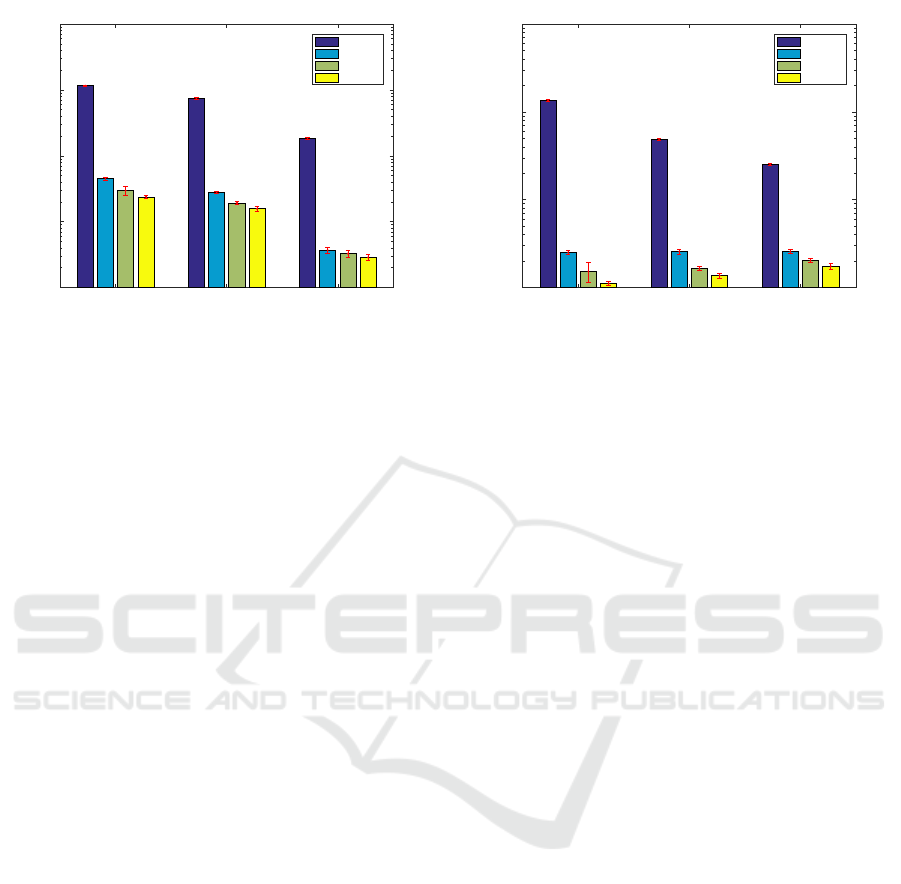
1024 # 768 640 # 480 320 # 240
Resolution
10
-2
10
-1
10
0
10
1
10
2
Time (s)
11.64
7.47
1.86
0.45
0.28
0.04
0.30
0.19
0.03
0.24
0.16
0.03
Analytical
Moving
Filt
Conv
(a) Each bar corresponds to the analisis of 600 images (200
for each ROI size).
3 # 3 5 # 5 7 # 7
ROI size
10
-1
10
0
10
1
10
2
Time (s)
13.54
4.90
2.53
0.25
0.26
0.26
0.15
0.16
0.20
0.11
0.14
0.18
Analytical
Moving
Filt
Conv
(b) Each bar corresponds to the analisis of 600 images (com-
plete data-set).
Figure 4: Analysis of the time required to process a single speckle image, lower is better. The bars values correspondent to
mean computation time needed to process one image laser speckle image. The error bars represented in red correspond to the
standard deviation. The temporal axis (y) is represented in a logarithmic scale.
orders of magnitude lower than the analytical algo-
rithm. It also gives better results than the ones ob-
tained with the implementation proposed by Duncan
and Kirkpatrick (Duncan and Kirkpatrick, 2008) (fil-
tering) due to the optimization of the MATLAB
R
function conv2. In this comparison, the performance
improvement is more visible for smaller ROI. In the
case of a ROI size equals to 3 × 3 pixels, the convolu-
tion algorithm achieved a computational time ≈26%
lower than the filtering implementation.
All the optimized implementations present result
of, at least, two orders of magnitude lower than the
reference method (analytical). This result is explained
by an absence of optimization of the analytical imple-
mentation.
4 CONCLUSION
Most papers using laser speckle imaging algorithm
optimization are performed using graphic processing
units (GPUs) (Liu et al., 2008). However, imple-
mentation efficiency is highly dependent on the pro-
gramming software used and can also be performed
by dedicated hardware. For this reason, there is no
gold standard implementation. Tom et al. (Tom et al.,
2008) presented an important overview of several al-
gorithms but applied to C programming language.
The proposed implementations, except for the an-
alytical one, are able to compute the contrast map
with overlapping ROI without increasing the compu-
tation time. Their application results in a contrast ma-
trix with the same resolution as the original image
(excluding the boundary constraints). The absence of
overlapping is obtained by selecting the central point
of each ROI.
In our conditions, the new proposed convolu-
tion algorithm achieves the best performance in all
the tests. The convolution method is simple and is
present in many image processing fields. The advan-
tage of this implementation over complex methods is
that high-performance FPGA-based implementations
can be found in literature (Perri et al., 2005; Carlo
et al., 2011). Since the used hardware platform and
programming style are extremely variable, this note
should be used as a guideline for other implementa-
tions rather than as a rule.
ACKNOWLEDGEMENTS
This work was partly supported by Fundac
˜
ao
para a Ci
ˆ
encia e Tecnologia (FCT) with a doc-
toral scholarship (SFRH/BD/89585/2012) and project
IF/01238/2013.
REFERENCES
Briers, D., Duncan, D., Kirkpatrick, S., Larsson, M.,
Stromberg, T., and Thompson, O. (2013). Laser
speckle contrast imaging : theoretical and practical
limitations. J. Bomedical Opt., 18(6):1–9.
Briers, J. and Webster, S. (1996). Laser speckle contrast
analysis (LASCA): A nonscanning, full-field tech-
nique for monitoring capillary blood flow. J. Biomed.
Opt., 1(2):174–179.
Carlo, S. D., Gambardella, G., Indaco, M., Rolfo, D.,
Tiotto, G., and Prinetto, P. (2011). An area-efficient
BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms
152

2-D convolution implementation on FPGA for space
applications. In IEEE 6th Int. Des. Test Work., pages
88–92. IEEE.
Cheng, H. and Duong, T. Q. (2007). Simplified laser-
speckle-imaging analysis method and its applica-
tion to retinal blood flow imaging. Opt. Lett.,
32(15):2188–2190.
Draijer, M., Hondebrink, E., van Leeuwen, T., and Steen-
bergen, W. (2009). Review of laser speckle contrast
techniques for visualizing tissue perfusion. Lasers
Med. Sci., 24(4):639–651.
Duncan, D. and Kirkpatrick, S. (2008). Spatio-temporal
algorithms for processing laser speckle imaging data.
In Opt. Tissue Eng. Regen. Med. II, number Febru-
ary, pages 685802–685802–6. International Society
for Optics and Photonics.
Huang, Y., Tran, N., Shumaker, P. R., Kelly, K., Ross, E. V.,
Nelson, J. S., and Choi, B. (2009). Blood flow dynam-
ics after laser therapy of port wine stain birthmarks.
Lasers Surg. Med., 41(8):563–571.
Humeau-Heurtier, A., Guerreschi, E., Abraham, P., and
Mah
´
e, G. (2013). Relevance of laser Doppler and
laser speckle techniques for assessing vascular func-
tion: State of the art and future trends. IEEE Trans.
Biomed. Eng., 60(3):659–666.
Kazmi, S. M. S., Richards, L. M., Schrandt, C. J., Davis,
M. a., and Dunn, A. K. (2015). Expanding appli-
cations, accuracy, and interpretation of laser speckle
contrast imaging of cerebral blood flow. J. Cereb.
Blood Flow Metab., 35(7):1076–1084.
Kirkpatrick, S., Duncan, D., Wang, R., and Hinds, M.
(2007). Quantitative temporal speckle contrast imag-
ing for tissue mechanics. J. Opt. Soc. Am. A. Opt.
Image Sci. Vis., 24(12):3728–3734.
Liu, S., Li, P., and Luo, Q. (2008). Fast blood flow vi-
sualization of high-resolution laser speckle imaging
data using graphics processing unit. Opt. Express,
16(19):2188–2190.
Perimed AB (2015). Pericam psi sytem.
https://www.perimed-instruments.com/
products/pericam-psi.
Perri, S., Lanuzza, M., Corsonello, P., and Cocorullo,
G. (2005). A high-performance fully reconfigurable
FPGA-based 2D convolution processor. Micropro-
cess. Microsyst., 29(89):381–391.
Rege, A., Thakor, N., Rhie, K., and Pathak, A. (2012). In
vivo laser speckle imaging reveals microvascular re-
modeling and hemodynamic changes during wound
healing angiogenesis. Angiogenesis, 15(1):87–98.
Roustit, M., Millet, C., Blaise, S., Dufournet, B., and Cra-
cowski, J. L. (2010). Excellent reproducibility of laser
speckle contrast imaging to assess skin microvascular
reactivity. Microvasc. Res., 80(3):505–511.
Ruaro, B., Sulli, A., Alessandri, E., Pizzorni, C., Ferrari, G.,
and Cutolo, M. (2013). Laser speckle contrast analy-
sis: a new method to evaluate peripheral blood perfu-
sion in systemic sclerosis patients. Ann. Rheum. Dis.,
pages annrheumdis–2013.
Steimers, A., Farnung, W., and Kohl-Bareis, M. (2016). Im-
provement of Speckle Contrast Image Processing by
an Efficient Algorithm BT - Oxygen Transport to Tis-
sue XXXVII. pages 419–425. Springer New York,
New York, NY.
Sturesson, C., Milstein, D. M. J., Post, I. C. J. H., Maas,
A. M., and van Gulik, T. M. (2013). Laser speckle
contrast imaging for assessment of liver microcircula-
tion. Microvasc. Res., 87:34–40.
Tom, W. J., Ponticorvo, A., and Dunn, A. K. (2008). Ef-
ficient processing of laser speckle contrast images.
Med. Imaging, IEEE Trans., 27(12):1728–1738.
Vaz, P., Pereira, T., Figueiras, E., Correia, C., Humeau-
Heurtier, A., and Cardoso, J. (2016a). Which wave-
length is the best for arterial pulse waveform extrac-
tion using laser speckle imaging? Biomed. Signal
Process. Control, 25:188–195.
Vaz, P. G., Humeau-Heurtier, A., Figueiras, E., Correia, C.,
and Cardoso, J. (2016b). Laser speckle imaging to
monitor microvascular blood flow: a Review. IEEE
Rev. Biomed. Eng., In press(99):1–1.
Performance Analysis of Spatial Laser Speckle Contrast Implementations
153
