Automatic Feature Selection in the SOPFs Dissolution Proﬁles Prediction

Problem

J. E. Salazar-Jim´enez

, J. D. S´anchez-Carvajal

, B. Quiros-G´omez

and J. D. Arias-Londo˜no

I&S Research group, Faculty of Engineering, Universidad de Antioquia, Cll 70 No. 52-21, Medell´ın, Colombia

Unidad de Investigaci´on e Innovaci´on, Humax Pharmaceutical S.A., Calle 97B Sur No. 50 - 95,

La Estrella, Antioquia, Colombia

Dpt. Of Systems Engineering and Computer Science, Universidad de Antioquia, Cll 70 No. 52-21, Medell´ın, Colombia

Keywords:

Automatic Feature Selection, Bioequivalence, Drug Development, Drug Dissolution Proﬁle Prediction, Solid

Oral Pharmaceutical Forms.

Abstract:

This work addressed the problem of dimensionality reduction in the drug dissolution proﬁle prediction task.

The learning problem is assumed as a multi-output learning task, since dissolution proﬁles are recorded in non-

uniform sampling times, which avoid the use of basic function-on-scalar regression approaches. Ensemble-

based tree methods are used for prediction, and also for the selection of the most relevant features, because

they are able to deal with high dimensional feature spaces, when the number of training samples is small.

All the drugs considered corresponds to rapid release solid oral pharmaceutical forms. Six different feature

selection schemes were tested, including sequential feature selection and genetic algorithms, along with a

feature scoring procedure, which was proposed in order to get a consensus about the best subset of variables.

The performance was evaluated in terms of the similitude factor used in the drug industry for dissolution

proﬁle comparison. The feature selection methods were able to reduce the dimensionality of the feature space

in 79.2%, without loss in the performance of the prediction system. The results conﬁrm that in the dissolution

proﬁle prediction problem, especially for different solid oral pharmaceutical forms, variables from different

components and phases of the drug development must be considered.

1 INTRODUCTION

The development of solid oral pharmaceutical forms

(SOPFs) must satisfy several requirements from tech-

nical, scientiﬁc and legal statements. Usually, the

whole development process is performed by adjust-

ing the design in the laboratory between the formu-

lation stage, and the veriﬁcation of complying indus-

trial manufacturing scaling standards (Gibson, 2005)

(Moon, 2011). One of the more important technical

requirements for SOPFs, is to assure that the pro-

duct has an appropriate biopharmaceutical behavior

(BPB), which includes the estimated time of effect or

duration, among other important clinic pharmaceuti-

cal properties (Shargel et al., 2007). A key element

of the BPB evaluation is the reconstruction of a time

curve known as dissolution proﬁle (DP), which pro-

vides the dissolution percentages of the drugs’ active

ingredient (AI) through time (Shargel et al., 2007).

In the generic pharmaceutical industry, the

development of SOPFs according to a Quality

by Design approach, must additionally satisfy a

pharmacokinetic-based measure known as Bioequi-

valence, which is a comparison between the DPs of

the generic drug and the reference product. The Bio-

equivalence lets generic laboratories to demonstrate

that their products are statistically similar in terms of

both, BPB and therapeutic properties, to those of the

reference drugs (Shargel et al., 2007). However, the

main drawback to get this objective, is the fact that the

DPs follow a no lineal behavior inﬂuenced by a large

number of variables including physical and chemi-

cal properties of the excipients and AIs, the interac-

tions that could occur between them, their respective

proportion in the formula, the manufacture param-

eters, the parameters of the dissolution test, among

others (Dokoumetzidis and Mahceras, 2006) (Ghayas

et al., 2013). Therefore, the task of obtaining a de-

sired DP sometimes becomes in the bottleneck of the

generic SOPFs design. Moreover, since the lack of

better techniques or optimization methods, the pro-

cess of getting a desired DP is approached by a “trial

Salazar JimÃl’nez J., SÃ ˛anchez Carvajal J., Quiros-GÃ¸smez B. and Arias-LondoÃ

so J.

Automatic Feature Selection in the SOPFs Dissolution Proﬁles Prediction Problem.

DOI: 10.5220/0006141800520058

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 52-58

ISBN: 978-989-758-214-1

and error” guided formulation design, supported ex-

clusively by the experience, expertise and knowledge

of drug development scientists (Aguilar, 2013).

In the last ﬁfteen years, many efforts have been

made in order to develop computational methods that

can provide a tool for the prediction/simulation of

DPs. Mechanistic and data-driven (phenomenologi-

cal) models have been used for this purpose (Siep-

mann and Siepmann, 2013) (Mendyk et al., 2015).

Mechanistic approaches are a more elegant and ac-

curate way to model the dynamic interaction among

the variables. However, they include many parame-

ters that are difﬁcult to estimate and require a deep

understanding of every law governing the interac-

tion among all the variables involved in the disso-

lution process, and much of them are still unknown

(Aguilar, 2013). On the other hand, computational

intelligence methods, and more speciﬁcally machine

learning (ML) techniques, are able to generate mod-

els trough a data-driven paradigm, with the advan-

tage that no a priori knowledge about the interactions

among the variables is required (Ibri´c et al., 2012).

Most of the ML-based approaches for DP prediction

focus their analysis in the use of Artiﬁcial Neural Net-

works (ANN) with different topologies. e.g., in (Shao

et al., 2007) a comparison between neurofuzzy logic

and a basic ID3 decision tree approaches is presented.

A total of 14 variables were included (4 formulation

variables, 2 process variables, and 8 tablet proper-

ties). No information about the number of AIs in-

cluded in the experiments is given by the authors. The

paper concluded that both models are able to provide

useful knowledge about the cause-effect relationships

among the variables and the quality of the product.

In another case study (Ibri´c et al., 2012), a review

of the application of ANNs in the formulation and

evaluation of modiﬁed release dosage forms is pre-

sented. Multi-layer perceptron and Elman neural net-

works are the most employed methods according to

the revision. In all the cases cited, the models are used

to predict DPs in highly controlled environments, i.e.

the data contain only one AI and few design varia-

bles, specially features related to formula composi-

tion. A more recent approach presented in (Mendyk

et al., 2015), compares the performance of ANN and

Genetic Programming (GP) in the modeling of drug

dissolution from the dosage form. The data set con-

tained results of dissolution tests carried out for 5 var-

ious formulations of lipid extrudates. Only two varia-

bles were included in the analysis. The authors found

GP to be the most robust model for DP prediction.

Bearing this in mind, the main limitation of the

computer-aided dissolution proﬁles prediction sys-

tems, to become in useful tools that really support the

design of a wider kind of SOPFs, is that they often

focus on speciﬁc dissolution phenomena, including

very scarce features and trained using data from only

one or maximum three different AIs. Therefore, they

serve limited purpose and their use in real develop-

ment environments could be considered narrow.

Building a ML-based tool able to simulate DPs of

different SOPFs, requires to consider a larger num-

ber of variables involved in the dissolution process,

because the dynamic response (DP) of some drugs

can drastically change by variations in features that

does not affect other kind of drugs. Nevertheless, by

increasing the number of variables to be considered

by complex data-driven models (such as ANN, whose

parameters increase exponentially with respect to the

number of variables), the model trained can likely be

affected by the curse of dimensionality, and overﬁts

to the training data.

From an statistical point of view, the prediction

of a DP from a set of formulation variables, corre-

sponds to a functional regression problem known as

Function-on-Scalar Regression (FoSR) (Reiss et al.,

2010), i.e., a regression problem where the respon-

ses are functions and the predictors are scalars. In

order to overcome the curse of dimensionality in the

DP prediction problem, a method for dimensionality

reduction on FoSR is required; however this is an al-

most unexplored ﬁeld in the state of the art, especially

for cases where the sampling times are not uniform

among the samples, which is precisely the case of

DPs, since the sampling times typically used in the

dissolution tests, are not uniform trough time and de-

pend on the duration or desired effect of the speciﬁc

drug being designed.

Bearing this in mind, an alternative way to ad-

dress the DP prediction problem, is to use a multi-

output ML-based approach, where the different va-

riables involved in the drug design and test, along

with the target dissolution times are used as inputs,

and the percentages of dissolution for the same tar-

get times are considered as outputs. This alternative

is suggested in (Contia and O’Hagan, 2010) for com-

plex non-uniform sampled dynamic models. Such a

model can be used as a wrapper criterion for feature

selection techniques, in order to reduce the number

of variables analyzed, avoid the overﬁtting of the pre-

diction model, and select the most relevant features

for the DP prediction problem.

In this sense, the present work explores the use

of heuristic-based methods, in order to address the

dimensionality reduction in the SOPFs’ DP predic-

tion problem. All the drugs considered correspond

to rapid release SOPFs, which have similar pharma-

cokinetics and are the most frequently type of SOPFs

Automatic Feature Selection in the SOPFs Dissolution Proﬁles Prediction Problem

produced by the pharmaceutical industry, specially

by generic laboratories (Shargel et al., 2007) (Qiu

and Zhou, 2011). The feature selection process eval-

uates 6 methods based on sequential feature selec-

tion and genetic algorithms, coupled with two super-

vised techniques, multi-output bagging of trees (BT)

and extremely randomized trees (ERT). Additionally,

BT and ERT are used themselves as feature selection

technique. In previous experiments, ANN and multi-

output support vector regressors were also evaluated,

but tree-based ensemble methods achieved better per-

formance. In order to follow a multi-output approach,

all the DPs were restricted to have the same number

of sampling times.

The rest of the paper is organized as follows: sec-

tion 2 presents the set of variables included, the re-

gression models and the feature selection techniques

employed. Section 3, describe the dataset and the va-

lidation methodology. Section 4 presents the results

obtained and ﬁnally section 5 includes some conclu-

sions.

2 METHODS

2.1 Variables Deﬁnition

A set of 168 variables were included for the study.

They were added for reasons of theoretical relevance

and availability. The input variables were classiﬁed

into 8 different groups, each one considered to be

essential in SOPFs’ DPs analytics:

1. Galenic features (number of initial features = 88):

Features Associated with drug design and formula

composition (e.g. %AI, and one hot encodingvec-

tor codifying the presence of a speciﬁc excipient,

etc.)

2. Pharmacotecnic features (number of initial fea-

tures = 11): Corresponding to variables, condi-

tions and parameters related to the manufacturing

process and drug development equipment (e.g.

mixing time, humidity, tablet hardness, etc.)

3. Final form physical features (number of initial

features = 16): Variables associated to dimen-

sional measures of the ﬁnal SOPF (e.g. tablet

thickness, length, etc.)

4. AIs’ physicochemical features (number of initial

features = 11): set of features associated with the

AIs’ physical and chemical characteristics (e.g.

AI molecular weight, logP, rotable bonds, etc.)

5. AIs’ pharmaco-molecularfeatures (number of ini-

tial features = 10): Variables related to the pre-

sence of speciﬁc molecular/chemical groups of

pharmaceutical interest (number of AI hydroxyls,

number of AI amines, etc.)

6. Formula physicochemicalfeatures (numberof ini-

tial features = 13): Similar to group 5, some

physicochemical characteristic of the tablet func-

tional components, (e.g. binder solubility in wa-

ter, surfactant particle size, etc.)

7. Drug dissolution test related features (number of

initial features = 16): All parameters and features

related to the analytic measure of %AI (e.g. sol-

vent used, analytic method, rotational speed, etc.).

8. Sampling times features (number of initial fea-

tures = 3): Corresponding to the 3 tested times

during the reconstruction of the PD.

The output or dependent variables correspond to

the dissolution percentage for every sampling time.

2.2 Prediction Models

Two different classiﬁcation models were used in this

work for DP prediction. In ﬁrst place a multi-output

bagging of Trees (BT) was used as predictor. This

corresponds to a set of decision trees estimated on

bootstrap samples extracted from the training data.

Ensemble methods have demonstrated to reach

comparable performance to complex parametric and

kernel based methods. Moreover, in this study they

were selected after a set of experiments where the

performance of BT was compared to ANN and multi-

output support vector regressors. For the dataset used

in this work, ensemble-based tree methods provided

the best results. This behavior could be explained be-

cause ANN and SVR require a larger number of sam-

ples to get a successful training phase, especially in

high dimensional feature spaces.

Additionally, a more computational efﬁcient tree-

based ensemble method was also used. Extremely

Randomized Trees (ERT) (Geurts et al., 2006) are a

class of tree-based ensemble methods, where for each

decision node, a random subset of candidate features

is used (instead of the whole set), and thresholds are

drawn also at random for each candidate feature. The

best of these randomly-generatedthresholds is picked

as the splitting rule. ERT provides a similar perfor-

mance than Random Forest, but they are computa-

tionally more efﬁcient (Geurts et al., 2006), which is

a desirable property especially when the methods are

going to be used as criterion for feature selection al-

gorithms.

In all the cases, the models were fed with the vari-

ables involved in the drug design and test, along with

the target dissolution times, and they were asked to

produce the corresponding dissolution percentage per

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms

every of the input times. Since the learning strategy

corresponds to a multi-ouput learning paradigm, all

the samples were restricted to have a constant num-

ber of times. As it as pointed before, in this work the

number of times was ﬁxed to 3, since according to the

methodology for dissolution test (FDA, 1997), a DP

must be evaluated with minimum 3 sampling times.

2.3 Feature Selection

Two Feature Selection Techniques (FSTs) were eval-

uated using wrapper methodsas selection criteria. Se-

quential Forward Selection (SFS) and Genetic Algo-

rithm (GA), were used as search algorithms.

• SFS is a bottom-up selection method which build

up a set of p features incrementally, starting with

the empty set and adding new features to the fea-

ture set one at a time, until the ﬁnal set is reached

(Webb, 2003). Suppose that during the iteration

t, p

features have been included into the selected

set of features X . For each of the features ν

not

yet selected, the criterion function J

= J(X + ν

)

is evaluated. The feature that yields the maximum

value of J

is chosen as the one that is added to

the set X . When the best improvement makes the

feature set worse, or when the maximum allow-

able number of features is reached, the algorithm

terminates (Webb, 2003).

• GAs are heuristic optimization and search tech-

niques inspired by principles of genetics and the

natural selection process. A GA allows a pop-

ulation composed of many individuals to evolve

under speciﬁc selection rules to a state that maxi-

mizes the “ﬁtness” (criterion function) (Haupt and

Haupt, 2004). In this work, a binary GA was

used, where each individual (a candidate subset of

features), was represented as a vector of binary-

valued components of length equal to the total

number of features. A ’1’ value in the j-th posi-

tion of one individual means that the j-th feature

is included in the candidate subset represented by

such an individual, otherwise such features is not

included. After convergence, the GA provides a

solution for the optimization problem, which in

this case corresponds to the ﬁnal subset of se-

lected features.

The criterion used for SFS and GA corresponds to

a wrapper method based on the two ensemble-based

trees learning algorithms described before (multi-

output ERT and BT). Additionally, ERT and BT were

used themselves as feature selection methods. This

type of models can be used as feature selectors, since

the learningstrategy in which they are based on, select

one feature to split the feature space in every internal

node of the tree. Therefore, the number of times that

a speciﬁc feature is used as splitting criteria (or sim-

ply to determine whether it is used for any internal

node or not), is directly proportional with the rele-

vance of such a feature for the prediction problem.

In this scenery, BT has and advantage over ERT, be-

cause BT analyses all the features in every internal

node, whilst ERT uses a random subset of candidate

features per node. However, the performance of both

models as feature selectors was evaluated. In total six

different FST methods were implemented. In all the

cases the main criterion for selection was the average

of the similitude factor f

given by

f2 = 50log





100

∑

t=1

− T

)

−0.5





(1)

where R

is the percentage of AI dissolved from a ref-

erence drug at a time t, and T

is the predicted value

by the model at the same time. n is the number of

sampling times. For all the samples in this work,

n = 3. Similitude factor f

was used, since it is the

criterion suggested by the US Food and Drug Admin-

istration (FDA) for dissolution test (FDA, 1997). A

detailed analysis of the f

factor, can show that it cor-

responds to a nonlinear mapping of the mean square

error, which is one of the classical measures for the

evaluation of regression models. f2 ranges in the in-

terval (−∞, 100], being 100 a perfect match between

the compared DPs.

The set of selected features must corresponds to

the one that provides the best average f

. Taking into

account that every FST would provide slightly dif-

ferent subsets of features, and in order to get a con-

sensus, a ranking strategy was implemented. Differ-

ent subsets of candidate features were ﬁnally tested,

according to their ranking, aiming to determine the

performance obtained by each one and the percentage

of reduction that the methods were able to ﬁnd. The

ranking strategy consisted in assigning one score to

every feature, according to the number of times that

each one was selected during the several runs of the

simulations. Moreover, the score also assign higher

values to features that were selected into small sub-

sets. The aim of this strategy is to ﬁnd smaller subsets

of features with the highest accuracies. Taking into

account that every FST was evaluated multiple times,

according to the validation methodology (see section

3.2), the ﬁrst step was to estimate a relevance factor

for each feature, which corresponds to the percentage

of times that the feature was included in the selected

subset, taking into account the total number of fea-

tures that were selected in any of the repetitions. For-

Automatic Feature Selection in the SOPFs Dissolution Proﬁles Prediction Problem

mally, let g

∈ {0, 1}, an indicator variable that takes

the value of 1, if the input variable f was included in

the ﬁnal subset during the experiment e, and 0 other-

wise. The score of the feature f is given by

∑

e=1

∑

e=1

∑

j=1

(2)

where n

is the number of experiments or repetitions

during the validation, and n

the number of varia-

bles. Additionally, the FST were evaluated for dif-

ferent number of trees in the bagging, therefore the

ﬁnal score per feature was estimates as the average of

the scores obtained for the different number of trees.

Several subsets of features were ﬁnally tested by

changing the minimum allowed score to be conside-

red a relevant feature.

3 EXPERIMENTAL SETUP

3.1 Data Set

Data was provided by Humax Pharmaceutical S.A.

and consisted of 658 records from about 60 different

products assays and about 50 AIs. Each formulation

assay or “record” had an associated output PD com-

posed by at least three sampling times. All the record-

ings where standardized to three sampling times, en-

suring that only one of the measurement be after 85%

dissolution (as suggested by FDA (FDA, 1997)). As it

was pointed out, all the drugs considered correspond

to rapid release SOPFs.

3.2 Validation Methodology

All the experiments were performed using a boot-

strapping validation strategy, with 70% of the sam-

ples for training and 30% for validation. Ten repeti-

tions for every experiment were carried out. The opti-

mal number of trees was selected according to a grid

search ranging from 10 to 100. In order to increase the

reliability of the subset of features ﬁnally selected, the

feature selection strategies were evaluated with differ-

ent number of trees, and all their results were taken

into account, as it was explained in section 2.3.

The performance of the methods were evaluated

according to the similitude factor f

(1). According

to the Guidance for Dissolution Testing of Immediate

Release SOPFs provided by the FDA (FDA, 1997),

two DPs are considered similar if the f

factor be-

tween them is greater than 50. Therefore, an addi-

tional error measure was estimated, by averaging the

number of times that the predicted DP did not exceed

such threshold. This error measure was called Err

4 RESULTS AND DISCUSSION

Table 1 shows the performance obtained using the

whole set of features described in section 2.1, using

an ERT-based predictor. This results are going to be

considered the base line for comparison purposes.

Table 1: Best results obtained for the whole set of features

using ERT.

Number of trees Average f

Average Err

10 58.93± 14.80* 28.03%± 3.8

20 60.20± 14.82 25.25%± 1.6

30 59.28± 14.87 27.17%± 2.9

40 59.04± 14.91 27.58%± 3.0

50 58.88± 15.23 29.14%± 3.4

60 59.26± 15.18 28.08%± 3.2

70 59.76± 14.82 26.41%± 2.0

80 59.74± 14.93 26.92%± 1.8

90 58.98± 14.79 27.73%± 2.1

100 59.27 ± 14.85 26.62%± 1.9

*mean ± standard deviation.

From table 1, is possible to observe that the av-

erage f

is not very sensitive to the number of trees.

However, for the largest number of trees evaluated,

the results are more stable in both, f

and Err

Therefore, the experiments for features selection were

performed using 80, 100 and 120 trees for every

method.

Figures 1 and 2 shows the percentage of reduc-

tion and similitude factors obtained for the different

FST evaluated, and changing the score threshold for

the variable inclusion. As a higher threshold is cho-

sen, more features are excluded, because the criterion

becomes stricter. This analysis allows to show how

different the subsets of features are per every run of

the different FSTs evaluated. If in every run of a FST

the subset of features is almost the same, such FST

is quite consistent and is able to select the best subset

of features even with a low score threshold. This is

the case of FSF-based selectors. Otherwise, if a FST

produce different results in every run, a larger score

threshold for the variable inclusion is required in or-

der to get a consensus.

The ﬁgures 1 and 2 shows the results before all the

methods started to reduce their performance, because

most of the features, or all of them, were excluded.

From ﬁgure 1 is possible to observe how SFS-based

methods are able to identify the “best” subset fea-

tures, even for small scoring threshold. This means

that the non-relevant features are excluded in almost

every run of the algorithm. Additionally, when BT

was used as wrapper criterion, the performance of the

selected subset of feature reach a higher f

(see ﬁg-

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms

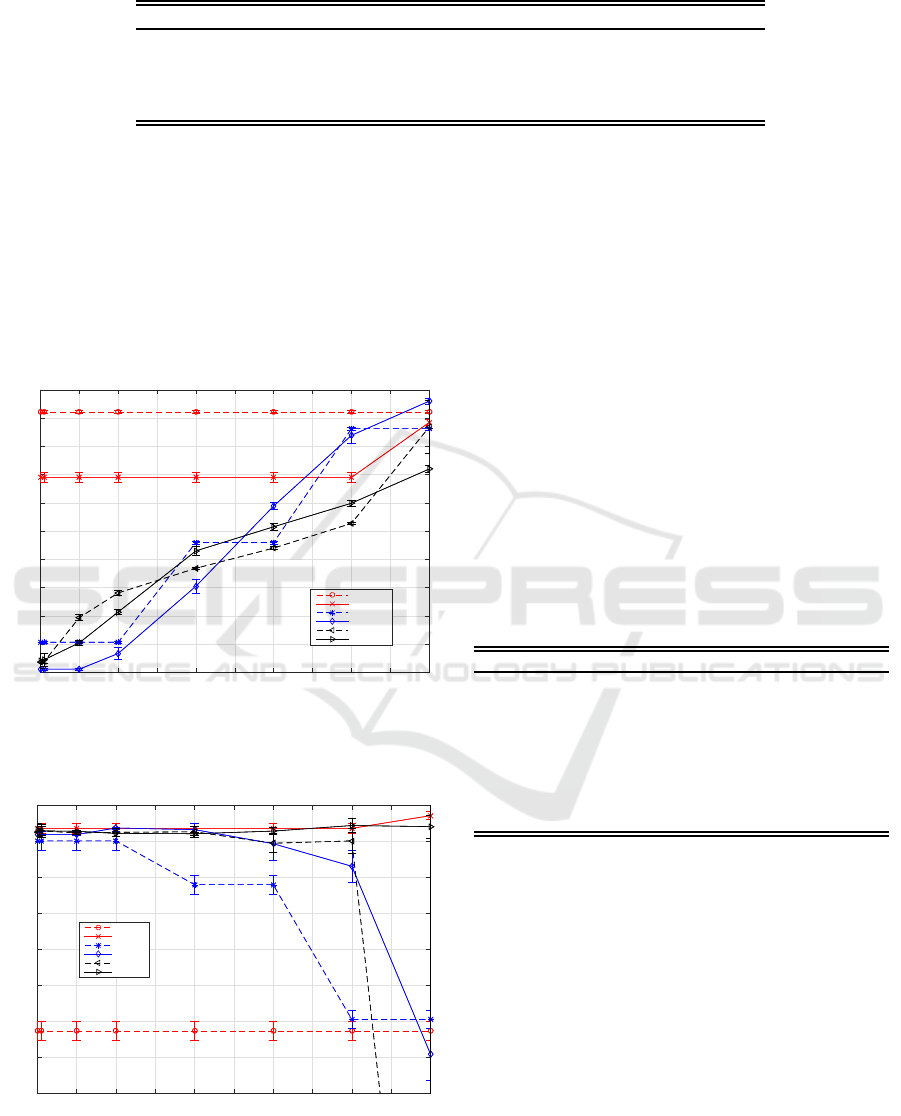
Table 2: Best results after the feature selection stage.

FST Average f

Average Err

Percentage of reduction

TB-120 60.03± 15.31 25.95%± 2.9 79.2%

SFS-TB-80 59.73± 15.00 26.29%± 2.4 89.2%

SFS-TB-120 59.84 ± 15.03 26.42%± 2.9 86.9%

TB-100 59.72± 15.07 26.67%± 2.3 70.8%

ure 2). Besides when BT was used alone as feature

selector, the performance was also high. This behav-

ior could be explained by the fact that BT evaluates all

the features in every decision node, whilst ERT evalu-

ates only a subset of randomly selected features. This

randomly selection provides ERT with a better com-

putational efﬁciency, but reduces their performanceas

feature selector.

Score

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

% of Features Reduced

100

Reduction Profile

SFSERT

SFSTB

GAERT

GATB

ERT

Figure 1: Percentage of reduction obtained for each FST

evaluated and different thresholds in the score.

Score

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

mean f2

Performance Profile

SFSERT

SFSTB

GAERT

GATB

ERT

Figure 2: Average similitude factor obtained for each FST

evaluated and different thresholds in the score.

Table 2 shows the best results obtained using the

different FSTs, and scoring thresholds. It is impor-

tant to note how feature selection using TB was able

to achieve a similar performance than those in table 1,

but with a reduction of 79.2% in the number of vari-

ables. Moreover, other SFS-based methods were also

able to yield similar performances, although some au-

thors assert that this kind of methods are suitable for

classiﬁcation but not for regression problems (Caste-

llano and Fanelli, 2000). . On the other hand, the use

of GA as search method did not produce satisfactory

results. Furthermore, its computational cost makes it

a less interesting option as feature selector.

Finally, table 3 shows how the feature dimensi-

onality reduction is split among the different groups

of variables considered. This is an interesting result,

since it conﬁrms that almost all the groups conside-

red are relevant for the prediction of DPs, whenever

the multi-output regression system have to work with

different SOPFs.

Table 3: Percentage of reduction according to every group

of variables analyzed.

Group of variables Percentage of reduction

Galenic 87.5%

Pharmacotecnic 45.5%

Final form 81.3%

AIs’ physicochemical 90.9%

AIs’ pharmaco-molecular 100%

Formula 76.9%

Dissolution test 81.3%

Sampling times 0.0%

5 CONCLUSIONS

The DP prediction problem is a complex task that can

be understood as a functional regression where the

responses are functions and the predictors are scalars.

In the case of DPs, the sampling times used dur-

ing dissolution test vary signiﬁcantly from one drug

to another, introducing additional challenges to the

modeling process. From a machine learning perspec-

tive, this problem can be addressed as a multi-output

learning task. The results show that the ensemble-

tree based methods are able to provide DP predictions

that, in average, exceed the minimum allowed value

to consider two DPs as similar (according to the US

Food and Drug Administration).

Automatic Feature Selection in the SOPFs Dissolution Proﬁles Prediction Problem

DP prediction from datasets that include many dif-

ferent solid oral pharmaceutical forms, requires the

introductionof features from different componentand

phases of the drug development process. This fact in-

creases the dimensionality of the feature space used

by the learning algorithm, whichcan be problematic if

the size of the training set is small. In this context, the

use of sequential feature selection techniques coupled

to wrapper criteria based on multi-output ensemble-

tree methods, becomes in an interesting alternative

that allows the identiﬁcation of relevant and reliable

subsets of features.

The results showed that a signiﬁcantly reduced

feature set can be found, and also that such subset is

able to provide a similar performance than the com-

plete set of features. Moreover, taking into account

that the database used contains different SOPFs, the

automatic selection also showed that almost all the

groups of variables considered, were found to be rel-

evant for the prediction of DPs.

Additional work must be done to include other

kind of ML based feature selection methods that can

also be adapted to this problem, as well as multi-input

multi-output feature extraction techniques.

ACKNOWLEDGEMENTS

This research was supported by Project No. CODIIA

15-1-01 funded by Universidad de Antioquia,

Medell´ın, Colombia and Humax Pharmaceutical S.A.

The authors had full access to all of the data in this

study and take complete responsibility for the in-

tegrity of the data and the accuracy of the data anal-

ysis, certifying that all ﬁnancial and material support

for the conduct of this study and/or preparation of this

manuscript is in compliance with ethical standards.

Moreover, the authors declare having taken part in the

research presented in this paper, having reviewed and

approved the manuscript being submitted. The au-

thors would like to thank Alba Ceballos and Rodrigo

Ochoa for useful discussions.

REFERENCES

Aguilar, J. (2013). Formulation tools for pharmaceutical

development, volume 44. Woodhead Publishing.

Castellano, G. and Fanelli, A. (2000). Variable selection

using neural-network models. Neurocomputing, 31(1-

4):1–13.

Contia, S. and O’Hagan, A. (2010). Bayesian emulation

of complex multi-output and dynamic computer mod-

els. Journal of Statistical Planning and Inference,

140(3):640–651.

Dokoumetzidis, A. and Mahceras, P. (2006). A century

of dissolution research: from noyes and whitney to

the biopharmaceutics classiﬁcation system. Int. J.

Pharm., 321(1-2):1–11.

FDA, U. (1997). Guidance for industry: Dissolution testing

of immediate-release solid oral dosage forms. Food

and Drug Administration, Center for Drug Evaluation

and Research (CDER).

Geurts, P., Ernst, D., and Wehenkel, L. (2006). Extremely

randomized trees. Machine Learning, 63(1):3–42.

Ghayas, S., Sheraz, M., Anjum, F., and Baig, M. (2013).

Factors inﬂuencing the dissolution testing of drugs.

Pak. J. Heal. Res., 1(1):1–11.

Gibson, M. (2005). Technlogy Transfer: An international

good practice guide for pharmaceuticals and allied

industries. DHI Publishing LLC.

Haupt, R. L. and Haupt, S. E. (2004). Practical genetic

algorithms. John Wiley & Sons.

Ibri´c, S., Djuriˇs, J., Parojˇci´c, J., and Djuri´c, Z. (2012). Ar-

tiﬁcial neural networks in evaluation and optimization

of modiﬁed release solid dosage forms. Pharmaceu-

tics, 4:531–550.

Mendyk, A., Gres, S., Jachowicz, R., Szlk, J., Polak, S.,

Winiowska, B., and Kleinebudde, P. (2015). From

heuristic to mathematical modeling of drugs dissolu-

tion proﬁles: Application of artiﬁcial neural networks

and genetic programming. Comput. Math. Methods

Med., 2015:1–9.

Moon, S. (2011). Pharmaceutical Production and Related

Technology Transfer. World Health Organization.

Qiu, Y. and Zhou, D. (2011). Understanding design and

development of modiﬁed release solid oral dosage

forms. J. Valid. Technol., 17(2):2332.

Reiss, P., Huang, L., and Mennes, M. (2010). Fast function-

on-scalar regression with penalized basis expansions.

The International Journal of Biostatistics, 6(1):Article

28.

Shao, Q., Rowe, R., and York, P. (2007). Comparison

of neurofuzzy logic and decision trees in discover-

ing knowledge from experimental data of an imme-

diate release tablet formulation. European Journal

of Pharmaceutical Sciences: Ofﬁcial Journal of the

European Federation for Pharmaceutical Sciences,

31(2):129136.

Shargel, L., Wu-pong, S., and Yu, A. (2007). Applied Bio-

pharmaceutics & Pharmacokinetics. McGraw-Hill’s

ACCESPHARMACY, 5th edition.

Siepmann, J. and Siepmann, F. (2013). Mathematical mod-

eling of drug dissolution. Int. J. Pharm., 453(1):1224.

Webb, A. R. (2003). Statistical pattern recognition. John

Wiley & Sons, 2nd edition.

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms