Automatic Visual Detection of Incorrect Endoscope Adaptions in

Chemical Disinfection Devices

Timo Brune

, Björn Brune

, Sascha Eschborn

and Klaus Brinker

University of Applied Sciences Hamm Lippstadt, Marker Allee 76-78, Hamm, Germany

Olympus Surgical Technologies Europe, Kuehnstraße 61, Hamburg, Germany

Keywords: Computer Vision, Feature Detection, Surf, Sift, Registration, Machine Learning, Supervised Learning,

Endoscopes, Disinfection.

Abstract: This paper presents a complete analyzing system for detecting incorrect endoscope adaptions prior to the

use of chemical disinfection devices to guarantee hygienic standards and to save resources. The adaptions

are detected visually with the help of an image registration algorithm based on feature detection algorithms.

On top of the processing pipeline, we implemented a k-nearest neighbor algorithm to predict the status of

the adaption. The proposed approach shows good results in detecting the adaptions correctly.

1 INTRODUCTION

Endoscopic diagnostic is the main application for

diseases of the gastrointestinal tract and has a huge

clinical relevance. An important part of endoscopes

is the quality of the preprocessing of the devices and

the resulting hygiene, to minimize the contamination

of the patient with microbes (Bader, 2002). In the

past microbes have developed resistances against

antibiotics. Consequent hygiene is therefore

indispensable. Muscarella (Muscarella, 2014)

showed that insufficient preprocessed endoscopes

are responsible for the contamination with CRE-

microbes. To guarantee an acceptable hygienic

standard, we need to disinfect the endoscopes. To do

this in a constant quality we apply supervising

preprocessing of the endoscopes.

So called cleaning and disinfection devices for

endoscopes (CDD-E) perform well in cleaning the

endoscope’s exterior and interior, where the

procedure of adaption is rather complex. Medical

employees often do not adapt the endoscopes

correctly to the CDD-E because of this complexity.

These adaption errors lead to a lack of hygiene. The

CDD-E is able to detect these errors and can

terminate the process of cleaning. An interruption

always costs operational time of up to 20 minutes,

water, cleaning chemicals and energy. We have

implemented a system tailored to detect those

adaption errors prior to the disinfection to save these

resources and ensure the quality of the

preprocessing.

We consider the margin between an endoscope

adapter and its adaption counterpart in the chemical

disinfection device in order to detect connection

faults. We have transformed the underlying problem

of determining the size of the gap between the

respective parts into an image registration problem

(Handels, 2009). Hence we want to try to align two

reference images of the two sides of the adapter to

an image of the disinfection device which contains

the endoscope and the adaption counterparts. Please

note that this new image is a 2d-projection of the

underlying 3d-scene. In this paper we make use of a

feature-based approach to image registration

(Zitova, 2003). The first step in this processing

pipeline is to detect feature points for each image

independently. In a second step corresponding

feature points on different images are matched.

We detect feature points with two different

feature detection algorithms which detect, describe

and match possible correspondences and compare

their performance on our problem. More precisely

we choose the algorithms scale-invariant feature

transform (SIFT) (Lowe, 2004) and speeded up

robust features (SURF) (Bay, 2008). We describe

these feature detection algorithms in more detail in

Chapter 2.2.4.

On top of the extracted features we use a simple

k-nearest neighbor algorithm to classify correct /

incorrect adaptions. More details are given in

Brune T., Brune B., Eschborn S. and Brinker K.

Automatic Visual Detection of Incorrect Endoscope Adaptions in Chemical Disinfection Devices.

DOI: 10.5220/0006143003050312

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 305-312

ISBN: 978-989-758-213-4

305

Chapter 2.2.5. Finally we show promising

experimental results on the accuracy of our

automatic error detection prototype in Chapter 3.

2 PROCEDURE

2.1 Hardware Setup

To accomplish the tasks of detecting errors in the

adaption, a complete prototype was built. The

system consists of a loading station wherein the

detection occurs and the integrated software which is

responsible for the processing pipeline of the

detection. As a basis for our image processing are

four images taken by four high-resolution cameras

from four different perspectives in order to capture

images without occlusions of relevant parts with a

high probability. Figure 1 shows an example of an

image which was taken by one of the cameras.

For optimal image processing it is important that

the scene is illuminated using controlled light

conditions (Bader, 2002). Because of that the

detection system is sealed in a cube to prevent

diffuse light entering the system. We enlighten the

detection system with a planar LED-Panel.

Camera sensors take 50% of the information

from the green interval of the spectrum. Green light

transfers approximately 72% of the luminance and is

there-fore most important for contrast and resolution

(Fukanaga, 1975) Because of that we chose an LED-

Panel with a color temperature of 6000 °K.

According to Wiens Law, the maximum radiation is

at 482.95 nm for 6000 °K which is within the green

part of the spectrum.

Figure 1: Example image of the scene, taken by one of the

four cameras.

The cameras are controlled using a serial interface

from the software to automate the system. With the

software we are also able to manipulate the settings

of the camera. So it is possible to adjust the aperture,

the ISO-value and the white balance. The white

balance is analogically set to 6000 °K. The other

values were set empirically , so that there is no over-

exposure and therefore no loss of information. We

use Canon EOS 750D cameras with a resolution of

24 Megapixel. A high resolution is essential for an

accurate detection.

Figure 2: Prototype.

We consider the task of detecting adaption errors

for a variety of different endoscopes and adapters. In

order to detect which endoscope is used, it is tagged

with an RFID chip. We use an RFID-reader, also

connected via a serial interface to differentiate

between them through their integrated RFID-tags.

On the basis of the detected endoscope the software

determines which and how many adapters should be

connected to the respective endoscope. The user gets

visual information on how to attach these adapters to

the detected endoscope. Figure 2 shows the general

setup of our prototype. At the front there is a door

which is not visible in the image.

2.2 Algorithmic Components

In order to classify whether an adapter is connected

correctly or not we use a pipeline of algorithms

which are explained in more detail in this chapter.

2.2.1 Image Registration

As explained in the introduction, we need to

measure the size of the gap between the two sides of

the adapter. We took several reference image pairs

of each adapter as shown in Figure

HEALTHINF 2017 - 10th International Conference on Health Informatics

306

Figure 3: left: two parts of the same adapter, right: both

adapters matched together show a complete view of the

adapter.

If we combine those two parts of the image we get a

complete view of the adapter. Our goal is to map and

accordingly register these two-dimensional reference

images independently on a two dimensional

projection of the scene. For image registration, two

images are needed. The first is called reference

image denoted 



, and the second is called template

image denoted 



. This leads to a mathematical

optimization problem. We search for a linear

mapping :



→



that maps the object on 



the

most exact to the object of 



. Depending on the

class of transformations we can differentiate

between rigid, affine and perspective transformation.

The positions of the endoscope and thus the adapters

are completely unknown and only depend on the

employee of the hospital. Therefore, we are not able

to reach our goal with a simple rigid or affine

transformation. We have to describe a three-

dimensional transformation in space as a two-

dimensional projection in the image layer (Schreer,

2005). A projection like this is defined as an

endomorph description of a scene (Fischer, 2014).

A property of perspective projection is the loss of

proportions. Objects that are further away from the

center of projection appear smaller.

We can define this transformation as a 33

matrix





=

cos



sin











cos

















(1)

which we apply to every position of the reference

image.

It is now known which form the transformation

matrix has to have to map a two-dimensional

reference image into the three-dimensional space

and map it again to a two-dimensional projection.

We have to determine the nine degrees of freedom

which uniquely define the matrix. To find the

required parameters, we need two sets of

corresponding points. is a set of points from the

reference image and ′ is a set of corresponding

points from the template image. Here 



is the

transformation matrix of the perspective projection.



∙







⟺









′

(2)

To determine the transformation matrix we need

to have correspondences of points in the reference

and template image. In the following chapter we

show how these correspondences are detected.

2.2.2 Feature Detection

Feature detection algorithms are methods from the

field of computer vision. We use them to detect so

called interest points and correspondences between

points in two images. These images typically show

the same object, but at a different time or from a

different perspective. In the experiments we will

analyze two well established algorithms to examine

which one is more appropriate for this application

field. The two algorithms are the scale-invariant

feature transform (SIFT) (Lowe, 2004) and the

speeded up robust features (SURF) (Bay, 2008).

These two algorithms have the same general

process, which is divided into three steps: 1. feature

detection, 2. feature description and 3. feature

matching.

The first step, feature detection, deals with the

detection of so-called interest points. These are

distinctive points in an image. They always depend

on their neighborhood.

The feature description deals with the description of

the detected interest points, enabling a comparison

between the reference and the template images. The

most significant feature is the surrounding of one

point. Since the surroundings of the interest points

are never exactly the same on the reference and the

template image, a pixelwise comparison would not

work robustly. Furthermore, the descriptors have to

be invariant against geometric, perspective and

illumination transformations and image noise. Both

algorithms are based on computing one gradient of

the complete neighborhood of an interest point, as

well as in their sub regions.

The final step of the feature detection algorithms

matches interest points in the reference and template

image. The challenge is to find correct

correspondences of points, which in fact show the

same points of an object (Szeliski, 2011).

Every interest point is described through a

multidimensional description vector. A similarity

can be evaluated with the Euclidean distance

between the two descriptors. The most accurate but

slowest method is to compare every interest point of

Automatic Visual Detection of Incorrect Endoscope Adaptions in Chemical Disinfection Devices

307

the reference image with every interest point of the

template image. Since accuracy is one of our main

goals, we make use of this algorithm in the

experimental section. Other possibilities are the

randomized k-d tree (Silpa-Anan, 2008) and the

priority k-means tree algorithm (Fukanaga, 1975).

These algorithms are up to two times faster, approx-

imate to 95% of correctness (Muja, 2014).

Despite the high accuracy of SIFT and SURF,

there are always a few correspondence errors which

have to be filtered. We filter these errors with the

well-established random sample consensus

algorithm (RANSAC) (Strutz, 2016). If these errors

were not filtered they would have a bad influence on

the computation of the transformation matrix.

2.2.3 Machine Learning

To classify if an adapter is adapted correctly we use

a simple k-nearest neighbor approach. As features

we use the Euclidean distance between the two

projections and the number of detected corres-

pondences. Figure 4 shows an example of registered

features on one of the adapters. In this example the

classes are linear separable.

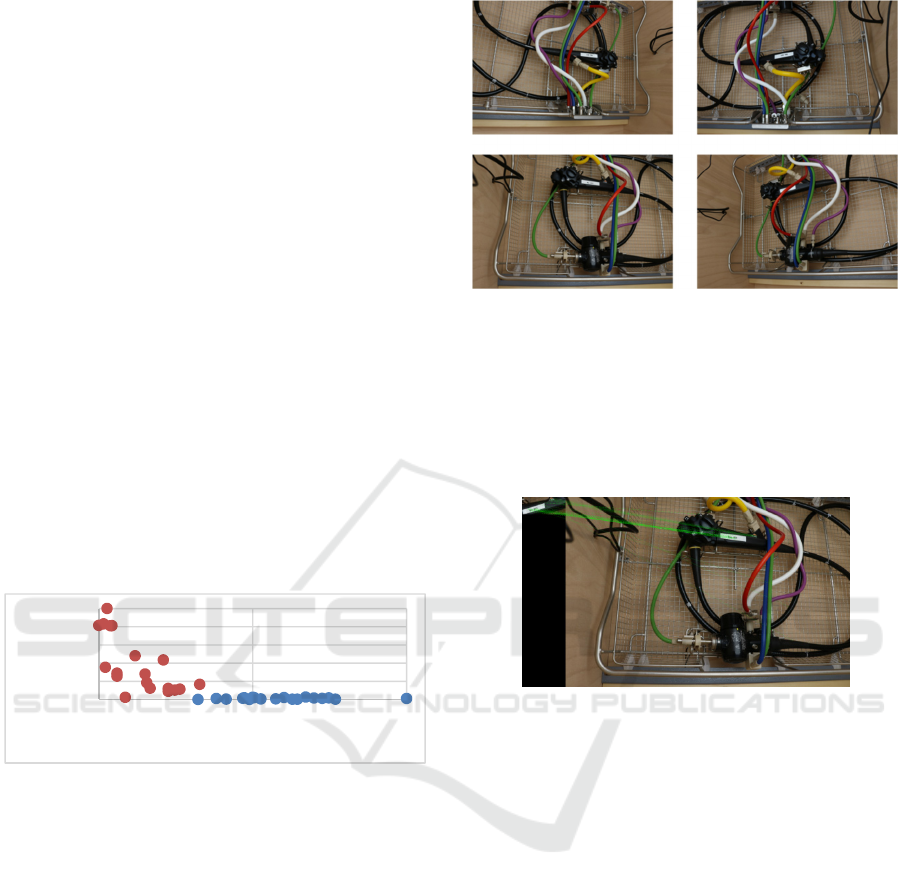
Figure 4: Normalized values of the Euclidean distances

and the number of correspondences, red: incorrect, blue:

correct.

2.2.4 Processing Pipeline

In this section we explain the complete processing

pipeline. Figure 5 shows four template images made

at runtime as explained previously.

We take five reference image pairs for every

adapter. One part of the pair shows the part of the

adapter at the endoscope, the other one the part of

the tube. The process is the same for every adapter.

Figure 5: Template images from four different

perspectives.

At first we intend to find the rough position of

the endoscope. For this purpose we use the feature

detection algorithm to find correspondences between

a reference image of the part of the adapter at the

endoscope.

Figure 6: Correspondence pairs between the reference

image and the template image to detect the rough position

of the adapter.

These interest points and correspondences are

easier to find because of the texts on the endoscope

which are very distinctive. We compute the mean of

all detected points in Figure 6 and crop that region

of the image depending on the size and geometry of

the adapter. This happens at a fourth of the

resolution to save time. The following computations

are made on the cropped images. This approach has

two advantages. First: The complex computations

are made on a much smaller image. Second: A

smaller image minimizes the probability of

correspondence errors.

When all subregions for all adapters were found,

the accurate registration of the reference image pairs

begins. For every adapter we have five reference

image pairs. As one can see in Figure 7 the adapters

not only have to be transformed in the space but may

have to be rotated longitudinally as well. For the

accurate registration we check all reference images

and choose the one with the most detected

0,2

0,4

0,6

0,8

00,51

Eucledean

Distance

Number of Correspondences

HEALTHINF 2017 - 10th International Conference on Health Informatics

308

correspondences.

Afterwards we detect and describe the interest

points of the chosen reference image of the adapter

on the side of the endoscope and the associated

reference image of the adapter on the side of the

tube. Then we identify correspondences between the

reference images and compute the transformation

matrices as shown in equations (1) and (2). With the

computed transformation matrices we map the

reference images into the template image we

identified previously. If the adaption is correct, the

projected reference images should intersect on the

inner edge as pictured in Figure 3. The same

matrices for mapping the reference images are used

to compute the center of the cutting edge. In Figure

8 one can see the two mapped reference images,

bounded in green rectangles. The midpoints of the

cutting edges are depicted by blue points. One can

recognize only one point at the left image because of

the optimal projections the two points overlap

completely. In the right image one can see an

incorrect adaption. The Euclidean distance between

the points is one feature for the classification of the

incorrect adaption.

Figure 7: A variety of reference images of the same

adapter because of the longitudinal rotations, which are

not detectable with the feature detection algorithms.

We use the two points to compute the Euclidean

distance between the two projections. An explorative

data analysis showed that the projection does not

work perfectly at all times. So it is not reliable as

single. Because of that we implemented a simple k-

nearest-neighbor Algorithm to classify the

adaptions. In addition to the Euclidean distance we

use the number of correspondences as a second

feature. This is depicted in Figure 4.

Figure 8: Mapped reference image pair on one template

image. The blue point marks the middle of their cutting

edges. Left: correct adaption, right: incorrect adaption.

3 EXPERIMENTAL RESULTS

As stated in the previous chapter, the detection of

interest points and correspondences is essential for a

correct projection of the reference images. The

quality of the transformation matrix is significantly

enhanced by detecting more correspondences. Vice

versa a faultless projection is impossible if there are

too many correspondence errors.. In this chapter we

describe the results of the detection processes and of

the classification.

We describe only the results of the reference

images on the side of the adapter. Because of the

high amount of letters on the endoscope itself, there

are a lot of interest points and the projection always

worked faultless.

Figure 9: Adapter set which we used for our experiments.

The quantitative results of the feature detection

algorithms are our first criteria for the quality of the

system. Figure

shows the adapter set we used for

our experiments. In the following tables we show the

statistic results of 40 processes for the first adapter

set. Table 1 shows the results for correct adaptions

generated with SURF.

The number of interest points and corres-

pondences - absolute and per pixel – is of special

importance here. In both categories one can see, that

the values are in the same order of magnitude for

most adapters. The adapters a, c, f and g have the

lowest values. This is because of the little body and

the few distinctive points on the adapters. So a

correct correspondence is more difficult to compute.

The adapters b, d and e have more distinctive points.

So the correspondences are easier to find. In Table 2

we see the statistical values for incorrect adaptions,

generated with SURF. The number of detected

interest points is similar. This makes sense, because

we use for both procedures images of the same size.

One can see the difference at the inspection of the

correspondences. For incorrectly adapted devices the

algorithm detects much less correspondences. This is

because the reference images were made with

correct adaptions.

Automatic Visual Detection of Incorrect Endoscope Adaptions in Chemical Disinfection Devices

309

Table 1: Correct adaptions, generated with SURF as pre-

processor.

Interest Points Correspondences

Adapter

Mean #

Minimum #

Maximum #

Per Pixel

Mean #

Minimum #

Maximum #

Per Pixel

824

90

764 995

3.4

E-3

139

25

105 189

5.8

E-4

367

24

331 382

2.1

E-3

12

81 115

5.0

E-4

349

8

339 357

1.0

E-3

13

23 65

1.6

E-4

572

12

561 586

1.,9

E-3

6

45 63

1.7

E-4

107

3

106 117

1.9

E-3

10

9 43

3.0

E-5

111

82

883

114

3.4

E-3

142

21

114 114

4.0

E-4

441

33

371 465

2.0

E-3

6

18 35

1.1

E-4

Table 2: Incorrect adaptions, generated with SURF as pre-

processor.

Interest Points Correspondences

Adapter

Mean #

Minimum #

Maximum #

Per Pixel

Mean #

Minimum #

Maximum #

Per Pixel

794

33

780 888

3.3

E-3

16

24 73

1.6

E-4

356

26

323 382

2.0

E-3

5

10 25

8.0

E-5

342

6

339 354

1.0

E-3

2

5 10

2.0

E-5

566

29

540 602

1.8

E-3

9

12 40

6.0

E-5

159

58

106 227

2.8

E-3

38

4 86

6.0

E-5

873

31

142

114

3.0

E-3

27

27 91

1.8

E-4

424

49

324 465

1.9

E-3

4

7 19

4.0

E-5

If there is an incorrect adaption in the template

image it is possible, that there are large perspective

changes. If the perspective changes are too high, the

SURF algorithm cannot detect them, so fewer

correspondences are found as one can see in Figure

10. In six of the seven cases there are more than

twice as many detected correspondences. The only

exception here is adapter g because of its simple

structure and few interest points. These experimental

evaluations demonstrate that the number of

correspondences is a meaningful feature for the

machine learning algorithm.

Table 3: Correct adaptions, generated with SIFT as pre-

processor.

Interest Points Correspondences

Adapter

Mean #

Minimum #

Maximum #

Per Pixel

Mean #

Minimum #

Maximum #

Per Pixel

402

5

391 407

1.7

E-3

13

54 91

3.3

E-4

135

8

121 140

8.0

E-4

5

38 51

2.6

E-4

157

13

140 170

5.0

E-4

5

7 26

1.0

E-5

321

20

278 336

1.0

E-3

7

15 33

7.0

E-5

8

41 58

9.0

E-4

3

5 13

1.5

E-4

697

18

206 776

2.0

E-3

208

10

191 220

6.3

E-4

238

40

199 339

1.0

E-3

5

10 28

7.0

E-5

In the following we outline the results of SIFT

for the same adapter set. The statistical values of

correct adaptions are shown in Table 3. Compared to

the SURF algorithm it attracts attention that SIFT

detects less interest points and correspondences than

SURF. The exact quotient is shown in Figure 11.

One can easily see that the SURF algorithm detects

more interest points and because of that more

Correspondences.

Figure 10: Comparison of the number of correspondences

between correct and incorrect adaptions.

In Table 5 one can see the statistical values for

incorrect adaptions, generated with SIFT. Analogue

to the SURF algorithm it is obvious that fewer

correspondences have been computed. This is

because of the similar procedure. Striking are the

detected minima of correspondences. If the

algorithm detects less than three correspondences, a

projection and following classification is impossible.

In summary we conclude, that the SURF algorithm

detects roughly twice as many correspondences than

100

150

abcdef g

Number of

Correspondeces

Correct - SURF Incorrect - SURF

HEALTHINF 2017 - 10th International Conference on Health Informatics

310

the SIFT algorithm. If we have too few corres-

pondences it is possible that the RANSAC algorithm

cannot filter the correspondence errors. The result is

an incorrect transformation matrix. Quantitatively

the SURF algorithm has to be preferred.

Figure 11: Comparison of the detected interest points and

correspondences.

Now we will focus on the quality and precision

of the classification. As outlined before we use a k-

nearest neighbor Algorithm for the binary

classification. The Euclidean distance of the

projection pairs and the number of correspondences

are the features of the algorithm. Experiments with

validation data gave us an optimal value for =5.

A first estimation of the quality of the processes

delivers the classification rate. In Figure 12 one can

see the classification rate per adapter for both

algorithms as pre-processing. All rates were

determined on test data experiments.

Figure 12: Comparison of the classification rates.

As predicted the process with SURF as pre-

processing has a significantly higher classification

rate of 92.86% compared to SIFT. The worst value

occurs at adapter e. This is because of the geometry

of the adapter. The Euclidean distance can be 0 for

this adapter although it is adapted incorrectly. This

adapter needs an additional physical rotation to be

correctly adapted. This can only be determined

through the number of detected correspondences.

Table 4: Confusion matrix of the classifications with

SURF as pre-processing.

SURF CORRECT

ADAPTIONS

INCORRECT

ADAPTIONS

PREDICTED

CORRECT

ADAPTIONS

TP = 64 FP = 4 P’ = 68

PREDICTED

INCORRECT

ADAPTIONS

FN = 6 TN = 66 N’ = 72

P = 70 N = 70

=140

Fawcett explains another possibility to evaluate

classifications (Fawcett, 2006). So called receiver

operating characteristics (ROC) graphs can be used

to evaluate and visualize the quality of a

classification. We divide the results of our experi-

ments in four groups: true-positive (TP), true-

negative (TN), false-positive (FP) and false-negative

(FN). These groups can be written in a so-called

confusion matrix (Fawcett, 2006), as one can see in

Table 4 and Table 6.

Table 5: Incorrect adaptions, generated with SIFT as pre-

processor.

Interest Points Correspondences

Adapter

Mean #

Minimum #

Maximum #

Per Pixel

Mean #

Minimum #

Maximum #

Per Pixel

339

5

397 409

1.7

E-3

9

24 51

1.6

E-4

136

7

121 140

8.0

E-4

6

3 19

5.0

E-5

160

35

140 256

5.0

E-4

2

3 8

1.0

E-5

317

21

278 336

1.0

E-3

6

9 30

5.0

E-5

131

99

41 246

2.3

E-3

25

3 76

4.6

E-4

711

10

557 776

2.2

E-3

142

53

44 209

4.3

E-4

203

14

190 239

9.0

E-4

3

4 13

3.0

E-5

The contents of the matrices were generated in 40

experiments and are a summary of all adapters.  is

the number of correct,  is the number of incorrect

adaptions. ′ is the number of positive, ′ is the

number of negative predictions. We can derive four

statistical values from these matrices: the true-

positive-rate (TPR), the false-positive-rate (FPR),

positive-predictive-value (PPV) and the accuracy

(ACC). We can now visualize the quality of the

classification with a ROC-Graph as shown in Figure

13.

300

600

900

1200

abcde fg

Count

Interest Points - SURF

Interest Points - SIFT

50%

100%

abcdef gØ

classification

rate

SURF SIFT

Automatic Visual Detection of Incorrect Endoscope Adaptions in Chemical Disinfection Devices

311

Table 6: Confusion matrix of the classifications with SIFT

as pre-processing.

SIFT CORRECT

ADAPTIONS

INCORRECT

ADAPTIONS

PREDICTED

CORRECT

ADAPTIONS

TP = 62 FP = 18 P’ = 80

PREDICTED

INCORRECT

ADAPTIONS

FN = 8 TN = 52 N’ = 60

P = 70 N = 70

=140

Ideally should the TPR be close to 1, the FPR close

to 0. The more the point is in the North-West, the

better is the classification. One can see in the

visualization that the processes with SURF as Pre-

Processing Algorithm is better than with SIFT. The

system needed in average 71/42 seconds for the

classification of the large/small adapter set.

Table 7: Statistical values from the confusion matrices.

SURF SIFT

TPR 0.914 0.886

FPR 0.057 0.257

PPV 0.941 0.775

ACC 0.928 0.814

Figure 13: ROC Graph.

4 CONCLUSION

This paper presents an automatic visual system for

detecting adaption errors in chemical disinfection

devices for endoscopes. Our experimental evaluation

shows promising results with respect to the

classification accuracy. With the SURF algorithm as

pre-processing tool, the prototype system yields a

classification accuracy of 92.86% for determining

the correctness of the adaptions in approximately

one minute of processing. Future work will aim in

enhancing the correctness of the prediction close to

100% and in installing the system directly into the

endoscope thermal disinfector to save even more

time and resources.

REFERENCES

Bader, L. et al, 2002 HYGEA (Hygiene in

Gastroenterology – Endoscope Reprocessing): Study

on Quality of Reprocessing Flexible Endoscopes in

Hospitals or Practice Setting. In Journal for

Gastroenterology 12 Pages 951-1000.

Muscarella, L., 2014 Risk of transmission of carbapanem-

resistant Enterobacteriaceae and related “superbugs”

during gastrointestinal endoscopy. In World Journal of

Gastrointestinal Endoscopy 6 Pages 951-1000.

Handels, H., 2009. Medizinische Bildverarbeitung,

Vieweg und Teubner. Wiesbaden, 2

edition.

Zitova, B., Flusser, J., 2003. Image registration methods: a

survey. In Image and Vision Computing Volume 21

Pages 977-1000.

Lowe, D, 2004, Distinctive Image features from Scale-

Invariant Keypoints. In International Journal of

Computer Vision 60 Pages 91-110.

Bay, H. et al, 2008, Speeded-Up Robust Features (SURF).

In Computer Vision and Image Understanding Pages

346-359.

Schreer, O., 2005. Stereoanalyse und Bildsynthese,

Springer Verlag. Berlin Heidelberg, 1

edition.

Fischer, G., 2014. Lineare Algebra, Springer Verlag.

Berlin Heidelberg, 18

edition.

Szeliski, R., 2011. Computer Vision, Springer Verlag.

Berlin Heidelberg, 1

edition.

Silpa-Anan, C., Hartley, 2008, R., Optimised KD-Tree for

fast image descriptor matching. In Computer Vision

and Pattern Recognition

Fukanaga, K., Narendra, P., 1975, A branch and bound

Algorithm for Computing k-Nearest Neighbors. In

IEEE Transactions on Computers C-24 Pages 750-

753.

Muja, M., Lowe, D., 2014, Scalable Nearest Neighbor

Algorithms for High Dimensional Data. In IEEE

Transactions on Pattern Analysis and Machine

Intelligence 36 Pages 2227-2240.

Strutz, T., 2016. Data Fitting and Uncertainty, Springer

Verlag. Berlin Heidelberg, 2

edition.

Fawcett, T., 2006, An introduction to ROC Analysis. In

Pattern Recognition Letters 27 Pages 861-874.

0,2

0,4

0,6

0,8

00,51

true positive rate

false positive rate

ROC - SURF ROC - SIFT

HEALTHINF 2017 - 10th International Conference on Health Informatics

312