A Robust Descriptor for Color Texture Classification
Under Varying Illumination
Tamiris Trevisan Negri
1,2,3
, Fang Zhou
2
, Zoran Obradovic
2
and Adilson Gonzaga
1
1
Department of Electrical and Computer Engineering, University of S
˜
ao Paulo, S
˜
ao Carlos, Brazil
2
Center for Data Analytics and Biomedical Informatics, Temple University, Philadelphia, U.S.A.
3
Federal Institute of Education, Science and Technology of S
˜
ao Paulo, Araraquara, Brazil
Keywords:
Color Texture, Texture Description, Illumination, Local Descriptors.
Abstract:
Classifying color textures under varying illumination sources remains challenging. To address this issue, this
paper introduces a new descriptor for color texture classification, which is robust to changes in the scene
illumination. The proposed descriptor, named Color Intensity Local Mapped Pattern (CILMP), incorporates
relevant information about the color and texture patterns from the image in a multiresolution fashion. The
CILMP descriptor explores the color features by comparing the magnitude of the color vectors inside the RGB
cube. The proposed descriptor is evaluated on nine experiments over 50,048 images of raw food textures
acquired under 46 lighting conditions. The experimental results have shown that CILMP performs better than
the state-of-the-art methods, reporting an increase (up to 20.79%) in the classification accuracy, compared to
the second-best descriptor. In addition, we concluded from the experimental results that the multiresolution
analysis improves the robustness of the descriptor and increases the classification accuracy.
1 INTRODUCTION
Texture analysis is an important and widely explored
field in computer vision. There are many existing
works studying a variety of models to describe tex-
tures, most of them designed for gray-scale images.
Although color is often ignored by many texture de-
scriptors, some works have shown the importance of
color in the process of describing a texture (Setchell
and Campbell, 1999; Drimbarean and Whelan, 2001;
Palm, 2004; Maenpaa and Pietikinen, 2004; Bianconi
et al., 2011).
In the last two decades, several descriptors were
developed to incorporate color information in differ-
ent tasks, such as classification, segmentation and
recognition. Statistical approaches based on co-
occurrence matrices together with color description
are used for image retrieval and texture classification
(Arvis et al., 2004; Vadivel et al., 2007). Wavelets
and Gabor Filters were also investigated for that pur-
pose (Maenpaa and Pietikinen, 2004; Campbell et al.,
1996; de Wouwer et al., 1999; Sengur, 2008; Palm
and Lehmann, 2002; Jain and Healey, 1998).
Local texture descriptors, such as local binary pat-
tern (LBP) (Ojala et al., 1996; Ojala et al., 2002), have
been extended to be applied to color textures. Op-
ponent color local binary pattern (OCLBP) combines
LBP histograms and opponent color texture features
for facial recognition (Chan et al., 2007). Intensity
color contrast descriptor (ICCD) and local color con-
trast (LCC) (Cusano et al., 2013; Cusano et al., 2014)
combine the LBP histogram with information associ-
ated to the color contrast of the image.
Experiments performed by Maenpaa and
Pietikainen (Maenpaa and Pietikinen, 2004) showed
that color descriptors perform better than the gray-
scale descriptors for texture classification tasks.
However, the same work showed that the color
texture descriptors are negatively affected by varying
illumination conditions.
To overcome the issue of varying illumination,
some authors proposed color normalization algo-
rithms as a pre-processing step for texture description
methods (Kandaswamy et al., 2012; Cusano et al.,
2014; Cusano et al., 2016). However, it has been
shown that the normalization requires an extra com-
putational cost only resulting in improvement in very
specific conditions (Cusano et al., 2016).
In this paper we propose a new color texture
descriptor robust to variations on the illumination
source. The proposed descriptor, named Color In-
tensity Local Mapped Pattern (CILMP), extends the
378
Negri T., Zhou F., Obradovic Z. and Gonzaga A.
A Robust Descriptor for Color Texture Classification Under Varying Illumination.
DOI: 10.5220/0006143403780388
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 378-388
ISBN: 978-989-758-225-7
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

local mapped pattern descriptor (LMP) presented in
(Ferraz et al., 2014) for color texture classification.
CILMP incorporates relevant information about the
color and texture patterns from the image. This infor-
mation can be extracted jointly or separately. Studies
about the human visual system show that texture and
color information are processed separately by the hu-
man brain (Poirson and Wandell, 1996). In (Maenpaa
and Pietikinen, 2004), the authors also concluded that
color and texture are separate phenomena and should
be treated individually. Therefore, the proposed de-
scriptor processes color and texture information sep-
arately to make it close to human perception.
The proposed descriptor incorporates color infor-
mation using the magnitude of the color vector inside
the RGB cube. Both color and texture information
are processed separately from different texture resolu-
tions to capture information from a range of frequency
patterns. The local patterns obtained from each reso-
lution are mapped to a histogram using a parametric
function. In this paper, we apply a genetic algorithm
to tune the parameters simultaneously in order to op-
timize the multiresolution analysis.
The proposed descriptor is evaluated on a large
dataset composed of 50,048 images of raw food tex-
tures designed especially to investigate the robust-
ness of texture descriptors when the scene illumina-
tion changes. The experimental results indicate that
combining different resolutions makes the descriptor
more robust, increasing the classification accuracy.
Moreover, CILMP outperforms the existing descrip-
tors considered in the comparison.
The remaining of this paper is organized as fol-
low: Section 2 provides a review of the local mapped
pattern descriptor and an extension of the method
designed for multiresolution analysis. Section 3
presents the proposed descriptor CILMP. The exper-
iments are reported and discussed in Section 4 and,
finally, we conclude the paper in Section 5.
2 LOCAL MAPPED PATTERN
In this section we first provide a brief description of
the local mapped pattern (LMP) descriptor (Ferraz
et al., 2014). Then, we present a natural extension of
this approach for circular neighborhoods, which al-
lows a multiresolution analysis.
The LMP descriptor was proposed by Ferraz et al.
(Ferraz et al., 2014) and originally designed for gray-
scale images. Let us consider a 3 × 3 local pattern as
shown in Fig. 1. Assuming that g
c
is the central pixel
in the local pattern, the LMP considers the differences
between g
c
and its neighboring pixels g
i
, i = 1, ... ,8,
as the argument of a weighting function which maps
each difference to a histogram bin.
𝑔
1
𝑔
2
𝑔
3
𝑔
4
𝑔
5
𝑔
6
𝑔
7
𝑔
8
𝑔
𝑐
Figure 1: Local Pattern 3 × 3.
A local pattern from a v = W ×W squared neigh-
borhood can be mapped to a histogram bin h
b
accord-
ing to
h
b
= round
∑
v−1
i=1
f
g
i
M(i)
∑
v−1
i=1
M(i)
(B − 1)
!
, (1)
where f is the mapping function applied to the differ-
ence between each neighbor g
i
and the central pixel
g
c
, B is the number of histogram bins and M is a
weighting matrix of predefined values for each pixel
position within the neighborhood. The mapping func-
tion, number of histogram bins and weighting matrix
can be set according to the application. In (Ferraz
et al., 2014) the mapping function is defined as the
sigmoid function, given by
f
g
i
=
1
1 + exp

−[g
i
−g
c
]
β

, (2)
where β is the steepness of the curve and [g
i
− g
c
]
is the difference between the central pixel g
c
and its
neighbors g
i
(i = 1, ... ,v − 1).
2.1 Sampled Local Mapped Pattern
The LMP methodology can be easily extended to cir-
cular neighborhoods around the central pixel. Given
the number P of neighboring pixels, g
p
corresponds to
the value of each sampled pixel P, equally spaced in a
circle of radius R (R > 0), forming a set of neighbors
of circular symmetry, in a counterclockwise order as
shown in Fig. 2.
𝑔
𝑐
𝑔
1
𝑔
2
𝑔
3
𝑔
4
𝑔
5
𝑔
6
𝑔
7
𝑔
8
Figure 2: Neighbors of a circular symmetry, where P = 8
and R = 1.
A Robust Descriptor for Color Texture Classification Under Varying Illumination
379

Assume that the corresponding central
pixel g
c
is located at (x, y) = (0,0), the
coordinates of each neighbor pixel g
p
are
(x,y) = (−Rsin(2πp/P), Rcos(2πp/P)). The
pixel values that are not located in the exact center
of each pixel are estimated through interpolation,
inspired by (Ojala et al., 2002).
This new version of LMP, called sampled-local
mapped pattern (S-LMP), is capable of sampling sev-
eral resolutions of radius (R) and number of neighbors
(P). The combination of different neighborhood con-
figurations (P,R) leads to a multiresolution analysis
which increases the power of the descriptor to extract
relevant features from the texture.
Each S-LMP pattern defined by P samples and ra-
dius R is mapped to a histogram bin h
b
using Eq. (3),
where B is the number of histogram bins and f is the
sigmoid mapping function given by Eq. (2) in which
β is the steepness of the curve. A weighting matrix
is not used in this approach, only the number of the
pixel samples P, which guarantees the rotation invari-
ant characteristic.
h
b
= round
∑
P
p=1
f
g
p
P
(B − 1)
!
. (3)
3 COLOR INTENSITY LOCAL
MAPPED PATTERN
The CILMP model is a parametric descriptor that
combines color and texture information in several res-
olutions to get high accuracy in classification tasks
under varying illumination. In this section, we in-
troduce how CILMP incorporates texture and color
information from the images to the feature vectors,
and propose the application of a genetic algorithm to
tune the descriptor parameters in order to optimize the
multiresolution analysis.
3.1 Feature Extraction
In CILMP, the texture information is extracted from
the image luminance by the S-LMP descriptor pre-
sented in Section 2.1. To get a multiresolution analy-
sis, the descriptor is applied using different neighbor-
hood configurations. The obtained histograms from
each neighborhood configuration are concatenated to
form the CILMP texture feature vector.
For the extraction of color information we propose
a novel approach based on the magnitude of the color
vectors inside the RGB cube. On a three-dimensional
color space, each axis represents a channel, and there-
fore each color can be represented as a point inside the
3-D space. For example, on the RGB color space, a
color is characterized by its primary components red,
green and blue (Gonzalez and Woods, 2008). A local
3 × 3 pattern of color texture is a three-dimensional
matrix where each pixel is described by three coordi-
nates g
i
= (R
i
,G
i
,B
i
).
To extend the S-LMP descriptor for color im-
ages, the difference between the squared magnitudes
of vectors in the RGB space is used as input of the
sigmoid function
f
g
p
=
1
1 + exp

−
(
||g
p
||
2
−||g
c
||
2
)
β

, (4)
where β is the steepness of the curve, g
c
is the central
pixel of the local pattern and g
p
is a neighbor of g
c
.
Symmetric circular neighborhoods are used to allow
a multiresolution analysis. The patterns are mapped
to a histogram bin h
b
according to Eq. (3). Figure 3
shows an RGB texture and its S-LMP map obtained
considering the sigmoid function presented by Eq. 4,
eight neighbors and radius equal to two.
Figure 3: Example of an RGB texture and its S-LMP map.
We apply the descriptor to color textures using
different neighborhood configurations. The obtained
histograms are concatenated to the texture histograms
provided by the S-LMP, forming the CILMP feature
vector.
Fig. 4 shows the multiresolution analysis per-
formed by the CILMP: different radius and number
of neighbors are used to extract texture information
from the luminance map and color information from
the RGB channels. Note that, for example, the neigh-
borhood (P,R) = (24, 5) just considers the pixel val-
ues which are distant five positions from the central
pixel. Combining different neighborhood resolutions
allows the descriptor to extract information from a
larger area, including more features in the feature vec-
tor.
3.2 Genetic Algorithm for Parameter
Tuning
The β parameter used in the sigmoid mapping func-
tion (Eq. 4) is related to the curve slope. It changes
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
380

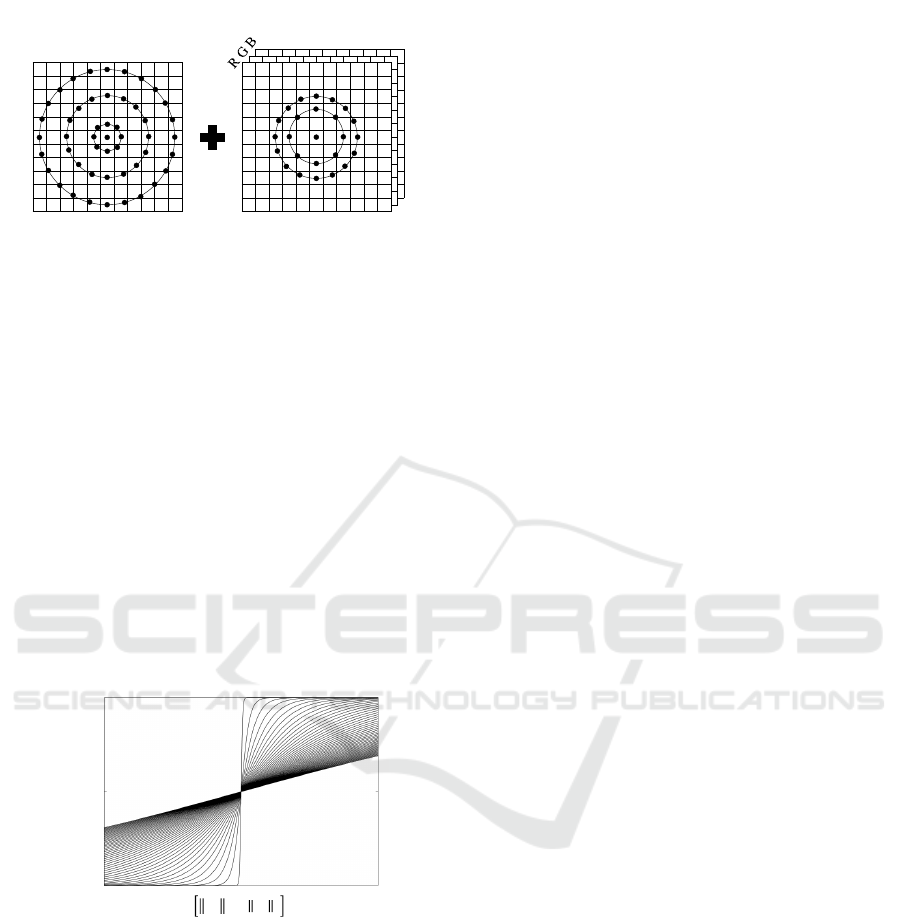
Luminance Map Local
Pattern
RGB Channel Local
Pattern
Figure 4: Example of a multiresolution analysis by the
CILMP using five configurations: (8,1) + (16,3) + (24, 5)
for the luminance map and (8,2) + (16,3) for the RGB
channels.
the sensitivity of the method to the nuances in the im-
age and directly affects the descriptor performance.
Note that β ∈ R, β 6= 0, in Eq. (2) . Since we are
not considering the absolute value in the argument of
the sigmoid function, we fix β > 0 to keep the curve
direction.
Fig. 5 shows the sigmoid curve behavior for a
range of β values. Small β values quickly saturate
the pixel differences to 0 or 1, resembling the LBP
(Ojala et al., 1996; Ojala et al., 2002). Large β val-
ues approximate the curve to a straight line parallel
to the abscissas axis, so that the pixel differences are
mapped to values around 0.5.
𝑔
𝑝
2
− 𝑔
𝑐
2
0
0.5
1
𝛽
𝑎
𝛽
𝑏
𝛽
𝑏
> 𝛽
𝑎
𝑓(𝑔
𝑝
, 𝑔
𝑐
)
Figure 5: Sigmoid curve behavior for a range of β values.
Small β values quickly saturate the pixel differences to 0 or
1. Large β values make the curve more flat.
For each neighborhood configuration we adopted
a different value of β. The CILMP showed in Fig.
4, for example, uses three configurations to extract
texture features and two for color features. So, five
β parameters need to be tuned.
Since the parameters from the five neighborhoods
influence each other when they are combined to form
the CILMP feature vector, we propose to adjust them,
simultaneously, by using genetic algorithm. The ac-
curacy is used as an objective function to be maxi-
mized.
4 EXPERIMENTS
4.1 Experimental Setup
In this work, the research problem is formulated as a
classification problem, that is, to predict which class
an image belong to. To evaluate the performance of
the CILMP descriptor we used the Raw Food Texture
(RawFooT) database, which was designed by Cusano
et al. (Cusano et al., 2016) specially to investigate the
robustness of color texture descriptors against lighting
changes in classification problems. The database con-
sists of 68 raw food textures of size 800 × 800 pixels,
acquired under 46 lighting conditions which differ in
direction, color, temperature, intensity and combina-
tion of these factors. The original images were di-
vided into 16 non-overlapping samples of 200 × 200
pixels: 8 samples for training and 8 samples for test.
There are 68 classes in this dataset and the goal is to
classify a sample in the correct class. The total num-
ber of samples is 68 × 46 × 16 = 50048, half of them
for training and the remaining for test. The 46 light-
ing conditions are listed below and illustrated in Fig.
6.
• (1-4) Intensity variations: Daylight at 6500 K
and four intensity levels: 100%, 75%, 50% and
25%;
• (5-13) Light direction: Daylight at 6500 K and
nine incident angles: 24
◦
, 30
◦
, 36
◦
, 42
◦
, 48
◦
, 54
◦
,
60
◦
and 90
◦
;
• (14-25) Daylight temperature: Daylight at
twelve different color temperatures from 4000 K
to 9500 K with steps of 500 K.
• (26-31) LED temperature: LED sources with
six different color temperatures: 2700 K, 3000 K,
4000 K, 5000 K, 5700 K and 6500 K;
• (32-40) Color and direction: combinations of
three colors (Daylight 6500 K, Daylight 9500 K
and LED 2700 K) and three incidence directions
(24
◦
, 60
◦
and 90
◦
);
• (41-43) Multiple illuminants: combinations of
two illuminants with different colors among Day-
light 6500 K, Daylight 9500 K and LED 2700 K;
• (44-46) Primary colors: pure red, green and blue
illuminants.
We performed the nine texture classification tasks,
same as (Cusano et al., 2016), using the RawFooT
database. Each task contains several subsets com-
posed by training and test images taken under the light
condition to be analyzed. For example, let us consider
task 2, which involves four different lighting intensi-
ties. If we assign the training samples acquired under
A Robust Descriptor for Color Texture Classification Under Varying Illumination
381

01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
Figure 6: Example of one of the textures (rice) in the Raw Food Texture database imaged under the 46 lighting conditions as
described in Section 4.1.
a light source of intensity level 100% as the training
group, we can form 3 subsets (training, test) consid-
ering the test samples taken under the other 3 inten-
sity levels: (100%, 75%), (100%, 50%) and (100%,
25%). Since there are four intensity levels, we can
form 4 × 3 = 12 subsets. Below is the brief descrip-
tion of the nine tasks.
1. No variations: 46 subsets. For each subset, train-
ing and test samples were taken under the same
light conditions.
2. Light intensity: 12 subsets, each one composed
of training and test samples taken under different
light intensities.
3. Light direction: 72 subsets, each one composed
of training and test samples taken under different
light directions.
4. Daylight temperature: 132 subsets, each one
composed of training and test sets with images
taken under different color temperatures.
5. LED temperature: 30 subsets, each one com-
posed of training and test sets with images taken
under different LED light temperatures.
6. Daylight vs. LED: 72 subsets combining the
twelve daylight temperatures with the six LED
temperatures.
7. Temperature or direction: 72 subsets combin-
ing the light conditions 32 to 40, where the train-
ing and test samples differ in color or direction or
both, color and direction.
8. Temperature and direction: 36 subsets comb-
ing the light conditions 32 to 40, where the train-
ing and test sets samples differ in both color and
direction.
9. Multiple illuminats: 6 subsets combining the
light conditions 41 to 43.
For each task, the CILMP descriptor is applied to
both training and test samples to extract feature vec-
tors. The dissimilarity between training and test sam-
ples, is measured by calculating the distance of the
feature vector from the test sample and the feature
vector of the training sample using the L
1
distance
D(S,M) =
∑
B
t
b=1
|
S
b
− M
b
|
, where S is the feature vec-
tor of a training sample, M is the feature vector of a
test sample and B
t
stands for the number of bins in the
feature vector.
In all the experiments we applied the K-nearest
neighbor classifier (K = 1) to estimate the label of
the test images: the feature vector of each test sample
is compared to all feature vectors of the training sam-
ples, and the class of the training sample which pro-
vides the smallest dissimilarity is considered as the
prediction of the test sample. Since there are several
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
382

subsets in each classification task, the performance
of the method is evaluated using three measurements:
the average over the accuracies provided by each sub-
set classification, the minimum accuracy among them
and the average rank of the descriptor over the nine
tasks.
In this work, the CILMP model uses five neigh-
borhood configurations: three configurations for the
luminance map – (8, 1), (16,3) and (24,5) and two
configurations for the RGB channels– (8, 2) and
(16,3) (as shown in Fig. 4). Considering the pixel in-
tensity variation is larger in the luminance image, we
use more resolutions to extract texture information.
Preliminary experiments showed that these five neigh-
borhood configurations are enough to get high accu-
racy. Increasing the number of neighborhoods con-
figurations produces similar results but increases the
size of the feature vector, therefore increasing compu-
tational cost.
The number of histogram bins B was set to 256
for each neighborhood configuration. So the CILMP
feature vector has 256 × 5 = 1280 positions.
4.2 Performance of the Individual
Descriptors
First, we analyze the performance of the individual
descriptors and the influence of the β parameter in
the classification rate. We selected a training and a
test set which contains images taken under multiple
light sources with different lighting conditions. Fig. 7
and Fig. 8 show the classification accuracies when the
β parameter varies between (0, 5] for each neighbor-
hood configuration separately. Since f is not defined
if β = 0, we chose 10
−10
as the minimum value for β.
Fig. 7 and Fig. 8 show that the optimal β is within
(0,1] for all the proposed configurations. Based on
that, we analyze the β behavior only in that interval.
Table 1 shows the worst and best accuracies for each
neighborhood configuration, and the corresponding β
50
55
60
65
70
75
80
85
90
95
100
0.00 0.25 0.50 0.75 1.00 1.25 1.50 1.75 2.00 2.25 2.50 2.75 3.00 3.25 3.50 3.75 4.00 4.25 4.50 4.75 5.00
Accuracy (%)
Beta
8,1 L 16,3 L 24,5 L
Figure 7: Accuracy obtained from the β parameters between
(0,5] considering different configurations of neighborhoods
for luminance maps.
50
55
60
65
70
75
80
85
90
95
100
0.00 0.25 0.50 0.75 1.00 1.25 1.50 1.75 2.00 2.25 2.50 2.75 3.00 3.25 3.50 3.75 4.00 4.25 4.50 4.75 5.00
Accuracy (%)
Beta
8,2 RGB 16,3 RGB
Figure 8: Accuracy obtained from the β parameters between
(0,5] considering different configurations of neighborhoods
for RGB channels.
Table 1: Lowest and highest classification accuracy (%)
and the respective β (0 < β ≤ 1) for each configuration of
(P,R).
(P,R) lowest acc. (β) highest acc. (β)
(8,1) L 55.51 (0.67) 90.99 (0.01)
(16,3) L 78.68 (0.85) 95.22 (0.02)
(24,5) L 81.07 (10
−10
) 94.12 (0.07)
(8,2) RGB 73.90 (10
−10
) 86.40 (0.71)
(16,3) RGB 76.29 (10
−10
) 86.76 (0.86)
values.
The configuration (P,R) = (16,3) applied to the
image luminance presents higher accuracy (95.22%)
than the others.The lowest accuracy for (P, R) =
(16,3) is 78.68%, so the difference between the low-
est and highest reaches 16.54%. Combining the five
configurations and using the β values, with which in-
dividual configuration gives the result of highest ac-
curacy, produce the classification accuracy 96.32%.
Moreover, using β values, with which individual de-
scriptor produces lowest accuracy, produce 95.22% of
accuracy, which is better than the performance of the
individual descriptors. Therefore, five descriptors to-
gether produces much better results than the individ-
ual one, and thus, is more robust to classify texture
acquired under different light sources.
4.3 Performance of CILMP
In this section, we describe the performance of the
proposed CILMP descriptor. The parameters pre-
sented in Table 1 are tuned separately, however, they
can influence each other on the feature vector com-
parison. Therefore, to get the optimal β values used
in the CILMP model, we apply a genetic algorithm
to tune all the parameters simultaneously. We con-
sider β ∈ (0, 1] (based on results of Fig. 7 and Fig.
8) and the accuracy was used as objective function to
be maximized. The maximum accuracy reported by
the genetic algorithm is 97.98%. So, we can conclude
A Robust Descriptor for Color Texture Classification Under Varying Illumination
383

that the classification rate is increased by tuning all
the parameters together.
After some preliminary experiments, we noticed
that the β parameters could be adjusted by using a
few images in the tuning process: just two samples
from each class are enough in the tuning set, and the
CILMP could achieve a good performance. Based on
that, a tuning set is generated by randomly selecting
two samples per class from the 25024 training images.
Since the database involves 68 classes, the tuning set
contains 168 images. The set of the five β parameters
that produces the highest accuracy in the tuning set is
used on the CILMP descriptor to perform the classifi-
cation tasks. To guarantee that the images chosen are
not affecting the results, we repeated the experiments,
using seven different sets of β. One of the β values set
is [0.08, 0.13,0.98,0.17,0.14] for the neighborhoods
(8,1) L, (16,3) L, (24,5) L, (8,2) RGB and (16,3) RGB
respectively.
Table 2 reports the average and standard deviation
of the average accuracy obtained for the nine tasks
presented in Subsection 4.1. We notice that the stan-
dard deviation is small for all the tasks, so that the
random selection of images does not affect the classi-
fication accuracy.
Table 2: Average over the average accuracy (%) and stan-
dard deviation from seven tuning sets obtained by CILMP.
Light Condition Changing Avg. Acc. Std. Dev.
No variations 97.98 0.0952
Light intensity 79.10 2.3215
Light direction 63.70 1.1156
Daylight temperature 97.09 0.1556
LED temperature 95.04 0.1682
Daylight vs. LED 93.95 0.0992
Temperature or direction 42.87 0.8114
Temperature and direction 28.72 0.9149
Multiple illuminant 95.59 0.3341
We compare the obtained accuracy using CILMP
to the results provided by Cusano et. al. (Cusano
et al., 2016) using other baselines. Among the meth-
ods presented in (Cusano et al., 2016), we selected
for comparison the traditional texture descriptors de-
signed for texture analysis, which is the focus of this
paper.
Table 3 reports a rank of the performance of each
descriptor over the nine tasks. Fig. 9 to 17 show the
average accuracy obtained for each descriptor accord-
ing to the task. Fig. 18(a) shows the improvement
achieved by CILMP over the other methods in terms
of average accuracy.
The accuracy presented in Fig. 9 to 17 is the aver-
age between the accuracies provided by several sub-
sets in a task, as explained in Subsection 4.1. We also
evaluate the descriptor considering the minimum ac-
curacy presented for each task. The improvement in
the minimum accuracy performed by CILMP, for each
task, is reported in Fig. 18(b). The data used in Fig. 9-
18 and Table 3 are provided by (Cusano et al., 2016).
As expected, most of the descriptors achieve high
accuracy when there are no changes in the illumina-
tion condition (task 1). Descriptors that were applied
to both color and luminance channels, such as LBP,
histogram, co-occurrence matrix, wavelet transform
and Gabor filter, performed better when the color was
considered, confirming the importance of color in the
process of describing a texture. CILMP achieves the
best accuracy (97.98%) for this task, with an im-
provement varying between 0.74% and 79.30% (Fig.
18(a)). The minimum accuracy achieved by the pro-
posed method is close to the best, as presented in Fig.
18(b).
CILMP also outperforms the other methods for
task 2, which considers changes in the light inten-
sity. The improvements in the average accuracy pro-
vided by the proposed descriptor are between 0.35%
and 75.78%. We can also notice from Fig. 18(b) that
the minimum accuracy performed by CILMP is very
close to the best minimum.
When the light direction changes (task 3), CILMP
achieves average accuracy of 63.70%, the 3rd best re-
sult for this task, 2.00% smaller than highest accuracy.
This is the only task in which the proposed descriptor
does not outperform the other methods in terms of av-
erage accuracy.
CILMP achieves excellent results for changes in
temperature when natural daylight (97.09%) and LED
lights (95.04%) are considered. High accuracy is also
reported when we compare images acquired under
daylight source to the images acquired under LED
light (93.65%). For these three tasks (tasks 4, 5 and
0
20
40
60
80
100
CILMP
Hist. rgb
Hist. HV
Opp Gabor RGB
OCLBP
Hist. RGB
LBP RGB
Gabor RGB
LCC
LBP Lab
DT-CWT
Granulometry
LBP I1I2I3
Chrom. mom.
LBP L
Hist. L
Gabor L
DT-CWT L
Gist RGB
HoG
Coocc. matr.
Coocc. matr. L
Accuracy (%)
Task 1 - No variations
Figure 9: Average accuracy (%) obtained by CILMP and
other texture descriptors for task 1.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
384

Table 3: Rank of performance of the proposed method and others texture descriptors.
Descriptor Reference Rank
CILMP Our model 1.22
LCC (Cusano et al., 2014; Cusano et al., 2016) 4.22
LBP Lab (Ojala et al., 2002; Cusano et al., 2016) 5.33
OCLBP (Maenpaa and Pietikinen, 2004; Cusano et al., 2016) 5.89
LBP L (Ojala et al., 2002; Cusano et al., 2016) 6.56
LBP RGB (Ojala et al., 2002; Cusano et al., 2016) 6.67
LBP I
1
I
2
I
3
(Ojala et al., 2002; Cusano et al., 2016) 7.11
Gabor RGB (Bianconi et al., 2011; Cusano et al., 2016) 9.11
Gabor L (Bianconi et al., 2011; Cusano et al., 2016) 9.44
Opp Gabor RGB (Jain and Healey, 1998; Cusano et al., 2016) 10.89
Granulometry (Hanbury et al., 2005; Cusano et al., 2016) 11.56
DT-CWT (Bianconi et al., 2011; Cusano et al., 2016) 11.89
Hist. H V (Cusano et al., 2016) 12.56
Hist. rgb (Cusano et al., 2016) 12.78
Gist RGB (Oliva and Torralba, 2001; Cusano et al., 2016) 13.00
Hist. RGB (Cusano et al., 2016) 14.78
Chrom. mom. (Paschos, 2000; Cusano et al., 2016) 15.56
DT-CWT L (Bianconi et al., 2011; Cusano et al., 2016) 16.22
HoG (Junior et al., 2009; Cusano et al., 2016) 17.22
Hist. L (Cusano et al., 2016) 18.33
Coocc. matr. (Cusano et al., 2016) 20.67
Coocc. matr. L (Cusano et al., 2016) 22.00
0
20
40
60
80
100
CILMP
OCLBP
LBP Lab
LBP RGB
Chrom. mom.
Hist. rgb
Gabor RGB
LBP I1I2I3
Granulometry
LCC
Gist RGB
LBP L
Gabor L
HoG
Hist. HV
DT-CWT
Opp Gabor RGB
Hist. RGB
DT-CWT L
Coocc. matr.
Hist. L
Coocc. matr. L
Accuracy (%)
Task 2 - Light intensity
Figure 10: Average accuracy (%) obtained by CILMP and
other texture descriptors for task 2.
6), the proposed descriptor performs the best, out-
performing the 2nd best (LCC descriptor) by large
margins: 8.33% for task 4, 20.79% for task 5 and
15.13% for task 6. Fig. 12-14 and Fig. 18(b) show
that CILMP also reports improvements larger than
18.20%, 24.45% and 25.09%, respectively, in terms
of minimum accuracy.
Tasks 7 and 8 include variations in the temperature
or/and direction of the light sources. We notice that
all the descriptors achieve poor performance in these
tasks. The best accuracy is achieved by CILMP with
0
20
40
60
80
100
OCLBP
Hist. rgb
CILMP
LBP I1I2I3
LBP Lab
LBP RGB
LCC
Chrom. mom.
Gabor RGB
Hist. HV
Opp Gabor RGB
DT-CWT
LBP L
Granulometry
Gist RGB
Hist. RGB
Gabor L
DT-CWT L
HoG
Hist. L
Coocc. matr.
Coocc. matr. L
Accuracy (%)
Task 3 - Light direction
Figure 11: Average accuracy (%) obtained by CILMP and
other texture descriptors for task 3.
42.87% of accuracy when either temperature or direc-
tion varies and 28.72% when both temperature and
direction vary. CILMP also provided the best mini-
mum rate for both tasks. It is clear that accounting for
changes in the direction of the light source is the most
challenging condition as shown by tasks 3, 7 and 8.
CILMP also has a superior performance in the last
task, when the images are taken under multiple illu-
minants and they vary between training and test sam-
ples. The proposed descriptor achieves the best aver-
age accuracy (95.59%) and the best minimum. The
A Robust Descriptor for Color Texture Classification Under Varying Illumination
385

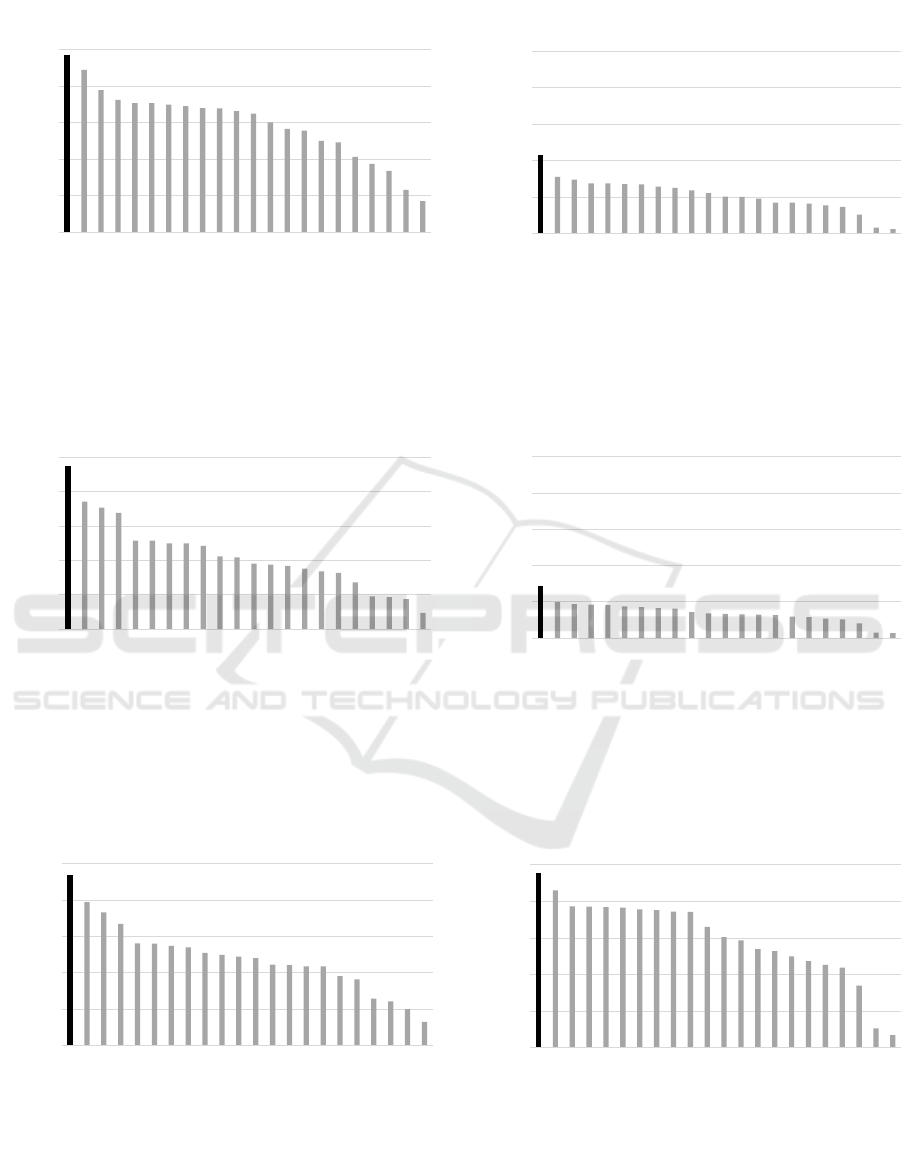
0
20
40
60
80
100
CILMP
LCC
LBP L
LBP RGB
LBP Lab
LBP I1I2I3
Granulometry
Gabor L
OCLBP
Opp Gabor RGB
DT-CWT
Gabor RGB
DT-CWT L
Hist. RGB
Gist RGB
Hist. L
Hist. HV
HoG
Hist. rgb
Chrom. mom.
Coocc. matr.
Coocc. matr. L
Accuracy (%)
Task 4 - Daylight temperature
Figure 12: Average accuracy (%) obtained by CILMP and
other texture descriptors for task 4.
0
20
40
60
80
100
CILMP
LCC
LBP L
Gabor L
Hist. HV
LBP Lab
OCLBP
LBP I1I2I3
LBP RGB
DT-CWT
Opp Gabor RGB
Gabor RGB
Hist. RGB
Gist RGB
HoG
Granulometry
DT-CWT L
Hist. L
Coocc. matr.
Chrom. mom.
Hist. rgb
Coocc. matr. L
Accuracy (%)
Task 5 - LED temperature
Figure 13: Average accuracy (%) obtained by CILMP and
other texture descriptors for task 5.
0
20
40
60
80
100
CILMP
LCC
LBP L
Gabor L
LBP RGB
LBP Lab
LBP I1I2I3
OCLBP
Opp Gabor RGB
DT-CWT
Granulometry
Gabor RGB
Hist. HV
DT-CWT L
Hist. RGB
Gist RGB
Hist. L
HoG
Hist. rgb
Chrom. mom.
Coocc. matr.
Coocc. matr. L
Accuracy (%)
Task 6 - Daylight vs. LED
Figure 14: Average accuracy (%) obtained by CILMP and
other texture descriptors for task 6.
0
20
40
60
80
100
CILMP
LCC
LBP L
Gabor L
LBP Lab
Gabor RGB
LBP I1I2I3
OCLBP
Gist RGB
LBP RGB
Granulometry
Opp Gabor RGB
Hist. rgb
DT-CWT
Chrom. mom.
HoG
Hist. HV
Hist. RGB
DT-CWT L
Hist. L
Coocc. matr.
Coocc. matr. L
Accuracy (%)
Task 7 - Temperature or direction
Figure 15: Average accuracy (%) obtained by CILMP and
other texture descriptors for task 7.
0
20
40
60
80
100
CILMP
LCC
LBP L
LBP I1I2I3
LBP Lab
Gist RGB
OCLBP
Gabor RGB
Gabor L
LBP RGB
Opp Gabor RGB
DT-CWT
DT-CWT L
Granulometry
Hist. rgb
HoG
Hist. HV
Chrom. mom.
Hist. RGB
Hist. L
Coocc. matr.
Coocc. matr. L
Accuracy (%)
Task 8 - Temperature and direction
Figure 16: Average accuracy (%) obtained by CILMP and
other texture descriptors for task 8.
0
20
40
60
80
100
CILMP
LCC
LBP Lab
LBP L
LBP RGB
OCLBP
LBP I1I2I3
Gabor RGB
Gabor L
Granulometry
DT-CWT
Gist RGB
Opp Gabor RGB
Hist. RGB
DT-CWT L
Hist. HV
Hist. L
Hist. rgb
HoG
Chrom. mom.
Coocc. matr.
Coocc. matr. L
Accuracy (%)
Task 9 - Multiple illuminant
Figure 17: Average accuracy (%) obtained by CILMP and
other texture descriptors for task 9 .
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
386

1 2 3 4 5 6 7 8 9
Tasks
-10
0
10
20
30
40
50
60
70
80
90
100
Improvement in average accuracy (%)
(a) Improvement obtained by CILMP in the average
accuracy compared to the other descriptors.
1 2 3 4 5 6 7 8 9
Tasks
-10
0
10
20
30
40
50
60
70
80
90
100
Improvement in minimum accuracy (%)
(b) Improvement obtained by CILMP in the mini-
mum accuracy compared to the other descriptors.
Figure 18: Improvement achieved by CILMP for the nine
tasks.
improvement in the average accuracy varies between
9.86% and 88.73%.
We notice from Fig. 18 that, in general, CILMP
performs a large improvement over the other methods.
The average improvement reached by CILMP is of
32.17% in the average accuracy and 34.49% in the
minimum accuracy.
Finally, considering all the tasks, the rank reported
in Table 3 shows that CILMP outperforms the existing
descriptors. The complexity of CILMP, first in the
rank, is similar to other methods, such as OCLBP and
Opponent Gabor RGB, which have average rank of
5.89 and 10.89, respectively.
5 CONCLUSIONS
In this paper we have introduced a new color tex-
ture descriptor (CILMP) for texture classification un-
der varying illumination. The proposed descriptor ex-
tends the local mapped pattern operator to color tex-
tures by combining color and texture information us-
ing multiresolution analysis. We applied a genetic al-
gorithm to tune the descriptor parameters simultane-
ously.
We performed descriptor evaluation over nine
tasks, which involve different cases of lighting
changes. The results show that combining different
resolutions of neighborhoods increases the classifica-
tion accuracy. The complexity of CILMP is similar
to others methods, and the proposed descriptor out-
performed them for eight tasks and provided the 3rd
best classification rate for the remaining task. CILMP
reported an increase in average accuracy of up to
20.79% compared to the second-best method.
We also highlight that it is hard for all the methods
to maintain high performance when the light source
direction changes, and this is also a limitation of the
proposed model. Thus, in future works, we plan to
investigate how to make the descriptor invariant to
changes in the light source direction, and we plan to
evaluate other color spaces besides RGB to extract
color information from texture.
ACKNOWLEDGEMENTS
The authors would like to thank the Sao Paulo Re-
search Foundation (FAPESP), grant #2015/20812-5.
REFERENCES
Arvis, V., Debain, C., Berducat, M., and Benassi, A. (2004).
Generalization of the cooccurrence matrix for colour
images: application to colour texture classification.
Journal of Image Analysis and Stereology, 23:63–72.
Bianconi, F., Harvey, R., Southam, P., and Fern
´
andez, A.
(2011). Theoretical and experimental comparison of
different approaches for color texture classification.
Journal of Electronic Imaging, 20(4).
Campbell, N. W., Thomas, B. T., and Troscianko, T. (1996).
Segmentation of natural images using self-organising
feature maps. In Proceedings of British Machine Vi-
sion Conference, pages 223–232.
Chan, C. H., Kittler, J., and Messer, K. (2007). Multi-
spectral local binary pattern histogram for component-
based color face verification. In First IEEE Int. Conf.
Biometrics: Theory, Appl. and Systems, pages 1–7.
A Robust Descriptor for Color Texture Classification Under Varying Illumination
387

Cusano, C., Napoletano, P., and Schettini, R. (2013). Il-
luminant invariant descriptors for color texture clas-
sification. In Computational Color Imaging, volume
7786 of LNCS, pages 239–249. Springer.
Cusano, C., Napoletano, P., and Schettini, R. (2014). Com-
bining local binary patterns and local color contrast
for texture classification under varying illumination.
J. Opt. Soc. Am. A, 31(7):1453–1461.
Cusano, C., Napoletano, P., and Schettini, R. (2016). Eval-
uating color texture descriptors under large variations
of controlled lighting conditions. J. Opt. Soc. Am. A,
33(1):17–30.
de Wouwer, G. V., Scheunders, P., Livens, S., and Dyck,
D. V. (1999). Wavelet correlation signatures for
color texture characterization. Pattern Recognition,
32(3):443 – 451.
Drimbarean, A. and Whelan, P. (2001). Experiments in
colour texture analysis. Pattern Recognition Letters,
22(10):1161 – 1167.
Ferraz, C. T., Junior, O. P., and Gonzaga, A. (2014). Feature
description based on center-symmetric local mapped
patterns. In Proceedings of the 29th Annual ACM
Symposium on Applied Computing, pages 39–44.
Gonzalez, R. C. and Woods, R. E. (2008). Digital Image
Processing (3rd Edition). Prentice-Hall, Upper Saddle
River, NJ, USA.
Hanbury, A., Kandaswamy, U., and Adjeroh, D. A. (2005).
Illumination-invariant morphological texture classifi-
cation. In Proceedings of the 7th Int. Symp. Mathe-
matical Morphology, pages 377–386.
Jain, A. and Healey, G. (1998). A multiscale represen-
tation including opponent color features for texture
recognition. IEEE Transactions on Image Processing,
7(1):124–128.
Junior, O. L., Delgado, D., Goncalves, V., and Nunes, U.
(2009). Trainable classifier-fusion schemes: An ap-
plication to pedestrian detection. In 12th Int. IEEE
Conf. Intell. Transp. Syst., pages 1–6.
Kandaswamy, U., Adjeroh, D. A., Schuckers, S., and Han-
bury, A. (2012). Robust color texture features under
varying illumination conditions. IEEE Trans. Syst.,
Man, and Cybern., Part B: Cybernetics, 42(1):58–68.
Maenpaa, T. and Pietikinen, M. (2004). Classification with
color and texture: jointly or separately? Pattern
Recognition, 37(8):1629 – 1640.
Ojala, T., Pietikainen, M., and Maenpaa, T. (2002). Mul-
tiresolution gray-scale and rotation invariant texture
classification with local binary patterns. IEEE Trans.
Pattern Anal. Mach. Intell., 24(7):971–987.
Ojala, T., Pietikinen, M., and Harwood, D. (1996). A com-
parative study of texture measures with classification
based on featured distributions. Pattern Recognition,
29(1):51 – 59.
Oliva, A. and Torralba, A. (2001). Modeling the shape of
the scene: A holistic representation of the spatial en-
velope. Int. J. Comput. Vision, 42(3):145–175.
Palm, C. (2004). Color texture classification by integra-
tive co-occurrence matrices. Pattern Recognition,
37(5):965 – 976.
Palm, C. and Lehmann, T. M. (2002). Classification of color
textures by gabor filtering. MG&V International Jour-
nal, 11(2/3):195–219.
Paschos, G. (2000). Fast color texture recognition using
chromaticity moments. Pattern Recognition Letters,
21(9):837 – 841.
Poirson, A. B. and Wandell, B. A. (1996). Pattern color
separable pathways predict sensitivity to simple col-
ored patterns. Vision Research, 36(4):515 – 526.
Sengur, A. (2008). Wavelet transform and adaptive neuro-
fuzzy inference system for color texture classification.
Expert Systems with Applications, 34(3):2120 – 2128.
Setchell, C. J. and Campbell, N. W. (1999). Using colour
gabor texture features for scene understanding. In 7th
International Conference on Image Processing and its
Applications, volume 1, pages 372–376.
Vadivel, A., Sural, S., and Majumdar, A. K. (2007). An inte-
grated color and intensity co-occurrence matrix. Pat-
tern Recogn. Lett., 28(8):974–983.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
388