Double Auction for Resource Allocation in Cloud Computing
Zhichao Zhao
1
, Fei Chen
2
, T-H. Hubert Chan
1
and Chuan Wu
1
1
The University of Hong Kong, Hong Kong
2
Noah’s Ark Lab, Huawei Technologies, Hong Kong
Keywords:
Cloud Resource Allocation, Double Auction, Truthful Mechanism.
Abstract:
Cloud computing has become more and more popular as more companies choose to deploy their services and
applications to the cloud. Particularly, trading unused cloud resources provides extra profits for companies
with rapidly changing needs. Cloud market enables trading additional resource between buyers and sellers,
where a buyer may have different valuations for different instances of the same resource due to factors such
as geographical location, configuration, etc. In this paper, we study double auctions with non-identical items
for cloud resource allocation, and develop a framework to decompose the design of truthful double auctions.
We propose two auctions based on the framework that achieve: (i) truthfulness; (ii) individual rationality; and
(iii) budget balance. We prove that the social welfare is constant-competitive to the (not necessarily truthful)
optimal auction under certain distributions. We run simulations to investigate the social welfare achieved by
our auctions. We use different probability distributions to capture various scenarios in the real world. Results
show that our mechanisms generally achieve at least half of the optimal social welfare, while one auction
achieves over a 0.9 fraction of the optimal in some circumstances.
1 INTRODUCTION
Motivation. Cloud computing has gained more atten-
tion in recent years (Zaman and Grosu, 2011; Zhang
et al., 2014; Zhao et al., 2014). It enables on-demand
delivery of computing resources such as computation
and data storage via the Internet. Compared to the
traditional approach where enterprises run their own
IT infrastructure, it has the advantage of lower main-
tenance cost and better scalability for both hardware
and software. As an example, Amazon EC2 (Ama-
zon, 2015d) and Google Compute Engine (Google,
2015) both provide resizable compute capacity in the
cloud. Both services provide a wide variety of config-
urations consisting of different CPU capacities, RAM
sizes and storage volumes. Furthermore, they pro-
vide virtual servers in multiple locations with differ-
ent charges, satisfying customers’ need for low net-
work latency worldwide. Cloud customers normally
buy long term contracts to reduce the average cost.
For example, Amazon EC2 reserved instances (Ama-
zon, 2015b) have a much lower price for long period
contracts than short period ones.
However, enterprises’ demand might change
1
This research was partially supported by the Hong
Kong RGC under the grant 17202715.
rapidly, which motivates the need for dynamic real-
location of cloud resources. A user can (1) offer un-
used cloud resource at a lower market price; and (2)
purchase additional cloud resource when the demand
increases. For instance, the aforementioned Ama-
zon EC2 has a marketplace (Amazon, 2015a) that en-
ables second-hand cloud resource trading for reserved
EC2 instances. Another company UCX, the Universal
Compute Xchange, also enables trading of computer
resources (UCX, 2015) that are measured and trans-
acted on UCX.
One issue that remains is how to allocate cloud re-
sources between multiple buyers and sellers to max-
imize resource utilization. As sellers and buyers aim
to maximize their individual utility, it is important to
design truthful mechanisms to deal with both sides.
Objectives. We aim at designing double auctions
with non-identical items for cloud resource allocation,
where both sellers and buyers are agents (bidders) and
a buyer’s valuations on the items may depend on fac-
tors such as geographical distance. We consider the
following properties (Dong et al., 2014):
• Truthfulness: Every agent has no incentive to lie
about its valuation to maximize its own utility.
• Individual rationality: Honest agents always have
non-negative utilities. That is, each buyer pays at
Zhao, Z., Chen, F., Chan, T-H. and Wu, C.
Double Auction for Resource Allocation in Cloud Computing.
DOI: 10.5220/0006145403010308
In Proceedings of the 7th International Conference on Cloud Computing and Services Science (CLOSER 2017), pages 273-280
ISBN: 978-989-758-243-1
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
273

most its bidding price and each seller gets paid at
least its bidding price.
• Budget balance: The party running the auction
has non-negative profit.
• Social Welfare: The auction is targeted to max-
imize the social welfare, which is defined as the
difference between sum of winning buyers’ val-
uations and sum of winning sellers’ valuations.
Intuitively, this means that allocation should be
made to buyers with higher valuations and sell-
ers with lower valuations. The performance ratio
is defined to be the ratio of the social welfare of
the auction to that of an (not necessarily truthful)
optimal auction.
In this paper we assume each agent is either a
buyer or a seller, but not both.
Limitation of Previous Work. To our knowledge,
most previous work that proposes auctions for cloud
computing considers one-sided auctions, where only
the buyers are agents (Zhang et al., 2014; Zhao
et al., 2014). Auctions have also been studied in
spectrum allocation settings. In some of the work
spectrum owners act as the auctioneer (Zheng et al.,
2014; Khaledi and Abouzeid, 2013), hence truthful-
ness of the sellers is not considered. In some of the
work (Zhou and Zheng, 2009; Dong et al., 2014;
Yang et al., 2014), double auctions are considered
and truthfulness of both the sellers and the buyers
are guaranteed. However spectrums are considered
to be identical, which ignores the differences between
items. Researchers do consider heterogeneous dou-
ble auction in spectrum settings recently (Feng et al.,
2012). However it relies heavily on the spectrum con-
flict graph to filter out some of the bids. In (Feng
et al., 2012), buyers are grouped into buyer groups us-
ing the conflict graph and only a single bid is consid-
ered by each group for winner determination. When
applied to auctions in cloud settings its performance
would decrease, due to the fact that cloud resource
cannot be shared simultaneously.
Another drawback of previous work lies in theo-
retical proofs. Some of the work does not have the-
oretical proofs (Feng et al., 2012), hence there is no
guarantee on the social welfare achieved by the auc-
tion. In some other work (Zheng et al., 2014) the
competitive ratio depends on the conflict graph, which
would not be satisfactory in cloud resource reloca-
tion setting. To the best of our knowledge, there is
no known truthful auction that can achieve optimal
social welfare. Hence, we use a different approach
and prove that our auction is constant competitive to
the (possibly untruthful) optimal auction under cer-
tain distributions. Though this is not a guarantee that
our auction works in all cases, it is a good indicator
that it will work in real applications.
Challenges. Most of previous work on double auc-
tion focuses on identical items. When each buyer has
the same valuation for all sellers, one can simply try
to assign a subset of sellers with smallest valuations
to a subset of buyers with largest valuations (Desh-
mukh et al., 2002). The presence of non-identical
items significantly complicates the design of auctions
with required properties. The one-sided VCG auc-
tion returns a maximum matching and allocates items
accordingly. On the other hand, a (possibly untruth-
ful) optimal double auction would indeed find a maxi-
mum weight matching, where valuations of sellers are
subtracted from the edge weights. Hence, one would
expect to find some matching in a truthful double auc-
tion. However, it could be a challenging problem to
analyze truthfulness (and budget balance) of auctions
that make use of bids from both sides at the same time.
To overcome this difficulty, we decompose the double
auction into multiple steps and strictly control the in-
formation used in each step.
Our Approach. One typical approach in designing
truthful auctions is to use VCG type of mechanisms
that are originally devised in the context of one-sided
auction. One useful gadget used in our approach is a
modified version of VCG auction (Fu, 2013). In this
setting there is a reserve price for each buyer, which
is the minimum amount the buyer should pay if cho-
sen. VCG auction with reserve price has also been
used in (Khaledi and Abouzeid, 2013) to determine
the payment. However, in their setting the spectrum
owner acts as the auctioneer, whose truthfulness is not
considered. On the contrary, in our setting the sellers
participate as bidders whose truthfulness needs to be
considered.
To design double auctions for non-identical items,
we introduce a framework consisting of two phases.
In the first phase, we identify a subset of “good” sell-
ers, which we call candidates. We set prices for the
candidates ensuring truthfulness for all the sellers. In
the second phase, we use a truthful one-sided auction
on the buyers whose needs are served by the candi-
dates. To achieve budget balance, we adopt the afore-
mentioned variant of VCG auction where the reserve
price is guaranteed to be at least the prices for candi-
dates.
With this framework we give our double auction.
We use the idea of learning (Balcan et al., 2005).
Particularly, we partition both sellers and buyers into
two subsets A
1
,A
2
and B
1
,B
2
. Then we use A
2
,B
2
to “learn” a good reserve price r
2
and apply it to the
auction between A
1
and B
1
. Similarly we use A
1
,B
1
to
learn another reserve price r
1
and apply it to the auc-
tion between A
2
and B
2
. Our evaluation results show
CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science
274

that the auction have good performance in general.
Our Contribution. We summarize our contributions
in this paper as follows.
• We consider double auctions in cloud resource
allocation setting. We propose a framework for
designing double auctions which decomposes the
task into two phases.
• We design a double auction under the framework
we propose. The auction is proved to satisfy truth-
fulness, individual rationality and budget balance.
• We prove the performance of Auction is constant
competitive to the (possibly untruthful) optimal
auction under certain probability distributions.
• We evaluate auction with probability distribu-
tions that correspond to scenarios in real applica-
tions. Our numerical results show that our auc-
tions achieve good social welfare.
2 RELATED WORK
Truthful auction has been an interesting topic in game
theory. One important result in the literature is VCG
auction (Vickrey, 1961; Clarke, 1971; Groves, 1973).
The auctioneer tries to sell a set of items to agents
(buyers) who have valuations for different outcomes
(all possible assignments). It is proved that VCG is
truthful and maximizes the social welfare, which is
the sum of valuations of buyers.
Maximizing the auctioneer’s profit has also been
considered. For example, in (Fiat et al., 2002) the au-
thors designed an auction that achieves at least
1
4
of
the optimal profit. They also considered a different
type of auction, cancellable auction, where the auc-
tioneer cancels the auction if the profit is smaller than
some predetermined value.
One-sided auctions have been extensively used
for cloud provider to determine the allocation of re-
sources. For example, (Zhang et al., 2014; Zaman
and Grosu, 2011; Zhao et al., 2014) studied auctions
for resource allocation problems in cloud computing
settings.
Double auctions with identical items have also
been considered. A third party (instead of the seller)
acts as the auctioneer who, in a high level, trades
with sellers and buyers based on bids from both sides.
Under this setting, McAfee’s mechanism (McAfee,
1992) is proved to be truthful, individual rational and
budget balanced. In (Deshmukh et al., 2002) a truth-
ful double auction was given that aims to maximize
the auctioneer’s profit.
Auctions have been considered for spectrum allo-
cation. In (Zheng et al., 2014; Khaledi and Abouzeid,
2013), the spectrum owners act as the auctioneer and
trade with the buyers. In (Zheng et al., 2014), the
competitive ratio is shown to be Ω(
1
m·∆
max
), where
∆
max
is the max degree of the conflict graph and m is
the number of items. Double auctions have also been
studied in spectrum allocation. In (Zhou and Zheng,
2009; Yang et al., 2014; Dong et al., 2014; Feng et al.,
2012), double auctions are applied to spectrum allo-
cation, where spectrum interference is taken into con-
sideration to maximize spectrum utilization.
3 PRELIMINARIES
3.1 The Problem Model
We consider a sealed-bid double auction with non-
identical items for cloud resource allocation. A seller
is a cloud service provider with one unit of resource.
A buyer is a user who is willing to buy one unit
of resource. For example, in the above mentioned
Amazon EC2 Reserved Instance Marketplace (Ama-
zon, 2015a), customers with redundant cloud EC2 in-
stances are willing to sell them for profit. They act
as sellers in our settings. Due to increasing needs,
other companies or individuals may want to expand
their cloud resource capabilities. They act as buyer
and trade with the sellers under the help of an auc-
tioneer.
Let A be the set of sellers and let B be the set
of buyers. Let n := |A| and m := |B| be the number
of sellers and buyers, respectively. Each seller i has
a valuation v
i
≥ 0 for its resource, the lowest price
at which it would still sell his resource. Each buyer
j has a valuation w
i, j
≥ 0 for the resource provided
by seller i, the highest price at which it would still
buy the resource from seller i. We note that the re-
sources from the sellers are essentially non-identical
items in the auction as w
i, j
and w
i
0
, j
can be unequal
when i 6= i
0
. This setting captures practical scenarios
where each user has different preferences on the ser-
vice providers. For instance, when a user is seeking
a server to host a website, the valuation could depend
on network latency, server capacity and etc.
We introduce some useful notations for double
auction. We shall use agent to refer to either a seller
or a buyer. Agents submit bids to an auction, where
the bids may not be the same as the true valuations.
In particular, a seller i submits
b
v
i
, and a buyer j sub-
mits
b
w
i
0
, j
for all sellers i
0
. Let
b
v := (
b
v
i
)
i∈A
and
b
w :=
(
b
w
i, j
)
(i, j)∈A×B
. The auction decides (i) an allocation
x : A × B → {0, 1}, where x
i, j
indicates whether seller
i is allocated to buyer j; and (ii) payment p
s
: A → R
+
to sellers and payment p
b
: B → R
+
from buyers. Ob-
serve that the allocation x, payment p
s
and p
b
are
Double Auction for Resource Allocation in Cloud Computing
275

functions of
b
v and
b
w. A valid allocation satisfies the
following properties:
•
∑
j∈B
x
i, j
≤ 1 for all i;
•
∑
i∈A
x
i, j
≤ 1 for all j.
Essentially, the inequalities guarantee that an item is
assigned to at most one buyer and a buyer can get
at most one item. Define x
s
i
:=
∑
j∈B
x
i, j
and x
b
j
:=
∑
i∈A
x
i, j
. A seller i is a winner if x
s
i
= 1, and a buyer j
is a winner if x
b
j
= 1. We require that p
s
i
= 0 if x
s
i
= 0
and that p
b
j
= 0 if x
b
j
= 0; in other words, the payment
is zero whenever the involved agent is not a winner.
We call the amount
∑
j∈B
p
b
j
−
∑
i∈A
p
s
i
the auctioneer’s
profit. The social welfare of the auction is defined as
S :=
∑
i∈A, j∈B
x
i, j
· w
i, j
−
∑
i∈A
x
s
i
· v
i
.
Let G be the complete bipartite graph between
sellers A and buyers B, where edge {i, j} between
seller i and buyer j has a weight w
i, j
−v
i
. Then, an al-
location can be represented by a matching in G. For a
matching M, let w(M) be the sum of weights of edges
in M. We say an agent x is covered in M if there exists
agent y such that {x,y} ∈ M. When the allocation is
represented by M, the auction achieves social welfare
S = w(M).
The utility for seller i is defined as u
s
i
:= p
s
i
−x
s
i
·v
i
.
The utility for buyer j is defined as u
b
j
:=
∑
i
x
i, j
·w
i, j
−
p
b
j
. Note that x
s
i
= 0 implies u
s
i
= 0 and that x
b
i
= 0
implies u
b
i
= 0. Let u
s
:= (u
s
i
)
i∈A
and u
b
:= (u
b
j
)
j∈B
.
Then u
s
and u
b
are functions of
b
v and
b
w. Also note
that in the double auction agents submit the bids to
maximize their individual utilities.
We now define some economic properties that
are investigated in this paper. For a vector V :=
(V
1
,. ..,V
n
), let (V
−i
,
b
V
i
) be the vector obtained from
V by replacing V
i
with
b
V
i
.
Definition 3.1 (Truthfulness). An auction is truth-
ful if for any v and w, the utilities for agents are
such that u
s
i
(v,w) ≥ u
s
i
((v
−i
,
b
v
i
),w) and u
b
j
(v,w) ≥
u
b
j
(v,(w
−(i, j)
,
b
w
i, j
)) for all i ∈ A, j ∈ B,
b
v
i
and
b
w
i, j
.
Definition 3.2 (Individual Rationality). An auction
achieves individual rationality if the utilities for
agents are such that u
s
i
≥ 0 for all i ∈ A and u
b
j
≥ 0
for all j ∈ B.
Definition 3.3 (Budget Balance). An auction
achieves budget balance if the auctioneer’s profit is
non-negative, i.e.,
∑
j∈B
p
b
j
−
∑
i∈A
p
s
i
≥ 0.
Our target is to design double auctions satisfy-
ing truthfulness, individual rationality and budget bal-
ance, with the goal to maximize the social welfare S.
Since the auctions designed in this paper are truthful,
we shall use v and w to denote the bids submitted by
agents.
3.2 One-sided Auction
We describe the one-sided auction setting that is gen-
eral enough for our use in this paper. There is a set
Y of m agents and a set Z of non-identical items.
There is also a collection T of possible outcomes,
each of which specifies an allocation of the items
among the agents. An agent j ∈ Y has a valuation
w
j
(T ) for outcome T ∈ T . Given bids from the
agents, an auction determines an outcome T and pay-
ment p on the agents, where the charge for agent j
is p
j
(T ). We say an agent is a winner in an out-
come T if it is allocated a positive number of items,
and the set W(T ) of winners is the winning set of T .
Each agent j aims to maximize its utility, which is
u
j
(T ) := w
j
(T )− p
j
(T ) if j ∈W (T ) and 0 otherwise.
If an auction returns an outcome T, then it achieves
social welfare
∑
j∈W(T )
w
j
(T ).
4 OUR SOLUTIONS
A natural idea to design a double auction for non-
identical items would be to find some maximum
matching to optimize the social welfare. Taking sell-
ers’ valuations into consideration, we would construct
some maximum weight matching with edge weights
w
0
where w
0
i, j
= w
i, j
−v
i
for seller i and buyer j. How-
ever this procedure is not budget balanced. Indeed
it is a challenging task to prove both budget balance
and truthfulness when we make use of bids from both
sellers and buyers at the same time (such as setting
w
0
i, j
= w
i, j
− v
i
). To overcome this difficulty, we di-
vide the interaction between sellers and buyers into
several steps, while restricting the information used
in each step. We introduce a framework consisting
of two phases extending the approach for identical
items (Dong et al., 2014).
(i) In the first phase, we construct a subset A
0
of sell-
ers, called candidates, from which winners are fi-
nally selected. We set reserve prices p for agents
in A
0
such that each seller in A
0
has non-negative
utility and no seller has the motivation to be dis-
honest, even if some candidates are not finally se-
lected. We specify a subset B
0
of buyers to serve
each candidate (which can be different), guaran-
teeing that the subset serving a candidate does not
influence its selection and reserve price.
(ii) In the second phase, we run a one-sided auction,
which is truthful and individual rational, on B
0
to
be served by the sellers A
0
.
Note that only a subset of sellers are considered to
be candidates. The intuition is that some seller can
be too expensive to be allocated to any buyers. More
CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science
276

importantly, the payment for the candidates should be
no smaller than the bid of any candidate, and hence an
expensive candidate would make it difficult to achieve
budget balance. Also only a subset of buyers is used
to serve a candidate since the information from other
buyers may be used in its selection and reserve price.
Throughout the procedure no seller has the motivation
to be dishonest as the input to the one-sided auction
is independent of the bids from A
0
, and no buyer has
the motivation to be dishonest as a buyer is either dis-
carded (if not in B
0
) or served by a truthful auction.
Individual rationality and budget balance can also be
easily checked.
4.1 VCG Auction with Reserve Price
Recall that the VCG auction (Vickrey, 1961; Clarke,
1971; Groves, 1973) is a one-sided auction that se-
lects the outcome T maximizing the social welfare.
We use p
j
(T ) to denote its charge to the selected
agents. The VCG auction with reserve price (VCG-
RP) (Fu, 2013) sets a reserve price r
j
for each agent,
hence charging j at price max{p
j
(T ),r
j
}. Assum-
ing that the sellers are always honest (i.e., sellers
are not agents), then the double auction reduces to a
one-sided auction, where all possible comes T is the
matchings between A and B. We adopt VCG-RP to
calculate the allocation as described below. We use
M to denote the returned matching and use p
b
{ j}
to
denote the charges.
When we invoke VCG-RP we always guarantee
the payments to the sellers p
s
{i}
’s are the same and
that we will use a higher reserve price r so that we
can achieve budget balance.
Proposition 4.1 ((Fu, 2013)). The VCG-RP auction
is truthful.
4.2 Our Double Auction
When the sellers are heterogeneous, a seller i may be
more favorable than i
0
even if v
i
> v
i
0
, when a large
portion of buyers have higher valuations for i than for
i
0
. In the auction, we exploit the valuations from both
sellers and buyers to determine the candidates (from
sellers).
We apply the idea of learning from (Balcan et al.,
2005). We partition both sellers and buyers into two
subsets, denoted by A
1
,A
2
and B
1
,B
2
. Then we use
A
1
,B
1
to calculate an optimal matching M
1
, and use
A
2
,B
2
to calculate an optimal matching M
2
. Intu-
itively, if the partitioning is done randomly the two
matchings should be close. Hence whatever learned
from one side can be applied to the other in winner de-
termination. We learn two thresholds p
1
and p
2
from
VCG-RP (A, B, w, r).
Input: Set A of sellers, set B of buyers with
bids w, reserve price r
Remove all edges {i, j} with w
i, j
< r from the
complete bipartite graph between A and B.
Let G be the resulting graph.
Compute a maximum weight matching M
∗
of
G.
foreach j ∈ B covered in M
∗
do
Suppose {i, j} ∈ M
∗
. Let G
0
be the graph
obtained from G with j and edges incident
to j removed.
Compute a maximum weight matching M
0
of G
0
.
Set p
j
:= max{w(M
0
) − (w(M
∗
) − w
i, j
),r}.
end
foreach j ∈ B not covered in M
∗
do
Set p
j
:= 0
end
Output: M
∗
and (p
j
)
j∈B
M
1
and M
2
. Concretely, this can be the average of
all seller bids or the maximum of all seller bids. Then
we use VCG-RP with reserve price p
1
between A
2
and
B
2
, ignoring sellers above p
1
. Similarly, we use VCG-
RP with reserve price p
2
between A
1
and B
1
, ignoring
sellers above p
2
. Note that in determining p
1
, p
2
we
can use various policies, e.g., maximum and average.
They both use similar ideas in guaranteeing truthful-
ness, individual rationality and budget-balance. We
focus on using average in our proof for simplicity. In
our simulations, we evaluate both variants.
We prove that this auction satisfies truthfulness,
individual rationality and budget-balance. We also
show that our auction is efficient on some distribu-
tion. Precisely, let D be the uniform distribution
over [a,b] and D + ∆ be the uniform distribution over
[a + ∆,b + ∆]. We consider sampling seller side valu-
ations from D and buyer side valuations from D + ∆.
We prove our auction is constant competitive under
this distribution for any a,b, ∆ ≥ 0.
Theorem 4.1. Auction is truthful, individual rational
and budget balanced.
The details of the proof are omitted due to space
limit. The proof for individual rationality and budget
balance is straight forward. For truthfulness, the idea
is to show no participant can benefit from reporting a
dishonest value.
Theorem 4.2 (Constant Approximation for Social
Welfare). Suppose the parameters a,b, ∆ ≥ 0 are
fixed. Moreover, there are n sellers whose valuations
are sampled independently from D := [a,b] uniformly
at random. Furthermore, there are m ≥ 2n buyers
Double Auction for Resource Allocation in Cloud Computing
277

Auction (A, B, v, w).
Input: Sellers A = {1,... ,n} with bids v,
buyers B = {1,... ,m} with bids w
Randomly partition A (B) into equally sized
subsets, denoted by A
1
and A
2
(B
1
and B
2
).
foreach k ∈ {1,2} do
Calculate a maximum weight matching M
k
between A
3−k
and B
3−k
, using w
i, j
− v
i
as
edge weights.
r
k
← Avg(v
i
: i ∈ M
k
) OR max(v
i
: i ∈ M
k
)
A
0
k
← {i ∈ A
k
: v
i
≤ r
k
}.
Run (M, p
0
) ←VCG-RP (A
0
k
,B
k
,w,r
k
)
Allocation:
foreach i ∈ A
k
and j ∈ B
k
do
Set x
i, j
:= 1 if {i, j} ∈ M and x
i, j
:= 0
otherwise.
end
Payment:
foreach i ∈ A
k
do
Set p
s
i
:= r
k
if i is covered in M, and
p
s
i
:= 0 otherwise.
end
foreach j ∈ B
k
do
Set p
b
j
:= p
0
j
.
end
end
whose valuations for each seller are sampled inde-
pendently from D + ∆ := [a + ∆, b + ∆] uniformly at
random. Then, for all 0 < ε ≤
1
8
, with probability
at least 1 − 2n exp(−
1
48
ε
2
n), Auction produces an as-
signment that achieves
1−4ε
8
fraction of the optimal
social welfare.
The proof is omitted due to space limit.
5 PERFORMANCE EVALUATION
In this section we simulate the proposed auctions. We
compare our algorithms to TAHES from (Feng et al.,
2012). Note that TAHES was originally designed for
spectrum auction, and we adapt it to our setting by
setting the conflict graph to be a complete graph. We
generate instances with valuations of sellers and buy-
ers taken from various probability distributions, and
study the impact on the social welfare achieved by
different auctions.
5.1 Simulation Setup
Note that the design goal of our algorithm is to max-
imize the social welfare S =
∑
i, j
x
i, j
· w
i, j
−
∑
i
x
s
i
· v
i
.
Since it is unclear what is the optimal truthful auc-
tion, we compare the social welfare to the optimal
(possibly untruthful) auction, which will output the
maximal weighted matching between sellers A and
buyers B, weighted by w
0
i, j
= w
i, j
− v
i
. Then, the
performance ratio of an auction A is defined to be
E[S(A )]/S
∗
, where S
∗
is the maximal matching and
S(A) is the social welfare by the auction.
We employ several distributions (for valuations of
sellers and buyers) to simulate different situations in
the real world. We use [α,β] to denote the (real num-
ber) interval from α to β. We use [α,β; δ] to denote
the values from α to β with step size δ.
(a) Uniform Distribution. We test our auctions in
a distribution similar to that in Theorem 4.2. Let
n := |A| and m := |B| be the number of sellers and
buyers respectively. There are four parameters α
s
,β
s
for sellers and α
b
,β
b
for buyers. For each seller i ∈ A,
we sample v
i
uniformly from [α
s
,β
s
]. For each seller-
buyer pair {i, j} ∈ A × B, we sample w
i, j
uniformly
from [α
b
,β
b
].
We choose different combinations of parameters
to study their influences. The parameters n and m
control the number of participants. We fix n, then ad-
just the number of buyers m to see the influence of
the ratio of sellers and buyers. Note the two inter-
vals [α
s
,β
s
] and [α
b
,β
b
] control how sellers’ and buy-
ers’ valuations diverge. We fix the sellers’ valuations
[α
s
,β
s
] and change the buyers’ valuation distributions
to study how different distributions affects the perfor-
mance.
(b) Geo-related Distribution. In a real world sce-
nario where companies rent cloud infrastructure to
host websites as buyers, they typically choose a server
location near their target clients. This is because the
network latency is the most influential factor in such
applications and a nearby server normally provides a
lower latency network. We simulate our auction using
Amazon EC2 as an example cloud provider consider-
ing the case when network latency is a critical issue.
We obtain the statistics on network latencies be-
tween cities from (Reinheimer and Roberts, 2015).
Then we combine it with the locations of Amazon
EC2 servers from (Amazon, 2015c) to estimate the
network latency from Amazon servers. In order to
simulate a real world sellers’ and buyers’ geograph-
ical distribution, we sample seller locations from
Amazon availability zones and buyer locations from
the checkin locations from Brightkite in (Amazon,
2015c). We assume that a buyer prefers service with
lower latency and its valuation decreases linearly with
the network latency. We use real Amazon selling
price (using t2.large) as the sellers’ bidding price.
While for buyers’ bidding price we use the formula
CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science
278

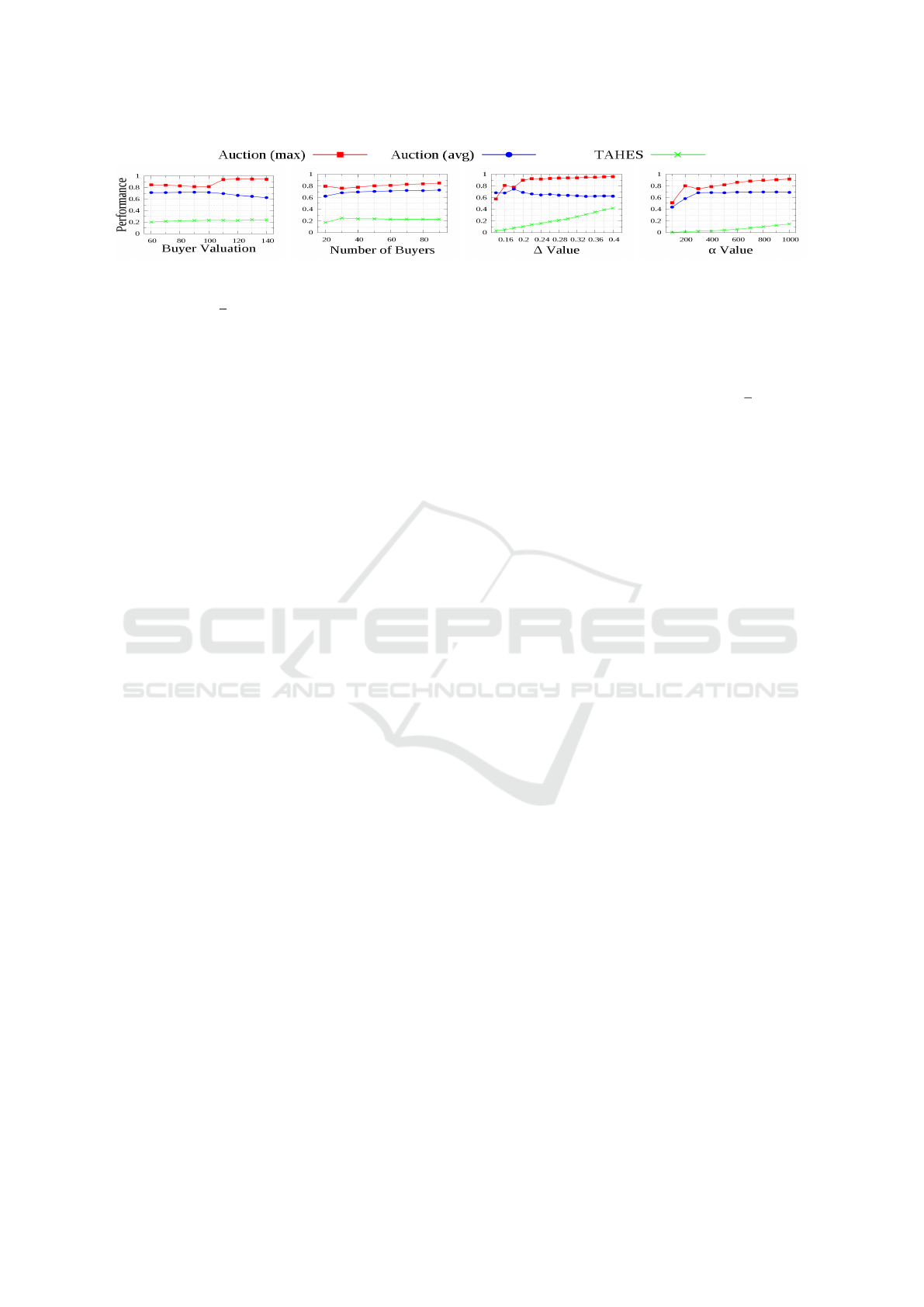
(a) (b) (c) (d)
Figure 1: Performances under different distributions.
w
i, j
= max{∆ −
1
α
· d
i, j
,0}, where d
i, j
is the network
latency from seller (server) i to buyer j.
5.2 Evaluation
In this section, we evaluate the performance of the
auctions under uniform and geo-related distributions.
We run both auctions on the distributions to see how
the parameters affect the performance ratio. We con-
sider two variants of Auction, namely Auction (max)
and Auction (avg). The difference is Auction (max)
uses the maximum of seller bids as the reserve price,
whereas the other one uses the average of seller bids.
(1) Impact of Valuations under Uniform Distri-
bution. We fix the sellers’ sampling interval to be
[0,100] and vary the buyers’ sampling interval. In
particular, for each β
b
∈ [60,140; 10], the valuation
for each buyer is sampled uniformly from [0, β
b
]. The
performance ratio is shown in Figure 1a, where the
x-axis shows the choice of β
b
.
Our auctions outperforms TAHES. Recall that
β
s
= 100, and thus when β
b
reaches 100 the sellers
and buyers have about the same valuations on aver-
age. When β
b
goes above 100, the performance ratio
of Auction (max) increases while that of Auction (avg)
decreases slightly. The reason of this phenomenon
is that Auction (avg) throws away many of the sell-
ers, and it damages the performance when buyers’
values are high enough. On the other hand, Auction
(max) can dynamically adjust the number sellers to
be thrown, resulting better performance.
(2) Impact of the Number of Agents under Uni-
form Distribution. We fix the number of sellers to
be 30 and vary the number of buyers in [20,90;10].
Then, we sample both the sellers’ and buyers’ val-
uations uniformly from [0,100]. This setting corre-
sponds to a market where there are more buyers than
sellers each with a similar valuation for the resources
to be traded. The performance ratio is shown in Fig-
ure 1b.
The performances of both variant of Auction in-
creases slightly with the number of buyers. Auc-
tion (max) has the highest performance ratio which
is slightly over 0.8. All our auctions have a relatively
high performance compared to TAHES. This is likely
because we can take advantage of multiple bids from
a single buyer compared to the TAHES auction.
(3) Impact of Valuations under Geo-related Dis-
tribution. Next, we study the impact of valuations
sampled under geo-related distribution on the perfor-
mance ratio. Recall that the valuation of buyer j for
seller i is calculated as w
i, j
= max{∆ −
1
α
· d
i, j
,0}.
We simulate a market with more buyers than sellers.
Specifically, we fix the number of sellers and buyers
to be 30 and 60 respectively and focus on the impact
of the choice of ∆ and α. Note that a typical Amazon
EC2 price (using t2.large) would be 0.1 USD to 0.2
USD per hour, and network latency varies from 5 ms
to 500 ms. Hence a reasonable choice of ∆ would be
from 0.2 to 0.4, and α from 100 to 1000.
First, we fix α to be 800 and investigate the effect
of the choice of ∆. It can be seen that with a larger ∆,
buyers tend to have relatively higher valuations. We
vary the ∆ in [0.14, 0.4;0.02]. The performance ratio
is shown in Figure 1c. It can be seen that with small
∆, all auctions benefits from higher ∆ values. After
∆ reaches 0.2, Auction (avg) decreases slightly. How-
ever the ratio of Auction (max) keeps increasing and
reaches 0.95. This is because Auction (max) can ad-
just its threshold automatically. Next we fix ∆ = 0.2.
Note that the weigh of network latency is especially
important in such circumstances. We vary the α value
from [100, 1000; 100]. Note that α adjusts the weight
of network latency. With a lower α the network la-
tency becomes more important. The performance ra-
tio is shown in Figure 1d.
From the numerical result, we can see that with
the increase of α the performance of all auctions in-
creases. This is likely because with larger α the buy-
ers have higher valuations, hence more edges can be
matched in the auctions. Auction (avg) reaches its
limit when the ratio reaches 0.7. However Auction
(max) keeps increasing as α increases and remains the
best auction.
6 CONCLUSION
In this paper we have developed techniques for the
design of truthful double auctions with non-identical
items for cloud resource allocation. We propose a
framework in which an auction can “learn” a good
Double Auction for Resource Allocation in Cloud Computing
279

subset of agents and appropriate payment policy. Un-
der certain distribution, we prove theoretically that
our auction achieves at least
1
8
of the optimal social
welfare. Then our auctions are evaluated on differ-
ent probabilistic distributions. Particularly, we use
data on network latencies between cities together with
Amazon EC2 server locations to simulate real world
situations where a buyer’s valuations depend on its
latency to the sellers (items). Our performance eval-
uation shows that the auctions achieve performance
ratios at least 0.5 in most cases, and Auction (max)
reaches a ratio of over 0.9 in certain cases.
REFERENCES
Amazon (2015a). Amazon EC2 reserved instance mar-
ketplace. http://aws.amazon.com/ec2/purchasing-
options/reserved-instances/marketplace.
Amazon (2015b). Amazon EC2 reserved in-
stances. http://aws.amazon.com/ec2/purchasing-
options/reserved-instances.
Amazon (2015c). AWS global infrastructure.
https://aws.amazon.com/about-aws/global-
infrastructure.
Amazon (2015d). Elastic compute cloud (EC2) cloud server
& hosting AWS. https://aws.amazon.com/ec2.
Balcan, M., Blum, A., Hartline, J. D., and Mansour, Y.
(2005). Mechanism design via machine learning.
In 46th Annual IEEE Symposium on Foundations of
Computer Science (FOCS 2005), 23-25 October 2005,
Pittsburgh, PA, USA, Proceedings, pages 605–614.
IEEE Computer Society.
Clarke, E. H. (1971). Multipart pricing of public goods.
Public choice, 11(1):17–33.
Deshmukh, K., Goldberg, A. V., Hartline, J. D., and Kar-
lin, A. R. (2002). Truthful and competitive double
auctions. In Algorithms - ESA 2002, 10th Annual
European Symposium, Rome, Italy, September 17-21,
2002, Proceedings, pages 361–373.
Dong, W., Rallapalli, S., Qiu, L., Ramakrishnan, K. K., and
Zhang, Y. (2014). Double auctions for dynamic spec-
trum allocation. In 2014 IEEE Conference on Com-
puter Communications, INFOCOM 2014, Toronto,
Canada, April 27 - May 2, 2014, pages 709–717.
Feng, X., Chen, Y., Zhang, J., Zhang, Q., and Li, B.
(2012). TAHES: truthful double auction for hetero-
geneous spectrums. In Greenberg, A. G. and Sohraby,
K., editors, Proceedings of the IEEE INFOCOM 2012,
Orlando, FL, USA, March 25-30, 2012, pages 3076–
3080. IEEE.
Fiat, A., Goldberg, A. V., Hartline, J. D., and Karlin, A. R.
(2002). Competitive generalized auctions. In Pro-
ceedings on 34th Annual ACM Symposium on Theory
of Computing, May 19-21, 2002, Montr
´
eal, Qu
´
ebec,
Canada, pages 72–81.
Fu, H. (2013). VCG auctions with reserve prices: Lazy or
eager. EC, 2013 Proceedings ACM.
Google (2015). Compute engine - google cloud platform.
https://cloud.google.com/compute.
Groves, T. (1973). Incentives in teams. Econometrica:
Journal of the Econometric Society, pages 617–631.
Khaledi, M. and Abouzeid, A. A. (2013). A reserve
price auction for spectrum sharing with heterogeneous
channels. In 22nd International Conference on Com-
puter Communication and Networks, ICCCN 2013,
Nassau, Bahamas, July 30 - Aug. 2, 2013, pages 1–
7. IEEE.
McAfee, R. (1992). A dominant strategy double auction.
Journal of Economic Theory, 56(2):434 – 450.
Reinheimer, P. and Roberts, W. (2015). Global ping statis-
tics. https://wondernetwork.com/pings.
UCX (2015). UCX expands trade of cloud (IaaS) on global
exchange. http://ucxchange.com/ucx-expands-trade-
of-cloud-iaas-on-global-exchange.
Vickrey, W. (1961). Counterspeculation, auctions, and
competitive sealed tenders. The Journal of finance,
16(1):8–37.
Yang, D., Zhang, X., and Xue, G. (2014). PROMISE: A
framework for truthful and profit maximizing spec-
trum double auctions. In 2014 IEEE Conference
on Computer Communications, INFOCOM 2014,
Toronto, Canada, April 27 - May 2, 2014, pages 109–
117.
Zaman, S. and Grosu, D. (2011). Combinatorial auction-
based dynamic VM provisioning and allocation in
clouds. In IEEE 3rd International Conference on
Cloud Computing Technology and Science, Cloud-
Com 2011, Athens, Greece, November 29 - December
1, 2011, pages 107–114.
Zhang, L., Li, Z., and Wu, C. (2014). Dynamic resource
provisioning in cloud computing: A randomized auc-
tion approach. In 2014 IEEE Conference on Computer
Communications, INFOCOM 2014, Toronto, Canada,
April 27 - May 2, 2014, pages 433–441.
Zhao, J., Li, H., Wu, C., Li, Z., Zhang, Z., and Lau, F. C. M.
(2014). Dynamic pricing and profit maximization for
the cloud with geo-distributed data centers. In 2014
IEEE Conference on Computer Communications, IN-
FOCOM 2014, Toronto, Canada, April 27 - May 2,
2014, pages 118–126.
Zheng, Z., Wu, F., Tang, S., and Chen, G. (2014). Unknown
combinatorial auction mechanisms for heterogeneous
spectrum redistribution. In Wu, J., Cheng, X., Li, X.,
and Sarkar, S., editors, The Fifteenth ACM Interna-
tional Symposium on Mobile Ad Hoc Networking and
Computing, MobiHoc’14, Philadelphia, PA, USA, Au-
gust 11-14, 2014, pages 3–12. ACM.
Zhou, X. and Zheng, H. (2009). TRUST: A general frame-
work for truthful double spectrum auctions. In IN-
FOCOM 2009. 28th IEEE International Conference
on Computer Communications, Joint Conference of
the IEEE Computer and Communications Societies,
19-25 April 2009, Rio de Janeiro, Brazil, pages 999–
1007.
CLOSER 2017 - 7th International Conference on Cloud Computing and Services Science
280