
Flow Parameters Derived from Impedance Pneumography after
Nonlinear Calibration based on Neural Networks
Marcel Mły
´
nczak
1
and Gerard Cybulski
1,2
1
Institute of Metrology and Biomedical Engineering, Faculty of Mechatronics, Warsaw University of Technology,
Boboli 8, 02-525, Warsaw, Poland
2
Department of Applied Physiology, Mossakowski Medical Research Centre, Polish Academy of Sciences,
Pawinskiego 5, 02-106 Warsaw, Poland
Keywords:
Ambulatory Monitoring, Impedance Pneumography, Calibration, Neural Networks.
Abstract:
Impedance pneumography (IP) is mainly used as a noninvasive method to measure respiratory rate, tidal
volume or minute ventilation. It could also register flow-related signals, after differentiation, from spirometry-
based forced vital capacity maneuvers or ambulatory-based signals reflecting flow values during natural activ-
ity. The aim of this paper is to assess the possibility of improving the accuracy of flow parameters calculated
by IP, by using nonlinear neural network correction (as opposed to simple linear calibration), and to evaluate
the impact of various calibration procedures and neural network configurations. Ten students carried out fixed
static breathing sequences, for both calibration and testing. A reference pneumotachometer and the Pneumoni-
tor 2 were used. The validation of calculating peak and mean flow value during each inspiration and expiration
was considered. A mean accuracy of 80% was achieved for a separate neural network with two hidden layers
with 10 neurons in each layer, trained individually for each subject and body position, using the data from the
longest, fixed calibration procedure. Simple linear modeling achieved only 72.5%.
1 INTRODUCTION
1.1 Problem and Related Works
Respiratory activity appears to be an important fac-
tor in physiological analyses, based on measurements
carried out both in the laboratory and under ambu-
latory conditions. Such studies need to extend be-
yond single spirometry evaluation, gathering the data
produced during natural functioning of the subjects
(Poupard et al., 2008; Koivumaki et al., 2012).
Impedance pneumography (IP) could be used to
measure ventilation non-invasively, even for long-
term monitoring, impacting the subject’s natural ac-
tivity during registration less than when using face
mask (Houtveen et al., 2006; Seppa et al., 2010;
Mły
´
nczak et al., 2015b).
Many studies have used impedance pneumog-
raphy to measure respiratory rate or tidal volume
(from which one could estimate minute ventilation)
(Houtveen et al., 2006; Seppa et al., 2010; Seppa
et al., 2011; Mły
´
nczak et al., 2015b; Mły
´
nczak et al.,
2015a; Gracia et al., 2015; Ansari et al., 2016). Those
three parameters are the main ones for respiratory
activity under unconstrained conditions, e.g., during
sleep (Roebuck et al., 2013; Seppa et al., 2016).
Impedance pneumography provides a volume-
related signal. However, it could also be used to mea-
sure flow values after differentiation. This could be
used to assess spirometry-based parameters, recorded
during forced vital capacity (FVC) maneuver (Seppa
et al., 2013b), or to enhance the information derived
from ambulatory impedance measurement. In the sec-
ond condition, peak and mean flow during each inspi-
ration and expiration could be calculated.
In a recent work, we assessed the accuracy and re-
producibility of linear calibration coefficients on es-
timation of tidal volume from impedance pneumog-
raphy (Mły
´
nczak et al., 2015a). Our analysis found
greater error in the calculated flow values than in
the calculated tidal volumes, compared to reference
pneumotachometry (PNT ). In most cases, the results
were underestimated, particularly for greater flow val-
ues. This could imply that linear calibration of the
impedance signal cannot faithfully reflect changes
in flow signal dynamics. Therefore, the assumption
made during volume calculations, that the best fitting
could be provided by linear regression modeling, ap-
peared to be wrong.
70
MÅ
´
CyÅ
ˇ
Dczak M. and Cybulski G.
Flow Parameters Derived from Impedance Pneumography after Nonlinear Calibration based on Neural Networks.
DOI: 10.5220/0006146800700077
In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 70-77
ISBN: 978-989-758-212-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

One of the possibilities to deal with this prob-
lem are hardware solutions, e.g., applying more so-
phisticated multifrequency application current signals
(multi-sinusoidal or binary one, with specific peaks of
frequencies) (Ojarand et al., 2013; Min and Paavle,
2013).
The other possibility may include an implemen-
tation of the more advanced signal processing of the
IP signal, including the way of handling the cardiac
component or the calibration strategy (the sequence
of differentiation and modeling in relation to the ref-
erence data).
Further, nonlinear corrections might be applied in
order to handle better signal dynamics. Artificial neu-
ral networks have been already used in other scientific
disciplines for such issue (Lai et al., 2015; Li et al.,
2015). They are also increasingly used in the analysis
of respiratory system activity in general (Jafari et al.,
2010; Lee et al., 2012; Baemani et al., 2008).
1.2 Objectives
The main objective of this paper is to assess the pos-
sibility of improving the accuracy of flow parame-
ters calculated by impedance pneumography, by us-
ing nonlinear neural-network correction (as opposed
to the simple linear model), based on flow-related sig-
nals.
The associated goals are to evaluate, what calibra-
tion procedure could provide the best data, leading
to the best accuracy in subsequent measurement anal-
ysis, and what neural network structure and order of
corrections is the most suitable for analysis of the flow
parameters.
2 METHODS
2.1 Subjects & Devices
Basic information about the study participants is pro-
vided in Table 1. All were generally healthy male stu-
dents (without any respiratory disease reported) and
were informed about the aim of the measurements and
gave written consent.
Table 1: Information about the study participants.
Minimum Mean Maximum
Weight [kg] 65.0 77.4 100.0
Height [cm] 171.0 179.3 187.0
BMI 20.75 24.14 33.41
Age 19 23 27
We used our impedance pneumography prototype,
Pneumonitor 2, to measure IP signals. We used the
tetrapolar method, in which two electrodes apply a
current signal and the remaining two measure volt-
age, which is related to the electrical impedance. The
configuration proposed by Seppa et al. was utilized
(Seppa et al., 2013a): receiving electrodes were posi-
tioned on the midaxillary line at about 5th-rib level,
and application electrodes on the same level on the
inner arms.
The Flow Measurement System (by Medikro Oy,
Kuopio, Finland) with a Spirometer Unit (M909), a
Fleisch-type Heatable Flow Transducer (5530), and a
Conical Mouthpiece (M9114), without any resistance,
were used as a reference PNT device. A 3L syringe
was used for daily system calibration to ensure accu-
rate flow values.
The sampling frequency of the reference PNT sig-
nal was 200Hz, while that of the Pneumonitor 2 is
f
s
= 250Hz. All signals were transformed (via inter-
polation) to the latter frequency.
2.2 Protocol & Analysis
The calibration was performed for three body posi-
tions (supine, sitting and standing), due to the signif-
icant impact of body posture on the calibration coef-
ficients (Mły
´
nczak et al., 2015b). Data for each po-
sition were gathered with three different calibration
protocols, differing by the duration of registration and
breathing regularity:
• free breathing registered for 30 seconds, hereafter
called ’Calibration Procedure 1’,
• free breathing recorded for 2 minutes, hereafter
called ’Calibration Procedure 2’, and
• fixed breathing, alternately shallow and deep, 4
breaths of each, for each of three frequencies, 6,
10, and 15 breaths per minute (BPM), to evalu-
ate whether signals containing various breathing
dynamics (rates and depths) may improve the cal-
ibration of flow-related signals, hereafter called
’Calibration Procedure 3’.
Data for testing were obtained with a fourth pro-
cedure, consisting of 6 normal breaths followed by 6
deep breaths (the difference in depth was subjective),
for three breathing rates (6, 10 and 15 BPM) and for
three body positions (the same as during each cali-
bration procedure). We automatically marked the ref-
erence breathing phases (inspiration, expiration, and
breathing pause) for each recording using simple am-
plitude thresholding of the flow-related raw PNT sig-
nal. We also included in the algorithm heuristics to
remove artifacts, very short phases and errors.
Flow Parameters Derived from Impedance Pneumography after Nonlinear Calibration based on Neural Networks
71

Both calibration and test IP signals were pro-
cessed by subtracting the noise component produced
by least mean square adaptive filtration from the raw
IP signal, then smoothing the difference with a 400
ms window. Then, flow-related signals were obtained
by second-order differentiation of all IP signals. After
differentiation, a simple moving-average smoothing
method with a 500 ms window was applied, striking
a balance between (necessary) removal of the cardiac
component and (undesirable) deterioration of the sig-
nal dynamics.
The basic calibration could be performed by cal-
culating the single linear coefficient between the
PNT reference and the processed, flow-related, IP-
differentiated signal, without needing to take into ac-
count the intercept coefficient of the linear model.
However, linear calibration for flow signals provides
much worse accuracy than for volume signals. In-
stead, we implemented nonlinear improvement, based
on neural networks, using the MATLAB Neural Net-
work Fitting App (described more precisely in the
next section) (Mathworks, 2016).
In order to compare flow parameters, absolute and
relative errors of maximum flow during inspiration (as
a positive value), maximum flow during expiration (as
a negative value), and mean flow values during each
phase, were calculated. We also provided T-test anal-
ysis to evaluate, whether the differences were statis-
tically significant, as well as box, compatibility, and
Bland-Altman plots.
Since some artifacts and very quick, unrepresen-
tative breathing phases remained after automatic seg-
mentation, we also provided the analysis after remov-
ing 5% outliers, from the inspiration and expiration
data, based on the reference PNT signal.
All analyses were performed using MATLAB.
2.3 Neural Network Correction
To fit the neural network, a basic perceptron archi-
tecture (with single-element-vector input, specific
numbers of sigmoid hidden layers and neurons in
those layers, and a linear output layer) was applied,
taking randomly selected signal samples in each it-
eration. IP was treated as input, and PNT as refer-
ence/output. During learning procedure the classic
Levenberg-Marquardt back-propagation method
was used, we chose the default division of calibra-
tion data into training (70%), validation (15%), and
test sets (15%).
We evaluated 13 approaches, listed below. ”Indi-
vidual training” refers to the separate use of the data
for each participant, for every calibration procedure
and for every body position, as input for a neural net-
work. ”Global training” indicates that the signals for
all conditions were combined and single neural net-
work was calculated.
1. Only simple linear modeling based on flow-
related signals.
2. Neural network with a single hidden layer with
10 neurons, trained individually.
3. Neural network with a single hidden layer with
20 neurons, trained individually.
4. Neural network with two hidden layers of 5 neu-
rons each, trained individually.
5. Neural network with two hidden layers of 10
neurons each, trained individually.
6. Simple linear modeling and then neural network
with a single hidden layer with 10 neurons,
trained individually.
7. Simple linear modeling and then neural network
with a single hidden layer with 20 neurons,
trained individually.
8. Simple linear modeling and then neural network
with two hidden layers of 5 neurons each,
trained individually.
9. Simple linear modeling and then neural network
with two hidden layers of 10 neurons each,
trained individually.
10. Simple linear modeling and then neural network
with a single hidden layer with 10 neurons,
trained globally.
11. Simple linear modeling and then neural network
with a single hidden layer with 20 neurons,
trained globally.
12. Simple linear modeling and then neural network
with two hidden layers of 5 neurons each,
trained globally.
13. Simple linear modeling and then neural network
with two hidden layers of 10 neurons each,
trained globally.
Those calibration approaches were performed for
signals obtained during each breathing protocol and
for all three body positions. In each case, we used
the Levenberg-Marquardt back-propagation learning
method. The neural networks’ architectures were set
arbitrarily, in order to evaluate their possible impact
on accuracy and learning time.
Due to the fact that the result of the neural network
training could be ”discontinuous”, we performed full
accuracy analysis for the best calibration procedure
with the addition of moving-average smoothing at the
end of the calibration calculations (with an arbitrary
window of 200 ms).
BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing
72
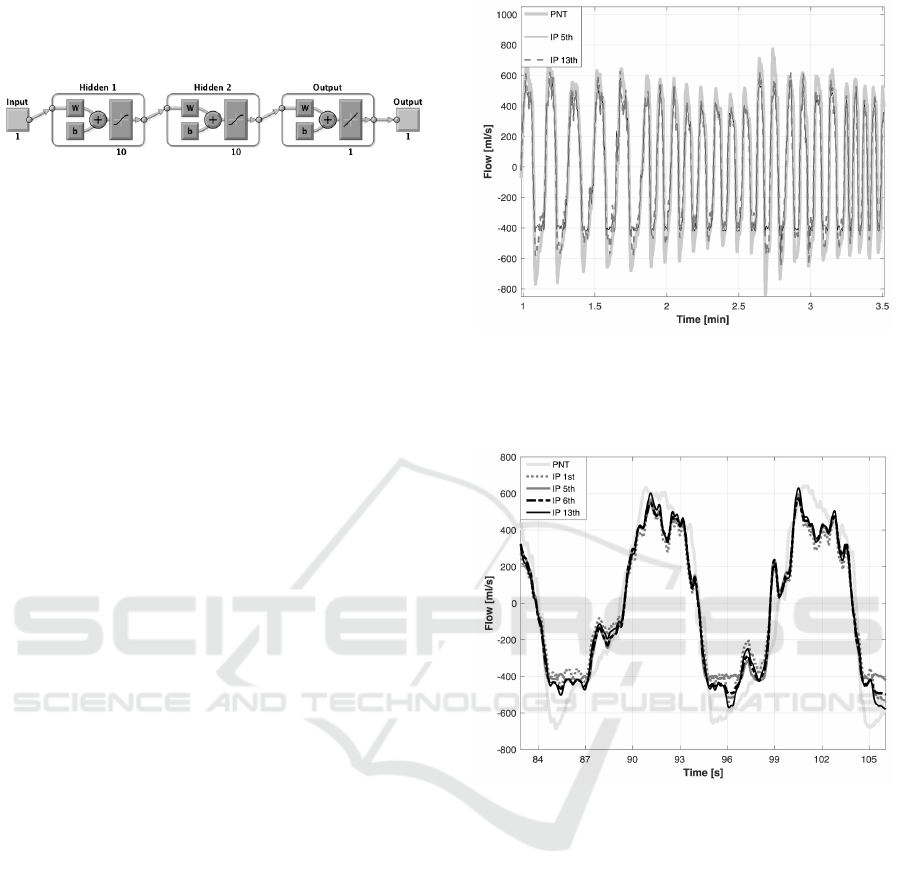
As an example, the neural network architecture
from the fifth approach is presented in Fig. 1.
Figure 1: Neural network architecture from the fifth ap-
proach (enumerated earlier); abbreviations: W - weight ma-
trix, b - bias vector (Mathworks, 2016).
3 RESULTS
A sample relationship between the reference PNT
signal and the flow-related IP signal, calculated by
the 5th, and 13th calibration approaches, for the sec-
ond participant in the sitting position, is presented in
Fig. 2. An excerpt of those signals (adding the ones
for the 1st and 6th calibration approaches), represent-
ing two consecutive breaths, is shown in Fig. 3.
Tables 2, 3, and 4 each present the absolute er-
rors, relative errors, and p-values of the maximum and
mean flow parameters for Calibration Procedures 1,
2, and 3, respectively (out of the 13 approaches, only
the 9 with the best outcomes for each procedure are
shown). For the best calibration procedure, we also
performed the analysis with smoothed calibration re-
sults (with a 200 ms window, hereafter called post-
hoc smoothing). The results appear in Table 5.
We did not observe any one participant sig-
nificantly contributing to the decrease in accuracy.
The flow parameters with the smallest overall error
were calculated for Calibration Procedure 3, with
the 6th calibration approach without any other post-
processing, and with the 5th with post-hoc smooth-
ing. It is worth noting that adding the smoothing to
the calibration result slightly increased the accuracy,
particularly for those calibration approaches in which
individually trained neural networks were used.
Generally, combining calculations for peak and
mean flow values, Calibration Procedure 3 and the 5th
calibration approach seemed best, with 80% mean ac-
curacy, compared to 72.5% for simple linear calibra-
tion.
We observed no statistically significant corre-
spondence between flow parameters using the first
calibration approach (only simple linear modeling).
More complicated calibration procedures yielded
lower numbers of neural-network-based approaches
in which there was statistically significant correspon-
dence between flow parameters. For the best combi-
nation, the differences in peak flow calculations were
statistically significant.
Figure 2: Sample comparison of the 5th, and 13th calibra-
tion approach results, calculated from the IP signal, in rela-
tion to the reference PNT signal, for the first participant in
a sitting position.
Figure 3: Excerpt of the sample comparison of the 1st, 5th,
6th, and 13th calibration approach results, calculated from
the IP signal, relative to the reference PNT signal, for the
first participant, sitting.
Individual neural-network learning was over 14
times faster than global one, comparing 36 seconds to
4 minutes and 12 seconds, on average, respectively.
The processing times were measured with the com-
puter processor Intel i5 (1200 MHz), with automati-
cally activated accelerations (up to 2700 MHz).
The box, compatibility, and Bland-Altman plots
for the calculated maximum flows for Calibration
Procedure 3 and the 6th calibration approach are pre-
sented in Fig. 4, 5, and 6, respectively. The same
analysis was provided for the 5th calibration approach
after applying post-hoc smoothing. The correspond-
ing box, compatibility, and Bland-Altman plots are
shown in Fig. 7, 8, and 9, respectively.
Flow Parameters Derived from Impedance Pneumography after Nonlinear Calibration based on Neural Networks
73
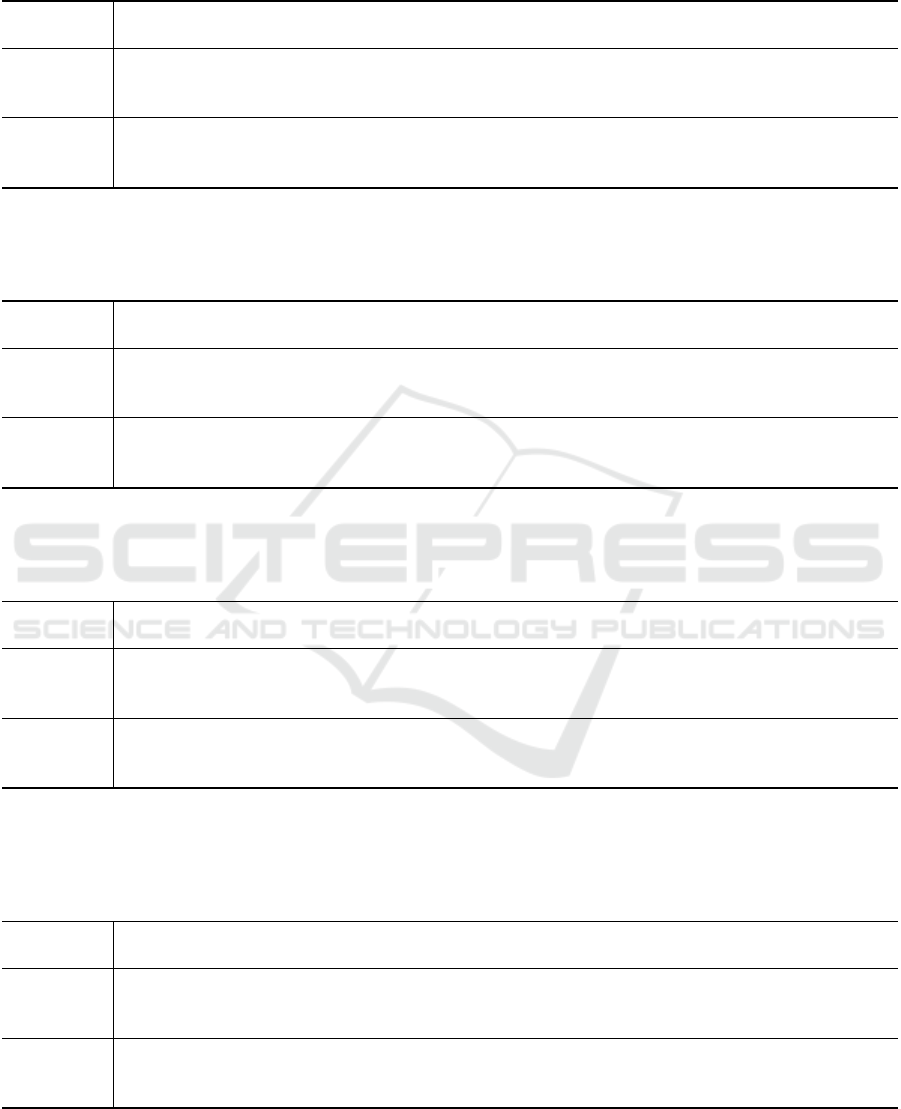
Table 2: Comparison of the maximum and mean flow values for the 9 most accurate approaches (considering average error
from maximum and mean flow calculations) for Calibration Procedure 1; A - absolute error in milliliters per second; R -
relative error in percents; p - approximate p-value of paired T test, accurate to the hundredths.
Calibration Approach
1 4 5 6 9 10 11 12 13
Max
Flow
A 200.7 246.3 220.9 216.7 233.1 178.9 174.3 175.1 173.6
R 34.6 35.9 31.3 30.9 33.5 25.5 24.8 24.9 24.8
p 0.09 <0.01 <0.01 <0.01 <0.01 <0.01 <0.01 <0.01 <0.01
Mean
Flow
A 187.6 182.1 169.8 173.5 189.6 145.6 145.2 145.8 145.2
R 43.7 38.2 34.0 34.1 37.9 30.7 30.3 30.4 30.3
p 0.58 <0.01 <0.01 <0.01 <0.01 <0.01 <0.01 <0.01 <0.01
Table 3: Comparison of the maximum and mean flow values for the 9 most accurate approaches (considering average error
from maximum and mean flow calculations) for Calibration Procedure 2; A - absolute error in milliliters per second; R -
relative error in percents; p - approximate p-value of paired T test, accurate to the hundredths.
Calibration Approach
1 2 5 6 9 10 11 12 13
Max
Flow
A 142.6 182.4 175.6 197.2 200.1 128.1 136.9 131.5 131.4
R 26.6 25.4 24.7 28.5 29.3 18.9 19.7 19.3 19.3
p 0.21 0.85 0.67 0.11 0.18 0.01 <0.01 <0.01 0.87
Mean
Flow
A 130.8 151.3 147.5 167.7 155.2 118.5 122.3 119.7 119.8
R 31.6 31.1 29.9 33.3 32.3 26.0 26.7 26.3 26.3
p 0.92 0.36 0.18 0.01 0.33 0.41 0.07 0.20 0.63
Table 4: Comparison of the maximum and mean flow values for the 9 most accurate approaches (considering average error
from maximum and mean flow calculations) for Calibration Procedure 3; A - absolute error in milliliters per second; R -
relative error in percents; p - approximate p-value of paired T test, accurate to the hundredths.
Calibration Approach
1 2 4 5 6 7 8 11 13
Max
Flow
A 144.3 126.8 132.3 118.4 118.5 120.7 118.9 133.0 134.3
R 28.6 21.1 22.6 20.9 20.8 22.9 20.0 23.9 24.3
p 0.37 0.04 0.04 0.05 <0.01 0.01 0.03 0.10 0.26
Mean
Flow
A 102.8 89.2 100.3 90.5 87.7 88.6 96.4 84.3 85.1
R 25.8 22.2 24.2 21.5 21.4 21.6 22.9 20.9 21.3
p 0.68 0.89 0.93 0.81 0.51 0.95 0.28 0.10 0.18
Table 5: Comparison of the maximum and mean flow values for the 9 most accurate approaches (considering average error
from maximum and mean flow calculations) for Calibration Procedure 3 after post-hoc smoothing of the calibration results
with a 200 ms window; A - absolute error in milliliters per second; R - relative error in percents; p - approximate p-value of
paired T test, accurate to the hundredths.
Calibration Approach
1 2 5 6 7 8 10 11 13
Max
Flow
A 144.3 119.0 109.1 109.7 110.0 113.6 130.5 123.7 125.3
R 28.6 19.5 18.4 19.0 19.3 18.7 22.8 21.6 22.3
p 0.37 0.04 <0.01 <0.01 <0.01 0.04 <0.01 0.18 0.36
Mean
Flow
A 102.8 90.1 91.4 88.6 89.5 97.4 87.9 85.0 85.9
R 25.8 23.4 21.6 21.7 22.0 23.2 22.4 21.0 21.4
p 0.68 0.88 0.80 0.50 0.93 0.28 0.01 0.10 0.18
BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing
74
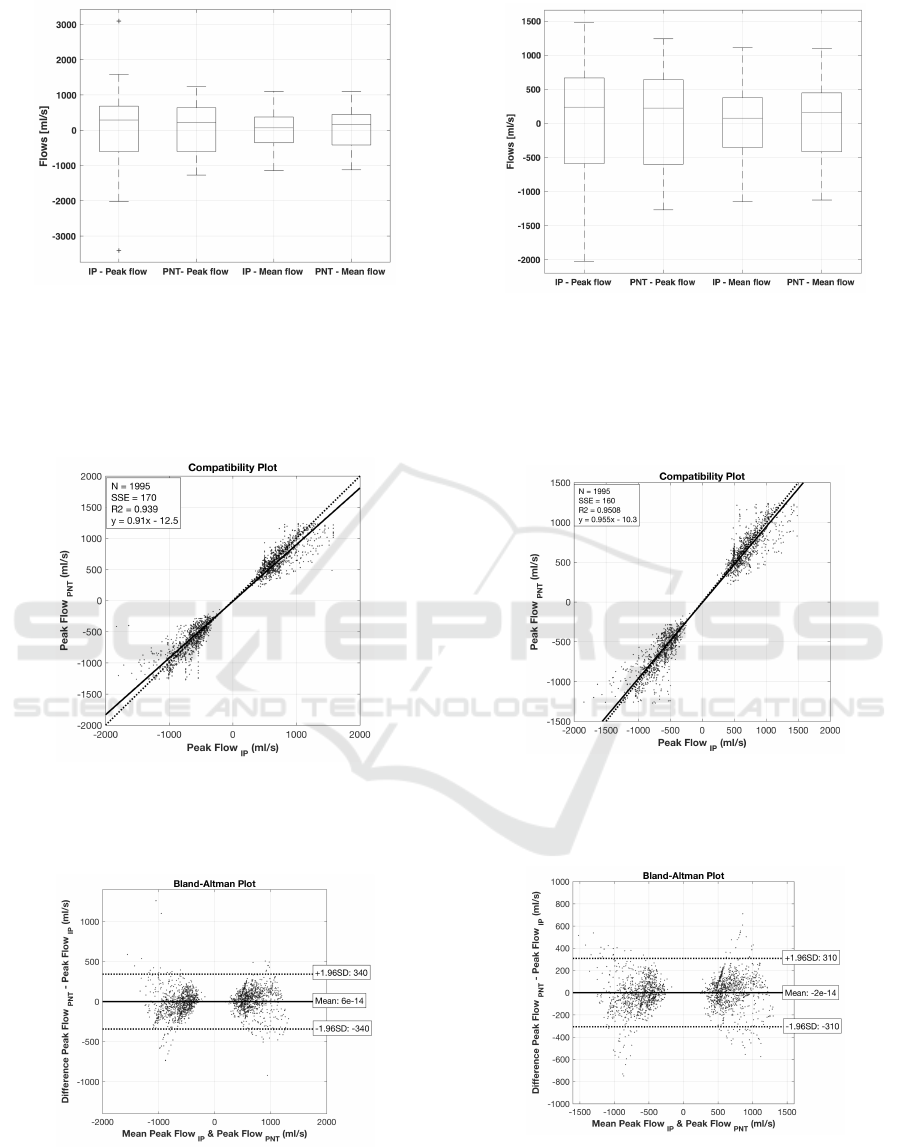
Figure 4: Box-plot comparing the maximum (peak) and
mean IP and PNT flow values and the differences between
them, calculated for both inspirations and expirations, for
all participants and body positions, for Calibration Proce-
dure 3 and the 6th calibration approach; positive values
correspond to inspiration flows, negative ones - to expira-
tion.
Figure 5: Compatibility plot for maximum flows, calculated
for both inspirations and expirations, for all participants and
body positions, for Calibration Procedure 3 and the 6th cal-
ibration approach.
Figure 6: Bland-Altman plot for maximum flows, calcu-
lated for both inspirations and expirations, for all partici-
pants and body positions, for Calibration Procedure 3 and
the 6th calibration approach.
Figure 7: Box-plot comparing the maximum (peak) and
mean IP and PNT flow values and the differences between
them, calculated for both inspirations and expirations, for
all participants and body positions, for Calibration Proce-
dure 3 and the 5th calibration approach after post-hoc
smoothing; positive values correspond to inspiration flows,
negative ones - to expiration.
Figure 8: Compatibility plot for maximum flows, calculated
for both inspirations and expirations, for all participants and
body positions, for Calibration Procedure 3 and the 5th cal-
ibration approach after post-hoc smoothing.
Figure 9: Bland-Altman plot for maximum flows, calcu-
lated for both inspirations and expirations, for all partici-
pants and body positions, for Calibration Procedure 3 and
the 5th calibration approach, after post-hoc smoothing.
Flow Parameters Derived from Impedance Pneumography after Nonlinear Calibration based on Neural Networks
75

4 DISCUSSION
In general, this paper touches the issue of improving
the accuracy of determining the respiratory flow pa-
rameters. As the more advanced method, the elec-
trical impedance tomography seems to provide bet-
ter set of data to estimate ventilation and perfusion as
by using ”single” signal in impedance pneumography
(Leonhardt and Lachmann, 2012).
Nevertheless, in this paper we evaluated the im-
provement of peak and mean flow estimation accu-
racy, using differentiated IP signal (convenient from
the point of view of long-term measurement), result-
ing from adding neural-network fitting correction or
separate modeling. The idea of using the nonlinear
correction approach stemmed from the observation
that the largest divergence between IP and reference
signals seemed to be near the peak value.
The verification was performed with different cali-
bration procedures (in order to check which one could
provide the best input data leading to the best results
during test measurements) and calibration approaches
(defining the order of applying linear and neural-
network models), with post-hoc smoothing provided
for the best calibration procedure (to check the pos-
sible impact of appearance of the cardiac component
on the calculation).
We used neural networks individually (for specific
subject and body position data) or globally (gathering
all data), with or without previously applying linear
calibration coefficients. The best accuracies were ob-
tained for Calibration Procedure 3, in which breath-
ing rates were fixed and depths of breathing forced.
Among them, individually trained neural-network ap-
proaches seemed the best in each assessed aspect. The
necessity of linear modeling before neural network
fitting remains important and in need of evaluation.
There is also the question of whether there is an opti-
mal network configuration (number of hidden layers
and neurons per layer), or whether it is dependent on
the specific subject and measurements being evalu-
ated.
It is worth remembering that the neural-network
approach is based on random selection of the input
and target data in the learning process. Without set-
ting the seed beforehand, we are unable to obtain the
same fit in subsequent repetitions of the training pro-
cess. Besides, the fitting could be discontinuous (due
to the specific data, particularly when there is an ar-
tifact in the signals). The subtle post-hoc smoothing
was added to deal with that issue.
The individual approach to neural-network fitting
reduces learning time. This could be useful with
regards to ambulatory monitoring and the prospect
of assessing different network configurations to see
which may be best suited to an individual.
The following limitations of this study require
mention:
• participants were only 10 males,
• measurements were carried out only under static
conditions,
• in ambulatory situations, recordings are longer
and more diversified, which may affect overall ac-
curacy,
• there was no distinction of breathing depths,
breathing rates, or body positions in the flow ac-
curacy assessment; the results were gathered into
the one set, and
• the neural network approach is compared to the
use of simple linear modeling calibration coeffi-
cient; there is no comparative analysis with an-
other nonlinear methods.
Future plans include:
• assessing the accuracy for models established sep-
arately for inspirations and expirations, and for
different depth of breathing,
• validating the accuracy in the case of a different
order of differentiation and calibration (e.g., linear
or nonlinear calibration for volume-related data
with differentiation as a final step, performed in
order to analyze flow values),
• comparing the results from presented neural-
network-based approach with the ones derived
from different nonlinear correction algorithm,
• checking the possibility to improve the accuracy
by removing the cardiac component adaptively in
the way, that the dynamics of the signal changes
(particularly for higher flows) is preserved in the
most optimal way, and
• evaluating more advanced methods of neural net-
work learning (Monteiro et al., 2016).
5 CONCLUSIONS
The following conclusions may be drawn:
• Non-linear neural-network-based correction of
the linear calibration model or a separate neural
network fitting model can improve the mean accu-
racy of peak and mean flow parameters calculated
from impedance pneumography signals.
• The longest considered calibration procedure,
consisting of fixed breathing with different rates
BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing
76

and depths, allows better coverage of possible
flow changes in test signals.
• Neural networks trained individually for every
body position of a particular subject seem to pro-
vide better results than ones trained with a global
set.
• We obtained 80% accuracy with the best combi-
nation (separate model based on a neural network
with two hidden layers of 10 neurons each, trained
individually on the data from 3rd calibration pro-
cedure), versus 72.5% for simple linear modeling.
ACKNOWLEDGMENTS
This study was supported by the research programs of
institutions the authors are affiliated with.
REFERENCES
Ansari, S., Ward, K., and Najarian, K. (2016). Motion Ar-
tifact Suppression in Impedance Pneumography Sig-
nal for Portable Monitoring of Respiration: an Adap-
tive Approach. IEEE J. Biomed. Heal. Informatics,
11(4):1–1.
Baemani, M. J., Monadjemi, A., and Moallem, P. (2008).
Detection of respiratory abnormalities using artifi-
cial neural networks. Journal of Computer Science,
4(8):663–667.
Gracia, J., Seppa, V. P., and Viik, J. (2015). Regional
impedance pneumography heterogeneity during air-
way opening pressure chirp oscillations. Int. J. Bio-
electromagn., 17(1):42–51.
Houtveen, J. H., Groot, P. F. C., and De Geus, E. J. C.
(2006). Validation of the thoracic impedance derived
respiratory signal using multilevel analysis. Int. J.
Psychophysiol., 59(2):97–106.
Jafari, S., Arabalibeik, H., and Agin, K. (2010). Classifica-
tion of normal and abnormal respiration patterns us-
ing flow volume curve and neural network. In Health
Informatics and Bioinformatics (HIBIT), 2010 5th In-
ternational Symposium On, pages 110–113. IEEE.
Koivumaki, T., Vauhkonen, M., Kuikka, J. T., and Haku-
linen, M. a. (2012). Bioimpedance-based measure-
ment method for simultaneous acquisition of respi-
ratory and cardiac gating signals. Physiol. Meas.,
33(8):1323–1334.
Lai, C.-L., Lee, J.-S., and Chen, J.-C. (2015). A curve fit-
ting approach using ann for converting ct number to
linear attenuation coefficient for ct-based pet attenu-
ation correction. IEEE Transactions on Nuclear Sci-
ence, 62(1):164–170.
Lee, S. J., Motai, Y., Weiss, E., and Sun, S. S. (2012). Ir-
regular breathing classification from multiple patient
datasets using neural networks. IEEE Transactions on
Information Technology in Biomedicine, 16(6):1253–
1264.
Leonhardt, S. and Lachmann, B. (2012). Electrical
impedance tomography: The holy grail of ventila-
tion and perfusion monitoring? Intensive Care Med.,
38:1917–1929.
Li, Y., Pan Fua, Z. L., Lia, X., and Lina, Z. (2015). Biax-
ial angle sensor calibration method based on artificial
neural network. Chemical Engineering, 46:361–366.
Mathworks (2016). Fit Data with a Neural Net-
work. https://www.mathworks.com/help/nnet/gs/fit-
data-with-a-neural-network.html. [Online; accessed
07-October-2016].
Min, M. and Paavle, T. (2013). Improved extraction of in-
formation in bioimpedance measurements. In J. Phys.
Conf. Ser., volume 434, pages 0120291–4.
Mły
´
nczak, M., Niewiadomski, W.,
˙
Zyli
´
nski, M., and Cybul-
ski, G. (2015a). Assessment of calibration methods
on impedance pneumography accuracy. Biomed. Eng.
/ Biomed. Tech.
Mły
´
nczak, M., Niewiadomski, W.,
˙
Zyli
´
nski, M., and Cybul-
ski, G. (2015b). Verification of the Respiratory Param-
eters Derived from Impedance Pnumography during
Normal and Deep Breathing in Three Body Postures.
In IFMBE Proc., volume 45, pages 162–165.
Monteiro, R. L. S., Carneiro, T. K. G., Fontoura, J. R. A.,
Da Silva, V. L., Moret, M. A., and De Barros Pereira,
H. B. (2016). A model for improving the learning
curves of artificial neural networks. PLoS One, 11(2).
Ojarand, J., Annus, P., and Min, M. (2013). Optimisation of
multisine waveform for bio-impedance spectroscopy.
In J. Phys. Conf. Ser., volume 434, pages 0120301–4.
Poupard, L., Mathieu, M., Sart
`
ene, R., and Goldman, M.
(2008). Use of thoracic impedance sensors to screen
for sleep-disordered breathing in patients with cardio-
vascular disease. Physiol. Meas., 29(2):255–267.
Roebuck, A., Monasterio, V., Gederi, E., Osipov, M., Behar,
J., Malhotra, A., Penzel, T., and Clifford, G. (2013). A
review of signals used in sleep analysis. Physiological
measurement, 35(1):R1.
Seppa, V. P., Hyttinen, J., Uitto, M., Chrapek, W., and
Viik, J. (2013a). Novel electrode configuration for
highly linear impedance pneumography. Biomed. Eng.
/ Biomed. Tech., 58(1):35–38.
Seppa, V.-P., Hyttinen, J., and Viik, J. (2011). A method
for suppressing cardiogenic oscillations in impedance
pneumography. Physiol. Meas., 32(3):337–345.
Seppa, V.-P., Pelkonen, A. S., Kotaniemi-Syrjanen, A.,
Makela, M. J., Viik, J., and Malmberg, L. P. (2013b).
Tidal breathing flow measurement in awake young
children by using impedance pneumography. J. Appl.
Physiol., 115(11):1725–31.
Seppa, V.-P., Pelkonen, A. S., Kotaniemi-Syrjanen, A.,
Viik, J., Makela, M. J., and Malmberg, L. P. (2016).
Tidal flow variability measured by impedance pneu-
mography relates to childhood asthma risk. Eur.
Respir. J., pages 1–10.
Seppa, V.-P., Viik, J., and Hyttinen, J. (2010). Assessment
of pulmonary flow using impedance pneumography.
IEEE Trans. Biomed. Eng., 57(9):2277–2285.
Flow Parameters Derived from Impedance Pneumography after Nonlinear Calibration based on Neural Networks
77
