Sampling Density Criterion for Circular Structured Light 3D Imaging

Deokwoo Lee

and Hamid Krim

Youngsan University, Yangsan, Gyeongnam, South Korea

Department of Electrical and Computer Engineering, North Carolina State University, Raleigh, NC, U.S.A.

dwoolee@ysu.ac.kr, ahk@ncsu.edu

Keywords:

3D Reconstruction, Structured Light Pattern, Sampling Theorem, Geometry.

Abstract:

3D reconstruction work has chieﬂy focused on the accuracy of reconstruction results in computer vision, and

efﬁcient 3D functional camera system has been of interest in the ﬁeld of mobile camera as well. The optimal

sampling density, referred to as the minimum sampling rate for 3D or high-dimensional signal reconstruction,

is proposed in this paper. There have been many research activities to develop an adaptive sampling theorem

beyond the Shannon-Nyquist Sampling Theorem in the areas of signal processing, but sampling theorem for

3D imaging or reconstruction is an open challenging topic and crucial part of our contribution in this paper.

We hence propose an approach to sampling rate (lower / upper bound) determination to recover 3D objects

(surfaces) represented by a set of circular light patterns, and the criterion for a sampling rate is formulated

using geometric characteristics of the light patterns overlaid on the surface. The proposed method is in a sense

a foundation for a sampling theorem applied to 3D image processing, by establishing a relationship between

frequency components and geometric information of a surface.

1 INTRODUCTION

3D Imaging research has been extensively performed

since a few decades in the areas of computer vision,

image processing and pattern recognition for diverse

applications. In 3D reconstruction, a number of meth-

ods have been proposed for the problem and the pas-

sive (Kolev et al., 2014) and the active ((Geng, 2011),

(Lei et al., 2013)) methods have been widely applied

in practice. Both methods are based on establishing

a geometrical relationship of high dimensional sig-

nal (or 3D object points) and a low dimensional one

(or 2D image projected on the image plane). Readers

also can refer to about recent research of the passive

and the active methods and a hybrid method that com-

bines the passive and the active method for the further

improvement on the quality of the 3D reconstruction

results ((Chan et al., 2008), (Song et al., 2014)). Con-

sider f ∈ R

and f

′

∈ R

, the problem is to then re-

cover f from given information of f

′

, where f

′

is de-

termined by a transformation P , such that

′

= P f, (1)

where P is usually a projection operator (Faugeras

et al., 2001), and the operator yields an approximately

perfect reconstruction of f. In the ﬁeld of image pro-

cessing and computer vision, the general principle

space in passive methods is triangulation using two

or more 2D image planes generated from a number of

cameras. The relative geometric relationship between

image planes located at different positions and a tar-

get object in 3D domain, and a successful correspon-

dence matching results provide sufﬁcient information

required to recover 3D coordinates of an object sur-

face. The passive methods, however, sometimes fails

high quality reconstruction results because there ex-

ists a inherent limitation and disadvantages due to the

occlusion problem, low textured surface, high com-

putational complexity of the correspondence match-

ing, etc. To alleviate the limitations of the passive

method, active method using structured light patterns

has been employed for 3D reconstruction . The active

method, an alternative to the passive methods, also

solves the reconstruction problems based on the ge-

ometrical relationship between the components (op-

tical center, 3D points on the surface, location of a

light source) by replacing one camera with a light

source generating structured light patterns. It is ob-

vious that data acquisition procedure and efﬁcient use

of data is crucial in reconstruction work in both pas-

sive and active methods. To achieve this efﬁciency,

reconstruction is closely related to sampling rate rep-

resented as the optimal number of light patterns. This

paper proposes an approach to a sampling theorem

for high dimensional signals and a sampling rate de-

478

Lee D. and Krim H.

Sampling Density Criterion for Circular Structured Light 3D Imaging.

DOI: 10.5220/0006147504780483

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 478-483

ISBN: 978-989-758-227-1

termination for structured light 3D imaging applica-

tions. In particular, we determine the lower and the

upper bound criterion of a sampling rate for the re-

construction using structured circular light patterns.

The active method on the basis of circular structured

light patterns provides simple, efﬁcient reconstruc-

tion algorithm, and the active method (Geng, 2011),

in general, achieve accurate reconstruction result in

contrast to the passive method. Once we have one di-

mensional continuous signal, we are interested in the

minimum sampling rate (f

) which is represented as

= 2 f

max

or the maximum sampling interval (T

max

Akin to 1D signal, once fully reconstructed, the sur-

face which is a (image) signal of interest, represented

as 3D Euclidean coordinates (triangle meshes com-

posed of vertices and faces), is considered a continu-

ous signal, which yields a natural question about an

optimal number of circular light patterns necessary

for reconstruction of surfaces. The spatial sampling

density (or sampling rate), is deﬁned as the minimum

number of circular patterns to be projected on a sur-

face. The minimum number of circular patterns leads

to the maximum sampling interval between neigh-

boring circular patterns. Determination of the mini-

mum number of the patterns is proposed in this paper.

The sampling rate determination in the ﬁeld of 3D re-

construction using the structured light pattern has not

gained much attention in contrast to the research for

improving accuracy of reconstruction itself. In this

paper, the sampling rate is ultimately obtained from

the spatial maximum frequency component which is

closely related to geometric characteristics of an ob-

ject surface. This paper proposes the approach to

derivation of the upper and the lower bound of a sam-

pling rate for the surface reconstruction and the sim-

ulations results are also shown to verify the proposed

approaches.

2 SAMPLING RATE

This section details the derivation of the minimum

sampling rate which leads to sufﬁcient representa-

tion of 3D characteristics of a target object surface.

This paper uses curvature information to determine

the minimum sampling rate, and frequency compo-

nents of the surface is derived by establishing a rela-

tionship between curvature and frequency. Intuitively,

required number of circular patterns is determined by

geometric surface shape, for instance, larger number

of the patterns is required for the surface which has

frequent variation of a surface shape. As previously

stated, surface shape deforms a set of concentric cir-

cular patterns. In other words, deformation can be

……

j=1 j=2

j=3

j=4

j=5

j=N

i=1

i=2 i=3

............

i=M

i=10

..........

Figure 1: i and j respectively index the number of points(M)

in each patterns, and the pattern’s position.

represented quantitatively by measuring curvatures of

the patterns projected onto the surface (i.e., original

circle has a constant curvature, but the curvatures are

not constant in deformed circles). These curvatures

can lead to developing a sampling criterion for a sur-

face reconstruction if the relationship between spatial

frequency components and curvature information is

established. This section establishes the relationship

to achieve sampling rate determination. In practice,

given small amount geometric information (i.e., high-

est curvature that is corresponding to a point of high-

est variation in the surface), sampling rate is directly

determined and leads to efﬁcient reconstruction (ap-

proximate geometric reconstruction) system. In this

paper, we assume that we are given the initial num-

ber of circular patterns that are sufﬁcient to represent

3D object (i.e., oversampled) to theoretically derive a

sampling criterion for a surface reconstruction. Once

3D coordinates of a surface are provided, we denote

the surface and the discretely sampled surface (sam-

pled by N concentric circular patterns) by S

and S

represented as

= {x

}, (2)

= {x

}, (3)

i = 1,2, ..., M, j = 1,2,.. . ,N,

where where i and j respectively index the number

of points in each patterns, and the pattern’s position

(Fig. 1). Since the present work aims at deriving the

minimum number of the patterns, this paper chieﬂy

deals with pattern-wise sampling rather than point-

wise sampling under the assumption that M is sufﬁ-

ciently large. Fig. 2, we view j = 1,2, ..., N as a time

index, and the signal of interest is given by

(t) = {x

(t), y

(t), z

(t)}, (4)

i = 1, 2,.. . ,M, j = 1, 2,.. . ,N.

A sufﬁciently large N makes S

(t) dense and close to

a continuous signal, which we in turn use to introduce

sampling technique using a 1D signal. S

(t) is deﬁned

Sampling Density Criterion for Circular Structured Light 3D Imaging

479

d d

Light

Projection

Onto

A Surface

1 2

d d

t=1

t=2

t=3

t=N

domain

Figure 2: Indices of the location of each curve alternatively

represented as time t to introduce a concept of a frequency

component of a surface.

in the continuous time and S

[n] = S

(nT) is deﬁned

is the discrete time domain. The Fourier transform of

(t), S

: R → R, is denoted by

(ω) =

∞

−∞

(t)e

−jωt

dt, (5)

where ω = 2πf, is a radian frequency. If we assume

that S

(t) is bandlimited, has a ﬁnite energy (square-

summable or square-intergrable in Lebesgue’s sense)

(Unser, 2000) and is sampled at the points t

= nT,

then S

(t) can be reconstructed with an appropriate T

as follows :

(nT) =

∞

∑

n=−∞

(t)ϕ

(t −nT), (6)

(t) = S

(nT) ⋆ ϕ

(nT)

∞

∑

n=−∞

(nT)ϕ

(t −nT), (7)

(8)

where ’⋆’ denotes the convolution operator, t can be

a time or a index of a sample (e.g., sampled pattern

in Fig. 1, and ϕ

(t) and ϕ

(t) are orthogonal basis

functions,

< ϕ

(k),ϕ

(k) >= δ(k −l), (9)

where ’<, >’ is an L

inner product operation and δ(t)

is the Dirac delta function. ϕ

(t) and ϕ

(t) are se-

lected appropriately to solve the reconstruction prob-

lem and are ideal lowpass ﬁlters in this paper (i.e.

sinc function) ((Higgins, 2003), (Jerri, 1977), (Mallat,

1989), (Papoulis, 1977), (Unser, 2000)). The recon-

struction process then can be written as

(t) =

∞

∑

n=−∞

(nT)sinc(ω

(t −nT)), (10)

where sinc(ω

(t − nT)) = sin(ω

(t − nT))/ω

(t −

nT) is a sinc function. Recovery of S

(t) from S

(nT)

is perfectly conducted by sampling the points from

(t), or by selecting an appropriate sampling fre-

quency f

, where f

= 1/T. Akin to determining the

sampling frequency for a 1D signal, our reconstruc-

tion of a surface, S

(t) will seek the maximal fre-

quency component f

max

, and this approach can be ap-

plied to any type of signals. We assume that the signal

of interest S

(t) is bandlimited or pre-processed by

appropriate ﬁlters (Eldar and Pohl, 2009). The sam-

pling rate f

provides a sufﬁcient criterion for a ge-

ometric signal recovery, and it is deﬁned in the unit

arc length or pixel. The minimum number of circular

patterns N

for the reconstruction is simply obtained

as follows :

= f

×N = 2 f

max

×N, (11)

where N is the initial number of circular patterns pro-

jected onto the surface to extract 3D coordinates, and

is the minimum number of patterns to reconstruct

the surface. In the experiments with synthetic data,

we initially determine N which can fully reconstruct

(or represent) 3D geometric information of a target

object surface.

2.1 Sampling Rate using the Two-Third

Power Law

Quantifying a surface shape is tantamount to extract-

ing sufﬁcient geometric information (e.g., tangent

vectors, curvatures, etc.) from a surface. To that end,

curvature, the ﬁrst derivative of a tangent vector, is ge-

ometric information for estimating spatial frequency

components, and the curvature is better to describe

geometric properties of 3D object because it is view-

point invariant. The Two-Third Power Law (Lee and

Krim, 2011), proposed by Paolo Viviani (Lacquaniti

et al., 1983) explains a relationship between an ab-

solute angular velocity and curvature for constrained

movements (Fig. 3). In this method, the constrained

movement of points comprises a curve, from which

we can estimate an angular velocity and curvature of

a curve composed of points. In Fig. 3, r is an Eu-

clidean distance from the reference point to any point

−→

T is a tangent vector, and κ is a curvature based on

an osculating circle where radius is R, and V is an an-

gular velocity which satisﬁes the following equations

(de’Sperati C and P, 1997):

V(t) = K ·

R(t)

1+ αR(t)

1−β

, (12)

V(t) = r(t)ω = 2πr(t) f,

where K depends on the movement duration, called

a velocity gain, α and β are parameters (α, β ∈ R).

Given R(t), and r(t), recall that our purpose here is

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

480

( )

ds R

! !

Figure 3: The Two-Thirds Power Law explains a relation-

ship between a geometrical information (i.e. curvature) and

an angular velocity of a curve. Angular velocity is com-

posed of a radius r and an angular frequency ω.

to estimate the maximal frequency component, f

max

Eq. (12) is rewritten as follows :

f =

2πr(t)

K ·

R(t)

1+ αR(t)

1−β

. (13)

Eq. (13) hence yields the maximal frequency compo-

nent and a sampling frequency estimation based on a

Nyquist rate :

max

= max

2πr(t)

K ·

R(t)

1+ αR(t)

1−β

(14)

≥ 2f

max

. (15)

Having established the algorithm for a spatial sam-

pling frequency estimation, sampling rate for 3D

object surface is considered. Extended to a 3-

dimensional signal, projected circular patterns on a

surface have two tangential vectors (Fig. 5). Hence,

two curvature components (κ

1ij

and κ

2ij

), the ﬁrst

derivative of tangential vectors, T

1ij

and T

2ij

are de-

ﬁned at P

with respect to the arc length. For a 3D

signal (i.e., surface), at any point P

, if two orthogo-

nal tangent vectors are selected, then two correspond-

ing curvatures are deﬁned as well.

We can hence acquire the frequency components

corresponding to κ

1ij

and κ

2ij

, respectively, and The

Two-Thirds Power Law for a 3D surface may also be

written as :

1ij

= 2π f

1ij

1+ αR

1ij

1−β

, (16)

2ij

= 2π f

2ij

1+ αR

2ij

1−β

, (17)

1ij

= r

2ij

= r

i = 1, 2,.. . ,M, j = 1,2,.. .,N,

1 1

, ,

ij ij ij ij

i j

P x y z

Figure 4: Example of 3D face model(fvinput data).

( 1)thj

1ij

2ij

th curve(pattern)j

( 1)thj

Figure 5: Vectors deﬁned on a point in a facial curve.

where R

1ij

and R

2ij

are 1/κ

1ij

and 1/κ

2ij

, re-

spectively, and M is the number of points on each

curve and N is the number of curves (patterns) on

the surface. To determine the minimum sampling

rate (2 ×max( f

)) consistent with the Nyquist Rate,

the maximum frequency component, max(f

) is re-

quired, and we deﬁne max(f

) as

max( f

) = max[sup( f

1ij

),sup( f

2ij

)]. (18)

Using the relationship between the frequency

component, f

and the corresponding r

, the maxi-

mum frequency is calculated. Prior to measuring the

global maximum f

, local maximum sup( f

1ij

) and

sup( f

2ij

) should be acquired, and each of which sat-

isﬁes the following,

sup( f

kij

) ≤

2π

sup

kij

1+ αR

kij

1−β

, k= 1,2.

(19)

Prior to the measurement of curvatures and r

’s of

all the points of the deformed circular patterns, a nor-

malization of data points is carried out. The normal-

ization yields the determination of the intrinsic char-

acteristics of each curve projection on the surface.

Sampling Density Criterion for Circular Structured Light 3D Imaging

481

2.2 Proposed Sampling Rate

Determination

In case of any dimensional signal, sampling rate can

be determined using curvature information. Using a

Fourier Series, any signal can be represented as a

combination of sinusoidal signal. Based on the princi-

ple of Fourier Series, a signal (or a curve) can ba rep-

resented as α(t) = [t,cosωt],where ω is a frequency

component of a signal. Once α(t) is determined, we

use the following information to estimate a curvature:

′

(t) =

dα(t)

= [1, −ωsinωt], (20)

′′

(t) =

dα(t)

= [0, −ω

cosωt]. (21)

For any regular curves, curvature is deﬁned as (Oprea,

2007)

κ =

|α

′

×α

′′

|α

′

, (22)

where α = α(t), × represents the outer product

between two vectors. To achieve the minimum sam-

pling rate, we do not have to measure all curvature

or frequency information. Because a maximal fre-

quency component contributes to the minimum sam-

pling rate. Thus, we represent the target signal as just

α(t) = [t,cosωt] or α(t) = [R(t),z(t)]. If we use cir-

cular patterns each of which has a radius R(t) = t, z(t)

can be represented as a combination of sinusoidal sig-

nals, and ω can be a dominant frequency component,

α(t) = [t,cosωt] is sufﬁcient representation. Curva-

ture can be written as

κ =

|−ωcosωt|



1+ ω

sin

ωt



3/2

≤



1+ ω

sin

ωt



3/2

. (23)

Then, κ is bounded by 0 ≤ κ ≤ ω

and the fre-

quency component can be written as

κ ≤ 4πf

f ≥

2π

√

κ. (24)

Since κ is any curvature value,

f ≥

2π

√

max

.  (25)

Although this approach is very simple and

straightforward, we only have minimum bound of a

frequency component, which is a drawback of the di-

rect method.

3 SIMULATION RESULTS

Having established representations for colored and

geometric faces, a sampling criterion determines the

minimum number of curves (patterns) to reconstruct

surfaces. Using the algorithms proposed above, the

sampling rate of the surface is shown in Table. I.

7 3D face models are used and they are composed

of vertices and faces. The estimated minimum sam-

pling rate, N

, derived from algorithms in the previ-

ous sections, for 5 real face models and 2 synthetic

ones, are shown in Table. I. As shown in Table. I, for

instance, 147 circular patterns are projected onto the

target 3D face and the reconstruction is carried out.

Once reconstructed with 147 patterns, the minimum

number of the patterns is derived based on Eq.s 19

and 25, and try to achieve reasonable reconstruction

result that does not have signiﬁcant loss of informa-

tion

4 SUMMARY AND CONCLUSION

In this paper, sampling rate determination for 3D re-

construction using structured light patterns has been

discussed. To the best of our knowledge, sampling

rate determination has not been of much interest in the

areas of computer vision and 3D imaging. Although

there have been extensive research about accurate 3D

reconstruction, the efﬁcient reconstruction employing

sampling theorem in 1D signal has been little inves-

tigated. The proposed approach is very efﬁcient and

simple from practical perspectives only by using cur-

vature information deﬁned in facial curves that are

projected light patterns. In practice, there also have

been extensive research about face recognition using

facial curves and our approach also can be used for

efﬁcient 3D face recognition work. Deformation of

a projected light pattern is important key to a recon-

struction and a sampling rate determination in this pa-

per. Although many works about reconstruction have

been done, this is very challenging work to use a cir-

cular pattern and to analyze a relationship of deforma-

tion of a 2D and a 3D image. In aspect of efﬁciency,

the optimal sampling rate was induced from a cur-

vature estimation. Before determining sampling rate,

we estimated curvatures of set of curveson the 3D ob-

ject. 3D curves are exactly mapped to 2D curves and

these are topologically equivalent to each other. The

highest curvature or the biggest distorted light pattern

on 3D surface is shown as the biggest distorted curve

on 2D image. This implies that values of curvature on

3D are also mapped to the values of curvature on 2D

image. Since a curvature estimation is a method of es-

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

482

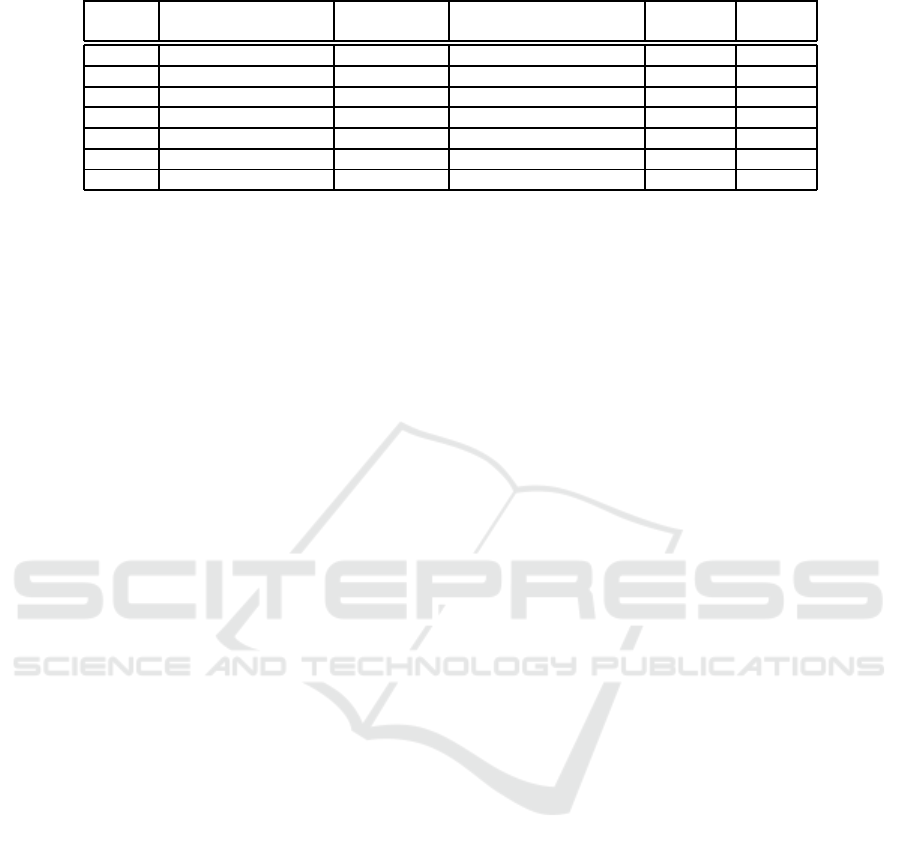
Table 1: Estimated minimum number of patterns.

N f

[1/arc length] N

(Initial number of patterns) (Sampling rate) (Minimum number of patterns) Size(vertex) Size(face)

Brian 147 0.38 56 15926×3 23526×3

Eric 153 0.40 62 17266×3 23567×3

Greg 142 0.33 47 16257×3 28023×3

Jeff 221 0.49 109 16080×3 18522×3

Weihong 271 0.33 90 15769×3 26959×3

fvgallary 89 0.30 27 5031×3 9999×3

fvinput 93 0.44 41 16092×3 32116×3

timation of curves’ shape, we used average curvature

of each curve in each unit space. So, curvature infor-

mation can tell us the characteristic of curves which is

matched to signal function. Given a maximal curva-

ture variation, we could ﬁnd the sampling rate and de-

termined the number of light patterns to be projected

for reliable 3D surface reconstruction. In addition,

we have presented an alternative algorithm to deter-

mine the sampling rate of a surface (or deﬁning the

minimum number of light patterns to be projected on

a surface whose maximal curvatures may be known)

subjected to an active light source probing. Such a

rate, in turn plays a key role in the efﬁcient represen-

tation of a surface and its subsequent reconstruction

from these patterns. While our primary application of

interest lies in the area of biometrics and face mod-

eling, the two-thirds-based sampling criterion may

be exploited in many different settings where surface

representation and sampling are of interest (e.g. sur-

face archiving). Although our sampling rate does not

recover the surface perfectly as the Shannon-Nyquist

Sampling Rate does for 1D signals, the sampling cri-

terion we proposed does not show a considerable in-

formation loss to be recognized. In the future, there

are some technical issues to be considered - quantify-

ing the algorithm efﬁciency (i.e. computational com-

plexity) and the reconstruction accuracy compared to

the previous methods is needed.

REFERENCES

Chan, Y., Delmas, P., Gimel’farb, G., and Valkenburg, R.

(2008). On fusion of active range data and passive

stereo data for 3d scene modelling. In Image and

Vision Computing New Zealand, 23rd International

Conference. IEEE.

de’Sperati C and P, V. (1997). The relationship between cur-

vature and velocity in two-dimensional smooth pur-

suit eye movements. The Journal of Neuroscience,

17(10):3932 – 3945.

Eldar, Y. C. and Pohl, V. (2009). Recovering signals from

lowpass data. CoRR, abs/0907.3576.

Faugeras, O., Luong, Q.-T., and Papadopoulou, T. (2001).

The Geometry of Multiple Images: The Laws That

Govern The Formation of Images of A Scene and Some

of Their Applications. MIT Press, Cambridge, MA,

USA.

Geng, J. (2011). Structured-light 3d surface imaging: atu-

torial. Adv. Opt. Photon., 3(2):128–160.

Higgins, J. (2003). A sampling theorem for irregularly

spaced sample points (corresp.). IEEE Transactions

on Information Theory, 22(5):621 – 622.

Jerri, A. J. (1977). The shannon sampling theorem - its

various extensions and applications: A tutorial review.

Proceedings of the IEEE, 65(11):1565 – 1596.

Kolev, K., Tanskanen, P., Speciale, P., and Pollefeys, M.

(2014). Turning mobile phones into 3d scanners. 2014

IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), 00(undeﬁned):3946–3953.

Lacquaniti, F., Terzuolo, C., and Viviani, P. (1983). The law

relating the kinematic and ﬁgural aspects of drawing

movements. Acta Psychologica, 54(13):115 – 130.

Lee, D. and Krim, H. (2011). A sampling theorem for a

2d surface. In Scale Space and Variational Methods

in Computer Vision - Third International Conference,

SSVM 2011, Ein-Gedi, Israel, May 29 - June 2, 2011,

Revised Selected Papers, pages 556–567.

Lei, Y., Bengtson, K., Li, L., and Allebach, J. (2013). De-

sign and decoding of an m-array pattern for low-cost

structured light 3d reconstruction systems. In Im-

age Processing (ICIP), 2013 20th IEEE International

Conference on.

Mallat, S. G. (1989). A theory for multiresolution sig-

nal decomposition: The wavelet representation. IEEE

Trans. Pattern Anal. Mach. Intell., 11(7):674–693.

Oprea, J. (2007). Differential Geometry and Its Applica-

tions. Mathematical Association of America, 2nd edi-

tion.

Papoulis, A. (1977). Signal analysis. Electrical and elec-

tronic engineering series. McGraw-Hill, New York,

San Francisco, Paris.

Song, Y., Glasbey, C. A., Polder, G., and van Heijden, G. W.

(2014). Non-destructive automatic leaf area measure-

ments by combining stereo and time-of-ﬂight images.

IET Computer Vision, 8(5):391–403.

Unser, M. (2000). Sampling—50 Years after Shannon. Pro-

ceedings of the IEEE, 88(4):569–587.

Sampling Density Criterion for Circular Structured Light 3D Imaging

483