Statistical Analysis of Window Sizes and Sampling Rates in Human

Activity Recognition

Anzah H. Niazi

, Delaram Yazdansepas

, Jennifer L. Gay

, Frederick W. Maier

Lakshmish Ramaswamy

, Khaled Rasheed

1,2

and Matthew P. Buman

Institute for Artiﬁcial Intelligence, The University of Georgia, Athens, Georgia, U.S.A.

Department of Computer Science, The University of Georgia, Athens, Georgia, U.S.A.

College of Public Health, The University of Georgia, Athens, Georgia, U.S.A.

School of Nutrition and Health Promotion, Arizona State University, Phoenix, Arizona, U.S.A.

Keywords:

Actigraph g3x+, Analysis of Variance, Body-worn Accelerometers, Data Mining, Human Activity Recogni-

tion, Random Forests, Sampling Rate, Weighted Least Squares, WEKA, Window Size.

Abstract:

Accelerometers are the most common device for data collection in the ﬁeld of Human Activity Recognition

(HAR). This data is recorded at a particular sampling rate and then usually separated into time windows be-

fore classiﬁcation takes place. Though the sampling rate and window size can have a signiﬁcant impact on the

accuracy of the trained classiﬁer, there has been relatively little research on their role in activity recognition.

This paper presents a statistical analysis on the effect the sampling rate and window sizes on HAR data classi-

ﬁcation. The raw data used in the analysis was collected from a hip-worn Actigraphy G3X+ at 100Hz from 77

subjects performing 23 different activities. It was then re-sampled and divided into windows of varying sizes

and trained using a single data classiﬁer. A weighted least squares linear regression model was developed and

two-way factorial ANOVA was used to analyze the effects of sampling rate and window size for different ac-

tivity types and demographic categories. Based upon this analysis, we ﬁnd that 10-second windows recorded

at 50Hz perform statistically better than other combinations of window size and sampling rate.

1 INTRODUCTION

The ﬁeld of Human Activity Recognition (HAR) is

dependent on a variety of instruments for data col-

lection — heart rate monitors, GPS, light sensors,

etc. — of which wearable triaxial accelerometers

are the most commonly utilized (Lara and Labrador,

2013), (Preece et al., 2009). Accelerometers are com-

mercially available in many formats, from modern

smartphones and consumer-grade activity-monitoring

products to high-grade research-oriented devices, the

consequences of which are wide degrees of quality in

data collection for HAR. When preparing for data col-

lection in a HAR study, two aspects of the accelerom-

eter to use should be strongly considered: the place-

ment of the device and the sampling rate at which it

gathers data.

The placement of the device depends greatly on

the context of the study. Many studies focusing on

ambulation activities (walking, running etc.) prefer

hip-worn or wrist-worn devices (Lara and Labrador,

2013), both of which have advantages and disadvan-

tages. Wrist-worn devices have trouble distinguishing

lower-body activities (for instance, walking and stair

climbing), while hip-worn devices can be problematic

when recognizing upper-body activities (for instance,

eating and brushing teeth). The impact of sampling

rate is discussed in later sections.

Once data has been collected — typically at a

ﬁxed sampling rate — it is prepared for classiﬁca-

tion by extracting relevant features such as means

and standard deviations and dividing the accelerom-

eter readings into windows. Often, windows of ﬁxed

length are used.

Both the sampling rate and window size of data

are crucial decisions in HAR which directly affect the

accuracy of developed classiﬁers. Though a literature

review revealed some relevant analyses (Section 2),

there appears to be a relative dearth of work directly

addressing sampling rate and window size in HAR.

This study is an attempt to remedy what we perceive

as a gap in the research. We have attempted to statisti-

cally identify the window size and sampling rate com-

bination which best suits activity recognition across

demographical and activity divisions.

The data used in this study was obtained from

77 demographically diverse subjects for 23 activities

in studies performed at Arizona State University in

Niazi A., Yazdansepas D., Gay J., Maier F., Ramaswamy L., Rasheed K. and Buman M.

Statistical Analysis of Window Sizes and Sampling Rates in Human Activity Recognition.

DOI: 10.5220/0006148503190325

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 319-325

ISBN: 978-989-758-213-4

319

Table 1: Description of Activities Performed.

# Activity Duration or Distance # of

sub-

jects

1 Treadmill at 27 młmin-1 (1mph) @ 0% grade 3 min 29

2 Treadmill at 54 młmin-1 (2mph) @ 0% grade 3 min 21

3 Treadmill at 80 młmin-1 (3mph) @ 0% grade 3 min 28

4 Treadmill at 80 młmin-1 (3mph) @ 5% grade (as tolerated) 3 min 29

5 Treadmill at 134 młmin-1 (5mph) @ 0% grade (as tolerated) 3 min 21

6 Treadmill at 170 młmin-1 (6mph) @ 0% grade (as tolerated) 3 min 34

7 Treadmill at 170 młmin-1 (6mph) @ 5% grade (as tolerated) 3 min 26

8 Seated, folding/stacking laundry 3 min 74

9 Standing/Fidgeting with hands while talking. 3 min 77

10 1 minute brushing teeth + 1 minute brushing hair 2 min 77

11 Driving a car - 21

12 Hard surface walking w/sneakers 400m 76

13 Hard surface walking w/sneakers hand in front pocket 100m 33

14 Hard surface walking w/sneakers while carry 8 lb. object 100m 30

15 Hard surface walking w/sneakers holding cell phone 100m 24

16 Hard surface walking w/sneakers holding ﬁlled coffee cup 100m 26

17 Carpet w High heels or dress shoes 100m 70

18 Grass barefoot 134m 20

19 Uneven dirt w/sneakers 107m 23

20 Up hill 5% grade w high heels or dress shoes 58.5m x 2 times 27

21 Down hill 5% grade w high heels or dress shoes 58.5m x 2 times 26

22 Walking up stairs (5 ﬂoors) 5 ﬂoors x 2 times 77

23 Walking down stairs (5 ﬂoors) 5 ﬂoors×2 times 77

2013 and 2014. Data was collected from a single hip-

worn triaxial accelerometer, an ActiGraph GT3X+, at

a sampling rate of 100Hz. By artiﬁcially downsam-

pling the data and creating differently sized windows,

we have obtained datasets at a cross section of 6 win-

dow sizes and 5 sampling rates. Multiple classiﬁers

were tested out and random forests was selected as

the standard classiﬁer for this study. We used our

standard classiﬁer to train these datasets with 10-fold

cross-validation and statistically observed the trends

using repeated measures two-way ANOVA. We then

further divided these datasets to observe how these ef-

fects change due to activity type or demographic fea-

tures of the subject.

It should be noted that this study, by necessity,

takes into account only certain aspects of HAR clas-

siﬁcation process. For example, we are utilizing data

from a single hip-worn accelerometer, as opposed

to other or multiple placements. Similarly, we use

only time- and frequency-based features with a sin-

gle classiﬁer (Random Forests) to further standardize

our tests. While feature sets and classiﬁer selection

certainly play a role in the outcomes of HAR classi-

ﬁcation research (Preece et al., 2009), to account for

all of them would lead to an signiﬁcant increase in

complexity which could be better examined in future

research.

Section 2 details the literature available in this do-

main. Section 3 describes the data collection and pre-

processing done to the data to obtain our data sets.

Section 4 gives the results of our classiﬁcation and

statistical analysis of these results. Finally, Section

5 states what we conclude from this work and how

these conclusions can be implemented in HAR data

classiﬁcation.

2 RELATED WORK

While a considerable amount of research has been

done in HAR using accelerometers, there has been

a lack of consensus on the methodology of collect-

ing and preprocessing data and thus this topic has

largely remained unanalyzed (Preece et al., 2009).

Lara and Labrador (2013) note that sampling rates in

HAR studies vary from 10Hz to 100Hz while win-

dow sizes range from less than 1 second to 30 sec-

onds. While there are some domain-related justiﬁca-

tions for such decisions, there is a lack of standardiza-

tion which likely impacts replicability.

Lau and David (2010) attempted a study similar

HEALTHINF 2017 - 10th International Conference on Health Informatics

320

to ours, in the sense that multiple data sets of dif-

fering window sizes (0.5, 1, 2 and 4 seconds) and

sampling rates (5, 10, 20 and 40 Hz) were gener-

ated from raw accelerometer data (gathered from a

pocketed smart phone) and the effects studied. While

they claim that these lower values are sufﬁcient for

good performance, their setup consisted of a single

test subject performing 5 activities. Maurer et al.

(2006), using 6 subjects, state that recognition accu-

racy does not signiﬁcantly increase at sampling rates

above 15-20Hz when their biaxial accelerometer is

used in conjunction with 3 other sensors (light, tem-

perature and microphone). Bieber et al. (2009) calcu-

late that 32Hz should be the minimum sampling rate

given human reaction time. Tapia et al (2007) varied

window length from 0.5 to 17 seconds and tested the

data sets with C4.5 decision tree classiﬁers, conclud-

ing that 4.2 seconds was the optimum window size for

their needs. Banos et al (2014) created data sets with

window sizes ranging from 0.25 to 7 seconds at inter-

val jumps of 0.25. They found that 1-2 seconds is the

best trade-off speed and accuracy for online training.

Larger windows were only needed if the feature set

was small.

Statistical analysis of classiﬁer performance ap-

pears infrequently performed. Most studies, such

as the ones cited above, simply state a performance

measure (often accuracies and f-measures) but do

not present any statistical evaluation. Demsar (2006)

comments on the lack of statistical analysis of classi-

ﬁer performance and prefers non-parametric tests for

comparing classiﬁers over parametric ones. The pa-

per also notes that replicability is a problem for most

experiments machine learning domain, hence experi-

ments should be tested on as many data sets as possi-

ble.

3 DATA COLLECTION,

PREPROCESSING AND

METHODOLOGY

3.1 Collecting Data

The data used in the present study was collected in

Phoenix, AZ from volunteers recruited through Ari-

zona State University. Participants were ﬁtted with an

ActiGraph GT3X+ activity monitor positioned along

the anterior axillary line of the non-dominant hip. The

monitor was ﬁxed using an elastic belt. The Acti-

Graph GT3X+ (ActiGraph) is a lightweight monitor

(4.6cm x 3.3cm x 1.5 cm, 19g) that measures triaxial

acceleration ranging from -6g to +6g. Devices were

initialized to sample at a rate of 100hz. Accelerometer

data was downloaded and extracted using Actilife 5.0

software (ActiGraph LLC, Pensacola, FL). The sub-

jects performed a number of activities which can be

observed in Table 1.

Data from 77 subjects (53 female and 24 male)

was used to train the classiﬁers. The 77 subjects were

taken from a larger group of 310 subjects who partici-

pated in the study. They were chosen for their relative

diversity in both demographics and the activities they

performed. Table 1 describes the activities performed

while Table 2 provides demographic information on

the subjects.

Table 2: Subject Demographics.

Mean Standard Deviation Range

Age (Years) 33.2 9.7 18.2 - 63.2

Height (cm) 167.9 7.9 152.6 -188.9

Weight (kg) 72.1 12.1 48.3 - 105.5

BMI 25.6 3.9 17.7 - 35.4

3.2 Generating Datasets

As noted earlier, the raw data was collected at a sam-

pling rate of 100Hz. From this, 30 data sets with

varying window sizes (of 1, 2, 3, 5 and 10 seconds)

with sampling rates (5, 10, 20, 25, 50 and 100Hz)

were created. To create data sets for sampling rates

< 100Hz, we downsampled from the original data

sets, e.g., 50Hz is generated by using every 2nd ac-

celerometer record (100/50), 25Hz using every 4th

record (100/25), etc. The number of records in a win-

dow then depends on the sampling rate as well as the

window size. E.g., A 1-second window at 100 Hz

contains 100 records (100x1), a 3-second window at

25Hz contains 75 records (3x25), and so on. As sum-

marized in Table 3, the window size affects the num-

ber of records in the data set, a fact that will become

signiﬁcant during analysis.

It should also be noted that, in some situations,

partial windows are formed; in these, not enough data

exists to form a complete window. Such partial win-

dows were discarded in order to provide the classiﬁer

a data set with a uniform format.

Table 3: Number of Records in the Datasets.

Window Size (s) No. of Records

1 175284

2 88557

3 59666

5 36533

10 19186

Statistical Analysis of Window Sizes and Sampling Rates in Human Activity Recognition

321

3.3 Feature Extraction and Selection

246 features were extracted using the raw accelerom-

eter data which were then reduced to a 32 feature

data set with time- and frequency-based features. The

32 feature set was reduced through correlation-based

feature selection, as well as from experts in the do-

main of human activity recognition. For more infor-

mation on feature selection, see (Niazi et al., 2016).

• Features in the Time Domain: These features in-

clude the mean, standard deviation and 50th per-

centile of each axis (x, y and z) and their vector

magnitude as well as the correlation values be-

tween the axes.

• Features in the Frequency Domain: These fea-

tures include the dominant frequency and its mag-

nitude for each axis (x, y and z) as well as their

vector magnitude.

3.4 Methodology

Random forest classiﬁers perform very well with this

data set (Niazi et al., 2016) and so this was chosen

as our standard classiﬁer. Each data set was divided

and evaluated in 10 folds. Further divisions were

carried out for certain activity groups (see Table 4)

or demographic groups. The accuracy on the test

fold was recorded. WEKA software packages (Hall

et al., 2009) were used in conjunction with custom

Java code for training and testing the data sets.

RStudio (RStudio Team, 2015) was used to eval-

uate results. A two-way factorial ANOVA was car-

ried out with weighted least squares to calculate the

expected average value (EV) for every combination.

It was found that window size and sampling rate as

well as their interaction were statistically signiﬁcant.

By determining the maximum expected accuracy (the

maximum EV), we discovered the accuracy remained

signiﬁcant at the 95% conﬁdence level. The next

section details the analysis and results of our exper-

iments.

Table 4: Division of activities in the clusters.

Non-Ambulatory Activities

8,9,10,11

Ambulatory Activities

Walking 1,2,3,4,12,13,14,15,

16,17,18,19,20,21

Running 5,6,7

Upstairs 22

Downstairs 23

4 STATISTICAL ANALYSIS OF

RESULTS

4.1 Weighting

From Table 3, it is clear that window size directly af-

fects the number of records in the data set. Table 5

shows that the variance increases as window size in-

creases, and so the weighting function should be in-

versely proportional to the variance. For the weighted

least squres, we use 1/WindowSize as an approxima-

tion.

Although sampling rate can also be seen to have

a small effect on the variance, it appears negligible.

All experiments use this weighting function to nor-

malize the distributions.

Table 5: Standard Deviations.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.0035 0.0034 0.0032 0.0029 0.0027 0.0021

2 0.0051 0.0031 0.0048 0.0032 0.0057 0.0032

3 0.0049 0.0071 0.0076 0.0066 0.0040 0.0054

5 0.0045 0.0057 0.0092 0.0108 0.0107 0.0071

10 0.0091 0.0129 0.0074 0.0082 0.0098 0.0096

How the standard deviation varies according to window

size and sampling rate for the data.

Subsection 4.2 describes in detail the statistical

process followed by all the experiments.

4.2 All Activities and Demographics

Our ﬁrst test evaluated all the data available, i.e., for

23 activities as performed by 77 subjects. The ob-

jective was to ﬁnd the maximum average expected

value (EV ) and use this to determine if other values

can be considered statistically signiﬁcant. A two-way

analysis of variance (ANOVA) on a Weighted Least

Squares (WLS) linear regression model shows that

both window size and sampling rate have a signiﬁcant

effect on accuracy with 99% conﬁdence (p<0.001).

The linear model is then used to obtain EV s for all

window size/sampling rate combinations. These val-

ues are show in Table 6.

Table 6: All Activities/Demographics.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.5858 0.6868 0.7893 0.8050 0.8251 0.8292

2 0.6324 0.7355 0.8219 0.8334 0.8456 0.8435

3 0.6544 0.7551 0.8269 0.8385 0.8488 0.8411

5 0.6848 0.7752 0.8322 0.8379 0.8473 0.8282

10 0.7316 0.8050 0.8474 0.8529 0.8583 0.8126

Values shown are the average expected value (EV ) for

accuracy on each dataset

The weighting scheme was chosen after a consultation

with the University of Georgia Statistics Consulting Center.

HEALTHINF 2017 - 10th International Conference on Health Informatics

322

The 10s/50Hz data set has the highest expected

value (EV

max

) for accuracy (in bold underline in Ta-

ble 6) in this experiment. Next we determine if other

accuracy EVs are signiﬁcantly different than the max-

imum EV

max

. As the alternate hypothesis is that other

combinations will have lower EV s, we use a 1-sided

t-test with a 95% conﬁdence interval.

max

−

= t

290,0.95

∗

√

MSE ∗

W S

max

W S

(1)

Equation 1 is used to ﬁnd the critical distance

when the sample sizes are unequal but the variance is

assumed equal. As each EV represents 10 folds, we

have 290 degrees of freedom. The value of t

290,0.95

is found as 1.651. The MSE value is obtained from

ANOVA. W S represents window size of EV

max

while

W S

and n is the number of observations which in our

case is always 10. Having found the critical distance,

we can observe which EV values fall inside the mar-

gin.

In this experiment, the 10s/25Hz value (in bold

in Table 6) is less than the critical distance away from

max

. Hence, it can be concluded that it is statisti-

cally as accurate as EV

max

with 95% conﬁdence.

The procedure elaborated in this section is repli-

cated for all of the following experiments.

4.3 Activity Groups

In Table 7, ambulatory activities were separated

from non-ambulatory activities while in Table 8 they

were classiﬁed as walking, running or stairclimb-

ing activities. Both experiments represent a macro-

classiﬁcation and as such exhibit similar patterns to

Table 6 — the 10s/50Hz has EV

max

Tables 7-12 show the results of experiments on

different activity group classiﬁcations. These groups

were divided as shown in Table 4.

However, classiﬁcations at a micro-level, within

these activity groups, exhibit different results. Classi-

fying between ascending and descending stairs (Ta-

ble 9) achieves EV

max

of 97% at 2s/50Hz. How-

ever, statistically signiﬁcant EV s for the experiment

are spread across a wide range of window sizes and

sampling rates. Interestingly data at lower sampling

rates are also deemed signiﬁcant for larger window

sizes. Statistical values for non-ambulatory activities

(Table 10) show similar patterns. For walking and

running activities, the spread is smaller and concen-

trated towards higher sampling rates, though there is

a lot of variation in window size. Running in partic-

ular prefers smaller windows. This is in agreement

with the claim by Bieber, et al (2009) that the sam-

pling rate should be more than 32Hz for ambulatory

activities.

4.4 Demographics

For the next round of experiments, data was separated

into demographic groups to observe any signiﬁcant

effects. The data sets were then used to classify all 23

activities.

Division by gender, female (53 subjects) and male

(24 subjects) (Tables 13 and 14 respectively) display

similar results. EV

max

is at 10s/50Hz for both experi-

ments and there are very similar spreads in signiﬁcant

results. This indicates that there is an insigniﬁcant dif-

ference in HAR for genders and activity classiﬁcation

should be generalized for both cases.

Data was then divided into 4 age groups; 18 −25

(24 subjects), 26 −32 (24 subjects), 33 −44 (21 sub-

jects) and 49−63 (8 subjects). The results of these ex-

periments are recorded in Tables 15-18, respectively.

There is a visible trend of decreasing window size

with increasing age. The spread of signiﬁcant values

gets larger as well.

Similar patterns are noted when the data is divided

according to Body Mass Index (BMI) categories;

Normal (40 subjects), Overweight (28 subjects) and

Obese (9 subjects) (Tables 19-21). As BMI increases,

the signiﬁcance of the EV

max

decreases along with the

window size. Subjects with lower BMIs fare better

with larger windows than those with higher BMIs.

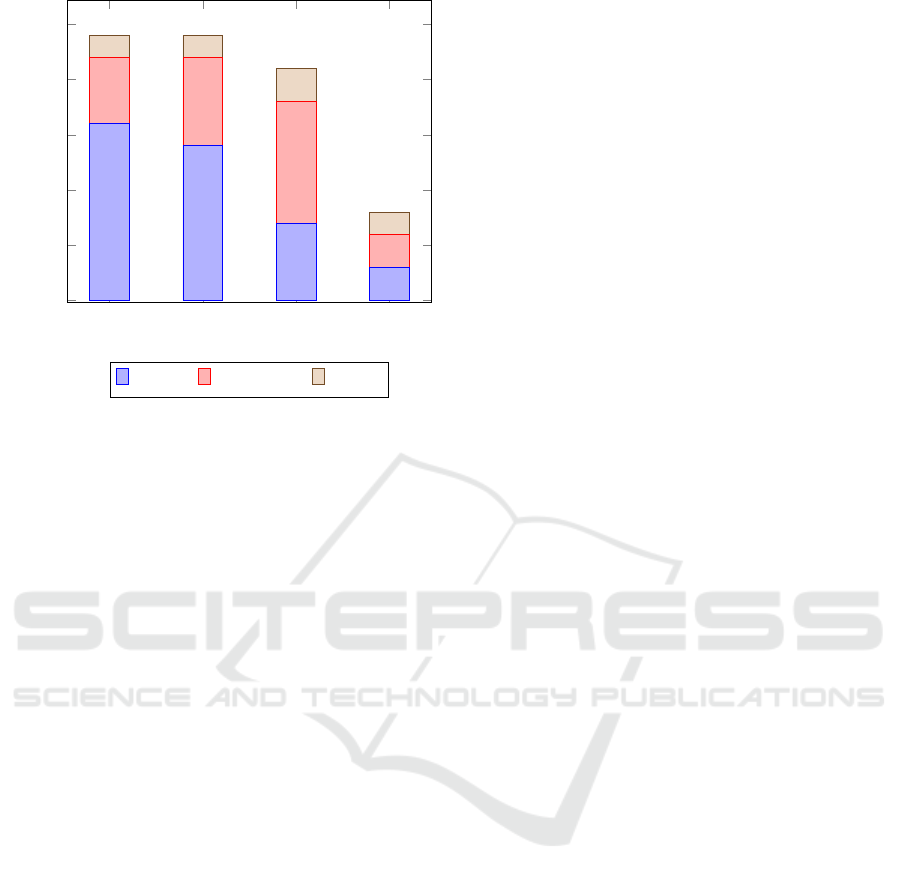
This can suggest a correlation between age and BMI

- elderly people are less likely to be active than young

people and are thus more likely to have high BMIs.

This hypothesis is supported in Figure 1 which shows

that the proportion of normal weighted people de-

creases with age in the dataset.

4.5 Summary of Analysis

Viewing all experiments together suggests that

10s/50Hz is the optimal combination of window size

and sampling rate, especially if the subjects of the

study are young, able-bodied and physically active.

Most high signiﬁcant EV are spread around high

sampling rates and window sizes, although there is

enough evidence to suggest there is not a very signiﬁ-

cant loss in accuracy if the sampling rate is decreased

to 25Hz or window size is decreased to 2s.

Statistical Analysis of Window Sizes and Sampling Rates in Human Activity Recognition

323

Table 7: Ambulatory vs. Non-Ambulatory Activites.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.6408 0.7295 0.8228 0.8369 0.8559 0.8590

2 0.6812 0.7735 0.8521 0.8634 0.8754 0.8730

3 0.7016 0.7957 0.8605 0.8688 0.8791 0.8725

5 0.7319 0.8127 0.8656 0.8727 0.8796 0.8634

10 0.7792 0.8419 0.8805 0.8876 0.8913 0.8537

Table 8: Ambulatory Activity Groups.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.8345 0.8720 0.9065 0.9106 0.9165 0.9170

2 0.8345 0.8872 0.9155 0.9177 0.9219 0.9195

3 0.8609 0.8951 0.9181 0.9211 0.9254 0.9200

5 0.8754 0.9045 0.9237 0.9267 0.9293 0.9180

10 0.9022 0.9264 0.9412 0.9411 0.9440 0.9169

Table 9: Stairs: Ascent vs. Descent.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.9555 0.9640 0.9675 0.9682 0.9690 0.9694

2 0.9599 0.9652 0.9681 0.9686 0.9697 0.9690

3 0.9611 0.9651 0.9670 0.9675 0.9690 0.9673

5 0.9618 0.9655 0.9668 0.9672 0.9670 0.9647

10 0.9650 0.9676 0.9676 0.9690 0.9687 0.9624

Table 10: Non-Ambulatory Activites.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.7854 0.8298 0.8609 0.8647 0.8711 0.8723

2 0.8086 0.8471 0.8726 0.8783 0.8795 0.8775

3 0.8161 0.8476 0.8734 0.8732 0.8780 0.8746

5 0.8246 0.8525 0.8682 0.8730 0.8726 0.8594

10 0.8406 0.8571 0.8713 0.8716 0.8716 0.8514

Table 11: Walking Activites.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.5556 0.6656 0.7916 0.8105 0.8329 0.8385

2 0.5976 0.7162 0.8274 0.8407 0.8581 0.8574

3 0.6189 0.7415 0.8344 0.8460 0.8598 0.8543

5 0.6474 0.7594 0.8374 0.8408 0.8527 0.8353

10 0.6875 0.7746 0.8387 0.8491 0.8557 0.8159

Table 12: Running Activites.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.7081 0.7795 0.8522 0.8688 0.9070 0.9140

2 0.7349 0.8191 0.8793 0.8961 0.9185 0.9210

3 0.7418 0.8321 0.8891 0.8968 0.9176 0.9177

5 0.7584 0.8266 0.8703 0.8863 0.8953 0.8972

10 0.7728 0.8333 0.8639 0.8714 0.8759 0.8553

Table 13: Gender: Female Subjects.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.6037 0.7132 0.8128 0.8227 0.8405 0.8430

2 0.6509 0.7606 0.8388 0.8490 0.8599 0.8554

3 0.6762 0.7762 0.8433 0.8529 0.8598 0.8498

5 0.7052 0.7937 0.8441 0.8490 0.8539 0.8351

10 0.7521 0.8164 0.8586 0.8595 0.8667 0.8169

Table 14: Gender: Male Subjects.

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.6439 0.7248 0.8139 0.8265 0.8474 0.8508

2 0.6857 0.7633 0.8412 0.8506 0.8653 0.8624

3 0.7017 0.7815 0.8478 0.8569 0.8675 0.8597

5 0.7226 0.7984 0.8484 0.8547 0.8641 0.8408

10 0.7759 0.8183 0.8636 0.8678 0.8736 0.8253

Table 15: Age: 18-26 Years

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.6207 0.7174 0.8094 0.8236 0.8432 0.8457

2 0.6662 0.7620 0.8362 0.8488 0.8588 0.8553

3 0.6857 0.7824 0.8443 0.8559 0.8629 0.8551

5 0.7196 0.8024 0.8484 0.8542 0.8623 0.8424

10 0.7633 0.8292 0.8627 0.8717 0.8753 0.8250

Table 16: Age: 27-33 Years

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.6614 0.7513 0.8343 0.8428 0.8590 0.8618

2 0.7043 0.7891 0.8564 0.8676 0.8746 0.8731

3 0.7198 0.8051 0.8623 0.8678 0.8779 0.8677

5 0.7390 0.8117 0.8573 0.8643 0.8679 0.8488

10 0.7784 0.8292 0.8658 0.8695 0.8720 0.8250

Table 17: Age: 34-44 Years

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.6651 0.7660 0.8442 0.8547 0.8689 0.8722

2 0.7085 0.8038 0.8654 0.8730 0.8849 0.8805

3 0.7271 0.8193 0.8651 0.8730 0.8807 0.8696

5 0.7482 0.8226 0.8596 0.8624 0.8721 0.8533

10 0.7833 0.8424 0.8733 0.8792 0.8822 0.8375

Table 18: Age: 49-63 Years

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.7593 0.8382 0.8892 0.8981 0.9065 0.9063

2 0.7856 0.8581 0.9043 0.9084 0.9135 0.9146

3 0.8046 0.8689 0.9040 0.9067 0.9101 0.9030

5 0.8201 0.8730 0.9031 0.9017 0.9084 0.8855

10 0.8503 0.8986 0.9114 0.9114 0.9119 0.8725

Table 19: BMI: Normal

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.6031 0.7074 0.8056 0.8188 0.8363 0.8393

2 0.6531 0.7525 0.8320 0.8437 0.8531 0.8503

3 0.6776 0.7753 0.8395 0.8493 0.8553 0.8478

5 0.7138 0.7946 0.8446 0.8482 0.8549 0.8376

10 0.7617 0.8204 0.8614 0.8615 0.8678 0.8149

Table 20: BMI: Overweight

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.6419 0.7381 0.8256 0.8391 0.8564 0.8597

2 0.6831 0.7762 0.8520 0.8609 0.8714 0.8689

3 0.7002 0.7940 0.8523 0.8612 0.8701 0.8637

5 0.7225 0.8064 0.8549 0.8619 0.8696 0.8494

10 0.7612 0.8287 0.8607 0.8674 0.8732 0.8252

Table 21: BMI: Obese

Sampling Rate (Hz)

5 10 20 25 50 100

Window

Size (s)

1 0.7423 0.8279 0.8803 0.8900 0.8998 0.9015

2 0.7817 0.8532 0.9008 0.9039 0.9164 0.9115

0.7968 0.8648 0.9010 0.9098 0.9167 0.9098

5 0.8164 0.8663 0.8943 0.9001 0.9070 0.8878

10 0.8368 0.8774 0.8994 0.9125 0.9091 0.8648

HEALTHINF 2017 - 10th International Conference on Health Informatics

324

18-26 27-33 34-44 49-63

2 2

# of subjects

Normal Overweight Obese

Figure 1: Distribution of BMI groups over age groups.

5 CONCLUSION

This study provides some basis for the selection of

sampling rates and window sizes for human activity

recognition. The analysis indicates that 10s/50Hz is

statistically the best combination for data collected

with a single hip-worn accelerometer. Most of the ex-

periments carried out preferred larger windows and

high sampling rates though some low intensity ac-

tivities and demographics can perform better with

smaller windows. Our analysis further suggests that

window size can vary between 2-10 seconds and sam-

pling rate 25-100Hz for different situations without

a signiﬁcant loss in performance. While our study

has shown that larger windows are preferable, smaller

windows can still provide signiﬁcant results if power

consumption is an issue. Additionally, lower values

are preferable for studies involving the less dynamic

activities or subjects who are more liable to be less

active.

Future work in this ﬁeld should be done to un-

derstand aspects of Human Activity Recognition bet-

ter. This study was performed under some assump-

tions that can be scrutinized. The placement of the

accelerometer could be shown to affect classiﬁer per-

formance for different activities — a combination of

sensors can also be used. Other sensors, such as heart

rate monitors or video image processors, provide new

avenues. This study can also be replicated using dif-

ferent classiﬁers or learning methods with different

feature sets. Extensive analysis on the statistical value

of other machine learning and data mining methods

could also help the ﬁeld as a whole.

REFERENCES

ActiGraph. Actisoft analysis software 3.2 user’s manual.

fort walton beach, ﬂ: Mti health services.

Banos, O., Galvez, J.-M., Miguel Damas, H. P., and Ro-

jas, I. (2014). Window size impact in human activity

recognition. Sensors, pages 6474–6499.

Beiber, G., Voskamp, J., and Urban, B. (2009). Activity

recognition for everyday life on mobile phones. Inter-

national Conference on Universal Access in Human-

Computer Interaction, pages 289–296.

Demsar, J. (2006). Statistical comparisons of classiﬁers

over multiple data sets. Journal of Machine Learning

Research, 7:1–30.

Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,

P., and Witten, I. H. (2009). The weka data min-

ing software: An update. SIGKDD Explor. Newsl.,

11(1):10–18.

Lara, O. D. and Labrador, M. A. (2013). A survey

on human activity recognition using wearable sen-

sors. IEEE Communication Surveys and Tutorials,

15:1192–1209.

Lau, S. and David, K. (2010). Movement recognition us-

ing the accelerometer in smartphones. IEEE Future

Network ands Mobile Summit 2010, pages 1–9.

Maurer, U., Smailagic, A., Siewiorek, D. P., and Deisher,

M. (2006). Activity recognition and monitoring using

multiple sensors on different body position. Interna-

tional Workshop on Wearable and Implantable Body

Sensor Networks.

Niazi, A., Yazdensepas, D., Gay, J., Maier, F., Rasheed, K.,

Ramaswamy, L., and Buman, M. (2016). A hierar-

chical meta-classiﬁer for human activity recognition.

IEEE International Conference on Machine Learning

and Applications.

Preece, S. J., Goulermas, J. Y., Kenney, L. P. J., Howard,

D., Meijer, K., and Crompton, R. (2009). Activ-

ity identiﬁcation using body-mounted sensorsa review

of classiﬁcation techniques. Physiological Measure-

ment, 30(4):R1.

RStudio Team (2015). RStudio: Integrated Development

Environment for R. RStudio, Inc., Boston, MA.

Tapia, E., Intille, S., Haskell, W., Larson, K., Wright, J.,

King, A., and Friedman, R. (2007). Real-time recog-

nition of physical activities and their intensities us-

ing wireless accelerometers and a heart rate monitor.

IEEE 11th IEEE international symposium on wear-

able computers, pages 37–40.

Yazdansepas, D., Niazi, A. H., Gay, J. L., Maier, F. W., Ra-

maswamy, L., Rasheed, K., and Buman, M. P. (2016).

A multi-featured approach for wearable sensor-based

human activity recognition. IEEE International Con-

ference on Healthcare Informatics (ICHI), Chicago,

IL.

Statistical Analysis of Window Sizes and Sampling Rates in Human Activity Recognition

325