
Optimized Limited Memory and Warping LCSS for Online Gesture
Recognition or Overlearning?
Baptiste Lemarcis
1
, Valère Plantevin
1
, Bruno Bouchard
2
and Bob-Antoine-Jerry Ménélas
1
1
Department of Mathematics and Computer Science, Université du Québec à Chicoutimi (UQAC), Chicoutimi,
QC, G7H 2B1, Canada
2
IEEE Senior, Chicoutimi, QC, Canada
Keywords: Online Gesture Recognition, Streaming, Template Matching Method, LCSS, LM-WLCSS.
Abstract: In this paper, we present and evaluate a new algorithm for online gesture recognition in noisy streams. This
technique relies upon the proposed LM-WLCSS (Limited Memory and Warping LCSS) algorithm that has
demonstrated its efficiency on gesture recognition. This new method involves a quantization step (via the K-
Means clustering algorithm). This transforms new data to a finite set. In this way, each new sample can be
compared to several templates (one per class) and gestures are rejected based on a previously trained rejection
threshold. Then, an algorithm, called SearchMax, find a local maximum within a sliding window and output
whether or not the gesture has been recognized. In order to resolve conflicts that may occur, another classifier
could be completed. As the K-Means clustering algorithm, needs to be initialized with the number of clusters
to create, we also introduce a straightforward optimization process. Such an operation also optimizes the
window size for the SearchMax algorithm. In order to demonstrate the robustness of our algorithm, an exper-
iment has been performed over two different data sets. However, results on tested data sets are only accurate
when training data are used as test data. This may be due to the fact that the method is in an overlearning state.
1 INTRODUCTION
In everyday communications, a large part of infor-
mation is conveyed thought gestures. As a result, it
appears that some benefits would certainly come in
exploiting gesture recognition technics in Human-
Computer Interactions. Gesture recognition has be-
come important in a wide variety of applications such
as gesture-to-speech in sign languages (Kılıboz and
Güdükbay, 2015, Rung-Huei and Ming, 1998). In the
past years, smartphones and smartwatches have be-
come omnipresent in everyday life (Guiry et al.,
2014), being equipped with multiple motion-related
sensors such as accelerometers, gyroscopes and mag-
netometers, they allow sensing raw data related to
movements of users. With the treatment of these data
streams, multiple techniques allow to detect per-
formed gestures. The literature regarding online ges-
ture recognition counts many methods such as Hidden
Markov Model (Hyeon-Kyu and Kim, 1999), Support
Vector Machine (Dardas and Georganas, 2011) and
Template Matching Methods (TMMs). TMMs ex-
press gestures as templates that are compared with the
data-stream afterward. The objective of such a com-
putation is to find similarities, where the highest af-
finity involves the recognition of the fittest gesture.
To do so, TMMs may employ Dynamic Time Warp-
ing (DTW) as similarity measure (Reyes et al., 2011).
Although DTW-based TMMs achieve accurate
results, the work described in (Vlachos et al., 2003)
shows that this method is not well suited to handle
time series and noise produced by inertial sensors. In
that sense, the LM-WLCSS (Limited Memory and
Warping Longest Common Sub-Sequence) aims at
overcoming issues brought by DTW. This method re-
lies upon the WLCSS method, an extension of the
LCSS problem. However, Roggen et al. (2015) did
not focus on class optimization and set arbitrary pa-
rameters for the clustering algorithm and the size of
the window. In this paper, we want to improve the
LM-WLCSS algorithm, hence we present a new
method based on that algorithm by focusing on the
class optimization process to spot gestures of a
stream. To achieve it, we train and optimize the LM-
WLCSS for each class. More precisely, the process
that convert the uncountable set of accelerometer data
to a countable one, called the quantization process, is
108
Lemarcis B., Plantevin V., Bouchard B. and MÃl’nÃl’las B.
Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?.
DOI: 10.5220/0006151001080115
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 108-115
ISBN: 978-989-758-229-5
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

performed for each gesture independently as the en-
tire recognition flow. The final decision is achieved
through a decision fusion.
The remainder of this paper is organized as fol-
lows. Section 2 reviews template matching methods
based on the longest common subsequence (LCSS).
Section 3 describes the proposed method. Next, sec-
tion 4 exposes data sets used for our experiments.
Section 5 reviews and discusses the results obtained.
Finally, Section 6 draws a conclusion.
2 RELATED WORK
In this paper we present a new approach, based on the
LM-WLCSS. Our state of the art briefly summarizes
related methods. We first introduce the training phase
of the Segmented and Warping LCSS. Then, the
recognition phase of these methods are described re-
spectively. We also present the LM-WLCSS as our
technique is derived from it. Finally, we present our
contributions to the LM-WLCSS.
Templates matching methods (TMMs) (Hart-
mann and Link, 2010) based on Dynamic Time Warp-
ing (Hartmann and Link, 2010), were demonstrated
as non-efficient in presence of noisy raw signals (Vla-
chos et al., 2003). To handle such data, Long-Van et
al. (2012) have introduced two new methods, based
on Longest Common Subsequence (LCSS), Segment-
edLCSS and WarpingLCSS. Both methods share the
same training phase. This training allows converting
accelerometer data into strings. This is due to the fact
that LCSS is based on a problem that relies upon
strings. For this, raw signals must be quantized. The
quantization step, proposed in (Long-Van et al.,
2012), involves computing clusters upon the training
data with the K-Means algorithm. Those centroids are
associated with pre-defined symbols to form strings.
Therefore, each gesture instance is represented as a
sequence of symbols. A LCSS score is associated
with each sequence. The higher the LCSS score is be-
tween two elements, the greater the similarity is. A
gesture instance is thus defined as a temporary tem-
plate. The final motif is chosen based on the one with
the highest average LCSS score. However, in order to
be able to compute whether a signal belongs to a ges-
ture class or not, a rejection threshold is associated
with the template. This threshold is defined as the
minimum LCSS between the previously elected tem-
plate and all other gesture instances of the same class.
Yet, Nguyen-Dinh et al. (2014b) have suggested a
new rejection threshold calculation, based on the
mean μ
c
and standard deviation σ
c
of LCSS scores for
the given class c. The resulting threshold ε is defined
as ε= μ
c
-h·σ
c
, where h is an integer that allows ad-
justing the sensitivity of the algorithm for this class.
In the Segmented LCSS recognition process, the
stream is stored in a sliding window OW. Each sam-
ple of this window is associated with previously gen-
erated centroids and its related symbol, based on the
minimum Euclidean distance. Then, this new string is
entirely compared to the template computed during
the training. If the resulting score exceeds the rejec-
tion threshold, of the associated class, then the gesture
is associated to c. However, a gesture may be spotted
as belonging to more than one class. To resolve such
conflicts, a resolver may be added, as proposed in
(Long-Van et al., 2012). It is based on the normalized
similarity
NormSim(A, B) = LCSS(A,B)/max(
‖
A
‖
,
‖
B
‖
), where
‖
‖
and
‖
‖
are respectively the length of A and B
strings. The class with the highest NormSim is then
marked as recognized. However, the Segmented
LCSS method implies to recompute the score each
time the sliding window is shifted. As a result, the
computation time is O(T
2
) (with T the size of the
longest template) in the worst case. However, without
OW the LCSS algorithm cannot find boundaries of in-
coming gestures. In this way, Long-Van et al. (2012)
have introduced a new variant of the LCSS called
WLCSS (WLCSS).
The WLCSS method removes need of a sliding
window and improves the computational cost as it au-
tomatically determines gesture boundaries. In this
new variant, quantized signals are still compared to
the template of a given class. Nevertheless, this ver-
sion only update the score for each new element,
starting from zero. This score grows when a match
occurs and decreases thanks to penalties otherwise.
The penalty consists of a weighted Euclidean distance
between symbols, whether it is a mismatch, a repeti-
tion in the stream or even in the template. In a newer
version presented in (Nguyen-Dinh et al., 2014b), the
distance is normalized. Once the matching score is
updated, the final result is output by the same decision
maker used in the SegmentedLCSS method. The re-
sulting time complexity for this new method is O(T).
Although the computational cost WLCSS is one order
of magnitude lower than the SegmentedLCSS, the
memory usage remains O(T
2
) in the worst case.
Recently, Roggen et al. (2015) have proposed a
new, microcontroller optimized, version of the
WLCSS algorithm called Limited Memory and
WLCSS (LM-WLCSS). Identically to previous meth-
ods, this one is designed to spot motif in noisy raw
signals and focuses on a single sensor channel. In this
way, a quantization step may not be required. More-
over, the training phase of this new variant has also
Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?
109

been modified to be embedded. This new step con-
sists in recording all gestures, and defining the first
instance as the template. The rejection threshold for
this template is then computed thanks to the LM-
WLCSS instead of the LCSS. As the WLCSS has
edged issues, authors have modified the formula, and
the resulting matching score is computed as follows:
M
j,i
0 ,ifi0orj0
M
j‐1,i‐1
R ,ifS
i
‐T
j
ε
max
M
j‐1,i‐1
‐P∙S
i
‐T
j
M
j‐1,i
‐P∙S
i
‐T
j
M
j,i‐1
‐P∙S
i
‐T
j
,ifS
i
‐T
j
ε
1
Where S
i
and T
j
are respectively defined as the first
i sample of the stream and the first j sample of the
template. The resulting score,
M
j,i
, starts from zero
and increases of reward R, instead of just one, when
the distance between the sample and the template
does not exceed a tolerance threshold
ε. Otherwise,
the warping occurs and the matching score
M
j,i
de-
creases of a penalty different from the WLCSS. This
last one is always equal to the weighted distance be-
tween
S
i
and T
j
, instead of relying on a mismatch, that
is to say, a repetition in the stream or even in the tem-
plate. Then, the resulting updated score is given to a
local maximum searching algorithm called Search-
Max, which filters scores exceeding the threshold
within a sliding window of size W
f
. Then, a one-bit
event is sent whether a gesture is spot or not. When a
match occurs, the start point of the gesture may be
retrieved by backtracking signals. This is performed
via a window of size W
b
to reduce unnecessary stored
elements. Thus, the overall memory usage, for a word
of size ws, is defined by NT∗wsNT∗WB with
NT representing the size of the template.
Moreover, in order to be able to manage multiple
acquisition channels with the LM-WLCSS technique,
two fusion methods were proposed. They are: the sig-
nal fusion (Nguyen-Dinh et al., 2014b, Long-Van et
al., 2012) and the decision fusion (Bahrepour et al.,
2009, Zappi et al., 2012). Observed performance
evaluations with these usages were obtained from the
Opportunity “Drill run”, representing 17 distinct ac-
tivities, and from 1 to 13 nodes. The resulting FScore
is 85% for the decision fusion and 80% for the signal
one. It demonstrates that higher is the number of
nodes, better is the recognition performance. Even
though other decision fusion methods have been pro-
posed in (Nguyen-Dinh et al., 2014a, Chen and Shen,
2014), there is no previous work, to the best of our
knowledge, that focus on optimizing the LM-WLCSS
for one class and perform a final decision fusion.
Hence, we introduce in this work a new variant of the
LM-WLCSS capable to handle multi-class, as well as,
a straightforward optimization for the quantization
and the windows size W
f
.
3 A NEW OPTIMIZED LIMITED
MEMORY AND WARPING
LCSS APPROACH FOR
ONLINE GESTURE
RECOGNITION
In this section, we introduce the Optimized LM-
WLCSS (OLM-WLCSS), our proposed approach for
online gesture recognition. This technique is robust
against noisy signals and strong variability in gesture
execution as well as methods we previously de-
scribed. This section first describes the quantization
step, following by the training phase. Then, the recog-
nition block for one class and the optimization pro-
cess are presented. Finally, we describe the decision-
making module.
3.1 Quantization
Similarly to the WLCSS, we use K-Means algorithm
to cluster the
data of the sensor in the quantization
step. Each sample from the sensor is represented as a
vector (e.g. an accelerometer is represented as a 3D
vector). Thus, each sensor vectors are associated with
their closest cluster centroid by comparing their Eu-
clidean distances. Since the WLCSS do store symbols
we suggest preserving centroids instead.
3.2 Training
This subsection presents the overall vision of our of-
fline training method on one class . In the case of
two or more classes, the process is repeated. Tem-
plates matching methods find similarities in the signal
and detect gesture via a motif. The template can be
elected as the best representation over the whole pos-
sible alternatives of the gesture in a training phase.
Such patterns maximize the recognition performance.
The overall process of our training is illustrated in
Figure 1. Raw signals are first quantized to create a
transformed training set. Next, this new data set is
used for electing a template. Finally, resulting motif
is given, as a parameter, to the rejection threshold cal-
culation method that output the tuple (template,
threshold).
HUCAPP 2017 - International Conference on Human Computer Interaction Theory and Applications
110
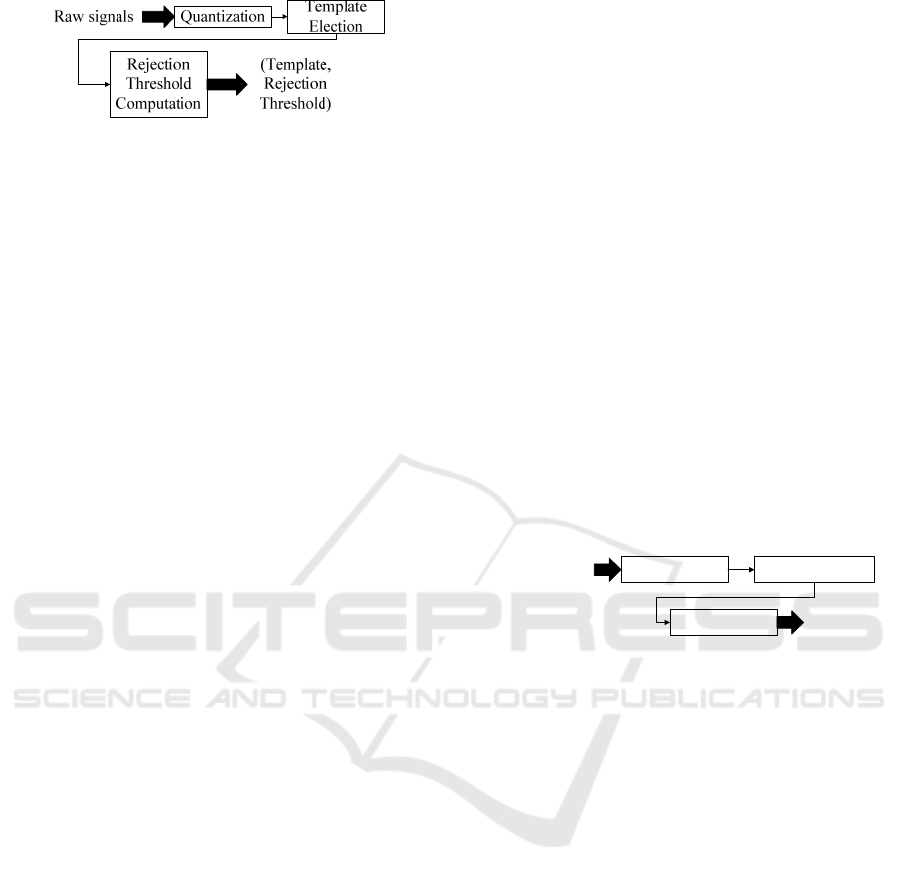
Figure 1: Overall training flow.
3.2.1 Template Election
Once the quantization phase is achieved, the next step
is to elect the best template. As described in (Long-
Van et al., 2012), such process is performed via the
LCSS method that has been modified to handle vector
instead of symbols. Each instance was defined as a
temporary template and then compared to the other
ones. The reference template is defined thanks to the
mean resulting score.
3.2.2 OLM-WLCSS
The core component of the presented method is the
computation of the matching score. This is achieved
thanks to the following formula:
M
j,i
0 ifi0orj0
M
j‐1,i‐1
R ifdS
,T
j
0
max
M
j‐1,i‐1
‐P
M
j‐1,i
‐P
M
j,i‐1
‐P
ifdS
,T
0
2
β∙d
S
,
T
(3)
Let d be the Euclidean distance between two cen-
troids,
the -th value of the quantized stream, and
the -th value of the template. Identically to its pre-
decessors, the initial value of the matching score
,
is zero. Then, this score is increased with the value of
R for every match when S
i
equal to T
j
. Otherwise, a
penalty P weighted by is applied. The resulting pen-
alty is expressed according to three distinct cases.
Firstly, when a mismatch between the stream and the
template occurs. Secondly, when there is repetition in
the stream and finally, when there is repetition in the
template. Similarly to the LM-WLCSS, only the last
column of the matching score is required to compute
the new one. It should be noted that a backtracking
method can be implemented to retrieve the starting
point of the gesture.
3.2.3 Rejection Threshold Calculation
The rejection threshold calculation is like the one pre-
sented in the LM-WLCSS algorithm. The score be-
tween the template and all the gesture instances of
class is computed with the core component of our
algorithm. Then, the matching score mean µ
c
and the
standard deviation σ
c
are calculated. The following
formula determines the resulting threshold:
Thd = µ - h · σ,h ∈
(3)
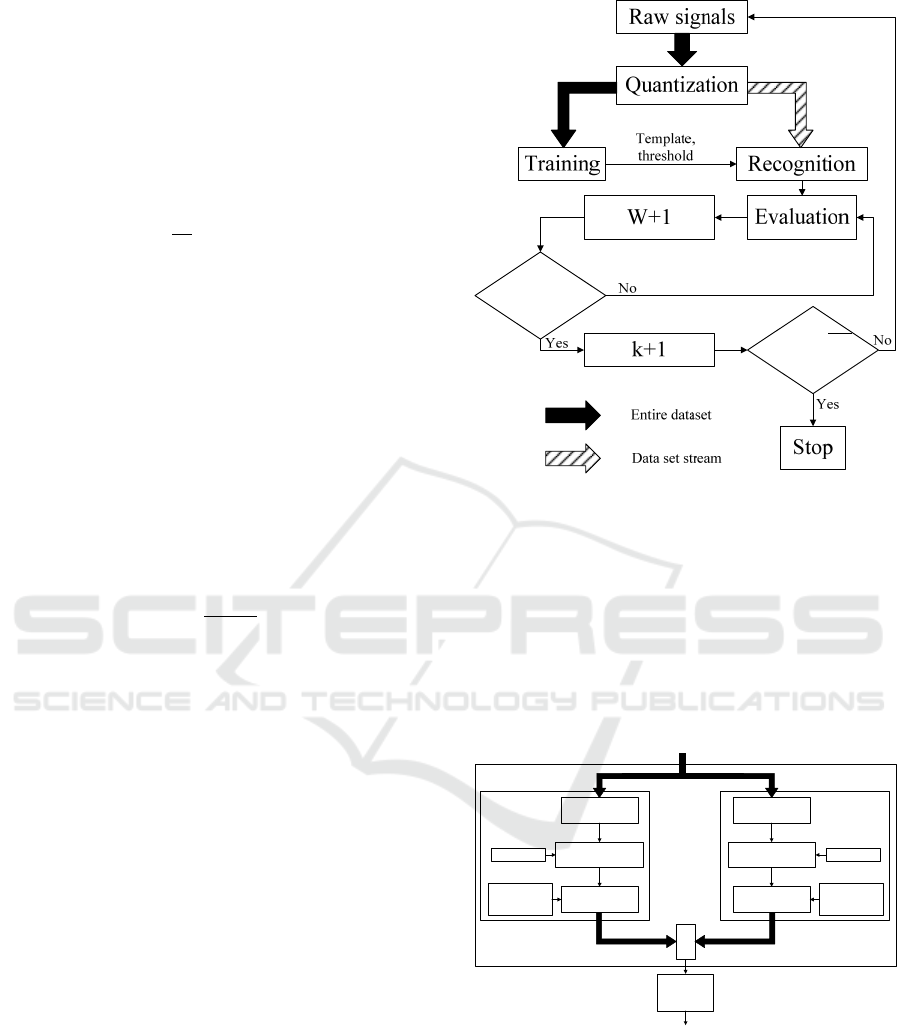
3.3 Recognition Blocks for One Class
The outcome of the previous phase is the best tuple
(template, rejection threshold) for each class. These
two elements define parameters that allow matching
a gesture to the incoming stream. Figure 2 illustrates
the recognition flow. As for the training, raw signals
are first quantized. The resulting sample and the pre-
viously elected template are given to the OLM-
WLCSS method presented in the training phase.
Next, the matching score is given to the SearchMax
algorithm that sends a binary event.
Quantization OLM-WLCSS
SearchMax
Raw Signals
Output
Figure 2: Overall single class recognition flow.
3.3.1 SearchMax
The matching score computed in previous steps
should increase and exceed the threshold if a gesture
is performed. However, noisy signals imply fluctua-
tions and undesired detections. To overcome such is-
sues, we used the SearchMax algorithm which was
introduced in (Roggen et al., 2015). Its goal is to find
local maxima among matching scores in sliding win-
dow W
f
. SearchMax loops over the scores and com-
pares the last and the current score to set a flag; 1 for
a new local maximum (Max
sm
) and 0 for a lower
value. A counter (K
sm
) is increased at each loop.
When K
sm
exceeds the size of W
f
the value of Max
sm
is compared to the threshold Thd. Eventually, the al-
gorithm returns a binary result; 1 if the local maxi-
mum is above Thd to indicate that a gesture has been
recognized, 0 otherwise.
3.4 Quantization and SearchMax
Optimization
The previously described quantization phase associ-
ates each new sample to the nearest centroid of the
Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?
111
class c. Thus, each class has a parameter
that de-
fined the number of clusters generated in the training
phase. In prior work, Long-Van et al. (2012) have de-
fined it with a value of 20 after they ran some tests. In
this way, we have also performed some tests with var-
ious cluster numbers. It appears that this parameter
highly impacts the performance of the algorithm.
Thus, we propose a straightforward optimization as
illustrated in Figure 3.This step consists of iteratively
running the training process with different
. There-
fore, we define 2,
N
c
as boundaries for
, where
N
c
is the number of samples used for the training of
the class c. For the same reason, we tried to vary the
sliding windows W
f
we previously introduced, and
noticed better performances from one to another.
Consequently, we choose to adopt the same way as
for
, and increment W
f
from zero to twice the tem-
plate size. The resulting best pair is elected based on
its performance. To perform the evaluation, we de-
cide to base the vote on the Cohen Kappa, as advice
in (Ben-David, 2007), instead of accuracy that could
be high due to a mere chance. The Kappa is computed
from observed probabilities (P
) and expected ones
(P
) as follows:
Kappa =
P
o
- P
e
1 - P
e
(4)
3.5 Final Decision
Previous steps were independently performed for
each gesture class. However, noise in raw signals and
high variations in gesture execution can lead to mul-
tiple detections. Several methods are available to re-
solve conflicts, such as the weighted decision de-
scribed in (Banos et al., 2012). In our system, we
choose to employ the lightweight classifier C4.5
(Quinlan, 2014), that requires a supervised training.
The overall representation of the recognition flow is
illustrated in Figure 4.
k>
N
c
W > W
u
Figure 3: Overall optimization process.
The training of C4.5 comes directly after the op-
timization step. It is performed using a 10-Fold cross-
validation on a data set previously created. This file
may be considered as a ∗ matrix, with is the
number of samples from the template training data
set, and M is the amount of recognition blocks. Each
element r
i,j
of this matrix represents the result of the
j-th recognition block for the i-th sample.
Raw signals
Quantization
OLM-WLCSS
SearchMax
d
1
⋮
d
m
Quantization
OLM-WLCSS
SearchMax
Template
Rejection
Threshold
Template
Rejection
Threshold
c
1
c
m
Decision
Making
FinalDecision
Decisionvector
Figure 4: Overall recognition flow for m class.
4 DATA USED FOR OUR
EXPERIMENTS
In order to evaluate the reliability of our algorithm,
we have exploited two different data sets. None of
HUCAPP 2017 - International Conference on Human Computer Interaction Theory and Applications
112
these sets are the ones used in (Roggen et al., 2015).
Indeed, in (Roggen et al., 2015) results were obtained
on a private data set with arbitrary parameter. In this
way a proper comparison with this algorithm is not
possible.
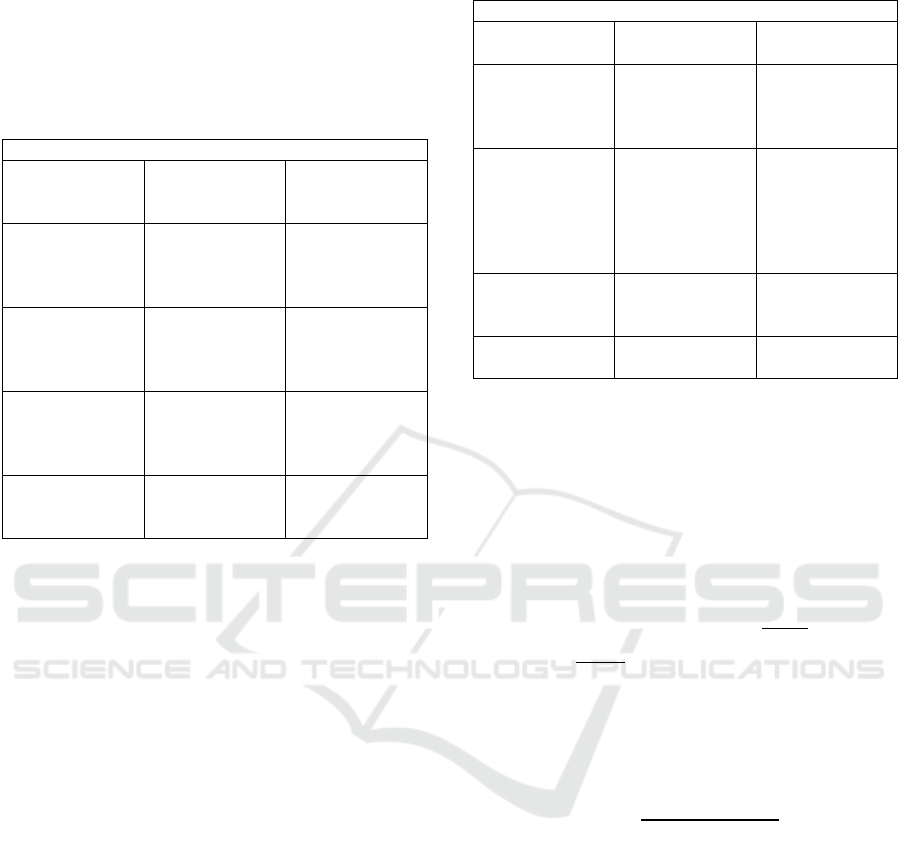
Table 1: All gestures of Make Coffee data set.
Make Coffee Gestures
opening the
brew basket lid
(G1)
getting the
measuring
spoon (G6)
getting the de-
canter (G11)
pushing the
shower head
(G2)
adding six
spoons of coffee
in the filter (G7)
pouring the wa-
ter into the wa-
ter reservoir for
5 seconds (G12)
putting filter
into the filter
basket (G3)
putting away
the measuring
spoon (G8)
putting the de-
canter onto the
warmer plate
(G13)
putting the cof-
fee box in front
of the coffee-
maker (G4)
closing the cof-
fee box (G9)
and closing the
water lid (G14)
opening the cof-
fee box (G5)
putting away
the coffee box
(G10)
The first focuses on a unique activity, to make cof-
fee. This activity is repeated 30 times. Since such an
activity admit 14 distinct gestures, we have split them
into 14 classes as enumerated in Table 1:.The data set
was created from data that came from two 9-DoF in-
ertial measurement units (LSM9DS0). Each sensor
was associated to an Intel Edison platform which was
powered with a Lithium battery. The sampling rate of
IMU was fixed at 20 Hz as advice in (Karantonis et
al., 2006), indeed, most of body movements are
largely under such a frequency. Once the configura-
tion of IMUs was completed, the two nodes were
placed on the subject’s wrists. Data were sent to the
computer via Wi-Fi. To record the activity, two mem-
bers of our team have been selected. The first one was
making coffee inside our laboratory, while the other
one was labeling each incoming sample. To ensure a
good execution, the activity was achieved several
times by the subject, as a training, without any record-
ing.
The second data set we use was suggested by the
Bilkent University (Altun et al., 2010). It includes
data from eight subjects, where each of them wore
five 9-DoF inertial measurement units (IMU). The
data set represents 19 daily or sports activities enu-
merated in Table 2:.The realized experiment only ex-
ploits records from the first subject.
Table 2: All gestures of Bilkent University data set.
Bilkent University Gestures
Sitting (A1)
moving around in
an elevator (A8)
exercising on a
cross-trainer (A14)
Standing (A2)
walking in a park-
ing lot (A9)
cycling on an exer-
cise bike in hori-
zontal and vertical
positions (A15-16)
lying on back and
on right side (A3-
4)
walking on a tread-
mill with a speed
of 4 km/h (in flat
and 15 deg in-
clined positions)
(A10-11)
rowing (A17)
ascending and de-
scending stairs
(A5-6)
running on a tread-
mill with a speed
of 8 km/h (A12)
j
umping (A18)
standing in an ele-
vator still (A7)
exercising on a
stepper (A13)
playing basketball
(A19)
4.1 Evaluation Metrics
The performance of the presented method was evalu-
ated on three well-known metrics: Accuracy (Acc),
FScore and Kappa measures. However, the last one
was prioritized and provides the recognition perfor-
mance of our algorithm. The first two were included
as comparison purpose since they are widely used in
classification problems. The FScore is based on the
precision expressed by, precision=
TP
TP+FP
and the re-
call recall =
TP
TP + FN
. Where TP is true positive values,
FP false positives, TN true negatives and FN false
negatives. These values were obtained after compu-
ting a confusion matrix. The final overall formula for
the FScore computation is given as follows:
FScore= 2 ∙
precision∙recall
p
recision+recall
(5)
5 RESULTS AND DISCUSSION
This section presents and discusses results we obtain
with the two previously described data sets. Figure 5
and Figure 6 summarize metric values for the data set
Make Coffee on the training and testing sets respec-
tively. Abscess values are the axis taken into account
for each iteration of the given method. We have taken
different sensors into account for each run. 3 axes rep-
resent the accelerometer, 6 refer to the accelerometer
and the gyroscope, 9 all the IMU and 18 the two
IMUs. The ordinate represents the Kappa, FScore and
Accuracy, expressed in percentages, for each combi-
nation.
Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?
113
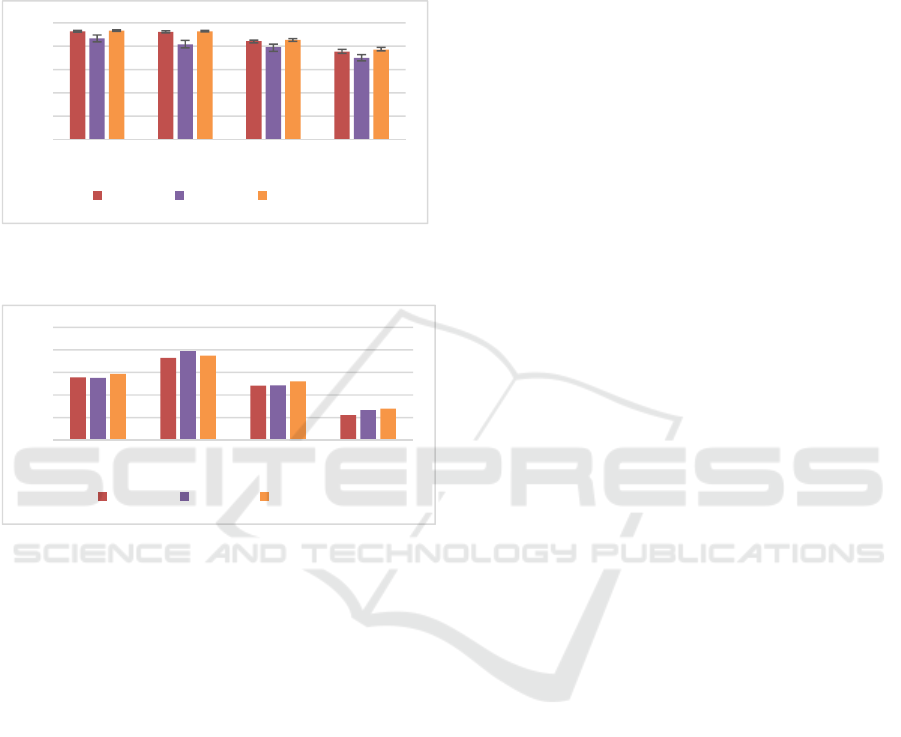
Performance results on the Make Coffee data set
show a considerable drop in the Kappa measure be-
tween the training set and the testing set for every
axis. The second data set present similar result with a
Kappa of 81% for the training set and 37% with the
testing set.
Figure 5: Results observed for the 10-Fold on the training
set, for the make coffee data set.
Figure 6: Results observed for supplied test set on the make
coffee data set.
The observed difference between obtained re-
sults, illustrates a significant limitation regarding the
performance. This contrast may be due to both the op-
timization of parameters (such as clusters from K-
Means and the size of the window for the SearchMax
algorithm) and of each classifier over training data.
We review some methods that falls in the same situa-
tion, meaning good results on training sets but low
ones on testing sets, that were identified as over-
learned (Gamage et al., 2011). Indeed, as described
by Witten and Frank (2005), a classifier trained and
optimized on the same set will achieve accurate re-
sults on this one, but should fall down with independ-
ent test data. Consequently, our proposed method
may be in an overlearning situation, explaining such
results. This is probably due to the fact that the pa-
rameters, of the proposed method, have been opti-
mized for the training data set.
6 CONCLUSIONS
In this paper, we have proposed a new TMM derived
from the LM-WLCSS technique which aims at recog-
nizing motifs in noisy streams. Several parameters
were evaluated such as a suitable number of clusters
for the quantization step, as well as, an adequate size
of the window. The evaluation we have performed
suggests promising results over the training set
(92.7% of Kappa for 3-axis), but we have observed a
serious drop with testing data (55.7% of Kappa for 3-
axis). Such a contrast may be due to the fact that our
method is overly dependent on the training data,
which refers to the proper definition of an overlearn-
ing situation. In a future work we plan to remove pa-
rameters from our method and don’t fall again into an
overlearning situation.
REFERENCES
Altun, K., Barshan, B. & Tunçel, O. 2010. CoAltun, K.,
Barshan, B. & Tunçel, O. 2010. Comparative study on
classifying human activities with miniature inertial and
magnetic sensors. Pattern Recognition, 43, 3605-3620.
Bahrepour, M., Meratnia, N. & Havinga, P. J. M. Sensor
fusion-based event detection in Wireless Sensor
Networks. Mobile and Ubiquitous Systems:
Networking & Services, MobiQuitous, 2009.
MobiQuitous '09. 6th Annual International, 13-16 July
2009 2009. 1-8.
Banos, O., Damas, M., Pomares, H. & Rojas, I. 2012. On
the use of sensor fusion to reduce the impact of
rotational and additive noise in human activity
recognition. Sensors, 12, 8039-8054.
Ben-David, A. 2007. A lot of randomness is hiding in
accuracy. Engineering Applications of Artificial
Intelligence, 20, 875-885.
Chen, C. & Shen, H. 2014. Improving Online Gesture
Recognition with Warping LCSS by Multi-Sensor
Fusion. In: Wong, W. E. & Zhu, T. (eds.) Computer
Engineering and Networking. Springer International
Publishing.
Dardas, N. H. & Georganas, N. D. 2011. Real-Time Hand
Gesture Detection and Recognition Using Bag-of-
Features and Support Vector Machine Techniques.
Instrumentation and Measurement, IEEE Transactions
on, 60, 3592-3607.
Gamage, N., Kuang, Y. C., Akmeliawati, R. & Demidenko,
S. 2011. Gaussian Process Dynamical Models for hand
gesture interpretation in Sign Language. Pattern
Recognition Letters, 32, 2009-2014.
Guiry, J. J., Van De Ven, P. & Nelson, J. 2014. Multi-sensor
fusion for enhanced contextual awareness of everyday
activities with ubiquitous devices. Sensors, 14, 5687-
5701.
0
20
40
60
80
100
3 axis 6 axis 9 axis 18 axis
Kappa FScore Accuracy
0
20
40
60
80
100
3 axis 6 axis 9 axis 18 axis
Kappa Fscore Accuracy
HUCAPP 2017 - International Conference on Human Computer Interaction Theory and Applications
114

Hartmann, B. & Link, N. Gesture recognition with inertial
sensors and optimized DTW prototypes. Systems Man
and Cybernetics (SMC), 2010 IEEE International
Conference on, 10-13 Oct. 2010 2010. 2102-2109.
Hyeon-Kyu, L. & Kim, J. H. 1999. An HMM-based
threshold model approach for gesture recognition.
Pattern Analysis and Machine Intelligence, IEEE
Transactions on, 21, 961-973.
Karantonis, D. M., Narayanan, M. R., Mathie, M., Lovell,
N. H. & Celler, B. G. 2006. Implementation of a real-
time human movement classifier using a triaxial
accelerometer for ambulatory monitoring. IEEE
Transactions on Information Technology in
Biomedicine, 10, 156-167.
Kılıboz, N. Ç. & Güdükbay, U. 2015. A hand gesture
recognition technique for human–computer interaction.
Journal of Visual Communication and Image
Representation, 28, 97-104.
Long-Van, N.-D., Roggen, D., Calatroni, A. & Troster, G.
Improving online gesture recognition with template
matching methods in accelerometer data. Intelligent
Systems Design and Applications (ISDA), 2012 12th
International Conference on, 27-29 Nov. 2012 2012.
831-836.
Nguyen-Dinh, L.-V., Calatroni, A., Tr, G., #246 & Ster
2014a. Towards a unified system for multimodal
activity spotting: challenges and a proposal.
Proceedings of the 2014 ACM International Joint
Conference on Pervasive and Ubiquitous Computing:
Adjunct Publication. Seattle, Washington: ACM.
Nguyen-Dinh, L. V., Calatroni, A. & Tröster, G. 2014b.
Robust online gesture recognition with crowdsourced
annotations. Journal of Machine Learning Research,
15, 3187-3220.
Quinlan, J. R. 2014. C4. 5: programs for machine learning,
Elsevier.
Reyes, M., Dominguez, G. & Escalera, S. Featureweighting
in dynamic timewarping for gesture recognition in
depth data. Computer Vision Workshops (ICCV
Workshops), 2011 IEEE International Conference on,
6-13 Nov. 2011 2011. 1182-1188.
Roggen, D., Cuspinera, L., Pombo, G., Ali, F. & Nguyen-
Dinh, L.-V. 2015. Limited-Memory Warping LCSS for
Real-Time Low-Power Pattern Recognition in Wireless
Nodes. In: Abdelzaher, T., Pereira, N. & Tovar, E.
(eds.) Wireless Sensor Networks. Springer International
Publishing.
Rung-Huei, L. & Ming, O. A real-time continuous gesture
recognition system for sign language. Automatic Face
and Gesture Recognition, 1998. Proceedings. Third
IEEE International Conference on, 14-16 Apr 1998
1998. 558-567.
Vlachos, M., Hadjieleftheriou, M., Gunopulos, D. &
Keogh, E. 2003. Indexing multi-dimensional time-
series with support for multiple distance measures.
Proceedings of the ninth ACM SIGKDD international
conference on Knowledge discovery and data mining.
Washington, D.C.: ACM.
Witten, I. H. & Frank, E. 2005. Data Mining: Practical
Machine Learning Tools and Techniques, Second
Edition (Morgan Kaufmann Series in Data
Management Systems), Morgan Kaufmann Publishers
Inc.
Zappi, P., Roggen, D., Farella, E., Tr, G., #246, Ster &
Benini, L. 2012. Network-Level Power-Performance
Trade-Off in Wearable Activity Recognition: A
Dynamic Sensor Selection Approach. ACM Trans.
Embed. Comput. Syst., 11, 1-30.
Optimized Limited Memory and Warping LCSS for Online Gesture Recognition or Overlearning?
115
