
Automated Multimodal Volume Registration based on Supervised 3D
Anatomical Landmark Detection
R
´
emy Vandaele
1
, Franc¸ois Lallemand
2
, Philippe Martinive
2
, Akos Gulyban
2
, S
´
ebastien Jodogne
2,3
,
Philippe Coucke
2
, Pierre Geurts
1
and Rapha
¨
el Mar
´
ee
1
1
Montefiore Institute, University of Li
`
ege, Grande Traverse 10, Li
`
ege, Belgium
2
Department of Radiotherapy and Oncology, University of Li
`
ege, Li
`
ege, Belgium
3
Department of Medical Physics, University of Li
`
ege, Li
`
ege, Belgium
{remy.vandaele, raphael.maree}@ulg.ac.be
Keywords:
Registration, Machine Learning, Oncology Applications, Radiation Therapy, Urology and Pelvic Organs,
Computed Tomography.
Abstract:
We propose a new method for automatic 3D multimodal registration based on anatomical landmark detection.
Landmark detectors are learned independantly in the two imaging modalities using Extremely Randomized
Trees and multi-resolution voxel windows. A least-squares fitting algorithm is then used for rigid registration
based on the landmark positions as predicted by these detectors in the two imaging modalities. Experiments
are carried out with this method on a dataset of pelvis CT and CBCT scans related to 45 patients. On this
dataset, our fully automatic approach yields results very competitive with respect to a manually assisted state-
of-the-art rigid registration algorithm.
1 INTRODUCTION
In radiotherapy, the 3D Computed Tomography Scan-
ner (CT-Scan) is used as the reference for treatment
dosimetry and patient positioning. During the treat-
ment itself, a Cone-Beam-CT-Scan (CBCT) is ac-
quired several times at the treatment machine to en-
sure the proper positioning of the patient with respect
to the simulation CT-Scan so as to correctly deliver
the treatment to the tumor. Registration of the two
modalities are thus needed in routine applications.
Usually, the registration is performed semi-manually
by a human operator.
The problem of multimodal rigid volume registra-
tion consists in finding the deformation (translations
and rotations) that will minimize the difference be-
tween the two images or volumes to register. This dif-
ference can be evaluated using several possible met-
rics such as voxel by voxel mutual information or
normalized correlation, but also, as in this paper, us-
ing the distance between common specific landmarks
identified in both volumes. Several general optimiza-
tion algorithms have been proposed for multimodal
rigid registration (Zitova and Flusser, 2003),(Pluim
et al., 2003). However, because the scanned regions
can differ between the two volumes to register, these
algorithms do not perform well enough without man-
Figure 1: Sample volumes (MIP projections) from our
dataset. On the left, a CT scan, on the right, a CBCT scan.
Notice the differences between the scanned body regions.
ual intervention for medical registration: an operator
is required to manually define in the two images the
region of interest (ROI) in which the registration pro-
cedure should be applied (Hill et al., 2001). For exam-
ple, as shown in Figure 1 for CT-CBCT registration
in radiotherapy, CT images will typically correspond
to large body scans, while CBCT images will corre-
spond to specific parts of the body (e.g. organs). The
application of out-of-the-box registration algorithms
such as 3D-Slicer (Fedorov et al., 2012) or Elastix
(Klein et al., 2010) on the whole CT and CBCT im-
ages will thus fail as it will try to register the full body
in CT to a specific organ in CBCT. The ROI for the
registration therefore needs to be manually selected in
both images, which significantly slows down the reg-
istration process.
In this paper, we propose, and evaluate, a novel
Vandaele R., Lallemand F., Martinive P., Gulyban A., Jodogne S., Coucke P., Geurts P. and MarÃl’e R.
Automated Multimodal Volume Registration based on Supervised 3D Anatomical Landmark Detection.
DOI: 10.5220/0006153803330340
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 333-340
ISBN: 978-989-758-226-4
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
333
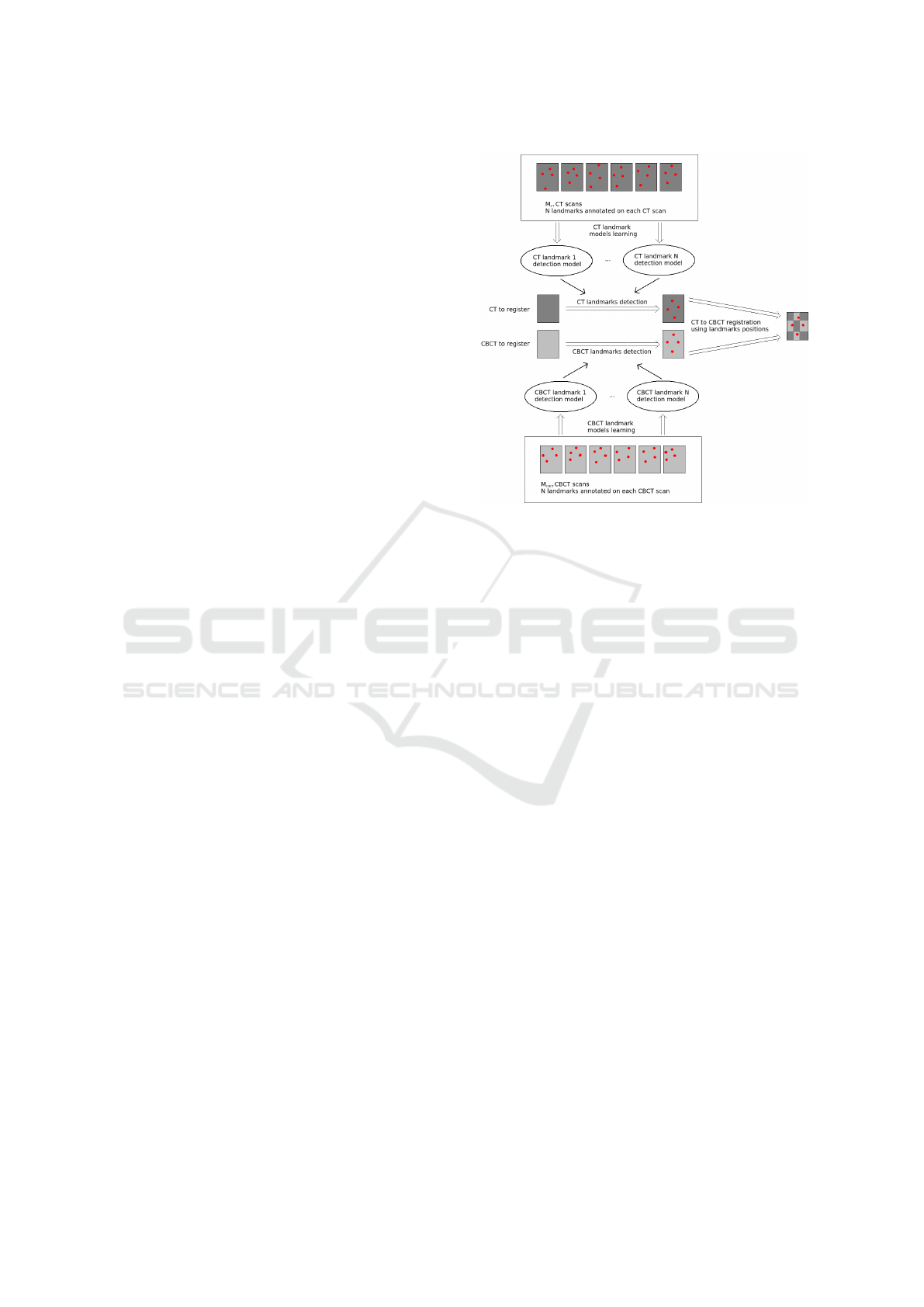
fully automated (i.e., free from any manual ROI selec-
tion) multimodal rigid volume registration algorithm.
The main idea of this approach is to first automati-
cally detect several 3D anatomical landmarks in each
image modality, using supervised machine learning
techniques, and then to register the two images only
on the basis of these landmarks. Our hypothesis is
that although patients have different appearances, a
specific anatomical landmark is likely to look very
similar among different patients in a given imaging
modality, hence each landmark appearance could be
learned in each modality. We want therefore to eval-
uate such an approach where anatomical landmarks
are detected independantly in each modality using su-
pervised learning, then registered, in contrast to com-
monly used approaches that rely on the design and
matching of invariant features accross modalities.
In Section 2, we present our 3D landmark detec-
tion method and explain how it is exploited for rigid
registration. In Section 3, we introduce our dataset of
simulation-CT and CBCT and summarize our land-
mark detection and registration results. Finally, we
conclude in Section 4.
2 METHOD
In our approach, landmark detection models are built
for each landmark and each modality independently
using training images and expert ground-truth land-
mark positions. If N landmarks have to be de-
tected, 2N detection models will be built (one for
each landmark and each modality). For new volumes,
once the landmarks are detected automatically in each
modality, the registration is then performed through
a matching point registration algorithm (Arun et al.,
1987) using all the detected landmark position pairs.
A graphical representation of our approach is given in
Figure 2.
In this section, we first describe the learning ap-
proach we used for the landmark detection, and then
the registration method we used in order to perform
the multimodal volume registration.
2.1 Supervised 3D Landmark Detection
Local, learning-based, feature detectors are promis-
ing approaches for landmark detection in 2D and 3D
images. They have been shown recently to outper-
form global landmark matching algorithms in various
applications (Fanelli et al., 2013; Wang et al., 2015).
Here, we extended the 2D landmark detection method
of (Stern et al., 2011) to 3D imaging.
Figure 2: Representation of our CT-to-CBCT registration
algorithm.
Our algorithm is based on supervised learning:
manually annotated volumes are used to train models
(Extremely Randomized Trees (Geurts et al., 2006))
able to predict the landmark positions in new vol-
umes. As in (Stern et al., 2011), we propose and
compare two approaches: in the first, a classifica-
tion model is trained for each landmark to predict if
a voxel corresponds to the landmark position. In the
second, a regression model is trained to predict the
euclidean distance between a voxel and the landmark
position.
Voxel Description. Each voxel v in the training
sample is described by D multi-resolution square
voxel windows of side size 2W + 1 centered on v
on each of the three axes. W and D are method pa-
rameters. It means that one voxel is described by
3D((2W + 1)
2
) features. In order to manage possi-
ble luminosity variations, the volume voxel values are
normalized and the feature values are computed as the
difference between each voxel value and the value of
the voxel v. Parameters W and D are illustrated in
Figure 3.
Classification Output. We consider a binary voxel
classification model. The voxels can either belong to
the landmark class (1) or to the non landmark class
(-1). Only one position in each image corresponds
to the landmark. If only these positions are consid-
ered as landmarks, and if N training images are avail-
able, only N positive examples will be available to
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
334

Figure 3: Illustration of the different parameters for one landmark in a CBCT scan. The multi-resolution windows describe
the landmark voxel.
train our voxel classification model. To extend the
set of positive examples, we consider as positive ex-
amples all voxels that are at a distance at most R
from the landmark, where R is a method parameter
illustrated in Figure 3. If the landmark is at posi-
tion (x
l
, y
l
, z
l
) in an image, then the output class of a
pixel at position (x, y, z) in the same image will be 1 if
(x−x
l
)
2
+(y−y
l
)
2
+(z−z
l
)
2
≤ R
2
, or −1 otherwise.
Regression Output. With the regression method,
the output associated to each voxel is the euclidean
distance between this voxel and the landmark position
in the training image. More formally, if the landmark
is at position (x
l
, y
l
, z
l
) in an image, then the output
value of a pixel at position (x, y, z) in the same image
will be
p
(x − x
l
)
2
+ (y − y
l
)
2
+ (z − z
l
)
2
Voxel Sampling Scheme. In both cases, the clas-
sification or the regression model is trained from a
learning sample composed of all the
4
3
πR
3
voxels that
are located within a distance d ≤ R to the landmark
position (the landmark class with the classification
approach) and P
4
3
πR
3
voxels located at random po-
sitions within a distance R < d ≤ R
max
to the land-
mark position (the non-landmark class for the classi-
fication approach), where P and R
max
are user defined
parameter. R and R
max
are represented in Figure 3.
In classification, sampling all the pixels inside the R
radius allows us to sample more landmark voxels in
the positive class than uniform sampling. For the re-
gression approach, this parameter allows us to sam-
ple more voxels close to the real landmark position,
which helps the model to perform a better differen-
tiation for the voxels close to the landmark position.
On the other hand, the effect of the R
max
parameter
is to artificially reduce the number of distant voxels,
which allows to reduce the size of the dataset, while
having little to no effect on the prediction accuracy, as
we will show in our experiments.
Model Training. The voxel classification or regres-
sion model is trained using the Extremely Random-
ized Trees algorithm (Geurts et al., 2006). This learn-
ing algorithm is a variant of the Random Forest al-
gorithm (Breiman, 2001) offering similar accuracy
than regular Random Forest while speeding up model
training. In this algorithm, an ensemble of T decision
or regression trees are built from the original train-
ing sample (no bootstraping), without pruning. At
each node, the best split is selected among K features
chosen at random, where K is a number between 1
and the total number of features. For each of the K
(continuous) selected features, a separation threshold
is chosen at random within the range of the feature
in the subset of the observations (i.e., voxels) in the
node. A score is computed for each pair of feature
and threshold, and the best pair according to a score
measure is chosen. We chose to use the Gini index
reduction score for classification, and the variance re-
duction score for our regression trees.
Landmark Prediction. During the radiotherapy
process, the patients are placed in the same position
according to the tumor location. When considering
specific tumor locations, the landmarks will be found
in close areas from one image to another. In con-
sequence, it would be inefficient to search for each
landmark in the whole volume. This is why instead
of thoroughly scanning the volume, we are consider-
ing another solution: in a new volume, we extract N
p
voxels taken at random locations following the nor-
mal distribution N (¯µ, Σ
2
), where ¯µ is the mean po-
sition of the landmark in the training dataset, and Σ
the corresponding covariance matrix. The predicted
position of the landmark in a new volume will either
be the median of the locations of the voxels predicted
as landmarks with the highest probability (classifica-
tion), or as the closest to the landmark position (re-
gression).
Automated Multimodal Volume Registration based on Supervised 3D Anatomical Landmark Detection
335

Parameter Setting. The method depends on sev-
eral parameters: the radius R and R
max
, the ration of
non-landmark versus landmark voxels P, the number
of voxels N
p
to extract for computing a prediction,
the number of trees T , the size of the window W and
the number of resolutions D. These parameters are
either set to their maximum value given the avail-
able computing resources (T, N
p
) or tuned through
cross-validation. Trees were fully grown (n
min
= 2)
and the K parameter was set to its default value
p
3D((2W + 1)
2
) (Geurts et al., 2006).
2.2 Multimodal Landmark-based Rigid
Registration
Once anatomical landmark coordinates have been
predicted in both images, the registration of the re-
sulting matching pairs of landmark positions is for-
mulated as the least-square optimization problem pre-
sented in (1).
min
X,T
N
∑
i=1
||p
0
i
− (X p
i
+ T )||
2
(1)
N is the number of landmarks, p
i
and p
0
i
are the co-
ordinates of the ith landmark in the two images, X
is a 3 × 3 rotation matrix, and T a 3 × 1 translation
vector. To solve this problem, we use the noniterative
SVD-based algorithm proposed in (Arun et al., 1987).
It is important to notice that, as opposed to volume
registration based on local feature detectors and in-
variant descriptors (e.g. (Lukashevich et al., 2011)),
our method does not require matching of landmark
descriptors accross modalities.
3 EXPERIMENTS AND RESULTS
In this section, we first describe our dataset, divided
into a training and a test set. Then, we study system-
atically the influence of the main parameters of our
landmark detection method by leave-one-patient-out
validation on the training set. Finally, we present reg-
istration results on the test set and compare them to
a semi-automated volume registration algorithm (Fe-
dorov et al., 2012).
3.1 Datasets
Our dataset contains images related to 45 patients
(male and female) and was acquired at the Radiother-
apy and Oncology Department, University of Li
`
ege,
Belgium. For each of these patients, we have one
pelvic CT scan as the reference (45 CTs in total), and
Table 1: Sets of values tested during cross-validation for
each parameter. In bold, the default value of each parameter
used in the first stage of cross-validation.
Parameter Tested values
R 2, 4, 5,6, 7, 8, 10,12, 14, 16
R
max
10, 25, 40,50, 75, 100, 200,500, 1000, 2000
P 0.1, 0.25, 0.5,1, 1.5, 2, 3,4, 6, 8
N
p
1, 10, 100,1000, 5000, 10000, 50000,
100000, 200000, 500000
T 1,5, 10, 25, 50,75, 100, 150, 200, 300
W 2, 3, 4,5, 6, 7, 8,9, 10, 12
D 1,2, 3, 4, 5,6, 7, 8, 9, 10
at least one corresponding CBCT scan of the pelvis
(68 CBCTs in total). We divided this dataset into a
training set of 30 patients, each with one CT and at
least one CBCT (i.e 53 CBCTs in total), and a test
set of 15 patients, each with exactly one CT and one
CBCT.
Because our algorithm works better with volumes
of identical resolutions and the original resolution
information is always available, each CT and each
CBCT were resized to 1 × 1 × 1mm voxel resolution.
Originally, CT scan resolutions were comprised be-
tween 0.5 and 3mm. The CBCT scans were acquired
with an Elekta XVI scanner, that were reconstructed
to 1 × 1 × 1mm resolution. More information about
the quality of the CBCT image acquisition procedure
can be found in (Kamath et al., 2011).
On each CT and each CBCT, 8 landmarks dis-
tributed in the pelvis were manually annotated two
times by the same skilled operator. The mean distance
between the two annotation runs is shown in Table 2
(Manual Err.). The position of each landmark is pre-
sented in Figure 4 for CT scans. We used as ground-
truth for each landmark the mean coordinates of the
two manual annotations provided by the operator.
3.2 Landmark Detection Results
3.2.1 Protocol
For our experiments, we fixed extremely random-
ized tree parameters to recommended values (K =
p
3D((2W + 1)
2
), n
min
= 2) (Geurts et al., 2006).
Other parameter values were evaluated in the ranges
presented in Table 1.
These values were tested for both the regression
and the classification approaches using leave-one-
patient-out in the training set. Since it is not possible
to explore all parameter combinations, we use a two-
stage approach. In the first stage, for each parameter
in turn, all its values were tested with the other pa-
rameters set to some default value (in bold in Table1).
In the second stage, the exact same procedure was ap-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
336
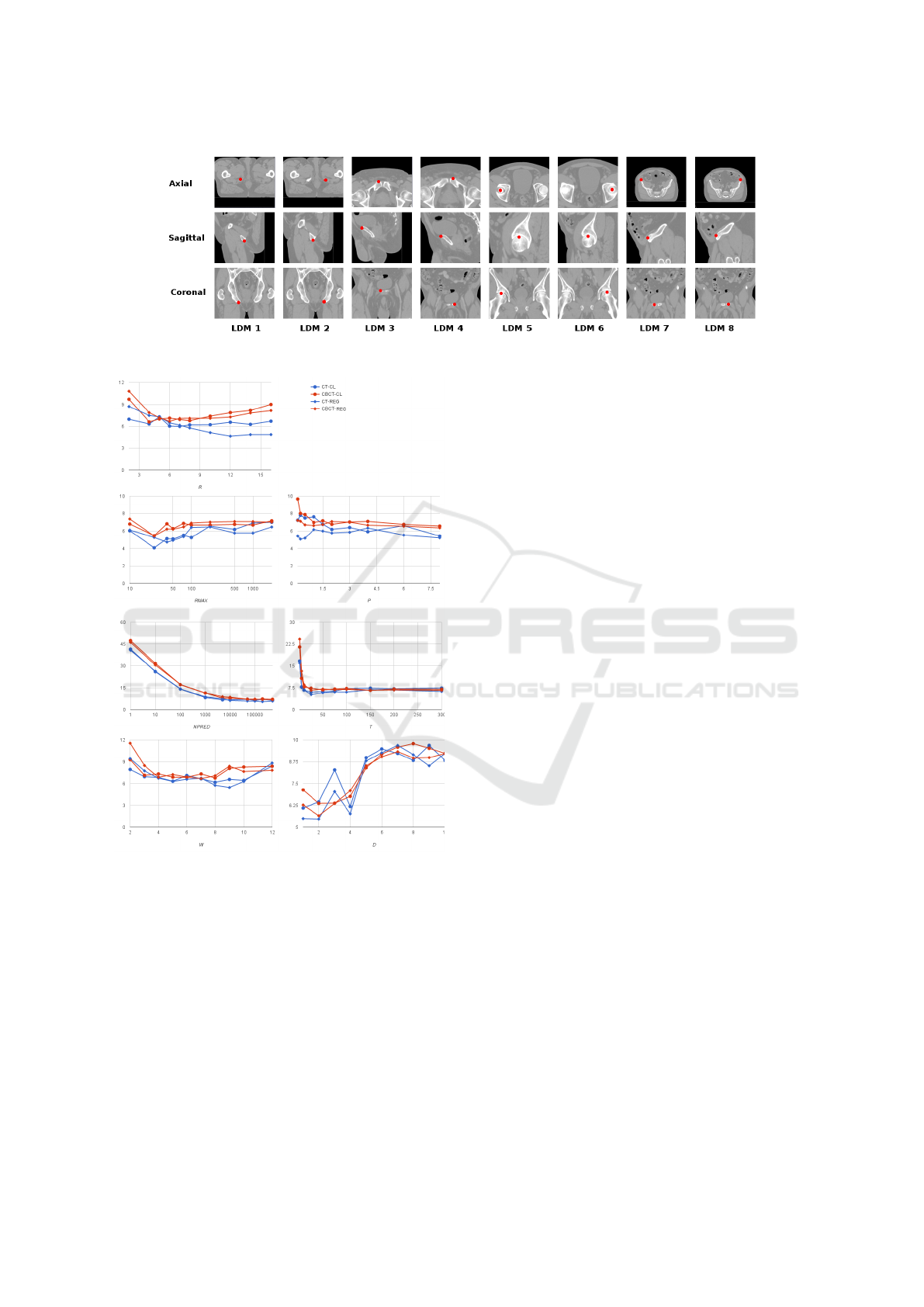
Figure 4: Representative pictures showing the position of the 8 landmarks on a CT-scan.
Figure 5: Influence of method parameters From top to bot-
tom, left to right: R, R
max
, P, N
p
, T,W, D. The y−axis is the
CV error (in mm) averaged over all landmarks.
plied by using as a new default value for each param-
eter the value that led to the lowest CV error (in aver-
age over all landmarks) in the first stage. The best val-
ues for each parameter in this second round were then
identified, this time for each landmark separately, and
used to retrain a model using all training images. In
total, 4480 parameter combinations were tested using
computer clusters.
3.2.2 Influence of Method Parameters
The influence of method parameters is shown in Fig-
ure 5. We did not notice major differences between
the classification and the regression approaches. For
some particular landmarks, the performance was
worse for the CBCT scans. We believe that this differ-
ence is mainly due to one particular patient for which
our algorithm had difficulties because of its particular
CBCT localization: the regions containing the land-
marks 3, 4, 7 and 8 was not acquired. For the classifi-
cation approach, the R parameter clearly needs to be
tuned: too small R will lead to too few positive ex-
amples in the dataset, while too large R will associate
too distant voxels to the positive class. The regres-
sion approach is less sensitive to too large R values.
We noticed that small values of R
max
(25-40 voxels)
work better for both classification and regression. We
explain that by the fact that the landmark structure is
unique inside the volume, and thus learning to dis-
criminate close voxels is more effective than com-
paring more distant voxels. Increasing the propor-
tion P improves the performance for classification but
smaller P values can be used for regression (which de-
creases the size of the dataset). Increasing the number
of predictions N
p
always improves the performance as
expected. However, optimal performance is already
attained with N
p
= 100000. The same effect is ob-
served with the number of trees T , with optimal per-
formance reached at T = 50. The windows size W
controls the number of features and the locality of the
information that is provided for each voxel. This pa-
rameter clearly needs to be tuned with values in the
range 6–8 being optimal in most cases. Increasing the
number of resolutions D quickly increases the error,
most likely because it leads to overfitting. Small val-
ues of D ' 2–3 are optimal in most cases.
3.2.3 Test Set Errors
Table 2 reports for each landmark the error obtained
on the test set (column ’Test Err’) using the optimal
Automated Multimodal Volume Registration based on Supervised 3D Anatomical Landmark Detection
337
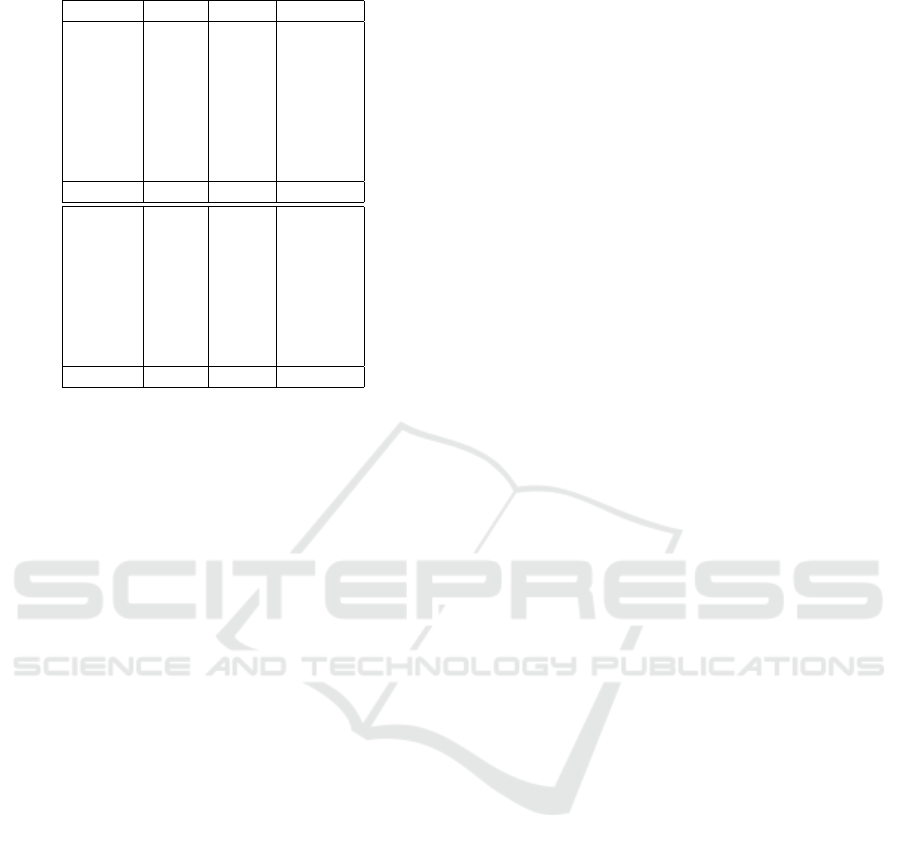
Table 2: Test set results (error in mm).
Landmark CV Err Test Err Manual Err
CT-1 3.23 3.33 1.04
CT-2 2.68 2.77 2.11
CT-3 2.84 2.71 1.81
CT-4 3.43 3.36 2.65
CT-5 2.83 3.28 0.73
CT-6 2.09 3.91 0.84
CT-7 2.92 3.2 0.94
CT-8 2.61 3.7 0.78
Avg 2.83 3.28 1.36
CBCT-1 3.49 3 2.01
CBCT-2 4.53 3.8 2.23
CBCT-3 9.44 4.98 1.34
CBCT-4 5.69 6.39 1.10
CBCT-5 2.84 4.03 1.41
CBCT-6 3.65 3.41 0.98
CBCT-7 8.75 3.56 1.50
CBCT-8 6.08 5.13 1.79
Avg 5.56 4.4 1.54
parameter setting determined with the two-stage CV
explained above. For comparison, columns ’CV Err’
and ’Manual Err’ provide respectively the optimal CV
error on the training set and the error between the two
manual annotations of the human operator.
Results are satisfactory although the difference
between the algorithmic and the manual errors remain
important. When interpreting these results, we have
to take into account the low resolution of the CT and
CBCT images that forced us to resize our voxels to a
1 × 1 × 1mm resolution. Given this resizing, an error
of only 2 or 3 voxels directly translates into an error
of 2 or 3mm. With CBCT scans of higher resolution,
we could have resized the images to a higher common
resolution, which should have led to a lower global
error (in mm). Performance on the CBCT scans are
worse than on the CT scans. We attribute this dif-
ference to poorer image acquisition quality (Kamath
et al., 2011).
3.3 Multimodal Volume Registration
Results
The registration results on all 15 CT-CBCT pairs in
the test set are shown in Figure 6. The quality of the
registration is measured by the average distance be-
tween the ground-truth positions of the landmarks in
the two images after their registration. LDM stands
for landmark registration. It corresponds to the pro-
posed approach, i.e., the application of the registra-
tion algorithm of (Arun et al., 1987) after the 8 pairs
of landmarks were automatically detected in the CT
and CBCT images using our algorithm. MANUAL
corresponds to the application of the same registration
algorithm but using the exact ground-truth positions
of the landmarks. Its error is thus a lower bound on
the error we can expect to achieve with our method.
For comparison, we also provide the error obtained
using the state-of-art (SOA) semi-automatic registra-
tion method implemented in 3D-slicer (Fedorov et al.,
2012) and described in (Johnson et al., 2007). We ap-
plied the method within the smallest box-sized ROI
surrounding all landmark positions and using the Mat-
tes mutual information, which we found to be the best
cost metric to use when compared to mean squared er-
ror and normalized correlation.
As shown in Figure 6, the performance of SOA
is unstable compared to our method and with respect
to manual ground truths. For most patients, our al-
gorithm performs much better. Globally, our results
are very good. They show that our fully automatic
approach performs better than (Johnson et al., 2007)
which in addition requires a manual intervention for
the delineation of the ROIs. The manual ground truth
approach is most of the time much better than our ap-
proach, suggesting that improving the quality of the
landmark detectors, e.g. by collecting more train-
ing images, could potentially improve even further the
performance of our method.
On a Ubuntu 15.04 8 × 2.4Ghz, our paralellized
python implementation of our algorithm takes 4 sec-
onds for the complete registration (T = 50, D =
3, N
p
= 100000). We only take into account the
CBCT landmark detection and the volume registra-
tion, given that in radiotherapy practice, CT land-
marks can be detected offline. On the same computer,
the registration of the box-sized ROI of the CT and
CBCT took approximately 7 seconds using 3D Slicer,
which is also parallelized (Johnson et al., 2007).
4 CONCLUSION
In this work, we proposed a simple but efficient
method for fully automated 3D multimodal rigid reg-
istration based on automated anatomical landmark de-
tection using supervised machine learning. We ap-
plied our approach for pelvis CT-CBCT registration
for patient positioning in radiotherapy. Our results
showed that our automated approach is competitive
with current state-of-art registration algorithms that
require manual assistance. Given any kind of body
location and modality, interesting landmarks to regis-
ter can be selected and detected by experts on a small
training dataset, and then multi modal registration can
be performed on new volumes by using our algorithm.
In future works, we would like to manage the possi-
bility to have landmarks out of the volume(s). Fu-
ture works will also focus on non-rigid registration,
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
338
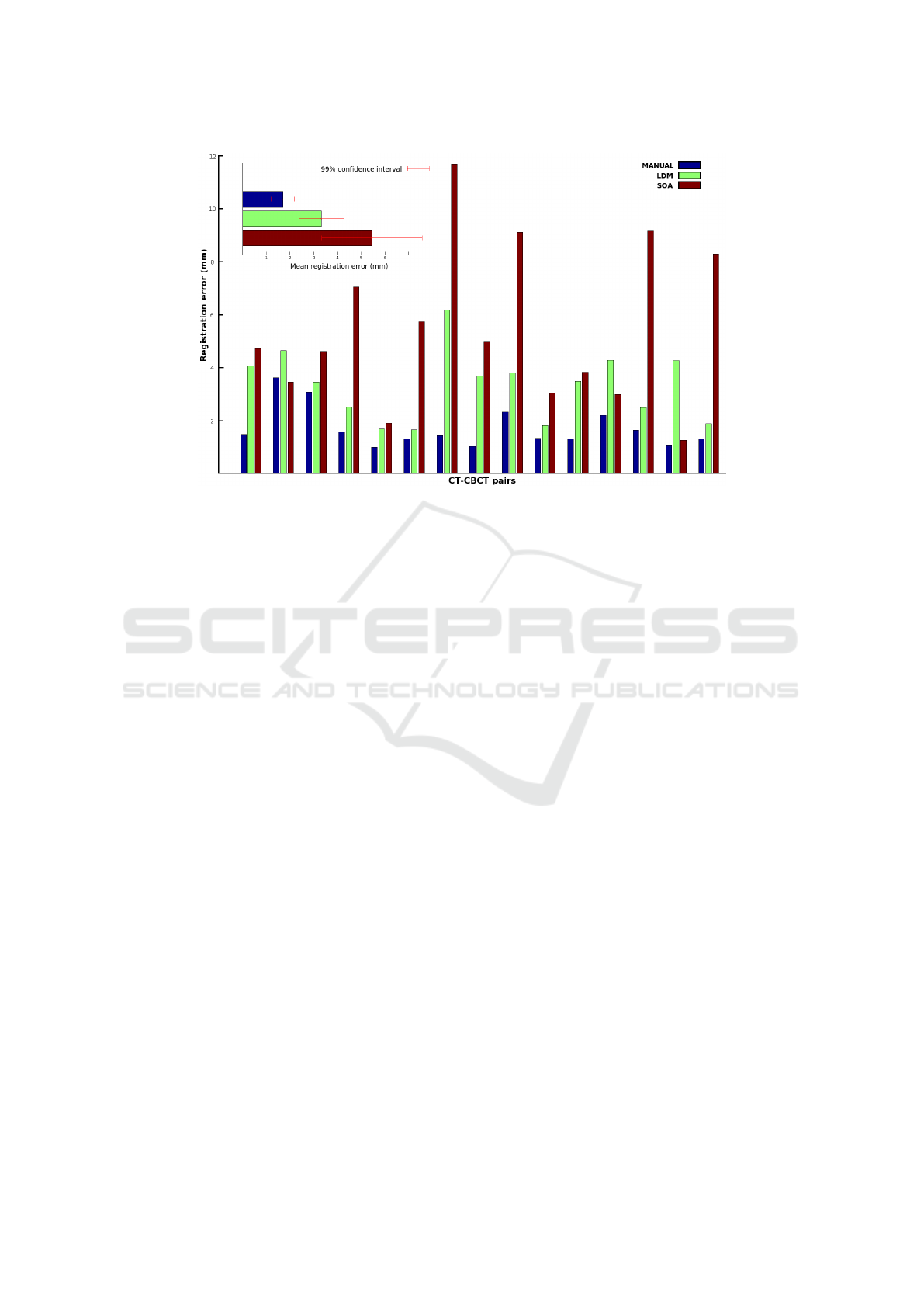
Figure 6: CT to CBCT registration results on the test set of 15 CT-CBCT pairs.
where a higher number of landmarks will most prob-
ably be required in order to perform plausible regis-
trations. To specifically address this issue, another in-
teresting future research direction would be to design
techniques for the automatic selection of the most ap-
propriate landmarks given pre-registered data. Be-
yond this specific application, we also think that our
3D landmark detection method could be interesting
in other areas such as morphometrics (Aneja et al.,
2015).
ACKNOWLEDGEMENTS
R.V. was supported by F.N.R.S T
´
el
´
evie grant, R.M
by research grant n1318185 of the Wallonia (DGO6).
The authors thank the GIGA and the SEGI for provid-
ing computing resources as well as the Consortium
des
´
Equipements de Calcul Intensif (C
´
ECI), funded
by the Fonds de la Recherche Scientifique de Bel-
gique (F.R.S.-FNRS) under Grant No. 2.5020.1.
REFERENCES
Aneja, D., Vora, S. R., Camci, E. D., Shapiro, L. G., and
Cox, T. C. (2015). Automated detection of 3d land-
marks for the elimination of non-biological variation
in geometric morphometric analyses. In IEEE 28th
International Symposium on Computer-Based Medi-
cal Systems, pages 78–83. IEEE.
Arun, K. S., Huang, T. S., and Blostein, S. D. (1987). Least-
squares fitting of two 3-d point sets. IEEE Trans-
actions on pattern analysis and machine intelligence,
(5):698–700.
Breiman, L. (2001). Random forests. Machine Learning,
45(1):5–32.
Fanelli, G., Dantone, M., Gall, J., Fossati, A., and Van Gool,
L. (2013). Random forests for real time 3d face
analysis. International Journal of Computer Vision,
101(3):437–458.
Fedorov, A., Beichel, R., Kalpathy-Cramer, J., Finet, J.,
Fillion-Robin, J.-C., Pujol, S., Bauer, C., Jennings,
D., Fennessy, F., Sonka, M., et al. (2012). 3d slicer
as an image computing platform for the quantita-
tive imaging network. Magnetic resonance imaging,
30(9):1323–1341.
Geurts, P., Ernst, D., and Wehenkel, L. (2006). Extremely
randomized trees. Machine learning, 63(1):3–42.
Hill, D. L., Batchelor, P. G., Holden, M., and Hawkes,
D. J. (2001). Medical image registration. Physics in
medicine and biology, 46(3):R1.
Johnson, H., Harris, G., Williams, K., et al. (2007). Brains-
fit: mutual information rigid registrations of whole-
brain 3d images, using the insight toolkit. Insight J,
pages 1–10.
Kamath, S., Song, W., Chvetsov, A., Ozawa, S., Lu, H.,
Samant, S., Liu, C., Li, J. G., and Palta, J. R. (2011).
An image quality comparison study between xvi and
obi cbct systems. Journal of Applied Clinical Medical
Physics, 12(2).
Klein, S., Staring, M., Murphy, K., Viergever, M. A., and
Pluim, J. P. (2010). Elastix: a toolbox for intensity-
based medical image registration. IEEE Transactions
on Medical Imaging, 29(1):196–205.
Lukashevich, P., Zalesky, B., and Ablameyko, S. (2011).
Medical image registration based on surf detector.
Pattern Recognition and Image Analysis, 21(3):519–
521.
Automated Multimodal Volume Registration based on Supervised 3D Anatomical Landmark Detection
339

Pluim, J. P., Maintz, J. A., and Viergever, M. A. (2003).
Mutual-information-based registration of medical im-
ages: a survey. IEEE Transactions on medical imag-
ing, 22(8):986–1004.
Stern, O., Mar
´
ee, R., Aceto, J., Jeanray, N., Muller, M.,
Wehenkel, L., and Geurts, P. (2011). Automatic lo-
calization of interest points in zebrafish images with
tree-based methods. In IAPR International Confer-
ence on Pattern Recognition in Bioinformatics, pages
179–190. Springer.
Wang, C.-W., Huang, C.-T., Hsieh, M.-C., Li, C.-H., Chang,
S.-W., Li, W.-C., Vandaele, R., Mar
´
ee, R., Jodogne,
S., Geurts, P., et al. (2015). Evaluation and com-
parison of anatomical landmark detection methods for
cephalometric x-ray images: a grand challenge. IEEE
Transactions on medical imaging, 34(9):1890–1900.
Zitova, B. and Flusser, J. (2003). Image registration
methods: a survey. Image and vision computing,
21(11):977–1000.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
340
