Assured Reinforcement Learning with Formally Veriﬁed Abstract Policies

George Mason

, Radu Calinescu

, Daniel Kudenko

and Alec Banks

Department of Computer Science, University of York, Deramore Lane, York, U.K.

Defence Science and Technology Laboratory, Salisbury, U.K.

Keywords:

Reinforcement Learning, Safety Constraint Veriﬁcation, Abstract Markov Decision Processes.

Abstract:

We present a new reinforcement learning (RL) approach that enables an autonomous agent to solve decision

making problems under constraints. Our assured reinforcement learning approach models the uncertain en-

vironment as a high-level, abstract Markov decision process (AMDP), and uses probabilistic model checking

to establish AMDP policies that satisfy a set of constraints deﬁned in probabilistic temporal logic. These for-

mally veriﬁed abstract policies are then used to restrict the RL agent’s exploration of the solution space so as

to avoid constraint violations. We validate our RL approach by using it to develop autonomous agents for a

ﬂag-collection navigation task and an assisted-living planning problem.

1 INTRODUCTION

Reinforcement learning (RL) is a machine learning

technique where an autonomous agent uses the re-

wards received from its interactions with an initially

unknown Markov decision process (MDP) to con-

verge to an optimal policy, i.e. the actions to take

in the MDP states in order to maximise the obtained

rewards (Wiering and Otterlo, 2012). Although suc-

cessfully used in applications ranging from gaming

(Szita, 2012) to robotics (Kober et al., 2013), stan-

dard RL is not applicable to problems where the poli-

cies synthesised by the agent must satisfy strict con-

straints associated with the safety, reliability, perfor-

mance and other critical aspects of the problem.

Our work addresses this signiﬁcant limitation of

standard RL, extending the applicability of the tech-

nique to mission-critical and safety-critical systems.

To this end, we present an assured reinforcement

learning (ARL) approach that restricts the explo-

ration of the RL agent to MDP regions guaran-

teed to yield solutions compliant with the required

constraints. Given limited preliminary knowledge

of the problem under investigation, ARL builds a

high-level abstract Markov decision process (AMDP)

(Marthi, 2007) model of the environment and uses

probabilistic model checking (Kwiatkowska, 2007)

to identify AMDP policies that satisfy a set of con-

straints formalised in probabilistic computation tree

logic (PCTL) (Hansson and Jonsson, 1994). The

constraint-compliant (i.e. “safe”) abstract policies

obtained in this way are then used to resolve some of

the nondeterminism of the unknown problem MDP,

inducing a restricted MDP that the RL agent can ex-

plore without violating any of the constraints.

As multiple safe abstract policies are generated

during the probabilistic model checking stage of

ARL, our approach retains only the abstract policies

that are Pareto-optimal with respect to optimization

objectives associated with the analysed constraints

and/or speciﬁed additionally. For example, the con-

straints for the RL problem from one of the case

studies described later in the paper specify a mea-

sure of the maximum healthcare cost permitted for an

assisted-living system. The Pareto-optimal abstract

policies that ARL retains for this RL problem (i) guar-

antee that this maximum threshold is not exceeded,

and (ii) cannot be replaced by (known) policies that

reduce both the healthcare cost and an additional op-

timization objective that reﬂects the level of distress

for the patient using the system.

Our ARL approach complements the recent re-

search on safe reinforcement learning (Garc

ıa and

Fern

andez, 2015). The existing results from this area

focus on specifying bounds for the reward obtained by

the RL agent or for simple measures associated with

this reward (Abe et al., 2011; Castro et al., 2012; De-

lage and Mannor, 2010; Geibel, 2006; Moldovan and

Abbeel, 2012; Ponda et al., 2013). In contrast to these

approaches, ARL uses probabilistic model checking

to formally establish safe AMDP policies associated

with the broad range of safety, reliability and perfor-

Mason G., Calinescu R., Kudenko D. and Banks A.

Assured Reinforcement Learning with Formally Veriﬁed Abstract Policies.

DOI: 10.5220/0006156001050117

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 105-117

ISBN: 978-989-758-220-2

105

mance constraints that can be formally speciﬁed in

PCTL (Hansson and Jonsson, 1994) extended with re-

wards (Andova et al., 2004). To the best of our knowl-

edge, these types of highly useful constraints are not

supported by any existing safe RL solutions.

To assess the effectiveness and generality of ARL,

we thoroughly evaluated its application through two

case studies that addressed different types of RL prob-

lems within different application domains. The ﬁrst

case study tackles a navigation problem based on the

benchmark RL ﬂag-collection domain (Dearden et al.,

1998), which we extended with an element of risk

that requires the application of ARL. The second case

study involves solving a planning problem to assist a

dementia sufferer perform the task of hand-washing,

and is adapted from a real-world application from the

assisted-living domain (Boger et al., 2006). In both

case studies, ARL generated Pareto-optimal sets of

safe abstract policies, which were successfully used

to drive the RL agents’ exploration towards solutions

satisfying a range of reliability and performance con-

straints associated with the two problems.

The rest of our paper is organized as follows.

In Section 2, we compare our work with related re-

search from the area of safe reinforcement learning.

Next, Section 3 introduces the terminology and tech-

niques that underpin the operation of ARL. Section 4

presents a motivating example that we use to illus-

trate the application of our ARL approach, which is

described in Section 5. The two cases studies that we

used to validate ARL are presented in Section 6, and

Section 7 concludes the paper with a brief summary

and a discussion of future work directions.

2 RELATED WORK

Our assured reinforcement learning approach be-

longs to a class of RL methods called safe rein-

forcement learning (Garc

ıa and Fern

andez, 2015).

However, existing safe RL research focuses on en-

forcing bounds on the reward obtained by the RL

agent or on simple measures related to this reward.

Geibel (2006) proposes a safe RL method that sup-

ports an inequality constraint on the reward cumu-

lated by the RL agent or a maximum permitted prob-

ability for such a constraint to be violated. Delage

and Mannor (2010) and Ponda et al. (2013) introduce

RL methods that enforce similar constraints through

generalizing chance-constrained planning to inﬁnite-

horizon MDPs. Thanks to the wide range of safety,

reliability and performance properties that can be ex-

pressed in PCTL, our ARL approach supports a much

broader range of RL constraints, which includes those

covered in (Delage and Mannor, 2010; Geibel, 2006;

Ponda et al., 2013).

Other recent research on safe RL includes the

work of (Moldovan and Abbeel, 2012), who introduce

an approach that enforces the RL agent to avoid irre-

versible actions by entering only states from which it

can return to the initial state. Similar approaches are

proposed by Castro et al. (2012) and Abe et al. (2010).

Thus, Castro et al. (2012) exploit domain knowledge

from ﬁnancial decision making and robust process

control to enforce constraints on the cumulative re-

ward obtained by the RL agent, on the variance of

this reward, or on a combination of the two. Along

the same lines, Abe et al. (2010) present a safe RL

method that enforces high-level business and legal

constraints during each value iteration step of the RL

process, and apply their method to a tax collection op-

timization problem. ARL is complementary to the ap-

proaches proposed in (Abe et al., 2011; Castro et al.,

2012; Moldovan and Abbeel, 2012) as it supports dif-

ferent types of constraints. In particular, the PCTL-

encoded constraints used by our approach are not spe-

ciﬁc to any domain or application like those from

(Castro et al., 2012) and (Abe et al., 2011).

ARL is unique in its use of an abstract MDP and

of probabilistic model checking to constrain the RL

agent’s exploration to safe areas of the environment.

Built with only limited knowledge about the problem

to solve, this AMDP has a signiﬁcantly smaller state

space and action set than the (unknown) MDP model

of the environment (Li et al., 2006; Marthi, 2007;

Sutton et al., 1999), allowing the efﬁcient analysis

of problem aspects associated with the required con-

straints. In contrast, existing safe RL methods mod-

ify the reward function to “penalize” agent actions as-

sociated with high variance in the probability of at-

taining the reward (Mihatsch and Neuneier, 2002) or

to avoid irreversible actions (Moldovan and Abbeel,

2012); or use domain knowledge to keep away from

unsafe states (Driessens and D

zeroski, 2004).

Unlike existing safe RL approaches, ARL synthe-

sises a Pareto-optimal set of safe AMDP policies that

correspond to a wide range of trade-offs between rele-

vant attributes of the optimisation problem. Although

multi-objective RL (MORL) research (Liu et al., 2015;

Vamplew et al., 2011) has considered the problem

of learning a policy that satisﬁes conﬂicting objec-

tives, existing MORL methods, e.g. (Barrett and

Narayanan, 2008; G

abor et al., 1998; Mannor and

Shimkin, 2004; Moffaert and Now

e, 2014), do not

support the broad range of optimisation objectives

that can be speciﬁed in ARL using reward-augmented

PCTL constraints.

Finally, our ARL approach builds on preliminary

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

106

results that we described in a recent work-in-progress

paper (Mason et al., 2016), which it signiﬁcantly ex-

tends through formalising the stages of the approach,

through the addition of an assisted-living case study

that conﬁrms the applicability of ARL to planning

problems, and through the inclusion of new experi-

mental results and insights from these experiments.

3 PRELIMINARIES

Markov Decision Processes (MDPs) (Wiering and

Otterlo, 2012) are a formalism for modelling sequen-

tial decision-making problems where an autonomous

agent can perceive the current environment state s and

select an action a from a set of actions. Performing

the selected action a results in the agent transitioning

to a new state s

and receiving an immediate reward

r ∈ R.

An MDP is formally deﬁned as a tuple (S,A,T, R),

where: S is a ﬁnite set of states; A is a ﬁnite set of ac-

tions; T : S×A×S → [0,1] is a state transition function

such that for any s,s

∈ S and any action a ∈ A that is

allowed in state s, T (s,a,s

) gives the probability of

transitioning to state s

when performing action a in

state s; and R : S×A×S → R is a reward function such

that R(s, a,s

) = r is the reward received by the agent

when action a performed in state s leads to state s

Given an MDP (S,A,T,R), we are interested in

ﬁnding a deterministic policy π : S → A that maps each

state in S to one of the actions permitted in that state

and maximizes the reward accrued by an autonomous

agent that follows the policy. When all MDP elements

are known, the problem can be solved using dynamic

programming, e.g. by means of value or policy it-

eration algorithms. In scenarios where the transition

function T and/or the reward function R are unknown

a priori, RL is employed as described below.

Reinforcement Learning (RL) is a machine learning

technique where an autonomous agent with no ini-

tial knowledge of an environment must learn about

it through exploration, i.e. by selecting initially arbi-

trary actions while moving from one state of an un-

known MDP to another. By receiving rewards af-

ter each state transition, the RL agent learns about

the quality of its action choices. The agent stores

this knowledge it gains about the quality of a state-

action pair (s, a) ∈ S × A in the form of a Q-value

Q(s,a) ∈ R. Updates to Q-values are done using

a temporal difference learning algorithm such as Q-

learning (Watkins and Dayan, 1992), whose formula

Q(s,a) ← Q(s,a) + α[r + γ · max

∈A

Q(s

) − Q(s,a)],

shows the Q-value Q(s,a) being updated after select-

ing action a in state s earned the agent a reward r and

took it to state s

, where α ∈ (0,1] is the learning rate

and γ ∈ [0,1] is the discount factor.

The Q-value updates propagate information about

rewards within the environment over the state-action

pairs, enabling the RL agent to exploit the knowledge

it has learned. Thus, when the agent revisits a state,

it can perform an action based on a pre-deﬁned pol-

icy instead of a randomly selected action. As an ex-

ample, with the ε-greedy policy the agent acts ran-

domly with probability ε and selects the highest Q-

value action with probability 1 − ε (Wiering and Ot-

terlo, 2012). Provided that each MDP state is visited

inﬁnitely many times and the learning rate α satisﬁes

certain conditions, the algorithm is guaranteed to con-

verge to an optimal policy. In practice, a ﬁnite num-

ber of learning iterations (i.e. episodes) is typically

enough to obtain a policy sufﬁciently close to the op-

timal policy.

Abstract MDPs (AMDPs) are high-level represen-

tations of MDPs in which multiple MDP states are

aggregated, e.g. based on their similarity (Li et al.,

2006), and the MDP actions are replaced by tempo-

rally abstract options (Sutton et al., 1999). As an ex-

ample, instead of an agent performing a sequence of

stepwise movements to transition through a series of

Cartesian coordinates from room A to enter room B

in a navigation problem, in an associated AMDP each

location would be a single state and the option would

simply be to “move” from room A to room B. Ac-

cordingly, an AMDP is orders of magnitude smaller

than its MDP counterpart, can often be built with very

limited knowledge about the environment, and can

be solved and reasoned about much faster (Marthi,

2007).

Consider an MDP (S,A,T,R) and a function

z : S →

S that maps each state s ∈ S to an abstract state

z(s) ∈

S such that

S = z(S). Then, the AMDP induced

by the state-mapping function z is a tuple (

T ,

R),

where:

S is the set of abstract states;

A is the set of op-

tions;

T :

S ×

A ×

S → [0,1] is a state transition func-

tion such that

T ( ¯s,o, ¯s

) =

∑

s∈S,z(s)= ¯s

∑

∈S,z(s

)= ¯s

P(s

|s,o)

for any ¯s, ¯s

∈

S and any option o ∈

A; and

R :

S ×

A ×

S → R is a reward function such that

R( ¯s, o) =

∑

s∈S,z(s)= ¯s

R(s,o)

for any ¯s ∈

S and any o ∈

A, where w

≥ 0 is the

weight of state s, calculated based on the expected

Assured Reinforcement Learning with Formally Veriﬁed Abstract Policies

107

frequency of occurrence of state s in the abstract state

z(s) (Marthi, 2007).

A parameterised AMDP uses parameters to spec-

ify which option to perform in each AMDP state (Xia

and Jia, 2013). An abstract policy selects the values

of these parameters, resolving the nondeterminism of

the AMDP, and thus transforming it into a discrete-

time Markov chain with a single option for each state.

Probabilistic model checking is a mathematically

based technique for establishing reliability, perfor-

mance and other nonfunctional properties of sys-

tems with stochastic behaviour (Kwiatkowska, 2007).

Given a Markovian model of the analysed system,

probabilistic model checking tools, such as PRISM

(Kwiatkowska et al., 2011) and MRMC (Katoen et al.,

2011), use efﬁcient symbolic algorithms to efﬁciently

examine its entire state space, producing results that

are guaranteed to be correct. The technique has been

successfully used to analyse nonfunctional properties

of systems ranging from cloud infrastructure (Cali-

nescu et al., 2012) and service-based systems (Ca-

linescu et al., 2013) to unmanned vehicles (Gerasi-

mou et al., 2014). Typical properties that can be es-

tablished using the probabilistic model checking in-

clude: ‘What is the probability that the agent will

safely reach the goal area?’ and ‘What is the expected

level of distress for the dementia patient?’ in the

ﬂag-collection navigation problem and in the assisted-

living planning problem from our case studies, re-

spectively.

Probabilistic model checking operates with MDPs

whose states are labelled with atomic propositions

that specify basic properties of interest that hold in

each MDP state, e.g. start, goal, or RoomA. MDPs la-

belled with atomic propositions enable the analysis of

properties that express probabilities and temporal re-

lationships between events and are speciﬁed in a prob-

abilistic variant of temporal logic called probabilistic

computational tree logic (PCTL) (Hansson and Jons-

son, 1994). Given a set of atomic propositions AP, a

state formula Φ and a path formula Ψ in PCTL are

deﬁned by the grammar:

Φ ::= true | a | ¬Φ | Φ

∧ Φ

| P

p

[Ψ]

Ψ ::= XΦ | Φ

U Φ

| Φ

≤k

, (1)

where a ∈ AP,  ∈ {<,≤,≥,>}, p ∈ [0,1] and k ∈

N; and a PCTL reward state formula (Kwiatkowska

et al., 2007) is deﬁned by the grammar:

Φ ::= R

r

] | R

r

≤k

] | R

r

[FΦ] | R

r

[S], (2)

where r ∈ R

≥0

. State formulae include the logical op-

erators ∧ and ¬, which allow the formulation of dis-

junction (∨) and implication (⇒).

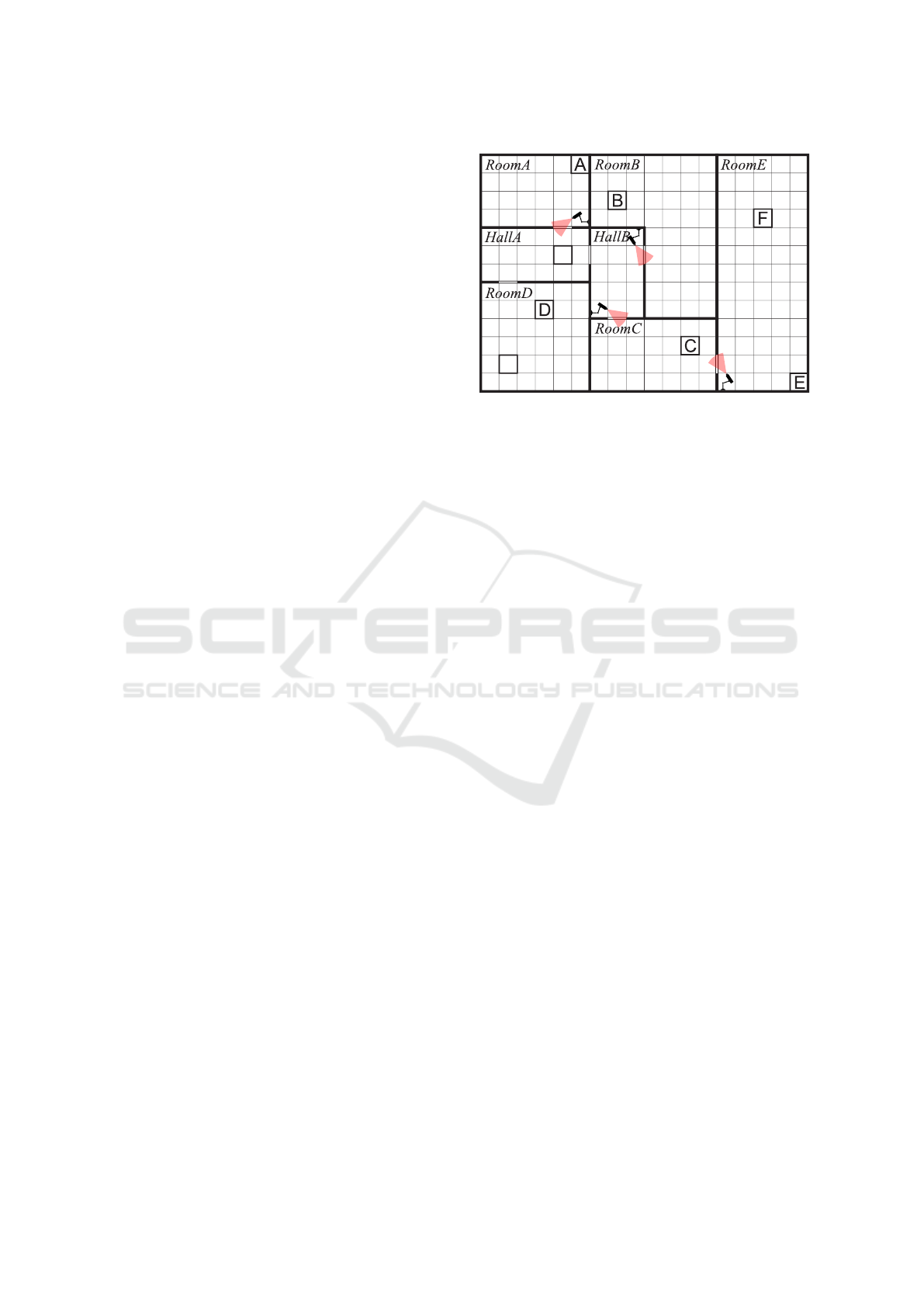
Start

Goal

Figure 1: Flag-collection mission. (Dearden et al., 1998)

extended with security cameras. The diagram shows the

ﬂag positions A–F, the start and goal positions for the agent,

and the cameras and their ﬁeld of view.

The semantics of PCTL are deﬁned with a sat-

isfaction relation |= over the states and paths of an

MDP (S,A, T,R). Thus, s |= Φ means Φ is satisﬁed

in state s. For any state s ∈ S, we have: s |= true;

s |= a iff s is labelled with the atomic proposition a;

s |= ¬Φ iff ¬(s |= Φ); and s |= Φ

∧ Φ

iff s |= Φ

and s |= Φ

. A state formula P

p

[Ψ] is satisﬁed in

a state s if the probability of the future evolution of

the system satisfying Ψ satisﬁes  p. For an MDP

path s

..., the “next state” formula X Φ holds

iff Φ is satisﬁed in the next path state (i.e. in state

); the bounded until formula Φ

≤k

holds iff

before Φ

becomes true is some state s

, x < k, Φ

is satisﬁed for states s

to s

x−1

; and the unbounded

until formula Φ

U Φ

removes the constraint x < k

from the bounded until. For instance, the PCTL

formula P

≥0.95

[¬RoomA U goal] formalises the con-

straint ‘the probability of reaching the goal without

entering RoomA is at least 0.95’.

The notation F

≤k

Φ ≡ trueU

≤k

Φ, and FΦ ≡

trueUΦ is used when the ﬁrst part of a bounded un-

til, and until formula, respectively, are true. The re-

ward state formulae (2) express the expected cost at

timestep k (R

r

]), the expected cumulative cost

up to time step k (R

r

≤k

]), the expected cumula-

tive cost to reach a future state that satisﬁes a property

Φ (R

r

[FΦ]), and the expected steady-state reward in

the long run (R

r

[S]).

Finally, probabilistic model checkers also support

PCTL formulae in which the bounds ‘ p’ and ‘ r’

are replaced with ‘=?’, to indicate that the compu-

tation of the actual bound is required. For example,

≤20

goal] expresses the probability of succeed-

ing (i.e. of reaching a state labelled goal) within 20

time steps.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

108

4 MOTIVATING EXAMPLE

We motivate the need for assured reinforcement learn-

ing using an extension of the benchmark RL ﬂag-

collection mission from (Dearden et al., 1998). In the

original mission, an agent needs to ﬁnd and collect

ﬂags scattered throughout a building by learning to

navigate through its rooms and hallways. In our ex-

tension, certain doorways between areas are provided

with security cameras, as shown in Figure 1. Detec-

tion by a camera results in the capture of the agent and

the termination of its ﬂag-collection mission.

Unknown to the agent, the detection effectiveness

of the cameras decreases towards the boundary of

their ﬁeld of view, so that the camera-monitored door-

ways comprise three areas with decreasing probabil-

ities of detection: direct view by the camera, par-

tial view, and hidden. We assume that the detec-

tion probabilities for the camera-monitored doorways

from Figure 1 and the camera-view areas have the val-

ues from Table 1.

Table 1: Agent detection probabilities.

Camera view

Camera

Direct Partial Hidden

HallA ↔ RoomA

HallB ↔ RoomB

HallB ↔ RoomC

RoomC ↔ RoomE

0.18 0.12 0.06

0.15 0.1 0.05

0.21 0.14 0.07

Consider now a real-world application where the

agent is an expensive autonomous robot pursuing a

surveillance mission or a search-and-rescue opera-

tion. In this scenario, its owners are interested in the

safe return of robot, but do not want it to behave “too

safely” or it will not collect enough ﬂags. Therefore,

they specify the following constraints for the agent:

The agent should reach the ‘goal’ area with pro-

bability at least 0.75.

The agent should cumulate more than two ﬂags

before it reaches the ‘goal’ area.

Subject to these constraints being satisﬁed, they are

interested to maximise:

The probability that the agent reaches the ‘goal’.

The number of collected ﬂags.

As a result, the agent owners additionally want to

know the range of possible trade-offs between these

two conﬂicting optimization objectives. In this way,

the right level of trade-off can be selected for each in-

stance of the mission. Note that formulating the con-

straints C

and C

into a reward function and using

standard RL to solve the problem is not possible be-

cause an RL agent aims to maximize its reward rather

than to maintain it within a speciﬁed range.

5 THE ARL APPROACH

Our ARL approach takes as input the following infor-

mation about problem to solve:

1. Partial knowledge about the problem;

2. A set of constraints C = {C

,.. . ,C

} that must

be satisﬁed by the policy learnt by the RL agent;

3. A set of objectives O = {O

,.. . , O

} that the

RL policy should optimise (i.e. minimise or max-

imise) subject to all constraints being satisﬁed.

The optimisation objectives O can be associated with

problem properties that appear in the constraints C

(like in our motivating example), or also with ad-

ditional problem properties (as in the assisted-living

planning problem from Section 6). The partial knowl-

edge must contain sufﬁcient information for the as-

sembly of an abstract MDP supporting the formali-

sation in PCTL and the probabilistic model checking

of the n >0 constraints and m ≥ 0 optimisation objec-

tives. For instance, for constraint C

from our moti-

vating example, it is enough to know the hidden-view

detection probabilities of the cameras (as the agent

should be able to learn the best area for crossing the

doorway). Note that the partial knowledge about the

environment assumed by ARL is necessary: no con-

straints could be ensured during RL exploration in the

absence of any information about the environment.

Furthermore, ARL assumes that sufﬁcient learning is

undertaken by the RL agent to ﬁnd an optimal policy

for safety requirements to be assured; suboptimal RL

policies may not satisfy the safety requirements.

Under these assumptions, our ARL approach:

(i) generates a Pareto-optimal set of “safe” abstract

policies that satisfy the constraints C and are Pareto

non-dominated with respect to the optimisation ob-

jectives O; and (ii) learns a (concrete) policy that sat-

isﬁes the constraints C and meets trade-offs between

objectives O given by a Pareto-optimal abstract policy

selected by the user. ARL comprises three stages:

1. AMDP construction – This stage devises a pa-

rameterised AMDP model of the RL problem

that supports the probabilistic model checking of

PCTL-formalised versions of the constraints C

and of the optimisation objectives O.

2. Abstract policy synthesis – This stage generates

the Pareto-optimal set of “safe” abstract policies.

3. Safe learning – This stage uses a user-selected

abstract policy from the Pareto-optimal set to en-

force state-action constraints for the exploration

of the environment by the RL agent, which sub-

sequently learns an optimal policy that complies

Assured Reinforcement Learning with Formally Veriﬁed Abstract Policies

109

with the problem constraints and meets the opti-

misation objective trade-offs associated with the

selected abstract policy.

The three ARL stages are described in detail in the

remainder of the section.

Stage 1: AMDP Construction. In this ARL stage,

all features that are relevant for the problem con-

straints and optimisation objectives must be extracted

from the available partial knowledge about the RL en-

vironment. This could include locations, events, re-

wards, actions or progress levels. The objective is to

abstract out the features that have no impact on the so-

lution attributes that the constraints C and objectives

O refer to, whilst retaining the key features that these

attributes depend on. This ensures that the AMDP is

sufﬁciently small to be analysed using probabilistic

model checking, while also containing the necessary

details to enable the analysis of all constraints and op-

timisation objectives.

In our motivating example, the key features are the

locations and connections of rooms and halls, the de-

tection probabilities of the cameras and the progress

of the ﬂags collected. Instead of having each Carte-

sian coordinate within a room or hall as a separate

state, the room or hall as a whole is considered a sin-

gle state in the AMDP. Also, we only consider the

hidden-view detection probability per camera since

these are the probabilities that the RL agent will learn

for the optimal points to traverse the doorways. These

abstractions yield a 448-state AMDP for our ﬂag-

collection problem, compared to 14,976 states for the

RL MDP (which is unknown to the agent). Note that

the number of AMDP states is larger than the number

of locations (i.e. rooms and halls) because different

AMDP states are used for each possible combination

of a location and a number of ﬂags collected so far.

The actions of the full RL MDP are similarly ab-

stracted. For example, instead of having the cardinal

movements at each location of the building from our

motivating example, abstract actions (i.e. options –

cf. Section 3) are speciﬁed as simply the movement

between locations. Thus, instead of the four possi-

ble actions for each of the 14,976 MDP state, the 448

AMDP states have only between one and four pos-

sible options each. The N options that are available

for an AMDP state correspond to the N ≥ 1 passage-

ways that link the location associated with that state

with other locations, and can be encoded using a state

parameter that takes one of the discrete values 1, 2,

. . . , N. The parameters for AMDP states with a single

passageway (corresponding to rooms A, B and E from

Figure 1) can only take the value 1 and are therefore

discarded. This leaves a set of 256 parameters that

Algorithm 1: Abstract policy synthesis heuristic.

1: function GENABSTRACTPOLICIES(M , C ,O)

2: PS ← {}

3: while ¬DONE(PS) do

4: P ← GETCANDIDATEPOLICIES(PS,M )

5: for π ∈ P do

6: if

c∈C

PMC

(M ,π,c) then

7: dominated = false

8: for π

∈ PS do

9: if DOM(π, π

,M ,O) then

10: PS ← PS \ {π

}

11: else if DOM(π

,π, M ,O) then

12: dominated = true

13: break

14: end if

15: end for

16: if ¬dominated then

17: PS ← PS ∪ {π}

18: end if

19: end if

20: end for

21: end while

22: return PS

23: end function

24: function DOM(π

,π

,M ,O)

25: return

∀o∈ O · PMC

(M ,π

,o)≥PMC

(M ,π

,o)∧

∃o∈ O · PMC

(M ,π

,o)>PMC

(M ,π

,o)

26: end function

correspond to approximately 4 × 10

possible ab-

stract policies.

Finally, this ARL stage is also responsible for la-

belling the AMDP with atomic propositions enabling

its probabilistic model checking, and for the PCTL

formalisation of the constraints C and optimisation

objectives O in terms of these atomic propositions.

For our ﬂag-collection mission, this involves associ-

ating an atomic proposition ‘goal’ with the AMDP

states corresponding to the agent reaching the ‘goal’

area (with any number of collected ﬂags), and formal-

ising the constraints and optimisation objectives from

Section 4 as follows:

: P

≥0.75

[F goal] O

: maximize P

[F goal]

: R

[F goal] O

: maximize R

[F goal]

Stage 2: Abstract Policy Synthesis. In this ARL

stage, the generic heuristic from Algorithm 1 is used

to ﬁnd constraint-compliant abstract policies for the

RL problem. Given an AMDP M , a set of constraints

C and a set of optimisation objectives O (all obtained

in Stage 1 of ARL), the function GENABSTRACT-

POLICIES from Algorithm 1 synthesises an approx-

imate Pareto-optimal set of abstract policies that sat-

isfy the constraints C and are Pareto non-dominated

with respect to the optimisation objectives O. The

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

110

abstract policy set PS returned by this function in

line 22 starts empty (line 2), and is assembled iter-

atively by the while loop in lines 3–21 until a termi-

nation criterion ¬DONE(PS) is satisﬁed. This crite-

rion (not shown in Algorithm 1) may involve ending

the while loop after a ﬁxed number of iterations, or

after several consecutive iterations during which PS

is left unchanged. Each iteration of the while loop

ﬁrst identiﬁes a set P of “candidate” abstract policies

in line 4, and then updates the Pareto-optimal policy

set in the for loop from lines 5–20. Our algorithm

is not prescriptive about the method used to get new

candidate policies. As such, the function GETCAN-

DIDATEPOLICIES from line 4 can be implemented

using a metaheuristic such as the genetic algorithm

used to synthesise Markovain models in (Gerasimou

et al., 2015), a simple heuristic like hill climbing, or

just random search.

To decide how to update PS, the for loop in lines

5–20 examines each candidate abstract policy π as

follows. First, the boolean function PMC

(which

invokes a probabilistic model checking tool) is used

to establish whether using policy π for the AMDP M

satisﬁes every constraint c ∈ C (line 6). If it does, π

is deemed “safe” and the inner for loop in lines 8–15

compares it to each of the abstract policies already in

PS by using the Pareto-dominance comparison func-

tion DOM deﬁned in lines 24–26, where the prob-

abilistic model checking function PMC

(M , π,o)

computes the value of the optimisation objective o ∈

O for the policy π of M .

Every policy π

∈ PS that

is Pareto dominated by π is removed from PS (lines

9–10). If π is itself Pareto-dominated (line 11), the

ﬂag dominated (initially false, cf. line 7) is set to true

in line 12 and the inner for loop is terminated early

in line 13. Finally, the new abstract policy is added

to the Pareto-optimal policy set if is not dominated by

any known policy (lines 16–18).

Stage 3: Safe Learning. The ﬁnal stage of ARL

exploits the previously obtained approximate Pareto-

optimal set of abstract policies. A policy is selected

from this set by taking into account the trade-offs that

different policies achieve for the optimisation objec-

tives used to assemble the set. The high-level op-

tions from the abstract policy are used as rules for

which of the corresponding low-level MDP actions

A policy π

is said to Pareto-dominate another policy

with respect to a set of objectives O iff π

gives superior

results to π

for at least one objective from O, and for all

other objectives π

it is at least as good as π

(Liu et al.,

2015). Without loss of generality, the deﬁnition of DOM

from Algorithm 1 assumes that all objectives from O are

maximising objectives.

the RL agent should, or should not, perform in order

to achieve the required constraints. For instance, as-

sume that the selected abstract policy for our motivat-

ing example requires the agent to never enter RoomA.

In this case, should the agent be at Cartesian coordi-

nates (5,9) (i.e. the position immediately to the North

of the Start position), the action to move North and

thus to enter RoomA is removed from the agent’s ac-

tion set, for this speciﬁc state. Disallowing actions

that are not associated with the safe options of the ab-

stract policy results in the RL agent learning low-level

behaviours that are guaranteed to satisfy the safety

constraints.

This restriction of actions necessarily reduces the

RL agent’s autonomy, however, it is not removed en-

tirely. Speciﬁcally, to ensure that the agent behaves

according to the safety requirements, exploration of

actions that can result in safety violations, i.e. those

actions which contradict the abstract policy, are re-

stricted. Otherwise, the agent is free to explore its

environment as it normally would. For example, in

the motivating example, the agent’s exploration is re-

stricted only by which rooms it can enter. The agent

must still explore the environment to learn the ﬂag lo-

cations within the rooms as well as the doorway areas

safest to cross, information which is unknown a priori

and therefore not contained within the abstract poli-

cies. Although abstract policy constraints may yield

suboptimal RL policies with respect to the RL model

in its entirety, this key feature assures safety.

6 EVALUATION

To evaluate the efﬁcacy and generality of ARL we ap-

plied it to two case studies from different domains.

The ﬁrst case study is based on the navigation task

described in Section 4, where the learning agent must

navigate a guarded building with the objective of col-

lecting ﬂags distributed throughout. The second case

study is a planning problem adapted from (Boger

et al., 2006), where a system has been designed to

assist a dementia sufferer perform the task of washing

their hands.

For each case study we conducted a set of four ex-

periments. An initial experiment was ﬁrst conducted

which was a traditional RL implementation of the

case study problem. This experiment serves as a base-

line which we contrast with the ARL experiments in

order to determine the effects of our method. Fol-

lowing the baseline experiment a further three exper-

iments were undertaken where RL in Stage 3 of ARL

was applied using a different abstract policy from the

Pareto-optimal set of abstract policies constructed in

Assured Reinforcement Learning with Formally Veriﬁed Abstract Policies

111

Stage 2 using an implementation based on random

search for function GETCANDIDATEPOLICIES from

Algorithm 1.

For all experiments we use a discount factor γ =

0.99 and a learning rate α = 0.1 which decays to 0

over the learning run, experiment-speciﬁc parameters

are shown where relevant in the remainder of this sec-

tion. All parameters have been chosen empirically in

line with standard RL practice. As is convention when

evaluating stochastic processes, we repeated each ex-

periment multiple times (i.e. ﬁve times) and we eval-

uated the ﬁnal policy for each experiment many times

(i.e. 10,000 times) in order to ensure that the results

are suitably signiﬁcant (Arcuri and Briand, 2011).

We evaluate the learning progress of each experi-

ment after each learning episode during a run. Error

bars for the standard error of the mean show the statis-

tical signiﬁcance of the learning over the ﬁve learning

runs that we performed for each experiment (Figures

3, 4, 7 and 8). Evaluation of the learned RL policies

was done once a learning run had ﬁnished (Tables 3

and 7).

6.1 Guarded Flag Collection

This case study is based on the scenario described in

Section 4 and referred to throughout Section 5. In the

interest of brevity, the details presented in these two

previous sections will not be repeated here.

In our RL implementation, the reward structure

was deﬁned as follows: the agent receives a reward

of 1 for each ﬂag it collects and an additional reward

of 1 for reaching the ‘goal’ area of the building. If

the agent is captured it receives a reward of -1 and

any ﬂags that have been previously collected are dis-

regarded.

We used the AMDP constructed during the ﬁrst

ARL stage as described in Section 5. In the sec-

ond ARL stage, we generated 10,000 abstract policies

with parameter values (i.e. state to action mappings)

drawn randomly from a uniform distribution. Out of

these abstract policies, probabilistic model checking

using the tool PRISM identiﬁed 14 policies that sat-

isﬁed the two constraints from Section 4. Figure 2

shows the QV results obtained for these 14 abstract

policies, i.e. their associated probability of reach-

ing the ‘goal’ area and expected number of ﬂags col-

lected. The approximate Pareto-front depicted in this

ﬁgure was obtained using the two optimization objec-

tives described in Section 5, i.e. maximizing the ex-

pected number of ﬂags collected and the probability

of reaching the ‘goal’ area of the building.

Three abstract policies were selected to use in

each of the ARL experiments during the safe learn-

0.8

0.85

0.9

3.5

4.5

Probability of reaching ‘goal’

Expected reward

Abstract policy

Pareto-front

Figure 2: Pareto-front of abstract policies that satisfy the

constraints from Section 4.

Table 2: Selected abstract policies to use for ARL in the

guarded ﬂag-collection.

Abstract

Policy

Probability of

Reaching ‘goal’

Expected

Reward

A 0.9 2.85

B 0.81 3.62

C 0.78 4.5

ing stage, as explained in Section 5. The properties of

these three abstract policies are shown in Table 2.

The baseline experiment, which was a standard

RL implementation of the case study, used an ε = 0.8

and performed 2 × 10

learning episodes, each with

10,000 steps. This did not, however, reach a global

optimum. Even after extensive learning runs, in ex-

cess of 10

learning episodes, conventional RL did

not attain a superior solution. In contrast, in our ex-

periments where ARL was used (cf. abstract policy

C, Table 3), a superior policy was learned much faster,

further demonstrating the advantages of our approach.

Figure 3 shows the learning progress for this experi-

ment.

0 0.2 0.4

0.6

0.8 1 1.2 1.4

1.6

1.8 2

·10

1.5

2.5

Episodes

Expected Reward

Figure 3: Learning for guarded ﬂag-collection with no ARL

applied.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

112

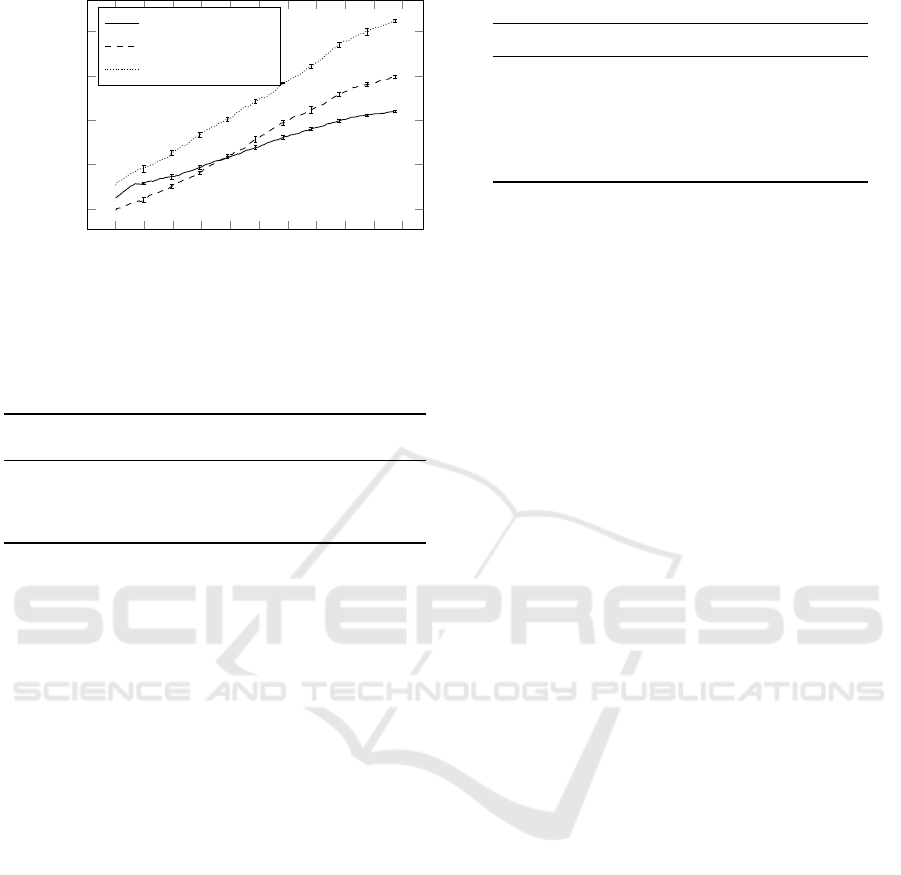
0 0.1 0.2 0.3 0.4

0.5 0.6

0.7 0.8 0.9 1

·10

1.5

2.5

3.5

Episodes

Expected Reward

Abstract policy A

Abstract policy B

Abstract policy C

Figure 4: Learning for guarded ﬂag-collection with ARL

applied using the selected abstract policies A, B and C.

Table 3: Results for baseline and ARL experiments for

guarded ﬂag-collection.

Abstract

Policy

Probability of

Reaching ‘goal’

Standard

Error

Expected

Reward

Standard

Error

None 0.72 0.0073 4.01 0.031

A 0.9 0.0012 2.85 0.0029

B 0.81 0.0019 3.62 0.0037

C 0.78 0.0012 4.5 0.0041

Next, we present the three ARL experiments, one

for each of the abstract policies from Table 2. Since

the abstract policy had the effect of guiding the agent

with regard to the locations to enter next, less explo-

ration by the agent was required and fewer learning

episodes were necessary. Therefore, we used ε = 0.6

which decayed to zero over the learning run and 10

episodes were needed for the learning to converge.

Figure 4 shows the RL learning progress for each of

the abstract policies used for ARL.

The learned policies for each of the experiments

were evaluated and the results summarized in Table 3.

The experiments where an abstract policy was ap-

plied resulted in an RL policy that: (a) satisﬁed the

problem constraints and optimisation objectives spec-

iﬁed in Section 4; and (b) matched the probability of

reaching the ‘goal’ area and the expected reward of

the abstract policy (cf. Table 2). The baseline exper-

iment gave results that do not satisfy our constraints,

which was expected given that only 14 of the 10,000

abstract policies synthesised by ARL satisﬁed these

constraints.

6.2 Autonomous Assistance for

Dementia Sufferer

Dementia is a common chronic illness with signiﬁ-

cantly debilitating consequences. As the illness pro-

gresses, it becomes increasingly difﬁcult for the suf-

Table 4: Hand washing subtasks.

Subtask Atomic proposition

Turn tap on on

Apply soap soaped

Wet hands under tap wet

Rinse washed hands rinsed

Dry hands dried

ferer to perform even simple tasks, making it neces-

sary for a caregiver to provide assistance with such

tasks.

To alleviate the duties of the caregiver and the cost

to healthcare, the project described in (Boger et al.,

2006) has developed an automated system that helps

a dementia patient perform the task of washing their

hands. For our second case study we used a simulated

version of this assisted-living system. For the purpose

of our system, the hand-washing task can be decom-

posed into the subtasks listed in Table 4. This table

also shows the atomic propositions (i.e. boolean la-

bels, cf. Section 3) that we will use in this section to

indicate whether each of the subtasks has been com-

pleted.

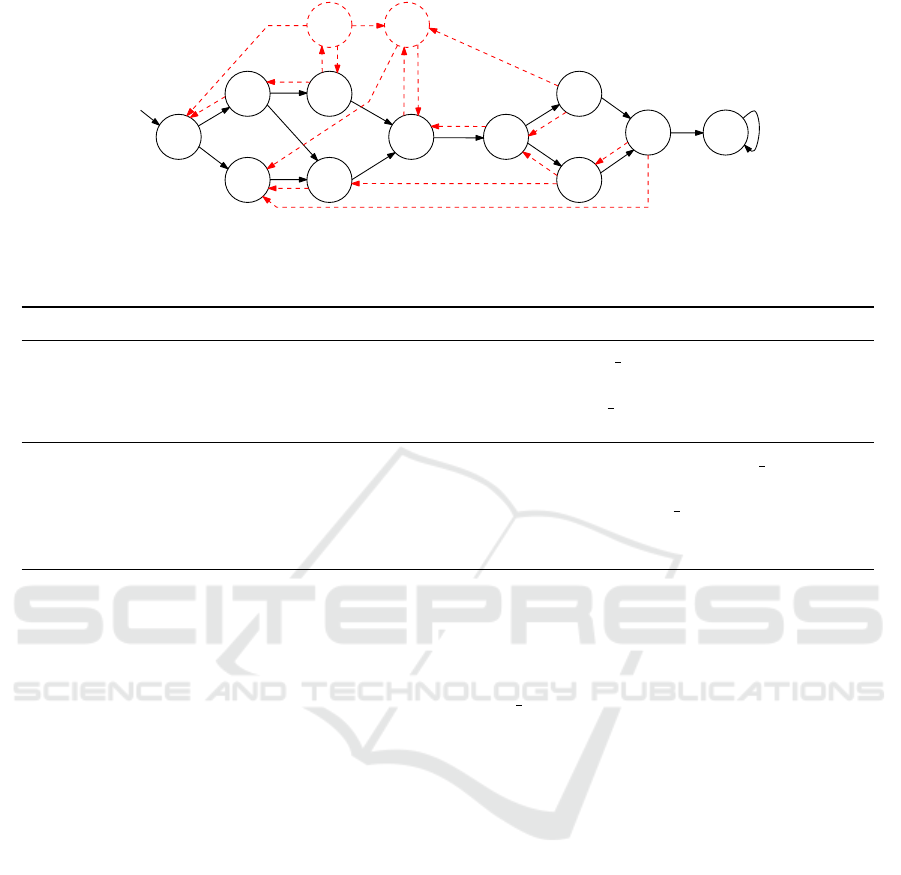
It is possible for the dementia sufferer to regress

in this task by repeating subtasks they have already

performed, or by performing the wrong subtask for

the stage of the hand-washing process they have

reached. Figure 5 depicts the workﬂow carried out

by a healthy person while progressing with the task

(black, continuous-line nodes and arrows) and the

possible regressions that a dementia sufferer could

make (red dashed-line nodes and arrows). For ease of

reference, the states of the workﬂow is labelled with

a state ID (s

to s

) and with the atomic propositions

that hold in that state.

The probabilities of the dementia sufferer pro-

gressing and regressing (not shown in Figure 5) vary

at each stage of the task and between sufferers. For

the purpose of our evaluation, we carefully decided

these probabilities based on the subtask complexity,

as indicated in (Boger et al., 2006).

The system is designed so that if the user fails to

perform one of the next correct subtasks then it may

provide a voice prompt instructing the user what sub-

task to do next. The system learns what style of voice

is most appealing to the user based on how conducive

different styles of prompt are at the user succeeding

with the overall task. Voice styles vary in gender,

sternness of the instructions (mild, moderate or strict)

and volume (soft, medium or loud). The appeal of the

voice style will induce an increase in the probabil-

ity that the dementia sufferer progresses compared to

no prompt being given, with the least appealing voice

Assured Reinforcement Learning with Formally Veriﬁed Abstract Policies

113

wet

done

dried

soaped

wet

soaped

rinsed

wet

rinsed

Figure 5: Workﬂow of washing hands, showing the subtasks at each stage of progress with the progression of a healthy person

in black continuous lines and the possible regressions of a dementia sufferer in red dashed lines.

Table 5: Constraints and optimisation objectives for the assisted-living system.

ID Constraint (C) or optimisation objective (O) PCTL

The probability that the caregiver provides as-

sistance should be at least 0.05

≥0.05

[F m = MAX MISTAKES]

The probability that the caregiver provides as-

sistance should be at most 0.2

≤0.2

[F m = MAX MISTAKES]

The level of dementia sufferer distress due to

multiple voice prompts should be minimised

minimise R

distress

[F done ∨ m = MAX MISTAKES]

The probability of calling the caregiver should

be minimised (subject to C

and C

being sat-

isﬁed)

minimise P

[F m = MAX MISTAKES]

yielding the smallest increase and the most appealing

yielding the largest increase.

For our system we wish to determine when to give

a prompt to the user and when it becomes necessary

to call the caregiver (because the user is not making

progress despite repeated prompts). Overloading the

user with prompts can become stressful, and therefore

each prompt has a negative reward of −1. Whilst call-

ing the caregiver will be of relief to the user as well as

ensuing the completion of the task, doing it too fre-

quently will become stressful to the caregiver or, in

a care home, will overstretch the personnel resources

available. Therefore, the caregiver should assist on

some occasions, but most of the time not; thus the

action to call the caregiver has a negative reward of

−300. Completing the task results in a reward of 500.

Note that the rewards for calling the caregiver and for

completing the task are only necessary in the RL sim-

ulation for learning to appropriately progress and are

not necessary in the AMDP.

Finally, we desire that the caregiver be present at

least once every one-to-four days, to ensure that the

sufferer receives the caregiver’s attention regularly.

Assuming that a person washes their hands approx-

imately ﬁve times a day, the probability that the care-

giver should assist the dementia sufferer during any

one hand-washing should be between

/20 and

/5, i.e.

between 0.05 and 0.2. This constraint, and an addi-

tional, manually-speciﬁed optimisation objective for

the abstract policy synthesis stage of ARL can be

formalised in PCTL as shown in Table 5, where m

is the number of mistakes made at any given time,

MAX MISTAKES is the threshold for the maximum

number of mistakes that result in calling the caregiver,

distress is the reward structure for stress to the demen-

tia sufferer, and done is the atomic proposition asso-

ciated with the completion of the hand-washing task

by the user (cf. Figure 5).

We constructed the AMDP for this system based

on the workﬂow shown in Figure 5, where each work-

ﬂow stage represents a different AMDP state. To ab-

stract the RL MDP we only used in the AMDP the

transition probabilities and the best style of prompt

which the RL agent aims to learn. We encoded an ab-

stract policy for this AMDP using an array of 12 pa-

rameters, one for each stage of the task from Figure 5

other than stage 10 (where the task is complete). The

parameter associated with each workﬂow stage rep-

resents the minimum number of total user mistakes

that warrant giving a prompt at that stage. Each pa-

rameter can take values between zero (always give

a voice prompt) and the maximum number of mis-

takes allowed before calling the caregiver (never give

a voice prompt).

We generated 10,000 abstract policies using ran-

dom search, and we used the probabilistic model

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

114

0.05

0.1

0.15

0.2

Probability of calling the caregiver

Distress to dementia sufferer

Abstract policy

Pareto-front

Figure 6: Abstract policies and Pareto-front for the assisted-

living system.

Table 6: Selected abstract policies used during the safe

learning stage of ARL for the assisted-living system.

Abstract

Policy

Probability of Calling

the Caregiver

Distress to

Dementia Sufferer

A 0.08 2.17

B 0.13 1.70

C 0.17 1.38

checker PRISM to identify the 786 abstract policies

that satisﬁed constraints C

and C

from Table 5. Two

optimisation objectives were used to assemble the ap-

proximate Pareto-front (and the set of Pareto-optimal

abstract policies) in the abstract policy synthesis stage

of ARL. The former objective was objective O

from

Table 5. The latter objective (O

from Table 5) was

derived from constraint C

, i.e. we aimed to min-

imise the probability of calling the caregiver. Figure 6

shows the entire set of safe abstract policies, as well as

the Pareto-front. For the last stage of ARL (safe learn-

ing), we carried out experiments starting from three

abstract policies from different areas of the Pareto-

front shown in Figure 6. Table 6 lists these three ab-

stract policies with their associated attributes (i.e. the

probability to call the caregiver and the level of dis-

tress to the dementia sufferer).

We chose a value of ε = 0.5 for all experiments

in this case study. Figure 7 shows the average learn-

ing of all ﬁve learning runs of the baseline experiment

(without ARL), with error bars used to show the stan-

dard error of the mean. For this experiment 1 × 10

episodes were necessary to reach an optimal policy

and each episode had a maximum of 1,000 steps.

Following the baseline experiment, we carried out

a series of experiments for each of the three selected

abstract policies from Table 6, the learning progress

of these experiments is shown in Figure 8. More

learning episodes were necessary for the ARL ex-

periments since for many states the abstract policies

0 0.2 0.4

0.6

0.8 1

·10

420

440

460

480

Episodes

Expected Reward

Figure 7: Learning for assisted-living system with no ARL

applied.

0.1 0.2 0.3 0.4

0.5 0.6

0.7 0.8 0.9 1

·10

420

440

460

Episodes

Expected Reward

A.P. A

A.P. B

A.P. C

Figure 8: Learning for assisted-living system with ARL ap-

plied using the selected abstract policies A, B and C.

prevented a prompt being given, delaying the agent’s

ability to explore and learn about different prompt

styles.

Contrasting the results from the baseline experi-

ment and the ARL experiments, it is clear that the ac-

tion constraints are having the expected effect on the

learned policy. In particular, comparing the probabil-

ities of calling the caregiver and the level of distress

to the dementia sufferer against those that were ver-

iﬁed for the abstract policies, the action constraints

are having the desired effect, with all the results being

close to or matching the values shown in Table 6. The

slight difference from the abstract policy C’s proba-

bility of calling the caregiver can be attributed to the

policy not being entirely optimal and further learning

should reduce the variance to zero.

7 CONCLUSION

For assured RL we proposed the use of an abstract

MDP formally analysed using quantitative veriﬁca-

tion. Safe abstract policies are identiﬁed and used as

Assured Reinforcement Learning with Formally Veriﬁed Abstract Policies

115

Table 7: Results from baseline and ARL experiments for the assisted-living system.

Abstract Policy

Probability of Calling

the Caregiver

Standard Error

Distress to

Patient

Standard Error

None 4.02 × 10

−4

4.28 × 10

−4

8.31 4.03 × 10

−3

A 0.08 4.95 × 10

−4

2.17 3.25 × 10

−3

B 0.13 5.17 × 10

−4

1.70 2.22 × 10

−3

C 0.18 4.27 × 10

−4

1.38 1.84 × 10

−3

a means to restrict the action set of an RL agent to

those actions that were proven to satisfy a set of re-

quirements, adding to the growing research on safe

RL. Through two qualitatively different case studies,

we demonstrated that the ARL technique can be ap-

plied successfully to multiple problem domains. ARL

assumes that partial knowledge of the problem is pro-

vided a priori, and makes the typical assumption that

with sufﬁcient learning the RL agent will converge to-

wards an optimal policy.

ARL supports a wide range of safety, performance

and reliability constraints that cannot be expressed us-

ing a single reward function in standard RL and are

not supported by existing safe RL techniques. Fur-

thermore, the use of an AMDP allows the application

of ARL where only limited knowledge of the prob-

lem domain is available, and ensures that ARL scales

to much larger and complex models than would other-

wise be feasible. Additionally, the expressive nature

of PCTL formulae and the construction of the AMDP

enables convenient on the ﬂy experimentation of con-

straints and properties without requiring modiﬁcation

of the underlying model.

Future work on ARL includes researching a

means of updating the AMDP should it not accurately

reﬂect the RL MDP. In the event that the RL agent

encounters information in the RL MDP that does not

correlate with the AMDP, or should the RL system

dynamics change during runtime, a means of feeding

back this information to update the AMDP can be de-

veloped, e.g. based on (Calinescu et al., 2011; Cali-

nescu et al., 2014; Efthymiadis and Kudenko, 2015).

After updating the AMDP the constraints will need to

be reveriﬁed and, if necessary, a new abstract policy

will be generated.

Additionally, we intend to exploit some of the

more sophisticated constraints that can be speciﬁed

in PCTL. For example, bounded until PCTL formu-

lae can place constraints on the number of time steps

taken to achieve a certain outcome, e.g. for our

assisted-living case study the formula P

≥0.75

[¬(s

∨

≤8

] requires the agent to ensure, with a proba-

bility of at least 0.75, that the user washes their hands

with water and soap and then rinses them (thus reach-

ing stage s

of the workﬂow from Figure 5) within

eight subtasks, without switching the tap on and off

unnecessarily (by entering stages s

or s

of the

workﬂow).

ACKNOWLEDGEMENTS

This paper presents research sponsored by the UK

MOD. The information contained in it should not be

interpreted as representing the views of the UK MOD,

nor should it be assumed it reﬂects any current or fu-

ture UK MOD policy.

REFERENCES

Abe, N., Melville, P., Pendus, C., et al. (2011). Optimiz-

ing debt collections using constrained reinforcement

learning. In 16th ACM SIGKDD Intl. Conf. Knowl-

edge Discovery and Data Mining, pages 75–84.

Andova, S., Hermanns, H., and Katoen, J.-P. (2004).

Discrete-time rewards model-checked. In Formal

Modeling and Analysis of Timed Systems, pages 88–

104.

Arcuri, A. and Briand, L. (2011). A practical guide for us-

ing statistical tests to assess randomized algorithms in

software engineering. In 33rd Intl. Conf. Software En-

gineering, pages 1–10.

Barrett, L. and Narayanan, S. (2008). Learning all optimal

policies with multiple criteria. In 25th Intl. Conf. Ma-

chine learning, pages 41–47.

Boger, J., Hoey, J., Poupart, P., et al. (2006). A planning

system based on markov decision processes to guide

people with dementia through activities of daily liv-

ing. IEEE Transactions on Information Technology in

Biomedicine, 10(2):323–333.

Calinescu, R., Johnson, K., and Raﬁq, Y. (2011). Using ob-

servation ageing to improve Markovian model learn-

ing in QoS engineering. In 2nd Intl. Conf. Perfor-

mance Engineering, pages 505–510.

Calinescu, R., Johnson, K., and Raﬁq, Y. (2013). Devel-

oping self-verifying service-based systems. In 28th

IEEE/ACM Intl. Conf. on Automated Software Engi-

neering, pages 734–737.

Calinescu, R., Kikuchi, S., and Johnson, K. (2012). Com-

positional reveriﬁcation of probabilistic safety prop-

erties for large-scale complex IT systems. In Large-

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

116

Scale Complex IT Systems. Development, Operation

and Management, pages 303–329. Springer.

Calinescu, R., Raﬁq, Y., Johnson, K., and Bakir, M. E.

(2014). Adaptive model learning for continual veriﬁ-

cation of non-functional properties. In 5th Intl. Conf.

Performance Engineering, pages 87–98.

Castro, D. D., Tamar, A., and Mannor, S. (2012). Policy

gradients with variance related risk criteria. In 29th

Intl. Conf. Machine Learning, pages 935–942.

Dearden, R., Friedman, N., and Russell, S. (1998).

Bayesian Q-learning. In 15th National Conference on

Artiﬁcial Intelligence, pages 761–768.

Delage, E. and Mannor, S. (2010). Percentile optimization

for Markov decision processes with parameter uncer-

tainty. Operations Research, 58(1):203–213.

Driessens, K. and D

zeroski, S. (2004). Integrating guid-

ance into relational reinforcement learning. Machine

Learning, 57(3):271–304.

Efthymiadis, K. and Kudenko, D. (2015). Knowledge revi-

sion for reinforcement learning with abstract MDPs.

In 14th Intl. Conf. Autonomous Agents and Multiagent

Systems, pages 763–770.

abor, Z., Kalm

ar, Z., and Szepesv

ari, C. (1998). Multi-

criteria reinforcement learning. In 15th Intl. Conf. Ma-

chine Learning, pages 197–205.

Garc

ıa, J. and Fern

andez, F. (2015). A comprehensive sur-

vey on safe reinforcement learning. Journal of Ma-

chine Learning Research, 16(1):1437–1480.

Geibel, P. (2006). Reinforcement learning for MDPs with

constraints. In 17th European Conference on Machine

Learning, volume 4212, pages 646–653.

Gerasimou, S., Calinescu, R., and Banks, A. (2014). Efﬁ-

cient runtime quantitative veriﬁcation using caching,

lookahead, and nearly-optimal reconﬁguration. In 9th

Intl. Symposium on Software Engineering for Adap-

tive and Self-Managing Systems, pages 115–124.

Gerasimou, S., Tamburrelli, G., and Calinescu, R. (2015).

Search-based synthesis of probabilistic models for

quality-of-service software engineering. In 30th

IEEE/ACM Intl. Conf. Automated Software Engineer-

ing, pages 319–330.

Hansson, H. and Jonsson, B. (1994). A logic for reasoning

about time and reliability. Formal Aspects of Comput-

ing, 6(5):512–535.

Katoen, J.-P., Zapreev, I. S., Hahn, E. M., et al. (2011).

The ins and outs of the probabilistic model checker

MRMC. Performance Evaluation, 68(2):90–104.

Kober, J., Bagnell, J. A., and Peters, J. (2013). Re-

inforcement learning in robotics: A survey. The

International Journal of Robotics Research, page

0278364913495721.

Kwiatkowska, M. (2007). Quantitative veriﬁcation: Mod-

els, techniques and tools. In 6th joint meeting of

the European Software Engineering Conference and

the ACM SIGSOFT Symposium on the Foundations of

Software Engineering, pages 449–458.

Kwiatkowska, M., Norman, G., and Parker, D. (2007).

Stochastic model checking. In 7th Intl. Conf. Formal

Methods for Performance Evaluation, volume 4486,

pages 220–270.

Kwiatkowska, M., Norman, G., and Parker, D. (2011).

PRISM 4.0: Veriﬁcation of probabilistic real-time sys-

tems. In 23rd Intl. Conf. Computer Aided Veriﬁcation,

volume 6806, pages 585–591.

Li, L., Walsh, T. J., and Littman, M. L. (2006). Towards a

uniﬁed theory of state abstraction for MDPs. In 9th In-

ternational Symposium on Artiﬁcial Intelligence and

Mathematics, pages 531–539.

Liu, C., Xu, X., and Hu, D. (2015). Multiobjective rein-

forcement learning: A comprehensive overview. IEEE

Transactions on Systems, Man, and Cybernetics: Sys-

tems, 45(3):385–398.

Mannor, S. and Shimkin, N. (2004). A geometric approach

to multi-criterion reinforcement learning. Journal of

Machine Learning Research, 5:325–360.

Marthi, B. (2007). Automatic shaping and decomposition of

reward functions. In 24th Intl. Conf. Machine learn-

ing, pages 601–608.

Mason, G., Calinescu, R., Kudenko, D., and Banks, A.

(2016). Combining reinforcement learning and quan-

titative veriﬁcation for agent policy assurance. In 6th

Intl. Workshop on Combinations of Intelligent Meth-

ods and Applications, pages 45–52.

Mihatsch, O. and Neuneier, R. (2002). Risk-sensitive re-

inforcement learning. Machine Learning, 49(2):267–

290.

Moffaert, K. V. and Now

e, A. (2014). Multi-objective re-

inforcement learning using sets of pareto dominat-

ing policies. Journal of Machine Learning Research,

15(1):3663–3692.

Moldovan, T. M. and Abbeel, P. (2012). Safe exploration

in Markov decision processes. In 29th Intl. Conf. Ma-

chine Learning, pages 1711–1718.

Ponda, S. S., Johnson, L. B., and How, J. P. (2013). Risk al-

location strategies for distributed chance-constrained

task allocation. In American Control Conference,

pages 3230–3236.

Sutton, R. S., Precup, D., and Singh, S. (1999). Between

MDPs and semi-MDPs: A framework for temporal

abstraction in reinforcement learning. Artiﬁcial Intel-

ligence, 112(1-2):181–211.

Szita, I. (2012). Reinforcement learning in games. In Rein-

forcement Learning, pages 539–577. Springer.

Vamplew, P., Dazeley, R., Berry, A., et al. (2011). Empirical

evaluation methods for multiobjective reinforcement

learning algorithms. Machine Learning, 84(1):51–80.

Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning. Ma-

chine Learning, 8(3):279–292.

Wiering, M. and Otterlo, M. (2012). Reinforcement learn-

ing and markov decision processes. In Reinforcement

Learning: State-of-the-art, volume 12, pages 3–42.

Springer.

Xia, L. and Jia, Q.-S. (2013). Policy iteration for parame-

terized markov decision processes and its application.

In 9th Asian Control Conference, pages 1–6.

Assured Reinforcement Learning with Formally Veriﬁed Abstract Policies

117