An Agent Trading on Behalf of V2G Drivers in a Day-ahead Price

Market

Ibrahem A. Almansour, Enrico H. Gerding and Gary Wills

Electronics and Computer Science, University of Southampton, U.K.

Keywords:

V2G, Driving Behaviour, Price Uncertainty.

Abstract:

Due to the limited availability of fuel resources, there is an urgent need for converting to use renewable sources

efﬁciently. To achieve this, power consumers should participate actively in power production and consumption.

Consumers nowadays can produce power and consume a portion of it locally, and then could offer the rest

of the power to the grid. Vehicle-to-grid (V2G) which is one of the most effective sustainable solutions,

could provide these opportunities. V2G can be deﬁned as a situation where electric vehicles (EVs) offer

electric power to the grid when parked. We developed an agent to trade on behalf of V2G users to maximize

their proﬁts in a day-ahead price market. We then ran the proposed model in three different scenarios using

an optimal algorithm and compared the results of our solution to a benchmark. We show that our solution

outperforms the benchmark strategy in the proposed three scenarios 49%, 51%, and 10% respectively in terms

of proﬁt.

1 INTRODUCTION

One of the most effective sustainable solutions is that

of electric vehicles(EVs), because of their power stor-

age capability. They could use solar and wind power

and signiﬁcantly decrease the amount of power that

are utilized for transportation because they are more

effective than internal combustion vehicles. More-

over, EV batteries could offset the volatility of wind

and solar production when they are plugged into the

grid. Vehicle-to-grid (V2G) has the potential to fur-

ther encourage consumers to change their vehicles

from fuel vehicles to EVs. This is due to its ability to

reduce the power cost, if used effectively. V2G can be

deﬁned as an approach whereby an EV offers electric

power to the grid when parked. (Kempton and Tomi´c,

2005) found that, most cars are not used 90% of the

time, so EVs can be used to provide power storage

and supplementary services to the smart grid during

this period when they not being used. Therefore, V2G

could be used to provide extra money. For example,

it is expected that, if an EV owners contribute in V2G

systems, they could take around (2500 to 3000) U.S.

dollars yearly (Tomas, 2013). Moreover, (Li et al.,

2015) found that the majority of V2G studies are dis-

cussed from the perspective of the power grid. In con-

trast, here we take the consumer’s perspective.

In this research there are a large number of diverse

actors with individual behaviours and incentives that

need to be considered such as the different power mar-

kets and V2G drivers’ behaviours. Thus, according to

Siegfried et al. (2009), an agent-based model might

be the ﬁrst choice to model the problem. Therefore,

our research models an agent to trade on behalf of

V2G in terms of maximising their proﬁt of using V2G

as a source of electricity with consideration to their

behaviours and their incentives.

The rest of the paper is organised as follows. The

related work will be discussed in Section 2. After-

ward, the proposed model will be described in Section

3. Then, Section 4 discusses the design of the optimi-

sation module. Next, the experimental evaluation will

be considered in section 5. Finally, the conclusion of

our study will be discussed in section 6.

2 RELATED WORK

V2G could be used to support the smart grid (Tomi´c

and Kempton, 2007), (Saber and Venayagamoorthy,

2011) and (White and Zhang, 2011). This offers V2G

drivers an opportunity to cut their power costs and re-

ceive money. To do so, they should have a clear un-

derstanding about how to deal with the power market.

However, there is a lack of knowledge among con-

sumers about how to deal with time varying prices in

Almansour, I., Gerding, E. and Wills, G.

An Agent Trading on Behalf of V2G Drivers in a Day-ahead Price Market.

DOI: 10.5220/0006156201350141

In Proceedings of the 3rd International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2017), pages 135-141

ISBN: 978-989-758-242-4

135

Figure 1: Picture showing our proposed model.

the power market (Mohsenian-Rad and Leon-Garcia,

2010) and (Han et al., 2010). To ﬁx that, (O’Neill

et al., 2010) study the price uncertainty problem used

reinforcement learning in the residential demand re-

sponse algorithm. In the same vein, (Conejo et al.,

2010) developed a real-time demand response algo-

rithm applied to a daily 24-hour horizon and used ro-

bust optimization to consider the price uncertainty in

their model (Conejo et al., 2010) and (O’Neill et al.,

2010) dealt with the real-time demand response prob-

lem. However, (Shi and Wong, 2011) discuss the

same issue in the context of V2G control.

V2G problems are more complicated if price un-

certainty is considered, as the price of electricity is de-

cided each hour, dynamically. (Shi and Wong, 2011)

discussed the real- time V2G control problem con-

sidering price uncertainty. Similar to (Shi and Wong,

2011), we study price uncertainty in the context of

V2G, but our study differs from theirs in that, Our al-

gorithm is more scalable, thus it could be used when

we consider the battery usage behavior as we plan for

our future work. Though, they applied Q-learning,

which does not work effectively when considering the

battery usage behavior as we concluded from (Guo

et al., 2004)

In contrast to the aforementioned studies, (Ghias-

nezhad Omran and Filizadeh, 2014), (Sanchez-Martin

et al., 2015),(Valogianniet al., 2014), (Gonzalez Vaya

and Andersson, 2013), and (Halvgaard et al., 2012)

studies will be used as references of our model when

we are going to model the driving behaviour in our

future work. In details, (Ghiasnezhad Omran and Fil-

izadeh, 2014) propose a procedure for location-based

prediction of the possible vehicular charging load at

charging stations. In order to emulate drivers’ charg-

ing behaviour they apply fuzzy decision-making sys-

tems. In a related vein, (Sanchez-Martin et al., 2015)

argue that applying stochastic behaviour to manage

EV charging points is more realistic and develop

a stochastic programming model to achieve optimal

management, taking into account price variations in

day-ahead price markets. Along the same line, (Halv-

gaard et al., 2012) use Economic Model Predictive

Control as a technique to reduce the cost of electricity

consumption for a single EV. Likewise, (Valogianni

et al., 2014) propose an algorithm termed Adaptive

Management of EV Storage, which is applied by a

learning agent that acts on behalf of individual EV

users and schedules EV charging over a weekly hori-

zon. They used reinforcement learning to learn user

consumption behaviour and schedule charging with

the objectives of maximizing user beneﬁt. The key

difference between our work and the aforementioned

studies is that they have not considered the V2G issue

but we have.

Speciﬁcally in V2G, a number of algorithms are

proposed to deal with different types of uncertain-

ties in V2G amid uncertainty in the production of re-

newable power (Pinson et al., 2009) (Panagopoulos

et al., 2012), together with that of EV driving be-

haviour (Ghiasnezhad Omran and Filizadeh, 2014)

(Shahidinejad et al., 2012). Moreover, several stud-

ies discuss uncertainty in power market prices, for

instance the work by (Shi and Wong, 2011). Fi-

nally, (Zareen et al., 2015) note that when the V2G

drivers charge or discharge their vehicles optimally in

the deregulated market, they not only maximize their

proﬁt but support the provision of regulation services

in emergencies. This claim could be used to highlight

the importance of our research.

3 THE MODEL

This section describes the model proposed to solve

the research problem. After that, the problem of price

uncertainty in the context of V2G is discussed.

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

136

3.1 Model Overview

In order to design our agent, a model has been pro-

posed as shown in Figure 1. In this model there

are two components that receive input from the V2G

driver, battery usage behaviour and user incentives.

Two factors will be considered to shape battery usage

behaviour: time, and vehicle usage (habit). In more

detail, V2G drivers determine the times when they

need to drive their car and when they can park their

car. one driving times are given, parking times can be

identiﬁed, which can be used to sell and buy the elec-

tricity. The second factor considered is vehicle usage

(habit). In this study, vehicle usage is deﬁned as the

daily driving distance and the average speed.

The data on battery usage behaviour and user in-

centives will be sent to the V2G agent, which is a ma-

jor component of this model, and it will use this infor-

mation to trade with the power market. Speciﬁcally,

this agent will buy and sell electricity from and to the

power market, trying to calculate the best time to buy

and sell by predicting price behaviour. In doing so, it

will maximize the V2G drivers’ utility, which is the

monetary proﬁt and the level of battery power that is

returned to the V2G driver at the end of a day. There is

a further important component in this model, namely

the power market, which models the real power mar-

ket. There are a number of factors that should be con-

sidered in designing such a market, such as the real

time pricing market.

The model shown in Figure 1 is of a simple mar-

ket, and is used to both understand the problem com-

prehensively and to design the model precisely. One

of the user incentives to be considered is price sensi-

tive. Furthermore, only a single type of power mar-

ket has been considered, namely the day-ahead price

(DAP) market. We chose the DAP market because

it is more practical to the people to plan for the fol-

lowing day power market price. In the DAP mar-

ket, quotes for day-ahead delivery of electricity are

offered together for every hour of the following day.

The information set to be used for quoting might not

be the same for every hour. Here, the V2G agent fo-

cuses on the power market side and in future work,

the driving behaviour and the user incentives will be

considered.

3.2 Problem Formulation

In more detail, the proposed model will incorporate

V2G driver behaviour, which has been deﬁned in this

study as usage time. Moreover, it will employ elec-

tricity prices for the next day, since we consider only

the day ahead price market. By using these two types

of information the model will maximize the V2G

driver utility function by deciding the the best action

for every hour of the day, apart from the usage time

allocated to users to drive their cars. The utility has

been deﬁned here as the monetary proﬁt and the level

of battery power that is returned to the V2G driver at

the end of a day. Table 1 has been used to explain the

notations in details.

Table 1: Overview of the main notations used.

notation Description

a The vector which contains the chosen

action for each hour

= 0 Do nothing

= 1 Charging

= -1 Discharging

B State of charge

des

Desired amount of battery level be-

fore using time

init

Initial value for the battery

n Total of hours day

electricity price at time t

T Number of time steps and can be de-

ﬁned as a T = {1, 2, ..., n}

Start of using time

End time of using

Available time which the agent can

charging or discharging or do nothing

V(x) Function represent the battery of

charge which left for the driver at the

end of the day

Before representing it mathematically, based on

the Table 1, the notations of our model will be dis-

cussed. We will explain using an example. Let us

assume a driver wants to use his or her car from time

until time T

, that will be considered as saying

to the agent that during this period of time it cannot

do anything represented in Equation 7. By exclud-

ing this usage time, the agent can deﬁne the period of

time during which it could charge a

= 1, discharge

= -1, or do nothing a

= 0, as represented in Equa-

tion 4. Agent will charge (buy) or discharge (sell)

from or to the market by considering the hour price

p. Moreover, let us assume the driver plans to go to

another city and he or she has an initial amount of bat-

tery at the start of the day of b

init

, and needs to have

a certain amount of battery b

des

to achieve this goal

without any delay; this issue has been determined by

Equation 8. At the end of the day the remaining bat-

tery state of charge has been represented as a func-

tion V(x), where is x ∈ B. Furthermore, we deﬁne the

utility as the monetary proﬁt and the level of battery

power that is returned to the V2G driver at the end

An Agent Trading on Behalf of V2G Drivers in a Day-ahead Price Market

137

of a day. Finally, the utility function can be deﬁned

as Equation 2, if conditions are satisﬁed, otherwise

U (

a) = −∞. After describing the notations, the prob-

lem will be mathematically represented as follows:

opt

= max

a∈



−1,0,1



U (

a) (1)

where

U (

a) = −

∑

t=1

) +V

init

∑

t=1

(2)

Subject to

T =



1, 2, 3, ..., n



(3)

a ∈



− 1, 0, 1



(4)

, T

∈ T (5)

init

, b

des

∈ B (6)

a = 0 ∀ T

≤ t ≤ T

(7)

init

∑

t=1

) ≥ b

des

(8)

= (T − (T

− T

)) (9)

∀t ∈ T : B = 0 ≤ b

init

∑

t=1

≤ 100 (10)

After representing the problem mathematically,

the main constraints will be explained. To ensure that

the car is available in the using time from T

until

time T

to the driver, we proposed this constraint in

Equation 7 which says to the agent during this period

that it cannot do anything. Moreover, to ensure that

the drivers will have their desired amount of battery

before their trip, we proposed this constraint in Equa-

tion 8. Further, to ensure the battery value does not

exceed its scope which is between 0 and 100 and to

calculates the battery amount after each step we pro-

posed constraint in Equation 10.

4 THE OPTIMIZATION MODULE

After formulating the problem in the previous section,

the design of this optimization module is discussed in

detail in this section.

To build an optimization module to maximize

the V2G driver utility function in day-ahead mar-

ket (DAP), discrete dynamic programming was used,

speciﬁcally backward induction. This is one of the

key approaches in mathematical optimization tech-

niques (Adda and Cooper, 2003). The backward in-

duction concept may be deﬁned as the process of rea-

soning backwards in time, starting from the end of a

problem, selecting a series of optimal actions. Start-

ing with the last time point and deciding on the best

action, it continues backwards to the ﬁrst time point,

at every step choosing the best action for each possi-

ble situation (Gibbons, 1992).

To apply the backward induction algorithm, the

study by (Fackler, 2004) was used. The authors claim

that, at discrete times or discrete states, there is a

Markova decision structure. An agent observes the

economics of the feasible state, B, in each point of

time, t, then chooses an action, a. In the present study,

the state space can be used to represent the battery

level, B. It can be represented mathematically as

B = { 0, 10, 20, ..., 100} (11)

The action, a, has three values: charging, discharging,

and doing nothing. The actions to be chosen depend

on the battery value. For instance, if it is 0, the agent

has just two actions: charging or doing nothing.

This section discusses the optimization module,

which is the main goal of this work and the next sec-

tion outlines the experimental evaluation.

5 EXPERIMENTAL EVALUATION

The experimental settings will be explained in this

section. Next, we will show the simulation results

using the benchmark strategy. After that, the exper-

imental scenarios will be discussed. Finally, we will

discuss the results.

5.1 Experimental Settings

The experimental settings are as follows:

• An unlimited budget;

• The price depends on the available supply;

• Only a single agent is considered;

• The pricing strategy is a ﬁxed price;

• We assume different price distributions, depend-

ing on time, and these are given by Table 2. This

assumption is used to test the model but it can

deal with any price distributions. For each period,

the prices are generated as an integer number that

ranged between start and the end for each period

selected with equal probability.

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

138

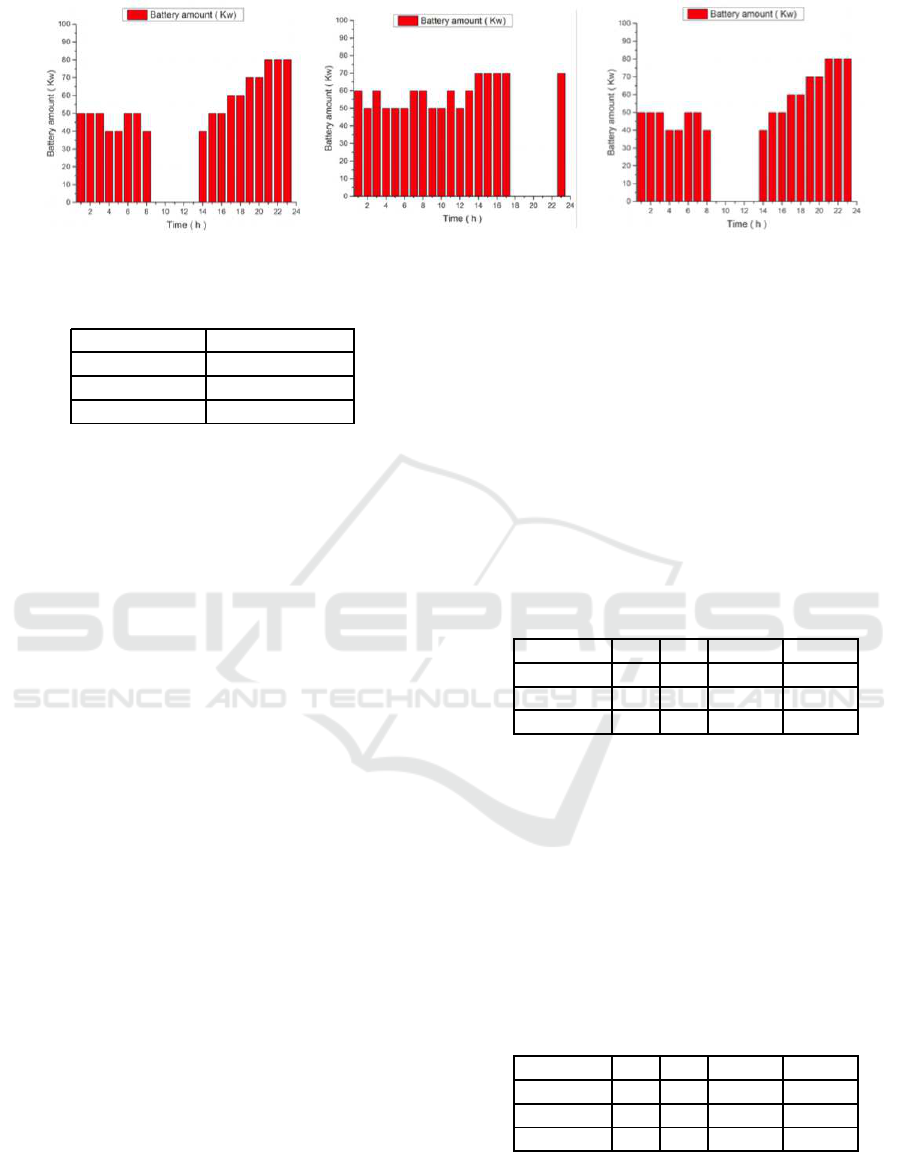
Figure 2: Bar charts of proposed scenarios with our solution.

Table 2: Assumptions for prices of electricity, based on

time.

Time (hours) Price (pounds)

1:00 - 8:59 1 - 6

9:00 - 17:59 40 - 60

18:00 - 23:59 7 - 27

Moreover, to evaluate our model, we ran it in dif-

ferent scenarios with our solution; after that, we ran

these scenarios with a benchmark strategy, will be ex-

plained in section 5.1.1. Finally, we compared our

solution results and those of a benchmark strategy. In

more detail, the comparison between these two algo-

rithms was divided into two stages. First, we ran the

simulation once per scenario with each algorithm to

show what happens at each run. Second, the simula-

tion was run a hundred times to obtain deﬁnite results.

5.1.1 Benchmark Strategy

Before discussing the results, the benchmark strategy

algorithm used to compare the model to evaluate our

solution will be explained. It starts at the ﬁrst avail-

able hour of the day, chooses its action by maximizing

the utility for each next step, compares the utility for

each choice, and selects the highest until reaching the

last available hour of the day.

5.1.2 Experimental Scenarios

Since our simulation has been assumed to work for

a single period per day, three people who drive their

cars at different periods of time are used to illustrate

scenarios to test this proposed optimization module.

All of these scenarios are uniformly distributed.

The ﬁrst scenario is of people who work normal

hours; we assume they start driving their car at any

hour of the period from 7:00 to 12:59.

The second scenario is of people who work

evenings: we assume that they use their car at any

hour of the period from 13:00 to 18:59.

The third scenario is of people who start work

early in the morning. We assume they start to drive

at any hour of the period from 1:00 to 6:59.

After discussing the experimental evaluation, the

next section discusses the results of running the sim-

ulation.

5.2 Results

We ﬁrst ran the simulation once per scenario with

each algorithm. We started by running our proposed

algorithm. Table 3 and Figure 2 show the results of

simulation runs.

Table 3: Summary table of proposed scenarios with our so-

lution.

Scenario T

utility

First 9 13 >= 40 104

Second 18 22 >= 50 43

Third 6 12 >= 40 116

Moreover, to evaluate the performance of our so-

lution, we compared it with that achieved by using

a benchmark strategy algorithm. The crucial differ-

ence between our solution and the benchmark strat-

egy, which explained in 5.1.1, is that the latter has no

information about the last point price. Thus, it will

trade to maximize the proﬁt for each feasible point,

while satisfying model constraints. Table 4 and Fig-

ure 3 provide the results of proposed scenarios after

applying a benchmark strategy.

Table 4: Summary table of proposed scenarios with bench-

mark strategy.

Scenario T

utility

First 9 13 >= 40 31

Second 18 22 >= 50 22

Third 6 12 >= 40 89

As shown in the results, the agent does not do any-

thing in the using time. Moreover, it is charging the

battery with the desired amount before the using time.

Furthermore, it is charging and discharging (buying

An Agent Trading on Behalf of V2G Drivers in a Day-ahead Price Market

139

Figure 3: Bar charts of proposed scenarios with benchmark strategy.

and selling) based on the changing on the price. Fi-

nally, to build robust results, we ran this simulation a

hundred times for each algorithm per scenario, then

the average of each scenario was calculated in terms

of ﬁnding which algorithm is better. Table 5 provides

the average results after running the simulation a hun-

dred times.

Table 5: The average utility results after running the simu-

lation 100 times.

Scenario Our solution Benchmark strategy

First 97 50

Second 79 39

Third 152 137

Through undertaking this comparison with the

ﬁrst scenario, our solution outperformed benchmark

strategy in 49%. Moreover, in the second scenario it

outperformed the benchmark strategy in 51%, while

in the third scenario our solution outperformed the

benchmark strategy in 10%.

6 CONCLUSIONS AND FUTURE

WORK

This study discussed the problem of the lack of

knowledge among customers about how to react to

prices varying in time in the power market, speciﬁ-

cally the V2G driver. Against this background, this

study focused on modelling an initial agent to trade

on behalf of V2G drivers in order to maximize their

proﬁts, speciﬁcally in the DAP market. A backward

induction algorithm was used to attain this aim. Three

reasonable scenarios were proposed to test this so-

lution, and were run under a benchmark algorithm.

The results of the proposed simulation were compared

with that of the benchmark algorithm. The results

show that our solution was better at maximizing the

V2G driver proﬁts in DAP and so it can represent a

baseline for future development.

For future work, driving behaviour will be mod-

elled in order to improve the proposed model through

using real data. Furthermore, the battery degradation

will be considered. Moreover, to make the proposed

model more realistic, a dynamic price market will be

considered. This task will be divided into two sub-

tasks. First, the real price market will be modelled to

behave as a market by means of using real data from

one of the European power markets. Second, the opti-

mization module that has been modelled in the current

research will be reﬁned to deal with dynamic prices.

REFERENCES

Adda, J. and Cooper, R. W. (2003). Dynamic economics:

quantitative methods and applications. MIT press.

Conejo, A. J., Morales, J. M., and Baringo, L. (2010).

Real-time demand response model. Smart Grid, IEEE

Transactions on, 1(3):236–242.

Fackler, P. L. (2004). Applied computational economics and

ﬁnance. MIT press.

Ghiasnezhad Omran, N. and Filizadeh, S. (2014). Location-

based forecasting of vehicular charging load on the

distribution system. Smart Grid, IEEE Transactions

on, 5(2):632–641.

Gibbons, R. (1992). Game theory for applied economists.

Princeton University Press.

Gonzalez Vaya, M. and Andersson, G. (2013). Optimal bid-

ding strategy of a plug-in electric vehicle aggregator

in day-ahead electricity markets. In European Energy

Market (EEM), 2013 10th International Conference

on the, pages 1–6. IEEE.

Guo, M., Liu, Y., and Malec, J. (2004). A new q-learning

algorithm based on the metropolis criterion. IEEE

Transactions on Systems, Man, and Cybernetics, Part

B (Cybernetics), 34(5):2140–2143.

Halvgaard, R., Poulsen, N. K., Madsen, H., Jorgensen, J.,

Marra, F., and Bondy, D. E. M. (2012). Electric vehi-

cle charge planning using economic model predictive

control. In Electric Vehicle Conference (IEVC), 2012

IEEE International, pages 1–6. IEEE.

Han, S., Han, S. H., and Sezaki, K. (2010). Design of an

optimal aggregator for vehicle-to-grid regulation ser-

vice. In Innovative Smart Grid Technologies (ISGT),

2010, pages 1–8. IEEE.

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

140

Kempton, W. and Tomi´c, J. (2005). Vehicle-to-grid power

fundamentals: calculating capacity and net revenue.

Journal of power sources, 144(1):268–279.

Li, Z., Chowdhury, M., Bhavsar, P., and He, Y. (2015). Op-

timizing the performance of vehicle-to-grid (v2g) en-

abled battery electric vehicles through a smart charge

scheduling model. International Journal of Automo-

tive Technology, 16(5):827–837.

Mohsenian-Rad, A.-H. and Leon-Garcia, A. (2010). Op-

timal residential load control with price prediction

in real-time electricity pricing environments. Smart

Grid, IEEE Transactions on, 1(2):120–133.

O’Neill, D., Levorato, M., Goldsmith, A., and Mitra,

U. (2010). Residential demand response using re-

inforcement learning. In Smart Grid Communica-

tions (SmartGridComm), 2010 First IEEE Interna-

tional Conference on, pages 409–414. IEEE.

Panagopoulos, A. A., Chalkiadakis, G., and Koutroulis, E.

(2012). Predicting the power output of distributed re-

newable energy resources within a broad geographical

region.

Pinson, P., Papaefthymiou, G., Klockl, B., Nielsen, H. A.,

and Madsen, H. (2009). From probabilistic forecasts

to statistical scenarios of short-term wind power pro-

duction. Wind energy, 12(1):51–62.

Saber, A. Y. and Venayagamoorthy, G. K. (2011). Plug-in

vehicles and renewable energy sources for cost and

emission reductions. Industrial Electronics, IEEE

Transactions on, 58(4):1229–1238.

Sanchez-Martin, P., Lumbreras, S., and Alberdi-Alen, A.

(2015). Stochastic programming applied to ev charg-

ing points for energy and reserve service markets.

Power Systems, IEEE Transactions on, pages 198 –

205.

Shahidinejad, S., Filizadeh, S., and Bibeau, E. (2012). Pro-

ﬁle of charging load on the grid due to plug-in vehi-

cles. Smart Grid, IEEE Transactions on, 3(1):135–

141.

Shi, W. and Wong, V. W. (2011). Real-time vehicle-to-grid

control algorithm under price uncertainty. In Smart

Grid Communications (SmartGridComm), 2011 IEEE

International Conference on, pages 261–266. IEEE.

Tomas, M. (2013). European union energy policy inte-

gration: A case of european commission policy en-

trepreneurship and increasing supranationalism. En-

ergy policy, 55:435–444.

Tomi´c, J. and Kempton, W. (2007). Using ﬂeets of electric-

drive vehicles for grid support. Journal of Power

Sources, 168(2):459–468.

Valogianni, K., Ketter, W., Collins, J., and Zhdanov, D.

(2014). Effective Management of Electric Vehicle

Storage using Smart Charging.

White, C. D. and Zhang, K. M. (2011). Using vehicle-

to-grid technology for frequency regulation and

peak-load reduction. Journal of Power Sources,

196(8):3972–3980.

Zareen, N., Mustafa, M., AbuJarad, S. Y., and Moradi,

M. (2015). Optimal strategies modeling in electric-

ity market for electric vehicles integration in presence

of intermittent resources. Arabian Journal for Science

and Engineering, 40(6):1607–1621.

An Agent Trading on Behalf of V2G Drivers in a Day-ahead Price Market

141