Evaluation of a Dental Caries Clinical Decision Support System

Michel Bessani

, Daniel Rodrigues de Lima

, Emery Cleiton Cabral Correia Lins

and Carlos Dias Maciel

Department of Electrical and Computer Engineering, University of S

ao Paulo, S

ao Carlos, S

ao Paulo, Brazil

Department of Biomedical Engineering, Federal University of Pernambuco, Recife, Brazil

Keywords:

Clinical Decision Support System, Dental Caries Management, Bayesian Networks, Decision Support System

Evaluation.

Abstract:

Decision Support Systems (DSSs) aims to support professionals decision process. A speciﬁc area of ap-

plication is the Clinical one, resulting in Clinical Decision Support Systems (CDSSs), focusing on Clinical

Decision problems, like oncology, geriatrics, and dentistry. DSSs integrate expert knowledge through pattern-

based approaches. Bayesian Networks are probabilistic graph models that allow representation and inference

on complex scenarios. BNs are used in different decision-making ﬁelds, e.g., Clinical Decision Support Sys-

tems. Traditionally, such models are learned using established databases. However, in situations where such

data set is unavailable, the BN can be manually constructed converting expert knowledge in conditional prob-

abilities. In this paper, we evaluate a Dental Caries Clinical Decision Support System which uses a BN to

provide suggestions and represent clinical patterns. The evaluation methodology uses forward sampling to

generated data from the BN. The generated data are separated into three groups, and each one is analyzed.

The results show the certainty of the Bayesian Network for some scenarios. The analysis of the CDSS BN

indicates that the system efﬁciently infers according to the pattern presented in the literature.

1 INTRODUCTION

Decision Support Systems (DSSs) are a set of com-

putational tools to provide information for support-

ing decision-making (Power et al., 2015). Ex-

pert knowledge-driven systems, are a type of DSSs,

that derive solutions for stated problems (Desh-

pande et al., 2016) by integrating “expert knowl-

edge through pattern-based approaches” (Hogen-

boom et al., 2016).

Among the DSSs, exists the speciﬁc area of Clin-

ical DSSs (CDSSs) (Berner, 2007), which aims to

assist health professionals in diagnosis and the over-

all clinical process (Castaneda et al., 2015). Exam-

ples are present in different health areas, as oncology

(Lambin et al., 2013; Sesen et al., 2013), geriatrics

(Genes et al., 2016) and dentistry (Goh et al., 2016).

A CDSS usually displays a rank or probability for

each suggestion (Berner, 2007), which helps the clin-

ician decision-making process. A previous study de-

veloped a CDSS with Bayesian Networks (BNs) for

dental caries management (Bessani et al., 2014), The

CDSS is based on the modern caries management

(Selwitz et al., 2007; Zero et al., 2011a). It uses in-

dividual caries risk factors and scientiﬁc evidence on

treatment outcomes.

BNs are probabilistic graph-based models that

offer a formal, natural and intuitive theory to deal

with uncertainties and represent speciﬁc knowledge

of complex scenarios (Kjaerulff and Madsen, 2010).

BNs have many applications, for example genet-

ics (Villanueva and Maciel, 2010), social-behavioral

models (Walsh et al., 2010) and lung cancer care

CDSSs (Sesen et al., 2013).

Traditionally, BN models are learned using estab-

lished databases, such as the Asia (Lepar and Shenoy,

1998) network. However, in some scenarios, there is

no data set available, and in these cases, the BN model

can be manually constructed by converting certainty

expressions into probability distributions (Kjaerulff

and Madsen, 2010). For dental caries management,

there is also no data set describing all the variables,

in the (Bessani et al., 2014) study the BN model for a

dental caries CDDS was manually assembled.

In this paper, we evaluate the Bayesian network

of a previously developed Clinical Decision Sup-

port System for Dental Caries management (Bessani

et al., 2014) using the forward sampling methodology

198

Bessani M., de Lima D., Cleiton Cabral Correia Lins E. and Maciel C.

Evaluation of a Dental Caries Clinical Decision Support System.

DOI: 10.5220/0006168301980204

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 198-204

ISBN: 978-989-758-212-7

(Koller and Friedman, 2009). Sampled data are used

to analyze the pattern embedded in the probabilistic

model to validate the CDSS for dental caries manage-

ment. Such analysis is performed by evaluating the

uncertainty in different clinical scenarios.

In the next section, we present the background in-

formation regarding Bayes nets and the Dental Caries

CDSS. Section 3 presents the methodology of both,

the forward sampling process and the used analy-

sis to evaluate the probabilistic model embedding the

CDSS. Further, Section 4 shows the results, analysis

and discussions leading to the conclusions and next

steps presented in Section 5.

2 BACKGROUND

This section presents the background information

necessary to build the CDSS for dental caries man-

agement. It is organized as follows by the theory re-

garding Bayesian networks, and the construction of

Bessani’s CDSS.

2.1 Bayesian Networks

Bayesian Networks represent the interaction between

random variables (Holmes and Jain, 2008). It is

composed of nodes that represent random variables

and edges that represent dependence (Hayduk et al.,

2003). Each node is named according to its function

in the network: the one exercising inﬂuence is called

a parent, and the one receiving that affect is known as

a child (Salini and Kenett, 2009).

Formally, a BN can be deﬁned as a set of variables

(nodes) and a set of directed edges between variables

that form a Directed Acyclic Graph (DAG) (Jensen

and Nielsen, 2007). The variables have a ﬁnite set

of mutually exclusive states, and the edges link par-

ent nodes (Pr) to child nodes (C) representing a di-

rect dependency between variables (Pearl, 1988). The

dependencies can represent causal relations between

connected nodes.

In a BN, two distinct variables are called D-

Separated (Hayduk et al., 2003) if, for all paths be-

tween them, there is one variable that can be instanti-

ated. The D-separated variables become independent

if the intermediate variable assumes some ﬁxed state.

It is useful to reduce the dimension of the joint prob-

ability over the BN (Jensen and Nielsen, 2007).

Each BN node has a probability table, and

in the case of child nodes, they have a condi-

tional probability table (CPT) (Pearl, 1988). The

CPT contains the conditional probability distributions

P(C

|Pr

, ..., Pr

) of each child node state consider-

ing the possible states of it parents.

The CPT represents the interaction between nodes

(Peebles, 1993). It gives the probability for a to

variable assume one of its states, given that it par-

ents variables assumed some speciﬁc conﬁguration

state. If the parent’s nodes are independent of each

other, we can use the chain rule (Jensen and Nielsen,

2007) to decompose P(C

|Pr

, ..., Pr

) as (1), which

is also called the Noisy-OR assumption (Zagorecki

and Druzdzel, 2004):

P(C

|Pr

, ..., Pr

) =

∏

k=1

P(C

|Pr

) (1)

The BN model is used to infer about the probabilities

of some interest node given some evidence, or prob-

abilities, of others nodes in the network. It is well

known that the exact inference for BN has an expo-

nential complexity based on the number of nodes and

edges presents in the network (Guo and Hsu, 2002)

2.2 Dental Caries CDDS

The BN evaluated in this paper are a Dental Caries

CDSS. Dental Caries (Marcenes et al., 2013) are the

most common oral conditions and still an important

health problem. It is a chronic transmissible dis-

ease of multifactorial etiology (Limeback, 2012; Pitts,

2004). The knowledge of such factors, like risk, treat-

ment outcomes and incidence of caries is necessary

for the caries management reasoning (Selwitz et al.,

2007) and their judgment is open to each professional

(Baelum, 2008).

Such a scenario stimulated the previous study

(Bessani et al., 2014), which developed a Dental

Caries CDSS. Unfortunately, there is no database re-

lating all the variables necessary to caries manage-

ment reasoning. In (Bessani et al., 2014) the CDSS

BN was constructed based on the scientiﬁc litera-

ture outcomes. The network was created and mod-

eled using the software package GeNIe Modeler from

BayesFusion, LLC.

The BN construction was performed in two parts:

the structure (qualitative), and the probabilities (quan-

titative), as proposed by (Kjaerulff and Madsen,

2010). The BN was modeled using the causal reason-

ing present in the cariology scientiﬁc literature. The

resulting BN model is shown in the Figure 1.

In summary, it comprises the risk factors (Zero,

2004; Limeback, 2012; S

oderstr

om, 2014), treat-

ment and return aspects (Nyvad et al., 2003; Fer-

reira Zandon

a et al., 2012; Zero et al., 2011b) neces-

sary to caries clinical decision. The risk factors cover

causal and predictive aspects to infer risk classiﬁca-

tion. Treatment assumes clinical evidence together

Evaluation of a Dental Caries Clinical Decision Support System

199

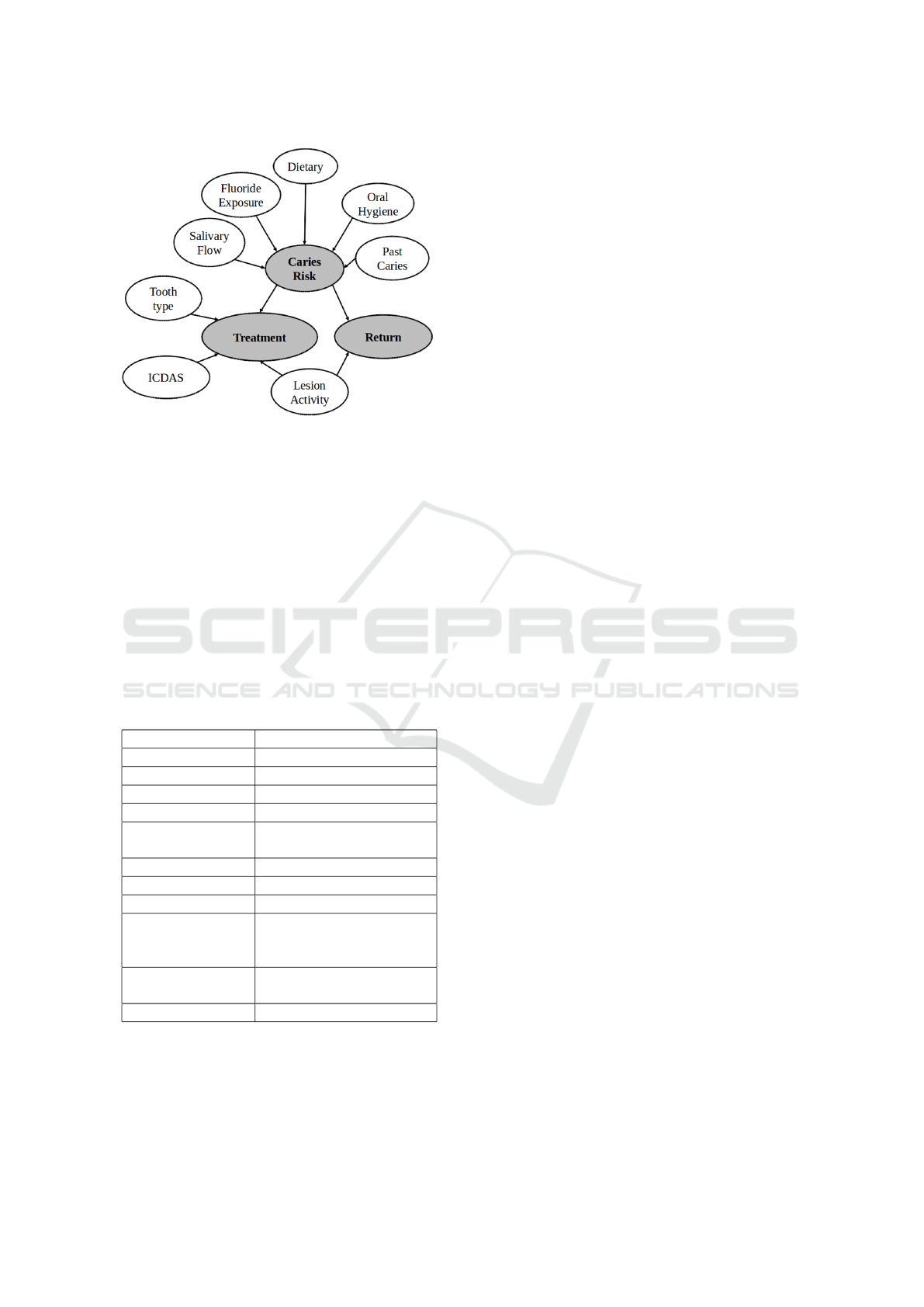
Figure 1: Bayesian Network modeled in a previous study

for a Dental Caries Clinical Decision Support System. The

white nodes are the system inputs, and the gray nodes are

the system suggestions.

with patient risk to infer the most indicate treatment.

The return is inferred considering lesion activity and

the patient risk.

Caries risk, treatment, and return are the sugges-

tions provided by the CDSS. The clinician needs to

supply the input variables states to the system, which

can be obtained by clinical examination, to get the

suggestions. The discrete states of each BN variable

are presented in Table 1.

Table 1: Bayesian Network variables and they respective

states.

Variable States

Dietary Good; Regular; Poor

Fluoride Exposure Yes; No

Salivary Flow Normal; Low

Oral Hygiene Good; Regular; Poor

Past Caries

Zero; Between 1 and 2;

3 or more

Teeth Type Molar; Premolar; Anterior

ICDAS 1&2; 3; 4; 5&6

Lesion Activity Yes; No

Treatment

Fluoride &/OR Sealants;

Restoration;

Endodontic treatment

Return

1 Year; 6 Months;

Before 6 Months

Caries Risk Low; Medium; High

3 METHODOLOGY

Due to lack of a database describing all the necessary

variables the BN evaluated here was manually con-

structed in a previous study. As a consequence, our

methodology consists of generating synthetic data by

forward sampling the CDSS BN (Koller and Fried-

man, 2009; Guo and Hsu, 2002).

In summary, a set of random samples is produced

according to the network CPTs. We also use the d-

separation property to divide the BN into three parts

named- Caries Risk, Treatment, and Return.

The forward sampling is done respecting the par-

tial order of the BN, ﬁrst sampling the nodes with-

out parents, and then sampling the child of such sam-

pled nodes. As a consequence, when sampling a child

node, the state of it parents are already sampled, and

the child sample is obtained from the CPT.

The random sampling of each variable uses

pseudo-random number generator. It gives a value

between 0 and 1 that is used to deﬁne the state of

the discrete variable, e.g., if the pseudo-random num-

ber generator return 0.6, the sampled variable have

P(X = 0) = 0.3 and P(X = 1) = 0.7, since 0.6 > 0.3

we set X = 1.

We divided the BN into three different parts,

Caries Risk, Treatment, and Return according to Sub-

section 2.2, and generated 20.000 random samples

from the CDDS BN. The data obtained are grouped

in the three mentioned parts.

All the possible states of the input variables were

considered allowing to evaluate how each one of their

states contributes to the CDSS suggestions. It will be

done considering the probabilities of the CDSS inputs

given the status of the system’ outputs, allowing an

assessment of how the uncertainties are handled by

the system and its capability of inferring on speciﬁc

scenarios.

4 RESULTS & DISCUSSION

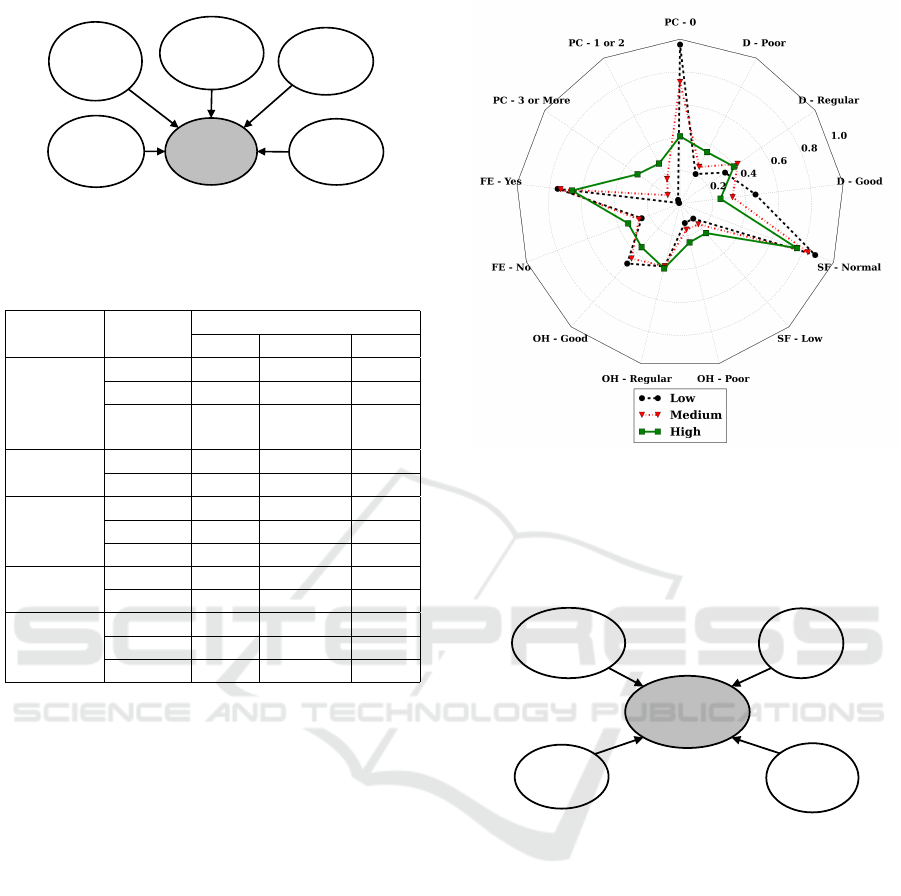
4.1 Caries Risk

The Caries Risk part of the BN is presented in Figure

2. The variables that were grouped from the random

samples are Past Caries, Salivary Flow, Fluoride Ex-

posure, Dietary and Oral Hygiene as input variables,

and Caries Risk.

Table 2 presents the samples grouped in a contin-

gency table and shows the relative frequencies of each

input variable state given the state of Caries Risk vari-

able.

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

200

Salivary

Flow

Past

Caries

Risk

Oral

Hygiene

Dietary

Fluoride

Exposure

Figure 2: BN part referent to Caries Risk suggestions.

Table 2: Conditional Probability Table for the variable

Caries Risk measured from the synthetic data generated.

Input State

Caries Risk

Low Medium High

Past

Caries

0 0,967 0,740 0,410

1 or 2 0,026 0,169 0,275

3 or

0,007 0,091 0,315

Fluoride

Exposure

Yes 0,751 0,733 0,662

No 0,249 0,267 0,338

Oral

Hygiene

Good 0,486 0,446 0,353

Regular 0,393 0,391 0,405

Poor 0,121 0,163 0,242

Salivary

Flow

Low 0,121 0,168 0,239

Normal 0,879 0,832 0,761

Dietary

Good 0,463 0,322 0,248

Regular 0,333 0,426 0,398

Poor 0,204 0,252 0,354

Figure 3 presents the relative frequencies of Table

2 as a radar chart. The three plots represent the rela-

tive frequency of each input state for the three states

of Caries Risk. It is possible to note that the frequen-

cies of the input variables states are different for each

state of Caries Risk.

Figure 3 also shows the relative frequencies of

each input state depending on the Caries Risk state.

For example, the state Past aries equal to zero is

present in 96,7% of the samples for Low Caries Risk,

reﬂecting how such input state is decisive to suggest

a Low Caries Risk.

In contrast, for high Caries Risk as shown in Fig-

ure 3, the input states that presented low frequencies

for Low Caries Risk have higher relative frequencies

for High Caries Risk, and the states with high fre-

quencies for Low Caries Risk have lower frequencies

for High Caries Risk.

4.2 Treatment

Treatment results refer to the sampling of the follow-

ing input variables: ICDAS, Tooth Type, Caries Risk

and Lesion Activity. The Treatment part of the BN is

Figure 3: Radar chart for the relative frequencies of Table 2

for the three states of the Caries Risk variable. PC refers to

Past Caries, SF to Salivary Flow, FE to Fluoride Exposure,

D to Dietary and OH to Oral Hygiene.

presented in Figure 4.

Caries

Risk

Tooth type

Treatment

Lesion

Activity

ICDAS

Figure 4: BN part referent to Treatment Suggestions.

Table 3 contains the samples grouped as a contin-

gency table showing the relative frequencies of each

input variable given the state of Treatment variable.

Figure 5 presents such same relative frequencies as a

radar chart. The three plots represents the three treat-

ment variable states.

We can note that ICDAS classiﬁcation is decisive

for endodontic treatment, with ICDAS 5 or 6 the en-

dodontic treatment is almost sure. ICDAS is the In-

ternational Caries Detection and Assessment System

and is deﬁned as a workﬂow for caries visual de-

tection and measurement, for more information see

(Zero et al., 2011b). On the other hand, for the other

Treatment suggestions, others variables become im-

portant.

Evaluation of a Dental Caries Clinical Decision Support System

201

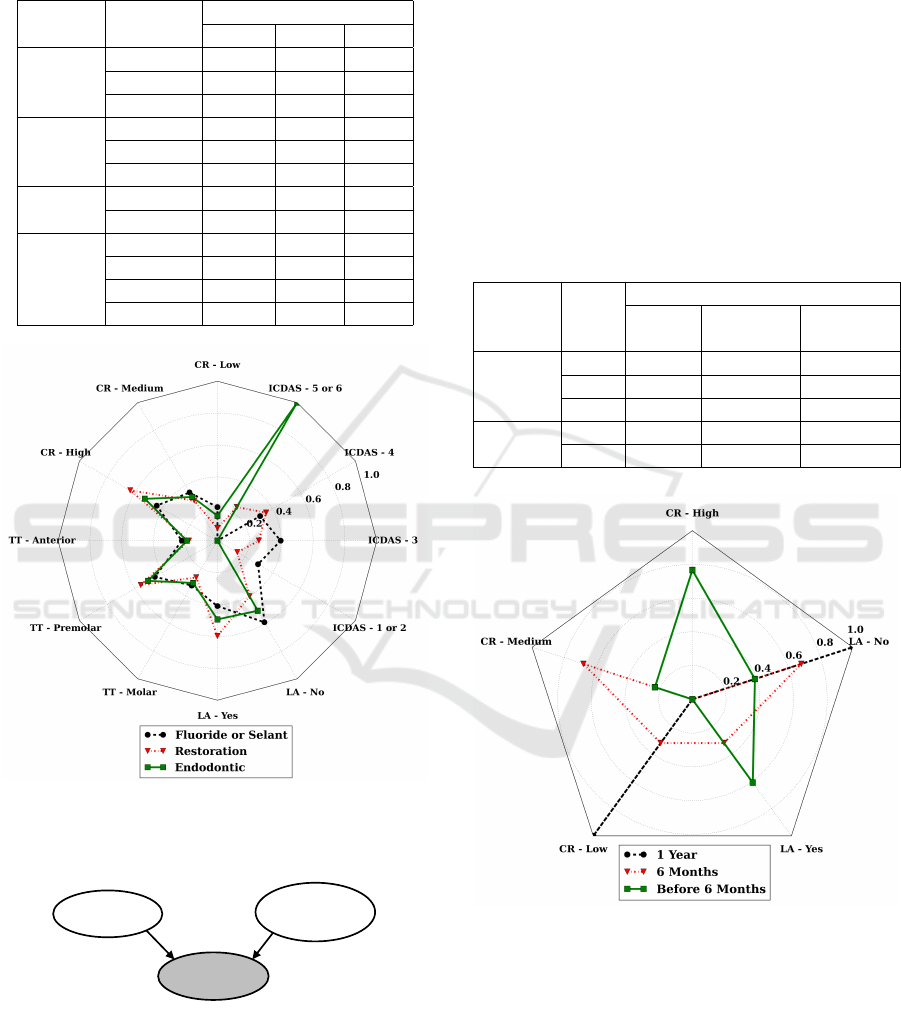
Table 3: Conditional Probability Table for the variable

Treatment measured from the synthetic data generated. F

or S is Fluoride or Sealant, R is Restoration, and E is En-

dodontic Treatments

Input State

Treatment

F or S R E

Caries

Risk

Low 0,211 0,078 0,157

Medium 0,350 0,290 0,317

High 0,439 0,631 0,526

Type

Thooth

Molar 0,223 0,179 0,192

Premolar 0,453 0,556 0,503

Anterior 0,324 0,266 0,306

Lesion

Activity

Yes 0,410 0,598 0,493

No 0,590 0,402 0,507

ICDAS

1 or 2 0,294 0,144 0,000

3 0,396 0,260 0,000

4 0,309 0,353 0,000

5 or 6 0,000 0,243 1,000

Figure 5: Radar chart for the relative frequencies of Table 3

for the three states of the Treatment variable. TT refers to

Tooth Type, CR to Caries Risk and LA to Lesion Activity.

Caries

Risk

Lesion

Activity

Return

Figure 6: BN part referent to Return suggestions.

4.3 Return

The Return part of the BN is shown in Figure 6. The

variables grouped to analyze this part of the network

are Caries Risk and Lesion Activity. Table 4 presents

the data as a contingency table.

We performed the same analysis for the Return

variable and Table 4 summarizes the random sam-

pling result. Likewise, Figure 7 displays the radar

chart for each Return state. We can see the importance

of each variable for the system return suggestion. For

a 1-year return, only a low Caries Risk and no Lesion

Activity is necessary. In contrast, other variables sta-

tus become important for a faster patient return. Such

graphical results are in agreement with the literature

used to model the BN (Bessani et al., 2014).

Table 4: Conditional Probability Table for the variable Re-

turn measured from the synthetic data generated. H is High,

M is Medium and L is Low Caries Risk

Input State

Return

1 Year 6 Months

Before

6 Months

Caries

Risk

H 0,00 0,00 0,77

M 0,00 0.68 0,23

L 1,00 0,32 0,00

Lesion

Activity

Yes 0,00 0,32 0,61

No 1,00 0,68 0,39

Figure 7: Radar chart for the relative frequencies of Table

4 for the three states of the Return variable. CR refers to

Caries Risk and LA to Lesion Activity.

5 CONCLUSION

In this paper, we evaluated a BN using forwarding

sampling. The generated data were used to analyze

the network. The BN evaluated is associated with a

CDDS for caries management and was developed in

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

202

a previous study. Due to the lack of data correlat-

ing all the necessary variables It was modeled using

a manual construction methodology, certainty expres-

sions from the scientiﬁc literature were converted into

probabilities.

The analysis was divided into three parts: Caries

Risk, Treatment, and Return. The sampled data were

presented in contingency tables and in radar charts,

allowing a visual analysis of the dependence of the

CDSS suggestions and input variables states.

Results showed the behavior of CDDS model in

different scenarios. The certainty about suggestions

is present in some scenarios, e.g., the patient return

is equal to 1 year if Caries Risk is low, and Lesion

Activity is no. For return before 6 moths, Lesion Ac-

tivity variable needs to be true, and Caries Risk needs

to be high. In contrast, uncertainty is present in oth-

ers suggestions states, e.g., in scenarios with a Low

Caries Risk.

The analysis shows the system deals with the un-

certainty inherent in the clinical processes. Further-

more, its infers according to the clinical standards pre-

sented in the literature of cariology. It can be helpful

as a second opinion during dental caries clinical man-

agement. The next steps are to quantify the different

levels of uncertainty present in the model and evalu-

ate the performance of the system by comparison with

experts decisions.

ACKNOWLEDGMENTS

The authors would like to thank CAPES - Brazil-

ian Federal Agency for Support and Evaluation of

Graduate Education within the Ministry of Educa-

tion of Brazil; and to CNPq - National Counsel of

Technological and Scientiﬁc Development - Project

475064/2013-5.

REFERENCES

Baelum, V. (2008). Caries management: technical solutions

to biological problems or evidence-based care? Jour-

nal of oral rehabilitation, 35(2):135–51.

Berner, E. S. (2007). Clinical decision support systems:

theory and practice. Springer Science & Business

Media.

Bessani, M., Lins, E. C. C. C., Delbem, A. C. B., and Ma-

ciel, C. D. (2014). Construction of a Clinical Decision

Support System for Dental Caries Management using

Bayesian Networks. In XXIV Brazilian Congress on

Biomedical Engineering - CBEB 2014, pages 517–

520.

Castaneda, C., Nalley, K., Mannion, C., Bhattacharyya, P.,

Blake, P., Pecora, A., Goy, A., and Suh, K. S. (2015).

Clinical decision support systems for improving di-

agnostic accuracy and achieving precision medicine.

Journal of clinical bioinformatics, 5(1):1.

Deshpande, R. R., DeMarco, J., Sayre, J. W., and Liu, B. J.

(2016). Knowledge-driven decision support for as-

sessing dose distributions in radiation therapy of head

and neck cancer. International journal of computer

assisted radiology and surgery, pages 1–13.

Ferreira Zandon

a, A., Santiago, E., Eckert, G. J., Katz, B. P.,

Pereira de Oliveira, S., Capin, O. R., Mau, M., and

Zero, D. T. (2012). The natural history of dental caries

lesions: a 4-year observational study. Journal of den-

tal research, 91(9):841–6.

Genes, N., Kim, M. S., Thum, F. L., Rivera, L., Beato, R.,

Song, C., Soriano, J., Kannry, J., Baumlin, K., Hwang,

U., et al. (2016). Usability evaluation of a clinical de-

cision support system for geriatric ed pain treatment.

Applied clinical informatics, 7(1):128–142.

Goh, W. P., Tao, X., Zhang, J., and Yong, J. (2016). Deci-

sion support systems for adoption in dental clinics: a

survey. Knowledge-Based Systems, 104:195–206.

Guo, H. and Hsu, W. (2002). A survey of algo-

rithms for real-time bayesian network inference. In

AAAI/KDD/UAI02 Joint Workshop on Real-Time De-

cision Support and Diagnosis Systems. Edmonton,

Canada.

Hayduk, L., Cummings, G., Stratkotter, R., Nimmo, M.,

Grygoryev, K., Dosman, D., Gillespie, M., Pazderka-

Robinson, H., and Boadu, K. (2003). Pearl’s d-

separation: One more step into causal thinking. Struc-

tural Equation Modeling: A Multidisciplinary Jour-

nal, 10(2):289–311.

Hogenboom, F., Frasincar, F., Kaymak, U., de Jong, F., and

Caron, E. (2016). A survey of event extraction meth-

ods from text for decision support systems. Decision

Support Systems, 85:12–22.

Holmes, D. and Jain, L. (2008). Introduction to bayesian

networks. In Holmes, D. and Jain, L., editors, Inno-

vations in Bayesian Networks, volume 156 of Stud-

ies in Computational Intelligence, pages 1–5. Springer

Berlin Heidelberg.

Jensen, F. and Nielsen, T. (2007). Bayesian networks and

decision graphs. Springer Science+Business Media,

New York, 2nd ed edition.

Kjaerulff, U. B. and Madsen, A. L. (2010). Bayesian Net-

works and Inﬂuence Diagrams: A Guide to Construc-

tion and Analysis. Springer Publishing Company, In-

corporated, 1st edition.

Koller, D. and Friedman, N. (2009). Probabilistic graphical

models: principles and techniques. MIT press.

Lambin, P., van Stiphout, R. G., Starmans, M. H., Rios-

Velazquez, E., Nalbantov, G., Aerts, H. J., Roelofs,

E., van Elmpt, W., Boutros, P. C., Granone, P., et al.

(2013). Predicting outcomes in radiation oncology-

multifactorial decision support systems. Nature Re-

views Clinical Oncology, 10(1):27–40.

Lepar, V. and Shenoy, P. P. (1998). A comparison of

lauritzen-spiegelhalter, hugin, and shenoy-shafer ar-

chitectures for computing marginals of probability

Evaluation of a Dental Caries Clinical Decision Support System

203

distributions. In Proceedings of the 14th Confer-

ence on Uncertainty in Artiﬁcial Intelligence (UAI-98,

pages 328–337. Morgan Kaufmann.

Limeback, H. (2012). Comprehensive Preventive Dentistry.

John Wiley & Sons, Ltd.,, West Sussex, UK.

Marcenes, W., Kassebaum, N. J., Bernab

e, E., Flaxman,

A., Naghavi, M., Lopez, A., and Murray, C. J. L.

(2013). Global burden of oral conditions in 1990-

2010: a systematic analysis. Journal of dental re-

search, 92(7):592–7.

Nyvad, B., Machiulskiene, V., and Baelum, V. (2003). Con-

struct and Predictive Validity of Clinical Caries Diag-

nostic Criteria Assessing Lesion Activity. Journal of

Dental Research, 82(2):117–122.

Pearl, J. (1988). Probabilistic reasoning in intelligent sys-

tems: networks of plausible inference. Morgan Kauf-

mann, San Maeto, 1 edition.

Peebles, P. Z. (1993). Probability, Random Variables, and

Rabdom Signal Principles. McGraw-Hill Inc., 3rd

edition edition.

Pitts, N. B. (2004). Are we ready to move from operative to

non-operative/preventive treatment of dental caries in

clinical practice? Caries research, 38(3):294–304.

Power, D. J., Sharda, R., and Burstein, F. (2015). Decision

support systems. Wiley Online Library.

Salini, S. and Kenett, R. S. (2009). Bayesian networks of

customer satisfaction survey data. Journal of Applied

Statistics, 36(11):1177–1189.

Selwitz, R. H., Ismail, A. I., and Pitts, N. B. (2007). Dental

caries. Lancet, 369(9555):51–9.

Sesen, M. B., Nicholson, A. E., Banares-Alcantara, R.,

Kadir, T., and Brady, M. (2013). Bayesian networks

for clinical decision support in lung cancer care. PloS

one, 8(12):e82349.

oderstr

om, U. (2014). A retrospective analysis of caries

treatment and development in relation to assessed

caries risk in an adult population in Sweden. BMC

Oral Health, 14(1):126.

Villanueva, E. and Maciel, C. D. (2010). Modeling asso-

ciations between genetic markers using Bayesian net-

works. Bioinformatics, 26(18):i632–i637.

Walsh, S., Dalton, A., Whitney, P., and White, A. (2010).

Parameterizing Bayesian Network Representations of

Social-Behavioral Models by Expert Elicitation A

Novel Application of Conjoint Analysis. In Artiﬁcial

intelligence in medicine, pages 227–232.

Zagorecki, A. and Druzdzel, M. J. (2004). An empirical

study of probability elicitation under noisy-or assump-

tion. In FLAIRS Conference, pages 880–886.

Zero, D. T. (2004). Sugars - the arch criminal? Caries

research, 38(3):277–85.

Zero, D. T., Zandona, A. F., Vail, M. M., and Spolnik, K. J.

(2011a). Dental caries and pulpal disease. Dental

Clinics of North America, 55(1):29–46.

Zero, D. T., Zandona, A. F., Vail, M. M., and Spolnik, K. J.

(2011b). Dental caries and pulpal disease. Dental

clinics of North America, 55(1):29–46.

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

204