Synchronization between Two Fixed Cavity Mode Locked Lasers
Shree Krishnamoorthy
1,2
, Satyajit Mayor
2
and Anil Prabhakar
1
1
Indian Institute of Technology, Madras, Chennai, India
2
National Center for Biological Sciences, Bangalore, India
Keywords:
Mode Locked Lasers, Injection-locked, Fibre Ring Laser, Synchronization, Pulsed Laser.
Abstract:
An active mode locked fibre ring laser is designed as a slave laser, driven by a commercial Ti:Sapphire laser
acting as a master. The master-slave synchronization was stabilized for frequency detuning, but the output
pulse width of the slave laser was observed to increase. The increase in pulse width was asymmetric about
the ring cavity resonance frequency, a consequence of an asymmetry in the detuning range of the higher order
cavity modes. We find that the detuning range decreases as the square of the mode number, in agreement with
theory.
1 INTRODUCTION
The fields of chemistry and biology widely use lasers
to probe both spatial and temporal aspects of systems
under study. In particular, microscopes extensively
use lasers for imaging of tissues, cells and organelles.
Over the years, microscopy techniques have evolved
and are now capable of imaging finer and finer details
of samples ((Nienhaus and Nienhaus, 2016)). Fur-
ther, the field has been challenging the very physical
limits of optics using nanoscopy techniques like stim-
ulated emission and depletion (STED), total internal
reflection fluorescence (TIRF) microscopy etc ((Fara-
hani et al., 2010; Klar et al., 2000; Takasaki et al.,
2013)). Similarly, spectroscopy has also evolved to
levels where many techniques in time resolved spec-
troscopy use optical pump and probe methods with
multiple lasers working in tandem, e.g. in time re-
solved CARS ((El-Diasty, 2011)). Both microscopy
with STED and spectroscopy like time resolved co-
herent anti-Stokes Raman scattering (CARS), require
two pulsed lasers working in synchronization to ob-
tain the desired results. In a simultaneous develop-
ment, fibre lasers have begun to compete with solid
state lasers, both in pulse energy and in repetition
rates. In this article we describe our efforts to use
a Ti:Sapphire laser as a master laser, while driving a
ytterbium doped fibre (YDF) ring laser in a master-
slave configuration.
Mode locking of the resonant cavity modes of a
laser will typically yield Fourier limited pulse widths
((Haus, 1975)). The technique is commonly used to
Figure 1: Schematic of master and slave lasers in synchro-
nization. Synchronization signal is in RF. Optical pulses are
depicted with solid lines.
generate fs pulses from a Ti:Sapphire laser. How-
ever, when we set up a master-slave laser system, we
are limited in our freedom to operate provided by the
commercial lasers. Femto-second lasers have limited
tuning in wavelength, pulse width and pulse repeti-
tion rates e.g. the Ti:Sapphire laser that is a com-
mon workhorse will typically work at approximately
80 MHz repetition rates. In some experiments, an ad-
ditional pulse stretching module is adopted that con-
verts a part of the femto-second laser output into a
picosecond laser ((Wu et al., 2015; Takasaki et al.,
2013)). The additional module achieves synchroniza-
tion, but enforces wavelength restriction on the pi-
cosecond laser as it is coupled to the femto second
laser pulses directly as its source ((Lauterbach et al.,
2013)). In other implementations a separate laser is
electronically controlled to achieve pulsed lasers and
Krishnamoorthy S., Mayor S. and Prabhakar A.
Synchronization between Two Fixed Cavity Mode Locked Lasers.
DOI: 10.5220/0006169402730282
In Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2017), pages 273-282
ISBN: 978-989-758-223-3
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
273

synchronization((Honigmann et al., 2014; Takasaki
et al., 2013)).
One way to set up optical synchronization, with
a Ti:Sapphire laser as a master and a fibre laser as
the slave, is to use a part of the optical pulse en-
ergy from the master to injection lock the fibre laser.
Fraction spectrum amplification (FSA) extracts and
amplifies the speectral energy available above 1 µm
from a Rainbow laser ((Li et al., 2010)) and amplifies
it using a ytterbium fibre amplifier. In another ap-
proach, we could seed the slave laser with sufficient
optical energy from the master laser to induce cross
phase modulation, as was demonstrated by synchro-
nizing a ytterbium doped fibre laser to a ns pulsed
diode laser ((Rusu et al., 2004)). In this article, we
propose an alternate method of using a pulsed elec-
trical signal derived from the Ti:Sapphire to injection
lock a ring fibre laser. The ring fibre laser needs to
be designed to have a cavity resonance close to the
repetition rate of the Ti:Sapphire, allowing the fibre
laser to also achieve mode locking. This active mode
locking configuration is shown schematically in Fig.2.
We use a MaiTai, from Spectra-Physics, as the mas-
ter laser. For the slave laser, we built an active fibre
mode locked laser at 1064 nm using Yb
3+
doped fi-
bre in a ring cavity with an electro-optic modulator
(EOM) which would yield about 100 ps pulses. These
pulses were then amplified and frequency doubled to
green ((Krishnamoorthy et al., 2014b; Krishnamoor-
thy et al., 2014a)). This master-slave configuration al-
lows us to explore two photon fluorophore excitation
with pico-second pulsed depletion, in a STED micro-
scope. The primary advantage over other methods is
that we are able to derive picosecond slave pulses with
electrical injection from the master.
The Ti:Sapphire laser provides the electrical in-
jection signal to the slave laser, that will then pro-
duce optical pulses synchronized to the master laser’s
pulses. The electrical signal is generated by a mon-
itor photodiode internal to the Ti:Sapphire laser. In
our STED experiments, the Ti:Sapphire is typically
tuned to obtain the best two photon excitation of the
fluorophore. Hence, we must consider the effect of
tuning the wavelength of the master laser on the slave
laser. Since we are modulating the EOM in the slave
laser with a pulsed electrical signal, we found that
the slave laser would produce pulses for all the wave-
lengths of the master laser. However, we also found
that the pulse width of the slave laser varied over the
wavelength range due a change in repetition rate of
the master laser pulses, and a loss of mode-locking.
Hence, we must consider the effect of varying the
synchronization signal’s repetition rate, as the slave
laser is detuned away from the resonant frequency of
Figure 2: Schematic of slave laser operating at 1064nm.
its ring cavity. We observed that the detuning behav-
ior of the ring cavity was asymmetric about its reso-
nant frequency, with the output pulse width increasing
more rapidly for injection frequencies greater than the
cavity resonance frequency. To understand the asym-
metry in response to frequency detuning, we have
studied the Fourier spectrum of the optical pulse train
and observed that the locking range of the upper and
lower frequency components have a slightly differ-
ent dependence on the cavity mode number (n), al-
though both depend on n
2
. This dependence on n is
underpinned by our theoretical understanding of ac-
tive mode locking ((Haus, 1975)) and is similar to
the asymmetric detuning behavior in electrical phase
locking ((Razavi, 2004)).
2 EXPERIMENTS AND RESULTS
The setup consists of a commercial Ti:Sapphire
femto-second laser source and a custom built 1064 nm
actively mode locked fibre laser. The Ti:Sapphire
laser acts as the master laser which provides an elec-
trical synchronization signal to the 1064nm mode
locked laser. The 1064 nm mode locked laser in turn
acts as the slave laser by producing laser pulses in
synchronization with the master laser’s signal.
The Ti:Sapphire laser produces pulses with a rep-
etition rate ( f
i
) of 80 MHz, and pulse width of 80 fs.
The laser can be tuned in the wavelength range of
690 − 1020 nm. An internal photodetector detects a
fraction of the light in the Ti:Sapphire laser cavity
and produces RF pulses with amplitude A
i
. The RF
pulses have the same repetition rate f
i
as the op-
tical laser pulses at the output of the master laser.
The RF pulses are amplified and used as input to the
electro-optic modulator (EOM) within the cavity of
the wavelength stabilized fibre ring laser, as shown
in Fig.2. The EOM acts as a loss modulation ele-
ment in the 1064 nm fibre laser cavity. The fibre ring
laser is constructed with polarization maintaining sin-
gle mode fibre with Yb:fibre as the gain medium. The
Yb:fibre is pumped by a 980 nm diode laser through
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
274

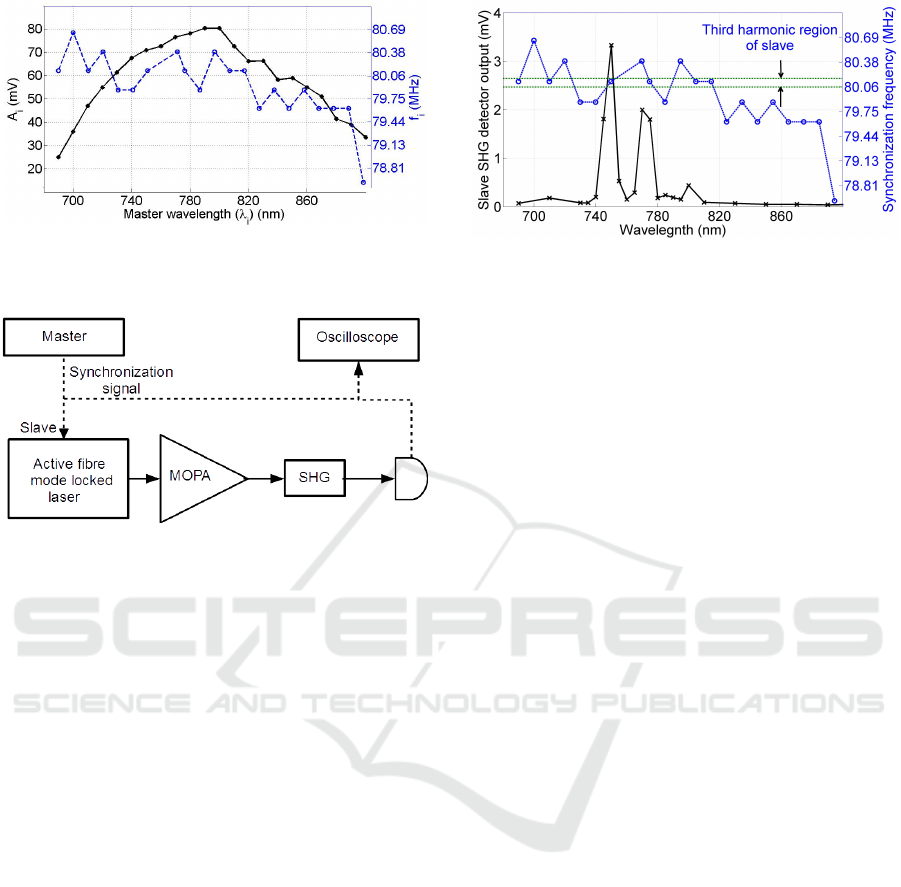
Figure 3: Synchronization signal voltage (A
i
) and fre-
quency (f
i
) with changing operating wavelength (λ
i
) of the
master laser.
Figure 4: Schematic for observing the frequency of syn-
chronization signal and the intensity of slave laser pulses
using SHG.
a wavelength division multiplexer (WDM). Unidirec-
tional propagation is ensured by a circulator in the
loop. Wavelength selection and line-width narrow-
ing is achieved by using a reflective fibre Bragg grat-
ing (FBG). Lasing occurs at λ
0
= 1064nm with a
line-width of ∆λ = 0.4nm. The corresponding cen-
tral optical frequency is f
optical
= 187.97 THz with a
bandwidth of f
L
= 70.66 GHz. The overall length of
the cavity is 7.49 m, which corresponds to a cavity
resonance at f
0
= 26.7 MHz ((Krishnamoorthy et al.,
2014a)).
2.1 Wavelength Tuning of Master Laser
The Ti:Sapphire laser can be tuned to operate at a
wavelength (λ
i
) between 690 and 1020 nm by con-
trolling a dispersive element in the cavity. Changing
λ
i
changes the peak amplitude A
i
and the repetition
rate f
i
of the master laser pulses. The RF monitor out-
put provided in the laser is used to measure A
i
and f
i
on a digital oscilloscope. We find that, the laser out-
put maximum occurs at 800 nm, as shown in Fig.3.
As the wavelength λ
i
is changed, f
i
changes between
78.8 and 80.7MHz ((Krishnamoorthy et al., 2014b)).
The RF monitor signal from the master laser is
fed to the fibre MLL. The slave laser produces optical
pulses at 1064 nm corresponding to the RF pulse train
injected from the master laser. Over the wavelength
Figure 5: Synchronization signal frequency with changing
operating wavelength of the master laser affects the pulse
width in the slave laser as measured by observing the output
power after SHG conversion.
range of the master laser, we find that pulse to pulse
synchronization between the master and slave laser
pulses is maintained. However, slave laser’s pulse
width changes as we tune λ
i
of the master laser.
To characterize the pulse width variation, average
power at the output of a second harmonic genera-
tion (SHG) stage is observed as shown in Fig.4.The
output of SHG depends on the intensity of the in-
put pump. For constant average power, repetition
rate and SHG optical configuration; the intensity of
laser pulse increases as the pulse width of the slave
laser decreases. So, an increase in the output power
of SHG (P
SHG
) indicates decrease in the slave laser
pulse widths. We use 1064 nm slave laser pulses as
source for SHG. The SHG stage is constructed using
commercial periodically poled LiNbO
3
crystal to pro-
duce at 532nm output in a single pass configuration.
The slave laser pulses are amplified by 21 dB using
two amplifier stages consisting of a Yb:fibre ampli-
fier followed by a master oscillator power amplifier
(MOPA). The amplified pulses are then fed to a SHG
stage to produce pulses at 532nm ((Krishnamoorthy
et al., 2014b)). For a fixed average power in the
1064nm pulse train, P
SHG
will depend nonlinearly on
the input pulse width. We find that regions where
P
SHG
increases appear as peaks at 750 nm, 770 nm and
805nm, as shown in Fig.5. At these regions, the rep-
etition rate f
i
is ∼ 80.07 MHz.
The frequency range around 80.07MHz corre-
sponds to the third harmonic frequency (3 f
0
) of the
slave laser. This region is indicated by the dashed
lines in the plot. We find that the peak pulse power
and pulse width are not constant in this frequency
range as shown in Fig.6. it is observed that every
third pulse produced by the slave laser has a larger
amplitude than the others. The modulation effect in
the slave pulses could be due to a slight detuned input
frequency f
i
from 3 f
0
in the synchronization signal.
Synchronization between Two Fixed Cavity Mode Locked Lasers
275

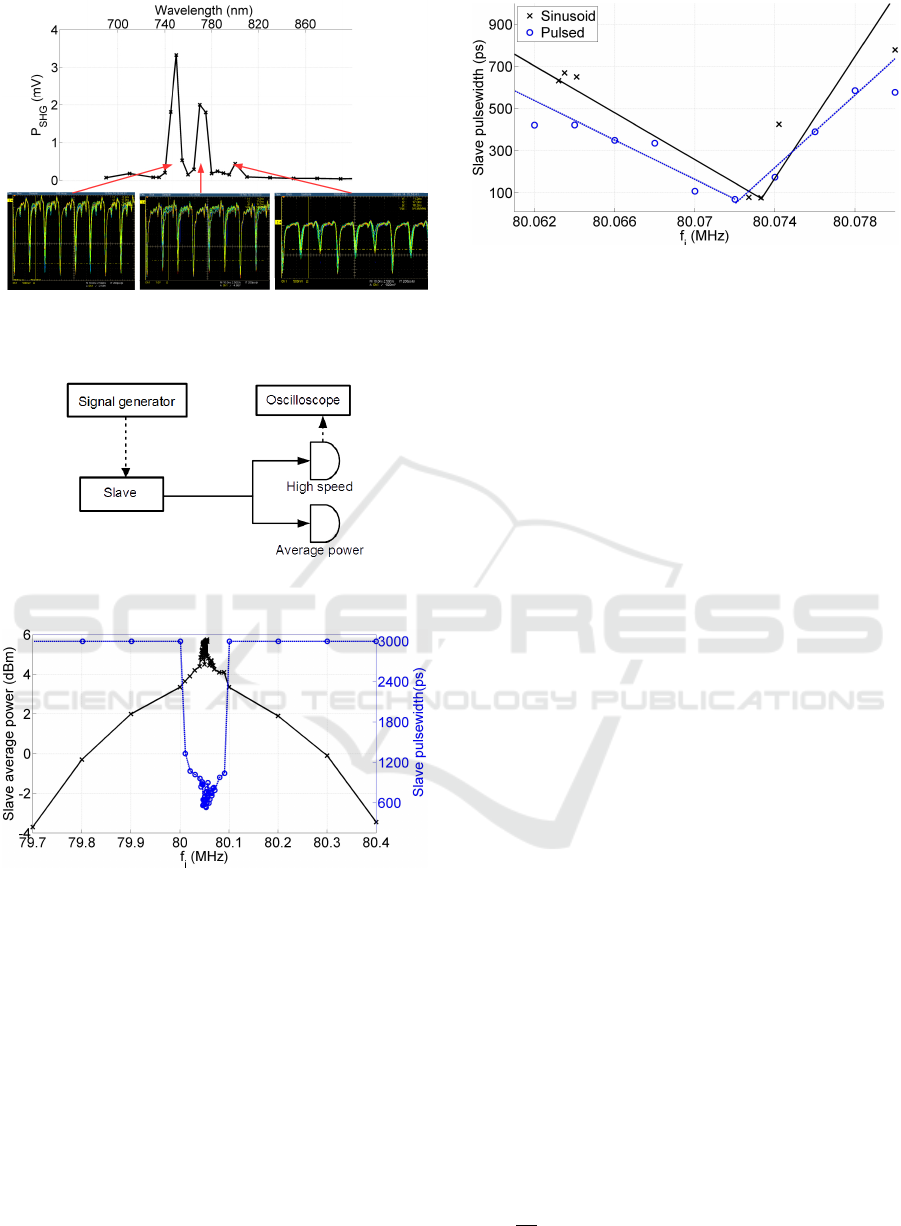
Figure 6: Slave laser pulse traces for the different operating
wavelengths. Every third pulse being intense indicates the
dominance of fundamental.
Figure 7: Schematic for characterizing slave laser at third
harmonic using a signal generator.
Figure 8: Average power and pulse width over the expected
operating range of slave laser.
2.2 Actively Mode Locked Fibre Laser
We investigate the effect of detuning f
i
from 3 f
0
by
using a signal generator in place of the master laser to
produce synchronization signal. The signal generator
drives the EOM of the slave laser with a sinusoidal
signal. The pulsed RF input is also generated with
repetition rate of f
i
and RF pulse width of 4 ns using
the signal generator. The generated optical pulse train
is monitored at the output of the slave laser as shown
in Fig.7.
Figure 9: Closer look at effect of detuning on pulse width
around 3 f
0
.
2.2.1 Third Harmonic Experiments
The repetition rate of the synchronization signal f
i
varies over a range of 500 kHz. The slave fibre laser
is expected to operate over this range. We measured
the average power on an optical detector and the pulse
width of the pulses using a high speed (10 GHz band-
width) detector as shown in Fig.7. We find that the
output power is significant over f
i
= 79.8 − 80.3MHz
range as shown in Fig.8. There is a further increase
in the output power for the range f
i
= 80 −80.1 MHz.
The output optical pulses in this range have smaller
pulse widths in pico-seconds as seen in Fig.8. Thus,
the slave laser produces ns pulses in ranges of f
i
=
{79.8 − 80, 80.1 − 80.2}MHz, and narrow pulses of
ps range in the region f
i
=
{
80 − 80.1
}
MHz.
A Fourier limited pulses are observed when the
laser is mode locked at 3 f
0
. The pulse widths increase
as the input to the EOM is detuned from the mode
locking frequency. A minimum pulse width of 69 ps
is observed at 3 f
0
as shown in Fig.9. As the synchro-
nization repetition rate f
i
is detuned from 3 f
0
, we find
that the pulse width increases. The increase in pulse
width is not symmetrical about the 3 f
0
frequency for
either sinusoidal or pulsed RF inputs. Slopes for the
pulse width change, for both sinusoid and pulsed RF
inputs, for frequencies f
i
greater than 3 f
0
is twice as
that for f
i
smaller than 3 f
0
. Upon further detuning,
a loss of mode locking occurs and we obtain broader
optical pulses. Beyond the mode locking range, opti-
cal pulses are produced due to modulation of the CW
laser by the EOM.
2.2.2 Fundamental Detuning
In Fig.9, the increase in pulse width is not symmetri-
cal about the central locking frequency. We have also
observed that there is modulation in the pulse peak
power due to dominance of the fundamental mode at
f
0
=
3 f
0
3
, as seen in the traces in Fig.6. As established
in Fig.8 and Fig.9, detuning of f
i
around the fun-
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
276

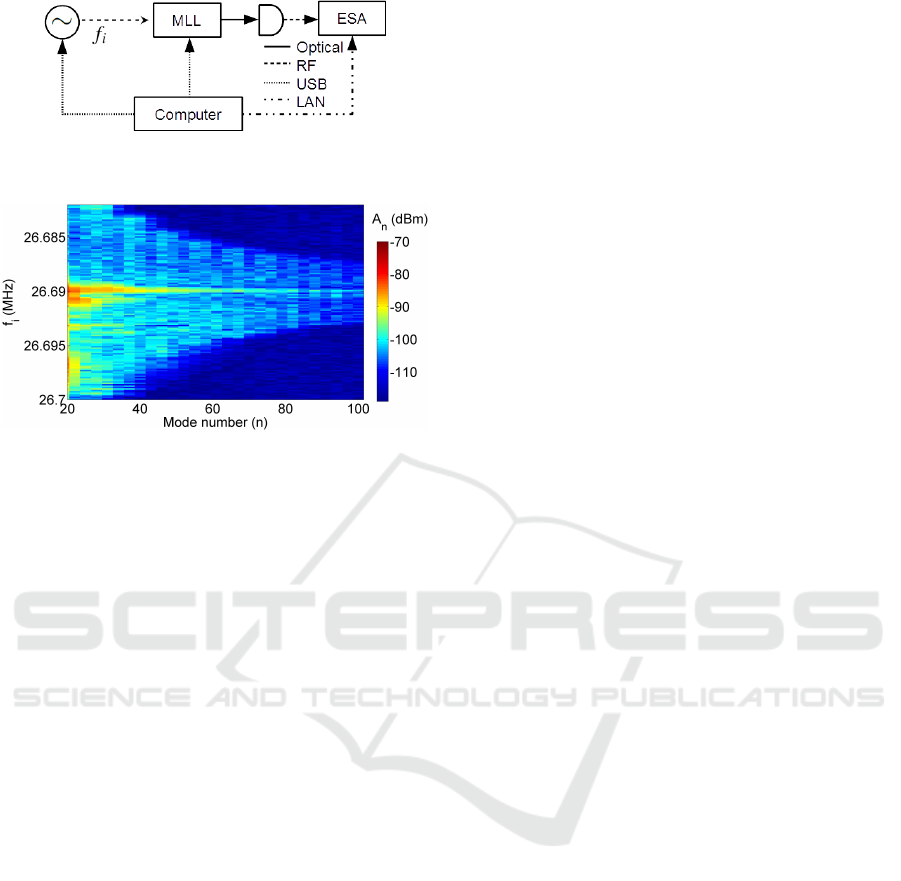
Figure 10: Schematic for finding the electrical amplitude
spectrum for the modes of the pulses.
Figure 11: Amplitude A
n
for each mode n of the pulse as
the input frequency f
i
is varied around the resonance f
0
=
26.69MHz.
damental resonance results in broadening of pulses.
We investigate the asymmetric increase in pulse width
around the fundamenta at f
0
.
From Fourier theory, we know that while the low-
est frequency components in a spectrum contributes
to average power, the pulse width is determined by
the higher frequency components. The electric field
in the laser can be described by
¯
E(¯r, t) =
∑
n
¯e
n
(¯r)exp( j2π f
optical
t)p(t), (1)
where the axial modes, given by ¯e
n
(¯r), are not time
varying. The optical frequency occurs at f
optical
.
The time varying electric field amplitude associated
with each axial mode n forms the pulse p(t) ((Haus,
1975)). For a Fourier limited pulse, the frequency
components of the field amplitude p(t) occur at mul-
tiples of the repetition rate of the pulse, i.e for an input
frequency of f
i
, the electric field amplitude can be de-
scribed as
p(t) =
∑
n
A
n
exp( j2πn f
i
t), (2)
where, A
n
is the complex amplitude for the n
th
har-
monic at frequency n f
i
in the frequency spectrum of
the pulse p(t). For a harmonic mode n, if the ob-
served frequency location
e
f
n
is same as the expected
harmonic frequency of n f
i
, then we can say that the
harmonic mode is locked to the input synchronization
signal at the frequency f
i
. If the observed frequency
e
f
n
and the expected frequency n f
i
do not match, i.e,
the deviation ∆ f
n
defined as,
∆ f
n
,
e
f
n
− n f
i
(3)
is nonzero then the mode is not locked. Thus, the fre-
quency location
e
f
n
of each harmonic n would show
if the pulse is mode locked or not. To quantify this,
we look at the electrical spectrum of the pulses and
capture the behavior of the harmonics that are first
to get unlocked with detuning. We use an electronic
spectrum analyzer (ESA) after a fast photodetector of
bandwidth of 10GHz to look at the different harmon-
ics as shown in Fig.10. We record the location of the
peak frequency
e
f
n
and the corresponding amplitude
A
n
for each harmonic (or mode number) n for the in-
put synchronization signal frequency f
i
. The signal
generator and the data collection on the ESA are auto-
mated using Virtual Instrument Software Architecture
(VISA) standards. For a given signal generator fre-
quency f
i
, the ESA is programmed to record the peak
frequency
e
f
n
and the corresponding amplitude A
n
for
each mode n. The ESA’s resolution bandwidth is set
to 500 Hz, allowing the ESA to resolve two closely
spaced frequency components up to a resolution of
500Hz. The observation frequency range set on the
ESA is limited to 500 kHz around the expected fre-
quency. We repeat the data collection for the different
input frequencies f
i
on the signal generator around
the fundamental frequency f
0
. First, we look at the
amplitude A
n
of the modes. We find that at the reso-
nant frequency f
0
= 26.69 MHz the power in all the
modes is highest as shown in Fig.11. As the input fre-
quency f
i
is detuned from the resonant frequency of
26.69MHz, we find that the power in all the modes
declines. For each input frequency f
i
, the peak fre-
quency location
e
f
n
for each mode n is collected. The
input frequency f
i
is detuned around the resonance f
0
and the deviation ∆ f
n
as defined in (3) is calculated
for each mode. This is shown Fig.13. We observe
that when f
i
= f
0
= 26.69 MHz all modes follow the
expected frequency, i.e. the deviation is
|
∆ f
n
|
= 0 for
all the modes n. For a range of input frequencies
around the resonance, the modes are locked and de-
viation is zero. For the recorded deviation range, the
modes lower than 25 do not deviate and follow the
expected Fourier frequency which implies that they
are still in their injection ranges. For the modes be-
tween 30 − 45, we see that the deviation in higher
mode builds up faster than for lower modes, as shown
in Fig.12.
To identify the spectral regions where mode lock-
ing for each mode occurs, we extract the upper and
the lower limits f
(U,n)
, f
(L,n)
respectively from the
frequency deviations. The limits are found as the
points where the deviations start to increase from
Synchronization between Two Fixed Cavity Mode Locked Lasers
277

Figure 12: Frequency deviation
|
∆ f
n
|
for each mode n of
the pulse as the input frequency f
i
is varied around the res-
onance f
0
= 26.69MHz.
zero. Since the resolution bandwidth on the ESA was
set to 500 Hz, we consider deviations of the order of,
or lesser, than the instrument resolution bandwidth to
be null. From the calculated deviation data in Fig.13,
we find the upper limit f
(U,n)
as
f
(U,n)
= max

e
f
n
:
|
∆ f
n
< 100 Hz
|

. (4)
Similarly we define the lower limit as the the mini-
mum frequency where the deviation is zero, i.e
f
(L,n)
= min

e
f
n
:
|
∆ f
n
< 100 Hz
|

. (5)
This is shown in Fig.14. We find that the both upper
and lower limits decrease as mode number increases,
indicating that the injection range narrows for higher
modes. However, the slope of decrease for upper limit
is larger by about three times when compared to the
lower limit. The region where the deviation in the fre-
quency is nearly zero is the region with mode locking
for any given mode, we define this as the the injection
range R
n
of the mode n ((Adler, 1946; Buczek et al.,
1973; Haus, 1975; Kurokawa, 1973)). The range R
n
is
bound by an upper frequency

f
(U,n)

and a lower fre-
quency

f
(L,n)

. Thus, we can define injection range
as
R
n
, f
(U,n)
− f
(L,n)
. (6)
Upon further detuning away from R
n
, the higher
modes lose mode locking. We calculate from The
difference between the two limits f
(U,n)
∼ f
(L,n)
as
the injection range R
n
for each mode n as shown in
Fig.15. We see that the injection range decreases with
increase in mode number. The reduction in the injec-
tion range is proportional to the mode number as n
2
as found by the fit to the ranges.
3 CONCLUSION AND
DISCUSSION
We have investigated the feasibility of using electri-
cal modulation of an active fibre mode locked laser
Figure 13: Deviation ∆ f
n
of each mode around the reso-
nance. Lower modes do not deviate in the narrow detuning
range and the higher modes deviate faster than the lower
modes.
Figure 14: Upper

f
(U,n)

and lower

f
(L,n)

limits of the
injection region.
Figure 15: Injection range R
n
for each mode n on a loga-
rithmic scale showing the dependency on the mode number.
in a master-slave configuration to obtain picosecond
optical pulses synchronized to the femto-second pulse
train of a commercial Ti:Sapphire laser. We have built
an active mode locked Yb:fibre laser as a slave laser,
at a fixed operating wavelength of 1064nm, as con-
structed in Fig.2. We find that the fibre mode locked
laser can be used as a pulsed slave laser, synchro-
nized to the master. The master laser had an operating
wavelength, λ
i
, in the range 690 − 920 nm. The rep-
etition rate f
i
of the Ti:Sapphire laser in wavelength
range is found to vary between 78.8 − 80.7 MHz as
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
278

shown in Fig.3. When the electronic synchronization
signal from the Ti:Sapphire is fed to the fibre MLL,
the fibre MLL produces fully mode locked pulses only
at the wavelengths where the repetition rate of the
Ti:Sapphire laser is close to the third harmonic 3 f
0
of the fundamental mode locking frequency f
0
of the
fibre laser. as shown in Fig.5
To further investigate the behavior of the fibre
laser for different synchronization signal repetition
rates, we closely observed the widening of the out-
put pulses from the slave laser. We found that there
was significant power over an input synchronization
frequency range of f
i
= 79.8 − 80.3 MHz. The fi-
bre laser was found to operate at its third harmonic
in this range, but as f
i
− 3 f
0
becomes large, we ob-
serve a modulation of the pulse train, as seen in Fig.8.
For f
i
→ 3 f
0
, a minimum pulse width of 69 ps was
obtained, shown in Fig.9. However, the change in
pulsewidth for f
i
6= 3 f
0
was asymmetric about 3 f
0
.
Also, upon detuning from the third harmonic, the
fundamental becomes dominant as seen in the pulse
train at 810 nm in Fig.6. The narrowing of pulses as
f
i
→ 3 f
0
is due to generation and locking of higher
order cavity modes as the EOM modulates the field
in the cavity. The injection of signal from lower,
and more stable modes into the higher modes causes
the higher cavity modes to be locked with the lower
modes. With detuning, the higher modes lose stability
and are not mode locked. We observed that this loss
in mode locking was determined by the extent of de-
tuning, | f
i
− 3 f
0
|, but did not explain the asymmetry
in locking.
To further investigate the detuning and pulse width
increase in the laser pulses, we operate the fibre laser
at the fundamental harmonic from a signal genera-
tor, and eliminate spurious effects due to variations in
the synchronization pulse from the master laser. We
found that the power in all modes was a maximum at
resonance, i.e. at f
i
= f
0
, as shown in Fig.11. We
then looked at the deviation in the frequency
|
∆ f
n
|
at
each mode n and we found that the deviation was a
minimum at f
0
, as shown in Fig.12. We observed that
the deterioration in the mode locked pulses was due
to detuning of the higher modes in the fibre laser. The
lower modes followed the input frequency harmonics
faithfully for a range larger than the measured detun-
ing. When we looked at the limits where the mode
locking occured for each mode, we found that the
upper limits f
(U,n)
and the lower limits f
(L,n)
for the
modes depend on the mode number, as n
2
. However,
the slope of the dependency for the limits are different
as shown in Fig.14. This indicates that for frequencies
above the resonance, i.e f
i
> f
0
, the modes lose lock-
ing rapidly with detuning. The rapid loss in locking
for higher modes indicates that the pulses are not of
Fourier nature and the pulse widths quickly increases
with detuning. On the other hand, when f
i
< f
0
, the
loss in locking for the modes is gradual and the pulse
width increases slowly as the input frequency is de-
tuned. The asymmetric dependency of the upper and
lower limits of the injection range explain the asym-
metry in the pulse width in frequency detuning as ob-
served in Fig.9. This asymmetry was also previously
reported in electrical circuits ((Razavi, 2004)).
We have defined an injection range R
n
for each of
the modes, and the range progressively decreases for
higher modes as shown in Fig.15. The effective in-
jection locking range of the entire fibre laser is thus
limited by the range of the highest mode of the laser,
which in turn is limited by the line-width of the laser.
In our experiments, we restricted the line-width of the
laser to 0.4nm at 1064 nm operating wavelength using
an FBG. We were also able to observe only up to the
100
th
as limited by the detector. From mode locking
theory, we are aware that the lower frequency modes
inject into the higher modes, but we report that the
onset of the injection is different for different modes.
In the injection range, as expected, the power in the
mode is higher than when the mode acts as a free run-
ning oscillator behavior.
Thus, an active mode locked ring fibre laser can
be operated in synchronization with another femto
second mode locked laser, by locking the ring cavity
to a harmonic of the lowest cavity resonance. When
the locking signal is detuned from the harmonic fre-
quency of the fibre laser, the fundamental cavity mode
becomes dominant, and manifests itself as an ampli-
tude modulation on the optical pulse train. Upon fur-
ther detuning, the pulse width further increases and
the laser operates in a modulation regime, driven by
the modulation produced by the EOM. This implies
that the operating regimes of the slave fibre laser will
depend on the repetition rate of the master laser’s syn-
chronization signal. By relying on cavity locking of
the slave, we obtain a wavelength independent syn-
chronization mechanism that offers us the ability to
synchronize two pulsed lasers over a wide range of
repetition rates. We do not vary the cavity length of
the fibre cavity but instead operate the master laser
within the detuning range of all the cavity modes of
the slave laser. To obtain the narrowest pulses from
the slave laser, the repetition rate of the synchronizing
master laser needs to be at a harmonic of the locking
frequency of the slave laser, with the available detun-
ing range decreasing as n
2
as we attempt to lock n
cavity modes together.
We believe that we are the first to report on
the asymmetric injection range of cavity modes in
Synchronization between Two Fixed Cavity Mode Locked Lasers
279

a Yb:fibre model locked ring laser. We have been
able to produced slave optical pulses in the range of
70ps − 2 ns, suitable for use as depletion pulses in a
STED microsocpe.
4 APPENDIX
We, now look at the effect of detuning the modulation
frequency f
i
on the axial modes of the laser. When
electrically modulated with a sinusoid at frequency
f
i
, the n
th
cavity mode occurs at the harmonic fre-
quency of the input frequency at f
n
= n f
i
. At cavity
resonance f
i
= f
0
, all the modes n are locked and oc-
cur at the respective harmonic at frequencies n f
0
with
mode amplitudes A
n
. The input frequency is detuned
to f
0
+ δ f , where δ f is the detuning. The detuning
causes a shift in the frequency locations of the modes
from f
n
= n f
0
to f
n
= n f
0
+ nδ f and the correspond-
ing mode amplitude A
n
changes to A
n
+δA
n
. We look
at the variation (δA
n
) when f
i
is detuned from the cav-
ity resonance f
0
by δ f .
Following the approach in ((Haus, 1975)), we em-
ploy perturbation analysis to find the variation δA
n
in
the mode amplitude of the n
th
mode due to a pertur-
bation δ f to f
i
= f
0
. We look at the perturbation to
the input frequency f
i
itself and find the effective per-
turbation of mode n’s amplitude A
n
, unlike the pertur-
bation to f
n
as done in ((Haus, 1975)). From ((Haus,
1975)), we have injection locking mode amplitude in
frequency domain given by
(
1 + jb − g
"
1 −

n f
0
f
L

2
#
+ j
n f
0
f
L
(σ + g)
)
A
n
= M
{
A
n−1
− 2A
n
+ A
n+1
}
.
(7)
On right, we have injection from the adjacent
modes n + 1 and n − 1 into mode n via sideband
generation by the modulator of strength M modulated
by a sinusoidal input. On left, the effect of the
resonant cavity and the gain medium on the mode
amplitude A
n
is described. The deviation in optical
frequency f
optical
is encapsulated in the term b. The
negative conductance g is produced by the gain
medium. The detuning of input frequency from the
empty cavity resonance f
c
is lumped in σ given by
σ =

1 −
f
c
f
0

2Q
f
L
f
optical
. (8)
Where, Q is the quality factor of the laser. The num-
ber of active axial modes in the laser is given by the
ratio of linewidth f
L
and f
0
, i.e
f
L
f
0
. In eq.(7), we intro-
duce the perturbation f
in
→ f
0
+ δ f , this causes vari-
ation in A
n
→ A
n
+ δA
n
, g → g + δg and σ → σ + δσ.
We get,
(
1 + jb − (g + δg)
"
1 −

k ( f
0
+ δ f )
f
L

2
#
+ (9)
j
k ( f
0
+ δ f )
f
L
((δσ + σ) + (g + δg))

(A
n
+ δA
n
) =
M
{
(A
n−1
+ δA
n−1
) − 2 (A
n
+ δA
n
) + (A
n+1
+ δA
n+1
)
}
.
The perturbation is applicable to the stable mode
locked state where equality of eq.(7) is valid. We look
at the perturbation from stable mode locked state at
f
i
= f
0
. The perturbation induced does not alter the
optical frequency f
optical
of the electric field in the
laser cavity, i.e. b = 0. We have small perturbation
in the input frequency that does not change the power
in the laser, thus, the variation in gain is negligible,
i.e. δg = 0. All second order perturbations are too
small, so approximated to 0. The detuning parameter
has a dependency on resonance frequency as evident
in (8), and the variation in the detuning parameter is
δσ = δ f

f
c
f
2
0
2Q
f
L
f
optical

. Everywhere, we assume
synchronized operation with ((σ + g) = 0). Variation
in all modes is of similar order, the injection signal
variation is negligible, so δA
n−1
− 2δA
n
+ δA
n+1
= 0.
The gain parameter g is a fractional value, this is
negligible compared to 1. With the assumptions dis-
cussed, we have,
(
1 − g
"
1 −

n f
0
f
L

2
#
+ j
n f
0
f
L
(σ + g)
)
(A
n
)+
(
1 − g
"
1 −

n f
0
f
L

2
#
+ j
n f
0
f
L
(σ + g)
)
(δA
n
)+

g

2k
2
f
0
δ f
f
2
L

+ j
n f
0
f
L
δσ + j
kδ f
f
L
(σ + g)

(A
n
)
= M
{
A
n−1
− 2A
n
+ A
n+1
}
+
M
{
δA
n−1
− 2δA
n
+ δA
n+1
}
. (10)
Simplifying the above equation, we have z

g

2n
2
f
0
f
2
L

+ j
n f
0
f
L

f
c
f
2
0
2Q
f
L
f
optical

(A
n
δ f )
+ (δA
n
) = 0. (11)
We rewrite the equation to show the fractional per-
turbation and mode amplitude as
δA
n
A
n
= −
δ f
f
0
(
2g

n f
0
f
L

2
+ jk

2Q
f
c
f
optical

)
.
(12)
We see that δA
n
is complex, the real part increases
as a function of n
2
, where as the imaginary part in-
creases linearly with n. Due to dependency on n
2
of
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
280

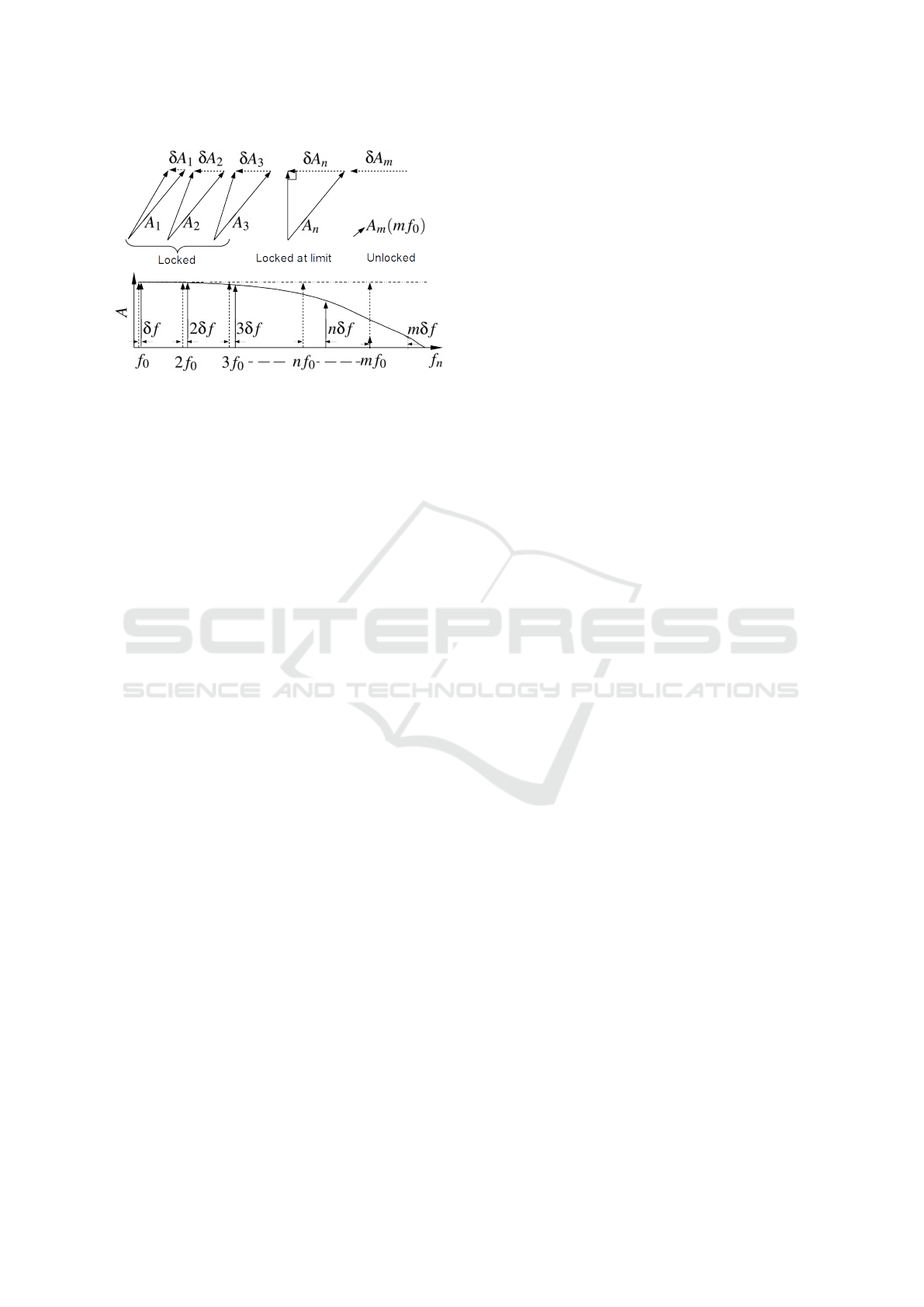
Figure 16: Effect on axial mode amplitudes with detun-
ing δ f . In the mode amplitude spectra, the mode enve-
lope deviates to the solid line envelope from ideal mode
locked envelope shown in dotted-dashed line. The mode
locations in frequency follow the Fourier frequencies of
( f
n
= n f
0
+ nδ f ), until mode n, that is still in the locking
limit , the further modes (m > n) are unlocked and oscillate
at m f
0
. The locking limit is where the injection signal is in
quadrature to the signal in the cavity as shown in the above
schematic.
the variation in the Re (δA
n
), the amplitude change is
larger the phase change with increasing mode number
n. The modes occur at f
n
= n f
0
, as shown as dotted
delta functions at the mode locations. For detuning
of δ f , the modes occur at f
n
= n f
0
+ nδ f which is a
nδ f frequency deviation from the mode locked state
for each mode. The detuned state is shown with solid
delta functions in frequency spectrum at the bottom
of Fig.16. Once the frequency deviation nδ f is out-
side the locking range R
n
for the mode, the mode is
no longer locked. This is shown for mode m which is
at a higher frequency than the modes n that are within
the locking range. This mode acts as free running os-
cillator, and the frequency of oscillation is same as at
resonance, i.e. n f
0
. However, the phase of the os-
cillation is no longer related to the rest of the modes
((Adler, 1946; Razavi, 2004)). In these modes, the
mode locked behavior is lost as they have frequency
deviation nδ f greater than the locking range R
n
of the
mode. These modes are said to be unlocked.
In the unperturbed, mode locked state, the ampli-
tudes A
n
for all modes are equal. This makes the spec-
tral envelope of the frequency spectrum uniform, as
shown by the dotted horizontal line in Fig.16. On de-
tuning, the spectral envelope deviates from the mode
locked envelope as shown by the solid curve in the
frequency spectrum. The amplitude deviation (re-
ferred to as deviation from here), is a function of n
2
as derived in eq.(12). The δA
n
for each mode is the
change in strength of injection for the mode. When
the mode frequency f
n
is within the locking range R
n
for the mode, the deviation is the difference phasor
between the mode amplitude A
n
at resonance, and the
resulting mode amplitude A
n
+ δA
n
after perturbation
((Razavi, 2004)). The phasors for different modes wrt
the amplitude deviation δA
n
are shown at the top of
the respective mode at n f
0
in the frequency spectrum.
As long as the resulting mode amplitude A
n
+δA
n
and
deviation δA
n
are within 90
◦
of each other, the mode
can be in locked state. The frequency f
n
, in mode is at
the edge of the injection range at either f
(U,n)
or f
(L,n)
.
A condition where the deviation and the resulting am-
plitude are at quadrature to each other is shown for
the mode n in Fig.16. We can see that the maximum
deviation supported by any mode is thus δA
n,Max
, cor-
responding to the limit of locking at either f
(U,n)
or
f
(L,n)
. Mode m greater than n is unlocked, the pha-
sor A
m
+ δA
m
makes an angle greater than 90
◦
with
the deviation δA
m
. The large phase required to main-
tain the angle between the injection and the resultant
mode amplitude cannot be provided by the laser, thus
the mode is not locked and acts as a free running oscil-
lator. The resulting frequency of the unlocked mode
is m f
0
and not m f
0
+ mδ f as would be expected for
a locked mode as is shown in Fig.16. Thus, due to
the large deviation δA
m
> δA
n,Max
, the mode m will
not be locked. In this manner we can relate the injec-
tion range R
n
to a deviation threshold δA
n,Max
for each
mode. In this manner we relate the injection range R
n
to a deviation threshold δA
n,Max
for each mode n.
REFERENCES
Adler, R. (1946). A study of locking phenomena in oscilla-
tors. Proc. IRE, 34(6):351–357.
Buczek, C. J., Freiberg, R. J., and Skolnick, M.
(1973). Laser injection locking. Proc. of the IEEE,
61(10):1411–1431.
El-Diasty, F. (2011). Coherent anti-stokes raman scatter-
ing: Spectroscopy and microscopy. Vibrational Spec-
troscopy, 55(1):1 – 37.
Farahani, J., Schibler, M., Bentolila, L., Mendez-Vilas,
A., and Diaz, J. (2010). Stimulated emission deple-
tion (sted) microscopy: from theory to practice. Mi-
croscopy: Science, Technology, Applications and Ed-
ucation, 2:1539.
Haus, H. A. (1975). A theory of forced mode locking.
Quant. Electronics, IEEE J. of, 11:323–330.
Honigmann, A., Sadeghi, S., Keller, J., Hell, S. W.,
Eggeling, C., and Vink, R. (2014). A lipid bound actin
meshwork organizes liquid phase separation in model
membranes. eLife, 3:e01671.
Klar, T. A., Jakobs, S., Dyba, M., Egner, A., and Hell, S. W.
(2000). Fluorescence microscopy with diffraction res-
olution barrier broken by stimulated emission. Proc.
of the Nat. Acad. of Sc., 97(15):8206–8210.
Krishnamoorthy, S., Jayavel, D., Prabhakar, A., Mathew,
M., and Mayor, S. (2014a). Depletion laser for pulsed
Synchronization between Two Fixed Cavity Mode Locked Lasers
281

sted using wavelength stabilized actively mode locked
lasers. In ICOL. Dehradun, India.
Krishnamoorthy, S., Mathew, M., Prabhakar, A., and
Mayor, S. (2014b). Actively mode locked fiber laser
for synchronized pulsed depletion in sted. In 6th EPS-
QEOD Europhoton Conference. Neuch ˇatel, Switzer-
land.
Kurokawa, K. (1973). Injection locking of microwave solid-
state oscillators. Proc. IEEE, 61(10):1386–1410.
Lauterbach, M. A., Guillon, M., Soltani, A., and Emiliani,
V. (2013). Sted microscope with spiral phase contrast.
Scientific reports, 3.
Li, W., Hao, Q., Li, Y., Yan, M., Zhou, H., and Zeng,
H. (2010). Ultrafast laser pulse synchronization. In
Duarte, F. J., editor, Coherence and Ultrashort Pulse
Laser Emission. InTech.
Nienhaus, K. and Nienhaus, G. U. (2016). Where do
we stand with super-resolution optical microscopy?
Mol. Bio., J. of, 428(2, Part A):308 – 322. Study of
biomolecules and biological systems: Proteins.
Razavi, B. (2004). A study of injection pulling and locking
in oscillators. In Custom Integrated Circuits Confer-
ence. Proc. IEEE, pages 305–312.
Rusu, M., Herda, R., and Okhotnikov, O. G. (2004). 1.05-
µm mode-locked ytterbium fiber laser stabilized with
the pulse train from a 1.54-µm laser diode: errata. Opt.
Express, 12(22):5577–5578.
Takasaki, K. T., Ding, J. B., and Sabatini, B. L. (2013).
Live-cell superresolution imaging by pulsed {STED}
two-photon excitation microscopy. Biophys. J.,
104(4):770 – 777.
Wu, Y., Wu, X., Toro, L., and Stefani, E. (2015). Resonant-
scanning dual-color sted microscopy with ultrafast
photon counting: A concise guide. Methods, 88:48–
56.
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
282