Understanding Jump Landing as an Oscillating System: A Model-based

Approach of Balance and Strength Analyses

Sandra Hellmers

, Sebastian Fudickar

, Lena Dasenbrock

, Andrea Heinks

, J

urgen M. Bauer

and Andreas Hein

Assistive Systems and Medical Technologies, Carl von Ossietzky University Oldenburg, Oldenburg, Germany

Department of Geriatric Medicine, Carl von Ossietzky University Oldenburg, Oldenburg, Germany

Chair of Geriatric Medicine, Heidelberg University, Agaplesion Bethanien Hospital Heidelberg, Heidelberg, Germany

Keywords:

Force Platform, Counter Movement Jump, Vertical Jump, Balance, Strength, Geriatric Assessment, Jump

Landing, DPSI.

Abstract:

Counter movement jumps (CMJ) are well-suited to measure the muscle power and balance. Since it has been

clariﬁed that well accepted CMJ ampliﬁcation-based balance measures (such as TTS or CoP) are signiﬁcantly

inﬂuenced by algorithmic, and measurement settings and thus, measurement results have limited meaning-

fulness among force platforms, we introduce a new model-based approach measuring the postural stability.

In this, during the landing and recovery phases after vertical jumps, the lower extremities can be represented

by an oscillating system and the corresponding transfer function is described by a second-order delay (PT2)

element.

In an initial prospective study with 20 subjects aged over 70 years, we observed an inverse relationship be-

tween the calculated parameter w and the jump height and could also identify an inﬂuence of sex, and body

weight on the jump height. Furthermore, we also found a relation between the parameter w and the dynamic

postural stability index (DPSI), even though these results must be ensured statistically using a larger cohort,

due to the current limited number of subjects.

Nevertheless, we could conﬁrm the general applicability of the Systems and Control Technology perspective

on describing human movements in a potentially more robust manner than current ampliﬁcation based ap-

proaches. Further investigations on our model and the oscillating behavior in the phase of landing are needed

to improve our system and to interpret the calculated parameters in a technical and physiological point of view.

1 INTRODUCTION

Geriatric assessments are well-established instru-

ments to identify early changes associated with func-

tional and cognitive decline, as they can occur in com-

mon geriatric syndromes, such as frailty or sarcopenia

(Clegg et al., 2013; Cruz-Jentoft et al., 2010; Elsawy

and Higgins, 2011). Thus, the assessments gain in-

creasing relevance with the ongoing age-related de-

mographic shift. Therefore, it exists a strong research

interest to identify degrading abilities very early in

geriatric assessments or with technical monitoring

systems (Hein et al., 2010; Fudickar et al., 2012), like

for example with systems in domestic environments

to identify changes in the user behavior (Steen et al.,

2013), to trigger preventive measures.

Nevertheless, for a self-determined healthy life

and low fall risk, functional abilities and physical ﬁt-

ness are fundamental for healthy aging. Muscular

strength of the lower extremities, balance, and en-

durance are essential factors (Granacher et al., 2013)

for the fall risk, frailty, and sarcopenia.

Due to the relevance of muscular strength of the

lower extremities, postural stability, and endurance,

these factors are covered by various standardized as-

sessments and tests (see Table 1). Most of these

assessments and tests consist of several assessment

items. For example, the Short Physical Performance

Battery (SPPB) consists of a walk test, a static balance

test, and the chair rising test and can cover strength

and balance only in the combination of the assessment

items. Consequently, among the common assess-

ments, only the Counter Movement Jump (CMJ) is

well-suited to test both components, strength, and bal-

ance within a single item. In detail, the CMJ allows to

measure postural stability (balance) (Granacher et al.,

Hellmers S., Fudickar S., Dasenbrock L., Heinks A., Bauer J. and Hein A.

Understanding Jump Landing as an Oscillating System: A Model-based Approach of Balance and Strength Analyses.

DOI: 10.5220/0006171101590168

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 159-168

ISBN: 978-989-758-213-4

159

Table 1: Selection of assessment items in our geriatric study (Hellmers et al., 2016), their test duration, and classiﬁcation

regarding the components of physical ﬁtness (- none, + to +++ increasing signiﬁcance). The test durations are based on

literature and estimated on own experiences (*) in a study with 250 participants. The values in brackets are the durations with

introduction and instructions or a test jump.

Geriatric Assessments Balance Strength Endurance Test Duration

de Morton Mobility Index ++ - - 9 min

-static balance ++ - -

-dynamic balance ++ - -

Short Physical Performance Battery ++ ++ - 15 min

-static balance ++ - -

-chair rise test - ++ -

Frailty Index - ++ - 10-17 min

∗

-grip strength - ++ - 3-5 min

Stair Climb Power Test - ++ - 2-(5) min

∗

6 Minute Walk Test - + ++ 6 min

Counter Movement Jump ++ ++ - 5-(6) min

∗

2013) via the time to stability (TTS) during the land-

ing and stabilization phase and muscle performance

of the lower extremities (strength) via muscle power

ahead of jumps (Buehring et al., 2015; Rittweger

et al., 2004; Dietzel et al., 2015; Kalyani et al., 2014).

The assessment of patients’ functional status for

balance and muscle strength through a single test

item instead of several tests lowers costs and personal

efforts (supporting an increased assessment density)

and can reduce stress and potential fatigue for pa-

tients, which hold the risk that assessments results

lose signiﬁcance (Siglinsky et al., 2015). Conse-

quently, the CMJ is a well-suited assessment item to

cover both muscle strength of the lower extremities

and postural stability.

However, since relying just on the force ampli-

ﬁcation, current CMJ-based balance measures (such

as COP and TTS) have been shown to be signiﬁ-

cantly prone to algorithmic and technical variations

thus have limited viability regarding the generaliza-

tion of classiﬁcation and measurements.

Thus, we propose a robust approach to measure

postural stability based on the natural frequencies dur-

ing the landing and recovery phase of CMJs and eval-

uate its practicability for 20 subjects with an age of 71

to 82 years.

2 COUNTER MOVEMENT JUMP

Within this section, the characteristics of CMJs are

discussed and are followed by a description of the

technically supported measurement of ground reac-

tion forces.

2.1 Biomechanical Characteristics

Counter movement jumps (CMJs) are vertical jumps

that are performed from standing, and according to

(Palma et al., 2008) consist of the following phases

(as shown in Figure 1): In the ﬁrst phase (a) the par-

ticipant is standing. Phase (b) is characterized by the

preparation (b) with a downward movement by the

ﬂexion of the knees and hips, followed by an imme-

diate and impulsive extension of the knees and hips

again to jump vertically up and take-off (c) and ﬂight

(d). At the end of the jump, a stage of landing (e) with

the absorption of the forces of the impact, and a stage

of recovery (f) of the balance can be identiﬁed, fol-

lowed by a standing phase after compensation of the

forces (a).

Figure 1: Counter movement jump and its separate phases:

standing (a), preparation (b), take-off (c), ﬂight (d), landing

(e), and recovery (f). The marks indicate the participant’s

center of mass in each jump phase.

2.2 Common Technical Measurements

via Force Platforms

Since pure observational evaluations are difﬁcult, due

to the fast progress of a jump, analyses are typi-

HEALTHINF 2017 - 10th International Conference on Health Informatics

160

cally technology supported via force platforms, con-

tact mats or optical systems (Bui et al., 2015). Force

platforms measure the ground reaction force intensity

and distribution.

Due to the speciﬁc force distribution characteris-

tics, the phases of a CMJ can be identiﬁed by varia-

tions of the ground force (if measured by ground force

reaction platforms or similar devices), as shown ex-

emplarily in Figure 2 and discussed in the following:

The transition from standing or rest (a) to preparation

(b) can be clearly recognized by changes in the ampli-

tudes of the force, which was nearly constant during

the standing phase. Take-off (c) is characterized by

the decrease of force affecting on the platform. Dur-

ing the ﬂight phase (d), the force amounts to zero. In

the moment of landing (e), the force increases to a

maximum. In the phase of recovery (f), the subject

tries to compensate the forces, in order to enter the

phase of standing or resting (a) again.

Figure 2: Variations over time of force intensities per axis

during a counter movement jump. The force was measured

by a force platform. The phases of the counter movement

jump are marked in the graph: standing (a), preparation (b),

take-off (c), ﬂight (d), landing (e), and recovery (f).

Figure 3 shows the coordinate orientation of the

force platform. It is clear that the mean force acts per-

pendicular to the force plate in the vertical (z) direc-

tion. But there are also reaction forces in the medio-

lateral (y) and especially in the anteroposterior (x) di-

rection. In the anteroposterior direction is a peak dur-

ing the take-off phase pushing the feet off the ground,

and during the landing while the toes and heels strike

the ground and compensate the movements.

Force platforms can estimate power, velocity and

the related jump height (Samozino et al., 2008). The

physical relationships between the measured force

and the power, as well as the jump height, is shown

in Section 3. The peak force measurements during

the preparation and take-off phases e.g. of CMJs are,

as long as being considered relative to the body mass,

signiﬁcantly related to muscle strength (Nuzzo et al.,

2008; Markovic et al., 2014). The strength can be an-

alyzed by the take-off phase of the jump, and the bal-

ance was shown to be estimated based on the force-

intensities and distributions during the landing and

recovery phase of jumps. For example, the time to

stabilization (TTS) is the time it takes for an individ-

ual to return to a stable state following a jump or hop

landing, and it is a used factor for balance analyses.

Thereby, a longer TTS indicates more difﬁculty con-

trolling the posture of landing and might indicate im-

paired neuromuscular control (Fransz et al., 2015).

Figure 3: The dimensions of the used AccuPower ground

reaction force platform of AMTI with its coordinate orien-

tation. The footprint symbolizes the orientation of the sub-

jects during the jumps.

3 STATE OF THE ART

The jump power, as an indicator of muscle strength,

can be identiﬁed by the force measurements during

the vertical jump, especially in the phase of the take-

off.

Force plates measure the force acting on the plate.

According to Newton’s second law, the force F is

equal to the mass m of an object times its accelera-

tion a.

F = m ·a (1)

In the example of Figure 2, we can clearly see the in-

ﬂuence of the mass of the jumper on the force F

act-

ing perpendicular to the surface of the plate. The off-

set at rest amounts about 1500 N, which corresponds

approximately to a mass of 150kg.

The power P is deﬁned by the force F times the

velocity v:

P = F · v (2)

In many studies, the maximum jump power is ob-

served and seems to be a sensitive indicator of the

muscle performance and the strength (Dietzel et al.,

2015; Kalyani et al., 2014).

Understanding Jump Landing as an Oscillating System: A Model-based Approach of Balance and Strength Analyses

161

A further important parameter for jump analyses

is the jump height. The jump height h can be esti-

mated by the following equation:

h = (v

·t)−

· g ·t

, (3)

where v

is the vertical velocity of the center of mass

of the jumper at take-off, t is the time to peak ﬂight

and g the gravity.

Besides measuring muscle strength, force plat-

forms can be utilized to measure dynamic postu-

ral stability, which has been shown as related to

balance and ankle stabilities. Therefore, functional

deﬁcits such as chronic functional ankle instability

(FAI) (Hertel, 2002), can be indicated based on the

recorded vertical, anteroposterior or mediolateral re-

action forces, which enable the calculation of time

to stabilization (TTS) and variations over time of the

center of pressure (COP), range of motion (ROM),

and the dynamic postural stability index (DPSI) as ac-

cepted measures for postural stability and FAI. The

DPSI is at least as accurate and precise as TTS but

provides a comprehensive measurement of dynamic

postural stability that is sensitive to change in 3 direc-

tions.

DPSI provides a comprehensive measurement of

dynamic postural stability that is sensitive to change

in all directions since combining three (vertical, an-

teroposterior and mediolateral) stability indexes and

considers as well the subject’s weight for the vertical

stability and thus has been shown to be a reliable mea-

sure (Wikstrom et al., 2005b; Meardon et al., 2016).

While COP and ROM have shown mixed correlations

to FAI stabilities, TTS is a well-accepted measure to

quantify performance. Typically, the force is con-

sidered in order to measure the TTS, as a measure

of the ability to stabilize posture (which is applied

within numerous studies). TTS typically ranges from

0 to 7s. By investigating 20 TTS calculation meth-

ods (as identiﬁed via a structured literature review),

Fransz et al. (Fransz et al., 2015) have shown that all

use threshold-based approaches based on the ground

force and 90% can be described based on four aspects:

(1) the input signal, (2) signal processing, (3) the sta-

ble state (threshold), and (4) the deﬁnition of when

the (processed) signal is considered stable.

Wikstrom et al. identiﬁed a signiﬁcant variabil-

ity among TTS measurements due to differences be-

tween the TTS calculation methods used in various

studies (Wikstrom et al., 2005a). By evaluating the in-

ﬂuences of parameter variations, Fransz et al. (Fransz

et al., 2015) have indicated that the TTS measure does

produce non-standardized parameters if estimated via

ground forces reaction parameter. They indicated

variations of the TTS of up to 56% for sample rate

(100 to 1000 Hz), 37% for ﬁlter settings (no ﬁlter, 40,

15 or 10 Hz), 28-282% for trial lengths (20, 14, 10, 7,

5 and 3 s), as well as calculation methods. Thereby

they clariﬁed the difﬁculties to compare TTS results

recorded among different systems based on the power

measure.

While these analyses are performed based on sin-

gle jump measurements for 25 healthy younger adults

(20-53 years), its insights will generally apply due to

the indicated computational differences and the dras-

tic effect sizes.

Consequently, alternative measures are desired,

which are more robust regarding measurement-

variations such as sample rates.

Ideally, these measures should be equally appli-

cable to rather mobile measurement devices such as

inertial measurement units (IMU), which will be in-

creasingly applied due to their lower price and the

higher grade of mobility (Choukou et al., 2014; Elvin

et al., 2007; Milosevic and Farella, 2015).

4 SYSTEMS AND CONTROL

TECHNOLOGY

Considering the situation, that a system is stimulated

by an action (input signal). Usually, the system re-

acts on this stimulation in any manner (output signal).

Now we want to describe this system to predict the

reaction of the system to an action. In the systems

and control technology the relation of an input and

an output function, and therefore, the system can be

described by a transfer function (see Figure 4).

Figure 4: Relation between the output function Y (s), the

transfer function H(s) and F(s) the input function.

The mathematical relation is given by:

Y (s) = H(s)F(s), (4)

where Y (s) is the output function, H(s) the transfer

function and F(s) the input function. If assuming,

that the landing and recovery phase of a vertical jump

(Figure 2 (e)) is an oscillating system, the transfer

function is described by a second-order delay element

(PT2-element).

H(s) =

Y (s)

F(s)

+ bs + 1

(5)

HEALTHINF 2017 - 10th International Conference on Health Informatics

162

Considering the general second-order system of an

oscillator H(s) can be described by

H(s) =

Kω

+ 2Dω

s + ω

, (6)

where ω

is the natural frequency, K the DC gain

of the system and D the damping ratio. It is as-

sumed, that the error resulting from the use of the

time-continuous model is small, because of a rela-

tively high sampling ratio of 200 Hz. The natural

frequency determines how fast the system oscillates

during the response. The damping ratio determines

how much the system oscillates as the response de-

cays toward a steady state. These parameters can be

deduced from equation 6, after transferring it in the

form of equation 5:

H(s) =

(

2Ds

+ 1)

(7)

and D =

bω

(8)

Therefore, the natural frequency and the damping ra-

tio can characterize the landing phase, the absorption

of the impact, and the restoring of the balance and

stability. As we will see in the next section, these

parameters might be an alternative possibility to char-

acterize the balance ability, the muscle strength, and

allow conclusions to postural stabilization and neuro-

muscular control.

5 MODEL-BASED APPROACH

We propose the use of the oscillation behavior

as an alternative approach to drawing conclusions

about muscle strength, balance ability, postural sta-

bility, and neuromuscular control instead of using

the DPSI, TTS, COP or ROM. The advantage of

the model-based approach of the oscillation behav-

ior (during landing and recovery phase) over existing

ampliﬁcation-based methods might be its potentially

lower dependability on sample rates, and trial lengths.

In detail, we aim to model (as schematically illus-

trated in Figure 5) the human’s lower extremities as a

spring that oscillates during the landing and recovery

phase. During free fall the spring is slack and will be

compressed at the impact on the ﬂoor and the landing

phase and depresses during the recovery phase to the

steady state in one or more oscillations.

From a physical point of view, this system can be

described by

F = −kx, (9)

Figure 5: Comparing of the human’s lower extremities with

a spring during the landing and the recovery phase of a

jump. The spring will be compressed during the landing

(e-e1) and depresses during the recovery phase (f-f1) to the

steady state in one or more oscillations.

with the force F, the displacement x and the spring

constant k. The frequency can be estimated with

k/m. (10)

This equation shows that the frequency correlates to

the spring constant k.

In our model, the spring is characterized by the

spring constant. Consequently, if comparing the

spring with the muscles of the humans’ lower extrem-

ities, the spring constant characterizes the stiffness of

the muscles in a ﬁrst approximation. Therefore, the

natural frequency ω

of our system describes the abil-

ity to absorb the impact at the landing and character-

izes the muscles of the lower extremities.

The damping ratio D indicates the inﬂuence

within or upon an oscillatory system that has the ef-

fect of reducing its oscillations and might also be a

relevant parameter for the characterization of the bal-

ance ability and the postural stability.

6 EVALUATION

6.1 Study Design

Each of the 20 considered healthy older adults of

our study (12 subjects are female (60%) and 8 male

(40%)) has performed three sequential CMJs with a

rest of 1 min between the jumps to avoid signs of fa-

tigue. Further characteristics of the subjects are listed

in Table 2. The group covers a typical range of age,

weight, and height for the group of pre-frail elderlies.

The test procedures were approved by the local ethics

committee (ethical vote: Hannover Medical School

No. 6948) and conducted in accordance with the Dec-

laration of Helsinki.

Understanding Jump Landing as an Oscillating System: A Model-based Approach of Balance and Strength Analyses

163

Table 2: Population characteristics of our study with the

minimum (min.), maximum (max.), mean values and stan-

dard deviation (SD).

n=20 min. max. mean SD

age [years] 71 82 75.1 3.02

weight [kg] 51.6 97.25 74.87 12.49

height [cm] 154.1 189.1 167.25 9.92

The jumps have been performed on an AMTI Ac-

cuPower ground reaction force plate, which is spec-

iﬁed for jumping and power analyses and is an ac-

cepted gold standard. Figure 3 shows the coordinate

orientation and the dimensions of the plate. The sam-

pling rate amounts 200Hz. The AccuPower sensitiv-

ity is based on a 8900 N full-scale F

capacity and a

12 bit internal AD (±2048 bit) or about 4.3 N/bit.

The transfer functions and FPE (as describing the

transfer functions ﬁt) have been estimated for each (of

the 3x20) performed CMJs with Mathworks’ MAT-

LAB (version R2015a) using the System Identiﬁca-

tion Toolbox (version 9.2).

Per subject, the jump with the best ﬁt estimation

was taken into account in our analyses, whereby ﬁts

below 70% are rejected. Thereby, the function for the

ﬁt corresponds to the form of equation 5. An impulse

function with the height of the impact force at landing

will be assumed for the input signal. Figure 6 shows

a typical input function.

Figure 7 shows a characteristic phase of landing

and recovery and is assumed as an output function.

To take the force in all directions into account, the

absolute values for each axis are summed up. In the

step of reprocessing the means are removed. In accor-

dance with the theoretical considerations of Section 4,

the number of poles is set to 2 and the number of zeros

to 0 for the model of the transfer function, to describe

an oscillating system (see equation 6). A discrete-

time spectrum with T=0.005 s is chosen, because of

the sampling rate of 200 Hz of the force plate.

6.2 Natural Frequency and Damping

Ratio

The natural frequency ω

and damping ratio D were

determined as described in section 4. The results

for the natural frequency are in the range of about

1Hz. Due to the literature, we expected higher fre-

quencies (Wakeling et al., 2001). The analyze of the

poles of the poles of the determined transfer functions

show that there are only two real poles, which indicate

a non-oscillating function instead of complex pole

pairs, which lead to exponentially modulated oscilla-

tions. Consequently, the calculated parameter (called

Figure 6: Typical impulse function as an input function.

Figure 7: Typical phase of landing and recovery as an output

function. The dashed line indicates the previous progress of

the force during the ﬂight phase.

w) is not equivalent to the natural frequency ω

and

describes rather a damping factor. Nevertheless, the

parameter w seems to be signiﬁcant: Figure 8 shows

the parameter w in relation to the jump height h. A

linear regression results in

d = −0.0013 · h + 1 (11)

The relation shows an inverse relationship between

these parameters. Therefore, the parameter w de-

creases with an increasing jump height.

Figure 9 shows the relation between jumping

height and the calculated parameter d for the damp-

ing ratio D. Within the study group, the parameter

d’s effect size is small, since varying only in a small

range. As an approximative assumption, the damping

is linearized. Hence, an inverse relationship between

the jumping height and the damping ratio was also

recognized. The relation is not signiﬁcant, due to the

small effect size. It needs further investigations via

data of both larger cohorts and heterogeneous groups,

and additionally if the parameter d is equivalent to the

damping ratio D.

HEALTHINF 2017 - 10th International Conference on Health Informatics

164

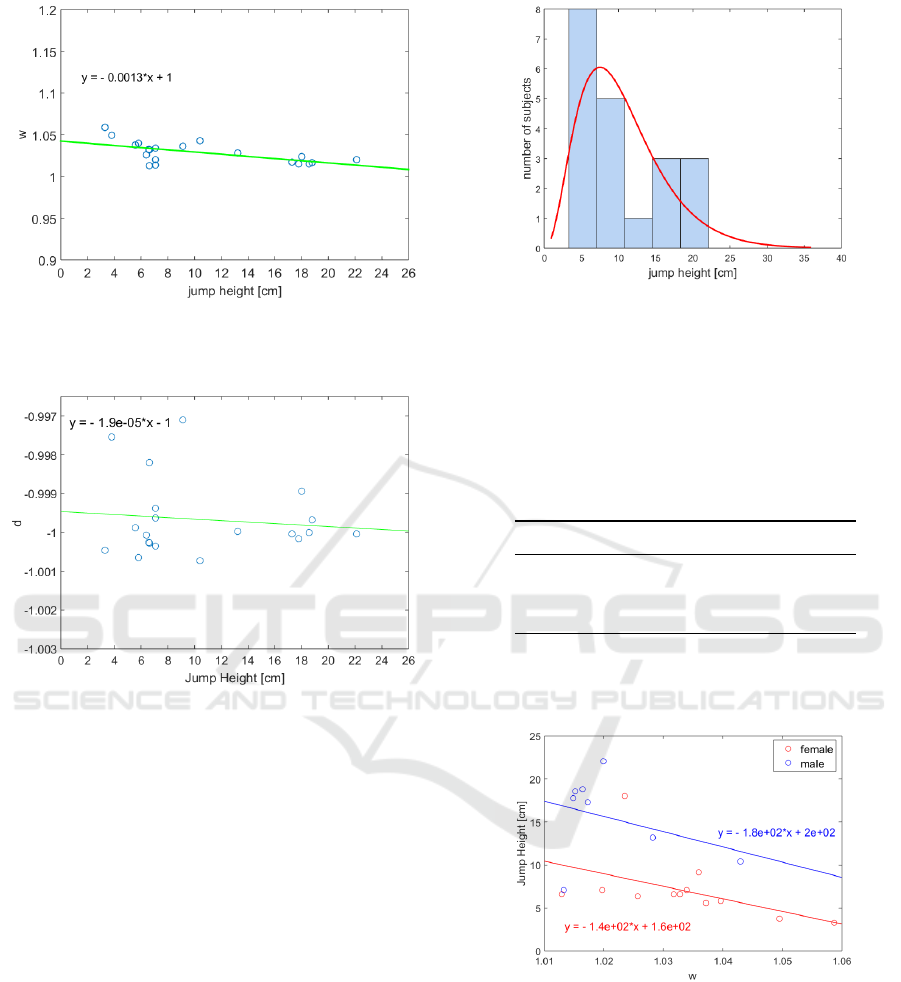
Figure 8: The parameter w is shown in relation to the jump

height h. There is an inverse relationship between this pa-

rameter and the jump height.

Figure 9: The estimated parameter d is shown in relation to

the jump height h. The variation of this parameter lies only

in a small range.

6.3 Major Factors of Inﬂuence

Due to the fact, that several factors can inﬂuence the

parameters w and d, we analyzed the inﬂuence of the

age, the sex, the body weight, the body height, w and

d as a function of the jump height.

Therefore we used a generalized regression

model. Due to the left skewed distribution of jump

height (see Figure (10)) we estimated a gamma-

distribution. Considering the jump height as clearly

observable element, we performed a stepwise model

selection by the Akaike information criterion (AIC).

The results of the regression analyses are listed in

Table 3. As mentioned in Section 6.2 the parameter

d varies only in a small range and is not signiﬁcant.

Also, the body height has no inﬂuence on the jumping

height. But we can see a small inﬂuence of the body

weight and an inﬂuence of the sex and the parameter

Table 3 shows the changes of the jump height for a

Figure 10: Distribution of the jump height and the estimated

gamma-distribution (red line).

one unit change of the listed parameters. For example,

the sex has an inﬂuence of about 7cm. The change of

0.01 unit of w results in a mean change of 1.5 cm of

jump height.

Table 3: Inﬂuence of weight, sex, and w depending on the

jump height.

Estimation SD p(> |t|)

w -152.20 43.02 <0.01

weight -0.073 0.04 0.08

sex -7.34 1.95 <0.01

Figure 11 illustrates the differences between male

and female subjects in jump height as a function of w.

Figure 11: Comparison of the jump height as a function of

w of male and female subjects.

Considering equation 10 in Section 5 and the sim-

pliﬁed comparison of a human as a spring, the natural

frequency increases with increasing spring constant

and therefore increasing stiffness. On the assumption

that the jump height h corresponds with the muscle

strength S, there seems to be a relationship between

jump height, the paramter w, muscle strength, and

spring constant k:

Understanding Jump Landing as an Oscillating System: A Model-based Approach of Balance and Strength Analyses

165

h ∼ S ∼

∼

. (12)

Thus, our model explains the inverse relation between

jump height and the parameter w.

In order to analyze the postural stability, the dy-

namic postural stability index (DPSI) was determined

in accordance with the approach of (Wikstrom et al.,

2005b) by equation 13.

DPSI =

∑

(0 − F

)

∑

(0 − F

)

∑

(m − F

)

(13)

where F

, F

are the forces in anteroposterior

(x), mediolateral (y) and vertical(z) direction, m the

body weight, and n the number of data points. Fig-

ure 12 shows the resulting distribution of the DPSI

over the considered CMJs of our study population.

Next to the normal distribution of the DPSI values and

the distribution-range (in relation to other age-related

groups such as in (Wikstrom et al., 2005b; Meardon

et al., 2016)) conﬁrms the suitability of the DPSI for

the considered group.

Figure 12: Distribution of the DPSI over our study popula-

tion with a normal distribution ﬁt.

In order to investigate the relation between w

and postural stability (represented by the DPSI), we

also analyzed the inﬂuence of the factors age, body

weight, and w as a function of the DPSI. Table 4 lists

the results.

Table 4: Inﬂuence of weight, sex and w depending on the

DPSI.

Estimation SD p(> |t|)

w -1244.73 791.75 0.14

weight 2.25 0.816 0.01

age 7.71 3.37 0.04

We found an inﬂuence of these factors on the

DPSI: For example, a change of 0.01 units in w re-

sults in a change of 12 of the DPSI-value. A change in

the age of 10 years causes a change of 77 of the value

of DPSI. While a signiﬁcant correlation of the weight

and age with the DPSI was found, the strong inﬂu-

ence of w (indicated by an estimate of 1244.73, which

is 161 times stronger than for age, the next strongest

estimate) could not yet be statistically ensured due to

the low number of subjects (n=20). Consequently, we

are looking forward to conﬁrming the expected signif-

icant correlation in an upcoming analysis with a larger

study group.

7 CONCLUSION

While the CMJ is well-suited to measure muscle

power and strength within a single assessment item,

common traditional ampliﬁcation-based balance mea-

sures for CMJ (such as TTS or CoP) have been shown

to be signiﬁcantly inﬂuenced by measurement set-

tings including trial length, sample rate, and ﬁlter set-

tings. Thus, a reliable alternative approach to detect

balance ability for vertical jumps is required.

As an alternative approach, we propose to model

the human body during the landing after a jump

from a Systems and Control Technology perspective.

Therefore, we used an impulse function of the maxi-

mum force at the impact on the ground as input func-

tion and the landing and recovery phase of a jump as

output function. This phase is characterized by the

balance and muscle strength of a subject.

Since the landing and recovery phase of vertical

jumps can be represented by an oscillating system,

the transfer function is described by a second-order

delay element (PT2-element), where the natural fre-

quency determines the systems oscillation frequency,

and the damping ratio determines the system oscilla-

tion intensity as the response decays towards a steady

state.

In an initial prospective study with 20 elderly

probands, we could not observe the expected oscillat-

ing behavior in the phase of landing. Nevertheless, an

inverse relationship between the calculated parameter

w and the jump height and an inverse relation to the

muscle strength could be determined. We could iden-

tify an inﬂuence of sex, weight, and w on the jump

height.

Furthermore, a potential correlation between

DPSI (as a common standard-index for balance) and

w was seen but could not be clearly clariﬁed due to

the limited group size. Thus, we will investigate these

effects in a further larger study.

Moreover, we considered in our model only

one dynamic mode (one modal mass and one fre-

quency). Using two-dimensional models of the mus-

HEALTHINF 2017 - 10th International Conference on Health Informatics

166

culoskeletal system (Blache and Monteil, 2013) or

even an anatomically realistic three-dimensional mus-

culoskeletal model (Farahani et al., 2016) could open

perspectives for more robust models.

ACKNOWLEDGEMENTS

The study is funded by the German Federal

Ministry of Education and Research (Project No.

01EL1422D). We would also like to thank Dr. Fabian

Sobotka for his support.

REFERENCES

Blache, Y. and Monteil, K. (2013). Effect of arm swing

on effective energy during vertical jumping: experi-

mental and simulation study. Scandinavian Journal of

Medicine & Science in Sports, 23(2):e121–e129.

Buehring, B., Krueger, D., Fidler, E., Gangnon, R., Heider-

scheit, B., and Binkley, N. (2015). Reproducibility of

jumping mechanography and traditional measures of

physical and muscle function in older adults. Osteo-

porosis International, 26(2):819–825.

Bui, H. T., Farinas, M.-I., Fortin, A.-M., Comtois, A.-

S., and Leone, M. (2015). Comparison and analysis

of three different methods to evaluate vertical jump

height. Clinical Physiology and Functional Imaging,

35(3):203–209.

Choukou, M.-A., Laffaye, G., and Taiar, R. (2014). Re-

liability and validity of an accelerometric system for

assessing vertical jumping performance. Biology of

Sport, 31(1):55.

Clegg, A., Young, J., Iliffe, S., Rikkert, M. O., and Rock-

wood, K. (2013). Frailty in elderly people. The

Lancet, 381(9868):752–762.

Cruz-Jentoft, A. J., Baeyens, J. P., Bauer, J. M., Boirie, Y.,

Cederholm, T., Landi, F., Martin, F. C., Michel, J.-P.,

Rolland, Y., Schneider, S. M., et al. (2010). Sarcope-

nia: European consensus on deﬁnition and diagnosis

report of the european working group on sarcopenia

in older people. Age and Ageing, 39:412423.

Dietzel, R., Felsenberg, D., and Armbrecht, G. (2015).

Mechanography performance tests and their associa-

tion with sarcopenia, falls and impairment in the ac-

tivities of daily living-a pilot cross-sectional study in

293 older adults. Journal of Musculoskeletal and Neu-

ronal Interactions, 15(3):249–256.

Elsawy, B. and Higgins, K. E. (2011). The geriatric assess-

ment. American Family Physician, 83(1):48–56.

Elvin, N. G., Elvin, A. A., and Arnoczky, S. P. (2007).

Correlation between ground reaction force and tibial

acceleration in vertical jumping. Journal of Applied

Biomechanics, 23(3):180.

Farahani, S. D., Andersen, M. S., de Zee, M., and Ras-

mussen, J. (2016). Optimization-based dynamic pre-

diction of kinematic and kinetic patterns for a human

vertical jump from a squatting position. Multibody

System Dynamics, 36(1):37–65.

Fransz, D. P., Huurnink, A., de Boode, V. A., Kingma, I.,

and van Die

en, J. H. (2015). Time to stabilization

in single leg drop jump landings: An examination of

calculation methods and assessment of differences in

sample rate, ﬁlter settings and trial length on outcome

values. Gait & Posture, 41(1):63–69.

Fudickar, S., Karth, C., Mahr, P., and Schnor, B. (2012).

Fall-detection simulator for accelerometers with in-

hardware preprocessing. In Proceedings of the 5th

International Conference on Pervasive Technologies

Related to Assistive Environments, page 41. ACM.

Granacher, U., Gollhofer, A., Hortob

agyi, T., Kressig,

R. W., and Muehlbauer, T. (2013). The importance

of trunk muscle strength for balance, functional per-

formance, and fall prevention in seniors: A systematic

review. Sports Medicine, 43(7):627–641.

Hein, A., Winkelbach, S., Martens, B., Wilken, O., Eichel-

berg, M., Spehr, J., Gietzelt, M., Wolf, K.-H.,

usching, F., H

ulsken-Giesler, M., et al. (2010). Mon-

itoring systems for the support of home care. Infor-

matics for Health and Social Care, 35(3-4):157–176.

Hellmers, S., Fudickar, S., B

use, C., Dasenbrock, L.,

Heinks, A., Bauer, J. M., and Hein, A. (2016). Tech-

nology supported geriatric assessment. In Ambient As-

sisted Living. Springer. (in press).

Hertel, J. (2002). Functional anatomy, pathomechanics, and

pathophysiology of lateral ankle instability. Journal of

Athletic Training, 37(4):364.

Kalyani, R. R., Corriere, M., and Ferrucci, L. (2014). Age-

related and disease-related muscle loss: the effect of

diabetes, obesity, and other diseases. The Lancet Dia-

betes & Endocrinology, 2(10):819–829.

Markovic, S., Mirkov, D. M., Nedeljkovic, A., and Jaric,

S. (2014). Body size and countermovement depth

confound relationship between muscle power output

and jumping performance. Human Movement Science,

33:203–210.

Meardon, S., Klusendorf, A., and Kernozek, T. (2016). In-

ﬂuence of injury on dynamic postural control in run-

ners. International Journal of Sports Physical Ther-

apy, 11(3):366.

Milosevic, B. and Farella, E. (2015). Wearable inertial sen-

sor for jump performance analysis. In Proceedings of

the 2015 Workshop on Wearable Systems and Appli-

cations, pages 15–20.

Nuzzo, J. L., McBride, J. M., Cormie, P., and McCaulley,

G. O. (2008). Relationship between countermovement

jump performance and multijoint isometric and dy-

namic tests of strength. The Journal of Strength &

Conditioning Research, 22(3):699–707.

Palma, S., Silva, H., Gamboa, H., and Mil-Homens, P.

(2008). Standing jump loft time measurement-an ac-

celeration based method. In Biosignals (2), pages

393–396.

Rittweger, J., Schiessl, H., Felsenberg, D., and Runge, M.

(2004). Reproducibility of the jumping mechanogra-

phy as a test of mechanical power output in physically

competent adult and elderly subjects. Journal of the

American Geriatrics Society, 52(1):128–131.

Understanding Jump Landing as an Oscillating System: A Model-based Approach of Balance and Strength Analyses

167

Samozino, P., Morin, J.-B., Hintzy, F., and Belli, A. (2008).

A simple method for measuring force, velocity and

power output during squat jump. Journal of Biome-

chanics, 41(14):2940–2945.

Siglinsky, E., Krueger, D., Ward, R. E., Caserotti, P.,

Strotmeyer, E. S., Harris, T. B., Binkley, N., and

Buehring, B. (2015). Effect of age and sex on jumping

mechanography and other measures of muscle mass

and function. Journal of Musculoskeletal & Neuronal

Interactions, 15(4):301.

Steen, E.-E., Frenken, T., Eichelberg, M., Frenken, M., and

Hein, A. (2013). Modeling individual healthy behav-

ior using home automation sensor data: Results from a

ﬁeld trial. Journal of Ambient Intelligence and Smart

Environments, 5(5):503–523.

Wakeling, J. M., Von Tscharner, V., Nigg, B. M., and Ster-

giou, P. (2001). Muscle activity in the leg is tuned in

response to ground reaction forces. Journal of Applied

Physiology, 91(3):1307–1317.

Wikstrom, E., Tillman, M., and Borsa, P. (2005a). Detec-

tion of dynamic stability deﬁcits in subjects with func-

tional ankle instability. Medicine & Science in Sports

& Exercise, 37(2):169–175.

Wikstrom, E., Tillman, M., Smith, A., and Borsa, P.

(2005b). A new force-plate technology measure of

dynamic postural stability: the dynamic postural sta-

bility index. Journal of Athletic Training, 40(4):305–

309.

HEALTHINF 2017 - 10th International Conference on Health Informatics

168