Impact of Feature Extraction and Feature Selection Techniques on
Extended Attribute Profile-based Hyperspectral Image Classification
Rania Zaatour, Sonia Bouzidi and Ezzeddine Zagrouba
Research team SIIVA, LIMTIC laboratory, Higher Institute of Computer Science (ISI), University of Tunis El Manar,
2 Street Abou Rayhane Bayrouni, 2080 Ariana, Tunisia
Keywords:
Dimensionality Reduction, Principal Component Analysis (PCA), Local Fisher Discriminant Analysis
(LFDA), Independent Component Analysis-based Band Selection, Extended MultiAttribute Profile (EMAP),
Hyperspectral Image Classification.
Abstract:
Extended multiattribute profiles (EMAPs) were introduced as morphological profiles built on the features of a
hyperspectral image extracted using Principal Component Analysis (PCA). In this paper, we propose to replace
PCA with other dimensionality reduction techniques. First, we replace it with Local Fisher Discriminant
Analysis (LFDA), a supervised locality preserving DR method. Second, we replace it with two band selection
techniques: ICAbs, an Independent Component Analysis (ICA) based band selection, and its modified version
that we propose in this article and which we are calling mICAbs. In the experimental part of this paper, we
compare the accuracies of classifying the sparse representations of the EMAPs built on features obtained
using each of the aforementioned dimensionality reduction techniques. Our experiments reveal that LFDA
gives, amongst all, the best classification accuracies. Besides, our proposed modification gives comparable to
higher accuracies.
1 INTRODUCTION
Hyperspectral remote sensing images (HSI) are data
cubes formed out of hundreds of tight correlated spec-
tral bands. This type of data offers rich spectral and
spatial information permitting a better distinction of
the objects contained in the acquired scene, which
leads to higher classification accuracies.
Most of the traditional HSI classification tech-
niques exploit only the spectral information provided
by the image. But, given the richness of the informa-
tion offered by HSIs, it is obvious that combining both
spectral and spatial information delivers more accu-
rate classification results.
A few years ago, Extended MultiAttribute Pro-
files (EMAP) (Dalla Mura et al., 2010) have been in-
troduced as morphological profiles allowing the ex-
traction of both spatial and spectral information from
HSIs.
Since first introduced, EMAPs were tested in sev-
eral HSI classification tasks through which it has been
proven that they enable the detailed modeling of the
structural information of an image’s objects while
preserving the geometrical information as well as the
spectral information of the data (Dalla Mura et al.,
2010; Dalla Mura et al., 2011; Song et al., 2014; Li
et al., 2014). This modeling depends on the type of at-
tributes used to compute the EMAPs and therefore no
prior knowledge of the processed image is required.
This morphological profile is defined as the con-
catenation of a set of images generated after filter-
ing the features of a reduced HSI. These features
are obtained after applying a dimensionality reduction
method, as a preliminary step, to the given HSI.
Dimensionality reduction techniques are destined
to lower the processing time and complexity, by min-
imizing the redundancy and reducing the hundreds of
bands, while assuring to keep most of the information
required to guarantee the effectiveness of the task to
perform. To do so, dimensionality reduction methods
act in one of the following ways: (a) extracting fea-
tures, or (b) selecting features.
Feature extraction methods decorrelate the HSI’s
information and eliminate its redundancy by project-
ing the original data on a new lower-dimensional fea-
ture space, and then selecting the first few relevant
features that contain most of the information in the
data. On the other hand, feature selection techniques
select a subset from the original data cube. These
methods reduce the highly-dimensional data without
Zaatour R., Bouzidi S. and Zagrouba E.
Impact of Feature Extraction and Feature Selection Techniques on Extended Attribute Profile-based Hyperspectral Image Classification.
DOI: 10.5220/0006171305790586
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 579-586
ISBN: 978-989-758-225-7
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
579

changing its features. Interestingly enough, some fea-
ture selection techniques relate to feature extraction
methods to select the most relevant bands.
When it comes to reducing the HSI’s dimension-
ality before building its EMAP, only feature extrac-
tion techniques were used in the literature. When first
introduced, EMAP was defined as a morphological
profile built upon the first few principle components
(PC) generated by PC Analysis (PCA) (Dalla Mura
et al., 2010). This feature extraction method is the
most commonly used technique to reduce HSI before
building their EMAP.
Other than PCA, in the literature, EMAPs were
built on the features obtained using other feature
extraction techniques such as Independent Compo-
nents Analysis (ICA) (Dalla Mura et al., 2011), Dis-
criminant Analysis Feature Extraction (DAFE), De-
cision Boundary Feature Extraction (DBFE), and
Nonparametric Weighted Feature Extraction (NWFE)
(Ghamisi et al., 2014).
The only way where feature selection techniques
were used in the context of classifying HSIs using
their EMAP, was to reduce the profile built using all
the original bands of the given image. Hence, in this
case, we are generating a huge profile and then we
are selecting the most representative features that will
enhance the classification process.
Some of the feature selection techniques used for
this purpose, mostly based on genetic algorithms, can
be found in (Pedergnana et al., 2013; Ghamisi and
Benediktsson, 2015; Tuia et al., 2014).
In this paper, we are interested in the HSI dimen-
sionality reduction prior to the generation of EMAPs.
For this purpose, we are proposing the use of three
dimensionality reduction techniques that, to the au-
thors’ knowledge, were never used in such context.
First, we propose to use Local Fisher Discriminant
Analysis (LFDA) instead of the most common PCA.
Since EMAPs are computed based on the connected
components of an original or transformed HSI, and
since LFDA accounts for locality, we believe that the
use of this feature extraction method will help gener-
ating more representative EMAPs. Moreover, LFDA
overcomes the limitations of PCA as (a) it is super-
vised and (b) it discards the assumption of a Gaussian
distribution of the data. Consequently, we strongly
believe that this dimensionality reduction technique
would give better results than the traditional PCA.
Second, we investigate the efficiency of feature se-
lection techniques to reduce the HSI dimensionality
prior to the generation of EMAPs. We are particularly
interested in a feature selection method that exploits
the transformation matrix of a feature extraction tech-
nique, namely ICA. This ICA-based band selection
technique, hereinafter referred to as ICAbs, selects the
bands that contribute the most to the ICA transforma-
tion. To do so, ICAbs evaluates ICA’s unmixing ma-
trix and selects the bands having the highest absolute
average coefficient.
Moreover, in this article, we propose a new fea-
ture selection technique consisting in a slightly mod-
ified version of ICAbs. This new method that we are
calling mICAbs, like modified ICAbs, is the same as
the original band selection technique, except the fact
that each one of them uses its own criterion to decide
of the bands to be selected.
All the aforementioned dimensionality reduction
techniques will be compared in the same HSI classi-
fication context using a sparse representation classi-
fication framework. These methods will be evaluated
according to the classification accuracies we get when
using them.
The rest of the paper is structured as follows: first,
in section 2, we describe how to build an EMAP and
how to use it in a HSI classification task based on
sparse representations. Section 3 recalls the bases
of PCA and LFDA and theoretically compares them.
Section 4 details the algorithm of the original ICA-
based band selection and introduces our proposed
modification. Section 5 describes the used HSI and
performs a comparison of the studied dimensionality
reduction techniques. Finally, section 6 concludes the
article.
2 HSI CLASSIFICATION USING
EMAP SPARSE
REPRESENTATION
In this section, we represent the way an EMAP is
generated, and we introduce the sparse classification
framework we will be using in the experimental part.
2.1 Extended Multi-Attribute Profile
(EMAP)
We can think of an EMAP as a cube of grayscale
images resulting from the application of attribute fil-
ters to the connected components of every feature se-
lected/extracted from a HSI.
Attribute filters proceed depending on whether an
attribute A (e.g., area, standard deviation, moment of
inertia) computed on a connected component C
i
of the
concerned feature meets a predefined condition on a
threshold value λ (e.g., A(C
i
) > λ). If A(C
i
) meets
the condition, C
i
is kept unaltered. Otherwise, it is
merged to the nearest connected component having a
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
580

lower (respectively greater) gray level, and this merg-
ing is called thinning γ (respectively thickening φ).
If we apply several thickenings and thinnings to
the same feature f using a set of ordered thresholds
{λ
1
, ...,λ
n
}, we obtain an Attribute Profile (AP):
AP( f ) = {φ
n
( f ), ..., φ
1
( f ), f , γ
1
( f ), ..., γ
n
( f )} (1)
Since a reduced HSI rh is a stack of r features,
concatenating the APs generated from every feature f
i
leads us to the definition of Extended Attribute Profile
(EAP):
EAP(rh) = {AP( f
1
), AP( f
2
), ..., AP( f
r
)} (2)
If we decide to use multiple attributes and gener-
ate an EAP based on each one of them, the concatena-
tion of the generated profiles is the so called EMAP.
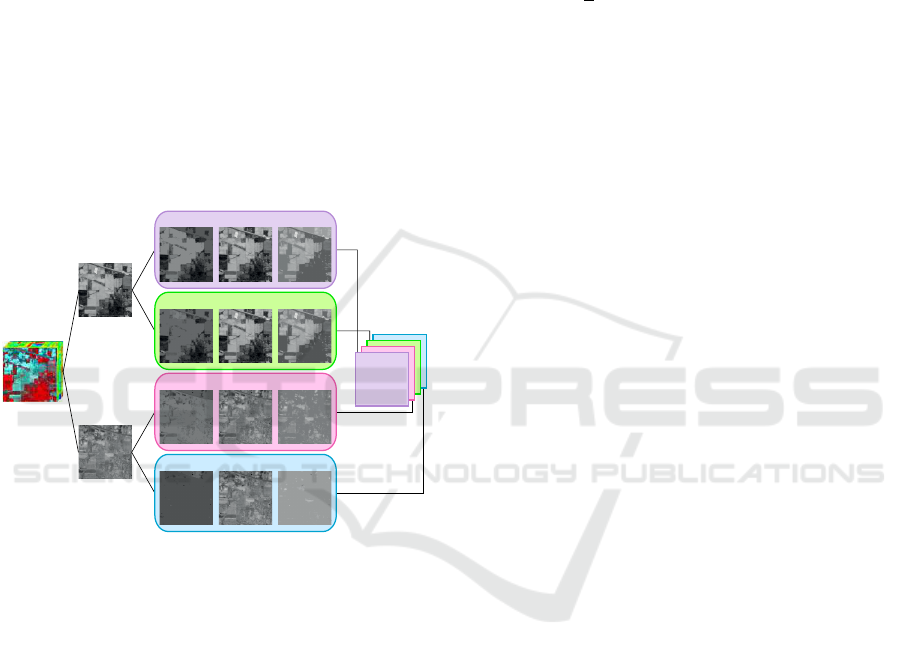
Fig. 1 summarizes the above mentioned steps of
building an EMAP.
EMAP
Reduced HSI
Feature 1
Feature 2
AP using attribute A1
AP using attribute A2
AP using attribute A1
AP using attribute A2
Figure 1: Simplified process of building an EMAP using a
2-feature reduced HSI and only 2 attributes.
2.2 Sparse Classification Framework
We chose to compare the studied DR techniques
through a classification task using a sparse represen-
tation classification framework to better represent the
highly dimensioned EMAPs.
Let D ∈ R
a×l
be a training dictionary made of a
l-dimensional atoms representing c classes such that
D = {d
1
, ..., d
a
} = {D
1
, ..., D
c
}, where D
k
contains
the a
k
samples of class k, and
∑
c
k=1
a
k
= a. Consid-
ering that a signal y can be represented by a linear
combination of D’s atoms, we have :
y ≈ d
1
x
1
+ ... + d
a
x
a
= [d
1
, ..., d
a
][x
1
, ..., x
a
]
>
= Dx + ε
(3)
where ε is the representation error and x =
[x
1
, ..., X
a
]
>
= [X
>
1
, ..., X
>
c
]
>
is a sparse a-dimensional
vector whose every value X
i
is the regression coeffi-
cients vector of the class i. If y belongs to class i,
we assume that it is well approximated by D
i
X
i
(Song
et al., 2014; Chen et al., 2011). Then, x is a sparse
vector where X
j
= 0 ∀ j 6= i.
To classify a signal y, we need to find an approxi-
mation of the sparse vector x subject to y = Dx +ε by
solving the following constrained optimization prob-
lem:
min
x
1
2
k
y − Dx
k
2
2
+ τ
k
x
k
1
, x ≥ 0 (4)
where τ is a Lagrange multiplier, which tends to 0
when ε tends to 0.
In our context, the dictionary’s atoms are EMAPs
of randomly selected samples from each class and y
is the EMAP of the current pixel to be classified. The
whole classification process consists in attributing to
the current pixel, whose EMAP is y, the class label
of the dictionary’s atom that has the highest non-null
coefficient in the approximated x.
3 PRINCIPAL COMPONENT
ANALYSIS VS. LOCAL FISHER
DISCRIMINANT ANALYSIS
Generally, the conventional feature extraction tech-
nique used to reduce HSIs is Principal Component
Analysis (PCA) (Hotelling, 1933). This unsupervised
second-order statistics-based method transforms the
original bands, using a linear combination, into decor-
related and variance maximizing Principle Compo-
nents (PC), then, the first few r PCs are selected.
These extracted features, and since they represent
most of the information that the original data offer,
were exploited to build EMAPs, when this profile was
introduced and in most cases where it was used after-
ward.
Nevertheless, in certain cases, when used prior
to classification, PCA may fail to reduce the dimen-
sions while keeping all the useful and representative
information. This is due to the facts that (a) PCA
assumes that class distribution is Gaussian although
real-life data is more likely to have a complex mul-
timodal distribution (Mart
´
ınez and Kak, 2001), (b) it
tends to omit some information that might be useful
to the classification process (Prasad and Bruce, 2008)
and (c) due to its unsupervised nature, PCA does not
count for class labels and thus, might lead to a more
complex class separability (Varghese et al., 2012).
A feature extraction technique that claims over-
coming these limitations is the Local Fisher Dis-
criminant Analysis (LFDA). It was introduced in
(Sugiyama, 2007) as the combination of two well
Impact of Feature Extraction and Feature Selection Techniques on Extended Attribute Profile-based Hyperspectral Image Classification
581

known dimensionality reduction techniques: Fisher
Discriminant Analysis (FDA) (Fisher, 1936) and Lo-
cality Preserving Projection (LPP) (Niyogi, 2004).
LFDA can be thought of as a localized version of
FDA where multimodal input data are handled effec-
tively and the local structure of nearby samples in the
original space is preserved (Li et al., 2012).
Let X = {x
1
, x
2
, ....., x
p
}, x
i
∈ R
n
be a set of p sam-
ples and y
i
∈ {1, 2, ...., c} be the class labels, where c
represents the total number of classes and p
l
repre-
sents the number of samples of class l (
∑
c
l=1
p
l
= p).
LFDA computes a local between-class scatter matrix
S
lb
and a local within-class scatter matrix S
lw
defined
respectively in (5) and (6).
S
lb
=
1
2
p
∑
i, j=1
W
lb
i, j
(x
i
− x
j
)(x
i
− x
j
)
>
(5)
S
lw
=
1
2
p
∑
i, j=1
W
lw
i, j
(x
i
− x
j
)(x
i
− x
j
)
>
(6)
where W
lb
and W
lw
are p × p matrices, respectively
defined as in (7) and (8), using A
i, j
which is the p ×
p LPP affinity matrix that characterizes the distance
between data samples.
W
lb
i, j
=







A
i, j
(
1
p
−
1
p
l
) i f y
i
= y
j
= l,
1
p
i f y
i
6= y
j
,
(7)
W
lw
i, j
=



A
i, j
p
l
i f y
i
= y
j
= l,
0 i f y
i
6= y
j
.
(8)
Using both the local between-class and the local
within-class scatter matrices, defining LFDA’s trans-
formation matrix, T , is reduced to the maximization
of an objective function, as shown in (9).
T = argmax[tr((T
>
S
lw
T )
−1
T
>
S
lb
T )]
(9)
where T ∈ R
n×r
and r is the new reduced dimension.
4 ICA-BASED BAND SELECTION
TECHNIQUES
In order to generate the final independent components
(IC), IC Analysis (ICA) defines a transformation ma-
trix that unmixes the original signal sources based on
their statistical independency measured by mutual in-
formation (Wang and Chang, 2006).
Let S be the original set of mixed source signals.
ICA aims at separating these signals in order to pro-
vide a new set of statistically independent sources X.
To do so, ICA searches for an unmixing matrix U,
such that:
X = US (10)
When ICA is used as a HSI DR technique, S is an
n × p matrix referring to the concerned HSI contain-
ing n bands and p pixels. On the other hand, X refers
to the reduced r × p set of the resulting ICs. There-
fore, U is an r × n matrix, where:
x
i j
=
n
∑
k=1
u
ik
s
k j
, i = 1, ..., r, j = 1, ..., p (11)
If we consider that u
ik
is the weight of informa-
tion the k
th
band is containing regarding to the i
th
IC,
u
k
= [u
1k
, ..., u
rk
] is then the vector of contributions
of the k
th
band to the ICA transformation. From this
assumption, the ICA-based band selection technique
we mentioned earlier in the introduction (Du et al.,
2003), hereinafter referred to as ICAbs, looks for the
bands having the higher average absolute weight ¯u
k
given in (12), and selects them for having the highest
contribution to the ICA transformation.
¯u
k
=
1
r
r
∑
i=1
|u
ik
| (12)
In this paper, we are proposing a modified version
of ICAbs. This technique that we will call mICAbs,
like modified ICAbs, will follow the same steps as the
original method. What we are changing is the crite-
rion according to which we will be considering that
a band is having a higher contribution than an other
one. Instead of looking for the bands having the high-
est average absolute weight, we will look for those
having the highest entropy.
This information theory concept is a statistical
measure of randomness that is related to the amount
of information a random variable is containing: the
higher the entropy is, the larger the amount of infor-
mation in the data is (Bajcsy and Groves, 2004). Our
choice of the entropy is encouraged by the fact that
ICA already uses it to define its ICs. Then, as long as
we are concerned, we believe that the use of entropy
will ameliorate the band selection process.
So, our proposed approach is to replace (12) by
(13), where we calculate the entropy of the contribu-
tion vector u
k
instead of its average absolute weight.
Eu
k
= Entropy(u
k
) = −
r
∑
i=1
p(u
ik
) log p(u
ik
) (13)
where p(u
ik
) represents the mass probability of
an event u
ik
from a finite set of possible values
(Mart
´
ınez-Us
´
o et al., 2007) .
Once the entropy of every contribution vector u
k
is computed, we obtain a sequence of band contribu-
tion’s entropies defined in (14).
[Eu
1
, ..., Eu
k
, ..., Eu
n
] (14)
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
582

Each Eu
k
of this sequence tells how informative
the contribution of the k
th
band to ICA’s transforma-
tion matrix is. Hence, selecting the bands having the
same indexes as those of the highest elements in this
sequence is equivalent to selecting the bands that con-
tribute the most to the ICA’s transformation.
5 EXPERIMENTAL RESULTS
This experimental section is organized as follows.
First, we compare the accuracies of classifying
EMAPs built upon features extracted by LFDA to the
ones obtained using features extracted by PCA. Then,
we compare the accuracies of classifying EMAPs
built upon bands selected by ICAbs to the ones ob-
tained using bands selected by mICAbs.
In our context, EMAPs are built using the reduced
data which is rescaled to the range [0, 255] and con-
verted to integers before applying the AFs. The em-
ployed attributes are (a) area, which measure the size
of regions, using threshold values ranging from 50 to
500 with a stepwise increment of 50, and (b) standard
deviation, which measures the homogeneity of the
pixels in every region, using threshold values rang-
ing from 2.5% to 20% with a stepwise increment of
2.5%.
The dictionary is made of the EMAPs of 10% of
every class’ total samples. In order to guarantee a
maximum of equal chances to all compared methods,
all the dictionaries used in this experimental part are
made of the EMAPs of the same randomly selected
pixels.
In the literature, it has been proven that Sparse
UNmixing by variable Splitting and Augmented La-
grangian (SUnSAL) is more efficient at solving equa-
tion (4) than other classifiers (Song et al., 2014). For
this reason, and since our aim is to compare the DR
methods and not the classification process, we will be
using only SUnSAL for our experiments.
The HSI we used to test our approach is
the well known hyperspectral image captured by
the Airborne Visible/Infrared Imaging Spectrometer
(AVIRIS) over the Indian Pines region situated in the
Northwest of Indiana, USA, in june 1992. This im-
age, known as AVIRIS Indian Pines
1
, is composed of
145 × 145 pixels and 220 spectral bands which have
been reduced to 200 bands in order to avoid both noise
and water absorption phenomena. Fig. 2 shows the
AVIRIS Indian Pines’ ground truth with it’s corre-
sponding color legend.
1
Available online at https://purr.purdue.edu/
publications/1947/1
Alfalfa
Buildings-Grass-Trees-Drives
Stone-Steel-Towers
Soybean-clean
Soybean-mintillSoybean-notill
Corn Corn-notill
WoodsWheatHay-windrowed
OatsCorn-mintill Grass-pasture
Grass-trees Grass-pasture-mowed
Figure 2: Ground truth of the AVIRIS Indian Pines.
In order to evaluate the effectiveness of the clas-
sification process we used the following metrics: the
average accuracy (AA), the overall accuracy (OA) and
the average reliability (AR).
5.1 Comparison of Classification
Results using LFDA and PCA
Fig. 3 illustrates the AAs we got using PCA and
LFDA, according to the variation of the number of
extracted features.
5 10 15 20 25 30 35 40 45 50
Reduced dimensions
84
86
88
90
92
94
96
Average Accuracy
LFDA
PCA
Figure 3: Average accuracy (AA) using LFDA and PCA
according to DR variation.
From Fig. 3, we can deduce that LFDA outper-
forms PCA in all the tested cases. The gap between
the AAs of both techniques rises as the number of kept
features rises, and reaches up to 7.9% when EMAPs
are built upon 50 features.
Furthermore, we can remark that LFDA is less
sensitive to the curse of dimensionality. This curse,
also known as Hughes Phenomenon (Hughes, 1968),
consists in the fact that the higher the number of fea-
tures is, the lower the classification accuracy is.
In Fig. 4, we can deduce that both feature ex-
traction techniques give very close OAs when using a
small number of features. Besides, PCA outperforms
LFDA in some cases. But, starting from 20 features,
LFDA mostly keeps its high accuracies while the OAs
obtained using PCA decline.
When using a small number of features, we can
remark that the AAs and OAs give opposite behav-
iors. In fact, when LFDA gives higher AA, PCA gives
Impact of Feature Extraction and Feature Selection Techniques on Extended Attribute Profile-based Hyperspectral Image Classification
583

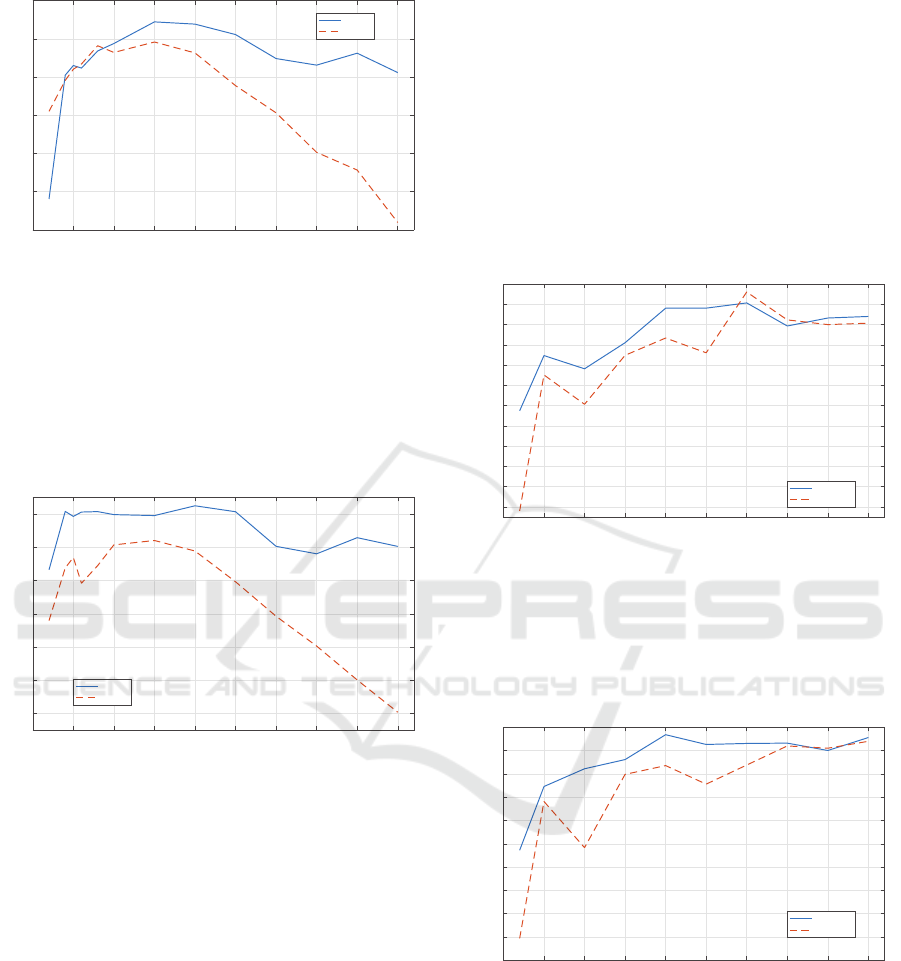
5 10 15 20 25 30 35 40 45 50
Reduced dimensions
88
89
90
91
92
93
94
Overall Accuracy
LFDA
PCA
Figure 4: Overall accuracy (OA) using LFDA and PCA ac-
cording to DR variation.
higher OA. This can be explained by the fact that PCA
gives better representations of larger classes, and so
gives a better OA, while LFDA gives a good represen-
tation of both small and large areas, and that is why it
has a better AA.
According to Fig. 5, LFDA is more reliable than
PCA in all the tested cases.
5 10 15 20 25 30 35 40 45 50
Reduced dimensions
90
91
92
93
94
95
96
Average Reliability
LFDA
PCA
Figure 5: Average reliability (AR) using LFDA and PCA
according to DR variation.
To conclude this part of the experimentation,
we can assert that LFDA enhances the accuracy of
EMAP-based HSI classification, when used, instead
of the most commonly used PCA, to reduce HSI’s di-
mensionality prior to generating its EMAP.
5.2 Comparison of Classification
Results using ICA-based Band
Selection Techniques
In this part of the experimentation, we evaluate and
compare ICAbs and our proposed mICAbs as feature
selection techniques used to reduce HSI’s dimension-
ality prior to the generation of EMAPs.
We can already assume that the results we will
be getting using feature selection techniques would
not be as accurate as the ones obtained with the fea-
ture extraction ones. This is due to the fact that fea-
ture extraction transformations exploit the whole orig-
inal data in order to extract the most pertinent fea-
tures. However, feature selection techniques select
the bands as they are without altering them or con-
solidating them.
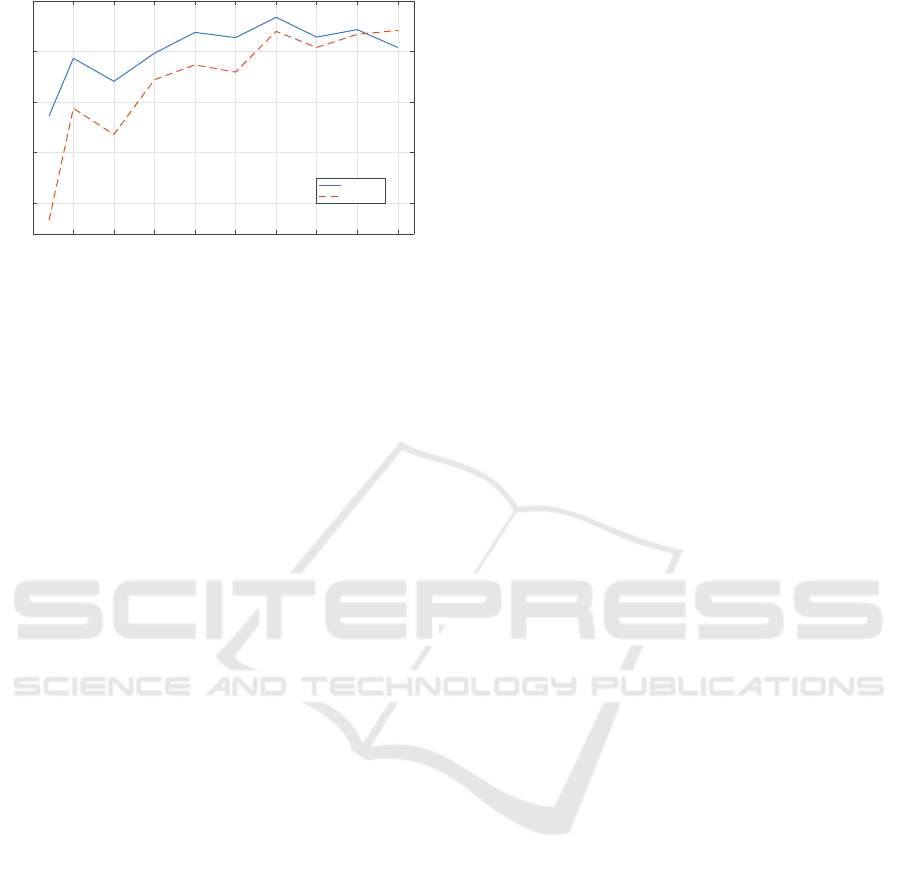
Fig. 6 illustrates the AAs obtained using both
ICA-based band selection techniques. We can deduce
that both methods give comparable accuracies, with
mICAbs giving better results in most of the tested
cases. This improvement is measured by a difference
reaching up to 4.4%.
5 10 15 20 25 30 35 40 45 50
Reduced dimensions
70
72
74
76
78
80
82
84
86
88
90
92
Average Accuracy
mICAbs
ICAbs
Figure 6: Average accuracy (AA) using ICAbs and mICAbs
according to DR variation.
The same conclusion can be made from compar-
ing the OAs, shown in Fig. 7, where mICAbs en-
hances the accuracy by a difference reaching up to
6.8%,
5 10 15 20 25 30 35 40 45 50
Reduced dimensions
72
74
76
78
80
82
84
86
88
90
92
Overall Accuracy
mICAbs
ICAbs
Figure 7: Average accuracy (OA) using ICAbs and mICAbs
according to DR variation.
Moreover, Fig. 8 confirms one more time that both
ICA-based band selection techniques give very close
results with mICAbs outperforming ICAbs in most of
the studied cases.
Besides, we can conclude that with both feature
selection techniques, unlike with feature extraction
ones, the classification is not affected by the curse of
dimensionality. That is to say, we do not notice a high
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
584

5 10 15 20 25 30 35 40 45 50
Reduced dimensions
75
80
85
90
95
Average Reliability
mICAbs
ICAbs
Figure 8: Average accuracy (AR) using ICAbs and mICAbs
according to DR variation.
decreasing in accuracies when using a higher number
of features (selected bands in this case).
This might be explained by the fact that, when us-
ing feature selection techniques, we are selecting the
most representative bands from a highly correlated
and redundant data. Thus, we are selecting bands that
are not necessarily very similar, and consequently, we
are minimizing the redundancy. Instead, in the fea-
ture extraction context, we are generating features that
accumulate most of the information contained in the
original data. Then, we will have a high redundancy
since we are trying to put the maximum of informa-
tion in each feature.
It is worth noting that the obtained accuracies
show a lot of tops and bottoms, unlike the ones
we got in the feature extraction case, which tend
to be monotonous. In fact, in every application,
LFDA/PCA apply the same transformation to the
original data and rank the features according to the
information they hold. Hence, using a bigger number
of reduced dimensions is equivalent to keeping the old
features and adding new ones so that the new set holds
even more information.
In contrast, the feature selection techniques we
used here are based on ICA which, when defining its
unmixing matrix, starts with random initial projection
vectors. Due to this randomness, the ICA transfor-
mation is not the same at every run. Therefore, the
mICAbs to ICAbs comparisons made above are not
based on the same unmixing matrix.
In fact, at every execution, a new ICA transforma-
tion matrix is defined and then the selection process
is made according to this matrix. Consequently, when
selecting bands from the Indian Pines, whether using
ICAbs or mICAbs, we will not be getting the same
exact set of bands at every run neither, therefore, the
same accuracy. This latter may rise or fall according
to the used ICA transformation matrix, which can ex-
plain the changing accuracies we had in the last three
figures.
6 CONCLUSION
In this paper, we proposed to replace PCA, the com-
mon feature extraction technique used to reduce a
HSI’s dimensionality before generating its EMAP, by
other dimensionality reduction techniques.
On one hand, as a feature extraction technique, we
proposed the use of LFDA which proved to be, ac-
cording to the experimental results, better than PCA.
This might be explained by the fact that LFDA takes
into consideration both the locality and the class la-
bels in order to maximize the between-class variance
while minimizing the within-class variance. Thus,
LFDA gives a reduced version of the image where
classes are easily discriminated.
On the other hand, we explored the effectiveness
of some feature selection techniques in the same con-
text. In fact, we proposed to replace PCA with two
ICA-based band selection methods: ICAbs, which is
existent in the literature, and mICAbs, our proposed
modified version of ICAbs.
Both feature selection techniques are based on the
unmixing matrix of ICA. The only difference between
them is the criterion according to which bands are se-
lected: ICAbs is based on the average absolute con-
tribution and mICAbs is based on the entropy of con-
tributions.
Both used feature selection techniques proved to
give close results that are not as good as those we get
when using feature extraction techniques. Moreover,
our proposed mICAbs proved to enhance the classifi-
cation accuracy, compared to the original ICAbs.
ACKNOWLEDGEMENT
The authors would like to thank Mr. Mauro Dalla
Mura for providing the AP implementation.
REFERENCES
Bajcsy, P. and Groves, P. (2004). Methodology for hyper-
spectral band selection. Photogrammetric Engineer-
ing & Remote Sensing, 70(7):793–802.
Chen, Y., Nasrabadi, N. M., and Tran, T. D. (2011). Hyper-
spectral image classification using dictionary-based
sparse representation. IEEE Transactions on Geo-
science and Remote Sensing, 49(10):3973–3985.
Dalla Mura, M., Benediktsson, J. A., Waske, B., and Bruz-
zone, L. (2010). Extended profiles with morpho-
logical attribute filters for the analysis of hyperspec-
tral data. International Journal of Remote Sensing,
31(22):5975–5991.
Impact of Feature Extraction and Feature Selection Techniques on Extended Attribute Profile-based Hyperspectral Image Classification
585

Dalla Mura, M., Villa, A., Benediktsson, J. A., Chanus-
sot, J., and Bruzzone, L. (2011). Classification of hy-
perspectral images by using extended morphological
attribute profiles and independent component analy-
sis. IEEE Geoscience and Remote Sensing Letters,
8(3):542–546.
Du, H., Qi, H., Wang, X., Ramanath, R., and Snyder, W. E.
(2003). Band selection using independent component
analysis for hyperspectral image processing. In Ap-
plied Imagery Pattern Recognition Workshop, 2003.
Proceedings. 32nd, pages 93–98. IEEE.
Fisher, R. A. (1936). The use of multiple measurements in
taxonomic problems. Annals of eugenics, 7(2):179–
188.
Ghamisi, P. and Benediktsson, J. A. (2015). Feature selec-
tion based on hybridization of genetic algorithm and
particle swarm optimization. IEEE Geoscience and
Remote Sensing Letters, 12(2):309–313.
Ghamisi, P., Benediktsson, J. A., and Sveinsson, J. R.
(2014). Automatic spectral–spatial classification
framework based on attribute profiles and supervised
feature extraction. IEEE Transactions on Geoscience
and Remote Sensing, 52(9):5771–5782.
Hotelling, H. (1933). Analysis of a complex of statistical
variables into principal components. Journal of Edu-
cational Psychology, 24.
Hughes, G. P. (1968). On the mean accuracy of statistical
pattern recognizers. Information Theory, IEEE Trans-
actions on, 14(1):55–63.
Li, J., Zhang, H., and Zhang, L. (2014). Supervised seg-
mentation of very high resolution images by the use of
extended morphological attribute profiles and a sparse
transform. IEEE Geoscience and Remote Sensing Let-
ters, 11(8):1409–1413.
Li, W., Prasad, S., Fowler, J. E., and Bruce, L. M.
(2012). Locality-preserving dimensionality reduction
and classification for hyperspectral image analysis.
IEEE Transactions on Geoscience and Remote Sens-
ing, 50(4):1185–1198.
Mart
´
ınez, A. M. and Kak, A. C. (2001). Pca versus lda. Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, 23(2):228–233.
Mart
´
ınez-Us
´
o, A., Pla, F., Sotoca, J. M., and Garc
´
ıa-Sevilla,
P. (2007). Clustering-based hyperspectral band selec-
tion using information measures. IEEE Transactions
on Geoscience and Remote Sensing, 45(12):4158–
4171.
Niyogi, X. (2004). Locality preserving projections. In Neu-
ral information processing systems, volume 16, page
153. MIT.
Pedergnana, M., Marpu, P. R., Dalla Mura, M., Benedik-
tsson, J. A., and Bruzzone, L. (2013). A novel tech-
nique for optimal feature selection in attribute profiles
based on genetic algorithms. IEEE Transactions on
Geoscience and Remote Sensing, 51(6):3514–3528.
Prasad, S. and Bruce, L. M. (2008). Limitations of principal
components analysis for hyperspectral target recogni-
tion. IEEE Geoscience and Remote Sensing Letters,
5(4):625–629.
Song, B., Li, J., Dalla Mura, M., Li, P., Plaza, A., Bioucas-
Dias, J. M., Benediktsson, J. A., and Chanussot, J.
(2014). Remotely sensed image classification using
sparse representations of morphological attribute pro-
files. IEEE transactions on geoscience and remote
sensing, 52(8):5122–5136.
Sugiyama, M. (2007). Dimensionality reduction of multi-
modal labeled data by local fisher discriminant anal-
ysis. The Journal of Machine Learning Research,
8:1027–1061.
Tuia, D., Volpi, M., Dalla Mura, M., Rakotomamonjy, A.,
and Flamary, R. (2014). Automatic feature learn-
ing for spatio-spectral image classification with sparse
svm. IEEE Transactions on Geoscience and Remote
Sensing, 52(10):6062–6074.
Varghese, N., Verghese, V., Gayathri, P., and Jaisankar, N.
(2012). A survey of dimensionality reduction and
classification methods. International Journal of Com-
puter Science and Engineering Survey, 3(3):45.
Wang, J. and Chang, C.-I. (2006). Independent component
analysis-based dimensionality reduction with applica-
tions in hyperspectral image analysis. IEEE transac-
tions on geoscience and remote sensing, 44(6):1586–
1600.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
586