
Pose Interpolation for Rolling Shutter Cameras using Non Uniformly
Time-Sampled B-splines
Bertrand Vandeportaele
1
, Philippe-Antoine Gohard
1,2
, Michel Devy
1
and Benjamin Coudrin
2
1
LAAS-CNRS, Universit
´
e de Toulouse, CNRS, UPS, Toulouse, France
2
Innersense, Ramonville-Saint-Agne, France
{bertrand.vandeportaele, philippe-antoine.gohard, michel.devy}@laas.fr, benjamin.coudrin@innersense.fr
Keywords:
Rolling Shutter, Camera Geometric Model, Perspective n-Points Algorithm, Simultaneous Localization and
Mapping, B-splines interpolation.
Abstract:
Rolling Shutter (RS) cameras are predominant in the tablet and smartphone market due to their low cost and
small size. However, these cameras require specific geometric models when either the camera or the scene is
in motion to account for the sequential exposure of the different lines of the image. This paper proposes to
improve a state-of-the-art model for RS cameras through the use of Non Uniformly Time-Sampled B-splines.
This allows to interpolate the pose of the camera taking into account the varying dynamic of the motion by
adding more control points where needed while keeping a low number of control points where the motion is
smooth. Two methods are proposed to determine adequate distributions for the control points, using either an
IMU sensor or an iterative reprojection error minimization. Results on simple synthetic data sets are shown to
prove the concept and future works are introduced that should lead to the integration of our model in a SLAM
algorithm.
1 INTRODUCTION
In Augmented Reality applications for mobile devices
(smartphones and tablets), the realtime localization of
the device camera and the 3D modeling of the envi-
ronment are used to integrate virtual elements onto
the images of the real environment. This task is
usually performed by algorithms of Structure From
Motion (SFM: (Hartley and Zisserman, 2004)), and
Simultaneaous Localization and Mapping (SLAM:
MonoSLAM(Davison, 2003), PTAM(Klein and Mur-
ray, 2007) OrbSLAM (Mur-Artal et al., 2015)). Most
existing implementations assume that the cameras are
using a Global Shutter (GS), for which all the lines of
the image are exposed at the same time, ie. the image
is a projection of the scene at one instant t.
However, more than 90% of mobile devices are
equipped with Rolling Shutter (RS) cameras because
of their lower cost and smaller size than the classic GS
cameras. The advantages of RS cameras come with
some drawbacks; by the way they are designed, they
cause image distortions when observing a dynamic
scene or when the camera is moving. In these sensors,
all the lines of the image are exposed and transferred
sequentially at different times.
More complex geometric models are thus required
for RS cameras, to account for the the varying pose of
the camera. This paper extends the RS Camera model
presented in(Steven Lovegrove, 2013) and (Patron-
Perez et al., 2015) for the camera pose interpolation
using B-splines controlled by Control Points (CP) that
are Uniformly Distributed (UD) in time. Our im-
provement of the model consists in using an adaptive
Non Uniform Distribution (NUD) of the CP of the B-
spline over time. This allows to globally reduce the
number of CP required to model a given trajectory
with the same accuracy than using UD.
The paper firstly presents existing SLAM algo-
rithms and exhibits problems arising from using im-
ages captured with RS cameras. It then presents the
theoretical framework used for the modeling of the
RS cameras. First, the cumulative B-splines are in-
troduced to allow the interpolation of 6-dof camera
pose in continuous time. Second, the pinhole camera
model using interpolated poses is derived. Finally,
the iterative minimization used in the Perspective n-
Points algorithm is explained. Our contribution fo-
cused on the distribution of the CP is then studied
and two methods are proposed to determine adequate
NUD of the CP, using either information from an IMU
sensor or multiple iterations of reprojection error min-
imization. The two methods are evaluated on sim-
286
Vandeportaele B., Gohard P., Devy M. and Coudrin B.
Pose Interpolation for Rolling Shutter Cameras using Non Uniformly Time-Sampled B-splines.
DOI: 10.5220/0006171802860293
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 286-293
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ple synthetic data sets to prove the concept and future
works are introduced that should lead to the integra-
tion of our model in a SLAM algorithm.
2 RELATED WORK FOR SLAM
2.1 Global Shutter
A SLAM algorithm can recover the position and ori-
entation of a mobile camera. In the Augmented Re-
ality context, these camera parameters can be used
to synthesize images of virtual elements as if they
were seen by the real camera. To do so without prior
knowledge of the environment, it is necessary to map
it in realtime.
Early realtime methods used to solve the SLAM
problem in the literature were based on Extended
Kalman Filter (EKF)(Davison, 2003), (Roussillon
et al., 2012), (Gonzalez, 2013). The simplicity of this
method and it’s computing efficiency for small size
environment model has made it the most used SLAM
method for the past decade.
Other robust and realtime methods based on lo-
cal Bundle Adjustment like PTAM (Klein and Mur-
ray, 2007) have also been proposed. They minimize
the reprojection error over a subset of previously ac-
quired images, called keyframes (Engel et al., 2014),
(Mur-Artal et al., 2015), or over a sliding window of
frames (Mouragnon et al., 2006). They provide im-
proved robustness thanks to the modeling of outliers,
and (Strasdat et al., 2010) proved the superiority of
these Bundle Adjustment-based methods over filter-
ing one.
2.2 Rolling Shutter
Using a SLAM method designed for GS camera
model with RS camera produces deviations of the es-
timated trajectory and reconstructed 3D points. These
deviations increase with the velocity of the cam-
era. One of the first use of a RS camera model
in the SLAM context was the adaptation of PTAM
for smartphone (Klein and Murray, 2009). They es-
timated the angular velocity of the camera at the
keyframe using keypoints tracked between the previ-
ous and the next frame. This angular velocity was
then used to correct the measurements of the points
in the image using a first order approximation so they
can be used as if they where obtained by a GS camera.
(Hedborg et al., 2011) initially used a similar
method, and proposed in (Hedborg et al., 2012) a bun-
dle adjustment using a RS camera model. To estimate
the varying camera pose inside a frame, they interpo-
lated independently the rotations (using SLERP) and
the translations (using linear interpolation).
(Furgale et al., 2012) also used a system based on
B-splines to have a continuous time representation. In
their work, they interpolate rotations and translations
by two independent B-splines. Their Cayley-Gibbs-
Rodriguez formulation used for the poses had two ma-
jor issues according to (Steven Lovegrove, 2013):
• The used Rodrigues parameterization has a singu-
larity for the rotation at π radians.
• The interpolation in this space does not repre-
sent the minimum distance for the rotation group
hence the generated trajectories can correspond to
unrealistic motions.
To address these issues,(Steven Lovegrove, 2013)
proposed to use a continuous time trajectory formu-
lation using cumulative B-splines. Their theoretical
framework is the basis of our work and is derived
next.
3 THEORETICAL FRAMEWORK
FOR RS CAMERAS
3.1 Cumulative B-splines for Pose
Interpolation
A standard B-spline is defined by constant polynomial
basis functions B
i,k
(k −1 being the degree of the used
polynomial) and variable Control Points (CP) p
i
:
p(t) =
k−1
∑
i=0
p
i
B
i,k
(t) (1)
Let
˜
B
i,k
(t) =
∑
k−1
j=i
B
j,k
(t) be a cumulative basis func-
tions defined further in eq. (8). The eq. (1) can be re-
formulated using CP differences (p
i
− p
i−1
) to obtain
the cumulative B-splines expression:
p(t) = p
0
˜
B
0,k
(t)+
k−1
∑
i=1
(p
i
− p
i−1
)
˜
B
i,k
(t) (2)
This definition of the B-spline stands for multidi-
mensional spaces and thus allows the interpolation for
camera poses p(i) ∈ R
6
independently over its differ-
ent components (for instance 3 translation parameters
and 3 rotation parameters using Rodrigues parame-
terization). However this does not account for the
correlations between the components of the pose thus
some adaptations are required to overcome this, using
6DoF camera poses defined in the SE3 space. Such
poses can be expressed by transformation matrices T
Pose Interpolation for Rolling Shutter Cameras using Non Uniformly Time-Sampled B-splines
287
parameterized by a translation a and a rotation matrix
R:
T =
R a
0
T
1
,T ∈ SE3,R ∈ SO3,a ∈ R
3
(3)
While the cumulative B-splines interpolation in
R
6
involves the differentiation of CP (p
i
− p
i−1
), in
the special Euclidean group SE3 it requires more
complex operations. Let T
w,i
be the i
th
Control Poses
(indistinctly abbreviated as CP) relatively to the world
coordinate frame w, the transformation matrix ∆T
i−1,i
relating two poses T
w,i−1
and T
w,i
is obtained by com-
position:
∆T
i−1,i
= T
−1
w,i−1
T
w,i
(4)
The log function maps a pose (or variation) defined
in SE3 to its tangent space se3, where operations for
composing transformation are simpler, and allows to
express the summation of weighted CP variation by
simple addition. Let T
w,s
(t) be the interpolated pose
along the B-spline at instant t and ∆
t
be the time be-
tween the 2 poses. Let Ω
i−1,i
=
1
∆
t
log(∆T
i−1,i
), the
eq. (2) can be adapted to se3:
log(T
w,s
(t)) =
˜
B
0
(t)log(T
w,0
) +
k−1
∑
i=1
˜
B
i
(t)Ω
i−1,i
(5)
The inverse of the logarithmic map, the exponen-
tial map, projects a pose from se3 to SE3 and can
be used to recover T
w,s
(t)) = exp(log(T
w,s
(t))). Ob-
serving that additions in se3 maps to multiplications
in SE3, the eq.(5) can be reformulated for SE3. The
pose T
w,s
(t) (for the B-spline s and expressed in world
coordinates w) is interpolated between the two CP
T
w,i
and T
w,i+1
for different time t using :
T
w,s
(t) = exp(
˜
B
0
(t)log(T
w,0
))
k−1
∏
i=1
exp(
˜
B
i
(t)Ω
i−1,i
)
(6)
A change of variable is introduced to map the real
time t variable between two CP associated to times
t
i
and t
i
+ ∆
t
to a normalized time u ∈ [0, 1] interval,
using a constant time interval ∆
t
between the CP:
u = (t −t
i
)/∆
t
(7)
Using this normalized time, the time between 2 CP is
equal to one, so the factor
1
∆
u
vanishes and the ex-
pression of Ω
i−1,i
can be reformulated as Ω
i−1,i
=
log(∆T
i−1,i
)
(Steven Lovegrove, 2013) have chosen to use cu-
bic B-splines because of their C
2
continuity, which
allow to predict angular velocities and linear acceler-
ations. Hence the degree of the polynomial for the
basis is 3 and the B-splines are locally controlled by
4 CP (as k = 4), meaning that the knowledge of the 4
surrounding CP is sufficient to interpolate on the B-
spline. The used cumulative basis functions
˜
B
i,k
(u)
for k = 4 are expressed in the i
th
component of the
vector
˜
B(u) by:
˜
B(u) =
1
6
6 0 0 0
5 3 −3 1
1 3 3 −2
0 0 0 1
1
u
u
2
u
3
(8)
Using normalized time variable u and noting that
the first line of
˜
B(u) is
˜
B
0
(u) = 1, the eq.( 6) can be
simplified in:
T
w,s
(u) = T
w,0
k−1
∏
i=1
exp(
˜
B
i
(u)Ω
i−1,i
) (9)
3.2 Rolling Shutter Camera Model
An image from a RS camera can be seen as the con-
catenation of one dimensional images (rows) exposed
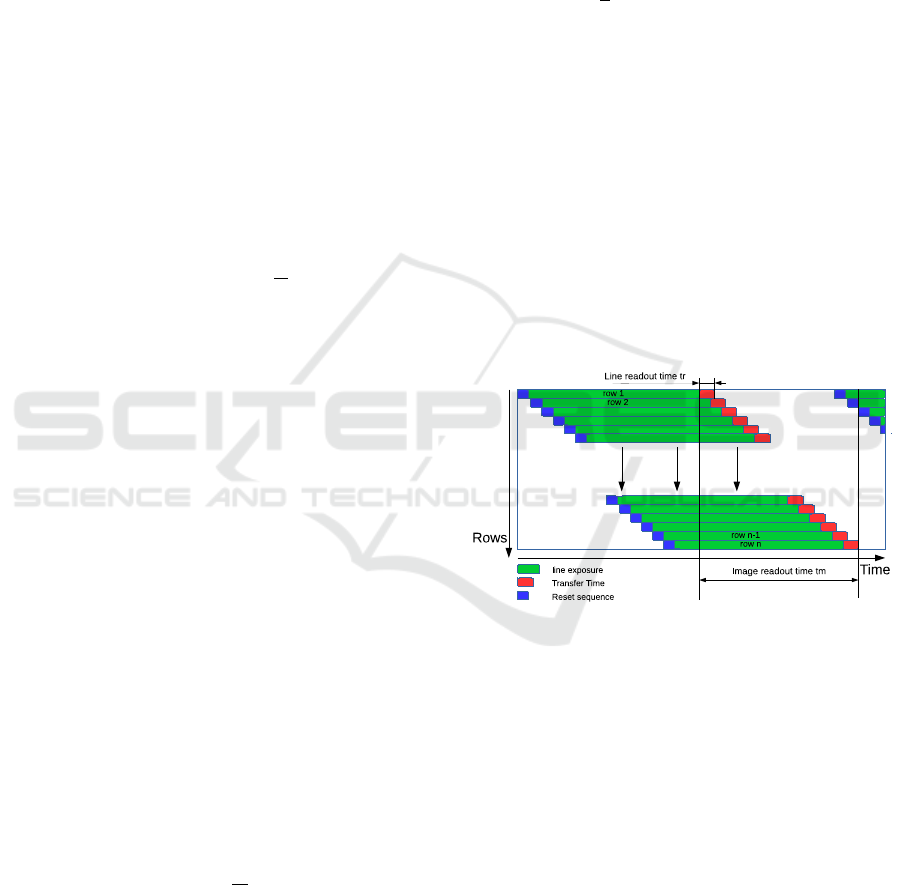
at different times as seen in the figure 1.
Figure 1: RS cameras expose the image lines sequentially,
thus if the first line is exposed at instant t
0
, then the n
th
line
is exposed at t
0
+ n.t
r
with t
r
the readout time of a line. The
time taken by the camera to fully expose an image is called
the readout time t
m
. (Li et al., 2013).
For a static scene and camera, there is no geomet-
ric difference between the GS and RS camera. But if
the camera is in motion relatively to the scene, each
line is a projection from a different camera viewpoint.
While the camera pose T ∈ SE3 is common to all the
pixels in a GS image, it varies over time as T(t) for
each individual line in the RS case.
The pinhole camera perspective projection model
is derived below. Let X be a 3D point defined in ho-
mogeneous coordinates in the world coordinate sys-
tem w. Let T
w,c
be the transformation matrix from
world w to camera c coordinate frame. Let K be the
camera matrix containing the intrinsic parameters and
π(.) be the perspective projection (mapping from P
2
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
288
to R
2
). The pinhole model projects X onto the image
plane to
x y
T
by:
x
y
:= π([K|0]T
w,c
X) (10)
To model the varying pose over time T
w,c
is pa-
rameterized by t as T
w,c
(t). The spline being defined
by eq.( 9) in the spline coordinate frame s (attached
to the IMU for instance) different from c, a (constant
over time) transformation T
s,c
is required to obtain
T
w,c
(t):
T
w,c
(t) = T
s,c
T
w,s
(t) (11)
The projection at varying time t is obtained by:
x(t)
y(t)
:= π([K|0]T
w,c
(t)X) = ω(X,T
w,c
(t)) (12)
This model does not yet represent the fact that at a
given time t corresponds a single line exposure. So
the projection
x(t
1
) y(t
1
)
T
of X at time t = t
1
will
actually be obtained only if the line y(t
1
) is exposed
at time t
1
.
(Steven Lovegrove, 2013) expressed the line ex-
posed at a time t as a function of s the frame start
time, e is the end frame time, and h is the height of
the image in pixels by:
y(t) = h
(t − s)
(e − s)
(13)
The figure 2 shows plotted in blue the image pro-
jections
x(t) y(t)
T
of a single 3D point obtained
by eq.( 12) using interpolation of the poses defined in
eq.( 9). The value of t is sampled to the different ex-
posure time of each individual row. The green line in-
dicates the row that is actually exposed when the y(t)
corresponds to the row number and the red cross at
the intersection is the resulting projection. For highly
curved trajectories, multiple projections of a single
3D point can be observed in a single image.
566 568 570 572 574 576 578 580 582 584
414
416
418
420
422
424
426
428
column
rows
Figure 2: Here is an example of the different projections of
a 3D point (in blue) in one image for each of the line poses,
in the case of a moving camera. The green line shows the
exposed rows at the time the 3D point is projected to it.
The projection(s)
x(t) y(t)
T
that is(are) effec-
tively observed by the RS camera is(are) obtained by
intersecting the curves corresponding to eq.( 12) and
eq.( 13). Determining t is an optimization problem
that (Steven Lovegrove, 2013) solve iteratively using
first order Taylor expansion of the 2 equations around
a time t:
y
b
(t + δt) = h
(t + δt − s)
(e − s)
(14)
x(t + δt)
y(t + δt)
= ω(X , T
w,c
(t))+ δt
dω(X,T
w,c
(t))
dt
(15)
This system of equations is reorganized as:
δt = −
ht + s(y
b
(t)− h) − ey
b
(t)
h + (s −e)
dω
y
(X,T
w,c
(t))
dt
(16)
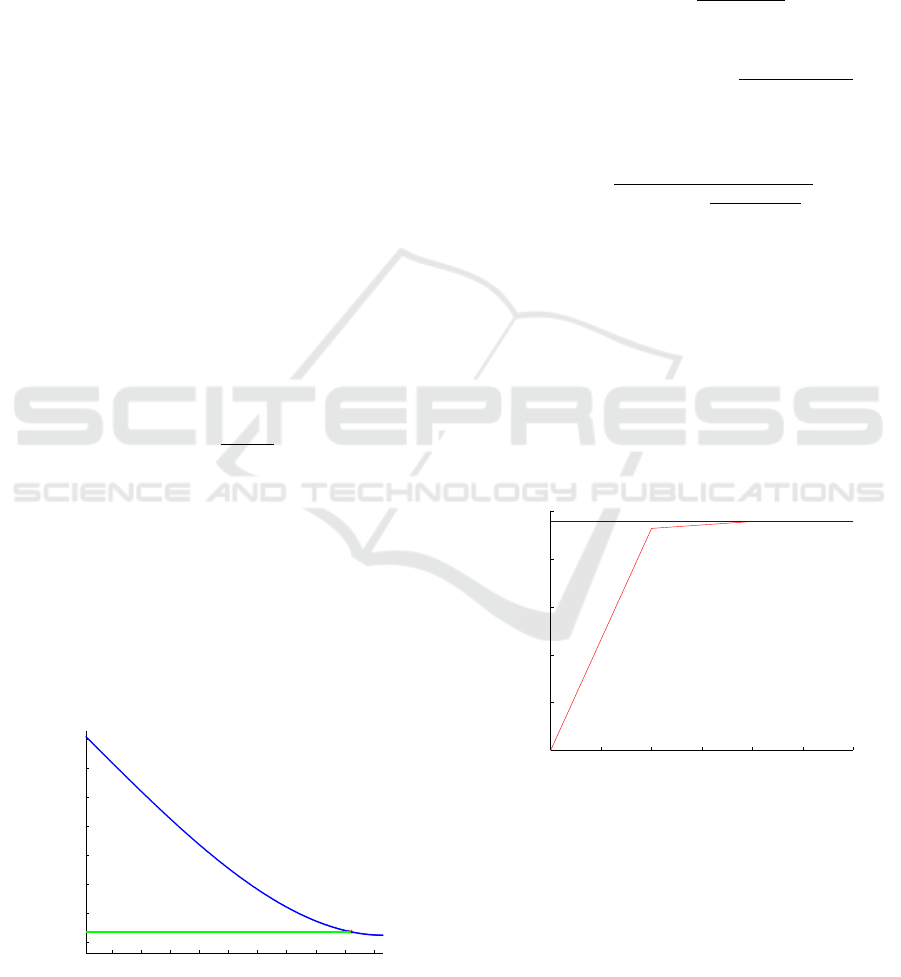
By updating t as t = t + δ
t
and iterating, t con-
verges generally in approximately 3 or 4 iterations
(see Figure 3). Once t is determined, the correspond-
ing projection is obtained using eq.( 12). For slow
motions, the initial value for t can be set at the time
corresponding to the middle row of the image and the
iterative algorithm is very likely to converge. How-
ever, for high dynamic motions, the initial value has
to be set wisely, as different initial values could lead
to different projections that correspond indeed to dif-
ferent actual projections.
0 0.5 1 1.5 2 2.5 3
2.35
2.4
2.45
2.5
2.55
2.6
iteration number
t
Figure 3: Evolution of t during three iterations.
3.3 Perspective n-Points Algorithm for
RS Camera
The Perspective n-Points, or PnP algorithm consists
in determining the pose of a camera given n corre-
spondences between 3D known points and their ob-
servations in the image. Here we describe the itera-
tive portion of the PnP algorithm that is used to refine
a first estimate.
Pose Interpolation for Rolling Shutter Cameras using Non Uniformly Time-Sampled B-splines
289

Let u
i,k
be a set of image measurements (corre-
sponding to time t
i
) of M 3D points X
k
inside a set
of N images and T
w,c
be related to a set of CP T
w,s
through eq.( 11).The reprojection error res(i,k) for in-
dividual point is defined by:
res(i,k) = ||u
i,k
− π([K|0]T
w,c
(t
i
)X
k
)|| (17)
The following cost function is minimized to de-
termine
ˆ
θ, the set of parameters T
w,s
that best fits the
model to the set of observations:
ˆ
θ = argmin
θ
N
∑
i=1
M
∑
k=1
res(i,k)
2
(18)
While a PnP algorithm for a GS camera optimizes
the pose of the camera itself, the RS version has to
optimize the CP used for the interpolation. Thus, the
parameters vector θ contains the required CP param-
eters.
The minimization is achieved using the
Levenberg-Marquardt algorithm, an iterative non-
linear least squares solver behaving between
Gauss-Newton and Gradient Descent. The initial
value for the parameters in θ is set from the IMU
measurements or by applying firstly a GS PnP.
The levenberg Marquardt algorithm uses the partial
derivatives (obtained by finite difference) of the cost
function with respect to the parameters to optimize.
It generally converges after several iterations but
is prone to converge to local minimum if the cost
function is not convex or if the initial value is too far
from the global minimum.
4 CP TEMPORAL SAMPLING
4.1 Uniform Distribution
(Steven Lovegrove, 2013) use an UD in time for
the CP, and use normalized times as shown in
eq.( 7). This UD of CP (chosen every 0.1 seconds in
(Steven Lovegrove, 2013)) leads to some limitations
in these two cases:
• For a camera grabbing frames at 30FPS, a CP
is defined each 3 frames leading to relatively
smoothed trajectory for fast camera motions, fail-
ing to accurately model it.
• For steady movement, the algorithm creates un-
necessary redundant CP.
The motion of hand-held device used for aug-
mented reality can be decomposed in three distinct
type of motions: high speed motion, low speed mo-
tion, and low range but high frequency motions when
the user’s hand is shaking. While the use of a small
UD interval ∆
t
between CP is a a simple solution to
model theses motions, it leads to an increase of the CP
number and consequently of the computational cost.
Doing so, unnecessary CP are used for low speed and
steady motions, adding no information/constraints to
the interpolated trajectory.
4.2 Non Uniform Distribution
To overcome this problem, we propose to relax the
UD constraint for the intervals ∆
t
between the CP.
This allows to locally increase the number of CP
where needed by lowering the time interval ∆
t
dur-
ing fast motion while keeping a low number of CP
for portions of the trajectory that correspond to slow
motions.
The mapping between u and t is then defined dif-
ferently from eq.( 7) by:
u =
t −t
i
t
i+1
−t
i
(19)
While the retrieving of the t
i
and t
i
+1 CP involved
only multiplication and rounding in the UD case, it re-
quires more complex computations with NUD as the
time value t
i
can be defined freely.
NUD provides the ability to create locally multi-
ple CP inside a single image. This leads to many CP
quartets required to interpolate the pose inside differ-
ent portions of the image (see Figure 4). As retrieving
the CP associated to a time t is an operation that is
done thousands of times per frame, some care is re-
quired to avoid wasting time searching over all the CP.
This is achieved by storing CP indices in an chrono-
logically ordered list and using hash tables for fast
access.
Figure 4: An example of multiple CP inside a single image,
and their influence for interpolating the pose for different
rows. 3 CP are time-stamped between the beginning and
the end of the image N: T
i+1
, T
i+2
and T
i+3
. The quartet
of CP used for interpolating pose at each row change three
time during the image exposure.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
290

4.3 CP Generation Methods
As our approach uses varying time intervals function
of the local properties of the motion, it requires to
generate the CP at the right time. We investigated two
different approaches involving either an IMU sensor
or the analysis of the reprojection error in the images.
The first one is better fitted for realtime applications
as the CP can be generated online using IMU mea-
surements while the second involves an iterative pro-
cess that predisposes it for offline computation.
4.3.1 Based on IMU
An IMU sensor is generally composed of a gyroscope
that measures the angular velocities and accelerom-
eters that provide accelerations. On current tablets
and smartphones, it generally delivers measurements
at about 100Hz, which is an higher frequency than the
frame rate of the camera.
We propose a simple analysis of the measurements
done by the IMU to determine when the CP are re-
quired. The figure 5 shows a generated trajectory
(in the two top plots). The left (resp. right) plots
corresponds to the translation (resp rotation) compo-
nents. The data provided by the IMU are plotted in
the middle plots. The bottom plots show respectively
the norm of the linear accelerations and angular ve-
locities. Different thresholding values (shown in red,
blue and black) are used to determine when more CP
are required. These threshold values th
i
are stored in
two (for acceleration and angular velocity) look up
table providing n(th
i
), the number of CP required per
unit of time. These lists of threshold values are gen-
erated empirically for the moment and correspond to
a tradeoff between accuracy of the motion modeling
and computational cost. For instance, if the angular
velocity norm is below the threshold th
1
, n(th
1
) CP
per unit of time are used while if its norm rises above
th
1
but below th
2
, n(th
2
) CP per unit of time are used
and so on. Once the CP are created, their parameters
are optimized using eq.( 18).
4.3.2 Based on Reprojection Error
We propose a second method to determine the tem-
poral location of the CP when a IMU in not avail-
able. This method involves an iterative estimation of
the trajectory using initial CP (set for instance with
an UD) as shown in eq.( 18). Let res
t
1
,∆
t
be the mean
of the residuals res(i,k) defined in eq.( 17) between
times t
1
and t
1
+ ∆
t
. Our method use an iterative
scheme consisting of the following two steps:
• The residuals are computed along the trajectory
and analyzed using a sliding window to measure
0 0.5 1
−0.2
0
0.2
Translation
0 0.5 1
−0.5
0
0.5
Orientation
0 0.5 1
−100
0
100
Acceleration
0 0.5 1
−4
−2
0
2
Angular Velocity
0 0.5 1
0
100
200
Acceleration norm
0 0.5 1
0
2
4
Angular velocity norm
Figure 5: Determination of the number of required CP per
unit of time using IMU measurements analysis (See the text
for details).
locally res
t
1
,∆
t
for varying t
1
. Maximums values
are detected and additional CP are generated at
the middle of the two corresponding neighboring
CP for time t
1
+
∆
t
2
.
• An iterative estimation of the trajectory eq.( 18)
is achieved with the added CP to refine the whole
set of CP.
The process is iterated until ∀t
1
: res
t
1
,∆
t
< threshold.
5 RESULTS
We evaluated our methods on simulated data sets con-
sisting of simple scenes (defined by sparse points
clouds) and trajectories (defined by B-splines using
manually defined ground truth CP that are NUD).
While the proposed methods have been tested to
model complex 6-dof trajectories, they cannot be eas-
ily drawn in this paper. Hence the plotted results are
for simple trajectories to allow the reader to interpret
them in 2D and serve as proof of concept. The syn-
thetic scene is projected to synthetic images using the
RS camera model, and the CP are optimized using
the iterative minimization. Even if the plotted results
only show the trajectories, they are computed using
the whole framework presented above ie. using the
PnP algorithm to compare the poses through the re-
projection error in the images using the RS camera
model.
5.1 Based on IMU
To test IMU-based CP generation, IMU measure-
ments are synthesized at 100Hz from the ground truth
trajectory using the first and second derivatives of
Pose Interpolation for Rolling Shutter Cameras using Non Uniformly Time-Sampled B-splines
291

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−0.5
0
0.5
b
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
100
200
c
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.05
0.1
a
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.02
0.04
0.06
0.08
d
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.02
0.04
0.06
0.08
e
Figure 6: Results for the IMU method (see text for details).
eq.( 6) (see (Steven Lovegrove, 2013) for details).
We set the first thresholds for the angular velocity
to th
d
Rot = 2rad/s and for the linear acceleration to
th
A
cc = 130cm/s
2
.
The figure 6 (a) shows a simple trajectory con-
sisting of a linear motion with a perturbation at t=0.5.
The plot 6 (b) shows the position of the camera during
the motion (using different colors for different axes,
the green being used for the vertical direction). The
plot 6 (c) shows the norm of the acceleration in green
while the first threshold is plotted in red. The angu-
lar velocities are not plotted in this simple example as
they have null values. The plot 6 (d) shows the B-
spline trajectory generated by our method while 6 (e)
shows the B-spline generated with the same number
of CP but using an UD. As expected, the NUD B-
spline is much closer to the ground truth while the
UD B-spline artificially smooths the trajectory, and
creates larger oscillations.
5.2 Based on Reprojection Error
For this second test, the same trajectory is used as
shown in figure 7 (a), but the synthetic IMU measure-
ments are not exploited. A first UD for the CP is used
to initiate the process and the resulting B-spline af-
ter one reprojection error minimization step is shown
in (b). The residuals mean value for the sliding win-
dows are shown in (c), and the maximum detected at
t = 0.5 permits to add a few (2) CP in the neighbor-
0.2 0.3 0.4 0.5 0.6 0.7 0.8
0
0.02
0.04
0.06
a
0.2 0.3 0.4 0.5 0.6 0.7 0.8
0
0.02
0.04
0.06
d
0.2 0.3 0.4 0.5 0.6 0.7 0.8
0
0.02
0.04
0.06
b
0.2 0.3 0.4 0.5 0.6 0.7 0.8
0
10
20
30
c
0.2 0.3 0.4 0.5 0.6 0.7 0.8
0
1
2
e
Figure 7: Results for the reprojection error method (see text
for details).
hood and iterate with error minimization step. The
process is stopped once the number of CP reaches the
same value than in the plot 6 (d) and (e) for com-
parison purpose. The obtained B-spline trajectory is
shown in 7 (d) and the corresponding residuals mean
value for the sliding windows in (e) shows a decrease
by an approximate 20X factor compared to (c) for a
increase of only 2 CP.
6 FUTURE WORKS
Our future researches will focus on multiple points:
• Some tests on real motions using hand held de-
vices will be conducted, the ground truth being
provided by a motion capture system.
• We will attempt to intricate in the same optimiza-
tion process the minimization of the residuals and
the CP generation in order to lower the time re-
quirements, especially for the method based on
reprojection error.
• Whereas the time associated to the CP are fixed
in our current study, it would be interesting to
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
292

optimize their values alongside the pose param-
eters. This added degree of freedom would allow
to adapt dynamically the distribution in time of
the CP avoiding the generation of new ones.
• We will try to integrate our model in a realtime
SLAM.
7 CONCLUSION
In this paper, we have enriched the B-splines trajec-
tory model from (Steven Lovegrove, 2013) to inte-
grate NUD for the CP in the RS Camera SLAM con-
text. We have shown that this NUD allowed to bet-
ter model trajectories than using an UD for the same
number of CP. We have proposed two methods to
generate the CP, using either IMU measurements or
iterative reprojection error minimization. The two
methods have been tested on synthetic trajectories and
proven to be efficient for the PnP problem resolution.
This enriched model will be integrated in a SLAM in
future works.
REFERENCES
Davison, A. J. (2003). Real-time simultaneous locali-
sation and mapping with a single camera. In 9th
IEEE International Conference on Computer Vision
(ICCV 2003), 14-17 October 2003, Nice, France,
pages 1403–1410.
Engel, J., Sch
¨
ops, T., and Cremers, D. (2014). LSD-SLAM:
Large-scale direct monocular SLAM. In ECCV.
Furgale, P., Barfoot, T. D., and Sibley, G. (2012).
Continuous-time batch estimation using temporal ba-
sis functions. In Robotics and Automation (ICRA),
2012 IEEE International Conference on, pages 2088–
2095.
Gonzalez, A. (2013). Localisation par vision multi-
spectrale. Application aux syst
`
emes embarqu
´
es. The-
ses, INSA de Toulouse.
Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-
ometry in Computer Vision. Cambridge University
Press, ISBN: 0521540518, second edition.
Hedborg, J., Forss
´
en, P. E., Felsberg, M., and Ringaby, E.
(2012). Rolling shutter bundle adjustment. In Com-
puter Vision and Pattern Recognition (CVPR), 2012
IEEE Conference on, pages 1434–1441.
Hedborg, J., Ringaby, E., Forss
´
en, P. E., and Felsberg, M.
(2011). Structure and motion estimation from rolling
shutter video. In Computer Vision Workshops (ICCV
Workshops), 2011 IEEE International Conference on,
pages 17–23.
Klein, G. and Murray, D. (2007). Parallel tracking and
mapping for small AR workspaces. In Proc. Sixth
IEEE and ACM International Symposium on Mixed
and Augmented Reality (ISMAR’07), Nara, Japan.
Klein, G. and Murray, D. (2009). Parallel tracking and map-
ping on a camera phone. In Proc. Eigth IEEE and
ACM International Symposium on Mixed and Aug-
mented Reality (ISMAR’09), Orlando.
Li, M., Kim, B., and Mourikis, A. I. (2013). Real-time mo-
tion estimation on a cellphone using inertial sensing
and a rolling-shutter camera. In Proceedings of the
IEEE International Conference on Robotics and Au-
tomation, pages 4697–4704, Karlsruhe, Germany.
Mouragnon, E., Lhuillier, M., Dhome, M., Dekeyser, F.,
and Sayd, P. (2006). Real time localization and 3d
reconstruction. In 2006 IEEE Computer Society Con-
ference on Computer Vision and Pattern Recognition
(CVPR’06), volume 1, pages 363–370.
Mur-Artal, R., Montiel, J. M. M., and Tard
´
os, J. D. (2015).
Orb-slam: A versatile and accurate monocular slam
system. IEEE Transactions on Robotics, 31(5):1147–
1163.
Patron-Perez, A., Lovegrove, S., and Sibley, G. (2015). A
spline-based trajectory representation for sensor fu-
sion and rolling shutter cameras. Int. J. Comput. Vi-
sion, 113(3):208–219.
Roussillon, C., Gonzalez, A., Sol
`
a, J., Codol, J., Mansard,
N., Lacroix, S., and Devy, M. (2012). RT-SLAM: A
generic and real-time visual SLAM implementation.
CoRR, abs/1201.5450.
Steven Lovegrove, Alonso Patron-Perez, G. S. (2013).
Spline fusion: A continuous-time representation for
visual-inertial fusion with application to rolling shut-
ter cameras. In Proceedings of the British Machine
Vision Conference. BMVA Press.
Strasdat, H., Montiel, J., and Davison, A. J. (2010). Real-
time monocular slam: Why filter? In Robotics and
Automation (ICRA), 2010 IEEE International Confer-
ence on, pages 2657–2664. IEEE.
Pose Interpolation for Rolling Shutter Cameras using Non Uniformly Time-Sampled B-splines
293
