Towards Non-rigid Reconstruction
How to Adapt Rigid RGB-D Reconstruction to Non-rigid Movements?
Oliver Wasenm
¨
uller, Benjamin Schenkenberger and Didier Stricker
German Research Center for Artificial Intelligence (DFKI), Kaiserslautern, Germany
Keywords:
RGB-D Reconstruction, Non-rigid, Human Body Capture, Sparse Warp Field.
Abstract:
Human body reconstruction is a very active field in recent Computer Vision research. The challenge is the
moving human body while capturing, even when trying to avoid that. Thus, algorithms which explicitly cope
with non-rigid movements are indispensable. In this paper, we propose a novel algorithm to extend existing
rigid RGB-D reconstruction pipelines to handle non-rigid transformations. The idea is to store in addition to
the model also the non-rigid transformation nrt of the current frame as a sparse warp field in the image space.
We propose an algorithm to incrementally update this transformation nrt. In the evaluation we show that the
novel algorithm provides accurate reconstructions and can cope with non-rigid movements of up to 5cm.
1 INTRODUCTION
The three-dimensional (3D) reconstruction of random
objects is a very active field in the Computer Vision
community. Several approaches using different types
of cameras where proposed, such as monocular cam-
eras , stereo cameras , depth cameras , spherical cam-
eras , etc. Most of them rely on one basic assumption:
The captured scene is rigid. This means, there is no
movement and the scene geometry is static. In case of
reconstructing buildings, streets, machines, etc. this
assumption holds and is very useful to simplify the
reconstruction problem. However, in reality this is
often not applicable, especially when living humans
are object of 3D reconstruction. Even if a human tries
to stand still, non-rigid movement is included due to
breathing, heart beat, muscle fatigue, etc. Thus, meth-
ods for handling this non-rigid movement in 3D re-
construction are indispensable.
Therefore, we propose in this paper a novel
pipeline performing RGB-D reconstruction by han-
dling explicitly non-rigid movements. We use RGB-
D cameras, since they have the advantage of giving
immediately information about the 3D geometry at
a given point in time. In the literature several ap-
proaches, like e.g. KinectFusion (Newcombe et al.,
2011), were proposed to perform rigid RGB-D recon-
struction. They demonstrate that – despite the cam-
eras low resolution and high noise level – high-quality
reconstructions are possible. Therefore, we use these
algorithms as basis and extend them in order to cope
(a) 1 frame (b) 250 frames
Figure 1: In this paper, we propose a non-rigid reconstruc-
tion pipeline for human body reconstruction. While parts of
the body can move up to 5cm during capturing, the recon-
struction stays rigid.
with non-rigid movements. More precisely our con-
tributions are
• an extension of a rigid reconstruction pipeline to
a non-rigid reconstruction,
• an incremental method to cope with non-rigid
transformations within the image space and
• an extensive evaluation on non-rigid as well as
rigid datasets.
The applications for non-rigid human body recon-
struction are numerous and cover amongst others an-
294
WasenmÃijller O., Schenkenberger B. and Stricker D.
Towards Non-rigid Reconstruction - How to Adapt Rigid RGB-D Reconstruction to Non-rigid Movements?.
DOI: 10.5220/0006172402940299
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 294-299
ISBN: 978-989-758-227-1
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

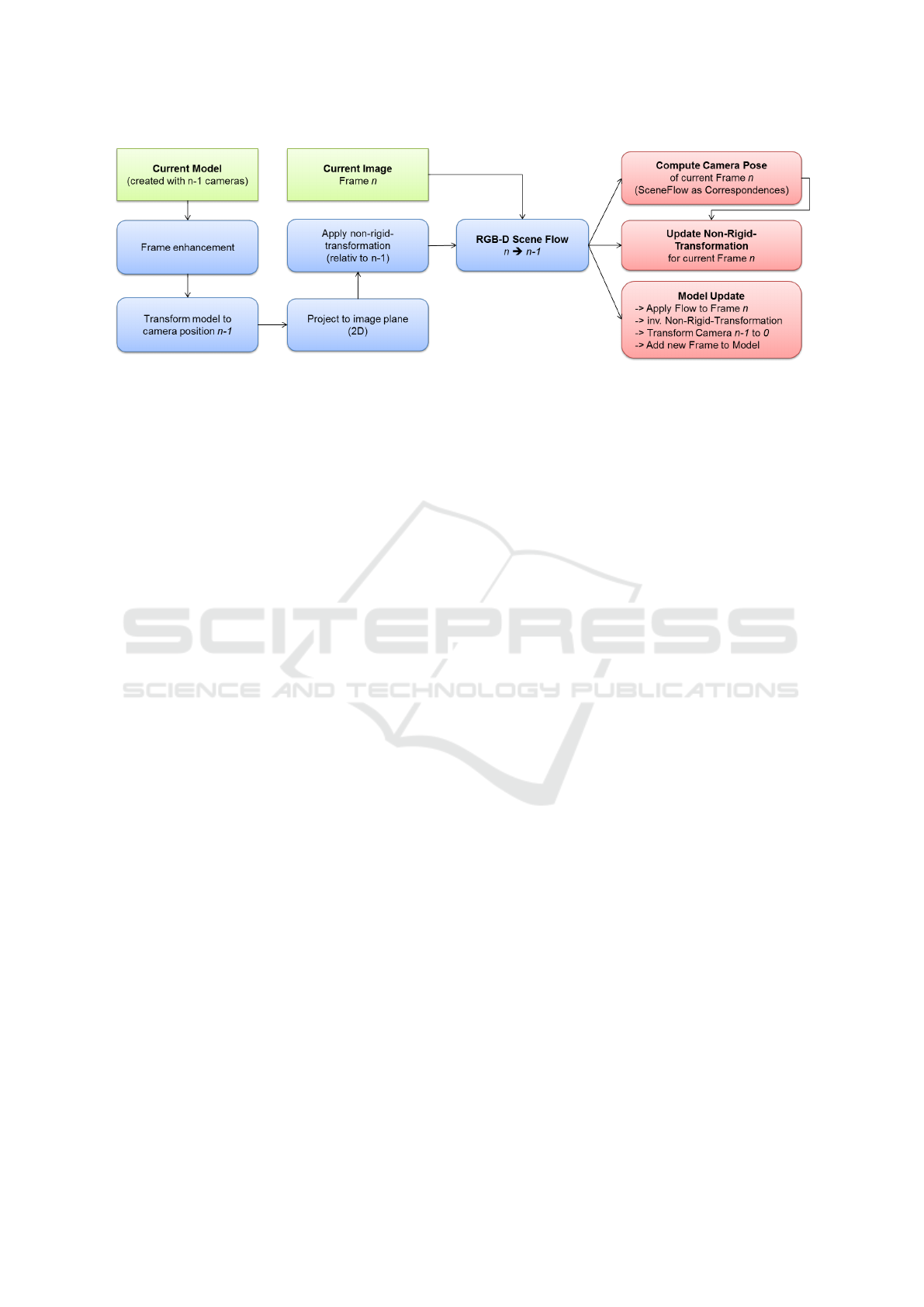
Figure 2: Overview of the proposed non-rigid reconstruction pipeline. In each iteration the model is prepared (cp. Section 3.2)
in order to show a similar geometry like the new input frame n. After applying a RGB-D scene flow algorithm three central
computations are performed (cp. Section 3.3): computation of new camera pose, computation of non-rigid-transformation for
next iteration and update of rigid model.
thropometric measurement extraction (Wasenm
¨
uller
et al., 2015), virtual try-on (Hauswiesner et al., 2011)
or animation (Aitpayev and Gaber, 2012).
2 RELATED WORK
In general, RGB-D reconstruction approaches can be
subdivided into online and offline approaches. On-
line algorithms use subsequent images and build an
updated reconstruction with each new frame. In con-
trast, offline approaches use a complete sequence
of images and try to find directly a reconstruction
based on all images. In the given literature sev-
eral approaches for offline non-rigid reconstruction
were proposed. Many approaches use an extended
non-rigid version of ICP to allow for non-rigid de-
formations (Brown and Rusinkiewicz, 2007). Often
they model the surface according to the as-rigid-as-
possible principle (Sorkine and Alexa, 2007). Quasi-
rigid reconstruction was proposed in (Li et al., 2013)
and others make use of known human kinematics
(Zhang et al., 2014). (Dou et al., 2013) utilize mul-
tiple fixed cameras by fusing all depth images into a
novel directional distance function representation.
Most online approaches in the literature target on
rigid reconstruction. A very famous algorithm is
KinectFusion (Newcombe et al., 2011), which was
the first approach for real-time 3D scanning with a
depth camera. This algorithm was extended in several
publications, trying to overcome its limitations (Whe-
lan et al., 2012). Other algorithms target on the pose
estimation of the camera (odometry), but use these
poses later for reconstruction. A famous approach
for RGB-D odometry is DVO (Kerl et al., 2013),
which was later extended for given applications or
cameras (Wasenm
¨
uller et al., 2016a). The first algo-
rithms for non-rigid online reconstruction were pro-
posed very recently. The first approach was Dynam-
icFusion (Newcombe et al., 2015), which extends
KinectFusion by a warping field to model the non-
rigid deformation. Later, this was extended in Vol-
umeDeform (Innmann et al., 2016) by making shape
correspondences more robust by SIFT features.
3 ALGORITHM
In this section we motivate and explain our novel al-
gorithm for extending rigid to non-rigid RGB-D re-
construction. An overview of the algorithm is given
in Figure 2. After presenting the basic idea in Section
3.1, we explain the model preparation (shown in blue
in Figure 2). In Section 3.2 we propose the model
processing, which is highlighted in red in Figure 2.
3.1 Idea
The basic idea of our novel algorithm is to extend an
existing rigid RGB-D reconstruction by modeling ex-
plicitly the non-rigid transformation. Hence, we try
to reconstruct an object under the assumption of be-
ing rigid and store the current non-rigid transforma-
tion nrt in addition. The non-rigid transformation has
the task to transform the current state of the scene
into a global rigid representation. The central chal-
lenge is to estimate the non-rigid transformation nrt
especially in case of larger displacements. A straight
forward approach would be to apply a scene flow al-
gorithm, which is designed for large displacements
(Hornacek et al., 2014). However, these approaches
require a high computation time and do currently not
have a sufficient robustness to cope with arbitrary
scenes. Therefore, we make use of fast (real-time)
Towards Non-rigid Reconstruction - How to Adapt Rigid RGB-D Reconstruction to Non-rigid Movements?
295

RGB-D scene flow algorithms (Jaimez et al., 2015),
which are indeed suitable for small displacements. To
cope with larger displacements we propose to store
the non-rigid transformation nrt incrementally. This
means, we compute for each new frame n the cur-
rent non-rigid transformation nrt
n
and apply it to the
global rigid model for the next frame. Since the non-
rigid transformations do not change rapidly, we can
compute it incrementally.
In our algorithm we propose to model the non-
rigid-transformation nrt as a warp field in the image
space, representing the transformation for each pixel
in the current frame. To speed-up the computation
and application of such a warp field we utilize a sparse
warp field. This means, we sample the field by sparse
points and interpolate between them. The reconstruc-
tion pipeline works then as follows in each iteration:
As an input we use the newly captured frame n as
well as the global rigid model, which was created out
of n − 1 frames. First, we need to prepare the recon-
structed rigid model to fit a new input frame n. There-
fore, we transform the model into the camera view
of the previous frame n − 1 and apply the non-rigid-
transformation nrt
n−1
. Thereafter, the prepared model
and the new frame should be similar in terms of their
geometric shape. In order to determine slight differ-
ences between them we apply a RGB-D scene flow
algorithm and receive dense correspondences. These
correspondences are used in the model processing to
estimate the new camera pose, to compute the up-
dated non-rigid-deformation nrt
n
and to update the
rigid scene reconstruction. We detail these steps in
the following sections.
3.2 Model Preparation
In this work we utilize the Microsoft Kinect v2 as an
RGB-D camera, since it is currently widely spread
and has overall a reasonable quality. In addition, it
has a global shutter which is perfectly suited for mov-
ing scenes. However, the depth images contain so-
called flying pixels close to depth discontinuities due
to the underlying Time-of-Flight (ToF) technology
(F
¨
ursattel et al., 2016). A sophisticated approach for
removing these pixels including the remaining noise
is required. In the literature several image filtering
(Kopf et al., 2007) and superresolution (Cui et al.,
2013) technologies were proposed. For this work we
decided to follow the approach of (Wasenm
¨
uller et al.,
2016b) due to its low runtime and high quality results.
The idea of this approach is to combine m subsequent
depth images to a single noise-free image. Therefore,
the m subsequent depth images are aligned by the reg-
istration algorithm ICP (Besl and McKay, 1992). For
our reconstruction pipeline we use m = 3 subsequent
depth images and assume negligible non-rigid move-
ment between them. The aligned depth images can
be fused by the approach described in (Wasenm
¨
uller
et al., 2016b).
The model preparation (shown in blue in Figure 2)
is the process of transforming the global rigid model
in such a way that its geometry is similar to a newly
captured frame. Since no information about the frame
n is known, we try to simulate the frame n − 1, which
was analyzed. One can assume that the geometry of
the frames n and n − 1 is quite similar, since the cam-
era has a high frame rate and the movements in the
application scenario are relatively small. Thus, we
transform the rigid model into the pose of the previ-
ous camera frame n − 1 and back-project it into the
image plane. This has mainly two reasons: First, we
need a 2D representation of the model and second we
stored the non-rigid-transformation nrt in the image
space. After that, we can apply the non-rigid transfor-
mation nrt that we estimated in the previous iteration.
Since nrt was stored as a sparse warp field, we use the
exact transformation for the image centers and inter-
polate the transformations in between them.
The result is a frame, whose geometry is similar
to the frame n − 1. One might argue that using the
frame n − 1 directly would have had the same effect,
but with the proposed model preparation a transfor-
mation from the frame n − 1 to the rigid model is
known. This transformation is essential to insert the
new frame n into the rigid model. In the next step
a RGB-D scene flow between the transformed model
and the new frame n is applied. As motivated in Sec-
tion 3.1 we use the RGB-D scene flow algorithm of
(Jaimez et al., 2015). The result are dense correspon-
dences between the two input models.
3.3 Model Processing
In the model processing three central computations
are performed: the computation of the new camera
pose, the computation of the non-rigid-transformation
nrt
n
for the next iteration and the update of the rigid
model. These three steps are detailed below.
The estimation of the camera pose of frame n is
required for the subsequent iteration as well as for the
non-rigid transformation computation. In our recon-
struction pipeline we estimate the camera pose based
on the scene flow result and the non-rigid transfor-
mation nrt
n−1
using RANSAC (Fischler and Bolles,
1981). Hence, we estimate the camera movement
with respect to the rigid object under pose n−1. That
has the advantage that compensating non-rigid trans-
formations nrt are not considered and also the influ-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
296

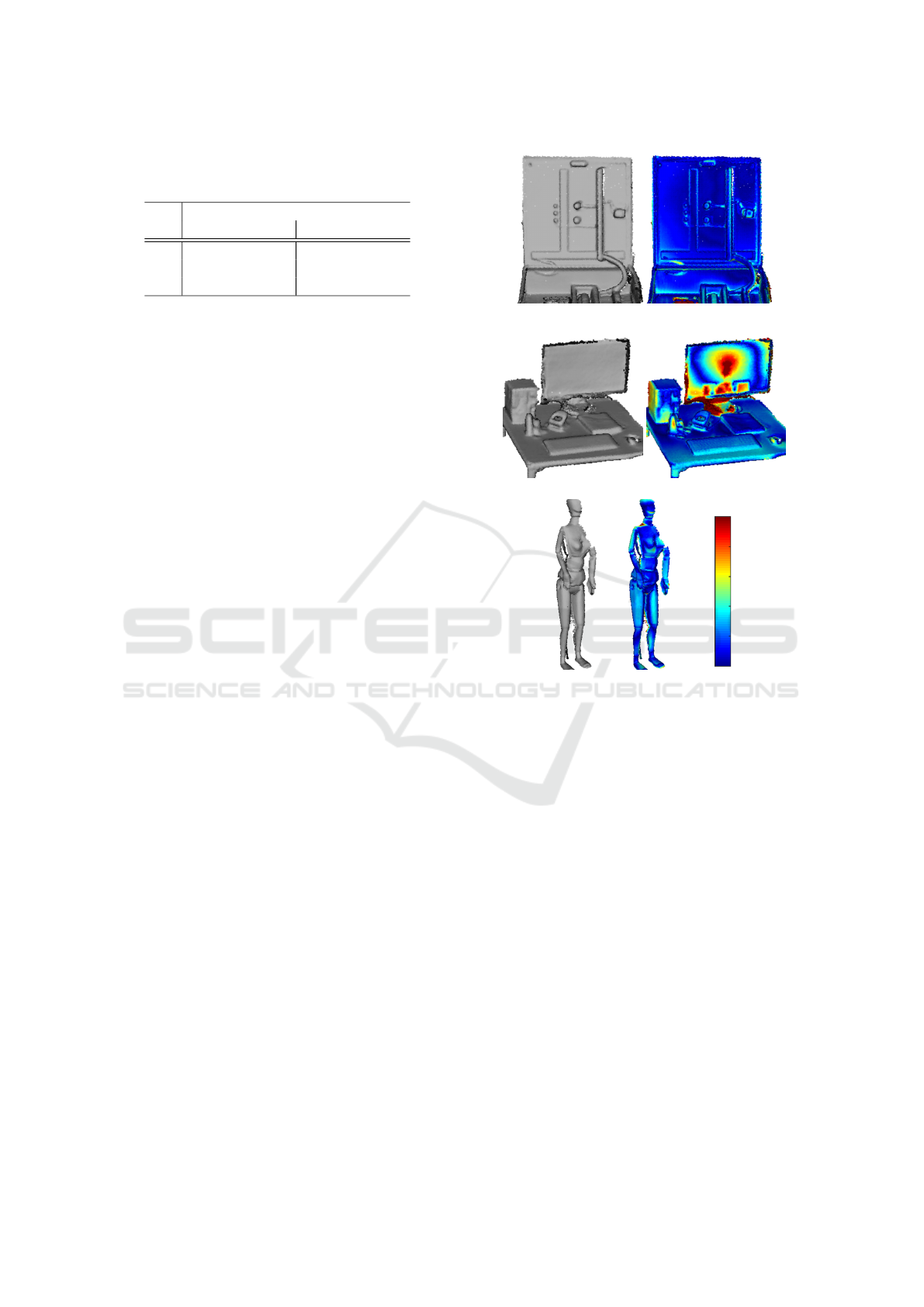
Table 1: Quantitative evaluation of the proposed algorithm
on the rigid CoRBS benchmark (Wasenm
¨
uller et al., 2016c).
A visual evaluation is provided in Figure 3.
KinectFusion Ours
mean RMSE mean RMSE
E5 0.017 0.026 0.014 0.023
D2 0.018 0.027 0.016 0.023
H2 0.015 0.025 0.013 0.022
ence of estimation errors is minimized. Estimating
the camera pose with RANSAC by using point cor-
respondences is a reliable method (from our experi-
ence) unless the non-rigid transformations get to large
(> 10cm). The traditional ICP-based camera pose es-
timation – like e.g. in KinectFusion – can also be ap-
plied here, but leads to less accurate results.
The next step is the computation of the non-rigid
transformation nrt
n
for the next iteration. We per-
form this computation by determining the start and
end points of the nrt
n
in the respective point clouds.
Since nrt
n
is computed with respect to the frame n,
the starting points for nrt
n
must be set according to
the corresponding pose. In order to do so we trans-
form the global rigid model with the camera pose n
and back-project all points into the image plane. This
gives us the starting points for nrt
n
, while the end
points are projected depth values of frame n. The cor-
respondences between the start and end points can be
determined by following the non-rigid transformation
nrt
n−1
of the previous frame n − 1 together with the
scene flow estimation. Due to occlusions it might
happen that for some points these correspondences
can not be estimated. But, under the as-rigid-as-
possible assumption (Sorkine and Alexa, 2007) these
correspondences can be propagated out of the local
neighborhood. As motivated in Section 3.1 we use a
sparse warp field to represent the non-rigid transfor-
mation nrt
n
. Thus, we estimate the nrt
n
for patches
in the image space with RANSAC using the esti-
mated start to end point correspondences. For each
patch we estimate a single transformation (consist-
ing of translation and rotation), which can be interpo-
lated between the patch centers. In our reconstruction
pipeline we use an uniform distribution of the patches.
Using the sparse warp field accelerates the runtime
clearly. Since the estimation of nrt
n
depend heavily
on nrt
n−1
and also the results are quite similar, this is
more an incremental update than a new calculation.
The last step in each iteration is to update to global
rigid model with the new measurements of frame n.
Obviously, they cannot be inserted directly due to the
non-rigid movements in the scene. In order to insert
new measurements correctly we try to compensate
all differences to the rigid model, which were intro-
(a) E5
(b) D2
0.03m
0.00m
(c) H2
Figure 3: Evaluation on the rigid CoRBS benchmark
(Wasenm
¨
uller et al., 2016c). The left side shows the re-
construction and the right side a color-coded comparison to
the ground truth. Quantitative values are given in Table 1.
duced by non-rigid movements. The combination of
the scene flow estimation and the non-rigid transfor-
mation nrt
n−1
contains these non-rigid movements.
Starting from the projected depth points of the frame
n we translate these points with the inverse scene flow.
This gives us a geometrically similar representation to
the prepared model (cp. Section 3.2). With a nearest
neighbor search we can find the corresponding points
between these two models. Based on that we can also
inverse the (in the beginning of the iteration) applied
non-rigid transformation nrt
n−1
. As a result we re-
ceive the input frame n transformed in such a way that
it corresponds to the global rigid model in the cameras
pose n − 1. Since also the pose n − 1 is known, the
points can be consistently inserted into the model. For
the representation of the global rigid model we use
the truncated signed distance function (TSDF) like
many rigid reconstruction pipelines (e.g. KinectFu-
sion (Newcombe et al., 2011)). This representation
has the advantage to remove remaining noise and to
Towards Non-rigid Reconstruction - How to Adapt Rigid RGB-D Reconstruction to Non-rigid Movements?
297

(a) frame 1 (b) frame 300 (c) comparison (d) frame 1 (e) frame 300 (f) comparison
0.02m
0.00m
Figure 4: Evaluation of the proposed algorithm on two non-rigid human body scenes. In both sequences the arms are moved
for up to 5cm. The images show the reconstructed global rigid model after the given number of frames. Despite the movement,
the reconstructed model stays rigid as confirmed in the comparison plots between the first frame and frame 300.
provide a smooth surface. After that step the next it-
eration with the input frame n + 1 starts.
4 EVALUATION
For the evaluation we use two different categories
of data. First, we use the rigid CoRBS benchmark
(Wasenm
¨
uller et al., 2016c) in order to show the func-
tionality and accuracy of our reconstruction pipeline
in the rigid case. Second, we use non-rigid sequences
of human bodies in order to show the functionality of
the proposed algorithm.
The rigid CoRBS benchmark (Wasenm
¨
uller et al.,
2016c) contains several image sequences of rigid
scenes together with a ground truth reconstruction
of the scene geometry. We use this benchmark
in order to show the full functionality of the pro-
posed incremental non-rigid transformation nrt. Ide-
ally, the nrt transformation should always be zero in
these sequences. In our evaluation experiments we
achieved very small nrt transformation, caused by mi-
nor measurement and estimation errors. Inaccurate
estimations get corrected in the subsequent iteration
of the reconstruction pipeline. Table 1 provides a
quantitative evaluation of the computed reconstruc-
tions against a ground truth. The accuracy achieves
state-of-the-art performance with an average error of
15mm. In Figure 3 this comparison is visualized.
The main parts of the three scenes are reconstructed
correctly. Only the black screen contains errors due
to imprecise raw depth measurements (Wasenm
¨
uller
et al., 2016b). From these experiments we can con-
clude that the proposed reconstruction works properly
and accurately for rigid scenes.
Furthermore, we try to evaluate the novel algo-
rithm for a non-rigid scene. Unfortunately, for non-
rigid scenes no benchmark with ground truth geom-
etry is existing. This makes it difficult to perform a
quantitative evaluation and to compare the algorithm
against other state-of-the-art approaches. Thus, we
recorded own scenes of human bodies with different
kinds of movement (e.g. moving arms, moving belly,
etc.) and perform a visual evaluation like recent re-
lated publications in this field. The persons in Figure
4 move their arms for up to 5cm during capturing.
The camera moves around the persons. The first im-
age shows the initial frame, which defines the pose of
the global rigid model. The second image shows the
reconstructed global rigid model after 300 iterations.
In between these frame the camera moved as well as
the persons moved non-rigidly. In oder to verify the
rigidity between these two models we visualize their
geometric difference in the third image. The differ-
ence is in most positions below 1cm, which is the raw
measurement accuracy (Wasenm
¨
uller et al., 2016b).
Thus, we can conclude that our novel algorithm
is able to reconstruct rigid models out of non-rigid
scenes. During our evaluation we tested several
datasets with different amount of non-rigid move-
ment. We realized that the novel algorithm can handle
non-rigid movements of up to 5cm; afterwards the re-
construction accuracy decreases clearly.
5 CONCLUSION
In this paper, we proposed a novel non-rigid RGB-
D reconstruction pipeline, which was adapted from
a state-of-the-art rigid reconstruction algorithm. We
showed that it is possible to reconstruct a global rigid
model under non-rigid movements in the scene, by
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
298

explicitly estimating and considering the non-rigid
transformation nrt of the scene. We proposed a novel
image based sparse warp field to compute, store and
apply this transformation efficiently. In the evaluation
we showed that the reconstruction achieves state-of-
the-art accuracy for rigid scenes and is able to recon-
struct non-rigid scene with up to 5cm movement.
ACKNOWLEDGEMENTS
This work was partially funded by the Federal Min-
istry of Education and Research (Germany) in the
context of the Software Campus in the project Body
Analyzer. We thank the Video Analytics Austria Re-
searchgroup (CT RTC ICV VIA-AT) of Siemens – es-
pecially Michael Hornacek and Claudia Windisch –
for the fruitful collaboration.
REFERENCES
Aitpayev, K. and Gaber, J. (2012). Creation of 3d human
avatar using kinect. Asian Transactions on Fundamen-
tals of Electronics, Communication & Multimedia.
Besl, P. J. and McKay, N. D. (1992). Method for registration
of 3-d shapes. In Robotics-DL tentative.
Brown, B. J. and Rusinkiewicz, S. (2007). Global non-
rigid alignment of 3-d scans. In ACM Transactions
on Graphics (TOG).
Cui, Y., Schuon, S., Thrun, S., Stricker, D., and Theobalt,
C. (2013). Algorithms for 3D shape scanning with a
depth camera. IEEE Transactions on Pattern Analysis
and Machine Intelligence (PAMI).
Dou, M., Fuchs, H., and Frahm, J.-M. (2013). Scanning
and tracking dynamic objects with commodity depth
cameras. In IEEE International Symposium on Mixed
and Augmented Reality (ISMAR). IEEE.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: a paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM.
F
¨
ursattel, P., Placht, S., Balda, M., Schaller, C., Hofmann,
H., Maier, A., and Riess, C. (2016). A comparative
error analysis of current time-of-flight sensors. IEEE
Transactions on Computational Imaging.
Hauswiesner, S., Straka, M., and Reitmayr, G. (2011). Free
viewpoint virtual try-on with commodity depth cam-
eras. In International Conference on Virtual Reality
Continuum and Its Applications in Industry. ACM.
Hornacek, M., Fitzgibbon, A., and Rother, C. (2014).
Sphereflow: 6 dof scene flow from rgb-d pairs. In
IEEE Conference on Computer Vision and Pattern
Recognition (CVPR).
Innmann, M., Zollh
¨
ofer, M., Nießner, M., Theobalt, C.,
and Stamminger, M. (2016). VolumeDeform: Real-
time volumetric non-rigid reconstruction. In Euro-
pean Conference on Computer Vision (ECCV).
Jaimez, M., Souiai, M., Gonzalez-Jimenez, J., and Cremers,
D. (2015). A primal-dual framework for real-time
dense rgb-d scene flow. In IEEE International Con-
ference on Robotics and Automation (ICRA).
Kerl, C., Sturm, J., and Cremers, D. (2013). Dense visual
slam for rgb-d cameras. In International Conference
on Intelligent Robot Systems (IROS).
Kopf, J., Cohen, M. F., Lischinski, D., and Uyttendaele, M.
(2007). Joint bilateral upsampling. In ACM Transac-
tions on Graphics (TOG). ACM.
Li, H., Vouga, E., Gudym, A., Luo, L., Barron, J. T., and
Gusev, G. (2013). 3d self-portraits. ACM Transactions
on Graphics (TOG).
Newcombe, R. A., Fox, D., and Seitz, S. M. (2015). Dy-
namicFusion: Reconstruction and tracking of non-
rigid scenes in real-time. In IEEE Conference on
Computer Vision and Pattern Recognition (CVPR).
Newcombe, R. A., Izadi, S., Hilliges, O., Kim, D., Davison,
A. J., Kohi, P., Shotton, J., Hodges, S., and Fitzgibbon,
A. (2011). KinectFusion: Real-time dense surface
mapping and tracking. In IEEE International Sym-
posium on Mixed and Augmented Reality (ISMAR).
Sorkine, O. and Alexa, M. (2007). As-rigid-as-possible sur-
face modeling. In Symposium on Geometry Process-
ing (SGP).
Wasenm
¨
uller, O., Ansari, M. D., and Stricker, D. (2016a).
DNA-SLAM: Dense Noise Aware SLAM for ToF
RGB-D Cameras. In Asian Conference on Computer
Vision Workshop (ACCV workshop). Springer.
Wasenm
¨
uller, O., Meyer, M., and Stricker, D. (2016b).
Augmented Reality 3D Discrepancy Check in Indus-
trial Applications. In IEEE International Symposium
on Mixed and Augmented Reality (ISMAR). IEEE.
Wasenm
¨
uller, O., Meyer, M., and Stricker, D. (2016c).
CoRBS: Comprehensive RGB-D Benchmark for
SLAM using Kinect v2. In IEEE Winter Conference
on Applications of Computer Vision (WACV).
Wasenm
¨
uller, O., Peters, J. C., Golyanik, V., and Stricker,
D. (2015). Precise and Automatic Anthropometric
Measurement Extraction using Template Registration.
In International Conference on 3D Body Scanning
Technologies (3DBST).
Whelan, T., Kaess, M., Fallon, M., Johannsson, H.,
Leonard, J., and McDonald, J. (2012). Kintinuous:
Spatially extended KinectFusion. In RSS Workshop on
RGB-D: Advanced Reasoning with Depth Cameras.
Zhang, Q., Fu, B., Ye, M., and Yang, R. (2014). Quality dy-
namic human body modeling using a single low-cost
depth camera. In 2014 IEEE Conference on Computer
Vision and Pattern Recognition. IEEE.
Towards Non-rigid Reconstruction - How to Adapt Rigid RGB-D Reconstruction to Non-rigid Movements?
299