A Multiscale Circum-ellipse Area Representation for Planar Shape
Retrieval
Taha Faidi
1,2
, Faten Chaieb
1
and Faouzi Ghorbel
1
1
Cristal Laboratory, ENSI, Manouba University, 2010, Manouba, Tunisia
2
Research and Studies Telecommunications Center (CERT), Technology Parc, Ariana, Tunisia
Keywords:
Shape Signature, Multiscale Representation, Affine Invariant, Triangle Circumscribed Ellipse.
Abstract:
In this paper, we propose a new Multiscale Circum-ellipse Area Representation (MCAR) for planar contours.
The proposed representation deals with a multiscale shape signature defined from the local area delimited by
the circumscribed ellipse of the triangle formed by three contour points and the contour. This shape signature
describes, at each scale level, the concavity/convexity at each contour point. Then, Fourier descriptors are
obtained by applying Fourier transform to the proposed multiscale signature. Thus, the proposed MCAR based
Fourier Descriptors handle the local and global shape characteristics. Furthermore, it is invariant to affine
transformation and robust to local deformations. The performance of our proposed method was evaluated
through the precision recall and bull’s-eye tests on the two well-known databases (MCD and MPEG7-setB).
Obtained results indicate that our method outperforms the shape signatures based Fourier descriptor proposed
in the literature.
1 INTRODUCTION
Shape representation and description of planar ob-
jects, which are subjected to certain viewpoint vari-
ation and partially occultation, is widely considered
as a fundamental subject in many applications of pat-
tern recognition and computer vision, such as robotic
vision, content-based image retrieval, and pose esti-
mation.
Deformations induced by capturing a planar object
from the real space in different viewpoint is often ap-
proximated by an affine transformation when the ob-
ject is far away from the camera. Thus, a shape de-
scriptor should be invariant under affine transforma-
tions which includes scaling, changes in orientation,
shearing and translation.
A variety of shape descriptors have been proposed in
the literature during the last decades that can be di-
vided in two main classes: contour based-techniques
and region based techniques.
In region based technique, all the pixel within a shape
are used to derive the shape representation, but only
the boundary points are used to obtain the contour
based shape representation technique.
Common region-based shape descriptors are,
moment based techniques including geometric,
Zernike, pseudo Zernike and Legendre moments (Hu,
1962; Lin and Chou, 2003), Angular radial transform
(ART) (Bober, 2001), shape matrix (Bober, 2001)
and generic Fourier descriptor.
In recent years, several contour based-shape descrip-
tors have been proposed in the literature due to its
good performance in different applications.
Fourier descriptors is a promising contour based
approach for shape retrieval. In general, the planar
contour is firstly converted to a periodic 1-D signa-
ture and followed by the application of the Fourier
transform. Many signatures have been proposed as
a Fourier descriptor in the literature (T.Zahn, 1972;
D.S.Zhang, 2005; I.Kunttu, 2007). Some of them
are, the complex coordinates (CC), the radial distance
(RD), the triangular centroid area (TCA),Angular ra-
dial coordinates (ARC) and the farthest point distance
(FPD)(A.El-Ghazal, 2007). Most of Fourier descrip-
tor are based on the magnitude of the Fourier trans-
form and ignore the phase information in order to
make descriptor invariant to rotation and independent
to starting point. To maintain the phase informa-
tion,(Bartolini et al., 2005) have proposed a Fourier
descriptor by using the magnitude and the phases of
Fourier transform. In (F.Chaker, 2003), an affine
and complete based Fourier Descriptors has been pro-
398
Faidi T., Chaieb F. and Ghorbel F.
A Multiscale Circum-ellipse Area Representation for Planar Shape Retrieval.
DOI: 10.5220/0006172803980404
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 398-404
ISBN: 978-989-758-225-7
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

posed.
Multiscale approaches are widely studied in the re-
cent years and they are based on a natural representa-
tion of shape information at multiple level of details.
In general multiscale descriptors could be classified
in two main categories: Those based on a multiscale
geometric contour representation and those based on
a multiscale signature definition. In the first category,
the contour is gradually smoothed and a shape sig-
nature is obtained from each contour scale. We can
cite the well-known MPEG 7 shape descriptor, called
Curvature scale space descriptor (CSS) (Abbasi et al.,
1999; Abbasi et al., 2000) where the initial contour is
gradually smoothed with an increasing value of Gaus-
sian kernel, and the shape signature is computed by
the ranking of the inflexion points at different scales.
Similar to the CSS, multiscale concavity/convexity
(MCC) (Adamek T., 2004), represent the shape con-
tour by the degree of the concavity/convexity between
two consecutive Gaussian contour scales. This rep-
resentation is invariant to Euclidian transformation
and robust to partial occultation but suffers from the
high time complexity needed to solve shape match-
ing problem. The Multi-resolution affine invariant
Fourier descriptor (FD-APS) proposed in (T.Faidi,
2015), is based on a multi resolution representation
of the contour. For each contour resolution, the
shape signature is computed as the area of the triangle
formed by the centroid points of the original contour
and two given points from respectively original con-
tour and the contour at a given scale. This representa-
tion is invariant to affine transformation and robust to
small occultation.
In the second approach, the descriptor is derived from
a multiscale definition of the signature such as the
Triangular area representation (TAR) (Alajlan et al.,
2007) and the multiscale contour flexibility based
Fourier descriptor(Xin Shu, 2015). The Triangular
area representation (TAR) define the multiscale
representation by a progressive triangle side length
at each point and take the area of each triangle as a
shape signature. The contour flexibility concept is
firstly introduced in (C.Xu, 2009) where an interior
and exterior neighboring regions centered to a land-
marks points in the contour are used to measure the
contour flexibility by an Euclidean distance function.
Recently, Xin Shu and al are extending flexibility
signature to a multiscale approach by taking different
level of bendable parameter in order to describe the
shape by a local and global representation (C.Xu,
2009). This representation it can reflect how ex-
tensively the neighborhood of a given point in the
contour are connected to the main body but it is not
invariant to affine transformation.
In this work we propose a new multiscale shape de-
scriptor, denoted MCAR, derived from a multiscale
signature definition based on the area of triangle
circum-ellipse. Furthermore, the proposed descriptor
is by definition invariant to affine transformations.
This paper is organized as follows: Section 2 in-
troduces the proposed multiscale shape signature
(MCAR). Section 3 describes the MCAR based
Fourier Descriptors obtained by applying Fourier
transform to the proposed multiscale signature. In
Section 4, experimental results are presented to eval-
uate our descriptor and compare it to state of the art
methods.
2 MULTISCALE
CIRCUM-ELLIPSE SHAPE
SIGNATURE
Let Γ = (x(t), y(t)) be a closed contour of a 2D planar
shape.
Figure 1: MCAR shape descriptor bloc diagram.
In figure1 we show the main steps needed to com-
pute our proposed multiscale shape signature. First,
the contour Γ is normalized by translating the con-
tour centroid to the origin of the 2D coordinate sys-
tem. Furthermore, the initial contour parametrization
would not be necessary the same for different views.
The descriptors computed from two different parame-
terizations of the same geometric curve are generally
different. This is due to parametrization dependance
on transformations. One solution to this problem con-
sist in performing a G-invariant reparametrization of
the curve where G is the considered geometric trans-
formations group.
In the case of affine transformations group, we carry
out a reparametrization by the normalized affine arc-
length defined as:
¯s
a
(t) =
1
L
a
Z
t
0
(||det(γ
0
(t), γ
00
(t))||)
1
3
dt, t ∈[0, T ].
(1)
where L
a
is the curve affine length.
A Multiscale Circum-ellipse Area Representation for Planar Shape Retrieval
399

Finally, a multiscale shape signature is computed.
This latter is detailed in the next section.
2.1 Formulation
In this section, we denote by {P
i
= {x
i
, y
i
}}
i=1···N
the discrete affine arc-length reparametrization of Γ
where N is the number of obtained contour points.
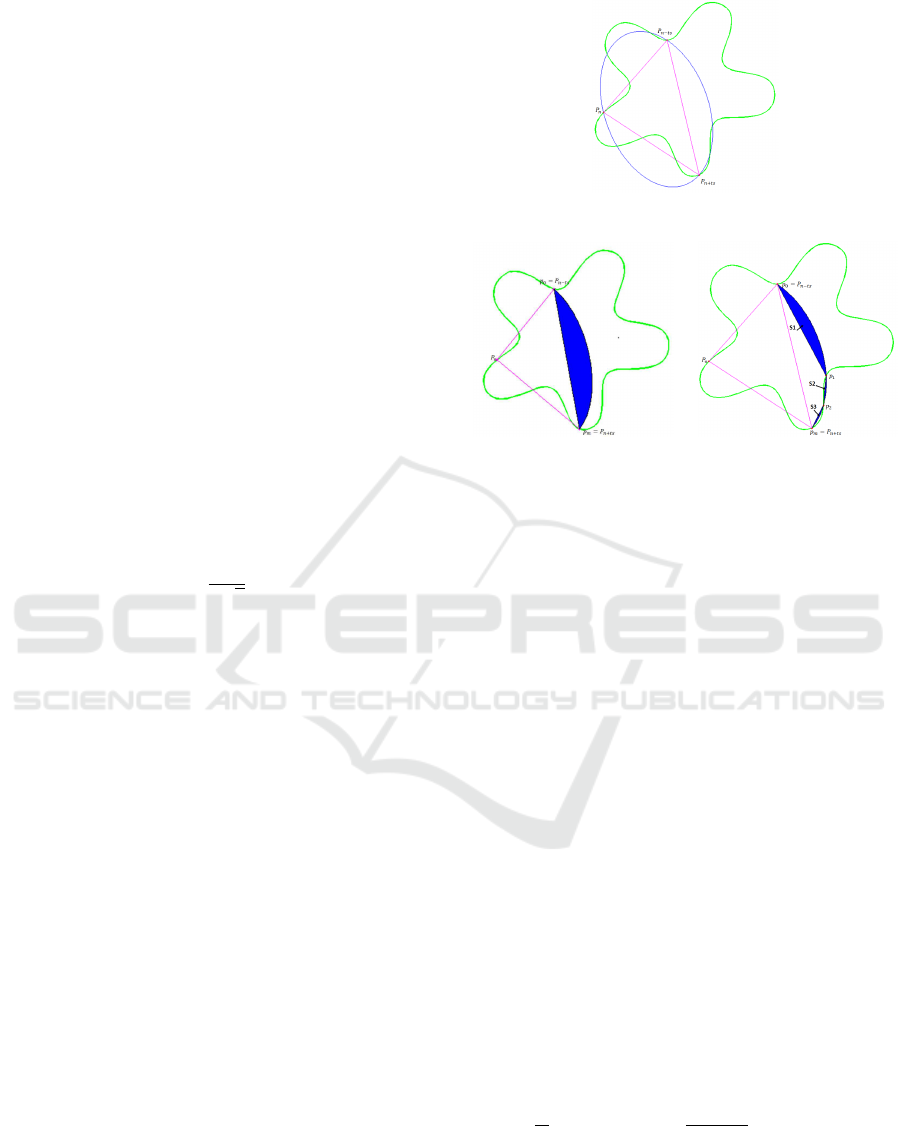
Let E
n,t
s
, the circumscribed ellipse of the triangle
4
n,t
s
= P
n−t
s
P
n
P
n+t
s
where P
n−t
s
= (x
n−t
s
, y
n−t
s
),
P
n
= (x
n
, y
n
) and P
n+t
s
= (x
n+t
s
, y
n+t
s
) are three
consecutive contour points and t
s
is the triangle side
length (See figure 2. a).
The multiscale signature at scale t
s
denoted by
W (n, t
s
) is defined according to the intersection be-
tween the arc γ
n,t
s
=
\
P
n−ts
P
n+t
s
of the ellipse E
n,t
s
and
the shape contour. Two cases can occur:
• case1 (See figure 2.b): γ
n,t
s
T
γ =
/
0.
The shape signature at scale t
s
is defined as
the area of the region delimited by γ
n,t
s
and the
segment [P
n−t
s
P
n+t
s
]. It’s given by:
W (n, t
s
) =
4π
9
√
3
Area(4
n,t
s
) (2)
• case 2 (See figure 2.c): γ
n,t
s
T
γ = {p
i
n
}
i=1···m
.
The shape signature at scale t
s
is defined as the
sum of the area of the regions {S
i
n,t
s
}
i=1···m
de-
limited by the elliptic arc \p
i
p
i+1
and the segment
[p
i
n
p
i+1
n
]. It’s given by the following equation:
W (n, t
s
) =
m
∑
i=0
Area(S
i
n,t
s
) (3)
2.2 Properties
Affine Invariance. The proposed shape descriptor
is invariant to affine transformations. Given a three
points A, B and C from the contour and A
0
, B
0
, C
0
their
image by an affine transformation. If E is the circum-
scribed ellipse of the triangle 4 = ABC then the cir-
cumscribed ellipse E
0
of the triangle 4= A
0
B
0
C
0
exist
and it’s the image of E by the same affine transforma-
tion. This property is verified due to the following
claims :
• The affine transformation maps an ellipse to an
ellipse and preserves the intersection between
curves.
• The uniqueness of the triangle circumscribed el-
lipse.
(a) E
ts
n
: Circumscribed
ellipse
(b) W (n, t
s
) : Shape signa-
ture (case 1)
(c) W (n, t
s
) : Shape signa-
ture (case 2)
Figure 2: Shape signature steps.
Discrimination Property. Figure3 shows the
MCAR shape signature of three shapes from two
different classes (figures 3 (a), (c) and (e)). We can
see that their corresponding shape signatures (figures
3(b), (d) and (f)) are similar for the same class shapes
(camel shape) and dissimilar for those from different
classes (camel and star shape).
Relation Between MCAR Signature and Contour
Concavity/Convexity. Figure 4 shows the signature
at different scales. We can notice that at the scales
(c, d, e and f) all the concavity/convexity parts of the
contours are described by the signature and only dom-
inant features persist over the scales (f and g).
3 MULTISCALE FOURIER
SHAPE DESCRIPTOR
Fourier Descriptors of the multiscale signature are
computed. The discrete Fourier transform of the
signature W (t, t
s
) is given by:
a
(ts)
n
=
1
N
N−1
∑
t=0
W (t, t
s
)exp(
−j 2πnt
N
), n = 0, ··· , N −1
. A Fourier descriptor of the signature W(t, t
s
) are
derived from the Fourier coefficients a
(t
s
)
n
as follows:
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
400

(a) (b)
(c) (d)
(e) (f)
Figure 3: MCAR Signature of For 3 shapes at scale ts=40.
(a) Shape boundary (b) Concavity/convexity at the
scale:ts=25
(c) ts=5 (d) ts=10 (e) ts=15
(f) ts=20 (g) ts=25
Figure 4: MCAR Signature at different scales
ts={5,10,15,20,25}.
DF
(t
s
)
= DF(W (t, t
s
)) =
(
|a
(t
s
)
n
|
|a
(t
s
)
0
|
)
n=1···p
, (4)
where p is the number of Fourier coefficients.
Therefore, the proposed descriptor is defined by
{J
k
}
k=1···N
:
{J
t
s
}
t
s
=1···T
s
= {DF
(t
s
)
}
t
s
=1···T
s
, (5)
where T
s
is the number of scales. In this work, we
consider
N
2
scales.
The similarity measure used to compare two shape
contours Γ1 and Γ2 is formalized as follows:
d(Γ1, Γ2) =
1
T
s
t
s
∑
k=1
kJ1
k
−J2
k
k
2
(6)
where T
s
is the number of contour scales and k.k
2
is
the L
2
norm.
Since the Fourier Descriptors of the signature are in-
variant to rotation and starting point, the proposed
descriptor is invariant to affine transformations and
starting point.
4 EXPERIMENTAL RESULTS
In this section, the performance of our proposed
method is shown using two standard shape datasets
MPEG7-setB and MCD.
Also, it’s compared with some commonly used sig-
natures such as Multiscale Contour flexibility shape
signature for Fourier descriptor, Curvature scale
space(CSS), Perimeter area function(PAF) and the
Multi-resolution Affine Invariant Planar Contour De-
scriptor(DFAP).
4.1 Datasets Description
The well-known MPEG-7 setB dataset (figure5), con-
sists of 1400 images classified into 70 classes. It’s
used for similarity-based retrieval accuracy and shape
descriptors robustness under various arbitrary shape
distortions, that include rotation, scaling, arbitrary
skew, stretching, defection, and indentation. The
Multiview Curve dataset (figure 6) is composed of
40 shape classes selected from MPEG-7 database,
where Each class contains 14 shape samples that cor-
respond to different perspective examples of the orig-
inal curve. This dataset is used in order to evaluate
shape descriptors under affine transformation.
4.2 Performance Evaluation
In order to evaluate the performance of our shape de-
scriptor in the context of image retrieval, we deal with
A Multiscale Circum-ellipse Area Representation for Planar Shape Retrieval
401

(a) (b)
Figure 5: MPEG7 setB dataset.
(a) (b)
Figure 6: MCD dataset.
the precision-recall and the bull’s-eye test which are
the most commonly used test measures.
The precision is defined as the number of relevant
shapes retrieved divided by the total number of shape
retrieved, while the recall is defined as the number of
relevant shapes retrieved divided by the total number
of relevant shapes in the class. The average of the pre-
cision and recall over all the database is used to plot
the precision-recall curve. In the case of the Bull’s-
eye test each shape from the database is used as a
query, if the retrieved shape is in the same class as the
query one then it is considered as a correct response.
The number of correct retrievals in the top 2M (where
M is the size of the class) ranks is counted, includ-
ing the query. Retrieval rate is the percentage of the
maximal possible number of correct retrievals shapes.
In order to be in the same conditions when comparing
our approach with other methods in the MPEG-7 Set
B data set, 128 points are sampled from each contour.
The bulls-eye test results obtained for the the
MPEG7-SetB database are shown in table 1 and
indicate that our descriptor outperforms Fourier
based shape signatures proposed in the literature such
as Fourier Decriptors of TAR, multiscale contour
flexibility descriptors and the DFAP proposed in
(T.Faidi, 2015). The MCAR signature’s performance
is equal to 71.41%. In fact, this is tied to the the-
oretical invariance property of our descriptor under
affine transformations and it’s capability to perfectly
capture the local and global information thanks to the
multiscale technique.
However, the CSS outperforms our descriptor in term
of bulls-eye test. It’s important to note that this de-
scriptor requires high complexity time to solve shape
matching problem. Our proposed descriptor is easy to
compute and uses a simple L
1
distance to measure the
distance between two shape signatures.
Table 1: The Bull-eyes test for our descriptor and other sig-
natures using MPEG-7 database setB.
Shape descriptor Bull-eyes
CSS 75.44
PAF+CD 74.36%
MCAR (proposed) 71.41%
TAR + Fourier descriptor 68.67%
Multiscale Contour flexibility
Fourier descriptor (W+)
67.57%
PAF 66.49 %
DFAP 66.46%
Multiscale Contour flexibility
Fourier descriptor (W+)
65.39%
Figure 7 shows ten random retrieval results from the
MCD database based on the proposed MCAR de-
scriptor. Incorrect responses are obtained for only one
query at the 8, 11, 12 and 13 ranks.
In figure 8, we show the average precision and recall
curves of MCD database for different shape descrip-
tors : Fourier Descriptors of TAR, DFPAS Descriptor
and the CSS descriptor. Our proposed descriptor out-
performs the others.
Figure 8: Average precision and recall of MCD database
retrieval.
5 CONCLUSION
In this paper, a closed-boundary multiscale shape sig-
nature invariant to affine transformation has been in-
troduced. It is defined from the local area delimited
by the circumscribed ellipse of the triangle formed by
three contour points and the contour. At each scale
level, the proposed shape signature, denoted MCAR,
depicts the contour point concavity/convexity. Then,
Fourier descriptors of the MCAR signature are gen-
erated. The multiscale approach combined with the
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
402

Query Retrieved Results
Figure 7: 10 random retrieval results from MCD database.
Fourier Descriptors captures both global and local ge-
ometric characteristics of the shape. Furthermore,
it is invariant to affine transformation and robust to
partial occlusion. The performance of our proposed
method was evaluated through the precision recall
and bull’s-eye tests on the two well-known databases
(MCD and MPEG7-setB). Obtained results indicate
that our method outperforms the shape signatures
based Fourier descriptor proposed in the literature.
ACKNOWLEDGEMENTS
This work is carried out as part of a MOBIDOC the-
sis financed by the European Union under the PASRI
1
program in partnership with the Research and Studies
Telecommunications Center CERT
2
and Cristal
3
lab-
oratory and was supported by the PHC Utique pro-
gram for the CMCU DEFI project (N
o
16G 1403).
REFERENCES
Abbasi, S., Mokhtarian, F., and Kittler, J. (1999). Curvature
scale space image in shape similarity retrieval. Multi-
media Syst, 7(6):467–476.
Abbasi, S., Mokhtarian, F., and Kittler, J. (2000). Enhanc-
ing css-based shape retrieval for objects with shallow
concavities. Image and Vision Computing, 18(3):199–
211.
Adamek T., O. N. (2004). A multiscale representation
method for nonrigid shapes with a single closed con-
1
http://www.pasri.tn/
2
http://www.cert.nat.tn/
3
http://www.arts-pi.org.tn/cristal.php/
tour. IEEE TRANSACTIONS, Circuit Syst,Video Tech-
nol, 14:742–753.
A.El-Ghazal, O.Basir, S. (2007). A new shape signature
for fourier descriptors. 14 th IEEE International Con-
ference on Image Processing SanAntonio,Texas,USA,
pages 161–164.
Alajlan, N., Rube, I., M.S.Kamel, and G.Freeman (2007).
Shape retrieval using triangle-area representation
and dynamic space warping. Pattern Recognition,
40(7):1911–1920.
Bartolini, I., Ciaccia, P., and Patella, M. (2005). Warp: ac-
curate retrieval of shapes using phase of fourier de-
scriptors and time warping distance. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
27(1):142–147.
Bober, M. (2001). Mpeg-7 visual shape descriptors. IEEE
Trans. Circuits and Systems for Video Technology,
11(6):716–719.
C.Xu, J.Liu, X. (2009). 2d shape matching by contour flex-
ibility. IEEE TRANSACTIONS ON PATTERN ANAL-
YSIS AND MACHINE INTELLIGENCE, 31.
D.S.Zhang, G. (2005). Study and evaluation of different
fourier methods for image retrieval. Image and Vision
Computing, 23:33–49.
F.Chaker, M.Bannour, F. (2003). A complete and stable
set of affine-invariant fourier descriptors. 12th In-
ternational Conference on Image Analysis and Pro-
cessing, pages 578–581.
Hu, M.-K. (1962). Visual pattern recognition by moment
invariants. Information Theory, IRE Transactions on,
8(2):179–187.
I.Kunttu, L. (2007). Shape-based retrieval of industrial sur-
face defects using angular radius fourier descriptor.
IET Image Processing, 1:231–236.
Lin, T.-W. and Chou, Y.-F. (2003). A comparative study of
zernike moments. In Web Intelligence, 2003. WI 2003.
Proceedings. IEEE/WIC International Conference on,
pages 516–519.
T.Faidi, F.Chaieb, F. (2015). A new multi-resolution affine
A Multiscale Circum-ellipse Area Representation for Planar Shape Retrieval
403

invariant planar contour descriptor. Image Analysis
and Processing-ICIAP 2015, 9280:494–509.
T.Zahn, R. (1972). Fourier descriptors for plane closed
curves. IEEE Transactions on Computers, 21:269–
281.
Xin Shu, Lei Pan, X.-J. W. (2015). Multi-scale contour flex-
ibility shape signature for fourier descriptor. Journal
of Visual Communication and Image Representation,
26:161167.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
404