
Efficient Resource Allocation for Sparse Multiple Object Tracking
Rui Figueiredo
1
, Jo
˜
ao Avelino
1
, Atabak Dehban
1
, Alexandre Bernardino
1
, Pedro Lima
1
and Helder Ara
´
ujo
2
1
Institute for Systems and Robotics, Instituto Superior T
´
ecnico, Lisboa, Portugal
2
Institute for Systems and Robotics, Universidade de Coimbra, Coimbra, Portugal
{ruifigueiredo, joao.avelino, atabak, alex, pal}@isr.tecnico.ulisboa.pt, helder@isr.uc.pt
Keywords:
Active Sensing, Constrained Resource Allocation, Multiple Object Tracking.
Abstract:
In this work we address the multiple person tracking problem with resource constraints, which plays a funda-
mental role in the deployment of efficient mobile robots for real-time applications involved in Human Robot
Interaction. We pose the multiple target tracking as a selective attention problem in which the perceptual agent
tries to optimize the overall expected tracking accuracy. More specifically, we propose a resource constrained
Partially Observable Markov Decision Process (POMDP) formulation that allows for real-time on-line plan-
ning. Using a transition model, we predict the true state from the current belief for a finite-horizon, and take
actions to maximize future expected belief-dependent rewards. These rewards are based on the anticipated
observation qualities, which are provided by an observation model that accounts for detection errors due to
the discrete nature of a state-of-the-art pedestrian detector. Finally, a Monte Carlo Tree Search method is em-
ployed to solve the planning problem in real-time. The experiments show that directing the attentional focci
to relevant image sub-regions allows for large detection speed-ups and improvements on tracking precision.
1 INTRODUCTION
Developing efficient adaptive sensing systems that are
capable of dealing with computational and power lim-
itations as well as timing requirements is of the ut-
most importance in a wide range of fields, including
automatic surveillance (Sommerlade and Reid, 2010),
sports analysis (Wang and Parameswaran, 2004) and
human-robot interaction (HRI) (Mihaylova et al.,
2002).
In multiple object tracking with resource con-
straints scenarios, the observer’s goal is to predict the
best regions in the visual field to attend, in the quest
to evaluate if they pertain to a given set of persons of
interest, and thus to prune the visual search space by
filtering out irrelevant image locations. Current state-
of-the art object detection algorithms are based on ex-
haustive search, sliding window approaches, which
are typically inefficient and agnostic to top-down tem-
poral context.
In this work, we propose a probabilistic frame-
work which poses the multiple object tracking-by-
detection problem as an on-line, resource constrained
decision making, aimed at minimizing the com-
bined targets’ state uncertainty, while coping with
computational processing limitations (see Figure 1).
More specifically, we pose our decision framework
within the Partially Observable Markov Decision
Processes (POMDPs) domain in order to account for
non-deterministic dynamics and partially observable
states. The derived dynamic resource allocation deci-
sion process combines prior knowledge about the tar-
gets’ state dynamics with accumulated probabilistic
information provided from sequentially gathered ob-
servations, in order to optimize multiple target loca-
tion estimation precision (i.e. minimize tracking un-
certainty). In the proposed formulation, actions are
taken from a low dimensional binary space. This
allows for finding decision policies in real-time us-
ing on-line, tree-based, planning algorithms for finite
horizon POMDPs (Ross et al., 2008). Our framework
relies on object detections with associated confidence
measures, obtained from visual information, that are
used to drive the observer’s attentional focus during
multiple object tracking.
Our main contributions are the following. First,
we model the state-dependent uncertainty that arises
during detection due to the discrete nature of the slid-
ing window based detector. Then, we apply an online
Monte Carlo Tree Search method to solve the plan-
ning problem in real-time. The computational bene-
fits of our methodology are demonstrated in a multi-
300
Figueiredo R., Avelino J., Dehban A., Bernardino A., Lima P. and AraÞjo H.
Efficient Resource Allocation for Sparse Multiple Object Tracking.
DOI: 10.5220/0006173103000307
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 300-307
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ple person tracking scenario, by combining it with a
state-of-the-art pedestrian detection algorithm (Doll
´
ar
et al., 2014). Moreover, we note that the proposed
decision making pipeline can be combined with any
general object detection algorithm. All the method-
ologies have been implemented in C++ to make them
suitable for video surveillance or real-time applica-
tions involving robotic platforms provided with vi-
sion.
The remainder of this paper is structured as fol-
lows. In section II we overview some related work
available in the literature. In section III we de-
scribe the various components involved in the pro-
posed adaptive tracking pipeline. In section IV we as-
sess the proposed methodology performance by eval-
uating the balance between efficiency (low computa-
tional requirements) and effectiveness in multiple ob-
ject tracking task-execution. Finally, in section V we
wrap up with some conclusions and future work.
2 BACKGROUND
Adaptive sensing is a trendy topic in many ar-
eas including computer vision (Gedikli et al.,
2007), robotics (Spaan et al., 2015) and neuro-
science (Van Rooij, 2008). Like biological systems,
artificial systems are equipped with limited compu-
tational and energetic resources, and thus, modeling
and replicating the observed mechanisms of selective
attention in humans, is of primordial importance to
develop more efficient and robust strategies for visual
tasks.
Current state-of-the art object detectors are based
on expensive binary classifiers which typically op-
erate over the full image space, in a sliding win-
dow manner. When combined with fast bottom-
up saliency-based approaches that generate object
bounding box proposals, the overall detection process
becomes more efficient (Zitnick and Doll
´
ar, 2014),
since regions that are unlikely to contain objects are
discarded for further processing. However, these ap-
proaches are agnostic to object dynamics, and are
solely based on low-level visual features.
Resource-constrained adaptive sensing, is within
a different line of research, and accounts for dynam-
ical uncertain environments and noisy sensors for se-
quential decision making. The temporal integration
of continuously gathered noisy detections is used to
predict future environment states and decide, in a top-
down manner, where to allocate the limited sensing
resources, according to some task-related goal. It has
been shown that adaptive sensing improves not only
processing efficiency but also estimation robustness
when compared to non-adaptive approaches (Malloy
and Nowak, 2014).
Adaptive sensing problems can be formulated as
POMDPs (Ahmad and Yu, 2013)(Butko and Movel-
lan, 2010)(Chong et al., 2008) that, depending on the
way they compute the policies, belong to two differ-
ent paradigms: Offline methods compute full policies
before run time. Despite achieving remarkable perfor-
mance in visual search tasks, these often require the
evaluation of many possible situations, via backward
induction, and hence take a considerable amount of
time (e.g. hours). Online decision approaches avoid
the computational burden of computing full policies
for many situations, by departing from the current be-
lief state and simulating future rewards for a finite
planning horizon (Ross et al., 2008).
Within the online POMDP domain, the work clos-
est to ours is the one in (Chong et al., 2008), which
proposed a formulation for general adaptive sensing
problems. The authors applied rollout techniques
which are guaranteed to improve upon a provided
base policy, that may be hard or impossible to com-
pute. Rollout techniques evaluate the candidate ac-
tions, by running many Monte-Carlo simulations and
returning the action with the best average outcome.
In this work we rely on a different, widely
known algorithm named Monte Carlo Tree Search
(MCTS) (Browne et al., 2012), which has recently
been given much attention by the Artificial Intelli-
gence community due to its outstanding performance
in the game Go (Gelly et al., 2012). MCTS combines
tree search with randomized rolllout simulations, be-
ing ideal for decision making under uncertainty. To
our knowledge we are the first to apply an online
tree-based POMDP solver in a stochastic resource-
constrained multiple object tracking scenario.
3 ADAPTIVE SENSING:
PROBABILISTIC MULTIPLE
PERSON TRACKING UNDER
RESOURCE CONSTRAINTS
A POMDP for general active sensing can be defined
as a 6-element tuple (X , A,Y , T,O,R) where X , A
and Y denote the set of the possible environment
states, perceptual actions and observations, respec-
tively. State transitions are modeled as a Markov
process and represented by the probability distribu-
tion function (pdf) T (x
t
,x
t−1
) = p(x
t
|x
t−1
). Observa-
tions are generated from states according to the pdf
O(x
t
,a
t
,y
t
) = p(y
t
|x
t
,a
t
).
Under the resource-constrained adaptive sensing
Efficient Resource Allocation for Sparse Multiple Object Tracking
301

Search Regions Proposals
...
Sliding Window-Based Detections
Probabilistic Multiple Pedestrian Tracking
...
Figure 1: The proposed resource-constrained multiple pedestrian tracking pipeline. Given a set of persons being tracked, our
decision making algorithm decides which sub-regions of the visual scene to attend. Then, a sliding window-based detector
is applied to the selected search regions, instead of the whole image. For each region a winning candidate is obtained via
maximum suppression and fed to the associated tracker with probabilistic measures queried from the observation model.
domain, the goal of the planning agent is to de-
vise control strategies that generate perceptual actions
from belief states, such that some intrinsic cumulative
reward is maximized, while accounting for perceptual
limitations. In the rest of this section we describe our
resource-constrained POMDP formulation for multi-
ple pedestrian tracking scenarios.
Let us consider a set of targets indexed by K =
{1,...,K}, being tracked in a 2D image plane I , with
state x
k
∈ X ⊂ R
3
given by
x
k
t
=
"
x
k,c
t
x
k,s
t
#
(1)
where x
k,c
= (u, v) and x
k,s
represent the bounding box
centroid image coordinates and scale, respectively.
Moreover, let us assume a stationary Markov chain
p(x
k
t
|x
k
t−1
) in order to model the object’s state transi-
tion between consecutive frames. Similarly to (Be-
wley et al., 2016) we assume sparsity-in-space and
independence among targets, and a linear constant-
velocity dynamics model, which is a good approxima-
tion for targets that move with low acceleration in 3D
and are not too close to the image plane. Finally, we
assume that the targets’ states are partially observable
and statistically explained by the observation model
distribution p(y
k
t
|x
k
t
).
3.1 Recursive Bayesian Estimation
Object tracking can be achieved by means of recursive
Bayesian estimation, according to
b
k
t
def
=p(x
k
t
|y
k
1
:
t
)
=ηp(y
k
t
|x
k
t
)
¯
b
k
t
(2)
where b
k
t
represents the belief posterior probability
over the target state x
k
t
, given the set of all gathered
observations y
k
1
:
t
taken up to time t, η is a normaliz-
ing factor and
¯
b
k
t
=
Z
p(x
k
t
|x
k
t−1
)b
k
t−1
dx
t−1
(3)
represents the belief after the prediction step. Further-
more, we assume Gaussian state transition and ob-
servation noises and hence tracking is optimally per-
formed using K independent Kalman filters. At each
time instant, each Kalman filter provides a parametric
posterior probability distribution function (pdf) over
the target state
b
k
t
= N ( ˆx
k
t
,Σ
k
t
) (4)
where
ˆx
k
t
=
"
ˆx
k,c
t
ˆx
k,s
t
#
(5)
is the estimated state and
Σ
k
t
=
"
σ
k,c
t
0
0 σ
k,s
t
#
(6)
is the error covariance matrix. Note that here we con-
sider a diagonal covariance matrix and aggregate the
centroid components in order to ease the notation.
3.2 Observation Model
The observations provided by the object detector are
localized bounding boxes, obtained with a pedestrian
detection algorithm. More specifically, at each time
instant the agent collects a set of observations
Y
t
=
n
y
k
t
,k = 1,...,K
o
(7)
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
302

each corresponding to a noisy projection of the k tar-
get state.
Detection noise has several origins, the easiest to
model being the one originated by the discrete nature
of the detector. The noise affecting the center of a
bounding box ε
x
k,c
t
has two origins, both depending
on the scale of the bounding boxes: ε
sl
, the error due
to the sliding window process and ε
sc
i
, the error due to
the uncertainty of the size of the bounding box. The
value of sliding window jumps Q
sl
depends on the
scale of the detection:
Q
n
sl
= s
n
Q
sl
(0) (8)
where Q
n
sl
is the number of pixels between two con-
secutive sliding window positions at scale n and s
n
is
the value of scale n, defined as:
s
n
= 2
n
N
(9)
where N is the number of scales per octave. The
present implementation of the detector has N = 8.
The value of the jumps of the bounding box
center-bottom due to scale change, depend on the
scale. The number of pixels is given by Q
scx
and
Q
scy
, for the x and y coordinates, respectively. In the
worst case scenario, a jump from the actual scale to
the coarsest one, these values are given by:
Q
n
scx
= w
0
(2
n+1
8
− 2
n
8
)/2 (10)
Q
n
scy
= h
0
(2
n+1
8
− 2
n
8
)/2 (11)
where w
0
and h
0
are the width and the height of the
smallest bounding box (n = 0).
Assuming a Gaussian distribution for these quan-
tization errors, the statistics of ε
sl
are given by
µ
n
sl
=
0
0
, Σ
n
sl
=
"
(Q
n
sl
)
2
0
0 (Q
n
sl
)
2
#
(12)
Regarding ε
sc
i
, we approximate the statistics of
these errors by the worst case which is given by
µ
n
sc
,
0
0
, Σ
n
sc
≈
"
(Q
n
scx
)
2
0
0 (Q
n
scy
)
2
#
(13)
Since both sources of noise are independent but
not additive, our observation model considers the
largest one at each time. This yields the final image
observation error ε
n
:
ε
n
∼ N (0,Σ
n
) (14)
where
Σ
n
= max(Σ
n
sl
,Σ
n
sc
) (15)
3.3 Dynamic Search Regions
Let us now consider different time-varying (dynamic)
regions of interest (i.e. bounding boxes) to be at-
tended, each delimiting a target instance hypothesis
u
t
=
[
k∈K
u
k
t
where u
k
t
⊂ X (16)
Search regions are deterministically and analytically
determined from beliefs according to the following
mapping function
f
:
ˆx
k
t
,Σ
k
t
→ u
k
t
(17)
which is defined as follows
u
k
t
=
h
ˆx
k,c
t
− α
c
σ
k,c
t
, ˆx
k,c
t
+ α
c
σ
k,c
t
i
× (18)
h
ˆx
k,s
t
− α
s
σ
k,s
t
, ˆx
k,s
t
+ α
s
σ
k,s
t
i
(19)
where α
s
and α
c
are user selected parameters that
control the width of the confidence bounds and thus
the size of the search regions. This definition accounts
for the confidence level of the true target state being
within the search region. The user selected parame-
ters permit balancing the trade-off between accuracy
and allocation effort (larger vs smaller regions).
Furthermore, we assume that each region has a de-
terministic, time-varying binary activation state
A = {a
k
∈ B, k ∈ K } = B
K
(20)
where B = {0, 1} with 0 and 1 meaning ”not process-
ing” and ”processing”, respectively. Decision making
is therefore performed in a finite multi-dimensional
binary action space and involves selecting which sub
regions of the image space to apply the sliding win-
dow detector to perform measurement update steps.
The belief becomes dependent on actions as follows
b
k
t
(a
k
t
) =
(
¯
b
k
t
if a
k
t
= 0
ηp(y
k
t
|x
k
t
)
¯
b
k
t
if a
k
t
= 1
(21)
where η is a normalizing constant. For attended re-
gions, the predicted belief is approximated by the ex-
pected expected observation uncertainty given by the
observation model, over a finite set of space points
corresponding to detection windows Y
k
⊂ X in the
search region k, according to
b
k
t
(a
k
t
) ≈ c
|Y
k
|
∑
i=1
p(y
k
t
|x
k,i
t
)
¯
b
k,i
t
if a
k
t
= 1 (22)
where c is a normalizing constant, |Y
k
| is the num-
ber of detection windows and
¯
b
k,i
t
= p(x
i
t
|
¯
b
k
t
). Each
p(y
k
t
|x
k,i
t
) is queried on-line from the learned observa-
tion model. Assessing multiple x
i
t
∈ u
k
t
instead of just
ˆx
t
should better approximate the error distribution.
Efficient Resource Allocation for Sparse Multiple Object Tracking
303

3.4 Resource Constrained POMDP with
Belief-dependent Rewards
As previously noted the decision making involved in
resource constrained multiple target tracking scenar-
ios can be formulated within the POMDP framework.
The perceptual agent tries to minimize tracking uncer-
tainty by prioritizing its limited attentional resources
to promising image regions. The instantaneous re-
ward function should thus reflect the action contri-
bution to maximizing the information regarding the
targets’ states. Similarly to (Araya et al., 2010) let us
define the instantaneous reward at time t as the nega-
tive entropy of the belief state, given by the following
expectation
r(b
k
t
(a
k
t
)) =
Z
b
k
t
logb
k
t
dx
t
(23)
For Gaussian beliefs this reward becomes simply
given by
r(b
k
t
(a
k
t
)) ≈ − log(|Σ
k
t
|) (24)
Inspired by the evidence of visual processing ca-
pacity limitations in humans (Xu and Chun, 2009), we
formulate the proposed resource constrained informa-
tion maximization as follows:
maximize
a
R
T
= E
"
T
∑
τ=1
γ
τ
K
∑
k=1
r(b
k
t+τ
(a
k
t+τ
))
#
subject to
K
∑
k=1
a
k
t+τ
≤ K
max
∀
τ∈{1,...,T }
K
∑
k=1
a
k
t+τ
|u
k
t+τ
|≤ S
max
A
p
∀
τ∈{1,...,T }
where T is the planning horizon, E [·] is the expecta-
tion operation, r(·) is the reward function, γ ∈ ]0,1]
is a discount factor, |u
k
t+τ
| is the area of the k search
region, K
max
is the maximum region-based activation
capacity, A
p
is the image pixel area and S
max
is the rel-
ative maximum image area that the visual system may
process per time-instant. The first constraint reflects
short-term memory limitations and allows reducing
the action space (assuming K
max
< K), and thus the
branching factor during planning. The second is mo-
tivated by computational effort and timing limitations
that arise during visual processing and contributes to
prune infeasible planning tree branches, by prioritiz-
ing resources to higher uncertainty targets.
3.5 Monte Carlo Tree Search (MCTS)
The MCTS algorithm relies on Monte-Carlo simula-
tions to assess the nodes of a search tree in a best-
first order, by prioritizing the expansion of the most
promising nodes according to their expected reward.
In a nutshell, the algorithm runs Monte Carlo sim-
ulations from the current belief state (i.e. input root
node), and progressively builds a tree of belief states
and outcomes. In the end, the most promising ac-
tion is returned. Each run comprises four phases (see
Fig. 2):
1. Selection: In the selection step a sequence of
actions are chosen within the search tree. Tree
descending is performed from the root until a
leaf node is reached. Action selection is typi-
cally carried out using an algorithm named Up-
per Confidence Bounds for Trees (UCT) (Kocsis
and Szepesv
´
ari, 2006), which elegantly balances
the exploration-exploitation trade-off, during ac-
tion selection. On the one hand, based on the cur-
rent accumulated simulated knowledge, the plan-
ning agent should select actions that may lead to
the best immediate payoffs (exploitation). On the
other hand, the agent should select unexplored ac-
tions since they may yield better long-term out-
comes;
2. Expansion: an action that leads to an unvisited
node is selected and the resulting expanded leaf
node is appended to the tree;
3. Simulation: From the expanded node, actions are
taken randomly in a Monte-Carlo depth-first man-
ner, until a predefined horizon or a terminal state
is reached. Simulation depth (i.e. time hori-
zon) is typically fixed, to deal with real-time con-
straints. Since sampling from a uniform distri-
bution over actions may be suboptimal, problem
specific knowledge should be incorporated to give
larger sampling probabilities to more promising
actions. In our specific problem, we bias this sam-
pling distribution such that regions with higher
entropy are prioritized.
4. Back-propagation: Finally, the simulation re-
wards are back-propagated to the root node. This
includes updating the reward rate stored at each
node along the way.
Finally, runs are repeated until a computational bud-
get (i.e. a triggering timeout or a maximum number
of iterations) is reached, and the best action from the
root node is selected.
3.5.1 Upper Confidence Bounds for Trees (UCT)
The idea of using Upper Confidence Bounds (Auer
et al., 2002) on rewards to deal with the exploration
exploitation dilemma in the face of uncertainty, has
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
304

Figure 2: Monte Carlo Tree Search (image taken from (Browne et al., 2012)).
been widely applied to reinforcement learning prob-
lems. In MCTS, Upper Confidence Bounds for Trees
(UCT) are typically employed in the selection phase,
while descending the tree. The upper confidence
bound accounts for the currently estimated value of
the action, and the estimated UCT variance, accord-
ing to
UCT (a) = r + c
r
logn
v
n
a
(25)
where r is the estimate for the value of the action
based on the simulated payoffs, n
v
is the number of
times the node has been visited, and n
a
is the num-
ber of times an action a has been tried from that node.
The constant c is a problem-dependent parameter that
balances the exploration-exploitation trade-off.
4 EXPERIMENTS
In order to evaluate the proposed resource-
constrained tracking approach we performed a
set of experiments on the TUD-Stadtmitte MOTChal-
lenge dataset (Leal-Taix
´
e et al., 2015), which allows
to evaluate tracking performance with the CLEAR
MOT metrics and known ground truth (Bernardin
and Stiefelhagen, 2008). This dataset comprises a
video sequence of 179 images, acquired with a static
camera with 640 × 480 image resolution. An average
of 8 pedestrians are present in the visual field, during
the video. To quantitatively assess the performance
of our methodologies we focused our evaluation in
the time speed-up gains and in the multiple object
tracking precision (MOTP), which is the total error
in estimated position for matched object-hypothesis
pairs over all frames, averaged by the total number of
matches:
MOTP =
∑
i,t
d
i
t
∑
t
c
t
(26)
where d
i
t
∈ [0, 100] quantifies the amount of overlap
(in percentage) between the true object o
i
and its as-
sociated hypothesis bounding boxes, and where c
t
is
the number of matches found for time t. The MOTP
shows the ability of the tracker to keep consistent tra-
jectories.
Our aim was to investigate the performance of the
proposed methodologies dependency on the resource-
constraints. We considered the following activa-
tion capacities K
max
∈ {1,2,3,4,5} and maximum
processing image areas S
max
∈ [0.1,1.0]. Since the
MCTS method is randomized, we performed 100 tri-
als for each combination of parameters. The region
size parameters where found empirically and were set
to α
c
= α
s
= 1. At each time step, the MCTS plan-
ning root node was set to the current tracking belief,
and the algorithm was allowed to run for 10ms. Fi-
nally, the simulation step depth was set to 3 and γ
was set to 0.9. The association between detections
and trackers was performed with the Hungarian Al-
gorithm (Burkard et al., 2009) using the Mahalanobis
distance. The tracking process is bootstrapped in the
first frame, by applying the pedestrian detector to the
whole image and instantiating a tracker for each de-
tection. These trackers are kept during the entire
video sequence, and every non-assigned detection is
discarded, i.e., trackers are not further created.
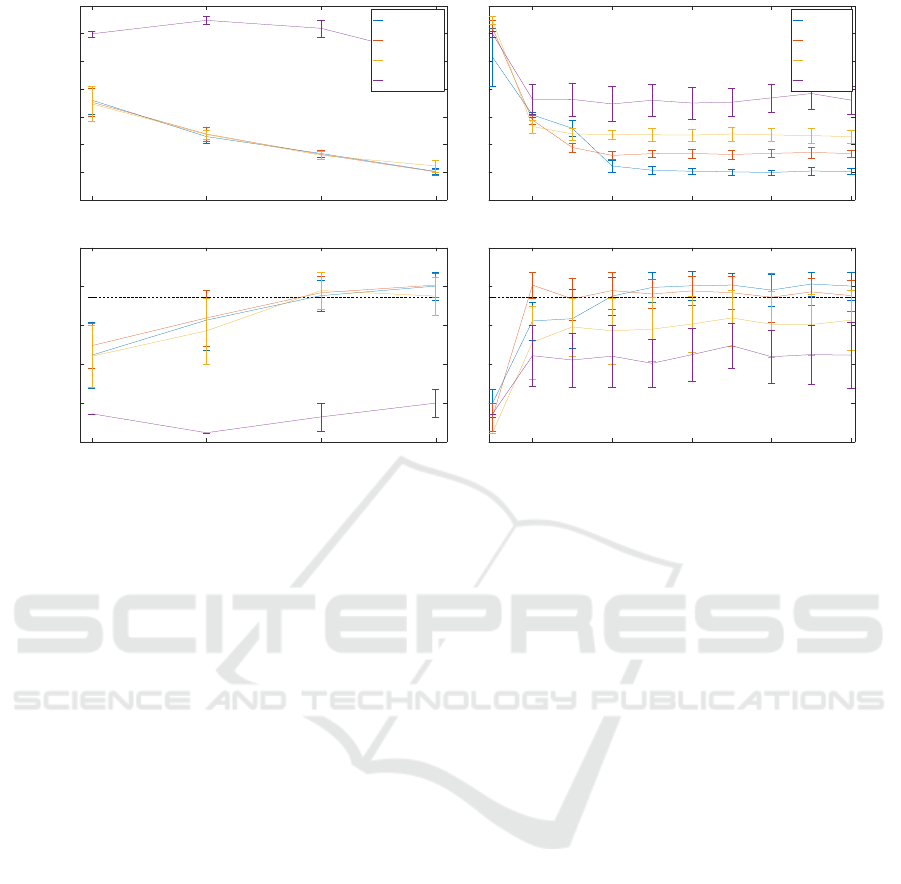
The results presented in Figure 3 demonstrate that
planning future resource allocations in a constrained
setting, improves simultaneously detection times and
tracking precision, when compared with the baseline,
Efficient Resource Allocation for Sparse Multiple Object Tracking
305
K
max
1 2 3 4
Gain
0
2
4
6
8
10
12
14
S
max
=1.0
S
max
=0.7
S
max
=0.4
S
max
=0.1
S
max
0.2 0.4 0.6 0.8 1
Gain
0
2
4
6
8
10
12
14
K
max
=4
K
max
=3
K
max
=2
K
max
=1
K
max
1 2 3 4
MOTP (%)
62
64
66
68
70
72
S
max
0.2 0.4 0.6 0.8 1
MOTP (%)
62
64
66
68
70
72
Figure 3: Speed-up gains and resulting Multiple Object Tracking Precision (MOTP). Bottom-row: Dashed black line repre-
sents the baseline full-window detector.
full-window detector.
As illustrated by the temporal gain plots (first row
of Figure 3), our method achieves detection times
around 12 times faster than the baseline detector
applied to the full-window (0.02 against 0.24 sec-
onds, for S
max
= 0.1), with comparable tracking per-
formance. Furthermore, the MOTP metric results
demonstrate that, on the one hand, constraining the at-
tention to regions with high probability of pertaining
a person, allows to improve detection accuracy and to
reduce the possibility of erroneous detections in the
targets’ vicinities, which may lead to bad detection-
tracker associations and hence degrade tracking preci-
sion. On the other hand, ignoring regions that are un-
likely to contain a person allows to reduce the number
of spurious wrong detections (i.e. False positives) that
may also contribute to tracking performance degrada-
tion.
In conclusion, in the constrained setting the allo-
cation of more computational resources yields better
tracking precision, at the cost of increased computa-
tional effort. Therefore, depending on the application
requirements, this trade-off can be easily balanced
by carefully selecting the K
max
and S
max
resource-
constraints.
5 CONCLUSIONS AND FUTURE
WORK
In this paper we have addressed the multiple object
tracking (MOT) problem with constrained resources,
which plays a fundamental role in the deployment of
efficient mobile robots for real-time applications in-
volved in HRI. We have framed the multiple object
tracking within the POMDP domain and proposed
a problem formulation that allows for on-line, real-
time, planning with a state-of-the-art Monte Carlo
Tree Search methodology. The results presented in
this work show that directing the attentional focci to
important image sub-regions allows for large detec-
tion speed-ups improvements on tracking precision.
The major limitation of our approach is still its
incapacity of dealing with non-sparse targets. In the
future, data association should also be considered dur-
ing planning by integrating data association method-
ologies such as joint probabilistic data-association
(JPDA) (Hamid Rezatofighi et al., 2015). Another
shortcoming of our methodology is its incapacity of
locating new pedestrians appearing on the scene, in
an efficient manner. However, this can be easily over-
come by considering proposals generated by bottom-
up saliency methods.
Finally, we note that the targets’ dynamics and the
observation distributions are extremely non-linear and
non-Gaussian. Therefore, a mixture of particle fil-
ters (Okuma et al., 2004) would be more appropriate
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
306

for our particular problem, and hence improve track-
ing accuracy at the cost of some additional computa-
tional effort.
ACKNOWLEDGMENT
This work has been partially supported by the
Portuguese Foundation for Science and Tech-
nology (FCT) project [UID/EEA/50009/2013].
Rui Figueiredo is funded by FCT PhD grant
PD/BD/105779/2014.
REFERENCES
Ahmad, S. and Yu, A. J. (2013). Active sensing as
bayes-optimal sequential decision making. CoRR,
abs/1305.6650.
Araya, M., Buffet, O., Thomas, V., and Charpillet, F.
(2010). A pomdp extension with belief-dependent re-
wards. In Advances in Neural Information Processing
Systems, pages 64–72.
Auer, P., Cesa-Bianchi, N., and Fischer, P. (2002). Finite-
time analysis of the multiarmed bandit problem. Ma-
chine learning, 47(2-3):235–256.
Bernardin, K. and Stiefelhagen, R. (2008). Evaluating mul-
tiple object tracking performance: the clear mot met-
rics. EURASIP Journal on Image and Video Process-
ing, 2008(1):1–10.
Bewley, A., Ge, Z., Ott, L., Ramos, F., and Upcroft, B.
(2016). Simple online and realtime tracking. CoRR,
abs/1602.00763.
Browne, C. B., Powley, E., Whitehouse, D., Lucas, S. M.,
Cowling, P. I., Rohlfshagen, P., Tavener, S., Perez,
D., Samothrakis, S., and Colton, S. (2012). A survey
of monte carlo tree search methods. IEEE Transac-
tions on Computational Intelligence and AI in Games,
4(1):1–43.
Burkard, R., Dell’Amico, M., and Martello, S. (2009). As-
signment Problems. Society for Industrial and Ap-
plied Mathematics, Philadelphia, PA, USA.
Butko, N. J. and Movellan, J. R. (2010). Infomax control
of eye movements. Autonomous Mental Development,
IEEE Transactions on, 2(2):91–107.
Chong, E. K., Kreucher, C. M., and Hero, A. O. (2008).
Monte-carlo-based partially observable markov deci-
sion process approximations for adaptive sensing. In
Discrete Event Systems, 2008. WODES 2008. 9th In-
ternational Workshop on, pages 173–180. IEEE.
Doll
´
ar, P., Appel, R., Belongie, S., and Perona, P. (2014).
Fast feature pyramids for object detection. PAMI.
Gedikli, S., Bandouch, J., von Hoyningen-Huene, N.,
Kirchlechner, B., and Beetz, M. (2007). An adaptive
vision system for tracking soccer players from vari-
able camera settings. In Proceedings of the 5th In-
ternational Conference on Computer Vision Systems
(ICVS).
Gelly, S., Kocsis, L., Schoenauer, M., Sebag, M., Silver,
D., Szepesv
´
ari, C., and Teytaud, O. (2012). The grand
challenge of computer go: Monte carlo tree search and
extensions. Communications of the ACM, 55(3):106–
113.
Hamid Rezatofighi, S., Milan, A., Zhang, Z., Shi, Q., Dick,
A., and Reid, I. (2015). Joint probabilistic data asso-
ciation revisited. In Proceedings of the IEEE Interna-
tional Conference on Computer Vision, pages 3047–
3055.
Kocsis, L. and Szepesv
´
ari, C. (2006). Bandit based monte-
carlo planning. In European conference on machine
learning, pages 282–293. Springer.
Leal-Taix
´
e, L., Milan, A., Reid, I., Roth, S., and Schindler,
K. (2015). MOTChallenge 2015: Towards a bench-
mark for multi-target tracking. arXiv:1504.01942
[cs]. arXiv: 1504.01942.
Malloy, M. L. and Nowak, R. D. (2014). Near-optimal
adaptive compressed sensing. IEEE Transactions on
Information Theory, 60(7):4001–4012.
Mihaylova, L., Lefebvre, T., Bruyninckx, H., Gadeyne, K.,
and Schutter, J. D. (2002). Active sensing for robotics
- a survey. In in Proc. 5 th Intl Conf. On Numerical
Methods and Applications, pages 316–324.
Okuma, K., Taleghani, A., De Freitas, N., Little, J. J., and
Lowe, D. G. (2004). A boosted particle filter: Multi-
target detection and tracking. In European Conference
on Computer Vision, pages 28–39. Springer.
Ross, S., Pineau, J., Paquet, S., and Chaib-Draa, B. (2008).
Online planning algorithms for pomdps. Journal of
Artificial Intelligence Research, 32:663–704.
Sommerlade, E. and Reid, I. (2010). Probabilistic surveil-
lance with multiple active cameras. In Robotics and
Automation (ICRA), 2010 IEEE International Confer-
ence on, pages 440–445. IEEE.
Spaan, M. T., Veiga, T. S., and Lima, P. U. (2015).
Decision-theoretic planning under uncertainty with
information rewards for active cooperative percep-
tion. Autonomous Agents and Multi-Agent Systems,
29(6):1157–1185.
Van Rooij, I. (2008). The tractable cognition thesis. Cogni-
tive science, 32(6):939–984.
Wang, J. R. and Parameswaran, N. (2004). Survey of sports
video analysis: research issues and applications. In
Proceedings of the Pan-Sydney area workshop on Vi-
sual information processing, pages 87–90. Australian
Computer Society, Inc.
Xu, Y. and Chun, M. M. (2009). Selecting and perceiving
multiple visual objects. Trends in cognitive sciences,
13(4):167–174.
Zitnick, C. L. and Doll
´
ar, P. (2014). Edge boxes: Locating
object proposals from edges. In ECCV.
Efficient Resource Allocation for Sparse Multiple Object Tracking
307
