Identification of Femoral-Acetabular Symptoms using sEMG Signals

during Dynamic Contraction

Zahra Karimi Tabar

, Chris Joslin

, Mario Lamontagne

and Giulia Mantovani

Systems and Computer Engineering, Carleton University, 1125 Colonel By Drive, Ottawa, Canada

School of Human Kinetics, University of Ottawa, 200 Lees Avenue, Ottawa, Canada

Keywords: Discrete Wavelet Transformation, DWT, EMG Signal Analysis, FAI, Hip Muscles, Non-Stationary Signal,

Signal Decomposition, Wavelet Decomposition.

Abstract: This paper focuses on development of an algorithm that automatically differentiates a Femoro-Acetabular

Impingement (FAI) patient from a healthy control person by comparing their surface electromyography

(sEMG) signal recorded from Gluteus Maximus (GMax), Tensor Fasciae Latae (TFL), and Rectus Femoris

(RF) muscles in the hip area. A discrete wavelet transform (DWT) method was used to analyse sEMG signals

by thirty-eight different wavelet functions (WFs) with 5 decomposition levels of dynamic contractions during

the three phases (descending, stationary, and ascending) of a squat task. The Bior3.9 WF was selected as it

provided higher amount of energy for most of the subjects and then the wavelet power spectrum was computed

for healthy control and FAI groups. The results show that the RF muscle is more active in the ascending phase

than the descending phase for FAI subjects, whereas it is more active in the descending phase for healthy

control. An independent sample t-test was used to check the activities of muscle in both groups. The results

demonstrate no significant difference for GMax (p=0.7477) and TFL (p=0.4997) muscles, while there is a

significant difference for RF muscle (p=0.0670).

1 INTRODUCTION

Femoro-Acetabular Impingement (FAI) is a

pathological condition in which the femoral head and

acetabular socket interact abnormally in the hip joint

(Myers, 1999). This abnormality reduces range of

motion and ability in patients (Keogh, 2008). In

young and active adults with FAI, the pain is usually

in the groin area (Samora, 2011). Hip bone

abnormalities can damage soft tissue structures and

limit the patients’ motion. Useful information can be

obtained from the muscles and such information has

clinical and engineering applications by measuring

Electromyography (EMG) signals. EMG is a

biomedical signal that provides a great source of

information to clinicians and researchers by

measuring the electrical currents generated in

muscles during contraction (Reaz, 2006). The

physiological and anatomical properties of muscles

can influence on the nervous system that controls the

EMG signal (Ahmed, 2009).

We propose an algorithm to discriminate a FAI

patient from a healthy person by comparing their

EMG signal recorded from hip muscles. The

proposed algorithm will produce a way to diagnose

FAI based on muscle activities, which can be a

complement to MRI and x-ray methods.

1.1 Background

An EMG signal recorded from muscles requires

advanced methods for detection, decomposition,

processing, and classification. To use the EMG signal

for diagnosis, a feature needs to be extracted before it

can be analysed or classified. This is due to the fact

that the raw EMG signal includes both useful

information and noise. EMG features can be

computed in various domains such as time,

frequency, time-frequency, and time-scale domains.

Analysis of EMG data requires rectification and

integration of signals or root mean square values to

extract information related to the amplitude of the

signal, which deals with the time domain

representation. However, the frequency content of

EMG is analysed using Fourier Transform (FT) that

is a unidimensional technique (Karlsson, 2001).

Traditional techniques for analysing surface EMG

signal are based on the FT method. The accuracy and

214

Karimi Tabar Z., Joslin C., Lamontagne M. and Mantovani G.

Identiﬁcation of Femoral-Acetabular Symptoms using sEMG Signals during Dynamic Contraction.

DOI: 10.5220/0006173802140222

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 214-222

ISBN: 978-989-758-212-7

reliability of this technique depends on the data

lengths’ and the signal requires to be stationary.

Moreover, a signal can be stationary or non-

stationary. If a signal is stationary, its properties are

statistically invariant over time; however the transient

events cannot be predicted in non-stationary signals.

The EMG signal is a non-stationary signal.

Furthermore, time-frequency methods that are

appropriate for non-stationary signal are used instead

of frequency methods to improve the EMG analysis

(Karlsson, 2001). Thus, for analysing EMG signals in

both time and frequency, the short-term Fourier

transforms (STFT) or wavelets can be used. The

former of the EMG signals usually has three steps:

recording the EMG signals, decomposition of signals

by signal processing techniques, and classification of

signals for diagnostic purpose.

In daily life activities or movements, subjects

perform more dynamic contractions instead of

isometric contractions. Moreover, in the field of

rehabilitation medicine, sports medicine, and etc.,

tasks similar to daily activities are performed. During

dynamic conditions, number of active motor units,

active muscle fibres, electrode geometry, muscle

fibre lengths, and innervation zone geometry

changes. These factors emphasize that the ME signals

are non-stationary. Therefore, time-frequency

methods have been introduced for the analysis of non-

stationary signals. These time-frequency

representation methods are: STFT, Wigner-Ville

distribution (WVD), Choi-Williams Distribution

(CWD), and wavelet transform (WT) that were

compared with recent studies for accuracy and

precision to analyse the ME signals (Karlsson, 2000

and 2001). A time-frequency analysis based on

wavelets (Meyer, 1993), which is introduced recently,

is an appropriate tool to overcome the limitations of

the traditional time-frequency methods. Karlsson

introduced the wavelet transform as a “mathematical

microscope” that help observe various parts of the

signal by setting the focus (Karlsson, 2000 and 2001).

The WT has some advantages over the other time-

frequency methods. WT uses short window for high

frequencies and long window for low frequencies,

although the STFT uses a single analysis window for

all frequencies (Rioul, 1991). Furthermore, the WT

can be used to analyse both stationary and non-

stationary signals in both time and frequency domain.

The WT is classified into continuous wavelet

transforms (CWT) and discrete wavelet transforms

(DWT). The wavelet transform requires the selection

of a mother wavelet depending on the application.

Wavelets are defined by the scaling function (also

called father wavelet) and wavelet function (or the

mother wavelet). The scale function in WT

determines wavelet dilation and compression of the

various wavelets from a mother wavelet.

Furthermore, the optimization of the WT is related to

the scale function, which is used for a specific signal.

The ability of DWT to extract features from the

signal is dependent on choosing an appropriate

mother wavelet function. The common standard

families of wavelet basis functions are Haar,

Daubechies (db1 to db10), Coiflet (coif1 to coif5),

Symmlet (sym2 to sym8), Morlet, and Mexican Hat.

Although there is not a specific rule for selecting a

wavelet basis function, some features of wavelets

cause a specific mother wavelet to be more

appropriate for a particular application and signal

type. According to Santoso et al. (Santoso, 1994)

state, for slow transient disturbances db8 and db10

wavelets were the best choice, whereas for short and

fast transient disturbances db4 and db6 were more

proper. Also, Walker (Walker, 1999) presented

general guidelines for selecting a wavelet such that

db4 was more appropriate for feature extraction and

coiflet6 provided better data compression results. In

order to select a more accurate wavelet function, it is

significant that the characteristic of signal should be

matched with the properties of the wavelet function.

For applying WT to the EMG signal various

mother wavelets and scale functions can be used

although no agreement has been reached regarding

the selection of the mother wavelet and the scale

function. For example, Karlsson et al. (Karlsson,

1999) used a Morlet mother wavelet with a linear

scale function (Karlsson, 1999, 2000, 2003) and Neto

et al. (Neto, 2007) applied Morlet with exponential

function. Von Tscharnar (Von Tscharnar, 2000), used

Cauchy mother wavelets with polynomial function.

Hostens et al. (Hostens, 2004) and Beck et al. (Beck,

2005) applied Daubechies mother wavelets to the

EMG signal with different scale functions. Hostens et

al. (Hostens, 2004), used a linear scale function while

Beck et al. (Beck, 2005) used a dyadic function.

The WT of the EMG signal has been used in

several studies related to muscle fatigue, EMG signal

processing, and muscle strength. Moreover, Neto et

al. (Neto, 2007, 2008), and Von Tscharner et al. (Von

Tscharnar, 2000, 2002, 2003, 2006), used the WT for

the EMG signals that were recorded during the sports.

Flanders (Flanders, 2002) used DWT to identify

the time of occurrence of EMG bursts. They chose

wavelet db2 and focused on the coefficient at an

intermediate scale (D3) because by plotting the peak-

to-peak range of the db2 weighting coefficient values

of several muscles, the D3 component had the largest

peak weighting coefficients based on their research.

Identiﬁcation of Femoral-Acetabular Symptoms using sEMG Signals during Dynamic Contraction

215

Thus, Flanders demonstrated that the simplest

wavelet such as db2 was suitable for recognizing

multiunit EMG bursts. Moreover, Kilby and Gholam

Hosseini (Kilby, 2004) also used mother wavelet that

had a different set of families to extract detailed

features of the sEMG signals. They used mother

wavelets that were available in LabVIEW® to

decompose the sEMG signals and reconstruct the

signal back. The reconstructed signals were

subtracted from the original signals in order to

calculate the errors to achieve statistical analysis.

Based on different errors of the various families of the

mother wavelets, they concluded the Daubechies

(db5) was the most appropriate mother wavelet for

analysing sEMG signals. However, they did not

consider several mother wavelets such as Morlet,

Meyer, and Mexican Hat because these mother

wavelets were not available by the software. Ahmed

et al. (Ahmed, 2009) illustrated a comparative study

of decomposing sEMG signals by using different

types of wavelets. Their goal was to choose a wavelet

based on the best possible energy localization in the

time-scale plane. In their algorithm, they decomposed

a signal using DWT for various wavelets and the

energy localization in time-scale plane was

calculated. From their results, db4, db5, and db6 were

shown to have the best energy localization compare

to other wavelets for normal and healthy muscle

EMG signal.

2 METHODOLOGY

The EMG data of Gluteus Maximus (GMax), Tensor

Fasciae Latae (TFL), and Rectus Femoris (RF)

muscles were recorded from 30 subjects during

dynamic contraction of a squat task (Fig. 1).

Figure 1: Descending, Stationary, and Ascending Phase of

Squat (Lamontagne, 2009).

During the squat, subjects were required to stand

with feet shoulder-width apart, parallel to one

another. Both arms were anteriorly extended, and

heels were in contact with the floor during the entire

squat. EMG signals were recorded during squat

cycles, thus each recorded signal was divided into

three regions based on squat phases (Descending,

Stationary, and Ascending phase). Five repetitions of

the same movement were executed (Lamontagne,

2009) The recorded sEMG signals formed two

groups: control (15 males and 1 female) and FAI (11

males and 3 females). Participant characteristics are

indicated in Table 1.

Table 1: Participant characteristics by group.

Group

Gender

Weight (Kg)

Height (cm)

Control (CON)

104.591

191.2

132.009

179

113.527

176

97.245

152

120.189

180.5

93.078

175.5

83.666

180.5

87.466

168

117.896

177.5

83.551

178

83.311

181

106.529

183

82.646

177

147.725

176

61.129

160.5

79.526

175.5

FAI (OR)

129.012

183.75

83.035

168

139.491

186

133.394

176.5

126.997

174.2

101.154

175

108.719

175

149.428

176

97.508

163

64.312

167

136.712

167

120.632

175

132.507

168.5

59.766

167

The sampling frequency of the signal was

1000Hz. The DC offset was removed from the raw

EMG signals. In order to be able to compare the EMG

activity in the same muscle on different subjects, the

signals have to be normalized. Normalization of

EMG signals were performed by dividing EMG

signals during a squat task to a reference EMG value

achieved from the same muscle of the same subject.

We utilized the Maximum Voluntary Isometric

Contraction (MVIC) method for normalization. To

measure the MVIC the participants were asked to lie

down on a testing bench, which was provided with

support beams and adjustable straps to limit the

movement of the limbs and hold it in place during

isometric contraction. The MVIC data were collected

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

216

for duration of 5 seconds for each muscle. MVICs for

GMax and RF muscles were measured when the

participants’ leg was straight, and they were asked to

push upwards against the Hand-Held Dynamometer

(HHD). Moreover, MVIC for TFL muscle was

collected when the participants were asked to push

diagonally against the HHD. After normalization,

EMG signals were full-rectified meaning that the

absolute value of the signal was used. The rectified

signals were passed through a 5

-order low-pass

Butterworth filter with cut off frequency of 10Hz.

This process provided the linear envelope of signals.

Furthermore, the filtered signals were amplitude-

normalized to the peak MVIC EMG (nEMG) and

then integrated to produce the integrated EMG

(IEMG) values.

2.1 EMG Analysis using Wavelet

Transforms

Data analysis was performed using the MATLAB

programming language with the signal processing

and Wavelet toolboxes (The Math Works, INC.). The

EMG values were recorded from GMax, TFL, and RF

muscles of the affected sides of the 30 subjects. There

were 5 repetitions for every subject with sampling

frequency of 1000Hz. The number of samples in each

EMG data set was very large, so EMG signals were

pre-processed by using the wavelet transform.

The analysis of the data commenced by removing

any DC offset in order to be ready for the wavelet

families’ analysis. The wavelet analysis was

performed by a function called mother wavelet. There

are different families or set of mother wavelets in the

Wavelet method which differ in their mathematical

principles named as Haar, Daubechies (db1 to db10),

Symlets (sym2 to 8), Coiflets (coif1 to 5),

Biorthogonal (bior1.1 to 6.8), Reverse biorthogonal

(rbio1.1 to 6.8), Meyer (meyr), Discrete

approximation of Meyer (dmey), Gaussian (gaus1 to

8), Mexican hat (mexh), and Morlet (morl). EMG

signals were decomposed using DWT with various

wavelet functions (WFs). We used discrete wavelet,

which allowed us to decompose our EMG signals

based on Haar, Daubechies (db1 to db10), Symlets

(sym2 to 8), Coiflets (coif1 to 5), Biorthogonal

(bior1.1 to 6.8), and discrete approximation of Meyer

(dmey) mother wavelets. Moreover, MATLAB code

was written to apply a DWT to the EMG signals. The

WT decomposes a signal into several multi-resolution

(levels) components based on basis functions or WFs.

These WFs are achieved by dilation, contraction, and

shifts of a unique function. Decomposition of the

signal into basis of wavelet functions implies the

computation of the inner products between the signal

and the basis function, leading to a set of coefficients

called wavelet coefficients.

The maximum level to apply the wavelet transform

depends on how many data points are contained

within our data set, while there is a down-sampling

by 2 operations from one level to the next level. We

used 5 levels of decomposition. Thirty eight different

wavelet functions exerted at decomposition level 1 to

5. The wavelet coefficients from each wavelet

function were used to calculate the energy of the

sEMG signals for each subject in each phase.

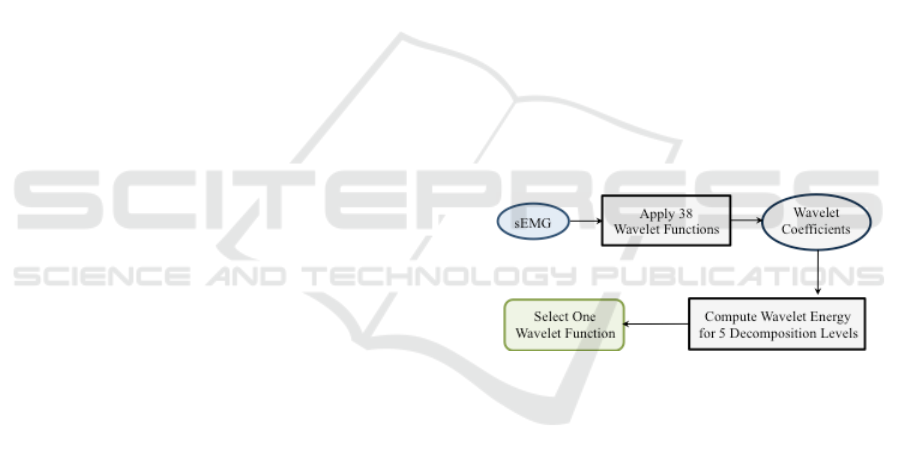
2.2 Wavelet Selection based on Energy

Calculation

The wavelet energy was computed for approximation

(Ea) and detail (Ed) coefficients. Ea is the percentage

of energy corresponding to the approximation and Ed

is the vector containing the percentage of energy

corresponding to the details. Ed for each sEMG signal

was collected after using 38 wavelet functions and the

highest five energies were highlighted for each

subject in three phases. Then, the highest repetition

wavelet function was chosen as our wavelet function.

This procedure is indicated in Fig 2.

Figure 2: Procedure of Selecting a WF.

2.3 Wavelet Power Spectrum

The wavelet power spectrum is a way to determine

the distribution of energy along the sEMG signal.

Wavelet coefficients of the selected wavelet function

were computed and the power spectrum was

measured during 5 levels of decomposition. The

distribution of power for each muscle during

descending, stationary, and ascending phase for both

CON and OR groups was determined. Fig. 3 shows

the block diagram for computing power and

discriminating two groups based on their power

spectrum.

Identiﬁcation of Femoral-Acetabular Symptoms using sEMG Signals during Dynamic Contraction

217

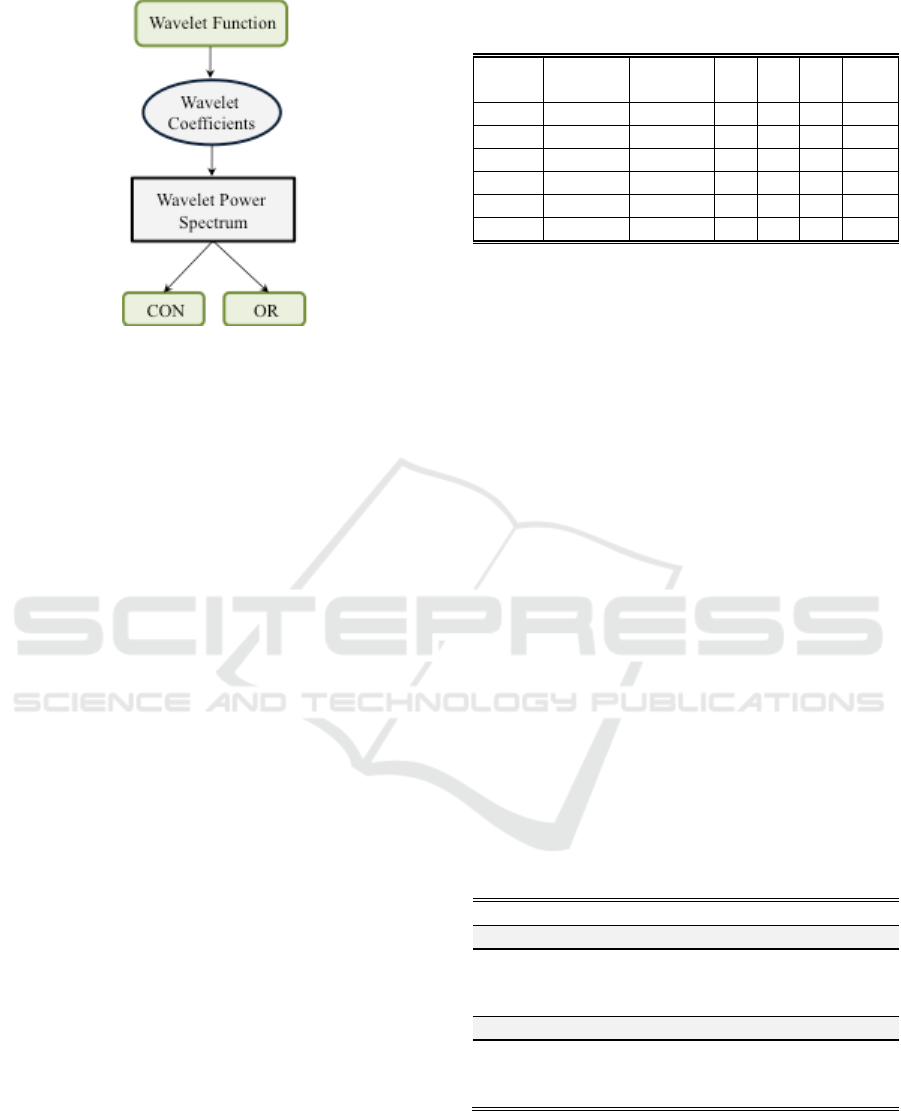
Figure 3: Block Diagram for Computing Power Spectrum.

3 RESULTS

The algorithm developed in this study evaluated for

its performance by discriminating the CON and OR

group from one another.

EMG signals, which were collected from three

muscles, were analysed by 38 wavelet functions with

5 levels of decomposition for three phases of dynamic

contraction during squat task. The five wavelet

functions that represented the highest amount of

energy for each subject were highlighted. The same

scenario was repeated for all subjects by analysing

EMG signals from all three muscles for each

descending (D), stationary (S), and ascending (A)

phase separately. The highest five energies occurred

in various levels for different subjects and muscles.

The five WFs that indicated the highest percentage of

energy were selected for each subject. The total

number of repetitions for the wavelet functions

between CON and OR group during three phases was

computed for each muscle separately. Bior3.9

wavelet function indicated the highest number of

repetitions between subjects for each muscle during

three phases except for muscle 1 of OR group which

Bior3.7 worked best (Table 2). As the difference

between Bior3.7 and Bior3.9 was not significant in

muscle 1 of OR group, Bior3.9 wavelet function was

used for further analyses.

Table 2: Selection of a WF with Highest Repetition of

Energy.

Subject

Muscle

Wavelet

Function

Total

CON

1 (GMax)

bior3.9

1 (GMax)

bior3.7

CON

2 (TFL)

bior3.9

2 (TFL)

bior3.9

CON

3 (RF)

bior3.9

3 (RF)

bior3.9

3.1 Wavelet Power Spectrum

The WT converts the data array, which is stored from

the EMG recorded signal, into a series of wavelet

coefficients. Each of these coefficients represents the

amplitude of the wavelet function at a specific

location in the array. The best way to specify the

distribution of energy within the data is to compute

the wavelet power. The power, which is the squared

absolute value of the wavelet coefficients, calculated.

The wavelet power spectrum for each muscle during

descending, stationary, and ascending phases was

computed by using Bior3.9 WF. This scenario was

repeated for all subjects from both groups. The

subjects were categorized based on calculated power

of each phase in Table 3. OR and CON groups were

divided into three categories based on the squat

phases. All 16 subjects in the CON group used their

muscle 1 in the ascending phase whereas; most of

them used muscle 2 and muscle 3 in their descending

phase. In OR group, muscle 1 was used in ascending

the same as CON group. However, muscle 2 was used

in ascending and muscle 3 in both descending and

ascending phases.

Table 3: Muscles used by CON and OR During Squat

Cycle.

Descending

Stationary

Ascending

Total

CON

Muscle 1

Muscle 2

Muscle 3

Muscle 1

Muscle 2

Muscle 3

Moreover, after calculating the power of the DWT

coefficients at various levels, the power was then

compared for the sEMG for OR and CON group of

three muscles (GMax, TFL, RF). Fig. 4 and Fig. 5

show the results of each muscle for both groups.

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

218

Figure 4: Muscles Power for CON Group.

Figure 5: Muscles Power for OR Group.

As indicated in above graphs, subjects from both

groups used higher power in descending and

ascending phases. In order to indicate whether there

is a significant difference between these two groups

in using their muscles during ascending and

descending phases, the actual A/D ratio for CON and

OR was computed.

By calculating the ratio, we can still see which

phase was the most active; however, we are also able

to see the extent of activity. Therefore, we calculated

the ratio of A/D for every subject in CON and OR

groups and then calculated the average. The resulting

average for each muscle is provided in Table 4 with

the standard deviation for each group.

Table 4: Average Ratio with Standard Deviation Values for

Each Muscle in CON and OR Groups.

CON

Muscle 1 (GMax)

13.38 ± 1.902

11.319 ±1.921

Muscle 2 (TFL)

1.33 ± 0.150

1.829 ± 0.205

Muscle 3 (RF)

0.613 ± 0.090

1.975 ± 0.260

The muscles power is plotted and shown in Fig. 6

for CON and OR group. In CON group muscle 1 and

2 were active in ascending phase whereas, muscle 3

was active in descending phase. Moreover, in the OR

group all three muscles were active in the ascending

phase.

Figure 6: Average Ratio Muscle Power for CON and OR.

In general, the described algorithm can be

summarized as follows:

The raw EMG signals are collected from a

participant for GMax, TFL, RF muscles during

descending, stationary, and ascending phases of squat

task. Then, the collected EMG signals are

normalized. The Bior3.9 wavelet function is applied

to normalized EMG signals and the wavelet

coefficients are computed. Based on wavelet

coefficients the wavelet power spectrum is calculated.

In addition, the ratio power which is the ratio of

ascending power over descending power is computed

in order to identify whether the subject has FAI or not.

If the ratio value for RF muscle is less than zero, it

means the participant used his/her RF muscle in

descending phase and he/she belongs to CON group.

Whereas, if the ratio value is greater than zero, it

means he/she used his/her muscle in ascending phase

and the subject belongs to FAI group.

3.2 Statistical Analysis

In this study an independent samples t-test was used

to check if the two means (averages) from CON and

OR groups are reliably different from one another.

Each t-value has a p-value that is the probability that

the pattern of data in the sample could be produced

by random data. The 2-tail t-test was applied to check

the activities of muscles for CON and OR groups.

Table 5 illustrates no significant difference was found

for GMax and TFL; whereas RF shows a significant

difference between CON and OR groups (p= 0.0670)

although the threshold (p=0.05) was not reached. This

can be due to the fact that the sample size in this study

was small and we require more samples for more

reliable results.

Identiﬁcation of Femoral-Acetabular Symptoms using sEMG Signals during Dynamic Contraction

219

Table 5: P-value for GMax, TFL, and RF Muscle.

P-value

Muscle 1 (GMax)

0.7477

Muscle 2 (TFL)

0.4997

Muscle 3 (RF)

0.067

4 DISCUSSION

Spectral properties of EMG signals have been defined

by their power spectra. The shape of the power

spectrum can be changed when the EMG signals are

generated from different types of Motor Unit (MU)

(Moritani, 1985; Gerdle, 1998; Elert 1992).

This study has indicated that the wavelet transform

method can be used to quantify features of the muscle

activity for dynamic contraction. The fundamental

properties of EMG spectra are conserved across

dynamic contraction, therefore the WT will be a

useful tool for studying EMG signals. The wavelet

power spectrum of OR and CON groups was analysed

for GMax, TFL, and RF muscles in the hip area by

using the Bior3.9 wavelet function in order to

discriminate the two groups. The power was

calculated for each muscle and an independent

sample t-test was used to check the activity of three

muscles in hip area to discriminate an OR patient

from a healthy person. The p-value for GMax, TFL,

and RF muscles is 0.7477, 0.4997, and 0.0670

respectively for 2-tail test. Therefore, RF muscle is

statistically significant although the threshold

(p=0.05) was not reached due to small sample size.

As a result, RF muscle is more active in ascending

than descending phase for OR people, whereas it is

more active in descending phase for CON people.

Muscle contraction is produced by a sequence of

electrical and chemical events, which start with an

action potential, which is created at the

neuromuscular junction. Individual muscle fibres are

classified into three primary muscle fibre types

named type I, type IIA, and type IIB based on their

contractile and metabolic properties. Type I is

referred to slow twitch oxidative, type IIA is fast

twitch oxidative and type IIB is fast twitch glycolytic

(Ethier, 2007). These three types of muscle fibres

have very different functional characteristics. Type I

fibre is characterized by low force, power, speed

production and high endurance. Type IIB has high

force, power, speed production and low endurance,

while type IIA indicates feature between the two

other types. The MU consists of a single motoneuron

and the group of muscle fibre it innervates. All

muscle fibres in a single MU contain the same muscle

fibre type. Three types of MUs (slow, fast fatigue-

resistant, and fast fatigable) are categorized on the

basis of their twitch speed and fatigability. The slow

twitch MU is small and can produce less force

compare to fast twitch MU. Type I muscle MUs

contract slower, and they reach to peak power slower

and highly resistant to fatigue compare to type II fast

twitch MUs. Type IIA and IIB are capable of the same

amount of peak force, however type IIA fibres take

longer to reach their peak power compare to type IIB.

Therefore, the total peak power by type IIB is higher

than type IIA. In other words, type I has low intensity,

lower frequency, and low power compare to type II.

The average ratio (ascending over descending phase)

power for GMax, TFL, and RF muscles, as indicated

in Table 4, presents the power of RF muscle is higher

in OR group than CON group. The faster motor units

generate higher frequencies in their power spectra

(Wakeling, 2004). Thus, the larger numbers of MUs

are recruitment in RF muscle for OR than CON.

Therefore, type II (fast twitch) MUs are active in OR

group, while in CON group type I (slow twitch) MUs

are used.

5 CONCLUSION & FUTURE

WORK

The algorithm developed in this study aimed to

automatically discriminate CON and OR groups

based on sEMG recorded from three hip muscles

(GMax, TFL, and RF) during dynamic contraction.

The program was capable of identifying OR from

healthy people by analysing the activity of hip

muscles.

The novel method developed in this study was used

to analyse EMG signals recorded from GMax, TFL,

and RF muscles for 16 CON and 14 OR subjects

during squat cycles. In this study the DWT was

selected and various wavelet functions from this WT

method were applied to EMG signals from three

muscles in order to select the best possible energy

localization in the time-frequency plane. This

analysis showed the Bior3.9 wavelet function

provided higher amount of energy for most of our

subjects. By selecting Bior3.9 the wavelet power

spectrum was computed for CON and OR during 5

levels of decomposition. The result indicated the RF

muscle (muscle 3) is more active in the ascending

phase than the descending phase for OR, while it is

more active in descending phase for CON.

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

220

During dynamic contraction there is a progressive

recruitment of faster MUs in OR group during

ascending phase. EMG activity at higher frequencies

correlated with higher contractile force, and with the

progressively faster types of MU, which can be

assumed to be recruited. Thus, during dynamic

contraction the higher wavelet power in RF muscle of

OR group demonstrates that faster MUs were active,

while lower power in CON group related to the fact

that slower MUs were active.

This research work showed that the proposed

algorithm can find a good solution for pre-screening

problem. Nevertheless, some more improvements

could be achieved. In this algorithm, only the three

muscles of hip area were considered, this might be

different if we consider all the muscles in the hip area.

Another limitation is that the physical activity and age

parameters of subjects were not available. Therefore,

research should be conducted in a wider range,

parameters like physical activity, age, and gender

could be considered.

Some future work from this thesis may consist of

considering a larger sample size for more accurate

and reliable values. The goal can be developing a

software application, which can assist doctors and

physicians to diagnose FAI faster and easier.

ACKNOWLEDGEMENTS

The work in this paper was funded and supported by

the Canadian NSERC Collaborative Health Research

Project.

REFERENCES

Myers, S.R., Eijer, H., Ganz, R. 1999, “Anterior

Femoroacetabular Impingement after Periacetabular

Osteotomy,” Clinical Orthopaedics & Related

Research, Vol. 363, pp. 93–99.

Keogh, M. J. Batt, M. E., 2008, “A Review of

Femoroacetabular Impingement in Athletes,” Sport

Med, Vol. 38(10), pp. 863–878.

Samora, J. B., Ng V. Y., Ellis, T. J. 2011,

“Femoroacetabular Impingement: A Common Cause of

Hip Pain in Young Adults,” Clinical Journal of Sport

Medicine, Vol. 21(1), pp. 51–56.

Reaz, M. B. I., Hussain, M. S., Mohd-Yasin, F., 2006,

“Techniques of EMG Signal Analysis: Detection,

Processing, Classification and Applications,”

Biological Procedures Online, Vol. 8(1), pp. 11–35.

Ahmed, S., Ahmed, S., Faruqe, M. O., Islam, M. R., 2009,

“EMG Signal Decomposition Using Wavelet

Transformation with Respect to Different Wavelet and

a Comparative Study,” Life and Medical Sciences, pp.

730–735.

Karlsson, J. S., Gerdle, B., Akay, M., 2001, “Analyzing

Surface Myoelectric Signal Recorded During Isokinetic

Contractions: A Time-Frequency Approach Using

Wavelet to Study Movements at Different Angular

Velocities,” IEEE Engineering in Medicine and

Biology, pp. 97–105.

Karlsson, S., Yu, J., Akay, M., 2000, “Time-Frequency

Analysis of Myoelectric Signal during Dynamic

Contractions: A Comparative Study,” IEEE

Transactions on Biomedical Engineering, Vol. 47(2),

pp. 228–238.

Meyer, Y., 1993 “Wavelets Algorithms and Applications”.

Philadelphia: Society of Industrial and Applied

Mathematics, pp. 1-4.

Rioul, O., Vetterli, M., 1991, “Wavelet and Signal

Processing,” IEEE Signal Process Magazine, Vol. 8,

pp. 14–38.

Santoso, S., Powers, E. J., Grady, W. M., 1994, “Electric

Power Quality Disturbance Detection Using Wavelet

Transform Analysis,” IEEE, pp. 166–169.

Walker, J. S., 1999, “A Primer on Wavelets and Their

Scientific Applications”. Boca Raton, FL: CRC.

Karlsson, S., Yu, J., Akay, M., 1999, “Enhancement of

Spectral Analysis of Myoelectric Signal During Static

Contractions Using Wavelet Methods,” IEEE

Transaction on Biomedical Engineering, Vol. 46(6), pp.

670–684.

Karlsson, J., Ostlundm, N., Larsson, B., Gerdle, B., 2003,

“An Estimation of the Influence of Force Decrease on

the Mean Power Spectral Frequency Shift of the EMG

During Repetitive Maximum Dynamic Knee

Extensions,” Journal of Electromyography and

Kinesiology, Vol. 13, pp. 461–468.

Neto, O.P., Magini, M., Pacheco, M.T., 2007,

“Electromyographic Study of a Sequence of Yau-Man

Kung Fu Palm Strikes with and without Impact,”

Journal of Sports Science and Medicine, Vol. 6, pp. 23–

27.

Von Tscharner, V., 2000, “Intensity Analysis in Time-

Frequency Space of Surface Myo-electric signal by

Wavelet of Specified Resolution,” Journal of

Electromyography and Kinesiology, Vol. 10, pp. 433–

445.

Hostens, I., Seghers, J., Spaepen, A., Ramon H., 2004,

“Validation of the Wavelet Spectral Estimation

Technique in Biceps Brachii and Brachioradialis

Fatigue Assessment During Prolonged Low-level Static

and Dynamic Contractions”. Journal of

Electromyography and Kinesiology, Vol. 14, pp. 205–

215.

Beck, T. W., Housh, T. J., Johnson, G. O., Weir, J. P.,

Cramer, J. T., Coburn, J. W., and Malek, M. H., 2005,

“Comparison of Fourier and Wavelet Transform

Procedures for Examining the Mechanomyographic

and Electromyographic Frequency Domain Responses

During Fatiguing Isokinetic Muscle Actions of the

Biceps Brachii,” Journal of Electromyography and

Kinesiology, Vol. 15, pp. 190–199.

Identiﬁcation of Femoral-Acetabular Symptoms using sEMG Signals during Dynamic Contraction

221

Neto, O., Magini, M., 2008 “Electromiographic and

Kinematic Characteristics of Kung Fu Yau-Man Palm

Strike,” Journal of Electromyography and Kinesiology,

Vol. 18, pp. 1047–1052.

Von Tscharner, V., 2002, “Time-Frequency and Principal

Component Methods for the Analysis of EMG

Recorded during a Mildly Fatiguing Exercise on a

Cycle Ergometer,” Journal of Electromyography and

Kinesiology, Vol. 12, pp. 479–492.

Von Tscharner, V., Goepfert, B., 2003 “Gender Dependent

EMGs of Runners Re- solved by Time/Frequency and

Principal Pattern Analysis,” Journal of

Electromyography and Kinesiology, Vol. 13, pp. 253–

272.

Von Tscharner, V., Goepfert, B., Nigg, B. M., 2003,

“Changes in EMG Signals for the Muscle Tibialis

Anterior while Running Barefoot or with Shoes

Resolved by Non-Linearly Scaled Wavelets,” Journal

of Biomechanics, vol. 36, pp. 1169–1176.

Von Tscharner, V., Goepfert, B., 2006, “Estimation of the

Interplay Between Groups of Fast and Slow Muscle

Fibers of the Tibialis Anterior and Gastrocnemius

Muscle While Running,” Journal of Electromyography

and Kinesiology, Vol. 16, pp. 188–197.

Flanders, M., 2002, “Choosing a Wavelet for Single-trial

EMG,” Journal of Neuroscience Methods, Vol. 116, pp.

165–177.

Kilby, J., Gholam Hosseini, H., 2004, “Wavelet Analysis of

Surface Electromyography Signals,” in Proceedings of

the 26th Annual International Conference of the IEEE

EMBS San Francisco, CA, USA, September 1-5.

Lamontagne, M., Kennedy, M. J., Beaule, P. E., 2009, “The

Effect of Cam FAI on Hip and Pelvic Motion during

Maximum Squat,” Clinical Orthopaedics and Related

Research, Vol. 467(3), pp. 645–650.

Moritani, T., Gaffney, F. D., Carmichael, T., Hargis, J.,

1985, “Interrelationships Among Muscle Fibre Types,

Electromyogram and Blood Pressure During Fatiguing

Isometric Contraction”, Biomechanics, Vol. IXA,

International Series on Biomechanics, Champaign,

Human Kinetics Publishers Inc., pp. 287-292.

Gerdle, B., Wretling, M. L., Henriksson-Larsen, K., 1988,

“Do the Fibre-Type Proportion and the Angular

Velocity Influence the Mean Power Frequency of the

Electromyogram?”, Acta Physiol. Scand, Vol. 134, pp.

341–346.

Elert, J. Rantapaa-Dahlqvist, S. B., Henriksson-Larsen, K.,

Lorentzon, R., Gerdle, B. U. C., 1992, “Muscle

Performance Electromyography and Fiber Type

Composition in Fibromyalgia and Work-Related

Myalgia,” Scand. J. Rheumatol, Vol. 21, pp. 29–34.

Ethier, C. R., Simmons, C. A., 2007, “Introductory

Biomechanics from Cells to Organisms”. Cambridge

University Press, pp. 332- 378.

Wakeling, J.M., Rozitis, A. I., 2004, “Spectra Properties of

Myoelectric Signals from Different Motor Unit in the

Leg Extensor muscles,” The Journal of Experimental

Biology, Vol. 207, pp. 2519–2528.

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

222