Consensus Clustering for Cancer Gene Expression Data

Large-Scale Analysis using Evidence Accumulation Approach

Isidora Šašić

, Sanja Brdar

, Tatjana Lončar-Turukalo

, Helena Aidos

and Ana Fred

Faculty of Technical Sciences,University of Novi Sad, Novi Sad, Serbia

BioSense Institute, Zorana Đinđića 1, Novi Sad, Serbia

Instituto de Telecomunicacoes, Instituto Superior Tecnico, Lisbon, Portugal

Keywords: Clustering, Consensus Clustering, Cancer Gene Expression.

Abstract: Clustering algorithms are extensively used on patient tissue samples in order to group and visualize the

microarray data. The high dimensionality and probe specific noise make the selection of the appropriate

clustering algorithm an uneasy task. This study presents a large-scale analysis of three clustering algorithms:

k-means, hierarchical clustering (HC) and evidence accumulation clustering (EAC) on thirty-five cancer gene

expression data sets selected to benchmark the performance of the clustering algorithms. Separated

performance analysis was done on data sets from Affymetrix and cDNA chip platforms to examine the

possible influence of the microarray technology. The study revealed no consistent algorithm ranking can be

inferred, though in general EAC presented the best compromise of adjusted rand index (ARI) and variance.

However, the results indicated that ARI variance under repeated k-means initializations offers useful

information on the need to implement more complex clustering techniques. If repeated K-means converges

to the same partition, also confirmed by the HC clustering, there is no need to run EAC. However, under

moderate or highly variable ARI in repeated K-means, EAC should be used to reduce the uncertainty of

clustering and unveil the data structure.

1 INTRODUCTION

Cancer genomics aims to uncover the molecular basis

of cancer. Different layers of genomic information

are used in cancer studies, with gene expression

profiles (transcriptome) being the most common.

Gene expression profiling provides an insight into

gene activity under different conditions. There is a

large amount of genome-wide gene expression data in

public archives (Rung et al, 2013) available to

identify the cancer signatures and more effective

diagnosis and treatment.

Clustering algorithms are extensively used on

patient tissue samples in order to group and visualize

the microarray data. Subgrouping of the similar

samples serves to reveal the new cancer subtypes and

to personalize the treatment approach. However, the

high dimensional and intrinsically noisy samples hide

the geometry of the clusters making the selection of

an appropriate clustering algorithm difficult. In the

clinical research, there is a prevalence of the simple

clustering methods, such as agglomerative clustering

and k-means (Alizadeh et al, 2000; Bredel et al, 2005;

D'haeseleer, 2005; Golub et al, 1999; Sorlie et al,

2003). The reason might be the ease of their use and

availability of implementations (de Souto et al.,

2008).

The data availability and modest variety of

implemented algorithms motivated a study by de

Souto et al. (2008) providing the first analysis of

several clustering algorithms combined with different

proximity measures and data normalization

techniques. The study uses 35 data sets from cDNA

or Affymetrix chip platforms (see Table 1), and

compares hierarchical clustering (HC), such as single,

complete and average linkage, mixture of

multivariate Gaussians (MMG), k-means, spectral

clustering and nearest neighbour methods (de Souto

et al, 2008). The overall performance of these

individual algorithms was the best in MMG, closely

followed by k-means, whereas HC proved as very

sensitive to noise.

The performance of the individual clusterings can

be significantly improved if they are combined,

similary to the ideas used in supervised learning

(classifier ensemble). In the unsupervised scenario,

176

aaÅ ˛aiÄ

G I., Brdar S., LonÄ ar-Turukalo T., Aidos H. and Fred A.

Consensus Clustering for Cancer Gene Expression Data - Large-Scale Analysis using Evidence Accumulation Approach.

DOI: 10.5220/0006174501760183

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 176-183

ISBN: 978-989-758-214-1

the clustering ensemble comprises multiple partitions

obtained by the base clusterings. The evidence on

data structure may be accumulated introducing

diversity in several ways (Fred and Jain, 2005; Iam-

on 2010): (1) combining the results of different

clustering algorithms; (2) resampling the data, thus

producing different results, (3) running the same

algorithm many times with different parameters or

initializations, (4) using different feature subsets for

individual clusterings. The way of combining the

results of the individual clusterings as well differs,

with most of the methods resulting in a pairwise

similarity matrix used to obtain the final partition.

The comprehensive performance evaluation of

consensus clustering methods on the gene expression

data sets used to evaluate individual algorithms does

not exist. In Iam-on et al (2010), the novel link-based

cluster ensemble (LCE) method is introduced and

compared with several consensus methods over a

subset of 10 data sets of the available cancer gene

expression collection from Table 1. Mimaroglu et al.

(2012) as well report on their results obtained on just

one input ensemble per data set.

In this study we evaluate the performance of a

consensus clustering approach - evidence

accumulation (EAC) versus conventionally used

individual algorithms: k-means and average-link and

Ward’s linkage hierarchical clustering. The

accumulation of evidence is achieved by running the

k-means algorithm multiple times with different

initializations (Fred and Jain, 2005). All 35 data sets

selected to benchmark the performance of the

clustering algorithms in the recovery of cancer type

were the ones used (de Souto et al., 2008), specified

in Table 1. The adjusted rank index (ARI) was used

to evaluate the clusters obtained against the true

labels (Hubert et al, 1985). A separate performance

analysis was done on data sets from Affymetrix and

cDNA chip platforms, to additionally examine the

possible influence of the microarray technology. Kuo

et al (2002) suggested that probe-associated factors

influence in a different manner measurements from

the two technologies, resulting in their poor

correlation. Based on the performance on the

individual data sets, we explored the difference in

ARI scores between EAC methods and the individual

clustering approaches: k-means and hierarchical

clustering. Additionally, we strived at categorizing

results across used data sets and making

recommendations on using EAC.

2 METHODS

2.1 Data Sets

The study included thirty-five data sets used for the

evaluation of individual clustering algorithms in de

Souto et al. (2008). The data sets differ by the type of

the chip technology, tissue, the number of available

samples denoted by N, the class number, k, the sample

distribution per classes, the original dimensionality

denoted by m and the dimensionality after feature

reduction, denoted by d (Table 1). The full list of

references corresponding to the data sets is provided

in de Souto et al. (2008).

In cDNA microarray, the gene expression levels

are measured as the ratio of the signal from mRNA

target sample and the reference sample, making the

comparison to the other technologies difficult (Kuo et

al, 2002). Affymetrix data are estimates of the

number of mRNA copies in a sample. Following the

de Souto et al. (2008), in Affymetrix data a lower and

un upper limit on gene expression levels was set to 10

and 16.0000, respectively. Additionally, for the large

variations in Affymetrix gene expression levels, the

data sets from this chip technology were rank

normalized.

All data sets were available only with reduced

feature sets, thus the influence of different data

dimensionality reduction techniques were not

analysed.

2.2 Clustering Techniques

2.2.1 K-means

The simplicity and the linear computational

complexity of the k-means make it, even 50 years

(Steinhaus, 1956; Lloyd,1952) beyond its proposal,

the most widely used partitioning clustering

algorithm (Jain, 2010). K-means clusters are

represented by their centers, i.e. their prototypes

characterizing all objects in each cluster. To assign

objects to the clusters the Euclidean distance is

typically used as a similarity measure, and the final

assignment is done by minimizing within-cluster sum

of the squared error (SSE): initial centers of the

clusters are set by randomly selecting k samples from

the given data set, where k equals the actual number

of the classes in a data set. In an iterative procedure,

K-means updates centers to minimize objective

function until convergence. In this work, the K-means

was repeated for 50 times on each data set with

random initializations of the cluster centers and and k

was fixed to the true number of classes.

Consensus Clustering for Cancer Gene Expression Data - Large-Scale Analysis using Evidence Accumulation Approach

177

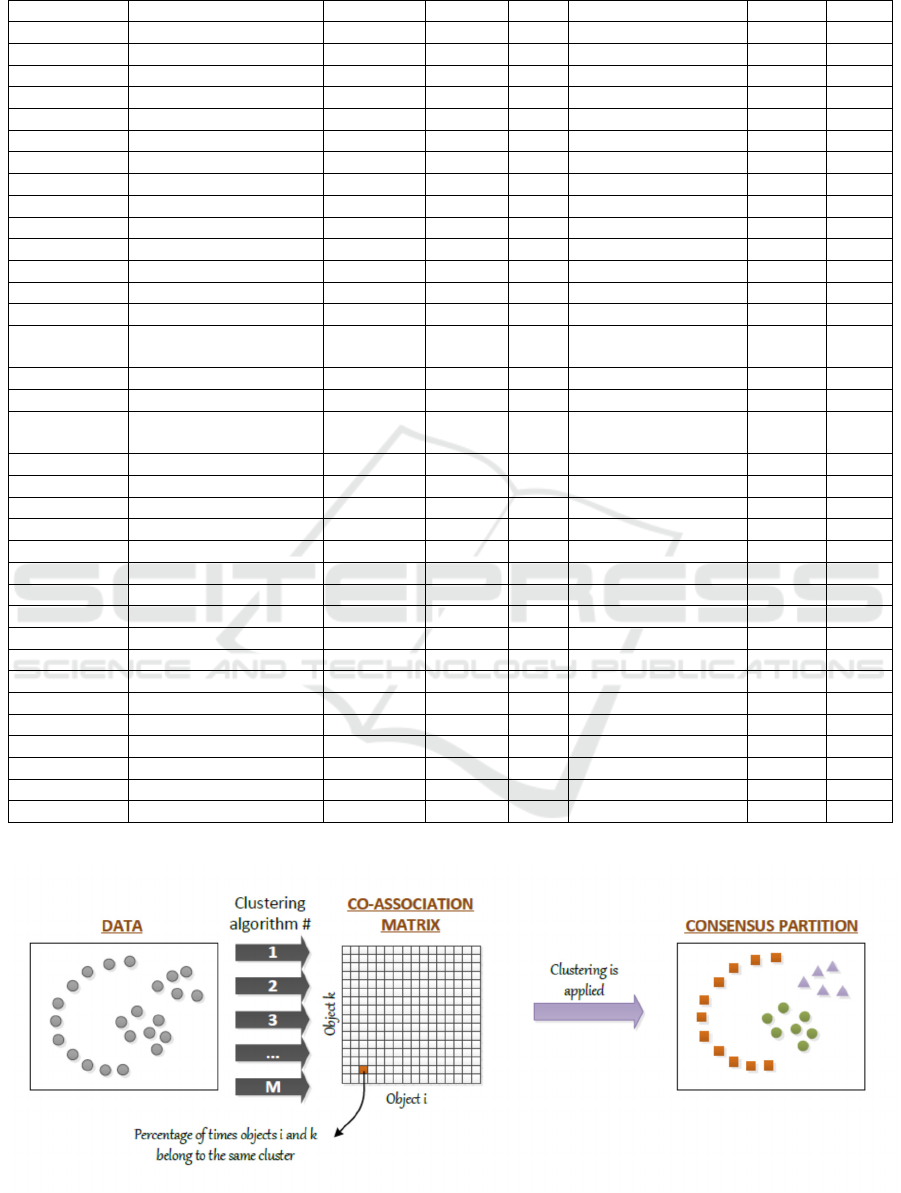
Table 1: Cancer gene expression data sets (full list of references in de Souto et al.(2008)).

Tissue Data set Chip N k Sample distribution m d

Blood Armstrong-V1 Affymetrix 72 2 24,48 12582 1081

Blood Armstrong-V2 Affymetrix 72 3 24,20,28 12582 1081

Lung / Bhattacharjee Affymetrix 203 5 139,17,6,21,20 12600 1543

Breast, Colon Chowdary Affymetrix 104 2 62,42 22283 182

Bladder Dyrskjot Affymetrix 40 3 9,20,11 7129 1203

Bone marrow Golub-V1 Affymetrix 72 2 47,25 7129 1877

Bone marrow Golub-V1 Affymetrix 72 3 38,9,25 7129 1877

Lung Gordon Affymetrix 181 2 31,150 12533 1626

Colon Laiho Affymetrix 37 2 8,29 22883 2202

Brain Nutt-V1 Affymetrix 50 4 14,7,14,15 12625 1377

Brain Nutt-V2 Affymetrix 28 2 14,14 12625 1070

Brain Nutt-V3 Affymetrix 22 2 7,15 1265 1152

Brain Pomeroy-V1 Affymetrix 34 2 25,9 7129 857

Brain Pomeroy-V2 Affymetrix 42 5 10,10,10,4,8 7129 1379

Multi-tissue Ramaswamy Affymetrix 190 14 11,10,11,11,22,10,11,

10,30,11,11,11,11,20

16063 1363

Blood Shipp Affymetrix 77 2 58,19 7129 798

Prostate Singh Affymetrix 102 2 58,19 12600 339

Multi-tissue Su Affymetrix 174 10 26,8,26,23,12,

11,7,27,6,28

12533 1571

Breast West Affymetrix 49 2 25,24 7129 1198

Bone marrow Yeoh-V1 Affymetrix 248 2 43,205 12625 2526

Bone marrow Yeoh-V2 Affymetrix 248 6 15,27,64,20,79,43 12625 2526

Blood Alizadeh-V1 cDNA 42 2 21,21 4022 1095

Blood Alizadeh-V2 cDNA 62 3 42,9,11 4022 2093

Blood Alizadeh-V3 cDNA 62 4 21,21,9,11 4022 2093

Skin Bittner cDNA 38 2 19,19 8067 2201

Brain Bredel cDNA 50 3 31,14,5 41472 1739

Liver Chen cDNA 180 2 104,76 22699 85

Lung Garber cDNA 66 4 17,40,4,5 24192 4533

Multi-tissue Khan cDNA 83 4 29,11,18,25 6567 1069

Prostate Lapointe-V1 cDNA 69 3 11,39,19 42640 1625

Prostate Lapoint-V2 cDNA 110 4 11,39,19,41 42640 2496

Brain Liang cDNA 37 3 28,6,3 24192 1411

Endometrium Risinger cDNA 42 4 13,3,19,7 8872 1771

Prostate Tomlins-V1 cDNA 104 5 27,20,32,13,12 20000 2315

Prostate Tomlins-V2 cDNA 92 4 27,20,32,13 20000 2315

Figure 1: Evidence accumulation clustering.

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms

178

2.2.2 Hierarchical Clustering

Agglomerative, bottom up, hierarchical clustering

was used with the Euclidean metric and several

linkages. Initially, each sample is assigned its own

cluster, which is further repeatedly merged using

certain linkage criteria until all samples are in one

cluster (Hastie et al., 2009). In this work Average and

Ward’s linkage (Ward, 1963) were tested. Average-

link groups the cluster pairs with the least mean

distance between the samples of each cluster, whereas

Ward’s linkage merges clusters resulting in the least

increase in within-cluster variance upon being

merged. The output hierarchy of the clusters can be

visualized in the form of a tree, called dendrogram. In

the dendrogram, each leaf node is an individual

sample, each inner node in the tree is the union of its

subclusters and the root is the cluster containing all

the samples. The final partition is obtained by cutting

the tree to result in the same number of clusters as the

number of classes k, in the given data set.

2.2.3 Evidence Accumulation Clustering

The simple use of a clustering algorithm, like K-

means, can give a diversity of solutions over the same

data set depending on the initialization, or of the

chosen k value. To overcome this issue, an approach

known as Clustering Ensemble has been proposed

that takes into account the diversity of solutions

produced by clustering algorithms. Clustering

ensembles can be generated from either different

clustering algorithms or from varying the algorithmic

parameters (Strehl and Ghosh, 2002; Ayad and

Kamel, 2008). To leverage clustering ensemble

results, Fred and Jain (2005) proposed an approach

known as Evidence Accumulation Clustering (EAC),

based on the combination of information of different

partitions, as illustrated in Figure 1.

The evidence accumulation clustering can be

summarized in the following steps: (i) building the

clustering ensemble, P, comprising the set of M

different partitions of a data set X.; (ii) combining

evidence from these partitions in a co-association

matrix; (iii) extracting the consensus partition. The

co-association matrix is built by taking the co-

occurrences of pairs of patterns in the same cluster as

votes for their association. The underlying hypothesis

is that patterns which should be grouped together, are

very likely to be assigned to the same cluster in

different data partitions. Therefore, the M data

partitions of N patterns yields a N x N

co - association matrix with elements:













(1)

where 



is the number of times the pattern pair (i,j)

is assigned to the same cluster among the M

partitions. The last step of the evidence accumulation

clustering consists of extracting the consensus

partition, which is found by applying a clustering

algorithm to the co-association matrix.

In this paper, the clustering ensemble was

produced by applying k-means M=200 times, with k

randomly chosen between[

√





√



]. The

extraction of the consensus partition was performed

by applying two hierarchical clustering algorithms:

average-link and Ward's linkage with the final

number of clusters equal to the true number of

classes. The whole procedure, from the clustering

ensemble generation was repeated 50 times, with the

same parameters and the results are averaged.

2.2.4 Clustering Validation Measure

The validation of each clustering algorithm in each

data set is performed using the Adjusted Rand Index

(ARI) (Hubert and Arabie, 1985), which compares

the partition obtained by a clustering algorithm C =

, C

, … , C

} against the ground-truth partition L

= {L

, L

, ..., L

}. This measure is an improved

version of Rand Index (RI) (Rand, 1971), which

quantifies agreement between two partitions by

counting the number of pairs of samples that are

clustered together or placed in different clusters in

both partitions, and the disagreement between

partitions by counting the number of pairs that are

clustered together in one partition but not in the other.

ARI corrects RI for a chance that random partitions

agree; it ensures that the value is then close to 0. The

maximum value of 1 is reached when external labels

and those assigned by clustering algorithms are

identical up to a permutation.

3 RESULTS AND DISCUSSION

Firstly, we present overall results by boxplots that

include results obtained on Affymetrix and cDNA

data sets (Figure 2 and 3). Box plots uncover how

agreements between clustering results and true labels

corresponding to cancer types highly vary, spanning

from 0 to 1, when results from all sets are analyzed

jointly. Median values of all methods, except for HC-

average, are approximately the same. Similar results

can be observed from box plots corresponding to

cDNA results.

Consensus Clustering for Cancer Gene Expression Data - Large-Scale Analysis using Evidence Accumulation Approach

179

Figure 2: Box plots for ARI over all Affymetrix data sets

when HC and EAC use a) average-link b) Ward’s linkage.

Figure 3: Box plots for ARI over all cDNA data sets when

HC and EAC use a) average-link b) Ward’s linkage.

Only the strongest patterns can be observed from such

graphs. Results presented in this way imply that HC-

average is inappropriate for clustering cancer

genomics samples. Other methods should be further

examined across data sets to draw conclusions.

To compare EAC against individual clustering

approaches, we measured differences in the mean

ARI scores. Figures 4 and 5 present how the

difference in mean scores change across Affymetrix

and cDNA data sets. We can easily notice where EAC

improved the results. The results unveil that EAC

enhanced results on many data sets. The largest

failure of EAC was observed on Gordon data set

(ward version, Figure 4b) and Alizadeh v2 data set

(Figure 5a and 5b). These results were additionally

examined in the following discussion. We further

explored the results obtained on different data sets.

Results can be grouped into three categories thus

allowing us to infer useful conclusions. Here we

selected a few data sets to demonstrate different

scenarios and provide recommendations on EAC

algorithms usage. The first group of the results is

characterized by the stable result of K-means – the

same partition produced on almost all of 50 runs of

the algorithm with random initialization. This

scenario was observed on 8 out of 35 data sets. We

can inspect outcomes of clustering on Gordon data set

in Figure 6. K-means discovered partition that

perfectly aligned with the class labels. The result of

HC-ward was slightly below, but HC-average

completely failed to reconstruct cancer types. EAC-

average produced the same result as K-means,

however, Ward’s version of EAC broke down. Our

general recommendation is not to use EAC for data

sets where K-means converges to the same partition,

especially when HC clustering (average and/or

Ward’s) also confirms obtained partition. If there is

no consensus among K-means, and both version of

HC it makes sense to use EAC, but we would suggest

revising the way ensemble is created.

Our analysis revealed the advantage of EAC in the

scenarios where k-means produced results of

moderate variability (13 data sets). Variability of K-

means impacts the diversity of the ensemble.

Additional diversity induced by choosing different K

for the ensemble helped EAC to better resolve

uncertainties in assigning gene expression samples to

the clusters. Results obtained on Ramaswamy data set

and Nutt data sets (Figures 7 and 8) demonstrate EAC

typical performance in the moderate diversity

scenarios. EAC here managed to be at the level of the

best of K-means in 50 runs or highly surpassed its

performance. Similar conclusions were derived from

the study on another data collection (Hadjitodorov

2006). Also, EAC is preferable option over HC

clustering. EAC-ward performs better in this scenario

compared to EAC-average. In the worst case the

result of EAC was at the level of the median result of

K-means, but with lower or no variation in the final

result.

The third scenario encompasses cases where K-

means varies highly (14 data sets). High diversity of

ensemble is challenging for evidence accumulation

algorithms. Example is provided in Figure 9. We can

observe that EAC converges to the median result of

K-means. Alizadeh v2, also belongs to this group of

data sets, where EAC converged to the median K-

means performance. The results across other sets

from this category fluctuated around the median

performance of K-means and only on few data sets

significantly overpassed the result of the K-means.

EAC-ward handled better higher diversity of the input

ensemble compared to EAC-average. The scenario

where K-means vastly diverge indicates at difficulties

in clustering underlying data. EAC can be used to

reduce the uncertainty of clustering, but some other

options for constructing the ensemble and internal

measures of clustering validation should be further

considered.

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms

180

Figure 4: Affymetrix data sets: differences in ARI a) when average-link b) Ward’s linkage is used in both HC and EAC.

Positive differences mean the improvement is introduced using EAC consensus clustering.

Figure 5: cDNA data sets: differences in ARI a) when average-link b) Ward’s linkage is used in both HC and EAC. Positive

differences mean the improvement is introduced using EAC consensus clustering.

Consensus Clustering for Cancer Gene Expression Data - Large-Scale Analysis using Evidence Accumulation Approach

181

Figure 6: Comparison of ARI scores produced by different

clustering algorithms on Gordon data set.

Figure 7: Comparison of ARI scores produced by different

clustering algorithms on Ramaswamy data set.

Figure 8: Comparison of ARI scores produced by different

clustering algorithms on Nutt v1 data set.

Figure 9: Comparison of ARI scores produced by different

clustering algorithms on Dyrskjot data set.

4 CONCLUSIONS

The study presented here systematically evaluates the

performance of EAC and compares it to the most

common individual clustering approaches in the

cancer genomics domain. As expected for the study

that encompasses a larger collection of data sets, the

absolute winner among examined method was not

detected, but useful conclusions can be made. EAC

strongly depends on the variability of K-means, i.e.

when there is a moderate diversity among K-means

partitions, we can expect that EAC will improve

results. On data sets that are intrinsically difficult to

cluster, EAC tends to converge to the median

partition. While other studies on this collection of

cancer genomic data did selective reporting on results

highlighting only benefits, we critically evaluated

methods and raised several important issues. In this

light, our study improves objectivity in the

assessment of clustering in cancer genomics.

Further work will focus on evaluating different

metrics, ensemble construction techniques, feature

subset selection and the identification of data set

properties informative on selection of the most

appropriate clustering approach.

ACKNOWLEDGEMENTS

The work was in part financed by: the COST Action

TD1405 ENJECT grant awarded to Tatjana Lončar-

Turukalo for short term scientific mission hosted by

prof. Ana Fred at Institute for Telecommunications,

Instituto Superior Technico, Portugal, by Serbian

Ministry of Education and Science (Project III 43002,

TR32040), and by the Portuguese Foundation for

Science and Technology, scholarship number

SFRH/BPD/103127/2014 and grant PTDC/EEI-

SII/7092/2014.

REFERENCES

Alizadeh, A. et al., 2000. Distinct types of diffuse large B-

cell lymphoma identified by gene expression profiling.

Nature, 403(6769), pp.503-511.

Ayad, H. and Kame, M., 2008., Cumulative Voting

Consensus Method for Partitions with Variable Number

of Clusters, IEEE Transactions on Pattern Analysis and

Machine Intelligence, 30(1),160-173.

Bredel,M. et al., 2005. Functional network analysis reveals

extended gliomagenesis pathway maps and three novel

MYC-interacting genes in human gliomas. Cancer

Research, 65, 8679–8689.

BIOINFORMATICS 2017 - 8th International Conference on Bioinformatics Models, Methods and Algorithms

182

de Souto,M. et al., 2008. Clustering cancer gene expression

data: a comparative study. BMC Bioinformatics, 9, 497.

D'haeseleer, P., 2005. How does gene expression clustering

work?. Nature Biotechnology, 23(12), pp.1499-1501.

Fred,A.L.N., and Jain,A.K., 2005. Combining multiple

clusterings using evidence accumulation. IEEE Trans.

Pattern Analysis and Machine Intelligence., 27, 835–

850.

Golub, T. et al, 1999. Molecular Classification of Cancer:

Class Discovery and Class Prediction by Gene

Expression Monitoring. Science, 286(5439), pp.531-

537.

Hadjitodorov, S. T., Kuncheva, L. I., Todorova, L. P. 2006.

Moderate diversity for better cluster ensembles.

Information Fusion, 7(3), pp. 264-275

Hastie, T., Tibshirani, R. and Friedman, J. (2009). The

elements of statistical learning. New York: Springer.

Hubert, L., & Arabie, P., 1985. Comparing partitions.

Journal of classification, 2(1), 193-218. Springer.

Iam-on, N., Tossapon, B., and Garrett, S., 2010, LCE: a

link-based cluster ensemble method for improved gene

expression data analysis, Bioinformatics, 26(12), pp.

1513-1519

Jain, A.K., 2010. Data clustering: 50 years beyond k-means,

Pattern Recognition Letters, 14 (4), pp. 327-344.

Kuo et al., 2002. Analysis of matched mRNA

measurements from two different microarray

technologies, Bioinformatics, 18(3), pp. 405-412.

Lloyd, S., 1982. Least squares quantization in PCM. IEEE

Transactions on Information Theory, 28, 129–137.

Originally as an unpublished Bell laboratories

Technical Note (1957).

Mimaroglu, S., Aksehirli, E., 2012. Diclens: Divisive

clustering ensemble with automatic cluster number.

IEEE/ACM Transactions on Computational Biology

and Bioinformatics (TCBB), 9(2), 408-420.

Sorlie,T. et al., 2003. Repeated observation of breast tumor

subtypes in independent gene expression data sets.

Proceedings of the National Academy of Sciences,

100(14), pp.8418-8423.

Steinhaus, H., 1956. Sur la division des corp materiels en

parties. Bulletin of Acad. Polon. Sci., IV(C1. III), 801–

804.

Strehl, A., and Ghosh, J., 2002., Cluster Ensembles - A

Knowledge Reuse Framework for Combining Multiple

Partitions, Journal of Machine Learning Research,3,

583-617.

Rand, W. M., 1971. Objective criteria for the evaluation of

clustering methods. Journal of the American Statistical

association, 66(336), 846-850.

Rung, J., Brazma, A., 2013. Reuse of public genome-wide

gene expression data," Nature Reviews Genetics, vol.

14(2), pp. 89-99.

Ward, H., 1963. Hierarchical Grouping to Optimize an

Objective Function. Journal of the American Statistical

Association. 58 (301): 236–244.

Consensus Clustering for Cancer Gene Expression Data - Large-Scale Analysis using Evidence Accumulation Approach

183