
Computational Study of Thermal Changes during the Non-invasive
Neuro-electrostimulation of the Nerve Structures in the Human Neck
Modelling Using Finite Element Method
Vladimir Kublanov
1
, Mikhail Babich
1
, Anton Dolganov
1
, Fedor Kornilov
2
and Anna Sajler
3
1
Research Medical and Biological Engeneering Centre of Hight Technologies, Ural Federal University, Mira, 19, 620002,
Yekaterinburg, Russian Federation
2
N. N. Krasovskii Institute of Mathematics and Mechanics of the Ural Branch of the Russian Academy of Sciences, Sofia
Kovalevskaya, 16, 620990, Yekaterinburg, Russian Federation
3
Ural State Medical University, Department of Human Anatomy, Repina, 3, 620028, Yekaterinburg, Russian Federation
Keywords: FEM Modelling, Neuro-electrostimulation, Human Neck, SYMPATHOCOR-01 Device.
Abstract: In the article methodology of FEM stimulation of thermal effects, caused by neck-region neuro-
electrostimulation was shown. Algorithm of the voxel model conversion to the 3-D objects represented as the
complex of the STL-files was described. The evaluation of the temperature in the biological tissues is based
on the association of the partial thermal changes, caused by the harmonics components of the pulsed neuro-
electrostimulation signal. Features of the thermal changes in the neck region were considered for the neuro-
electrostimulation by means of the current pulse field formed in the "SYMPATHOCOR-01" device. Results
have shown that for modulation frequencies in range 45-55 Hz, duration of the partial pulses 25-30 us, current
pulse amplitude less than 13 mA, the neuro-electrostimulation does not cause thermal changes higher
than 0.1 K.
1 INTRODUCTION
Non-invasive portable neuro-electrostimulation
devices are widely used in the contemporary medical
practice. These devices use low-frequency pulse
signals with single polarity for the stimulation. These
devices are used to treat patients with exogenously-
organic diseases of the central nervous system,
anxiety and depressive disorders, atrophic diseases of
the nervous system, and diseases accompanied by
cognitive, sensory, motor and autonomic disorders.
The peripheral nervous system is usually used as the
target for devices exposure. Among the variety of the
non-invasive devices, the multi-electrode systems are
the most promising. The effectiveness of the multi-
electrode systems arises from the spatial distribution
of current pulses in the stimulation zone.
The “SYMPATHOCOR-01” is an example of
such multi-electrode systems. Methods of the
“SYMPATHOCOR-01” device clinical application
implements the methodology of dynamic correction
of the activity of the sympathetic nervous system
(DCASNS) and provide correction of the autonomic
balance, determined by the ratio of activity of the
sympathetic and parasympathetic divisions of the
autonomic nervous system (ANS). The
“SYMPATHOCOR-01” device is included in the
State Registry of medical devices in Russia
(registration certificates №FSR 2007/00757 from
28.09.2007), and instructions for its use were
approved in August 1999, by head of the State control
of the Quality, Efficiency, and Safety of Medicines
and Medical Equipment Department of the Russian
Ministry of Health (Kublanov, 2008a).
During the neuro-electrostimulation procedure
via the “SYMPATHOCOR-01” device, Joule heating
of electric currents cause local heating zones.
Excessive heating of the biological tissues may
change normal functioning in the local zones or cause
thermal damage of tissue.
There is many papers that study heating processes
of biological tissues during electrostimulation.
However, as heating processes cannot be investigated
invivo, these processes are assessed by numerical
solving of the Pennes equation (Bergman and
Incropera, 2011) or by physical experiments (Su et
Kublanov V., Babich M., Dolganov A., Kornilov F. and Sajler A.
Computational Study of Thermal Changes during the Non-invasive Neuro-electrostimulation of the Nerve Structures in the Human Neck - Modelling Using Finite Element Method.
DOI: 10.5220/0006174702830290
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

al., 2014). Yet implementation of physical
experiments can be difficult.
Biological objects have a complex geometry.
Therefore, numerical solving of the Pennes equation
is usually performed by the finite element method
(FEM) (Cao et al., 2015). At present time, FEM
modelling does not allow transient simulation of the
pulsed current for frequency dependent
characteristics of biological tissues. Therefore, it is
advisable to produce decomposition of the pulse
currents into Fourier series, to perform modelling of
the harmonic components of the pulsed current, and
to combine partial effects of the harmonic
components.
The aim of the present work is to evaluate the
tissue heating process formed during nero-
electrostimulation of the human neck by the field of
the pulsed current.
2 MATHERIALS AND METHODS
To evaluate the tissue heating process, voxel model
of the human neck was used. In order to simplify the
simulation procedure, it is appropriate to consider a
pulse sequence as a superposition of harmonic
components, determined by Fourier series.
In current work COMSOL Multiphysics
(COMSOL Inc., USA) software was used for solution
of the Pennes bioheat equation for heat transfer.
Before the solution start, human body voxel model
was transformed into the STL-files. Every STL-file
represent particular 3-D biological object. For the
voxel body model transformation, the in-house script
was written in the Python language of with Anaconda
distribution (Continuum analytics, USA).
After solution solving by means of the FEM,
temperatures dependencies on the x, y, z spatial
coordinates have been exported to *.csv files.
Further by means of the in-house script in the
Python language with Anaconda distribution using
the set of *.csv files, maximum thermal changes in
the biological tissues of the human neck in
dependence on amplitude, frequency and duration of
the neuro-electrostimulation impulse signal were
plotted.
2.1 “SYMPATHOCOR-01” Device
Description
In the “SYMPATHOCOR-01” device for neuro-
electrostimulation of the nerve structures, the
spatially distributed rotating field of the current
pulses is formed. The field is created between two
multi-electrode arrays, located on the left and right
sides of the neck. The central electrode of each multi-
electrode array serve as anode, and is placed on the
projection of the cervical ganglia of the ANS. The
other electrodes in the multi-electrode array are
partial cathodes provide spatial patterns of the filed.
Partial current pulses, flowing from the anode of
one electrode array to partial cathodes of another
electrode array, form resulting current pulse filed.
Each of the partial pulses have an amplitude and
duration in the following ranges:
the pulse amplitude varies from 0 to 15 mA;
duration of each pulse ranges from 15 to 60 us.
Current pulse filed is modulated by frequency,
that ranges from 5 to 150 Hz. In that case for a single
period of the field formation, from 1 to 13 partial
current pulses can be generated. Each pulse follows
the previous one consequently.
The process of the thermal changes formation as
the result of the neuro-electrostimulation is formed by
set of partial current pulses, flowing between the
anode and the partial cathodes. Therefore, for
simulation formation of the current pulse field as the
superposition of the processes, caused by the
transition of the partial currents pulses between
anodes and one partial cathode.
The partial current pulses used in the
“SYMPATHOCOR-01” device has a very small
duty-cycle varying from 75*10E-6 to 9*10E-3.
Therefore 99% of the power is contained in first 2000
harmonics.
Low-frequency monopole pulse sequence of the
signal, formed in the “SYMPATHOCOR-01” device,
as any periodic signal can be decomposed into a
Fourier series as a sum of harmonics.
cos2π
θ
,
(1)
where: t – time, f(t) – neuro-electrostimulation signal
in time domain, a
0
– amplitude of constant part of
signal, n – number of harmonic component of the
signal, a
n
– amplitude of n-th harmonic component of
the signal, T – period of signal repetition, θ
n
– phase
of n-th harmonic component of the signal.
On the other hand, according to the Parseval's
theorem, the average power of the signal is the sum
of the power spectral densities of the components,
which does not depend on their phases (Arfken et al.,
2011).
,
(2)

where: P – average power of the signal, P
n
– average
power of n-th harmonic component of the signal.
According to the Newton’s law of cooling, power
is directly proportional to the thermal difference
between body and its surroundings.
∆,
(3
)
where: Q – thermal energy, h – heat transfer
coefficient, A – heat transfer source area, ΔT – thermal
difference between the body and its surroundings
(Bergman et al., 2011).
Thus, the total thermal difference between the
body and its surroundings as a result of current pulses
Joule heating can be determined as the sum of the
partial thermal differences between the body and its
surroundings caused by individual harmonic
components.
∆ ∆
,
(4
)
where: ΔT
n
– thermal difference between the body
and its surroundings caused by n-th harmonic
component of pulse signal.
Harmonic signals with constant amplitude were
used for simulation. Thermal effect of each harmonic
component was computed proportional to the ratio of
the signal components and simulation components
powers.
∆
∆
,
(5)
where: b
n
– harmonic signal amplitude used in FEM
solution, ΔTm
n
– thermal difference between the body
and its surroundings obtained after FEM solution for
n-th harmonic component of pulse signal.
Finally, the total thermal difference of biological
tissues caused by the current pulses Joule heating is
determined by the following equation.
∆
∆
.
(6)
2.2 Model Preparation
Model Duke from the Virtual Population ViP1
models has been used as the primary model of human
body(Christ et al. 2010). The Duke model provides
reliable information about the anatomy of the entire
human body, obtained with the help of magnetic
resonance imaging and the subsequent segmentation
of the results. This method of constructing the model
provides high accuracy of the simulation results.
The Duke model is a 3-D matrix. Each element
(voxel) of the 3-D matrix stores a value indicating
whether an element belongs to a particular biological
tissue. The model represents 77 types of various
biological tissues. Geometric size of one voxel is 1
mm x 1 mm x 1 mm.
The whole body model has been truncated to the
human’s neck area, in accordance with papers goals.
Truncated 3-D matrix has a size of 201 mm 222
mm 102 mm. Length and width of the truncated
matrix fully include the cross-section of the human
neck. Truncated matrix height is 7 times larger than
the standard electrode used in the
“SYMPATHOCOR-01” device for neuro-
electrostimulation procedures. For these procedures,
circular brass electrodes with 15 mm diameter and 0.2
mm thickness are uses (Kublanov, 2008b).The
boundaries of the model are far away enough from the
electrode application site and have a minimal impact
on the current distribution and the formation of local
heating zones in the neck.
Cross-section of the 3-D human neck model
matrix in the area of the electrodes placement is
shown in Fig 1. At Fig. 1 pixels, representing the
same biological tissue have the same brightness.
Figure 1: Cross-section of the three-dimensional human
neck model.
The COMSOL simulation software has no
possibility of using voxel models of geometric solids.
Therefore, it is necessary to transform a voxel model
to the format of 3-D models of objects, such as STL.
Block diagram of the algorithm for voxel models
to STL format conversion is shown in Fig. 2. This

algorithm has been implemented in Python using the
Anaconda distribution.
Figure 2: Block diagram of an algorithm for voxel models
to STL format conversion.
For COMSOL simulation software it is necessary
that objects do not contain zero thickness geometry.
Therefore, the algorithm includes a step of bringing a
voxel model to well-composed state. Feature of this
step is the increase of the voxel 3D-matrix resolution.
This leads to a significant increase of 3D-matrix
elements and, as the result, significant increase of the
requirements for computational resources. Pre-
decimation of the original 3D matrix model was
carried out for the optimization of computing
resources.
In the first step of the conversion algorithm
decimation (reduction in size) of 3-D voxel model of
the neck by a factor of 3 is executed for each
dimension. Decimation factor should be selected to
be the smallest among all possible values, in a way
that the number of elements obtained in the 3D-
matrix does not cause difficulties in solution of the
FEM model. Decimation procedure consists of the
following steps:
selection of the cube with the size 3 3 3
voxels in initial 3D-matrix;
picking of the most common value in the
selected voxel;
setting the most common value to appropriate
place into decimated matrix.
As a result, the algorithm creates a decimated
matrix comprising (x/3) (y/3) (z/3) voxels in each
dimension, where x, y, z the number of voxels in the
initial 3D-matrix. The size of each voxel in the
decimated 3D-matrix is increased to a value of 3 mm
x 3 mm x 3 mm.
Cross-section of the human neck model after
decimation is shown in Fig. 3. The vertical level of
the image is selected the same as in Fig. 1. At Fig. 3
pixels, representing the same biological tissue have
the same brightness.
Figure 3: Cross-section of the human neck model after
decimation.
Second step of the conversion algorithm is the
addition of the nervus vagus, sympathetic trunk,
nervus hypoglossus, nervus accessories to the
decimated neck model, in accordance with the
anatomic atlas of Netter and Frank (Netter, 2010). In
the original Duke model as well as in the model after
decimation nerve formations in the neck are not
represented. These nerve structures are the targets for
the "SYMPATOKOR-01" neuro-electrostimulation,
and therefore their presence in the model is needed.
At the third step of the conversion algorithm,
decimated voxel 3D-matrix has been improved to a
well-composed state. The criterion for well-
composed state is the absence in the model geometry
of zero thickness between geometric objects,
consisting of a same biological tissue (Gonzalez-Diaz
et al., 2015).
Algorithm of the 3D-matrix improvement to the
well-composed state consists of the following steps:
interpolation of the 3D-matrix with the
interpolation factor equaled to 3 for each
dimension based on zero-hold method
(Laughton and Warne, 2002);
search for not well-composed pairs of voxels in
the interpolated 3D-matrix;
modification of voxels, neighboring with found
not well-composed pairs so that the not well-
composed pair will become well-composed.

Interpolation factor is set to 3 because this is the
minimum value that will not cause a new not well-
composed pairs by removing the old ones. The
advantage of such algorithm is the preservation of the
topology model from changes. Cross-section model
of the well-composed human neck is shown in Fig. 4.
Figure 4: Cross-section model of the well-composed human
neck.
The vertical level of the image is selected the
same as in Fig. 1. At Fig. 4 points, consisting of the
same biological tissue have the same brightness.
After decimation, interpolation, improvement to
well-composed state steps the resulting 3D-matrix
size was 201 222 102 voxels with voxel size 1
mm 1 mm 1 mm. Using a model of this size
allows us to maintain a balance between accuracy and
required computation resources.
The last step of the algorithm is to convert models
in STL format files for further imports into FEM
simulation software. In order to convert voxel models
to STL format, each model is divided into a set of
binary voxel 3D-matrices. Each binary voxel 3D-
matrix for a certain type of biological tissue contains
a non-zero elements in the respective elements of
these biological tissue of the voxel 3D-matrix.
Each binary voxel 3D-matrix is divided into
connected components with connectivity set to 6.
Each connected component is stored in the form of
geometric bodies in separate STL file. The number of
geometrical bodies after saving was 172. The number
of unique types of biological tissue after save was 21.
After saving as a set of STL-files, the model of
human neck was imported into the COMSOL
Multiphisics 5.2a software. After the meshing
procedure, imported geometry model was presented
in the form of 1.5 million tetrahedra.
Figure 5: Appearance of the human neck 3D-model.
Each imported geometric body was set to its
appropriate biological tissue. All in all, the following
types of biological tissues were used: Blood, Bone,
Cerebrospinal Fluid, Connective Tissue, Esophagus,
Fat, Intervertebral disc, Larynx, Mandible, Bone
marrow red, Mucous, Muscle, Nerve, Subcutaneous
adipose tissue (SAT), Spinal Cord, Skin, Tendon
Ligament, Thyroid Gland, Tongue, Trachea,
Vertebrae. For each biological tissue in the model
physical characteristics were set based on IT'IS
Database for thermal and electromagnetic parameters
of biological tissues (Hasgall et al., 2012). The
following physical characteristics were set: electrical
conductivity, relative permittivity, density, heat
capacity, thermal conductivity, blood perfusion rate,
heat generation rate. Values of relative permittivity
and electrical conductivity physical characteristics
were set to be frequency dependent in range from 1
Hz to 100 MHz Therefore, the developed model took
into account the peculiarities of the formation of
thermal effects with the use of pulsed current.
2.3 Model Configuration
The electrode system in model is represented by two
cylindrical brass electrodes with 15 mm in diameter
and 10 mm thickness. The conductivity of brass is
much greater than the conductivity of the biological
tissues. Therefore, accurate transmission of the real
electrode geometry to model is not needed. The single
requirement to the model electrode is equality of
model electrode diameter to real electrode diameter
(Kublanov and Babich, 2015).
Appearance of the human neck 3D-model with
placed electrodes is shown in Fig. 5. The electrode
placement on Fig. 5 corresponds to one of the
possible variants of the partial current formation. The
left electrode is used as anode, and the right electrode
is used as cathode. The electrodes are marked in the
image in black.

For the model calculation, frequency stationary
study was used. This study calculates temperature
distribution by the model volume at thermal
equilibrium.
Temperature on boundaries, which were formed
after truncating model to the human’s neck area, was
set to 310 K.
For simulation, the frequency range from 1 Hz to
100 MHz was used. This range includes first 20000
harmonics of the neuro-electrostimulation signal.
Low-frequency components contain significantly
greater amount of energy than high. Therefore, the
frequency range for simulation was set to a
logarithmic scale as follows: (1, 3, 5, 7, 9, 10, 30, 50,
70, 90, 100, 300, 500, 700, 900, 1k, 3k, 5k, 7k 9k,
10k, 30k, 50k, 70k, 90k, 100k 300k, 500k, 700k,
900k, 1M, 3M, 5M, 7M, 9M, 10M, 30M, 50M, 70M,
90M 100M) Hz.
For simulation, amplitude of the harmonic current
components was set to 10 mA. Although it is possible
to conduct simulation with other values of the current.
In addition, we studied model without applied
partial currents. These results were used for the base
of the temperature distribution in human tissues in the
neck in the absence of neuro-electrostimulation
signal.
After computation of the models for all
harmonics, temperatures values depending on the
coordinates x, y, z were exported into *.csv files.
Each frequency corresponds to a separate *.csv file.
2.4 Preparation of Thermal Difference
Results
Python script has been written for the calculation and
analysis of the thermal changes during the neuro-
electrostimulation process on the basis of equation 6,
using the previously exported temperature
distributions, saved in set of * .csv files. This script
performs the following steps:
import of the *.csv files and convert them to the
form of thermal distribution 3D-matrices;
calculation of amplitudes and frequencies of
the Fourier series harmonics of the periodic
pulsed signal used for neuro-
electrostimulation;
3D-matrix calculation of thermal changes for
each harmonic used in simulation;
interpolation of existing thermal changes 3D-
matrices for decomposed harmonic frequencies
used for neuro-electrostimulation signal;
summation of 3D-matrix thermal changes for
each decomposed harmonic of neuro-
electrostimulation in accordance with equation
6.
The results of script execution are thermal
changes for the whole model volume depending on
neuro-electrostimulation pulse characteristics was
calculated.
3 RESULTS
The cross-section of the thermal increase distribution
of tissues human neck during neuro-
electrostimulation processes is shown in Fig. 6.
Neuro-electrostimulation pulse characteristics were:
1 mA amplitude, 30 us duration, and 50 Hz
frequency. The vertical level of the image is selected
the same as in Fig. 1.
Figure 6: The cross-section of temperature increase in the
human neck for neuro-electrostimulation current pulse
characteristics 1 mA amplitude, 30 us duration, and 50 Hz
frequency.
According to the image in the Fig. 6, the
maximum temperature increase (0.05 K) is located at
cathode and anode application points. Significant
thermal increase were not observed in the inner
biological tissues of neck area This can explained by
a decrease of the current density with increasing
depth of biological tissue location. One can note that
the maximal thermal increase under the cathode and
the anode are different. That can be explained by the
different thicknesses of the skin in electrode
application points of the Duke model. For human
neck model with a constant thickness of the skin
difference of maximum thermal increase under the
cathode and anode application points will not be
observed.
Maximal thermal increase was considered as the
integral parameter of thermal effects in the entire
volume of biological tissues caused by neuro-
electrostimulation.
Maximal thermal increase in biological tissues of
the human neck using neuro-electrostimulation
dependency on the signal duration and frequency for
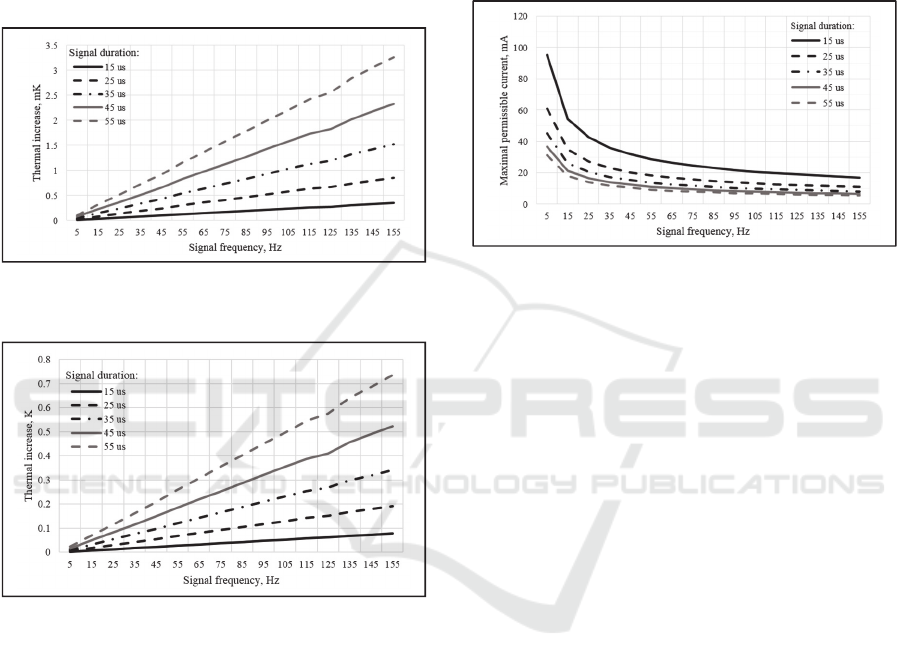
the 1 mA pulse amplitude is shown in Fig. 7.
Maximum thermal increase in biological tissues of
the human neck using neuro-electrostimulation
dependency on the signal duration and frequency for
the 15 mA pulse amplitude is shown in Fig. 8.
Figure 7: Maximal thermal increase against frequency, for
different durations, for the 1 mA pulse amplitude.
Figure 8: Maximal thermal increase against frequency, for
different durations, for the 15 mA pulse amplitude.
Fig. 7 and Fig. 8 show that maximal thermal
increase for 1 mA pulse amplitude is 3.5 mK and for
15 mA is 0.7 K. Comparison of the plots, presented
on Fig. 7 and Fig. 8 reveal quadratic dependency of
the maximal temperature on pulse current amplitude.
The thermal increase caused by the neuro-
electrostimulation, becomes stronger, as the pulse
modulation frequency and pulse duration increase.
This can be explained by the fact that the heating of
the tissues magnifies with the increase of the neuro-
electrostimulation duty-cycle.
Let us consider the maximal permissible current
for different stimulation pulse duration and frequency
characteristics with the condition: the maximal
thermal increase in the volume of biological tissue
does not exceed the 0.1 K. The tissue heating less than
0.1 K is considered non-thermal exposure and cannot
cause tissue damage (WHO | Electromagnetic fields
and public health 2016). Plot of the neuro-
electrostimulation current pulse amplitude against
frequency, for different pulse duration, under
condition that the maximum thermal rise in human
tissues of the neck is less than 0.1 K is shown in Fig.
9.
Figure 9: Maximal permissible current against frequency,
for different durations.
According to the Fig. 9 the application of the pulse
current with the frequencies in range 45-55 Hz,
duration 25-30 us and amplitude less than 13 mA, will
not cause significant thermal effects. These pulse
current features are the most frequently used ones for
the neuro-electrostimulation processes. For
application of the pulse current with higher
frequencies, one must reduce duration and amplitude
in order to prevent significant tissue heating.
4 CONCLUSIONS
The current work presented methodology of the FEM
simulation for thermal effects evaluation, caused by
the neck region neuro-electrostimulation. Algorithm
of the voxel model conversion to the 3-D objects
represented as the complex of the STL-files was
described. The evaluation of the temperature in the
biological tissues is based on the association of the
partial thermal changes, caused by the harmonics
components of the pulsed neuro-electrostimulation
signal.
Features of the thermal changes in the neck region
were considered for the neuro-electrostimulation by
means of the current pulse field formed in the
"SYMPATHOCOR-01" device. Results have shown
that for modulation frequencies in range 45-55 Hz,
duration of the partial pulses 25-30 us, current pulse
amplitude less than 13 mA, the neuro-

electrostimulation does not cause thermal changes
higher than 0.1 K.
In our future works, it is planned to carry out
verification of the heat distribution model in the
laboratory. Also in plans, to assess the impact of
deviations of the biological tissue physical
characteristics on the temperature distribution.
The developed methodology of the thermal effects
assessment caused by pulsed current neuro-
electrostimulation in the human neck will allow to
develop guidelines for choosing the parameters of the
current pulses field for each patient, taking into
account his anthropometric characteristics.
The height and body mass index (BMI) will be
used as the anthropometric characteristics of the
patient. It is assumed based on these characteristics, a
doctor will select appropriate model from a set of a
Virtual Population model group and then will produce
linear transformation of the model to meet the
patient’s height and BMI. Then, based on the
calculated model it is suggested to recommend ranges
of stimulation parameters.
ACKNOWLEDGMENTS
The work was supported by Act 211 Government of
the Russian Federation, contract № 02.A03.21.0006.
REFERENCES
Arfken, G.B., Weber, H.J., and Harris, F.E., 2011.
Mathematical methods for physicists: a comprehensive
guide. Academic press.
Bergman, T.L. and Incropera, F.P., 2011. Introduction to
heat transfer. John Wiley & Sons.
Bergman, T.L., Incropera, F.P., DeWitt, D.P., and Lavine,
A.S., 2011. Fundamentals of heat and mass transfer.
John Wiley & Sons.
Cao, X., Sui, X., Lyu, Q., Li, L., and Chai, X., 2015. Effects
of different three-dimensional electrodes on epiretinal
electrical stimulation by modelling analysis. Journal of
neuroengineering and rehabilitation, 12 (1), 1.
Christ, A., Kainz, W., Hahn, E.G., Honegger, K., Zefferer,
M., Esra Neufeld, Rascher, W., Janka, R., Bautz, W.,
Chen, J., Kiefer, B., Schmitt, P., Hans-Peter
Hollenbach, Shen, J., Oberle, M., Szczerba, D., Kam,
A., Guag, J.W., and Kuster, N., 2010. The Virtual
Family—development of surface-based anatomical
models of two adults and two children for dosimetric
simulations. Physics in Medicine and Biology, 55 (2),
N23.
Gonzalez-Diaz, R., Jimenez, M.-J., and Medrano, B., 2015.
3D well-composed polyhedral complexes. Discrete
Applied Mathematics, 183, 59–77.
Hasgall, P.A., Neufeld, E., Gosselin, M.C., Klingenböck,
A., and Kuster, N., 2012. IT’IS Database for thermal
and electromagnetic parameters of biological tissues.
IT’IS Foundation website.
Kublanov, V.S., 2008a. A hardware-software system for
diagnosis and correction of autonomic dysfunctions.
Biomedical Engineering, 42 (4), 206–212.
Kublanov, V.S., 2008b. [A hardware-software system for
diagnosis and corrections of autonomic dysfunctions].
Meditsinskaia tekhnika, (4), 40–46.
Kublanov, V.S. and Babich, M.V., 2015. Principles of
organization and control of multielectrode neuro-
electrostimulation device. In: Biomedical Engineering
and Computational Technologies (SIBIRCON), 2015
International Conference on. IEEE, 82–86.
Laughton, M.A. and Warne, D.F., 2002. Electrical
Engineer’s Reference Book. Newnes.
Netter, F.H., 2010. Atlas of human anatomy. Elsevier
Health Sciences.
Su, Y., Souffrant, R., Kluess, D., Ellenrieder, M.,
Mittelmeier, W., van Rienen, U., and Bader, R., 2014.
Evaluation of electric field distribution in
electromagnetic stimulation of human femoral head.
Bioelectromagnetics, 35 (8), 547–558.
WHO | Electromagnetic fields and public health: radars and
human health [online], 2016. WHO. Available from:
http://www.who.int/peh-
emf/publications/facts/fs226/en/ [Accessed 21 Oct
2016].
