
Rolling Shutter Camera Synchronization with Sub-millisecond Accuracy
Mat
ˇ
ej
ˇ
Sm
´
ıd and Ji
ˇ
r
´
ı Matas
Center for Machine Perception, Czech Technical University in Prague, Prague, Czech Republic
{smidm, matas}@cmp.felk.cvut.cz
Keywords:
Synchronization, Rolling Shutter, Multiple Camera, Photographic Flash.
Abstract:
A simple method for synchronization of video streams with a precision better than one millisecond is proposed.
The method is applicable to any number of rolling shutter cameras and when a few photographic flashes or
other abrupt lighting changes are present in the video. The approach exploits the rolling shutter sensor property
that every sensor row starts its exposure with a small delay after the onset of the previous row. The cameras
may have different frame rates and resolutions, and need not have overlapping fields of view. The method was
validated on five minutes of four streams from an ice hockey match. The found transformation maps events
visible in all cameras to a reference time with a standard deviation of the temporal error in the range of 0.3 to
0.5 milliseconds. The quality of the synchronization is demonstrated on temporally and spatially overlapping
images of a fast moving puck observed in two cameras.
1 INTRODUCTION
Multi-camera systems are widely used in motion
capture, stereo vision, 3D reconstruction, surveil-
lance and sports tracking. With smartphones ubiquit-
ous now, events are frequently captured by multiple
devices. Many multi-view algorithms assume tem-
poral synchronization. The problem of multiple video
synchronization is often solved by triggering the cam-
eras by a shared signal. This solution has disadvant-
ages: it is costly and might put a restriction on the
distance of the cameras. Cheaper cameras and smart-
phones do not have a hardware trigger input at all.
Content-based synchronization can be performed
offline and places no requirements on the data acquis-
ition. It has received stable attention in the last 20
years (Stein, 1999; Caspi et al., 2002; Tresadern and
Reid, 2003; Cheng Lei and Yee-Hong Yang, 2006;
Padua et al., 2010). Some of the methods require cal-
ibrated cameras, trackable objects, laboratory setting
or are limited to two cameras. The wast majority of
the methods requires overlapped views. For analysis
of high-speed phenomena, a very precise synchron-
ization is critical. The problem of precise sub-frame
synchronization was addressed in (Caspi et al., 2006;
Tresadern and Reid, 2009; Dai et al., 2006).
The research reported in this paper has been partly sup-
ported by the Austrian Ministry for Transport, Innovation
and Technology, the Federal Ministry of Science, Research
and Economy, and the Province of Upper Austria in the
frame of the COMET center SCCH.
Figure 1: Four cameras with rolling shutter sensors captur-
ing a scene when a photographic flash was fired. Part of
image rows integrated light from the flash. The leading and
trailing edges are easily detectable and on the ice rink also
clearly visible. The edges serve as very precise synchroniz-
ation points.
We propose a very simple yet sub-millisecond ac-
curate method for video data with abrupt lighting
changes captured by rolling shutter cameras. Such
lighting changes could be induced for example by
photographic flashes, creative lighting on cultural
events or simply by turning on a light source. In
controlled conditions, it is easy to produce necessary
lighting changes with a stock camera flash.
It is very likely that an existing multi-view ima-
ging system uses rolling shutter sensors or that a set
of multi-view videos from the public was captured by
rolling shutter cameras. The expected image sensor
238
Å
˘
amà d M. and Matas J.
Rolling Shutter Camera Synchronization with Sub-millisecond Accuracy.
DOI: 10.5220/0006175402380245
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 238-245
ISBN: 978-989-758-225-7
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

shipment share for CMOS in 2015 was 97% (IHS
Inc., 2012). Most of the CMOS sensors are equipped
with the rolling shutter image capture.
The proposed method assumptions are limited to:
• a few abrupt lighting changes affecting most of
the observed scene, and
• cameras with rolling shutter sensors.
The method does not require an overlapping field
of view and the cameras can be heterogeneous with
different frame rates and resolutions. The proposed
method works with frame timestamps instead of
frame numbers. This means that the method is robust
to dropped frames.
When a lighting abruptly changes during a rolling
shutter frame exposure, the transition edge can be re-
liably detected in multiple cameras and used as a sub-
frame synchronization point. An example of captured
frames with an abrupt lighting change caused by a
single photographic flash is shown in Figure 1.
Let us illustrate the importance of precise sub-
frame synchronization on an example of tracking ice
hockey players and a puck. Players can quickly reach
a speed of 7
m
/s (Farlinger et al., 2007) and the puck
36
m
/s (Worobets et al., 2006). When we consider
25fps frame rate, a player can travel 28 cm, and a
puck can move 1.44 m in the 40 ms duration of one
frame. When a synchronization is accurate up to
whole frames, the mentioned uncertainties can lead
to poor multi-view tracking performance.
2 RELATED WORK
The computer vision community keeps stable atten-
tion to the video synchronization problem. The issue
was approached in multiple directions. Synchroniza-
tion at the acquisition time is done either by a special
hardware or using a computer network to synchron-
ize time or directly trigger cameras. A more gen-
eral approach is video content-based synchronization.
The advantage is that it does not have special acquis-
ition requirements. We already mentioned a number
of content-based methods. We will review works that
make use of a rolling shutter sensor or photographic
flashes which are the most relevant to our method.
(Wilburn et al., 2004) construct rolling shutter
camera array that was able to acquire images at 1560
fps. The cameras were hardware synchronized, and
the rolling shutter effect was mitigated by outputting
slices of a spatio-temporal image volume.
(Bradley et al., 2009) approach the rolling shut-
ter image capture in two ways. First, they acquire
images with stroboscopic light in a laboratory set-
ting, and extract and merge only rows affected by a
light pulse that possibly span over two consecutive
frames. By changing the frequency and duration of
the flashes they effectively create a virtual exposure
time and a virtual frame rate. Second investigated ap-
proach merges two consecutive frames by a weighted
warping along optical flow vectors. This is similar to
the spatio-temporal method.
Cinematography focused methods for the rolling
shutter sensor acquisition were studied by (Hudon
et al., 2015). They analyse stroboscopic light artefacts
for the purpose of image reconstruction.
(Atcheson et al., 2008) applied the rolling shut-
ter flash based synchronization and spatio-temporal
volume slice approach to capture gas flows for a 3D
reconstruction.
The use of photographic flashes for synchroniz-
ation appeared to our knowledge first in (Shrestha
et al., 2006). They find a translation between two
video sequences by matching sequences of detected
flashes. The final synchronization is accurate to the
whole frames.
None of the rolling shutter or flash based ap-
proaches known to us pays attention to dropped
frames and a camera clock drift.
3 METHOD
The inputs for the synchronization algorithm are
frame timestamps extracted from video files or net-
work streams and detected transition edges of abrupt
lighting changes. We will refer to the transition edges
as synchronization events or simply events. We find
synchronization transformations s
c
( f , r) → t
ref
for all
cameras c (except a reference camera c
ref
) that map
each camera temporal position ( f ,r) to the reference
camera time t
ref
. The temporal position is defined by
a frame, row pair ( f ,r). The situation is presented in
Figure 3.
To correctly model the sub-frame accurate syn-
chronization transformation we have to take into ac-
count missing frames, different frame rates, a drift of
image sensors clock and hidden dark rows in image
sensors.
3.1 On Time Codes
An ideal timing of video frames assumes a stable
frame rate fps and no skipped frames. Time of the first
row exposure of a frame i is then t(i) = i ·
1
fps
+t
0
,i ∈
{0,1,...}. Unfortunately, this is not true for most of
the real-world video sequences. The most common
Rolling Shutter Camera Synchronization with Sub-millisecond Accuracy
239

Figure 2: Detection of an abrupt lighting change. A photographic flash fired during the acquisition of the frame I
n
. The flash
duration is shorter than the frame duration. Only the lines that were integrating light when the flash was illuminating the scene
were affected. The red dotted lines mark the leading and trailing edges of the bright region. The profiles on the right show
pixel intensity changes in the frame before the abrupt change and in the frame with the change.
c
1
c
ref
c
2
f
1
f
2
f
3
f
4
f
5
f
1
f
2
f
3
f
3
f
2
f
1
f
4
f
5
time
Figure 3: Sub-frame synchronization of the cameras c
1
and
c
2
with respect to the reference camera c
ref
. Frame rates,
resolution and temporal shifts between cameras differ. The
short black lines on the sides of frame rectangles represent
image rows. We find an affine transformation s
c
( f ,r) → t
ref
for every camera c that maps a time point specified by a
frame number f and a row number r to the reference camera
time t
ref
. The dotted lines show a mapping of time instants
when rows in c
1
and c
2
are captured to the reference camera
time.
deviation from the ideal timing is a dropped frame
caused by high CPU load on the encoding system.
When a frame is not encoded before the next one is
ready, it has to be discarded. Almost all video sources
provide frame timestamps or frame durations. This
information is necessary to maintain very precise syn-
chronization over tenths of minutes. We’ll briefly
present frame timing extraction from container format
MP4 and streaming protocol RTP.
Video container files encapsulate image data com-
pressed by a video codec. The timing data is stored
in the container metadata. The MP4
1
file format is
based on Apple QuickTime. Frame time-stamps are
encoded in Duration and Time Scale Unit entries. The
Time Scale Unit is defined as “the number of time
units that pass per second in its time coordinate sys-
tem”.
A frequent streaming protocol is Real Time Trans-
fer Protocol (RTP). The codec compressed video data
is split into chunks and sent typically over UDP to a
receiver. Every packet has an RTP header where the
Timestamp entry defines the time of the first frame in
the packet in units specific to a carried payload: video,
audio or other. For video payloads, the Timestamp
frequency is set to 90kHz.
1
officially named MPEG-4 Part 14
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
240

time in miliseconds
row
1
0
40 80
120
3
5
n
frame duration
exposure time
Figure 4: The figure illustrates rows exposure in time. The
green rectangles represent the time spans when a row is in-
tegrating light. In rolling shutter sensors the rows do not
start to integrate light at the same time. Instead the integra-
tion begins sequentially with small delays.
3.2 Rolling Shutter
Historically, cameras were equipped with various
shutter systems. To name the mechanical shutters,
prevalent were the focal plane shutters - where two
curtains move in one direction or the diaphragm shut-
ters where a number of thin blades uncover circular
aperture. The electronic shutters implemented in im-
age sensors are either global or rolling. CCD type
image sensors are equipped with a global shutter, but
are already being phased out of the market. Most of
the CMOS sensors have a rolling shutter. Recently, a
global shutter for the CMOS sensors was introduced,
but consumer products are still rare.
All shutter types except the global shutter exhibit
some sort of image distortion. Mostly different re-
gions of the sensor (or film) integrate light in a differ-
ent time or the exposure time differs.
The rolling shutter equipped image sensor integ-
rates light into the pixel rows sequentially. In the
CMOS sensor with the rolling shutter, an electrical
charge integrated in all pixels can not be read at once.
The readout has to be done row by row. For illus-
tration see Figure 4. To preserve constant exposure
time for all pixels on the sensor, the exposure starts
has to be sequential exactly as the readouts are. This
means that every row captures the imaged scene in a
slightly different moment. Typically a majority of the
row exposure time is shared by spatially close rows
(ON Semiconductor, 2015; Sony, 2014).
To properly compute the start time of a row expos-
ure we have to take into account hidden pixels around
the active pixel area. The most image sensors use
the hidden pixels to reduce noise and fix colour inter-
pretation at the sensor edges (Figure 5). This means
width
height R
h
r
R
0
R
1
Figure 5: The active pixel matrix on image sensor is sur-
rounded by a strip of hidden pixels, sometimes also called
“dark” pixels. They serve for black colour calibration or
to avoid edge effects when processing colour information
stored in the Bayer pattern (ON Semiconductor, 2015). The
rolling shutter model (Equation 1) assigns a sub-frame time
to a row r.
that there is a delay, proportional to R
0
+ R
1
, between
reading out the last row of a frame and the first row of
the next one. Camera or image sensor specifications
often include total and effective pixel count. The dif-
ference between the two values is the number of hid-
den pixels.
Now it is straightforward to compute sub-frame
time for a frame f and a row r as
t( f ,r) = t
f
+
R
0
+ r
R
0
+ R
h
+ R
1
· T
frame
, (1)
where R
0
,R
h
, R
1
are row counts specified in Figure 5,
t
f
is the frame timestamp and T
frame
is the nominal
frame duration. The constants R
0
and R
1
can be found
in the image sensor datasheet or the summary value
R
0
+R
h
+R
1
of total sensor lines can be estimated, as
demonstrated in Subsection 3.4.
3.3 Abrupt Lighting Changes
Abrupt lighting changes are trivially detectable and
are suitable for sub-frame synchronization with
rolling shutter sensors.
The only requirement is that the majority of
the observed scene receives light from the source.
Many multi-view recordings already fulfil the require-
ment. Professional sports photographers commonly
use flashes mounted on sports arena catwalks to cap-
ture photos during indoor matches
2
, mobile phones
or DSLRs flashes are used at many social occasions
2
http://www2.ljworld.com/news/2010/mar/21/behind-
lens-story-behind-those-flashing-lights-nca/
Rolling Shutter Camera Synchronization with Sub-millisecond Accuracy
241

flash duration
time
row
Figure 6: Short abrupt lighting event, e.g., photographic
flash, affects only part of the frame rows, in red colour, due
to the rolling shutter capture. Rows, depicted half filled in
green and red, are being captured at the time of the light-
ing change. Such rows integrate light of the lighting event
only partially. The longer the exposure time the more rows
capture an onset of an event.
Figure 7: Median line intensity difference between consec-
utive frames in a moment of a flash. Rows in range 950-
1700 were captured when the photographic flash has illu-
minated the scene. An exponential character of the leading
and trailing edges is related to the physical process of the
capacitor discharge in a flashtube.
that are recorded. Creative rapidly changing lighting
is frequent at cultural events such as concerts.
For photographic flashes (Figures 1, 6), it is pos-
sible to detect both leading and trailing edges. A flash
duration is typically one order of magnitude shorter
than a frame duration. Flashes produce light for
1
/1000
to
1
/200 of a second in contrast to 40 ms frame duration
of a 25fps recording.
An example profile of the captured light intensity
by a rolling shutter sensor is in Figure 7. The shape
of the profile is formed by two processes. The expo-
nential form of the transition edges corresponds to the
physical properties of the lighting source. The par-
tially affected rows at the start and end of an event
contribute with a linear ramp to the profile shape.
The detection of the abrupt lighting changes is ro-
bust and straightforward. As we require that the light-
ing affects most of the scene, the maximum of differ-
ence of median line intensity for a frame shows dis-
tinct peaks, see Figure 8. We simply threshold the
values to get the frames with the events. We use the
leading edge as the synchronization event. The event
row is found in the differences of median line intens-
Figure 8: Detection of the abrupt lighting changes. A me-
dian line intensity profile is computed for every frame. Then
the profiles in consecutive frames are subtracted. The dif-
ference maxima for range of frames is plotted above. The
clearly visible peaks correspond to the lighting changes. We
threshold the values and detect the events marked on the plot
by the red dots.
Algorithm 1: Detection of synchronization events.
Input: image sequences
Output: synchronization events
foreach camera do
foreach frame do
m
f
:= line median intensity (frame)
m
f
∈ N
n
, where n is frame height
end
foreach frame do compute difference profiles
d
f
:= m
f
− m
f −1
d
f
∈ Z
n
, where n is frame height
end
for f in { f | max(d
f
) > threshold} do
r := find raising edge row in d
f
event := ( f ,r)
end
end
return events
ity profiles, see Figure 2. The method is summarized
in Algorithm 1.
3.4 Synchronization
We model the time transformation s
c
( f , r) → t
ref
from
a camera c to a reference camera c
ref
as an affine
mapping similar to (Padua et al., 2010). Substan-
tial difference is that we operate on timestamps in-
stead of frame numbers. The transformation maps the
events detected in camera c to the same events in the
time of a reference camera c
ref
. The dominant part of
the transformation s
c
( f , r) is a temporal shift between
cameras c and c
ref
. The synchronization model con-
sisting of a constant temporal shift is usable only for
shorter sequences. We found out in experiments that
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
242

camera clocks maintain stable frame duration, but the
reported time units are not precisely equal. This de-
ficiency is known as the clock drift. We compensate
the drift by a linear component of the transformation.
The proposed transformation is
s( f , r;α,β) = αt
f
+ β + r ·
T
frame
R
, (2)
where α is the camera clock drift compensation, β is
the temporal shift, f is the frame number, r is the row
number, t
f
is the frame acquisition timestamp and R =
R
0
+ R
h
+ R
1
is the total number of sensor rows.
The goal of the synchronization is to find
s
c
( f , r;α
c
,β
c
) for all cameras in C =
{
c
1
,c
2
,...,c
n
}
except for a reference camera c
ref
.
For an event observed in camera c and c
ref
at
( f
c
,r
c
) and ( f
c
ref
,r
c
ref
) the synchronized camera time
and the reference camera time should be equal:
s
c
( f
c
,r
c
;α
c
,β
c
) = t
c
ref
( f
c
ref
,r
c
ref
). (3)
We have demonstrated how to detect abrupt light-
ing changes in Subsection 3.3. In the next step, we
manually align time in cameras c and c
ref
up to whole
frames, e.g., for the first matching event, and automat-
ically match the rest of the events to get:
E
c,c
ref
=
( f
c
1
,r
c
1
),
f
c
ref
1
,r
c
ref
1
(4)
,...,
( f
c
k
,r
c
k
),
f
c
ref
k
,r
c
ref
k
.
Now we can construct overdetermined system of
Equations 3 for k pairs of matching events E
c,c
ref
. The
least squares solution gives the unknowns α
c
,β
c
. Op-
tionally also the sensors properties T
c
row
:=
T
c
frame
/R
c
and T
c
ref
row
:=
T
c
ref
frame
/R
c
ref
can be estimated, when these
are not available in the image sensors datasheets.
When synchronizing more than two cameras, one
system of equations for all cameras has to be con-
structed to estimate the reference camera time per im-
age row T
c
ref
row
jointly.
We summarize the synchronization process in Al-
gorithm 2. The single global time for a frame f and
row r is computed using Equation 1 for a reference
camera and using Equation 2 for other cameras.
4 DATA
The ice hockey data consists of one complete USA
versus Russia match captured by 4 cameras. The
company Amden s.r.o. provided us the data recorded
on the International Ice Hockey Federation World
Algorithm 2: Multi-camera Synchronization.
Input: frame timestamps, detected synchronization
events, reference camera c
ref
Output: synchronization parameters
foreach {c ∈ C | c 6= c
ref
} do
E
c,c
ref
:= match events in c and c
ref
foreach event in E
c,c
ref
do
{
( f
c
,r
c
),( f
c
ref
,r
c
ref
)
}
:= event
t
c
:= time stamp for frame f
c
t
c
ref
:= time stamp for frame f
c
ref
add equation:
α
c
t
c
+ β
c
+ r
c
· T
c
row
= t
c
ref
+ r
c
ref
· T
c
ref
row
to the system of equations
end
end
solve the system in a least squares sense
return {α
c
,β
c
,T
c
row
| c ∈ C and c 6= c
ref
},T
c
ref
row
Championship 2015. Example images from the cam-
eras are on Figure 1. The cameras 1 and 2 are ob-
serving the ice rink from sides, the cameras 3 and
4 are focusing on the defending and attacking zones,
that is from the blue lines to the ends of the rink. The
camera pairs 1 and 2, and 3 and 4 are identical models
with the same lenses. The cameras 1 and 2 use camera
model Axis P1428E with resolution 3840 × 2160 px,
the cameras 3 and 4 are equipped with camera model
Axis P1354 with resolution 1280 × 720 px.
The data was delivered in the Matroska file format
and later converted to mp4. The frame timestamps
were extracted using ffprobe command line utility
included in the ffmpeg package.
5 EXPERIMENTS
The subsection 3.3 and Algorithm 1 describe the
method to detect synchronization events. We pro-
cessed the first 5 minutes of the ice hockey match in
the four video streams and detected 18, 22, 13 and
15 flashes in the cameras 1, 2, 3 and 4 respectively.
For the sake of simplicity, we omitted the flashes that
crossed the frame boundary. The event distribution is
depicted in Figure 9.
We performed two experiments, first we syn-
chronized four cameras jointly by solving a single
system of equations, secondly we synchronized cam-
era pairs independently. The results are presented in
Table 1 and Table 2. The deviation of the synchron-
ized time from the reference time for the detected
events, which in ideal case should be 0, can be inter-
preted as a measure of method accuracy. The stand-
ard deviation of the synchronization errors is 0.5 ms
for the joint synchronization and in range from 0.3 ms
Rolling Shutter Camera Synchronization with Sub-millisecond Accuracy
243
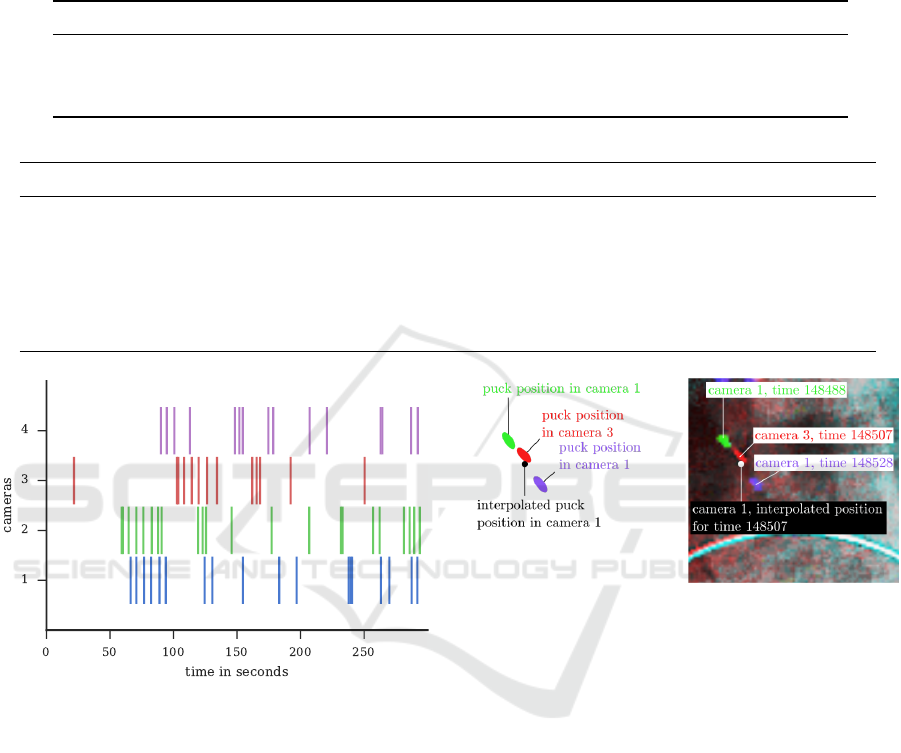
Table 1: Synchronization parameters and errors for a system of four cameras. The camera 1 was selected as the reference
camera c
ref
and the cameras 2, 3 and 4 were synchronized to the reference camera time. The found parameters of the
synchronization transformations (Eq. 2) are presented in the table below. The time per image row for the reference camera is
0.0154 ms. The clock drift is in column three presented as a number of rows per second that need to be corrected to maintain
synchronization. The standard deviation of the synchronized time from the reference time for the synchronization events is
presented in the last column.
camera c
ref
, c 1 - clock drift drift (in
lines
/s) shift (in ms) T
c
row
(in ms) std error (in ms)
1 2 8.39 ×10
−6
−0.56 6066.7 0.015 0.49
1 3 -3.12 ×10
−6
0.08 −37500.2 0.0394 0.44
1 4 -8.35 ×10
−6
0.2 −23858.7 0.0414 0.44
Table 2: Synchronization parameters and errors for independent pairs of cameras. For detailed description see Table 1.
c
ref
, c 1 - clock drift drift (in
lines
/s) shift (in ms) T
c
ref
row
(in ms) T
c
row
(in ms) std error (in ms)
1 2 8.47 ×10
−6
−0.57 6067.49 0.0159 0.0148 0.45
1 3 -8.55 ×10
−6
0.22 −37500.7 0.0158 0.0396 0.42
1 4 -7.04 ×10
−6
0.17 −23859 0.0151 0.0417 0.39
2 3 -14.52 ×10
−6
0.37 −43567.9 0.0149 0.0397 0.39
2 4 -17.37 ×10
−6
0.42 −29926 0.015 0.0416 0.33
3 4 -10.12 ×10
−6
0.2 13642.3 0.0477 0.05 0.27
Figure 9: Flashes detected in cameras 1-4. The temporal
position of the events is always in the camera specific time.
The inter camera shift is clearly visible unlike the clock
drift. The drift error accumulates slowly and is not notice-
able in this visualization.
to 0.5 ms for the camera pairs. We can claim that our
method is sub-millisecond precise.
We validated the found sub-frame synchronization
with an observation of a high-speed object in over-
lapping views. A puck is present in two consecutive
frames in the camera 1 and in the time between in the
camera 3. We interpolated the puck position in the
camera 1 to the time of the puck in camera 3. The
puck position in the camera 3 and the interpolated po-
sition should be the same. Figure 10 shows that the
interpolated puck position is close to the real one from
camera 3.
We implemented the system in Python with help
Figure 10: Synchronization validation. Moving blurred
puck is visible in two synchronized cameras. We show three
overlaid images of the same puck: two consecutive frames
in the camera 1 and single frame in the camera 3. The ac-
quisition time of the puck for all 3 frames was computed
considering frame f and row r of the puck centroid. Know-
ing the puck acquisition times it possible to interpolate a
position of the puck in the camera 1 for the time of acquis-
ition in the camera 3. The interpolated puck position in the
camera 1 and the real position in the camera 3 should be
equal. The situation is redrawn on the left, on the right are
the image data visualized in green and blue channels for the
camera 1 and in the red channel for the camera 3. The inter-
polated position in the camera 1 is depicted as a black circle
on the left and a white circle on the right. The interpolated
position and the real position in the camera 3 are partially
overlapping.
of the NumPy, Matplotlib and Jupyter packages
(Hunter, 2007; Perez and Granger, 2007; van der Walt
et al., 2011).
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
244

6 CONCLUSIONS
We have presented and validated a sub-frame time
model and a synchronization method for the rolling
shutter sensor. We use photographic flashes as sub-
frame synchronization events that enable us to find
parameters of an affine synchronization model. The
differences of the synchronized time at events that
should be ideally 0 are in range from 0.3 to 0.5 mil-
liseconds. We validated the synchronization method
by interpolating a puck position between two frames
in one camera and checking against the real position
in other camera.
We published
3
the synchronization code as an
easy to use Python module and the paper itself is
available in an executable form that allows anybody
to reproduce the results and figures.
ACKNOWLEDGEMENTS
Both authors were supported by SCCH GmbH un-
der Project 830/8301434C000/13162. Ji
ˇ
r
´
ı Matas has
been supported by the Technology Agency of the
Czech Republic research program TE01020415 (V3C
– Visual Computing Competence Center). We would
like to thank Amden s.r.o. for providing the ice
hockey video data.
REFERENCES
Atcheson, B., Ihrke, I., Heidrich, W., Tevs, A., Bradley, D.,
Magnor, M., and Seidel, H.-P. (2008). Time-resolved
3d capture of non-stationary gas flows. ACM Trans.
Graph.
Bradley, D., Atcheson, B., Ihrke, I., and Heidrich, W.
(2009). Synchronization and rolling shutter compens-
ation for consumer video camera arrays. In CVPR.
Caspi, Y., Irani, M., and Yaron Caspi, M. I. (2002). Spatio-
temporal alignment of sequences. PAMI.
Caspi, Y., Simakov, D., and Irani, M. (2006). Feature-based
sequence-to-sequence matching. IJCV.
Cheng Lei and Yee-Hong Yang (2006). Tri-focal tensor-
based multiple video synchronization with subframe
optimization. IEEE Trans. Image Process.
Dai, C., Zheng, Y., and Li, X. (2006). Subframe video syn-
chronization via 3D phase correlation. In ICIP.
Farlinger, C. M., Kruisselbrink, L. D., and Fowles, J. R.
(2007). Relationships to Skating Performance in
Competitive Hockey Players. J. Strength Cond. Res.
Hudon, M., Kerbiriou, P., Schubert, A., and Bouatouch, K.
(2015). High speed sequential illumination with elec-
tronic rolling shutter cameras. In CVPR Workshops.
3
http://cmp.felk.cvut.cz/
∼
smidm/flash synchronization
Hunter, J. D. (2007). Matplotlib: A 2D Graphics Environ-
ment. Comput. Sci. Eng.
IHS Inc. (2012). CMOS Image Sensors Continue March to
Dominance over CCDs.
ON Semiconductor (2015). 1/2.5-Inch 5 Mp CMOS Digital
Image Sensor. MT9P031.
Padua, F. L. C., Carceroni, R. L., Santos, G., and Kutulakos,
K. N. (2010). Linear Sequence-to-Sequence Align-
ment. PAMI.
Perez, F. and Granger, B. E. (2007). IPython: A System for
Interactive Scientific Computing. Comput. Sci. Eng.
Shrestha, P., Weda, H., Barbieri, M., and Sekulovski, D.
(2006). Synchronization of multiple video recordings
based on still camera flashes. In Int. Conf. Multimed.
Sony (2014). Diagonal 6.23 mm (Type 1/2.9) CMOS
Image Sensor with Square Pixel for Color Cameras.
IMX322LQJ-C.
Stein, G. (1999). Tracking from multiple view points: Self-
calibration of space and time. In CVPR.
Tresadern, P. and Reid, I. (2003). Synchronizing Image Se-
quences of Non-Rigid Objects. In BMVC.
Tresadern, P. A. and Reid, I. D. (2009). Video synchron-
ization from human motion using rank constraints.
CVIU.
van der Walt, S., Colbert, S. C., and Varoquaux, G. (2011).
The NumPy Array: A Structure for Efficient Numer-
ical Computation. Comput. Sci. Eng.
Wilburn, B., Joshi, N., Vaish, V., Levoy, M., and Horow-
itz, M. (2004). High-speed videography using a dense
camera array. In CVPR.
Worobets, J. T., Fairbairn, J. C., and Stefanyshyn, D. J.
(2006). The influence of shaft stiffness on potential
energy and puck speed during wrist and slap shots in
ice hockey. Sport. Eng.
Rolling Shutter Camera Synchronization with Sub-millisecond Accuracy
245
